Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact
Abstract
:1. Introduction
2. Modelling of Pantograph–Catenary with Reattachment Impact
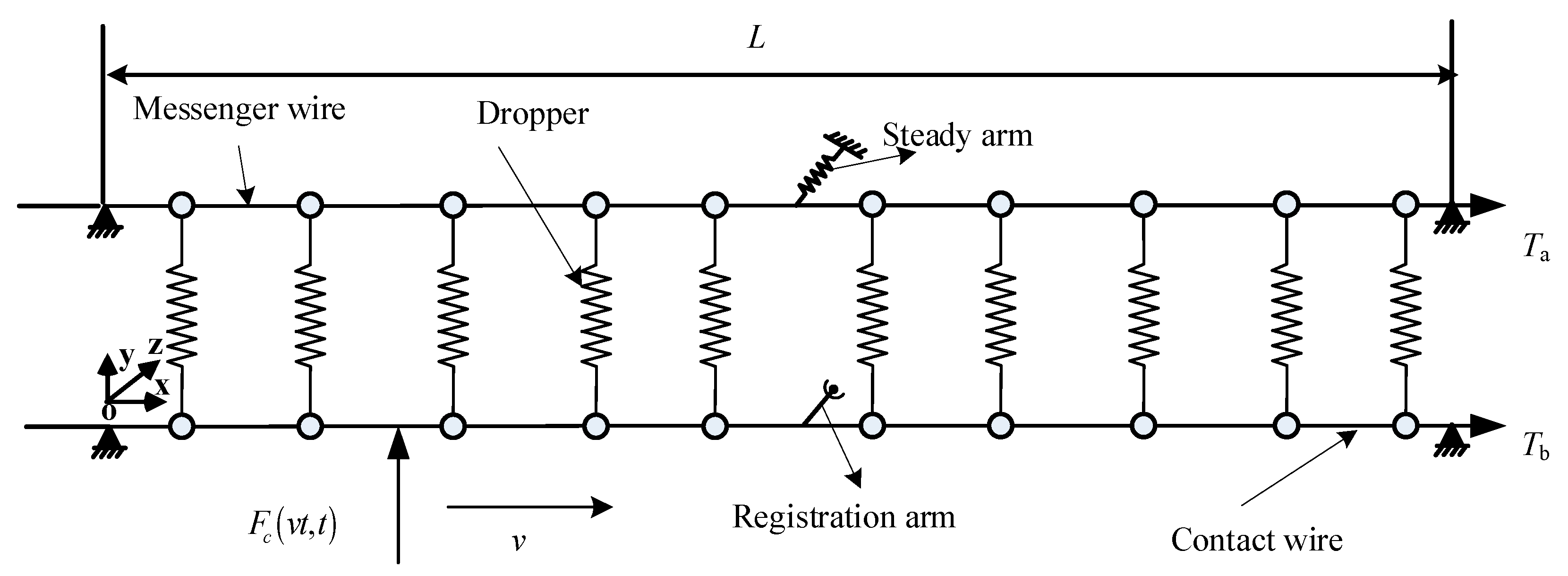
2.1. Equation of Motion for Catenary
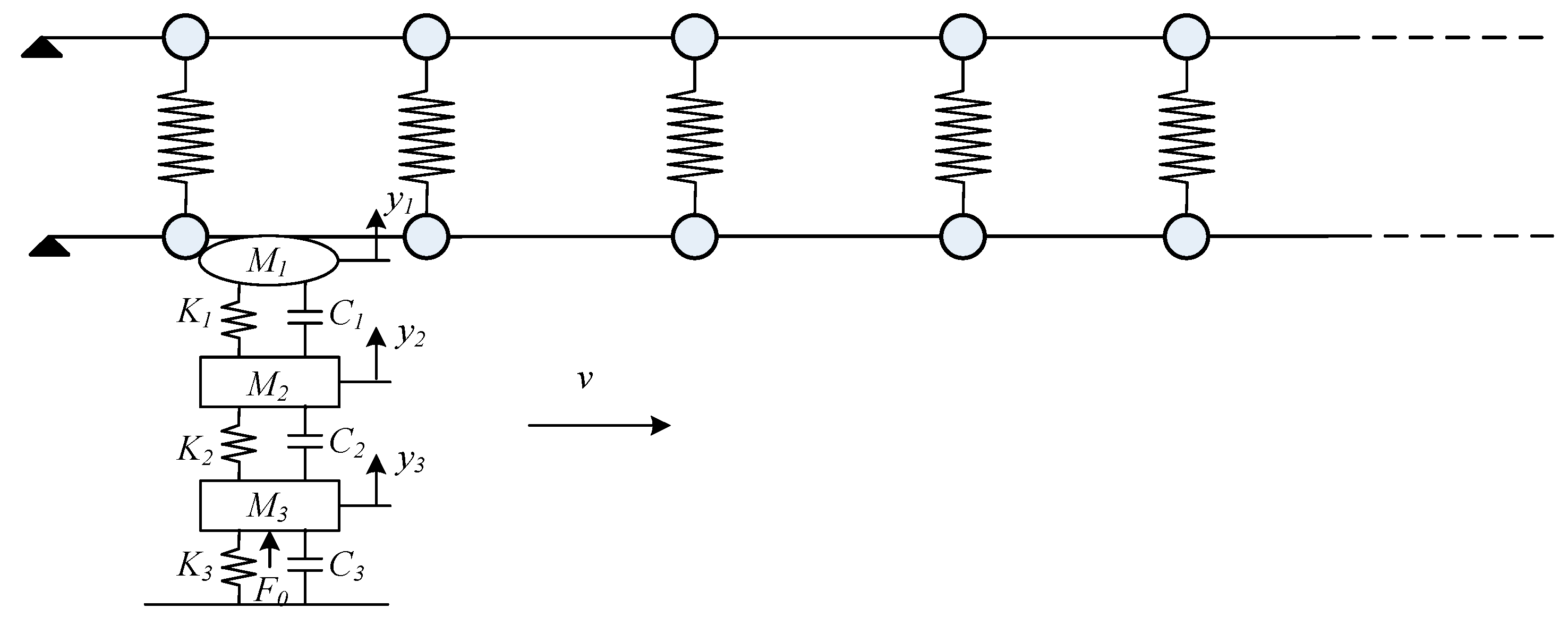
2.2. Contact Model of Pantograph–Catenary
2.3. Modelling of Reattachment Impact
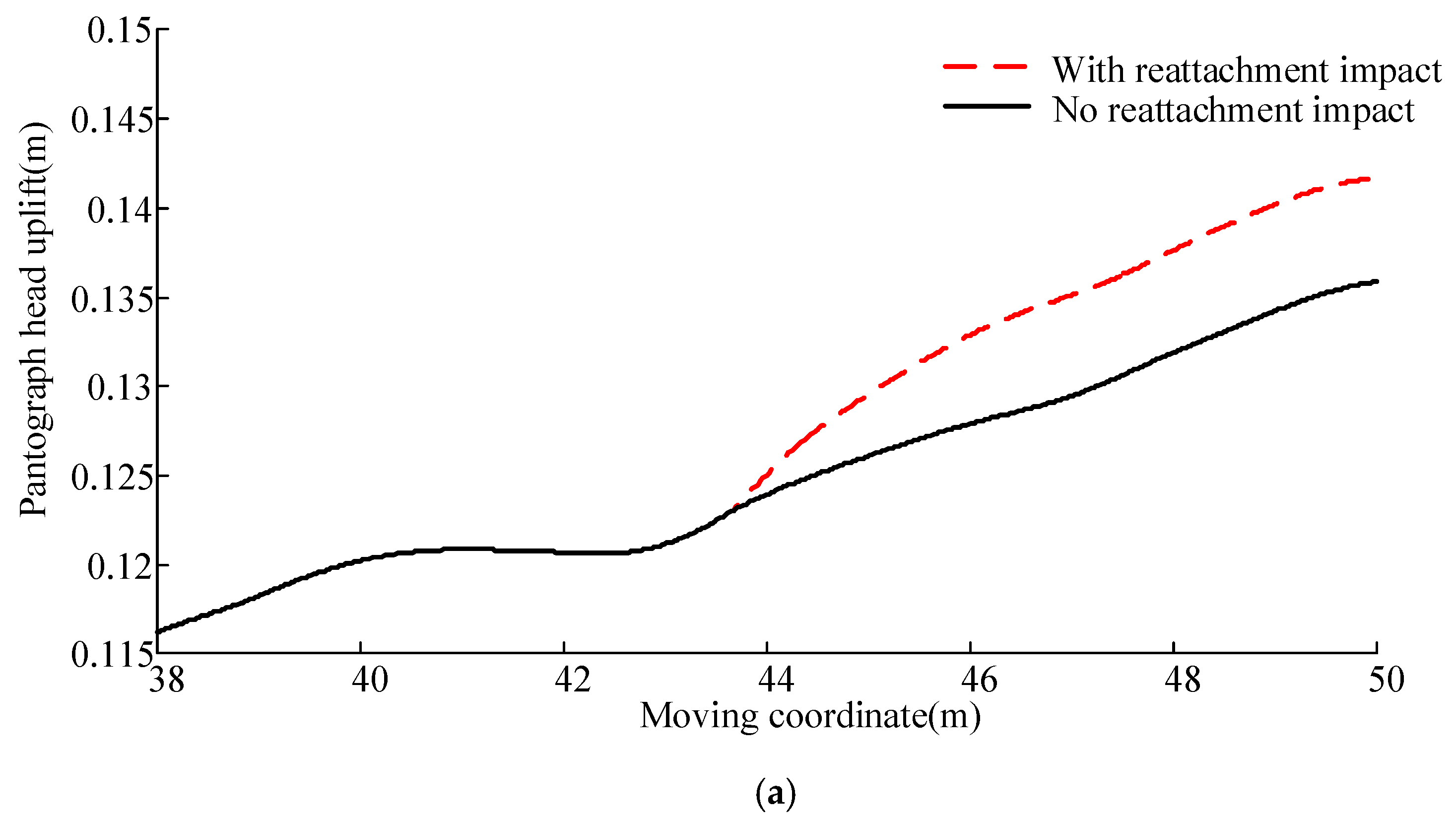
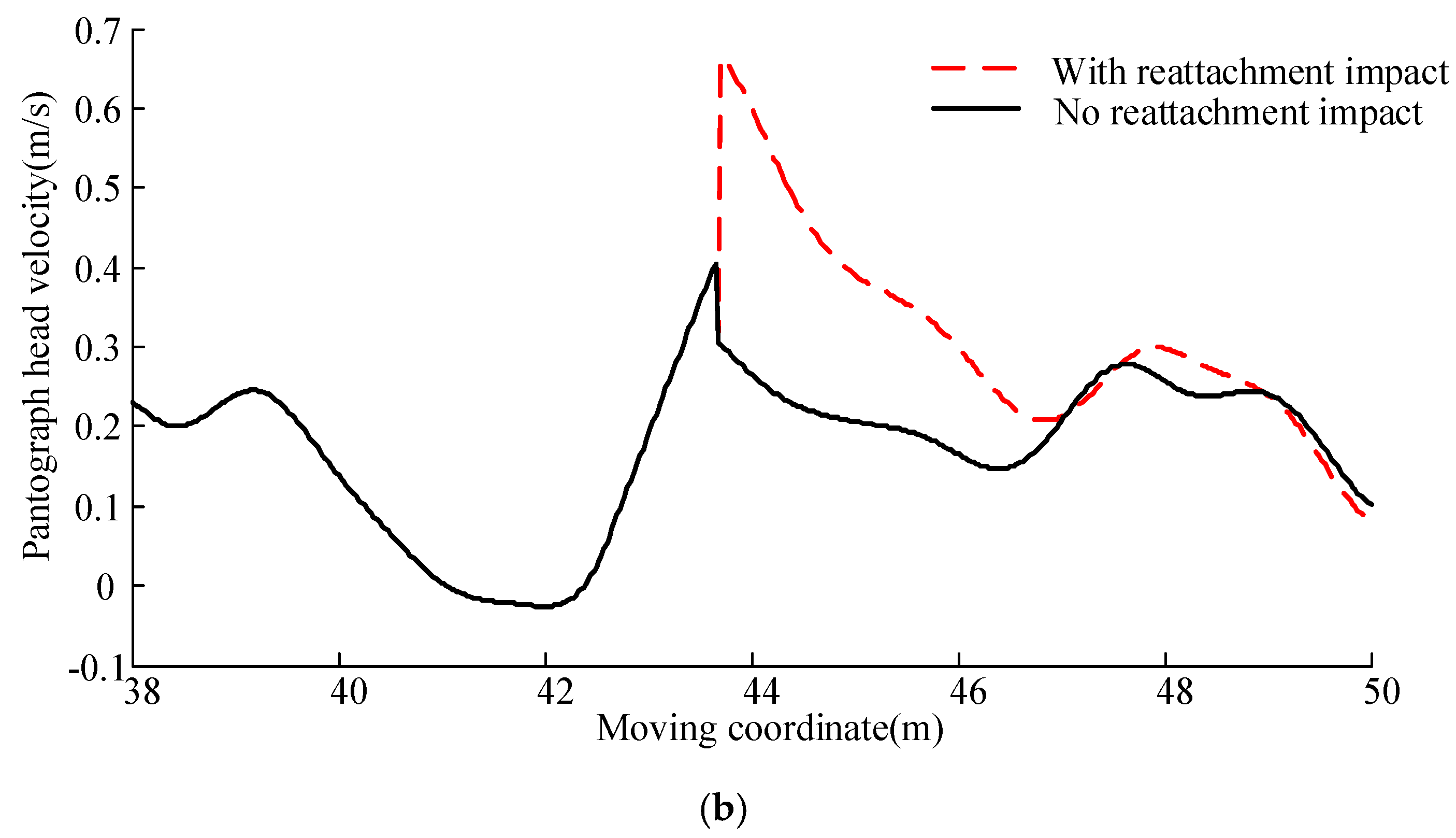
3. Analysis with Reattachment Impact
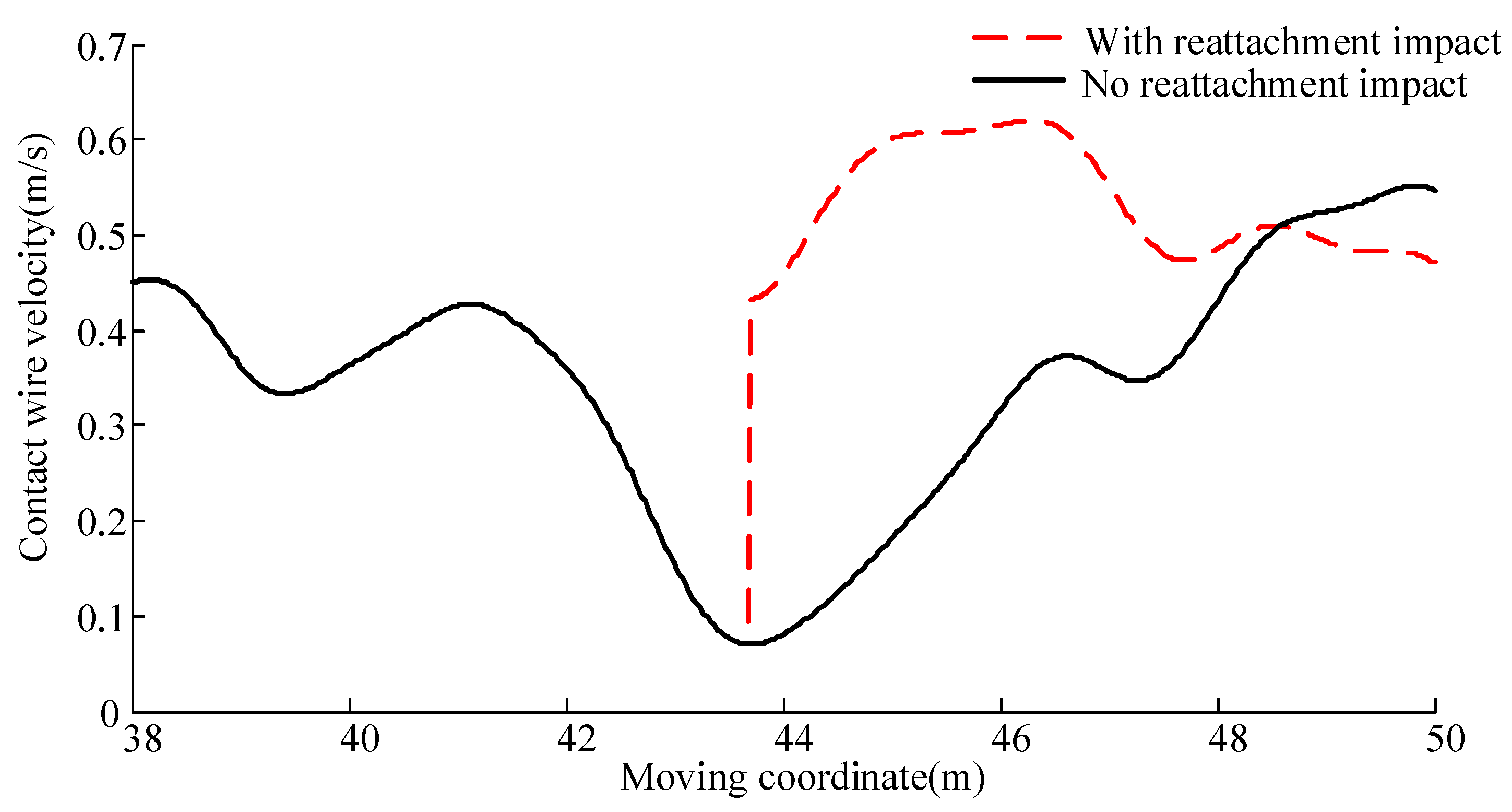
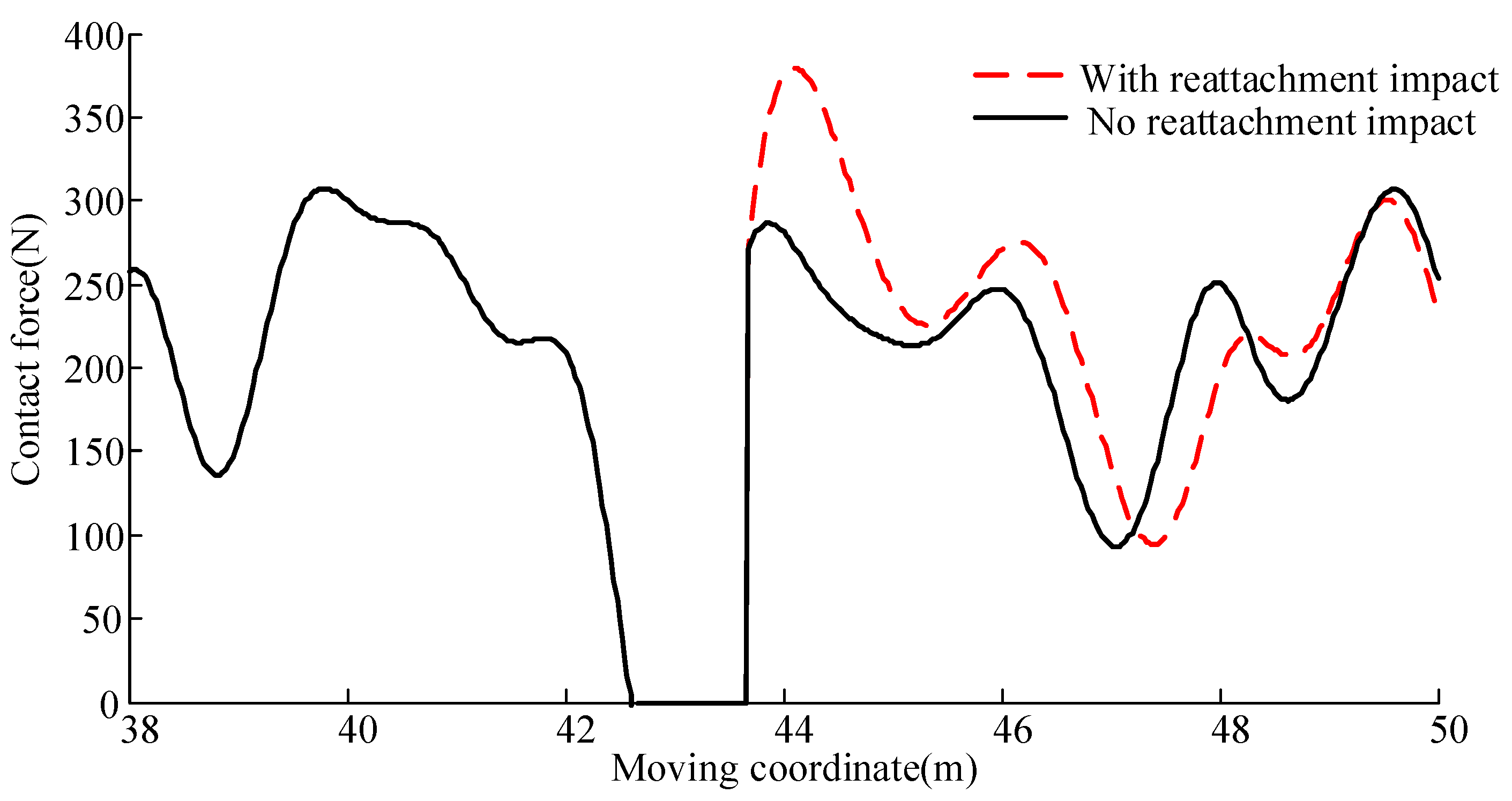
3.1. Analysis with 380 km/h
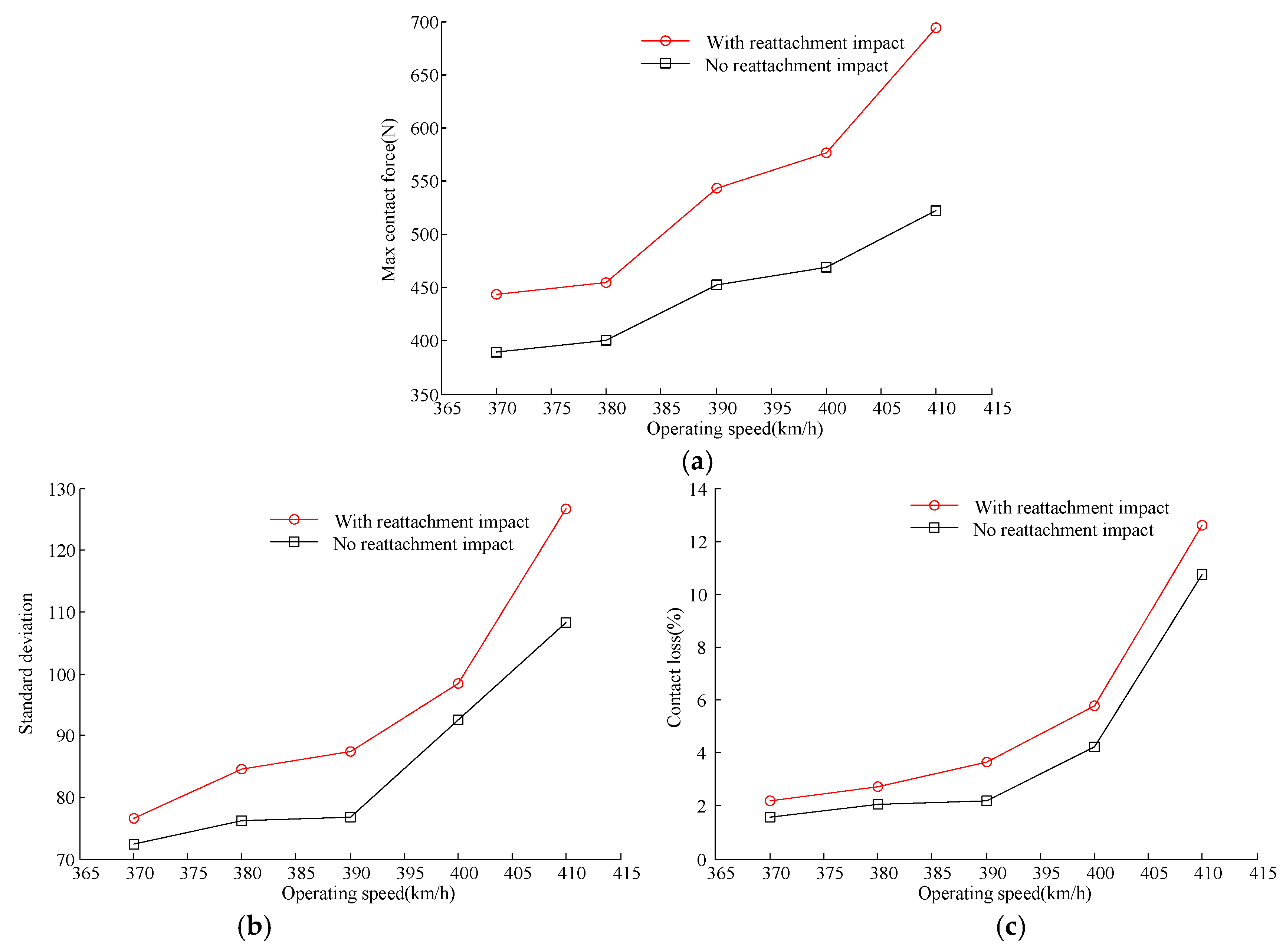
3.2. Analysis at Different Operating Speeds
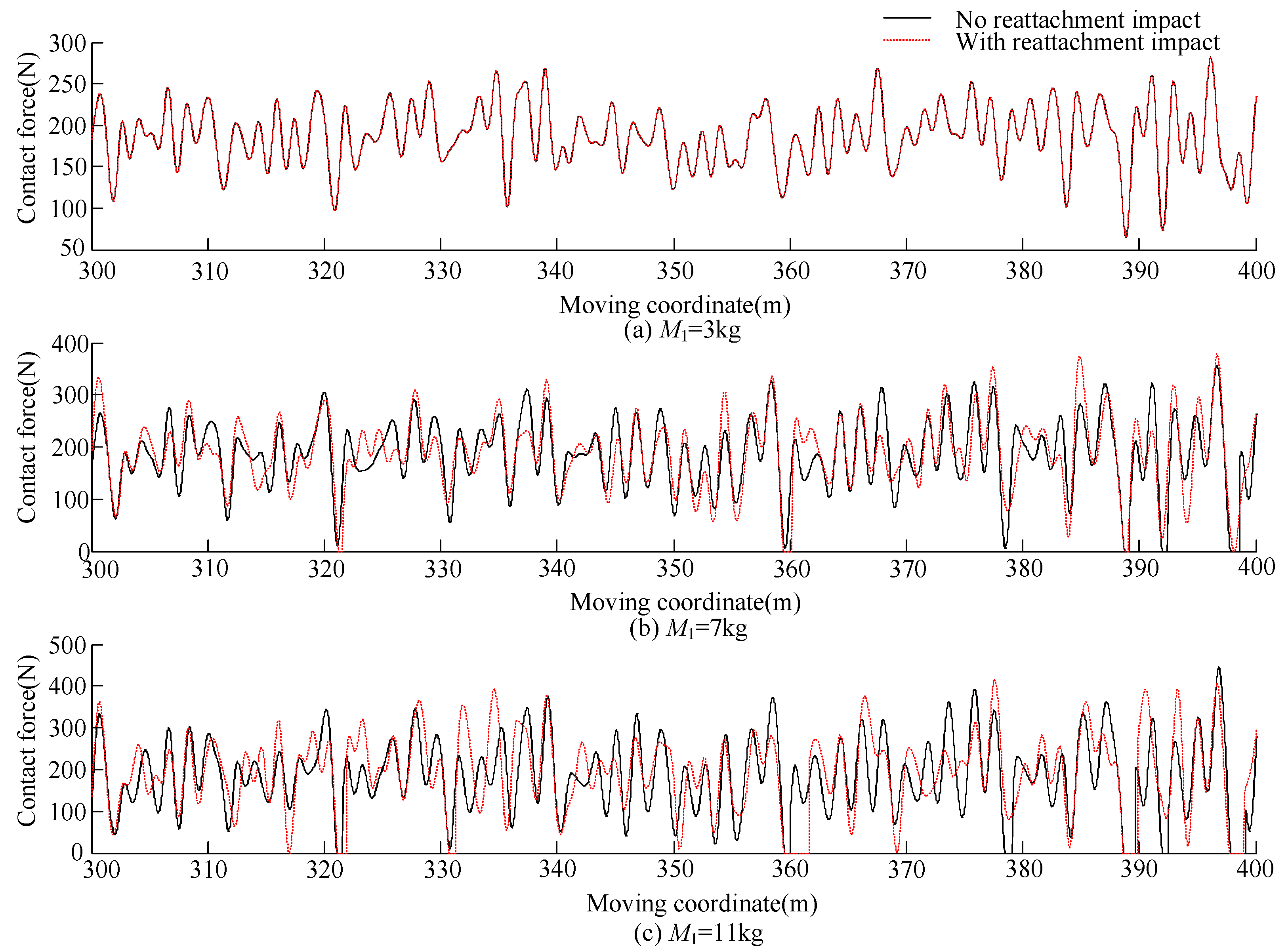
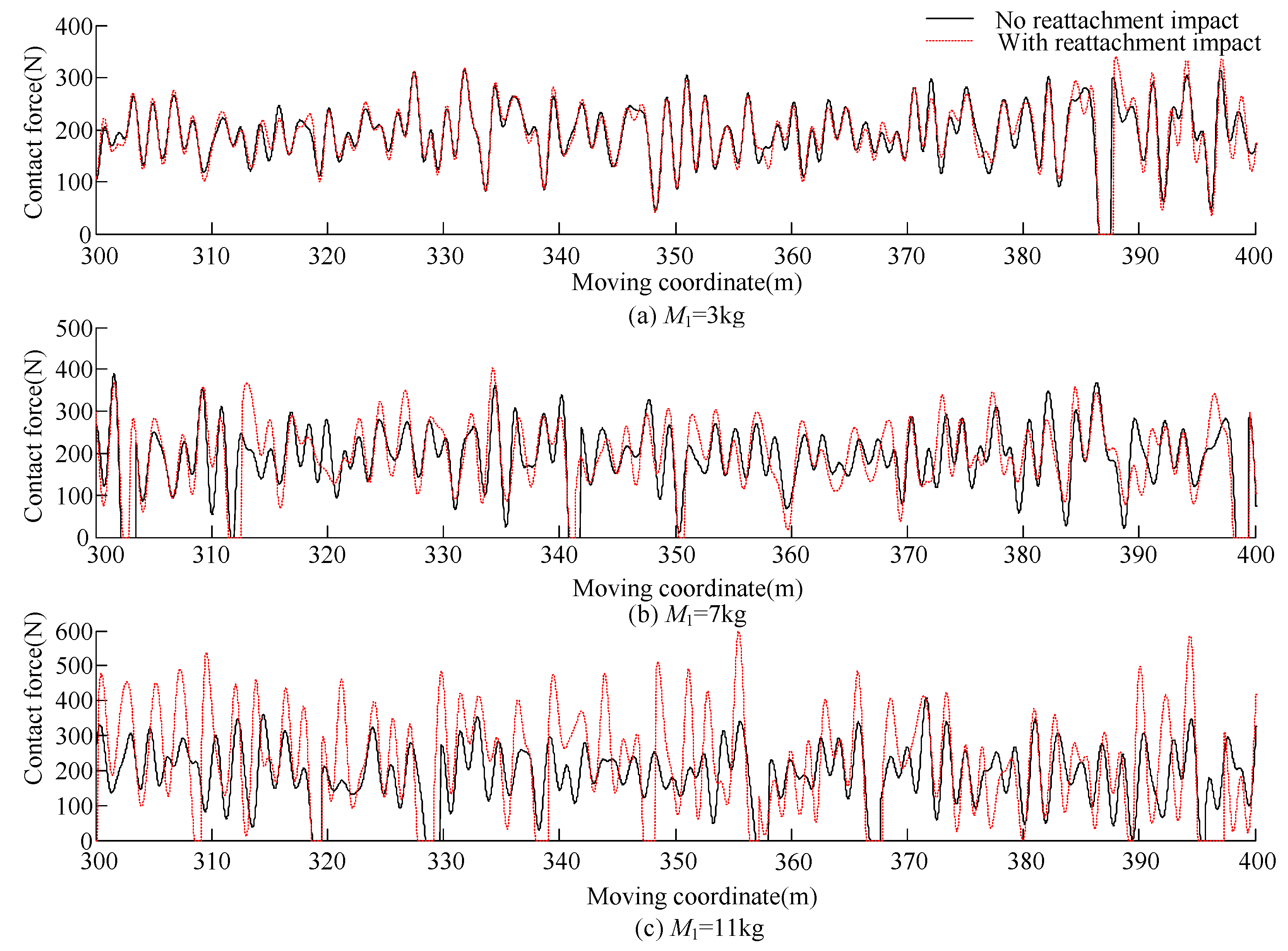
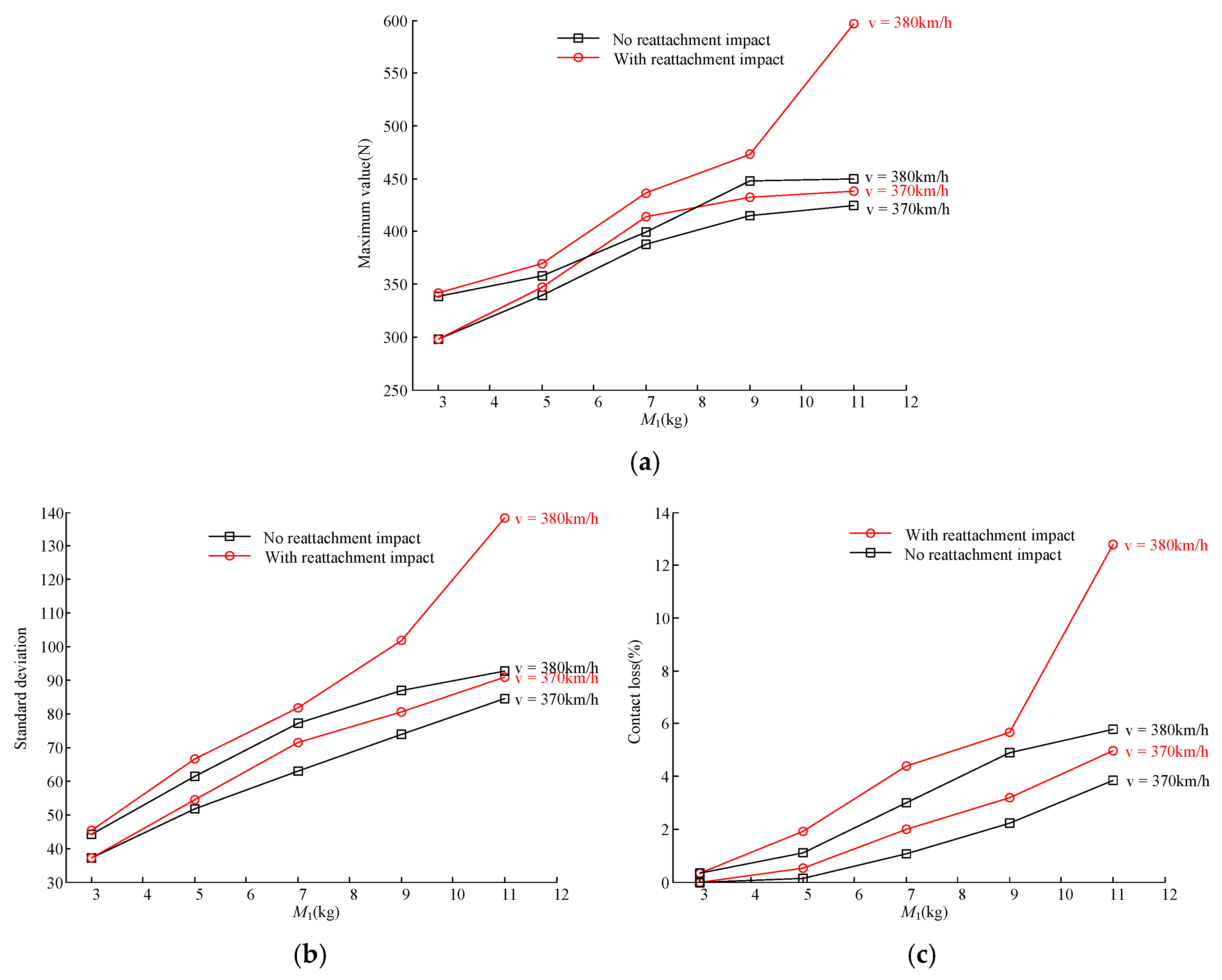
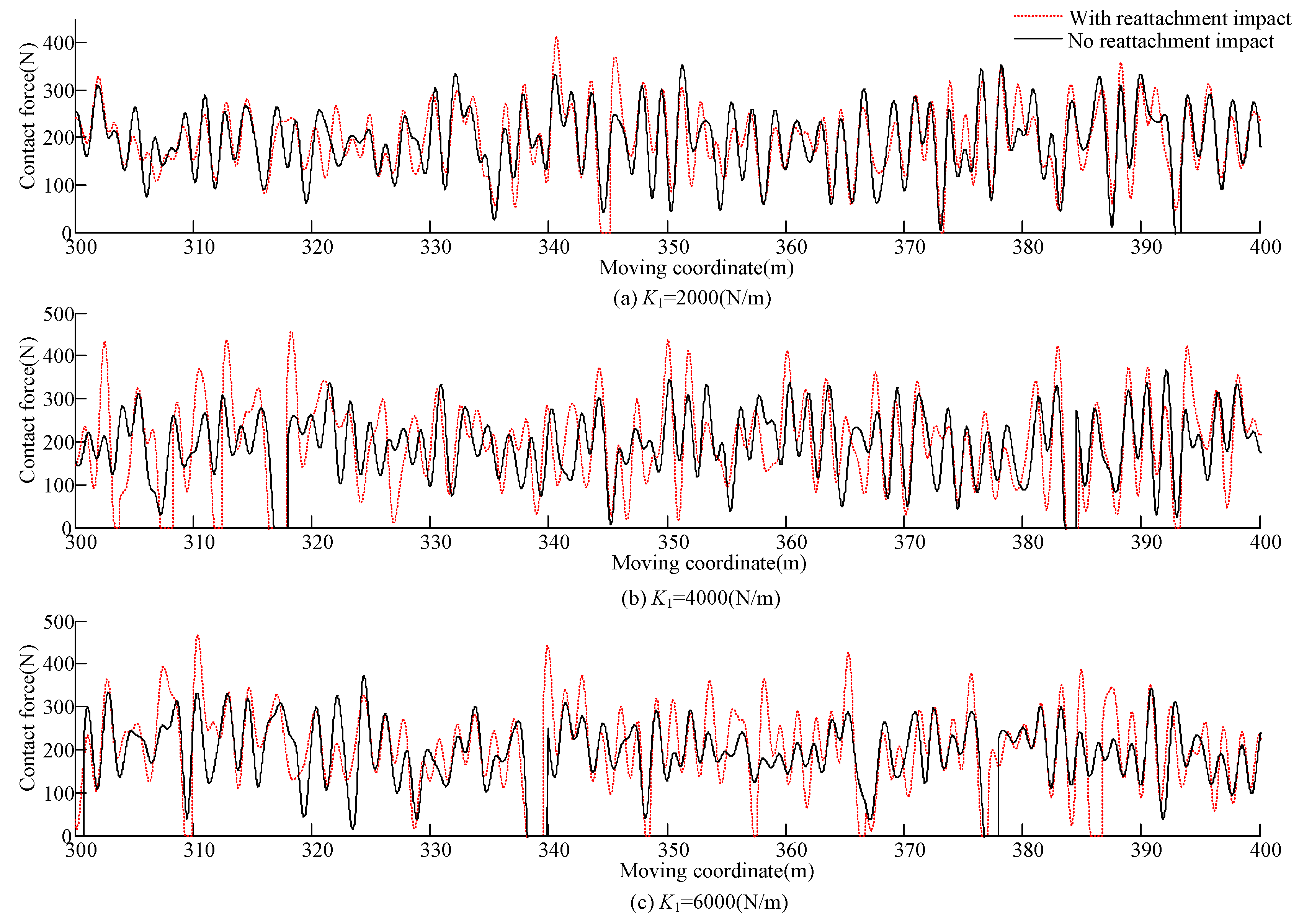
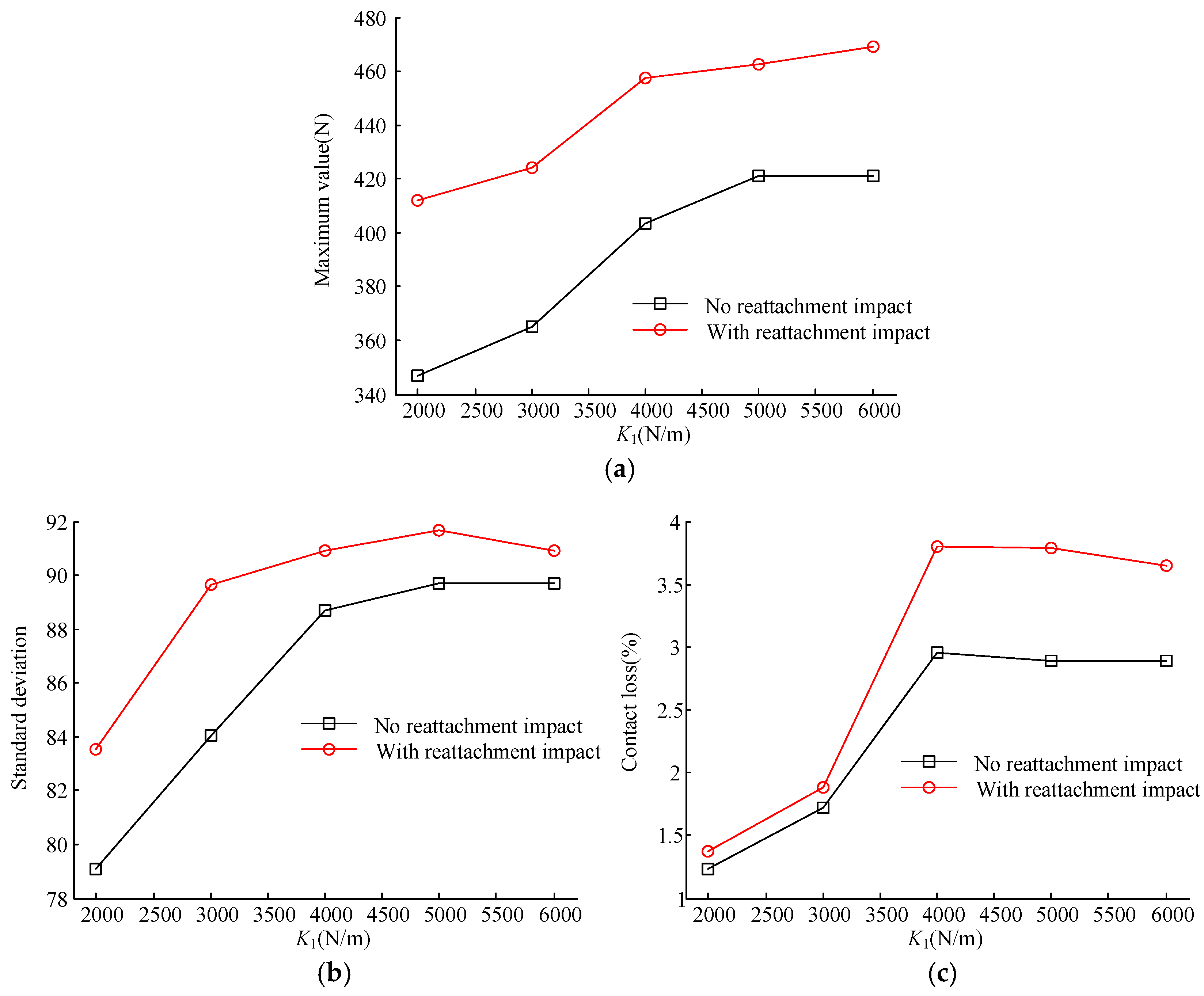
3.3. Analysis with Different Pantograph Head Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Poetsch, G.; Evans, J.; Meisinger, R.; Kortüm, W.; Baldauf, W.; Veitl, A.; Wallaschek, J. Pantograph/catenary dynamics and control. Veh. Syst. Dyn. 1997, 28, 159–195. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear analysis of wind-induced vibration of high-speed railway catenary and its influence on pantograph–catenary interaction. Veh. Syst. Dyn. 2016, 54, 723–747. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Duan, F.; Lu, X.; Wang, H. Study on wind-induced vibration behavior of railway catenary in spatial stochastic wind field based on nonlinear finite element procedure. J. Vib. Acoust. Trans. ASME 2018, 140, 011010. [Google Scholar] [CrossRef]
- Wang, Z.; Song, Y.; Yin, Z.; Wang, R.; Zhang, W. Random response analysis of axle-box bearing of a high-speed train excited by crosswinds and track irregularities. IEEE Trans. Veh. Technol. 2019, 68, 10607–10617. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Liu, Z.; Duan, F.; Xu, Z.; Lu, X. Wave propagation analysis in high-speed railway catenary system subjected to a moving pantograph. Appl. Math. Model. 2018, 59, 20–38. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Zhang, J.; Lu, X.; Duan, F. Analysis of the galloping behaviour of an electrified railway overhead contact line using the non-linear finite element method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 2339–2352. [Google Scholar] [CrossRef]
- Lopez-Garcia, O.; Carnicero, A.; Maroño, J.L. Influence of stiffness and contact modelling on catenary-pantograph system dynamics. J. Sound Vib. 2007, 299, 806–821. [Google Scholar] [CrossRef]
- Bruni, S.; Ambrosio, J.; Carnicero, A.; Cho, Y.H.; Finner, L.; Ikeda, M.; Kwon, S.Y.; Massat, J.P.; Stichel, S.; Tur, M.; et al. The results of the pantograph-catenary interaction benchmark. Veh. Syst. Dyn. 2015, 53, 412–435. [Google Scholar] [CrossRef]
- Collina, A.; Bruni, S. Numerical simulation of pantograph-overhead equipment interaction. Veh. Syst. Dyn. 2002, 38, 261–291. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements. Veh. Syst. Dyn. 2015, 53, 1455–1479. [Google Scholar] [CrossRef]
- Ambrósio, J.; Pombo, J.; Pereira, M.; Antunes, P.; Mósca, A. A computational procedure for the dynamic analysis of the catenary-pantograph interaction in high-speed trains. J. Theor. Appl. Mech. 2012, 50, 681–699. [Google Scholar]
- Pombo, J.; Ambrosio, J. Environmental and track perturbations on multiple pantograph interaction with catenaries in high-speed trains. Comput. Struct. 2013, 124, 88–101. [Google Scholar] [CrossRef] [Green Version]
- Pombo, J.; Ambrsio, J. Multiple pantograph interaction with catenaries in high-speed trains. J. Comput. Nonlinear Dyn. 2012, 7, 041008. [Google Scholar] [CrossRef]
- Seo, J.H.; Kim, S.W.; Jung, I.H.; Park, T.W.; Mok, J.Y.; Kim, Y.G.; Chai, J.B. Dynamic analysis of a pantograph-catenary system using absolute nodal coordinates. Veh. Syst. Dyn. 2006, 44, 615–630. [Google Scholar] [CrossRef]
- Song, Y.; Ouyang, H.; Liu, Z.; Mei, G.; Wang, H.; Lu, X. Active control of contact force for high-speed railway pantograph-catenary based on multi-body pantograph model. Mech. Mach. Theory 2017, 115, 35–59. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Xu, Z.; Zhang, J. Developed moving mesh method for high-speed railway pantograph-catenary interaction based on nonlinear finite element procedure. Int. J. Rail Transp. 2019, 7, 173–190. [Google Scholar] [CrossRef]
- Seo, J.H.; Sugiyama, H.; Shabana, A.A. Three-dimensional large deformation analysis of the multibody pantograph/catenary systems. Nonlinear Dyn. 2005, 42, 199–215. [Google Scholar] [CrossRef]
- Lee, K. Analysis of dynamic contact between overhead wire and pantograph of a high-speed electric train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 157–166. [Google Scholar] [CrossRef]
- Ouyang, H. Moving-load dynamic problems: A tutorial (with a brief overview). Mech. Syst. Signal Process. 2011, 25, 2039–2060. [Google Scholar] [CrossRef]
- Lee, U. Separation between the flexible structure and the moving mass sliding on it. J. Sound Vib. 1998, 209, 867–877. [Google Scholar] [CrossRef]
- Lee, U. Revisiting the moving mass problem: Onset of separation between the mass and beam. J. Vib. Acoust. Trans. ASME 1996, 118, 516–521. [Google Scholar] [CrossRef]
- Stǎncioiu, D.; Ouyang, H.; Mottershead, J.E. Vibration of a beam excited by a moving oscillator considering separation and reattachment. J. Sound Vib. 2008, 310, 1128–1140. [Google Scholar] [CrossRef]
- Ouyang, H.; Mottershead, J.E. A numerical-analytical combined method for vibration of a beam excited by a moving flexible body. Int. J. Numer. Methods Eng. 2007, 72, 1181–1191. [Google Scholar] [CrossRef]
- Dahlberg, T. Moving force on an axially loaded beam—With applications to a railway overhead contact wire. Veh. Syst. Dyn. 2006, 44, 631–644. [Google Scholar] [CrossRef]
- Cheng, Y.S.; Au, F.T.K.; Cheung, Y.K.; Zheng, D.Y. On the separation between moving vehicles and bridge. J. Sound Vib. 1999, 222, 781–801. [Google Scholar] [CrossRef]
- Lee, K.; Chung, J. Dynamic analysis of a hanger-supported beam with a movingoscillator. J. Sound Vib. 2013, 332, 3177–3189. [Google Scholar] [CrossRef]
- Lee, K.; Cho, Y.; Chung, J. Dynamic contact analysis of a tensioned beam with a moving massspring system. J. Sound Vib. 2012, 331, 2520–2531. [Google Scholar] [CrossRef]
- Zou, D.; Zhou, N.; Rui Ping, L.; Mei, G.M.; Zhang, W.H. Experimental and simulation study of wave motion upon railway overhead wire systems. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 934–944. [Google Scholar] [CrossRef]
- Zhang, W.H.; Mei, G.M.; Wu, X.J.; Chen, L.Q. A study on dynamic behaviour of pantographs by using hybrid simulation method. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2005, 219, 189–199. [Google Scholar] [CrossRef]
- Brogliato, B. Nonsmooth Mechanics: Models, Dynamics and Control, 3rd ed.; Springer: London, UK, 2016. [Google Scholar]
- Cháidez, S.T.; de la, S.T. Contribution to the Assessment of the Efficiency of Friction Dissipaters for Seismic Protection of Buildings; Universitat Politècnica de Catalunya: Barcelona, Spain, 2003. [Google Scholar]
- Zhao, Y.Y.; Wu, G.N.; Gao, G.Q.; Wang, W.G.; Zhou, L.J. Study on electromagnetic force of pantograph-catenary system. Tiedao Xuebao J. China Railw. Soc. 2014, 36, 28–32. [Google Scholar]
- EN 50367. Railway applications—Current Collection Systems—Technical Criteria for the Interaction between Pantograph and Overhead Line. 2012. Available online: https://standards.globalspec.com/std/10202019/EN%2050367 (accessed on 31 May 2012).
- Song, Y.; Liu, Z.; Ouyang, H.; Wang, H.; Lu, X. Sliding mode control with PD sliding surface for high-speed railway pantograph-catenary contact force under strong stochastic wind field. Shock Vib. 2017, 2017, 4895321. [Google Scholar] [CrossRef]
| Item | Value | Item | Value |
|---|---|---|---|
| Span | 48 m | Interval of droppers | 5/9.5/9.5/9.5/9.5/5 m |
| Contact wire tension | 27 kN | Simulated length | 10 spans |
| Messenger wire tension | 21 kN | Messenger wire type | CuMg0.5 AC 120 |
| Number of droppers | 5 | Contact wire type | BZ II 120 |
| Dropper stiffness | 1 × 105 N/m | Dropper mass | 0.4 kg |
| Messenger wire support stiffness | 1 × 107 N/m | Steady arm mass | 1.125 kg |
| Item | 1 | 2 | 3 |
|---|---|---|---|
| M (kg) | 6 | 7.12 | 5.8 |
| C (Ns/m) | 0 | 0 | 70 |
| K (N/m) | 9430 | 14,100 | 0.1 |
| Maximum operating speed: 350 (km/h); F0 = 0.00097 × v2 + 70 (N) | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, W.; Song, Y. Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact. Vibration 2020, 3, 18-33. https://doi.org/10.3390/vibration3010003
Chu W, Song Y. Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact. Vibration. 2020; 3(1):18-33. https://doi.org/10.3390/vibration3010003
Chicago/Turabian StyleChu, Wenping, and Yang Song. 2020. "Study on Dynamic Interaction of Railway Pantograph–Catenary Including Reattachment Momentum Impact" Vibration 3, no. 1: 18-33. https://doi.org/10.3390/vibration3010003





