Field Experiments and Numerical Analysis of the Ground Vibration Isolation of Shock Wave Propagation under Explosion Shock Loading
Abstract
:1. Introduction
2. Field Experiments and Numerical Analysis
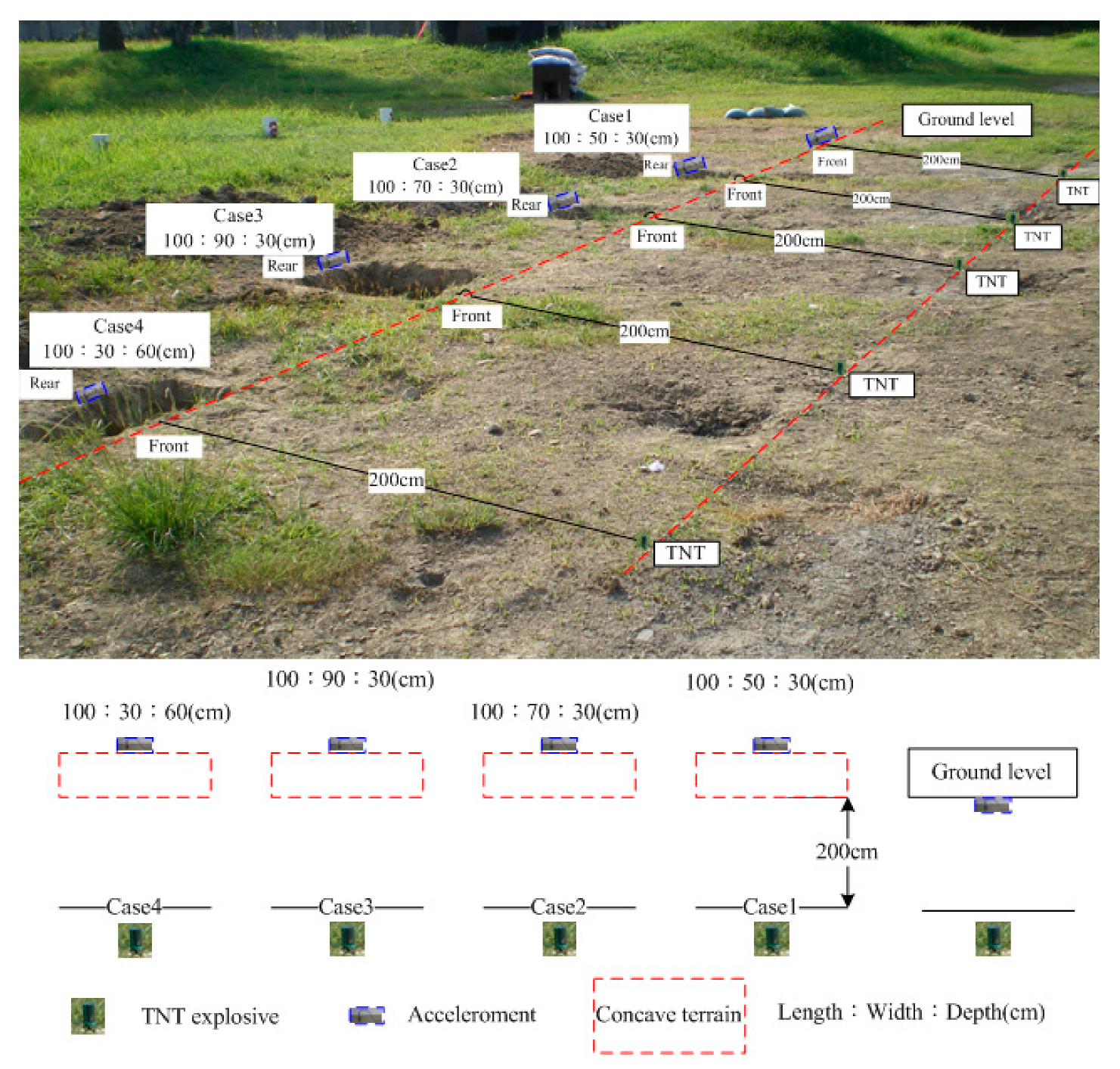
2.1. Explosion Tests
2.2. Numerical Analysis
3. Implementation of Numerical Analysis
3.1. Numerical Simulation Model
3.2. Mathematical Formulation of Material Parameters and Equation of State
4. Results and Discussion
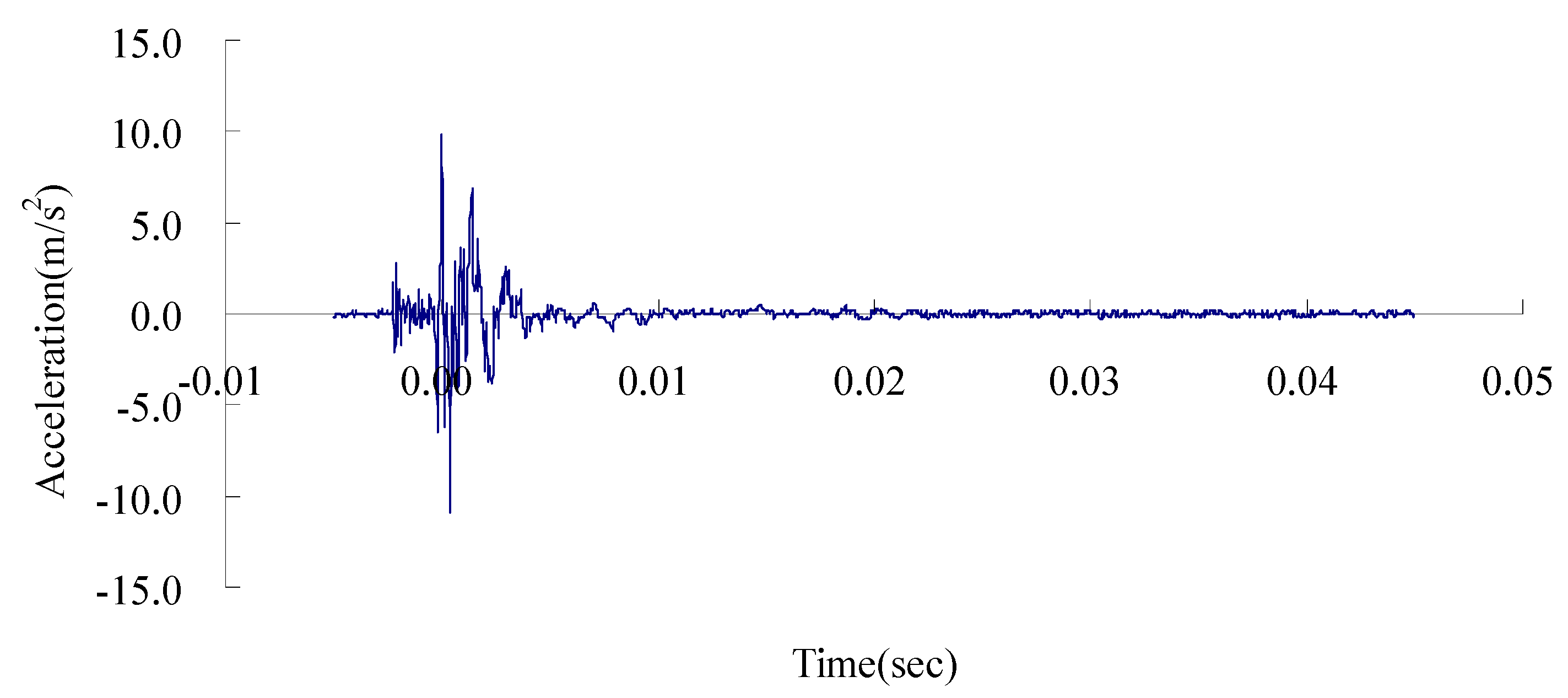
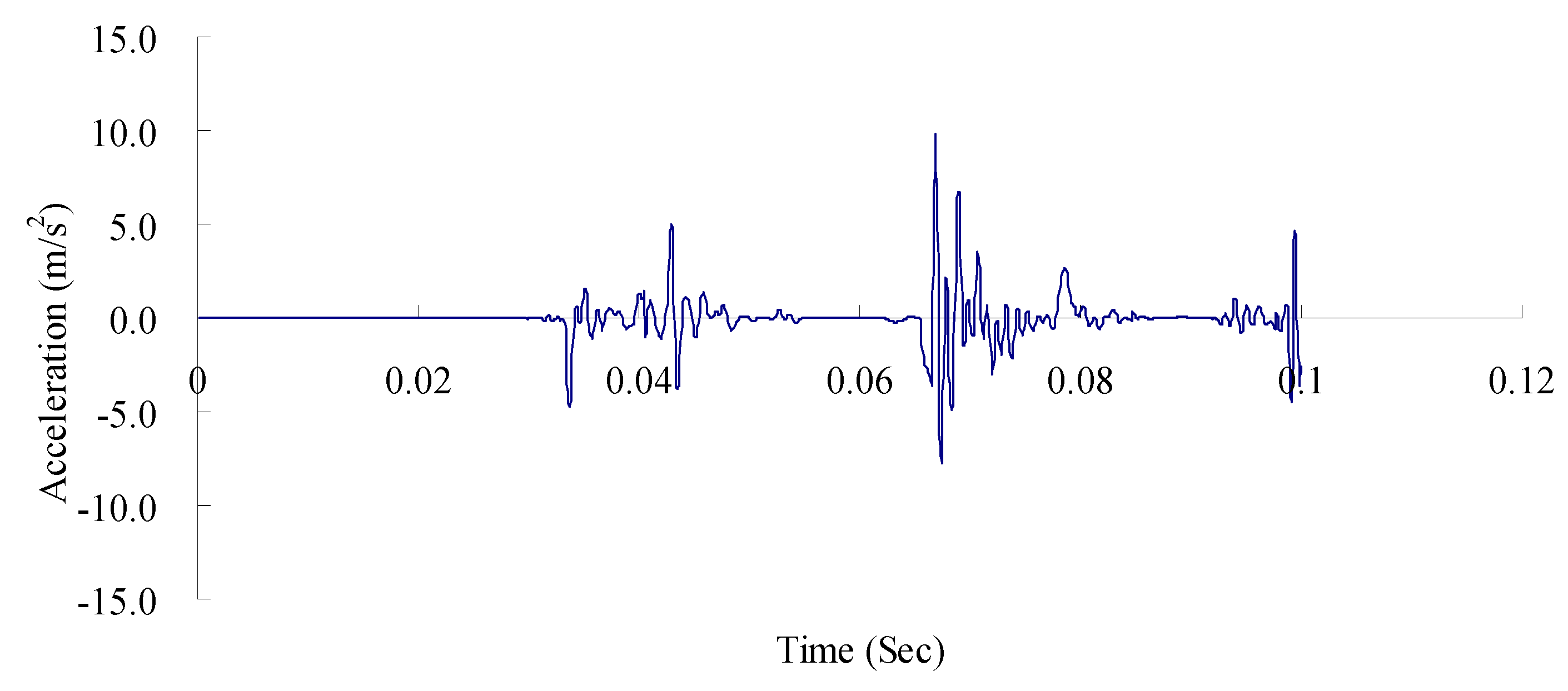
4.1. In Situ Explosion Tests
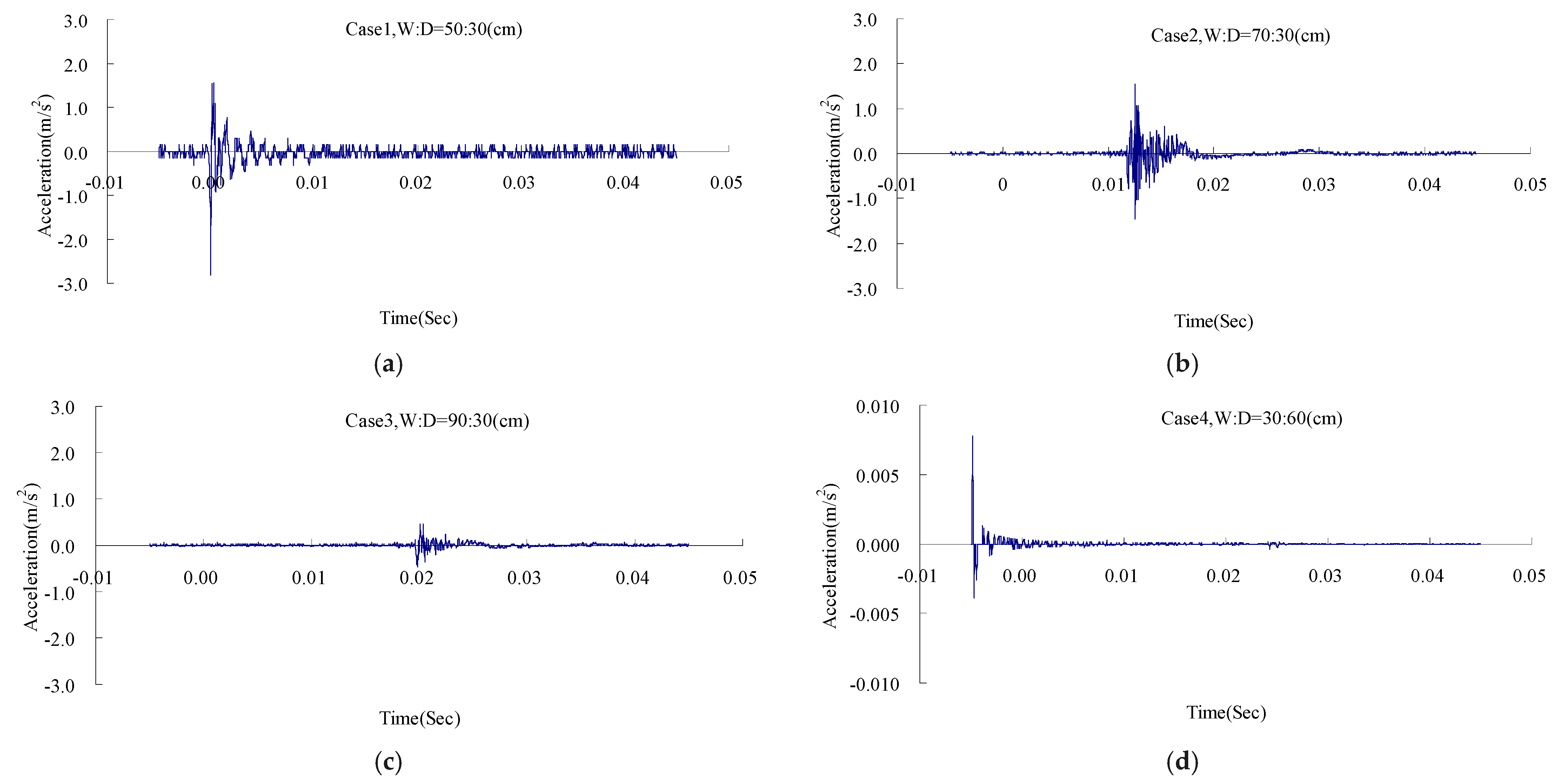
4.2. Comparison Simulation Results by the Explosion Tests
4.3. Topographical Effects of the Propagation of Blast Waves
5. Conclusions
- This study measured ground acceleration values during in situ explosion tests to verify the relative error by numerical analysis. The analysis results indicate that incorporating MMALE with eight-node solid elements, and constructing a numerical analysis model for explosions, is effective for analyzing fluid–solid coupling effects, solving dynamics problems (e.g., geometric nonlinearity, material nonlinearity, and contact nonlinearity), and facilitating an examination of the variations in blast wave energy, to provide a foundation for developing explosion hazard analysis models.
- Blast analysis involves transient dynamics problems. It is generally used for analyzing blasts with rapid loading times and high vibration frequencies, and involves highly nonlinear geometries and materials. The propagation of blast waves in a medium is affected by the properties of that medium. Concave terrain has considerable attenuation effects on the propagation of blast waves. The attenuation is associated with the width and depth of concave terrain, although the depth has a more pronounced effect. The horizontal attenuation effects from horizontal waves are more prominent than those from vertical waves, and the effects are subject to the direction in which the wave propagates. The propagation of blast waves in convex terrain exhibits both attenuation and amplification effects. In convex terrain, vertical blast waves have stronger amplification effects than horizontal ones, indicating that larger elevation differences lead to more noticeable amplification effects. The amplification effects decrease as the width of convex terrain increases. The study results may serve as a reference for vibration isolation engineering and disaster prevention construction.
- Seismic waves induced by explosions are a process of energy propagation and transfer. Therefore, to achieve the goals of vibration reduction, disaster prevention, and safety protection, designers of blast protection engineering projects can measure the energy of explosions that induce ground vibrations, to obtain a reference for vibration hazard control, secure structures with substantial elevation differences, and minimize blast wave hazards by digging vibration reduction trenches.
Funding
Conflicts of Interest
References
- Crandle, F.J. Ground vibration due to blasting and its effect upon structures. J. Boston Soc. Civ. Eng. 1949, 36, 222–245. [Google Scholar]
- Wang, J. Simulation of Landmine Explosion Using LS-DYNA 3D Software: Benchmark Work of Simulation in Soil and Air; DSTO-TR-1168; Aeronautical and Maritime Research Laboratory: Fishermans Bend, VIC, Australia, 2001; pp. 1–30. [Google Scholar]
- Wang, T.C.; Lee, C.Y.; Wang, I.T. Analysis of blasting vibration wave propagation based on finite element numerical calculation and experimental investigations. J. Vibroeng. 2017, 19, 2703–2712. [Google Scholar] [CrossRef]
- Goodman, H.J. Compiled Free-Air Blast Data on Bare Spherical Pentolite; BRL Report, No. 1092; Ballistic Research Laboratories: Aberdeen, MD, USA, 1960; pp. 3–46. [Google Scholar]
- Kivity, Y.; Ben-Dor, G.; Anteby, I.; Sadot, O. The blast wave resulting from an accidental explosion in an ammunition magazine. In Proceedings of the Military Aspects of Blast and Shock Symposium–19th International Conference, Calgary, AB, Canada, 2–6 October 2006. [Google Scholar]
- Koga, Y.; Matsuo, O. Shaking table tests of embankments resting on liquefiable sandy ground. Soil. Found. 1990, 30, 162–174. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Lu, Y. Numerical analysis on dynamic deformation mechanism of soils under blast loading. Soil. Dyn. Earthq. Eng. 2003, 23, 705–714. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Evaluation of blast-induced ground vibration predictors. Soil. Dyn. Earthq. Eng. 2007, 27, 116–125. [Google Scholar] [CrossRef]
- Ak, H.; Iphar, M.; Yavuz, M.; Konuk, A. Evaluation of ground vibration effect of blasting operations in a magnesite mine. Soil. Dyn. Earthq. Eng. 2009, 29, 669–676. [Google Scholar] [CrossRef]
- US Army Engineers Waterways Experimental Station. Fundamental of Protection Design for Conventional Weapons; Technical Manual TM 5-855-1; US Army Engineers Waterways Experimental Station: Washington, DC, USA, 1998. [Google Scholar]
- Ahmad, S.; Al-Hussaini, T.M. Simplified design for vibration screening by open and in-filled trenches. J. Geotech. Eng. 1991, 117, 67–88. [Google Scholar] [CrossRef]
- Klein, R.; Antes, H.; Le Houedec, D. Efficient 3D Modelling of Vibration Isolation by Open Trenches. Comput. Struct. 1997, 64, 809–817. [Google Scholar] [CrossRef]
- Spyros, S.; Fotis, R. Computer simulation of shock waves transmission in obstructed. J. Los. Pre. Pro. Ind. 2004, 17, 407–417. [Google Scholar]
- Dally, J.W.; David, L. A photoelastic analysis of propagation of Rayleigh waves past a step change in elevation. Bull. Seism. Soc. Am. 1968, 58, 539–563. [Google Scholar]
- Zhu, Z.; Yang, Y. Research on effect decreasing quake of groove on the building with dynamic photo elasticity. Exp. Shock Wav. 1989, 9, 55–60. [Google Scholar]
- Zhang, Q.; Bia, C.H.; Liu, Q.M. Experimental research on amplitude change of blasting seismic wave with topography. J. Be. Inst. Tech. 2000, 9, 237–242. [Google Scholar]
- LS-DYNA Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006.
- LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2009.
- Tai, Y.S.; Chu, T.L.; Hu, H.T.; Wu, J.Y. Dynamic response of a reinforced concrete slab subjected to air blast load. Theo. Appl. Fract. Mech. 2011, 56, 140–147. [Google Scholar] [CrossRef]
- Gebbeken, N.; Ruppert, M. On the safety and reliability of high dynamic hydrocode simulations. Int. J. Num. Meth. Eng. 1999, 46, 839–851. [Google Scholar] [CrossRef]
- Wang, I.T. Numerical and experimental verification of finite element mesh convergence under explosion loading. J. Vibroeng. 2014, 16, 1786–1798. [Google Scholar]
- Dobratz, B.M. LLNL Explosive Handbook Properties of Chemical Explosives and Explosive Simulants; Lawrence Livemore National Laboratory: Livermore, CA, USA, 1981. [Google Scholar]
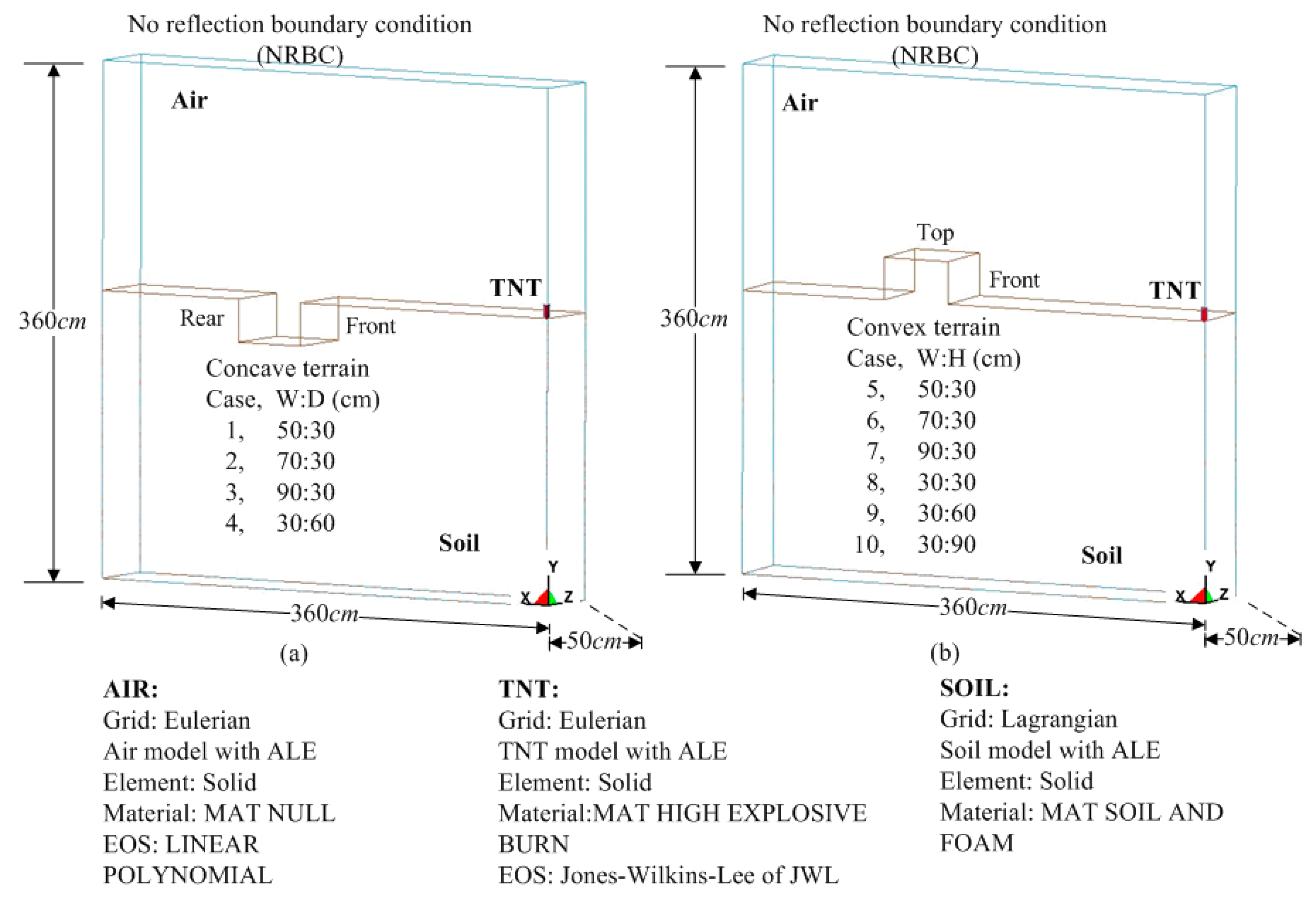

| Element | Material and Equation of State Parameters (Unit System: g, cm, μ-Second) | ||||||
|---|---|---|---|---|---|---|---|
| Air | MAT_NULL | ||||||
| RO | PC | MU | TEROD | CEROD | YM | PR | |
| 0.00129 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| EOS_LINEAR_POLYNOMIAL | |||||||
| C0 | C1, C2, C3, C6 | C4 | C5 | V0 | E0 | ||
| 0.0 | 0.4 | 0.4 | 1.0 | ||||
| TNT | MAT_HIGH_EXPLOSIVE_BURN | ||||||
| RO | D | PCJ | BETA | K | G | SIGY | |
| 1.63 | 0.693 | 0.21 | 0.0 | 0.0 | 0.0 | 0.0 | |
| EOS_JWL | |||||||
| A | B | R1 | R2 | OMEGA (ω) | E0 | V0 | |
| 3.712 | 0.03231 | 4.15 | 0.95 | 0.3 | 0.07 | 1.0 | |
| MAT_SOIL_AND_FOAM | ||||||
|---|---|---|---|---|---|---|
| Soil | RO | G | BULK | A0 | A1 | A2 |
| 2.6 | 0.000147 | 0.00729 | ||||
| Case | W:D (cm) | Experiment (m/s2) | Numerical Analysis (m/s2) | Relative Error (%) |
|---|---|---|---|---|
| Front of concave | 10.0500 | 9.7326 | −3.158 | |
| Rear of concave | ||||
| 1 | 50:30 | 2.7690 | 2.6309 | −4.987 |
| 2 | 70:30 | 1.5500 | 1.4946 | −3.574 |
| 3 | 90:30 | 0.4500 | 0.4135 | −8.107 |
| 4 | 30:60 | 0.0078 | 0.0074 | −4.600 |
| Case | W:D (cm) | Front of Concave (m/s2) | Rear of Concave (m/s2) |
|---|---|---|---|
| 1 | 50:30 | 9.6817 | 2.4275 |
| 2 | 70:30 | 1.1833 | |
| 3 | 90:30 | 0.4071 | |
| 4 | 30:60 | 0.0061 |
| Case | W:H (cm) | Vertical PGA (m/s2) | Horizontal PGA (m/s2) | ||
|---|---|---|---|---|---|
| Front of Convex | Central of Top | Front of Convex | Central of Top | ||
| 5 | 50:30 | 8.9179 | 40.0893 | 7.6326 | 19.5180 |
| 6 | 70:30 | 29.2753 | 14.4296 | ||
| 7 | 90:30 | 22.7200 | 10.8512 | ||
| 8 | 30:30 | 41.5224 | 20.2410 | ||
| 9 | 30:60 | 43.5458 | 21.7863 | ||
| 10 | 30:90 | 37.9214 | 18.1338 | ||
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, I.-T. Field Experiments and Numerical Analysis of the Ground Vibration Isolation of Shock Wave Propagation under Explosion Shock Loading. Vibration 2019, 2, 300-310. https://doi.org/10.3390/vibration2040019
Wang I-T. Field Experiments and Numerical Analysis of the Ground Vibration Isolation of Shock Wave Propagation under Explosion Shock Loading. Vibration. 2019; 2(4):300-310. https://doi.org/10.3390/vibration2040019
Chicago/Turabian StyleWang, Iau-Teh. 2019. "Field Experiments and Numerical Analysis of the Ground Vibration Isolation of Shock Wave Propagation under Explosion Shock Loading" Vibration 2, no. 4: 300-310. https://doi.org/10.3390/vibration2040019
APA StyleWang, I.-T. (2019). Field Experiments and Numerical Analysis of the Ground Vibration Isolation of Shock Wave Propagation under Explosion Shock Loading. Vibration, 2(4), 300-310. https://doi.org/10.3390/vibration2040019





