Review of Pedestrian Load Models for Vibration Serviceability Assessment of Floor Structures
Abstract
:1. Introduction
1.1. Background
1.2. Key Problems
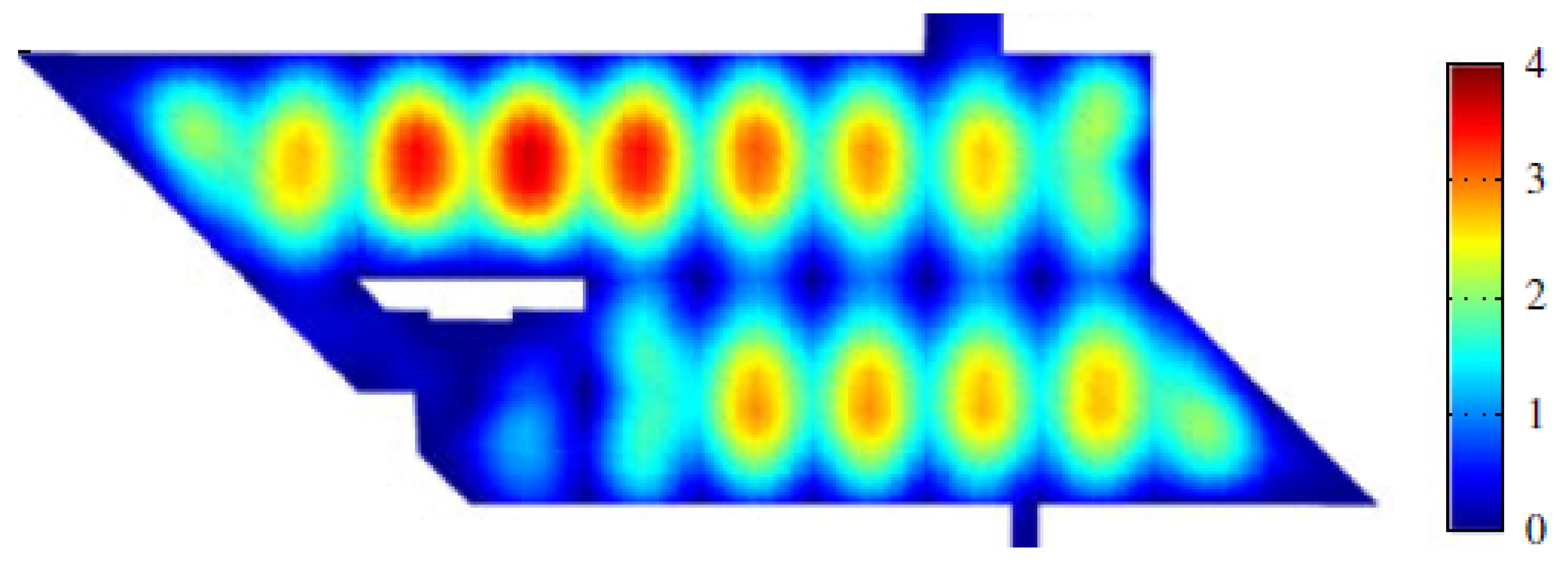
2. Characteristics of Vibration in Floors
2.1. Vibration Source (Input)
2.2. Transmission Path (System)
2.3. Receiver (Output)
3. Human Induced Loading
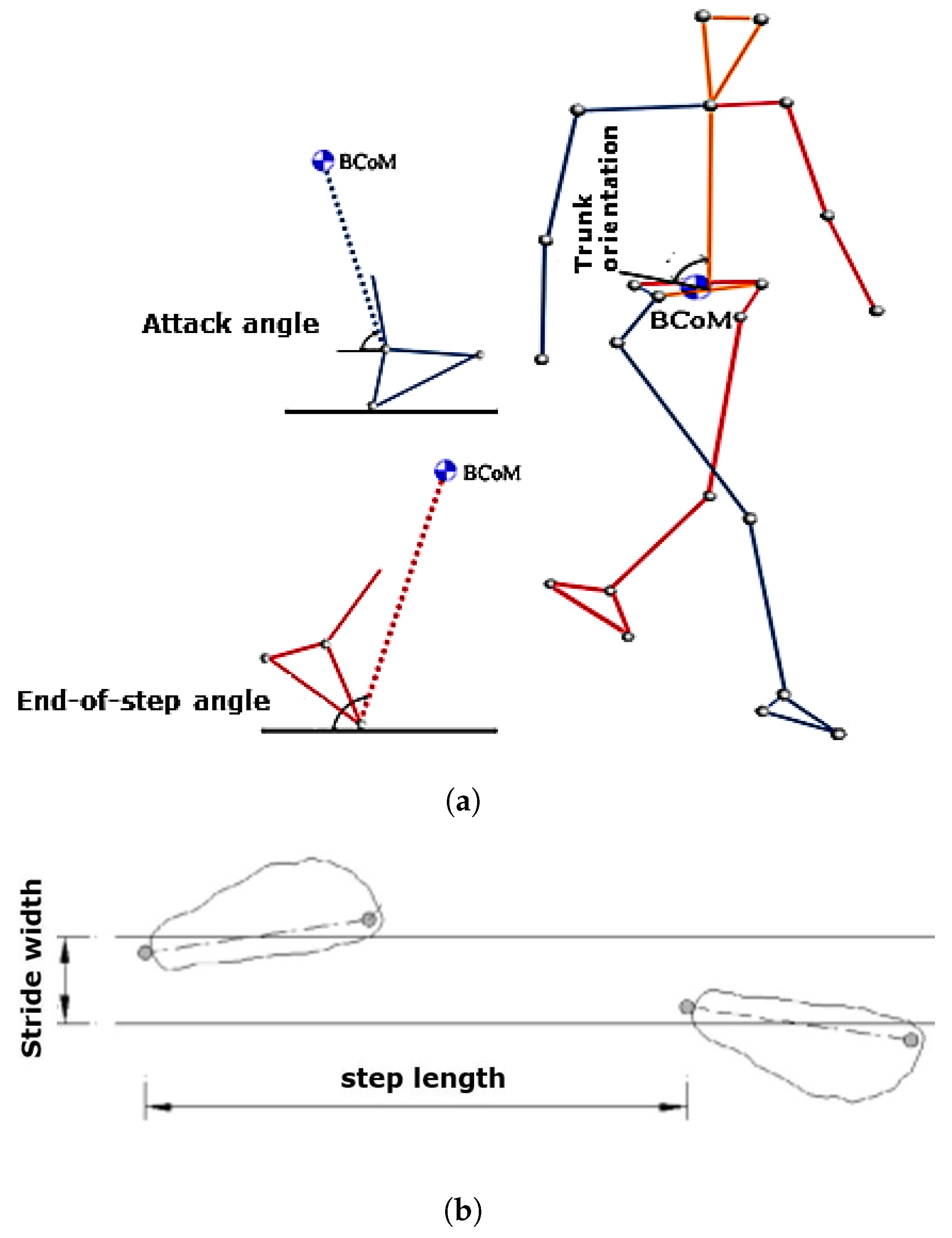
3.1. Walking Parameters
3.1.1. Spatio-Temporal Gait Parameters
3.1.2. Controlled Walking vs. Free Walking
3.1.3. Subject Variability
3.2. Walking Models
3.2.1. Deterministic Walking Models
3.2.2. Probabilistic Walking Models for Individual Pedestrians
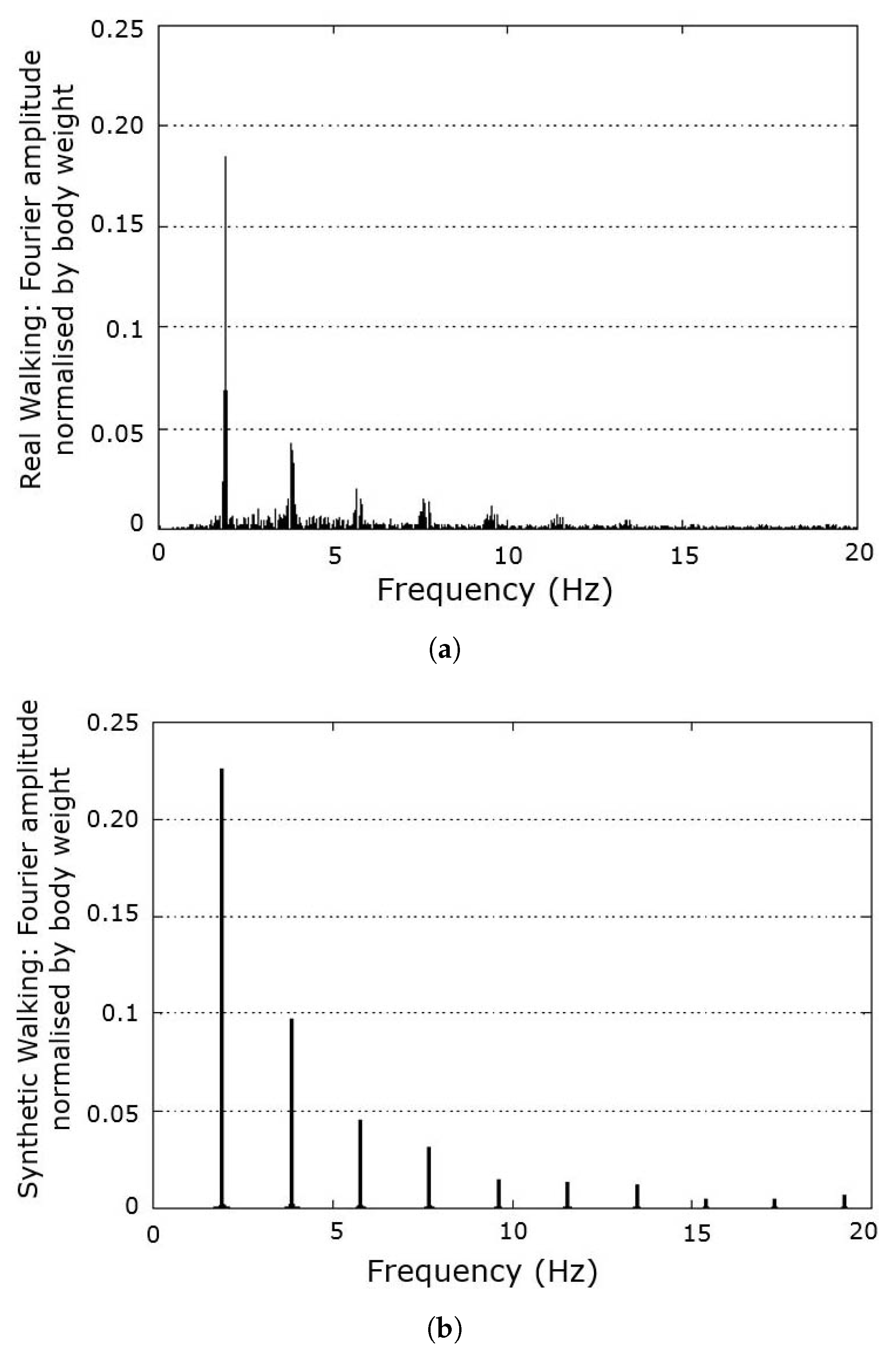
3.2.3. Response Spectrum in Walking Models
3.3. Statistical Modelling Approaches for Multiple Pedestrians
3.4. Walking Path (Route of Pedestrian)
4. Contemporary Design Guidelines and Codes of Practice
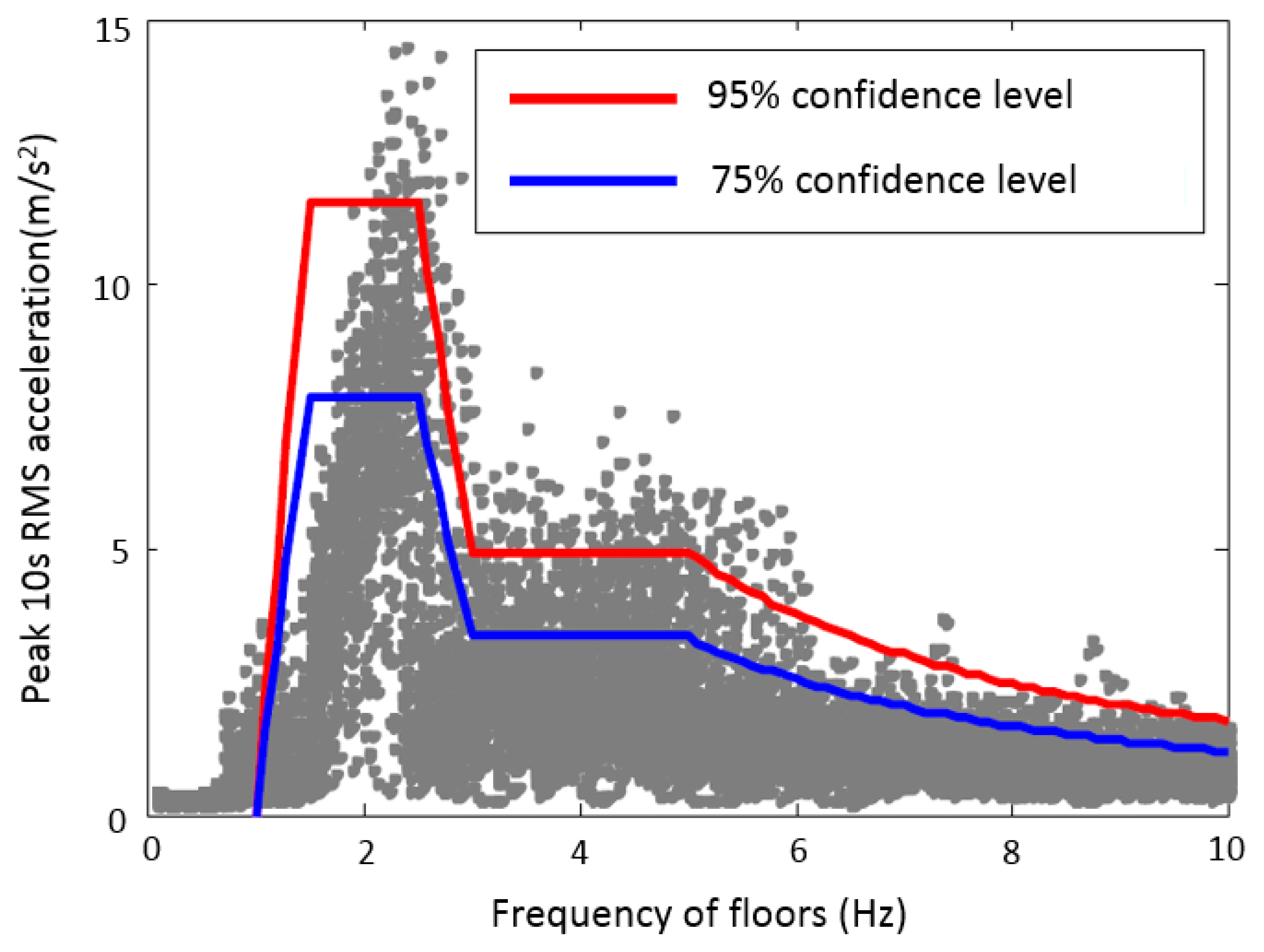
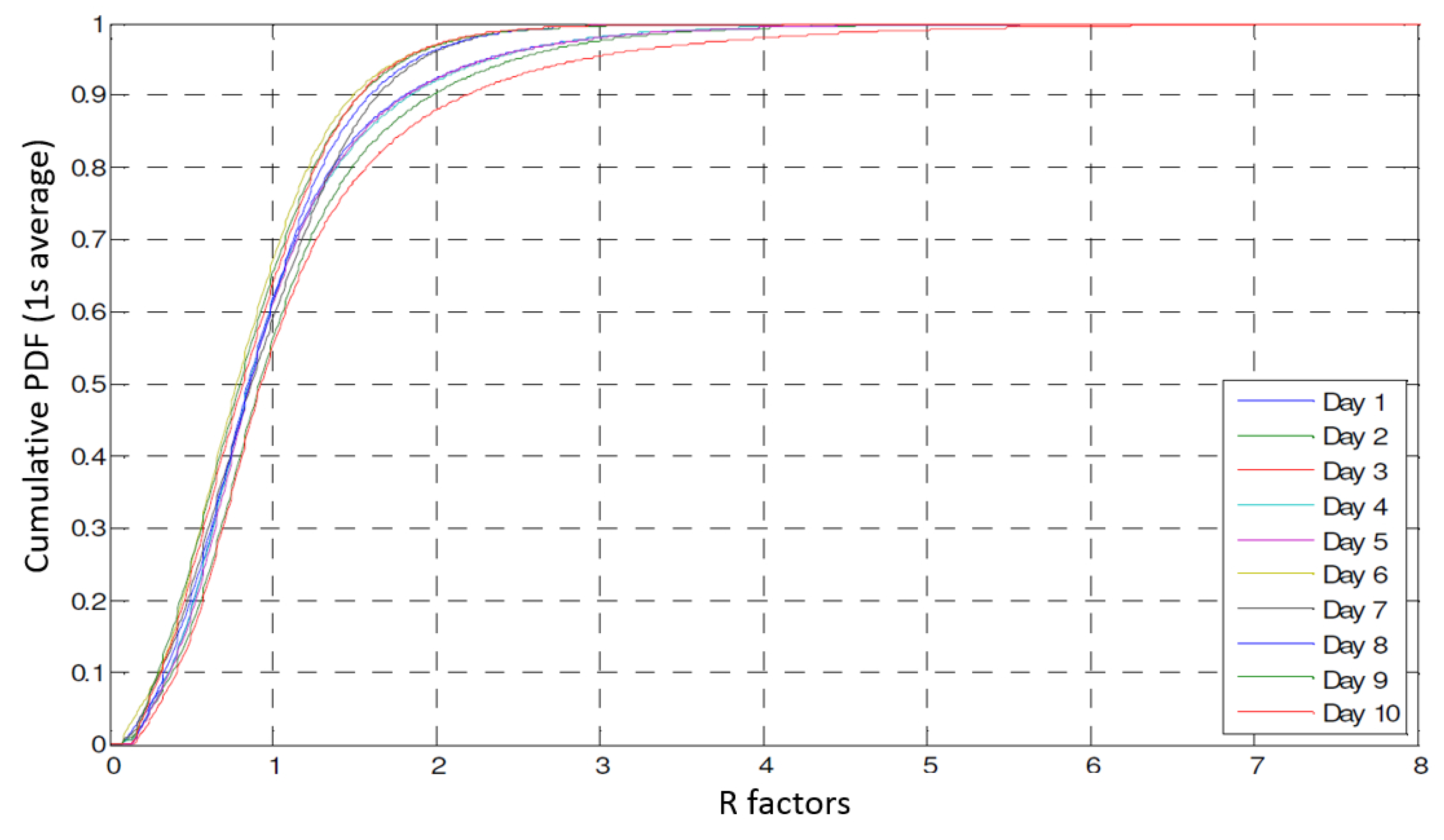
5. Probabilistic Response Distribution
6. Pedestrian Monitoring Techniques
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pavic, A.; Reynolds, P.; Waldron, P.; Bennett, K.J. Critical review of guidelines for checking vibration serviceability of post-tensioned concrete floors. Cem. Concr. Compos. 2001, 23, 21–31. [Google Scholar] [CrossRef]
- Pavic, A.; Reynolds, P. Vibration serviceability of long-span concrete building floors: Part 1—Review of background information. Shock Vib. Dig. 2002, 34, 191–211. [Google Scholar]
- Pavic, A.; Reynolds, P. Vibration serviceability of long-span concrete building floors: Part 2—Review of mathematical modelling approaches. Shock Vib. Dig. 2002, 34, 279–297. [Google Scholar]
- Hicks, S.; Devine, P. Vibration characteristics of modern composite floor systems. In Composite Construction in Steel and Concrete V; ASCE: Reston, VA, USA, 2006; pp. 247–259. [Google Scholar] [CrossRef]
- Nguyen, H.A.U. Walking Induced Floor Vibration Design and Control. Ph.D. Thesis, Swinburne University of Technology, Melbourne, VIC, Australia, 2013. [Google Scholar]
- Živanović, S.; Pavic, A.; Reynolds, P. Vibration serviceability of footbridges under human-induced excitation: A literature review. J. Sound Vib. 2005, 279, 1–74. [Google Scholar] [CrossRef]
- Kerr, S.C. Human Induced Loading on Staircases. Ph.D. Thesis, University College London, London, UK, 1998. [Google Scholar]
- Davis, B.; Avci, O. Simplified vibration serviceability evaluation of slender monumental stairs. J. Struct. Eng. 2015, 141, 1–9. [Google Scholar] [CrossRef]
- Jones, C.; Reynolds, P.; Pavic, A. Vibration serviceability of stadia structures subjected to dynamic crowd loads: A literature review. J. Sound Vib. 2011, 330, 1531–1566. [Google Scholar] [CrossRef]
- Catbas, F.; Celik, O.; Avci, O.; Abdeljaber, O.; Gul, M.; Do, T. Sensing and monitoring in stadium structures: A review recent advances and a forward look. Front. Built Environ. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Mouring, S.E.; Ellingwood, B.R. Guidelines to minimise floor vibrations from building occupants. J. Struct. Eng. 1994, 120, 507–526. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Liu, J. Vibration of prestressed cable RC truss floor system due to human activity. J. Struct. Eng. 2015, 142, 1–10. [Google Scholar] [CrossRef]
- Brownjohn, J.; Middleton, C. Procedures for vibration serviceability assessment of high-frequency floors. Eng. Struct. 2008, 30, 1548–1559. [Google Scholar] [CrossRef] [Green Version]
- Bhargava, A.; Al-Smadi, Y.; Avci, O. Vibrations assessment of a hospital floor for a magnetic resonance imaging unit (MRI) replacement. In Proceedings of the Structures Congress, Pittsburgh, PA, USA, 2–4 May 2013; ASCE: Reston, VA, USA, 2013; pp. 2433–2444. [Google Scholar] [CrossRef]
- Ebrahimpour, A.; Sack, R.L. A review of vibration serviceability criteria for floor structures. Comput. Struct. 2005, 83, 2488–2494. [Google Scholar] [CrossRef]
- Avci, O. Retrofitting steel joist supported footbridges for improved vibration response. In Proceedings of the Structures Congress, Chicago, IL, USA, 29–31 March 2012; ASCE: Reston, VA, USA, 2012; pp. 460–470. [Google Scholar] [CrossRef]
- Murray, T.M.; Allen, D.E.; Ungar, E.E.; Davis, D.B. Vibrations of Steel-Framed Structural Systems Due to Human Activity; American Institute of Steel Construction (AISC): Chicago, IL, USA, 2016. [Google Scholar]
- Smith, A.; Hicks, S.; Devine, P. Design of Floors for Vibration: A New Approach, 2nd ed.; Steel Construction Institute (SCI): Berkshire, UK, 2009. [Google Scholar]
- RFCS. Human Induced Vibrations of Steel Structures (HiVoSS)—Vibration Design of Floors: Background Document; European Comission-RFCS: Brussels, Belgium, 2007. [Google Scholar]
- Osborne, K.P.; Ellis, B. Vibration design and testing of a long-span lightweight floor. Struct. Eng. 1990, 68, 181–186. [Google Scholar]
- Chen, Y.; Aswad, A. Vibration characteristics of double tee building floors. PCI J. 1994, 39, 84–95. [Google Scholar] [CrossRef]
- Chen, Y. Finite element analysis for walking vibration problems for composite precast building floors using ADINA: modeling, simulation and comparison. Comput. Struct. 1999, 72, 109–126. [Google Scholar] [CrossRef]
- Hanagan, L.M.; Raebel, C.H.; Trethewey, M.W. Dynamic measurements of in-place steel floors to assess vibration performance. J. Perform. Constr. Facil. 2003, 17, 126–135. [Google Scholar] [CrossRef]
- Barrett, A.; Avci, O.; Setareh, M.; Murray, T. Observations from vibration testing of in-situ structures. In Proceedings of the Structures Congress, St. Louis, MO, USA, 18–21 May 2006; ASCE: Reston, VA, USA, 2006; pp. 1–10. [Google Scholar] [CrossRef]
- Toratti, T.; Talja, A. Classification of human induced floor vibrations. Build. Acoust. 2006, 13, 211–221. [Google Scholar] [CrossRef]
- Pavic, A.; Willford, M. Vibration Serviceability of Post-Tensioned Concrete Floors, 2nd ed.; Concrete Society: Slough, UK, 2005. [Google Scholar]
- Willford, M.; Young, P. A Design Guide for Footfall Induced Vibration of Structures; Concrete Centre (CC): Surry, UK, 2006. [Google Scholar]
- Fanella, D.A.; Mota, M. Design Guide for Vibrations of Reinforced Concrete Floor Systems; Concrete Reinforcing Steel Institute (CRSI): Schaumburg, IL, USA, 2014. [Google Scholar]
- Al-Anbaki, A.F. Footfall Excitation of Higher Modes of Vibration in Low-Frequency Building Floors. Ph.D. Thesis, The University of Exeter, Exeter, UK, 2018. [Google Scholar]
- Muhammad, Z.; Reynolds, P. Vibration serviceability of building floors: Performance evaluation of contemporary design guidelines. J. Perform. Constr. Facil. 2018, in press. [Google Scholar]
- Živanović, S.; Pavic, A. Probabilistic modeling of walking excitation for building floors. J. Perform. Constr. Facil. 2009, 23, 132–143. [Google Scholar] [CrossRef]
- Racic, V.; Brownjohn, J.M.W. Stochastic model of near-periodic vertical loads due to humans walking. Adv. Eng. Inform. 2011, 25, 259–275. [Google Scholar] [CrossRef]
- Zivanović, S. Modelling human actions on lightweight structures: Experimental and numerical developments. MATEC Web Conf. 2015, 24, 01005. [Google Scholar] [CrossRef]
- Živanović, S. Probability-Based Estimation of Vibration for Pedestrian Structures Due to Walking. Ph.D. Thesis, The University of Sheffield, Sheffield, UK, 2006. [Google Scholar]
- Hudson, E.J.; Reynolds, P. Implications of structural design on the effectiveness of active vibration control of floor structures. Struct. Control Health Monit. 2014, 21, 685–704. [Google Scholar] [CrossRef]
- Brownjohn, J.; Pavic, A.; Omenzetter, P. A spectral density approach for modelling continuous vertical forces on pedestrian structures due to walking. Can. J. Civ. Eng. 2004, 31, 65–77. [Google Scholar] [CrossRef] [Green Version]
- Middleton, C.J.; Brownjohn, J.M.W. Response of high frequency floors: A literature review. Eng. Struct. 2010, 32, 337–352. [Google Scholar] [CrossRef]
- Pavic, A.; Miskovic, Z.; Živanović, S. Modal properties of beam-and-block pre-cast floors. IES J. Part A Civ. Struct. Eng. 2008, 1, 171–185. [Google Scholar] [CrossRef]
- Willford, M.; Young, P.; Field, C. Improved methodologies for the prediction of footfall-induced vibration. In Proceedings of the SPIE: Buildings for Nanoscale Research and Beyond, San Diego, CA, USA, 31 July–1 August 2005; pp. 1–12. [Google Scholar] [CrossRef]
- Reynolds, P.; Pavic, A. Effects of false floors on vibration serviceability of building floors. II: Response to pedestrian excitation. J. Perform. Constr. Facil. 2003, 17, 87–96. [Google Scholar] [CrossRef]
- Younis, A.; Avci, O.; Hussein, M.; Davis, B.; Reynolds, P. Dynamic forces induced by a single pedestrian: A literature review. Appl. Mech. Rev. 2017, 69, 020802:1–020802:17. [Google Scholar] [CrossRef]
- ISO10137. Bases for Tesing O F Structures—Serviceability of Buildings And Walkways Against Vibrations; ISO: Geneva, Switzerland, 2007. [Google Scholar]
- Eriksson, P.E. Vibration of Low-Frequency Floors–Dynamic Forces and Response Prediction. Ph.D. Thesis, Chalmers University of Technology, Goteborg, Sweden, 1994. [Google Scholar]
- Živanović, S.; Pavic, A.; Racic, V. Towards modelling in-service pedestrian loading of floor structures. In Topics on the Dynamics of Civil Structures, Vol. 1: Proceedings of the 30th IMAC, A Conference and Exhibition on Structural Dynamics, Jacksonville, FL, USA, 30 January–2 February 2012; Springer International Publishing: New York, NY, USA, 2012; pp. 85–94. [Google Scholar]
- Avci, O. Amplitude-dependent damping in vibration serviceability: Case of a laboratory footbridge. J. Archit. Eng. 2016, 22, 1–15. [Google Scholar] [CrossRef]
- Ji, T.; Ellis, B. Floor vibration induced by dance type loads: Theory. Struct. Eng. 1994, 72, 37–44. [Google Scholar] [CrossRef]
- Hamdan, S.; Hoque, M.N.; Sutan, M. Dynamic property analysis and development of composite concrete floor (CCF) and vibration serviceability: A review. Int. J. Phys. Sci. 2011, 6, 7669–7693. [Google Scholar] [CrossRef]
- Middleton, C.J. Dynamic Performance of High Frequency Floors. Ph.D. Thesis, The University of Sheffield, Sheffield, UK, 2009. [Google Scholar]
- Reynolds, P.; Pavic, A. Reliability of assessment criteria for office floor vibrations. In Proceedings of the Experimental Vibration Analysis for Civil Engineering Structures (EVACES), Varenna, Italy, 3–5 October 2011; pp. 317–324. [Google Scholar]
- Reynolds, P.; Pavic, A. Reliability of assessment criteria for building floor vibrations under human excitation. In Proceedings of the 50th U.K. Conference on Human Responses to Vibratio, Southampton, UK, 9–10 September 2015. [Google Scholar]
- Muhammad, Z.; Reynolds, P.; Hudson, E. Evaluation of contemporary guidelines for floor vibration serviceability assessment. In Topics on the Dynamics of Civil Structures, Vol. 2: Proceedings of the 35th IMAC, A Conference and Exposition on Structural Dynamics, 2017; Springer International Publishing: New York, NY, USA, 2017; pp. 339–346. [Google Scholar] [CrossRef]
- Živanović, S.; Pavic, A. Quantification of dynamic excitation potential of pedestrian population crossing footbridges. Shock Vib. 2011, 18, 563–577. [Google Scholar] [CrossRef]
- Costa-Neves, L.; da Silva, J.; de Lima, L.; Jordão, S. Multi-storey, multi-bay buildings with composite steel-deck floors under human-induced loads: The human comfort issue. Comput. Struct. 2014, 136, 34–46. [Google Scholar] [CrossRef]
- Lythgo, N.; Wilson, C.; Galea, M. Basic gait and symmetry measures for primary school-aged children and young adults whilst walking barefoot and with shoes. Gait Posture 2009, 30, 502–506. [Google Scholar] [CrossRef] [PubMed]
- Lythgo, N.; Wilson, C.; Galea, M. Basic gait and symmetry measures for primary school-aged children and young adults. II: Walking at slow, free and fast speed. Gait Posture 2011, 33, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Rainer, J.H.; Pernica, G. Vertical dynamic forces from footsteps. Can. Acoust. 1986, 14, 12–21. [Google Scholar]
- Racic, V.; Pavic, A.; Brownjohn, J.M.W. Experimental identification and analytical modelling of human walking forces: Literature review. J. Sound Vib. 2009, 326, 1–49. [Google Scholar] [CrossRef]
- Dang, H.V.; Živanović, S. Experimental characterisation of walking locomotion on rigid level surfaces using motion capture system. Eng. Struct. 2015, 91, 141–154. [Google Scholar] [CrossRef]
- Ellis, B. On the response of long-span floors to walking loads generated by individuals and crowds. Struct. Eng. 2000, 10, 17–25. [Google Scholar]
- Kerr, S.C.; Bishop, N.W.M. Human induced loading on flexible staircases. Eng. Struct. 2001, 23, 37–45. [Google Scholar] [CrossRef]
- Pachi, A.; Ji, T. Frequency and velocity of people walking. Struct. Eng. 2005, 83, 36–40. [Google Scholar] [CrossRef]
- Chen, J.; Xu, R.; Zhang, M. Acceleration response spectrum for predicting floor vibration due to occupant walking. J. Sound Vib. 2014, 333, 3564–3579. [Google Scholar] [CrossRef]
- Jacobs, N.; Skorecki, J.; Charnley, J. Analysis of the vertical component of force in normal and pathological gait. J. Biomech. 1972, 5, 11–34. [Google Scholar] [CrossRef]
- Caprani, C.C. Application of the pseudo-excitation method to assessment of walking variability on footbridge vibration. Comput. Struct. 2014, 132, 43–54. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V. Structural vibration serviceability: New design framework featuring human-structure interaction. Eng. Struct. 2017, 136, 295–311. [Google Scholar] [CrossRef]
- Živanović, S.; Pavic, A.; Reynolds, P. Probability-based prediction of multi-mode vibration response to walking excitation. Eng. Struct. 2007, 29, 942–954. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F. Simplified procedures for vibration serviceability analysis of footbridges subjected to realistic walking loads. Comput. Struct. 2009, 87, 890–903. [Google Scholar] [CrossRef]
- Waarts, P.H.; Duin, F.V. Assessment procedure for floor vibrations due to walking. Heron J. 2006, 51, 251–264. [Google Scholar]
- Willford, M.R.; Young, P.; Field, C. Predicting footfall-induced vibration: Part 1. Proc. Inst. Civ. Eng. Struct. Build. 2007, 160, 65–72. [Google Scholar] [CrossRef]
- Setareh, M. Office floor vibrations: Evaluation and assessment. Proc. Inst. Civ. Eng. Struct. Build. 2014, 167, 187–199. [Google Scholar] [CrossRef]
- Rainer, J.H.; Pernica, G.; Allen, D.E. Dynamic loading and response of footbridges. Can. J. Civ. Eng. 1988, 15, 66–71. [Google Scholar] [CrossRef] [Green Version]
- Hamming, R.W. Numerical Methods for Scientists and Engineers, 2nd ed.; McGraw Hill: New York, NY, USA, 1973. [Google Scholar]
- Alexander, R.M.; Jayes, A. Fourier analysis of forces exerted in walking and running. J. Biomech. 1980, 13, 383–390. [Google Scholar] [CrossRef]
- Blanchard, J.; Davies, B.L.; Smith, J. Design criteria and analysis for dynamic loading of footbridges. In Proceeding of the Symposium on Dynamic Behaviour of Bridges, Transport and Road Research Laboratory, Crowthorne, Berkshire, UK, 19 May 1977; pp. 1–11. [Google Scholar]
- Murray, T.M.; Allen, G. Floor Vibrations: A New Design Approach; IABSE: Göteborg, Sweden, 1993; pp. 119–124. [Google Scholar] [CrossRef]
- Bachmann, H.; Ammann, W.J.; Deischl, F.; Eisenmann, J.; Floegl, I.; Hirsch, G.H.; Klein, G.K.; Lande, G.J.; Mahrenholtz, O.; Natke, H.G.; et al. Vibration Problems in Structures: Practical Guideline; Report; Birkhäuser Verlag: Zürich, Switzerland, 1995. [Google Scholar] [CrossRef]
- Obata, T.; Miyamori, Y. Identification of a human walking force model based on dynamic monitoring data from pedestrian bridges. Comput. Struct. 2006, 84, 541–548. [Google Scholar] [CrossRef]
- Bachmann, H.; Ammann, W. Vibrations in Structures Induced by Man and Machines, 2nd ed.; International Association for Bridge and Structural Engineering: Zürich, Switzerland, 1987. [Google Scholar]
- Brownjohn, J.; Racic, V.; Chen, J. Universal response spectrum procedure for predicting walking-induced floor vibration. Mech. Syst. Signal Process. 2016, 71, 741–755. [Google Scholar] [CrossRef]
- Krenk, S. Dynamic response to pedestrian loads with statistical frequency distribution. J. Eng. Mech. 2012, 138, 1275–1281. [Google Scholar] [CrossRef]
- Ohlsson, S.V. Floor Vibrations and Human Discomfort. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Sweden, 1982. [Google Scholar]
- Ebrahimpour, A.; Sack, R.L. Modeling dynamic occupant loads. J. Struct. Eng. 1989, 115, 1476–1496. [Google Scholar] [CrossRef]
- Ebrahimpour, A.; Hamam, A.; Sack, R.L.; Patten, W.N. Measuring and modeling dynamic loads imposed by moving crowds. J. Struct. Eng. 1996, 122, 1468–1474. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F. Equivalent spectral model and maximum dynamic response for the serviceability analysis of footbridges. Eng. Struct. 2012, 40, 445–456. [Google Scholar] [CrossRef]
- Pedersen, L.; Frier, C. Sensitivity of footbridge vibrations to stochastic walking parameters. J. Sound Vib. 2010, 329, 2683–2701. [Google Scholar] [CrossRef]
- Bocian, M.; MaCdonald, J.H.G.; Burn, J.F. Biomechanically inspired modeling of pedestrian-induced vertical self-excited forces. J. Bridge Eng. 2013, 18, 1336–1346. [Google Scholar] [CrossRef]
- Hicks, S. Vibration characteristics of steel concrete composite floor systems. Prog. Struct. Eng. Mater. 2004, 6, 21–38. [Google Scholar] [CrossRef]
- Maraveas, C.; Fasoulakis, Z.C.; Tsavdaridis, K.D. A review of human induced vibrations on footbridges. Am. J. Eng. Appl. Sci. 2015, 8, 422–433. [Google Scholar] [CrossRef]
- Mashaly, E.S.; Ebrahim, T.M.; Abou-Elfath, H.; Ebrahim, O.A. Evaluating the vertical vibration response of footbridges using a response spectrum approach. Alex. Eng. J. 2013, 52, 419–424. [Google Scholar] [CrossRef]
- Georgakis, C.; Ingolfsson, E.T. Vertical footbridge vibrations: The response spectrum methodology. In Proceedings of the Third International Conference FOOTBRIDGE 2008: Footbridges for Urban Renewal, Porto, Portugal, 2–4 July 2008; pp. 267–275. [Google Scholar]
- Živanović, S.; Pavic, A.; Ingólfsson, E.T. Modelling spatially unrestricted pedestrian traffic on footbridges. J. Struct. Eng. 2010, 136, 1296–1308. [Google Scholar] [CrossRef]
- Carroll, S.; Owen, J.; Hussein, M. A coupled biomechanical/discrete element crowd model of crowd–bridge dynamic interaction and application to the Clifton Suspension Bridge. Eng. Struct. 2013, 49, 58–75. [Google Scholar] [CrossRef]
- Venuti, F.; Racic, V.; Corbetta, A. Modelling framework for dynamic interaction between multiple pedestrians and vertical vibrations of footbridges. J. Sound Vib. 2016, 379, 245–263. [Google Scholar] [CrossRef]
- Sim, J.; Blakeborough, A.; Williams, M.S.; Parkhouse, G. Statistical model of crowd jumping loads. J. Struct. Eng. 2008, 134, 1852–1861. [Google Scholar] [CrossRef]
- Živanović, S. Benchmark footbridge for vibration serviceability assessment under the vertical component of pedestrian load. J. Struct. Eng. 2012, 138, 1193–1202. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Nishioka, T.; Shiojiri, H.; Matsuzaki, K. Dynamic Design of Footbridges; IABSE: Moscow, Russia, 1978; pp. 1–15. [Google Scholar]
- Nguyen, T.H.; Gad, E.; Wilson, J.; Lythgo, N.; Haritos, N. Evaluation of footfall induced vibration in building floor. In Proceedings of the Australian Earthquake Engineering Society 2011 Conference, Barossa Valley, South Australia, 18–20 November 2011. [Google Scholar]
- Macal, C.; North, M. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Helbing, D.; Molnar, P. Social force model for pedestrian dynamics. Phys. Rev. 1995, 51, 4282–4287. [Google Scholar] [CrossRef]
- Farina, F.; Fontanelli, D.; Garulli, A.; Giannitrapani, A.; Prattichizzo, D. Walking ahead: The headed social force model. PLoS ONE 2017, 12, e0169734. [Google Scholar] [CrossRef]
- Carroll, S.; Owen, J.; Hussein, M. Modelling crowd bridge dynamic interaction with a discretely defined crowd. Sound Vib. 2012, 331, 2685–2709. [Google Scholar] [CrossRef]
- Hicks, S.; Smith, A. Design of floor structures against human-induced vibrations. Steel Constr. 2011, 4, 114–120. [Google Scholar] [CrossRef]
- RFCS. Human Induced Vibrations of Steel Structures (HiVoSS)—Vibration Design of Floors: Guideline; European Comission-RFCS: Brussels, Belgium, 2007. [Google Scholar]
- Feldmann, M.; Heinemeyer, C.; Butz, C.; Caetano, E.; Cunha, A.; Galanti, F.; Goldack, A.; Helcher, O.; Keil, A.; Obiala, R.; et al. Design of Floor Structures for Human Induced Vibrations; Joint Rep EUR 24084 EN; European Commission-JRC: Luxembourg, 2009. [Google Scholar] [CrossRef]
- Sedlacek, G.; Heinemeyer, C.; Butz, C.; Volling, B.; Waarts, P.; Van Duin, F.; Hicks, S.; Devine, P.; Demarco, T. Generalisation of Criteria for Floor Vibrations for Industrial, Office, Residential and Public Building and Gymnastic Halls; Technik Report European 21972 EN; European Commission-JRC: Luxembourg, 2006. [Google Scholar]
- Mohammed, A.; Pavic, A.; Racic, V. Improved model for human induced vibrations of high-frequency floors. Eng. Struct. 2018, 168, 950–966. [Google Scholar] [CrossRef] [Green Version]
- Fahmy, Y.G.M.; Sidky, A.N.M. An experimental investigation of composite floor vibration due to human activities. A case study. Hous. Build. Natl. Res. Cent. J. 2012, 8, 228–238. [Google Scholar] [CrossRef]
- Hassan, O.A.B.; Girhammar, U.A. Assessment of footfall-induced vibrations in timber and lightweight composite floors. Int. J. Struct. Stab. Dyn. 2013, 13, 1–26. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamic of Structures, 3rd ed.; Computers and Structures, Inc.: Berkeley, CA, USA, 2003. [Google Scholar]
- Pavic, A.; Reynolds, P.; Prichard, S.; Lovell, P.A. Evaluation of mathematical models for predicting walking-induced vibrations of high-frequency floors. Int. J. Struct. Stab. Dyn. 2003, 3, 107–130. [Google Scholar] [CrossRef]
- Setareh, M. Vibration serviceability of a building floor structure. II: Vibration evaluation and assessment. J. Perform. Constr. Facil. 2010, 24, 508–518. [Google Scholar] [CrossRef]
- Ellis, B.R. Serviceability evaluation of floor vibration induced by walking loads. Struct. Eng. 2001, 79, 30–36. [Google Scholar] [CrossRef]
- Ellis, B. The influence of crowd size on floor vibrations induced by walking. Struct. Eng. 2003, 81, 20–27. [Google Scholar] [CrossRef]
- Willford, M.R.; Young, P.; Field, C. Predicting footfall-induced vibration: Part 2. Proc. Inst. Civ. Eng. Struct. Build. 2007, 160, 73–79. [Google Scholar] [CrossRef]
- Setareh, M. Vibration serviceability issues of slender footbridges. J. Bridge Eng. 2016, 21, 1–12. [Google Scholar] [CrossRef]
- BSI. Guide to Evaluation of Human Exposure to Vibration in Buildings. Part 1: Vibration Sources Other Than Blasting (BS6472-1); BSI: London, UK, 2008. [Google Scholar]
- Pedersen, L. Dynamic model of a structure carrying stationary humans and assessment of its response to walking excitation. In Topics on the Dynamics of Civil Structures: Proceedings of the IMAC-XXIV, A Conference and Exposition on Structural Dynamics, 2007; Springer International Publishing: New York, NY, USA, 2007. [Google Scholar]
- Devin, A.; Fanning, P.J.; Pavic, A. Nonstructural partitions and floor vibration serviceability. J. Archit. Eng. 2016, 22, 1–9. [Google Scholar] [CrossRef]
- Oasys. GSA v9.0 Structural Design & Analysis Software; Oasys Software: London, UK, 2018. [Google Scholar]
- Autodesk. Autodesk Robot Structural Analysis Professional; Autodesk: San Rafael, CA, USA, 2018. [Google Scholar]
- CSI. SAP2000 v20 Integrated Finite Element Analysis and Design of Structures; Computers and Structures Inc.: Berkely, CA, USA, 2018. [Google Scholar]
- CSI. ETABS v17 Integrated Analysis, Design and Drafting of Building Systems; Computers and Structures Inc.: Berkely, CA, USA, 2018. [Google Scholar]
- Živanović, S.; Racic, V.; El Bahnasy, I.; Pavic, A. Statistical characterisation of parameters defining human walking as observed on an indoor passerelle. In Proceedings of the Experimental Vibration Analysis for Civil Engineering Structures (EVACES), Porto, Portugal, 24–26 October 2007; pp. 219–225. [Google Scholar]
- Racic, V.; Pavic, A.; Brownjohn, J.M.W. Modern facilities for experimental measurement of dynamic loads induced by humans: A literature review. Shock Vib. 2013, 20, 53–67. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Lombaert, G.; Jonkers, I.; De Roeck, G.; Van Den Broeck, P. Characterisation of walking loads by 3D inertial motion tracking. J. Sound Vib. 2014, 333, 5212–5226. [Google Scholar] [CrossRef]
- Keogh, J.; Duignan, R.; Caprani, C. Characteristics of pedestrian crowd flow demand for vibration serviceability of footbridges. In Bridge Maintenance, Safety, Management and Life Extension; CRC Press: Boca Raton, FL, USA, 2014; pp. 370–377. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, L.; Racic, V.; Brownjohn, J. Measuring human-induced vibrations of civil engineering structures via vision-based motion tracking. Measurement 2016, 83, 44–56. [Google Scholar] [CrossRef] [Green Version]
- Fujino, Y.; Pacheco, B.M.; Nakamura, S.; Warnitchai, P. Synchronization of human walking observed during lateral vibration of a congested pedestrian bridge. Earthq. Eng. Struct. Dyn. 1993, 22, 741–758. [Google Scholar] [CrossRef]
- Kretz, T.; Grünebohm, A.; Kaufman, M.; Mazur, F.; Schreckenberg, M. Experimental study of pedestrian counterflow in a corridor. J. Stat. Mech. Theory Exp. 2006, 2006, P10001. [Google Scholar] [CrossRef]
- Corbetta, A.; Bruno, L.; Muntean, A.; Toschi, F. High statistics measurements of pedestrian dynamics. In Proceedings of the Conference on Pedestrian and Evacuation Dynamics 2014 (PED2014), Transportation Research Procedia, Delft, The Netherlands, 22–24 October 2014; pp. 96–104. [Google Scholar]
- Brandle, N.; Bauer, D.; Seer, S. Track-based finding of stopping pedestrians—A practical approach for analyzing a public infrastructure. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Transportation Research Procedia, Toronto, ON, Canada, 17–20 September 2006; pp. 115–120. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhammad, Z.; Reynolds, P.; Avci, O.; Hussein, M. Review of Pedestrian Load Models for Vibration Serviceability Assessment of Floor Structures. Vibration 2019, 2, 1-24. https://doi.org/10.3390/vibration2010001
Muhammad Z, Reynolds P, Avci O, Hussein M. Review of Pedestrian Load Models for Vibration Serviceability Assessment of Floor Structures. Vibration. 2019; 2(1):1-24. https://doi.org/10.3390/vibration2010001
Chicago/Turabian StyleMuhammad, Zandy, Paul Reynolds, Onur Avci, and Mohammed Hussein. 2019. "Review of Pedestrian Load Models for Vibration Serviceability Assessment of Floor Structures" Vibration 2, no. 1: 1-24. https://doi.org/10.3390/vibration2010001
APA StyleMuhammad, Z., Reynolds, P., Avci, O., & Hussein, M. (2019). Review of Pedestrian Load Models for Vibration Serviceability Assessment of Floor Structures. Vibration, 2(1), 1-24. https://doi.org/10.3390/vibration2010001




