Model Validation of a Porous Piezoelectric Energy Harvester Using Vibration Test Data
Abstract
:1. Introduction
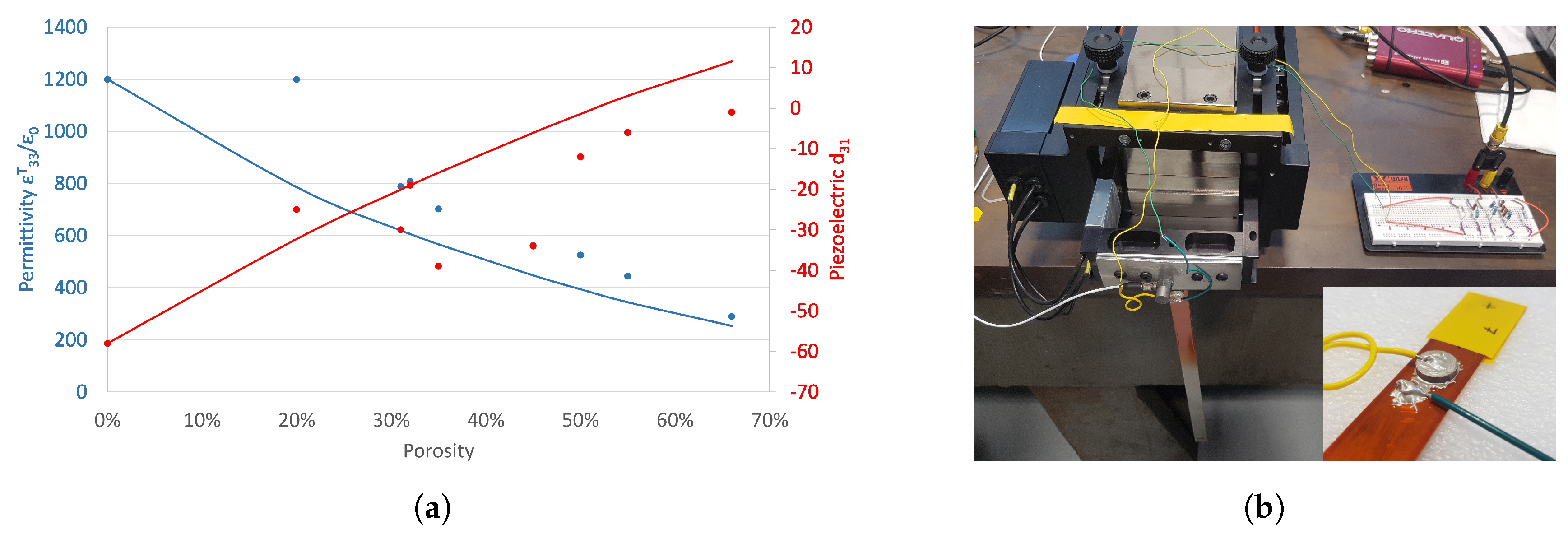
2. Manufacture Of Porous Material
3. Theoretical Homogenisation
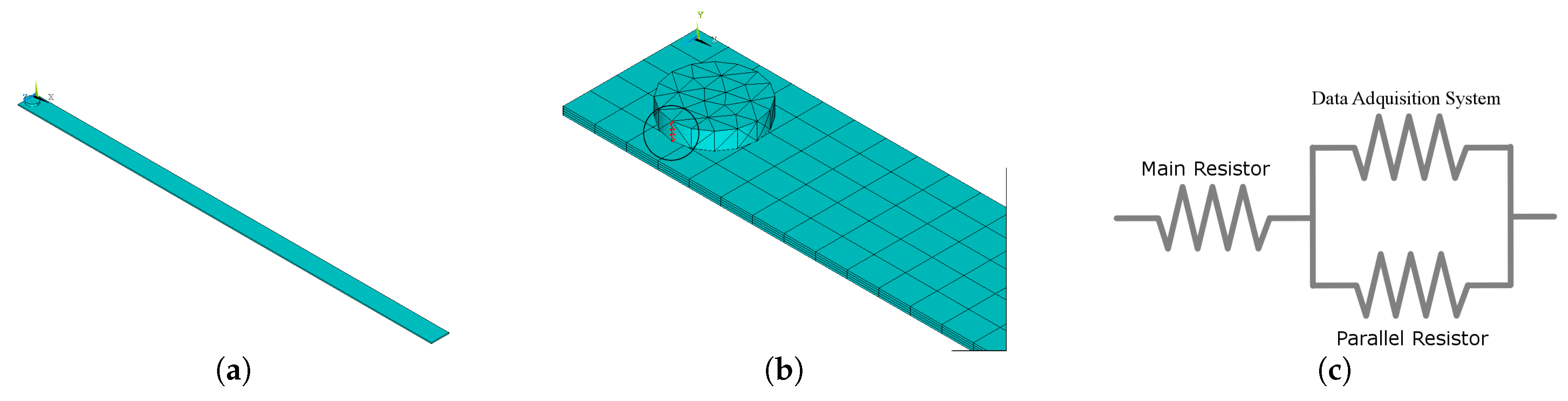
4. Numerical Model
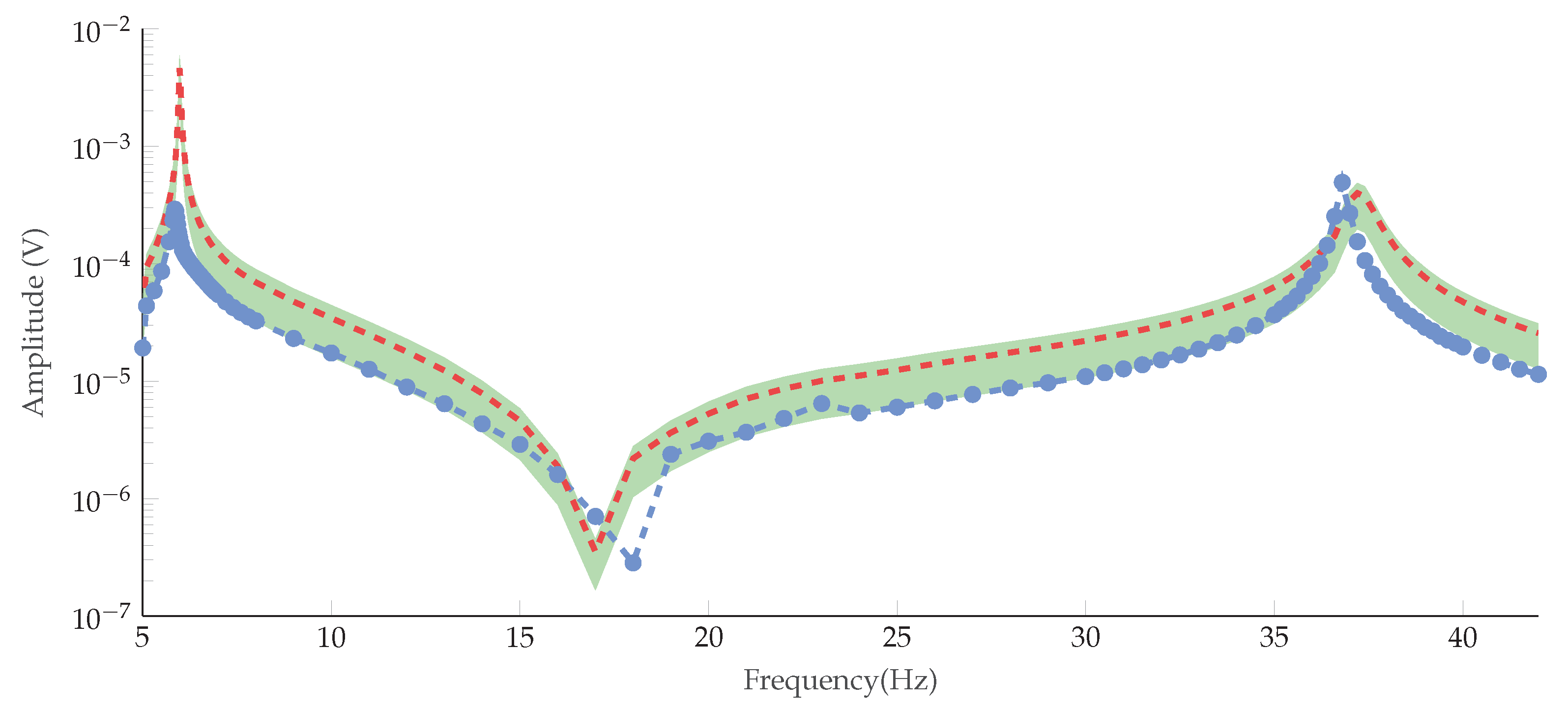
5. Experimental Validation
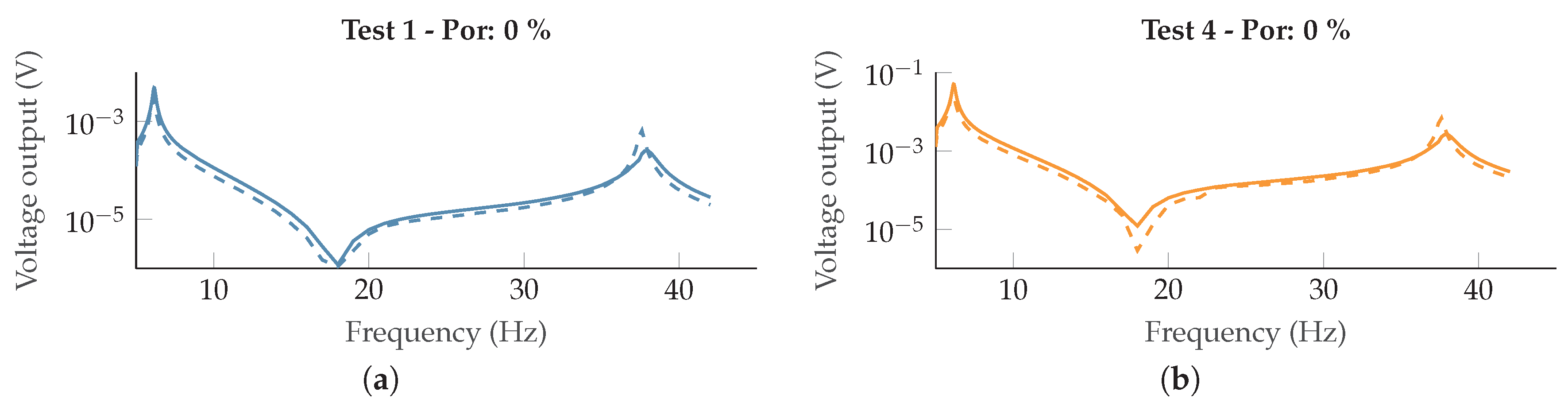
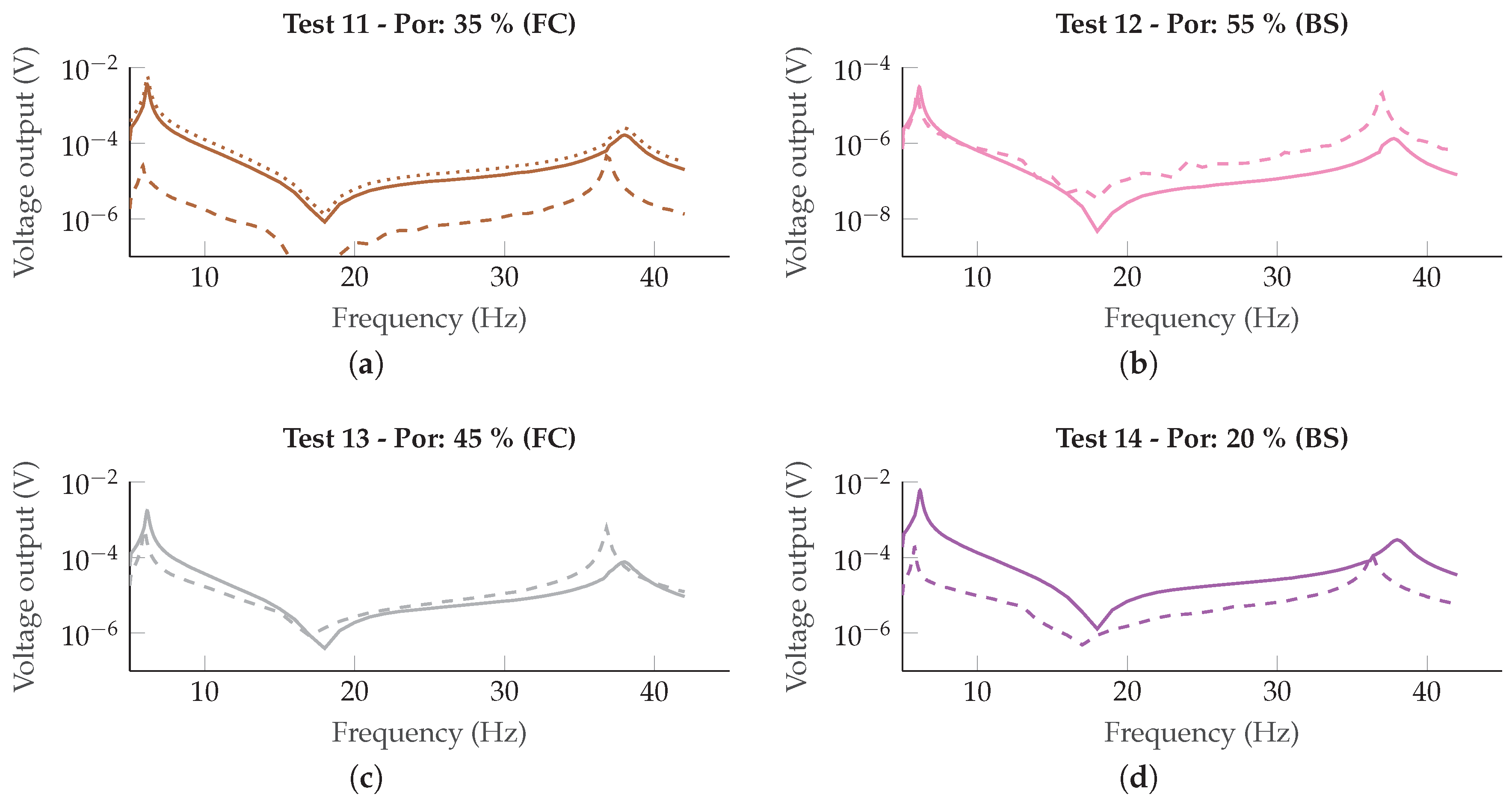
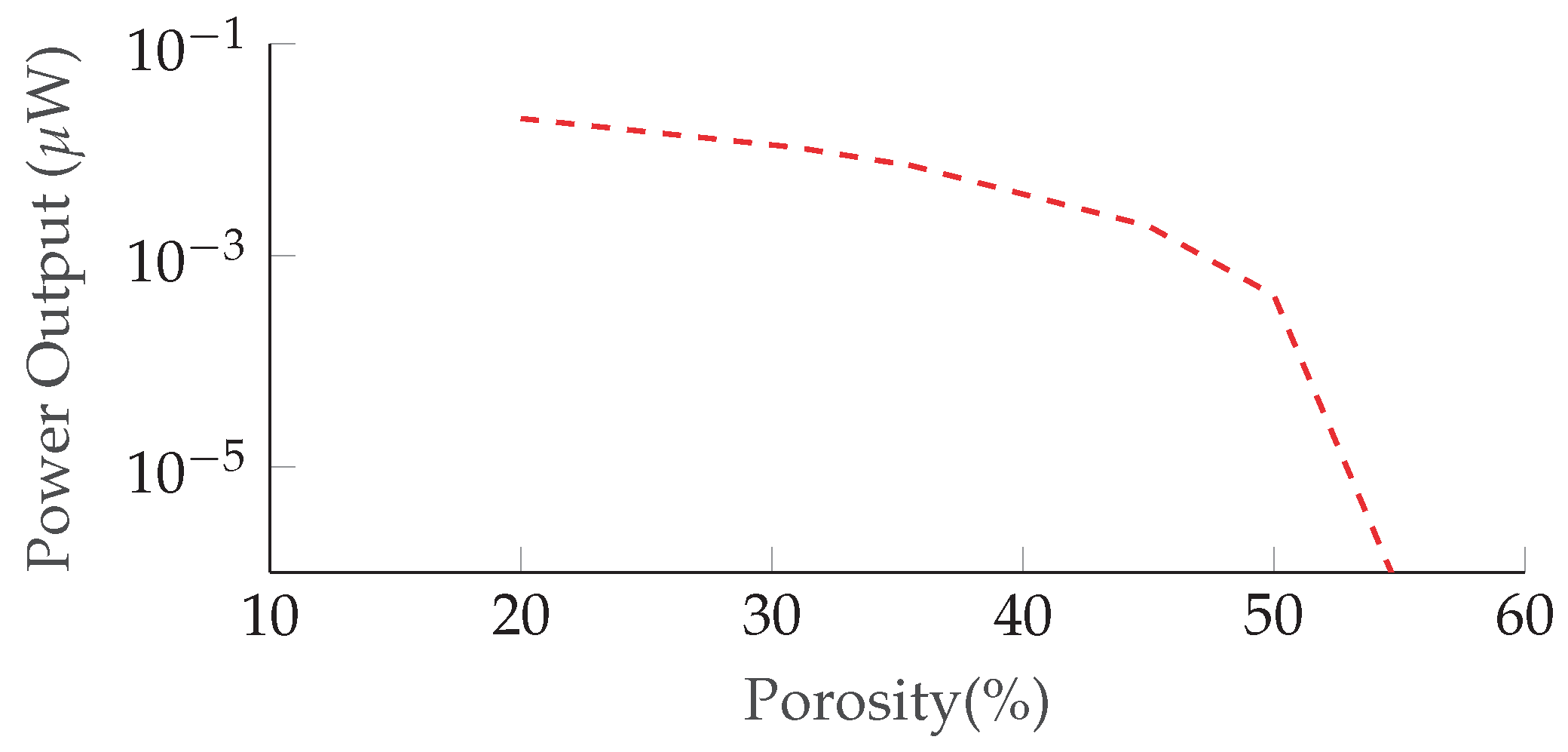
6. Experimental Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kelly, A. Why engineer porous materials? Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 364, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Miyoshi, T.; Itoh, M.; Akiyama, S.; Kitahara, A. ALPORAS aluminum foam: Production process, properties, and applications. Adv. Eng. Mater. 2000, 2, 179–183. [Google Scholar] [CrossRef]
- Bobyn, J.; Pilliar, R.; Cameron, H.; Weatherly, G. The optimum pore size for the fixation of porous-surfaced metal implants by the ingrowth of bone. Clin. Orthop. Relat. Res. 1980, 150, 263–270. [Google Scholar] [CrossRef]
- Göransson, P. Tailored acoustic and vibrational damping in porous solids–Engineering performance in aerospace applications. Aerosp. Sci. Technol. 2008, 12, 26–41. [Google Scholar] [CrossRef]
- Canham, L.T. Silicon quantum wire array fabrication by electrochemical and chemical dissolution of wafers. Appl. Phys. Lett. 1990, 57, 1046–1048. [Google Scholar] [CrossRef]
- She, J.; Yang, J.; Ohji, T. Thermal shock resistance of porous silicon nitride ceramics. J. Mater. Sci. Lett. 2003, 22, 331–333. [Google Scholar] [CrossRef]
- White, R.J.; Luque, R.; Budarin, V.L.; Clark, J.H.; Macquarrie, D.J. Supported metal nanoparticles on porous materials. Methods and applications. Chem. Soc. Rev. 2009, 38, 481–494. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.S.; Whang, D.; Lee, H.; Im Jun, S.; Oh, J.; Jeon, Y.J.; Kim, K. A homochiral metal–organic porous material for enantioselective separation and catalysis. Nature 2000, 404, 982–986. [Google Scholar] [CrossRef] [PubMed]
- Staszewski, W.; Boller, C.; Tomlinson, G.R. Health Monitoring of Aerospace Structures: Smart Sensor Technologies and Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Sodano, H.A.; Inman, D.J.; Park, G. A review of power harvesting from vibration using piezoelectric materials. Vib. Dig. 2004, 36, 197–206. [Google Scholar] [CrossRef]
- Jin, L.; Ma, S.; Deng, W.; Yan, C.; Yang, T.; Chu, X.; Tian, G.; Xiong, D.; Lu, J.; Yang, W. Polarization-Free High-Crystallization β-PVDF Piezoelectric Nanogenerator Toward Self-Powered 3D Acceleration Sensor. Nano Energy 2018, 50, 632–638. [Google Scholar] [CrossRef]
- Jaffe, B. Piezoelectric Ceramics; Elsevier: New York, NY, USA, 2012; Volume 3. [Google Scholar]
- Friswell, M.I.; Ali, S.F.; Bilgen, O.; Adhikari, S.; Lees, A.W.; Litak, G. Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I.; Inman, D.J. Piezoelectric energy harvesting from broadband random vibrations. Smart Mater. Struct. 2009, 18, 115005. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Madinei, H.; Khodaparast, H.H.; Adhikari, S.; Friswell, M.; Fazeli, M. Adaptive tuned piezoelectric MEMS vibration energy harvester using an electrostatic device. Eur. Phys. J. Spec. Top. 2015, 224, 2703–2717. [Google Scholar] [CrossRef]
- Neiss, S.; Goldschmidtboeing, F.; Kroener, M.; Woias, P. Piezoelectric Materials for Nonlinear Energy Harvesting Generators. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2013; Volume 476, p. 012035. [Google Scholar]
- Cammarano, A.; Neild, S.; Burrow, S.; Wagg, D.; Inman, D. Optimum resistive loads for vibration-based electromagnetic energy harvesters with a stiffening nonlinearity. J. Intell. Mater. Syst. Struct. 2014, 25, 1757–1770. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Chen, W.; Malakooti, M.H.; Cao, J.; Inman, D.J. Design and modeling of a flexible longitudinal zigzag structure for enhanced vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2017, 28, 367–380. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Electromechanical modeling and nonlinear analysis of axially loaded energy harvesters. J. Vib. Acoust. 2011, 133, 011007. [Google Scholar] [CrossRef]
- Fukui, Y.; Kakimoto, K.; Yamagiwa, K.; Mitsuoka, T.; Ohbayashi, K. Effect of Pore Shape on the Electrical Property of Porous LNKN Piezoceramics. Ferroelectrics 2008, 367, 133–138. [Google Scholar] [CrossRef]
- Bowen, C.R.; Perry, A.; Lewis, A.C.F.; Kara, H. Processing and properties of porous piezoelectric materials with high hydrostatic figures of merit. J. Eur. Ceram. Soc. 2004, 24, 541–545. [Google Scholar] [CrossRef]
- Roscow, J.I.; Taylor, J.; Bowen, C.R. Manufacture and characterization of porous ferroelectrics for piezoelectric energy harvesting applications. Ferroelectrics 2016, 498, 40–46. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Featherston, C.A. Energy harvesting using porous piezoelectric beam with impacts. Procedia Eng. 2017, 199, 3468–3473. [Google Scholar] [CrossRef]
- Roscow, J.I.; Topolov, V.Y.; Bowen, C.R.; Taylor, J.; Panich, A.E. Understanding the peculiarities of the piezoelectric effect in macro-porous BaTiO3. Sci. Technol. Adv. Mater. 2016, 17, 769–776. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, L.; Zeng, J.; Zhou, K.; Zhang, D. Aligned porous barium titanate/hydroxyapatite composites with high piezoelectric coefficients for bone tissue engineering. Mater. Sci. Eng. C 2014, 39, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Bao, Y.; Zhang, D.; Bowen, C.R. Porous PZT ceramics with aligned pore channels for energy harvesting applications. J. Am. Ceram. Soc. 2015, 98, 2980–2983. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Pierard, O.; Friebel, C.; Doghri, I. Mean-field homogenization of multi-phase thermo-elastic composites: A general framework and its validation. Compos. Sci. Technol. 2004, 64, 1587–1603. [Google Scholar] [CrossRef]
- Wu, T.T. The effect of inclusion shape on the elastic moduli of a two-phase material. Int. J. Solids Struct. 1966, 2, 1–8. [Google Scholar] [CrossRef]
- Dunn, M.L.; Taya, M. Electromechanical properties of porous piezoelectric ceramics. J. Am. Ceram. Soc. 1993, 76, 1697–1706. [Google Scholar] [CrossRef]
- Martinez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Featherston, C.A. Porous piezoelectric materials for energy harvesting. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 19–21 September 2016. [Google Scholar]
- Mikata, Y. Determination of piezoelectric Eshelby tensor in transversely isotropic piezoelectric solids. Int. J. Eng. Sci. 2000, 38, 605–641. [Google Scholar] [CrossRef]
- Martinez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Berger, H. Homogenization of porous piezoelectric materials. Int. J. Solids Struct. 2017, 113, 218–229. [Google Scholar] [CrossRef]
- Iyer, S.; Venkatesh, T. Electromechanical response of (3-0) porous piezoelectric materials: Effects of porosity shape. J. Appl. Phys. 2011, 110, 034109. [Google Scholar] [CrossRef]
- Roscow, J.; Zhang, Y.; Taylor, J.; Bowen, C. Porous ferroelectrics for energy harvesting applications. Eur. Phys. J. Spec. Top. 2015, 224, 2949–2966. [Google Scholar] [CrossRef] [Green Version]
- Dunn, M.L.; Taya, M. An analysis of piezoelectric composite materials containing ellipsoidal inhomogeneities. Proc. R. Soc. Lond. A 1993, 443, 265–287. [Google Scholar] [CrossRef]
- Kar-Gupta, R.; Venkatesh, T. Electromechanical response of porous piezoelectric materials: Effects of porosity distribution. Appl. Phys. Lett. 2007, 91, 062904. [Google Scholar] [CrossRef]
- Roscow, J.; Lewis, R.; Taylor, J.; Bowen, C. Modelling and fabrication of porous sandwich layer barium titanate with improved piezoelectric energy harvesting figures of merit. Acta Mater. 2017, 128, 207–217. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xie, M.; Roscow, J.; Bao, Y.; Zhou, K.; Zhang, D.; Bowen, C.R. Enhanced pyroelectric and piezoelectric properties of PZT with aligned porosity for energy harvesting applications. J. Mater. Chem. A 2017, 5, 6569–6580. [Google Scholar] [CrossRef] [PubMed] [Green Version]



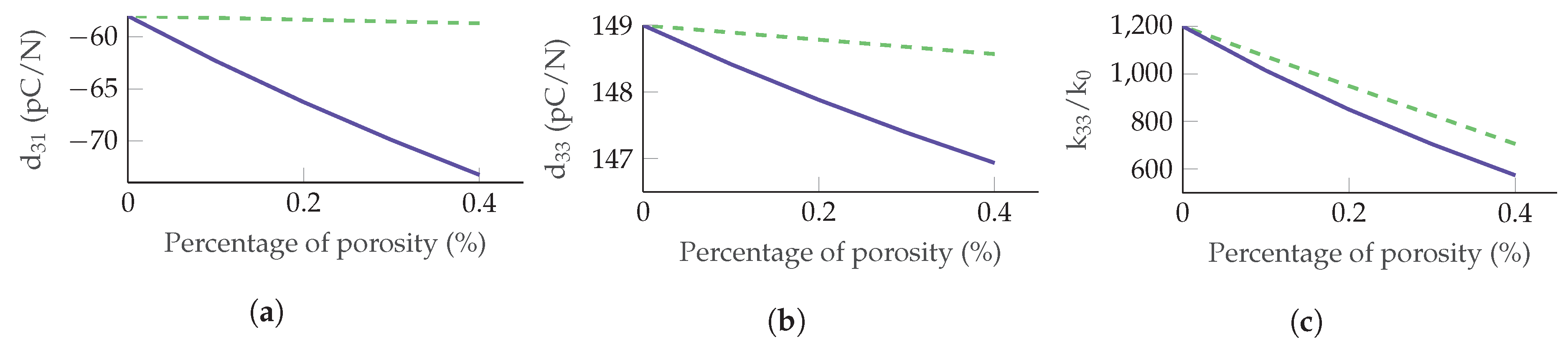
| PZT-5A | Aluminium | |||
|---|---|---|---|---|
| Density () | 7750 | Density () | 2700 | |
| () | 17.2 | Young’s Modulus (GPa) | 70 | |
| () | 16.7 | Poisson’s Ratio | 0.3 | |
| () | 409 | |||
| () | 176 | Beam Dimensions | ||
| 1800 | Length × Width × Thickness (mm) | 375 × 16 × 1 | ||
| Sample Number | Porosity (%) | Thickness (mm) | Diameter (mm) | Fabrication Method | Piezoelectric Coeff. () | Relative Permittivity |
|---|---|---|---|---|---|---|
| 1 | 66 | 2.07 | 11.137 | BURPS | −10 | 290 |
| 2 | 55 | 2.00 | 11.240 | BURPS | −60 | 445 |
| 3 | 50 | 1.86 | 11.273 | BURPS | −120 | 526 |
| 4 | 32 | 1.50 | 11.247 | BURPS | −190 | 808 |
| 5 | 20 | 1.27 | 11.260 | BURPS | −250 | 1199 |
| 6 | 45 | 1.78 | 9.940 | Freeze cast | −340 | 563 |
| 7 | 35 | 2.06 | 10.230 | Freeze cast | −390 | 702 |
| 8 | 31 | 1.70 | 10.640 | Freeze cast | −300 | 788 |
| Test Number | Sample Number | Method Fabrication | Porosity | Main Resistor in Series | Resistor in Parallel |
|---|---|---|---|---|---|
| 1 | #Ref | - | 0.0% | 10.042 M | 0.9951 k |
| 2 | #Ref | - | 0.0% | 14.677 M | 0.9951 k |
| 3 | #Ref | - | 0.0% | 14.677 M | 9.987 k |
| 4 | #Ref | - | 0.0% | 10.042 M | 9.987 k |
| 5 | #Ref | - | 0.0% | 10.042 M | 9.987 k |
| 6 | 7 | Free-casting | 35.0% | 10.042 M | 9.987 k |
| 7 | 8 | Free-casting | 31.0% | 10.042 M | 9.987 k |
| 8 | 3 | BURPS | 50.0% | 10.042 M | 9.987 k |
| 9 | 1 | BURPS | 66.0% | 10.042 M | 9.987 k |
| 10 | 2 | BURPS | 55.0% | 10.042 M | 9.987 k |
| 11 | 7 | Free-Casting | 35.0% | 10.042 M | 9.987 k |
| 12 | 2 | BURPS | 55.0% | 10.042 M | 0.9951 k |
| 13 | 6 | Free-Casting | 45.0% | 10.042 M | 9.987 k |
| 14 | 5 | BURPS | 20.0% | 10.042 M | 9.987 k |
| (pC/m) | (pC/m) | |||
|---|---|---|---|---|
| Percentage | Mean | S.D. | Mean | S.D. |
| 30 | 50.74 | 5.67 | −0.69 | 0.45 |
| 40 | 76.54 | 9.83 | −4.86 | 1.20 |
| 50 | 90.48 | 5.65 | −11.37 | 1.81 |
| 60 | 97.08 | 7.23 | −17.65 | 1.52 |
| 70 | 99.01 | 4.85 | −19.40 | 1.39 |
| 80 | 91.90 | 5.36 | −22.56 | 0.48 |
| 90 | 100.35 | 9.09 | −30.30 | 11.12 |
| Nominal | 149 | −59 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Ayuso, G.; Haddad Khodaparast, H.; Zhang, Y.; Bowen, C.R.; Friswell, M.I.; Shaw, A.D.; Madinei, H. Model Validation of a Porous Piezoelectric Energy Harvester Using Vibration Test Data. Vibration 2018, 1, 123-137. https://doi.org/10.3390/vibration1010010
Martínez-Ayuso G, Haddad Khodaparast H, Zhang Y, Bowen CR, Friswell MI, Shaw AD, Madinei H. Model Validation of a Porous Piezoelectric Energy Harvester Using Vibration Test Data. Vibration. 2018; 1(1):123-137. https://doi.org/10.3390/vibration1010010
Chicago/Turabian StyleMartínez-Ayuso, Germán, Hamed Haddad Khodaparast, Yan Zhang, Christopher R. Bowen, Michael I. Friswell, Alexander D. Shaw, and Hadi Madinei. 2018. "Model Validation of a Porous Piezoelectric Energy Harvester Using Vibration Test Data" Vibration 1, no. 1: 123-137. https://doi.org/10.3390/vibration1010010
APA StyleMartínez-Ayuso, G., Haddad Khodaparast, H., Zhang, Y., Bowen, C. R., Friswell, M. I., Shaw, A. D., & Madinei, H. (2018). Model Validation of a Porous Piezoelectric Energy Harvester Using Vibration Test Data. Vibration, 1(1), 123-137. https://doi.org/10.3390/vibration1010010








