Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation
Abstract
1. Introduction
2. Virtual Impulse Response Function
3. Regularized ARMA Time Series Model
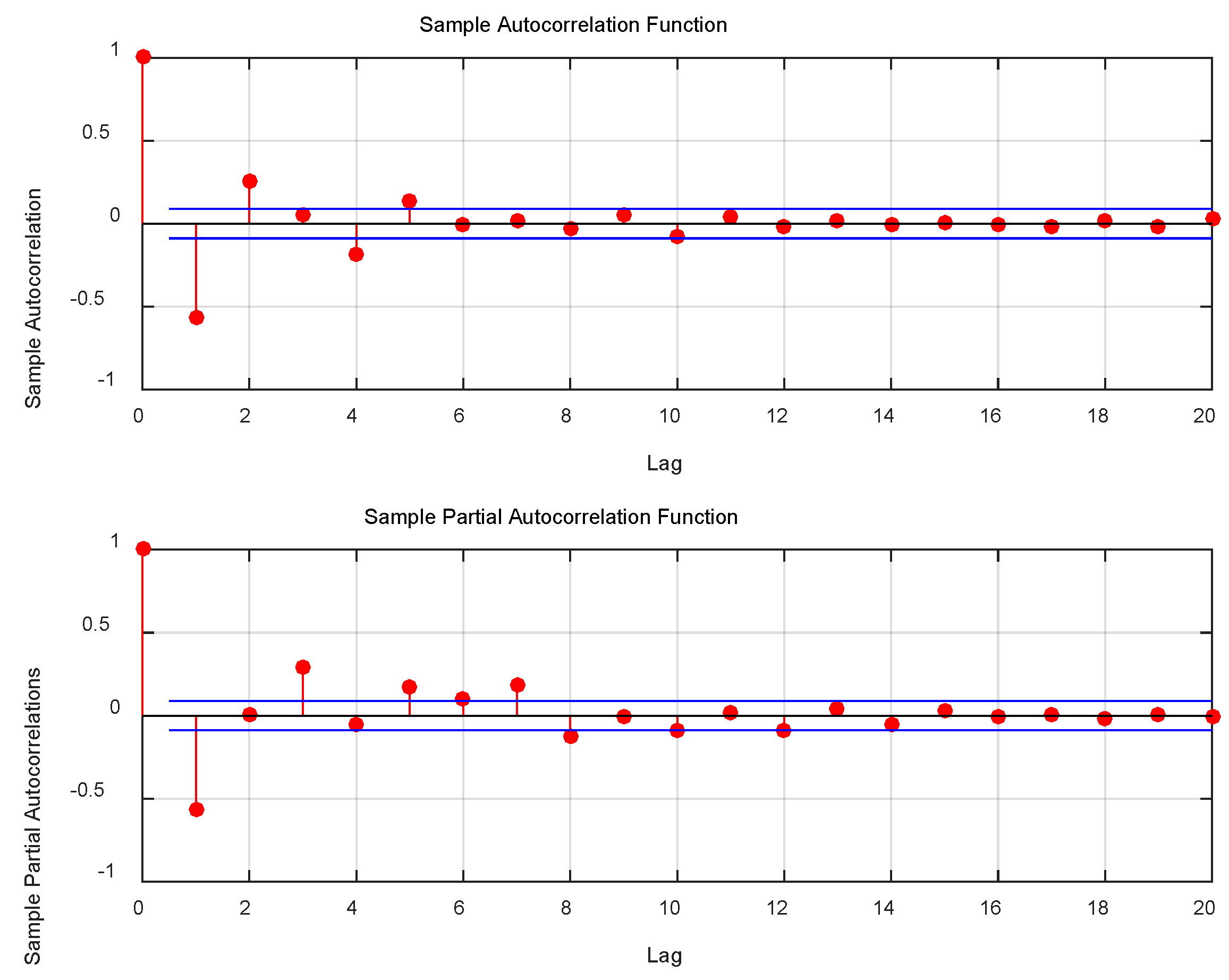
3.1. Introduction of ARMA Time Series Model
3.2. Regularization of ARMA Time Series
3.3. Derivation of Regularized ARMA Time Series
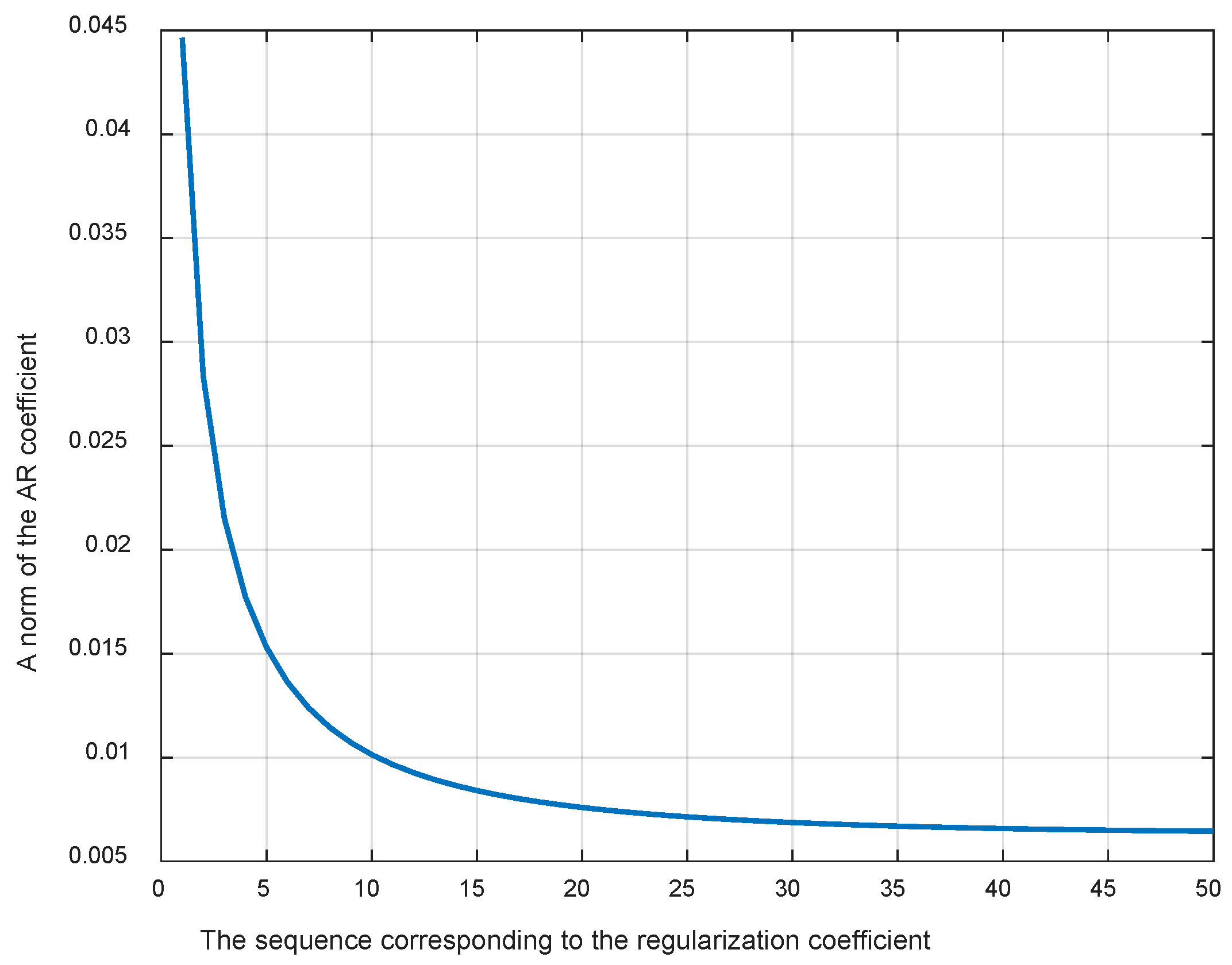
3.4. The Selection of Regularization Coefficient α
3.5. Regularized ARMA Time Series Modeling
- Determine the sample Auto Correlation Function (ACF) and Partial Auto Correlation Function (PACF) of the signal to be simulated.
- Choose the appropriate model based on the sample autocorrelation coefficient and partial autocorrelation coefficient properties.
- Determine the model order using AIC or other criteria.
- Validate the model. If the geometric model does not pass the test, go to Step 2, reselect the model, and fit again.
- Optimize the model. If the fitted model passes the test, then it still moves to Step 3, taking full consideration of the possibilities, creating a number of quasi-models, and selecting the optimal model from all the tested fitted models.
- Calculate regularization coefficients and regularization time series models based on optimal model parametric.
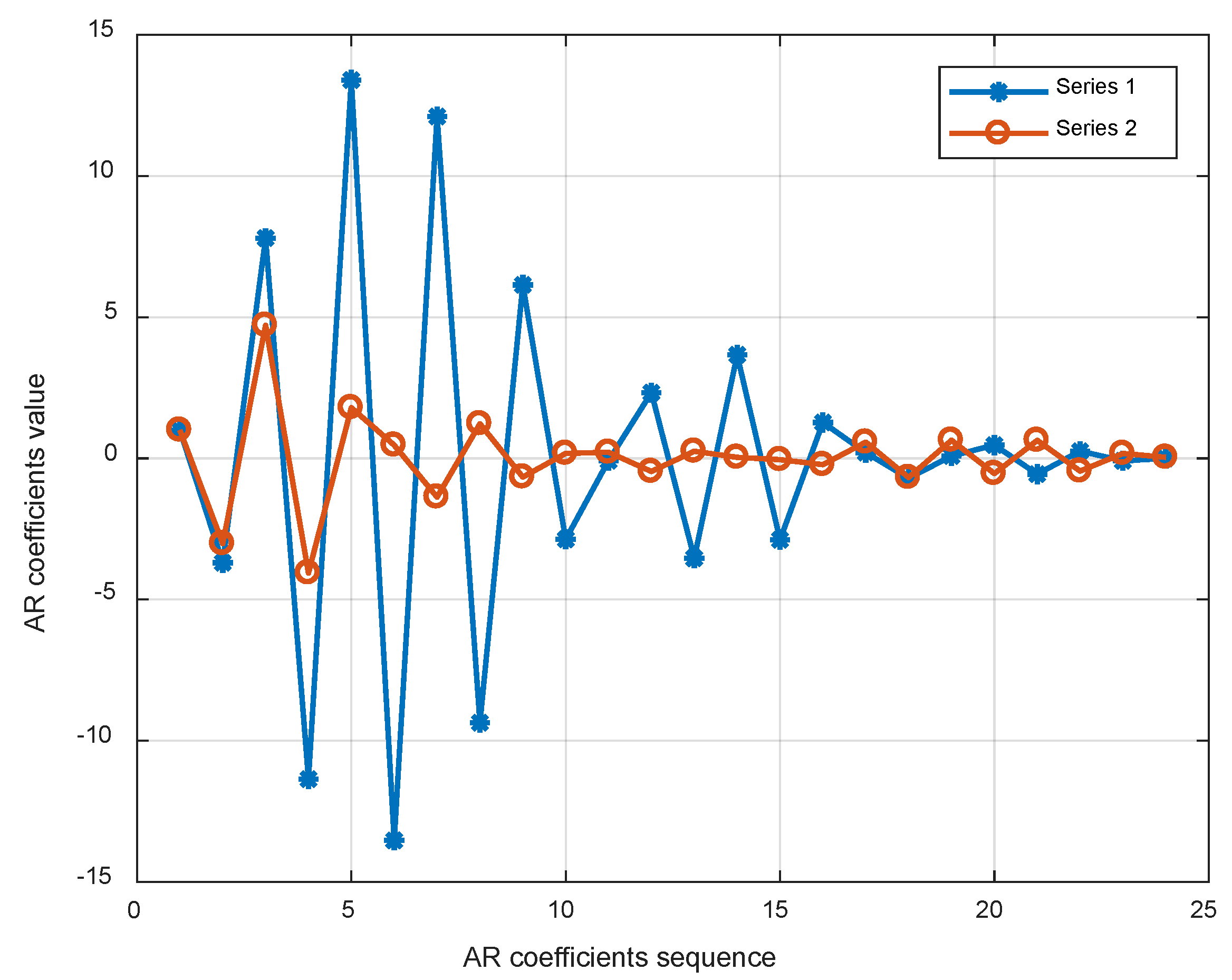
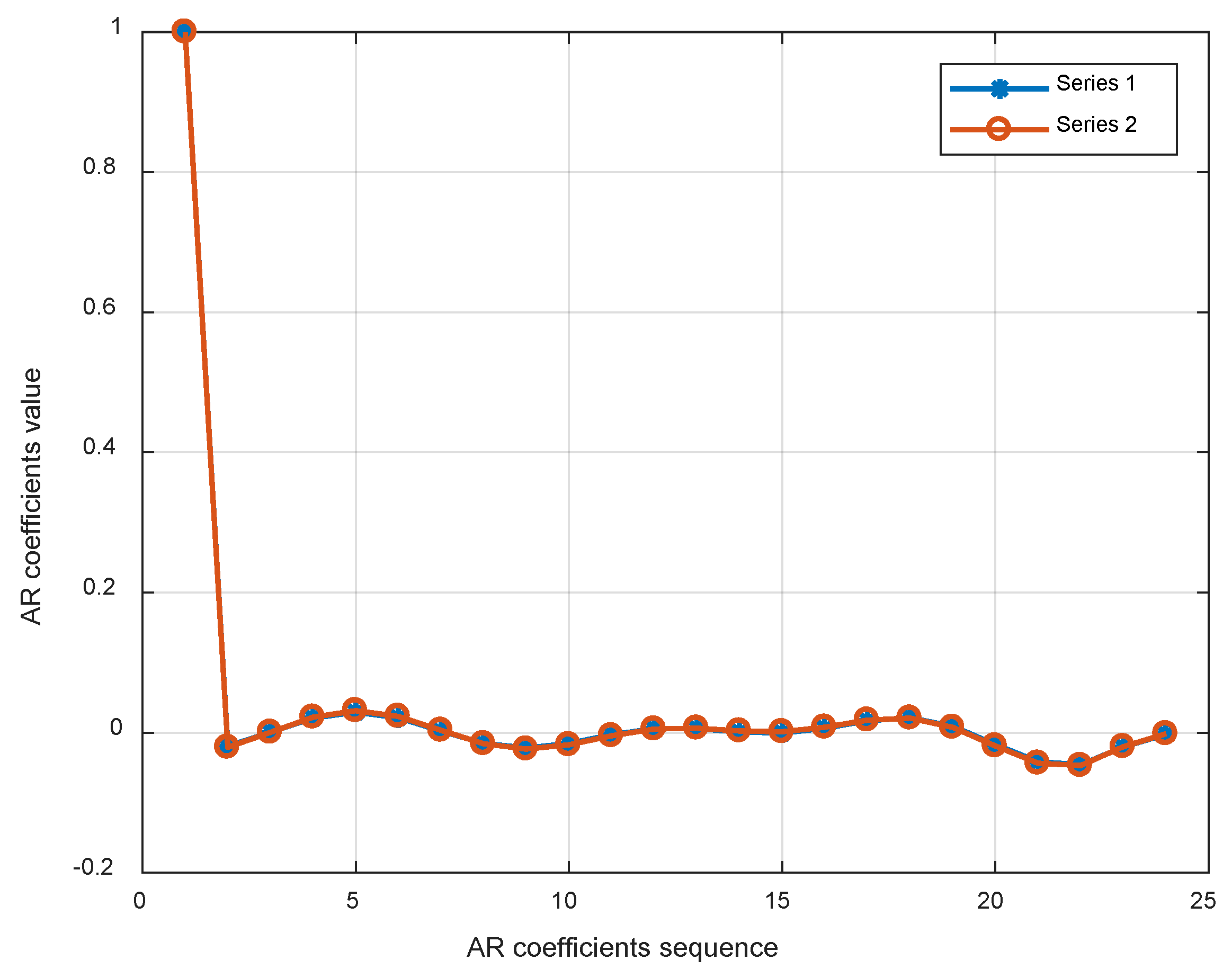
- Extract the AR coefficients as feature vectors from the regularized time-series fitting optimal model.
4. Damage Identification Procedure
- For a structured health monitoring system in which the sensors have been placed, the virtual impulse response function is obtained by comparing a large vibration response with another response where the damage may occur.
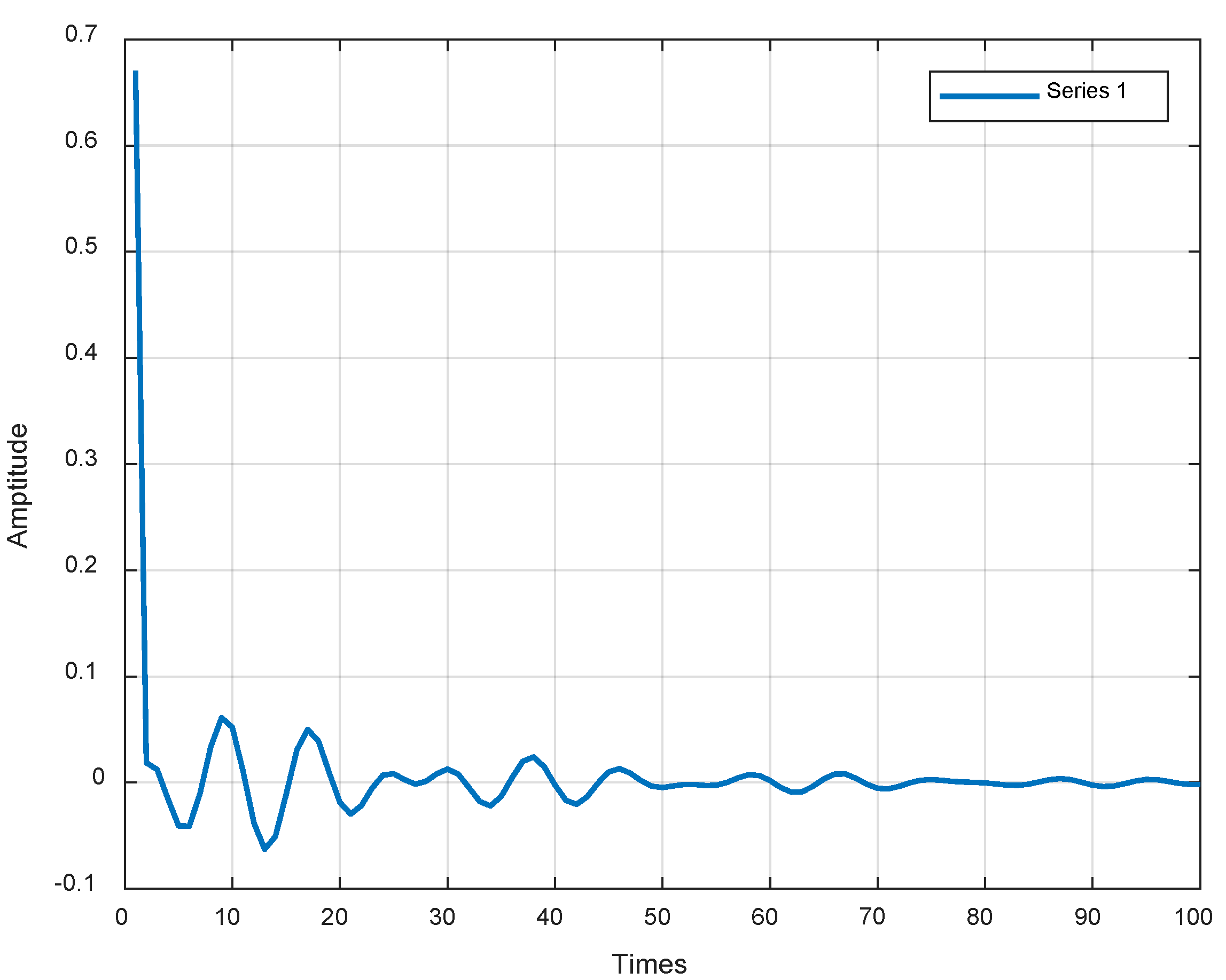
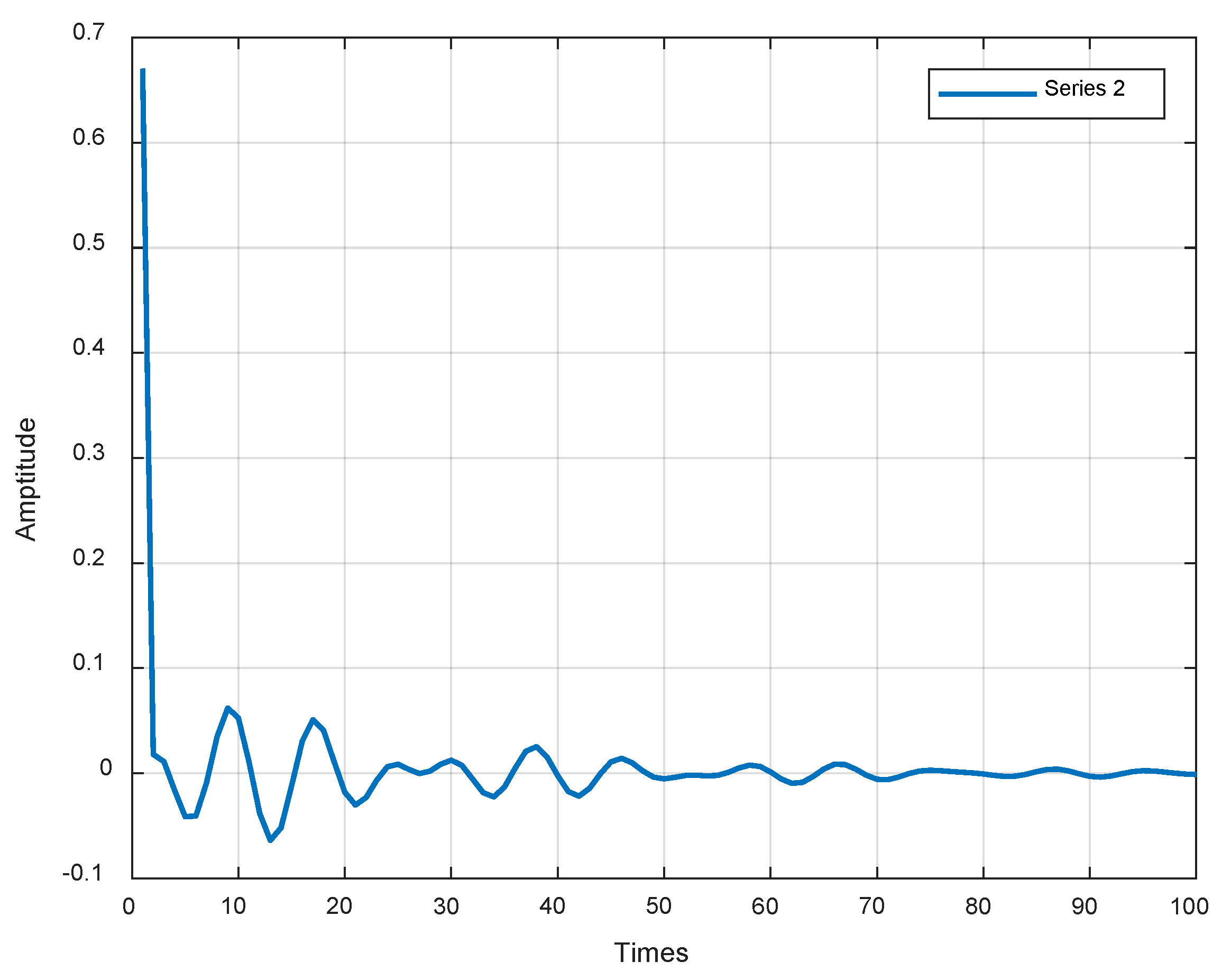
- Use the regularized ARMA time series model to fit the obtained virtual impulse response and extract the AR coefficient of the best-fit model as the damage feature vector.
- Compare the AR coefficient extracted from the undamaged working condition and damage condition and calculate the damage index.
5. Numerical Simulation
5.1. Three-Degrees-of-Freedom Chain Structure
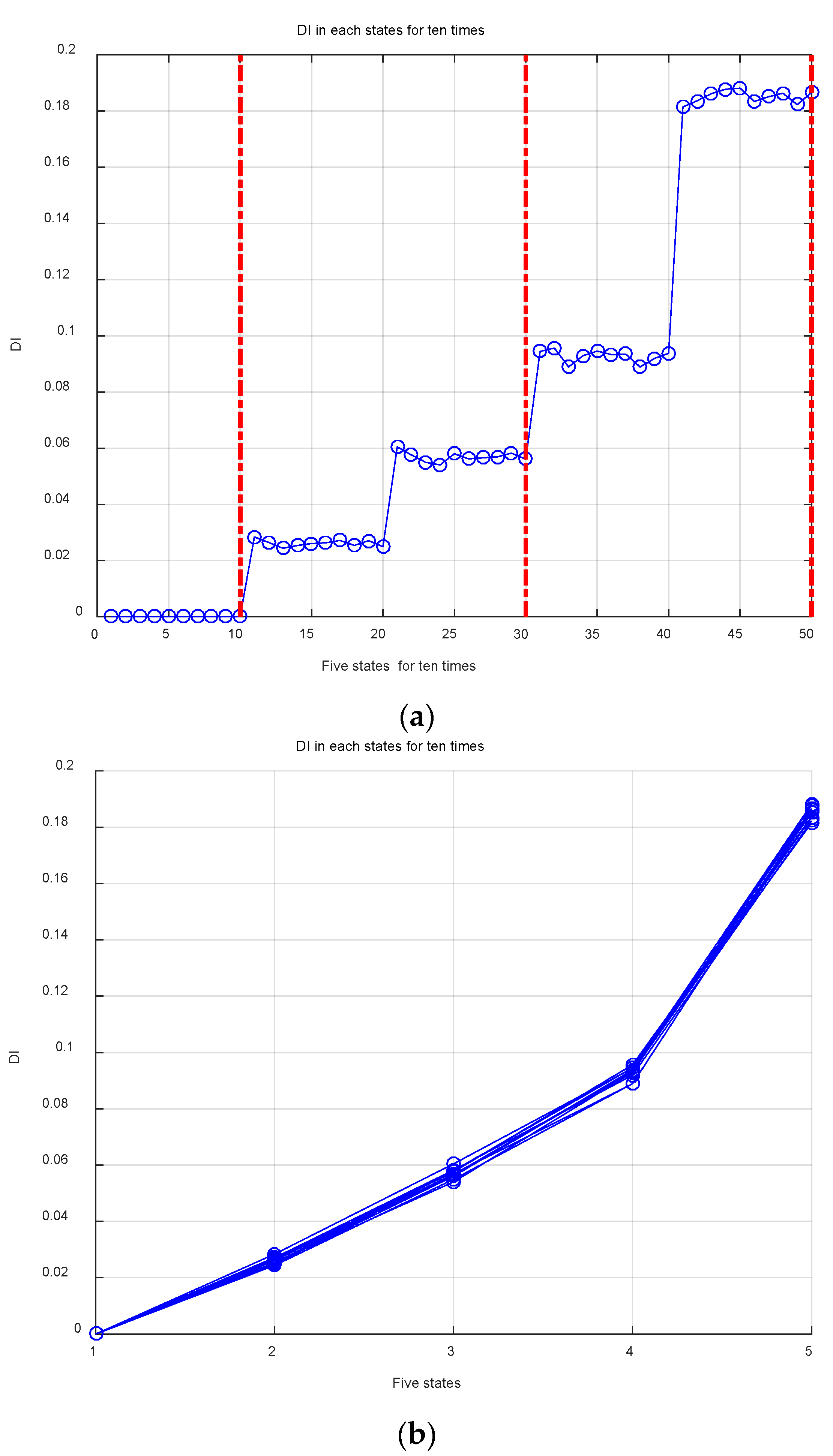
5.2. Damage Identification Process
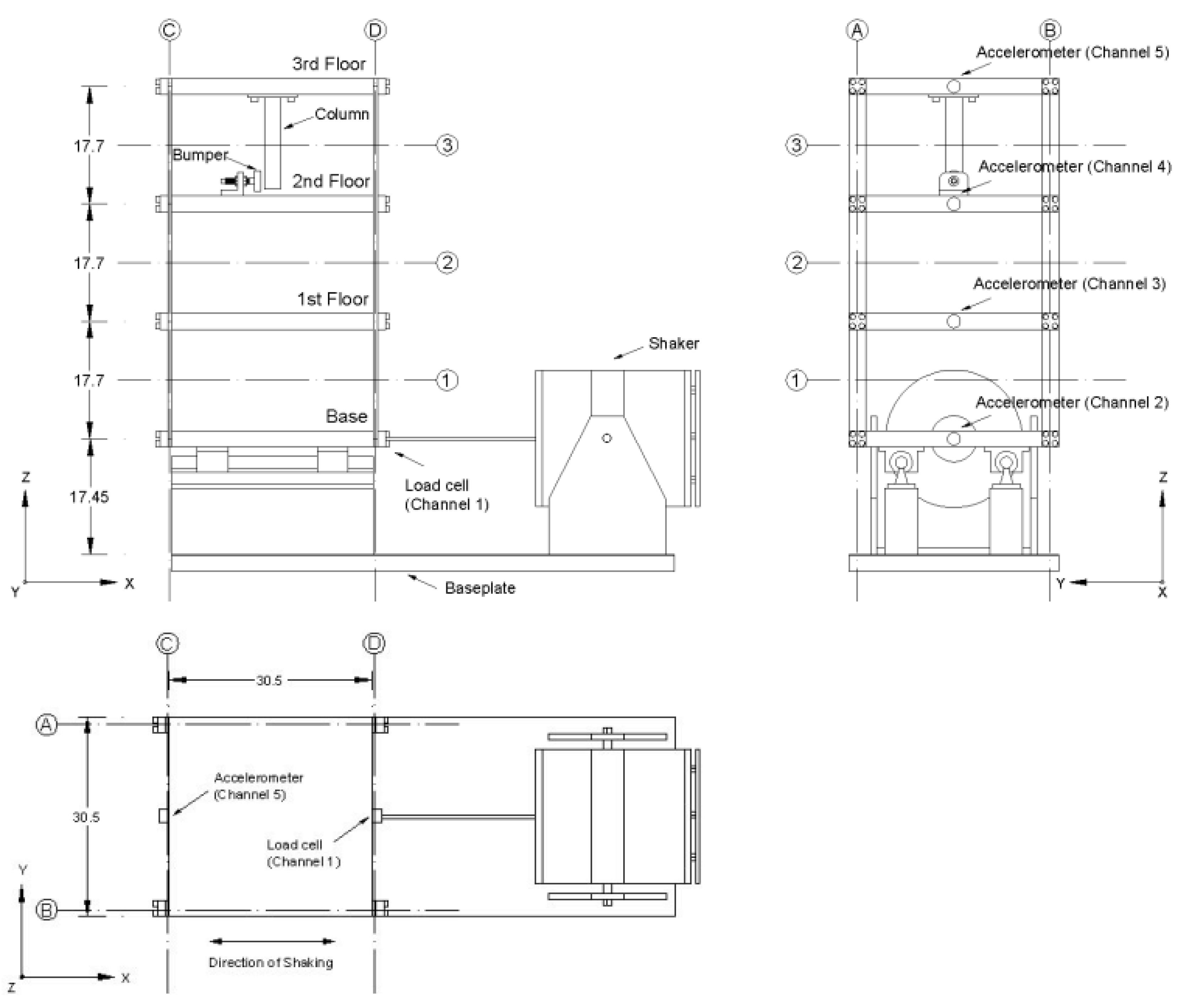
6. Verification Using the Data of the Alamos Three-Floor Shear Structure
6.1. Test Structure Description
6.2. Damage Identification Process
7. Discussion
8. Conclusions
- It has strong robustness to environmental excitation and can effectively identify damage based on environmental excitation.
- The direct use of structural vibration response for non-parametric damage identification has strong practicality and allows for real-time damage monitoring.
- The results of numerical simulations show that the method is sensitive to slight damage to the structure. Even a 5% reduction in stiffness can be identified.
Author Contributions
Funding
Conflicts of Interest
References
- Li, D.S.; Zhang, Y.; Ren, L. Sensor deployment for structural health monitoring and their evaluation. Adv. Mech. 2011, 41, 39–50. [Google Scholar]
- Wang, J.; Qin, L.; Song, W.; Shi, Z.; Song, G. Electromechanical Characteristics of Radially Layered Piezoceramic/Epoxy Cylindrical Composite Transducers: Theoretical Solution, Numerical Simulation and Experimental Verification. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Fan, S.; Bai, X.; Mo, Y.L.; Song, G. A novel embeddable spherical smart aggregate for structural health monitoring: Part I. Fabrication and electrical characterization. Smart Mater. Struct. 2017, 26, 095050. [Google Scholar] [CrossRef]
- Kong, Q.; Fan, S.; Mo, Y.L.; Song, G. A novel embeddable spherical smart aggregate for structural health monitoring: Part II. Numerical and experimental verifications. Smart Mater. Struct. 2017, 26, 095051. [Google Scholar] [CrossRef]
- Yin, H.; Wang, T.; Yang, D.; Liu, S.; Shao, J.; Li, Y. A smart washer for bolt looseness monitoring based on piezoelectric active sensing method. Appl. Sci. 2016, 6, 320. [Google Scholar] [CrossRef]
- Feng, D.M.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, M.; Li, T.; Song, G. ECG Signal de-noising and baseline wander correction based on CEEMDAN and wavelet threshold. Sensors 2017, 17, 2754. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt looseness detection based on piezoelectric impedance frequency shift. Appl. Sci. 2016, 6, 298. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, T.; Song, G.; Gu, H. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Signal Process. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Kong, Q.; Zhu, J.; Ho, M.; Song, G. Tapping and Listening: A New Approach to Bolt Looseness Monitoring. Smart Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Lu, G.; Feng, Q.; Li, Y.; Wang, H.; Song, G. Characterization of ultrasound energy diffusion due to small-size damage on an aluminum plate using piezoceramic transducers. Sensors 2017, 17, 2796. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Robert, R.H.; Silva, P.; Mo, Y.L. Cyclic crack monitoring of a reinforced concrete column under simulated pseudo-dynamic loading using piezoceramic-based smart aggregates. Appl. Sci. 2016, 6, 341. [Google Scholar] [CrossRef]
- Du, G.; Kong, Q.; Zhou, H.; Gu, H. Multiple cracks detection in pipeline using damage index matrix based on piezoceramic transducer-enabled stress wave propagation. Sensors 2017, 17, 1812. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Song, G.; Masri, S.F. Damage detection for a frame structure model using vibration displacement measurement. Struct. Health Monit. 2012, 11, 281–292. [Google Scholar] [CrossRef]
- Li, H.N.; Li, D.S. Safety assessment, health monitoring and damage diagnosis for structures in civil engineering. Earthq. Eng. Eng. Vib. 2002, 22, 82–90. [Google Scholar]
- Fan, W.; Qiao, P.Z. Vibration based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2010, 9, 83–111. [Google Scholar]
- Alamdari, M.M.; Samali, B.; Li, J. Damage localization based on symbolic time series analysis. Struct. Control Health Monit. 2015, 22, 374–393. [Google Scholar] [CrossRef]
- Siebel, T.; Friedmann, A.; Koch, M.; Mayer, D. Assessment of Mode Shape-Based Damage Detection Methods under Real Operational Conditions. In Proceedings of the 6th European Workshop on Structural Health Monitoring, Dresden, Germany, 3–6 July 2012. [Google Scholar]
- Tomaszewska, A. Influence of statistical errors on damage detection based on structural flexibility and mode shape curvature. Comput. Struct. 2010, 88, 154–164. [Google Scholar] [CrossRef]
- Wu, S.; Wei, Z.; Wang, S.; Wang, B.; Li, Y. Damage Identification Based on AR Model and PCA. J. Vib. Meas. Diagn. 2012, 32, 841–845. [Google Scholar]
- Gul, M.; Catbas, F.N. Statistical pattern recognition for Structural Health Monitoring using time series modeling: Theory and experimental verifications. Mech. Syst. Signal Process. 2009, 23, 2192–2204. [Google Scholar] [CrossRef]
- Lakshmi, K.; Rama Mohan Rao, A. A robust damage-detection technique with environmental variability combining time-series models with principal components. Nondestruct. Test. Eval. 2014, 29, 357–376. [Google Scholar] [CrossRef]
- Mei, Q.; Gul, M. An Improved Methodology for Anomaly Detection Based on Time Series Modeling; Springer: New York, NY, USA, 2013; pp. 277–281. [Google Scholar]
- Tributsch, A.; Adam, C. An enhanced energy vibration-based approach for damage detection and localization. Struct. Control Health Monit. 2018. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q.; Miao, C.Q. Structural damage alarming method based on wavelet packet analysis by ambient vibration test. Chin. J. Appl. Mech. 2008, 25, 366–370. [Google Scholar]
- Diao, Y.S.; Zhang, Q.L.; Meng, D.M. Damage Localization of Offshore Platform Based on the Virtual Impulse Response Function. Adv. Mater. Res. 2012, 368–373, 1676–1680. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.R.; Hunter, N.F.; Worden, K. Structural Health Monitoring Using Statistical Pattern Recognition Techniques. J. Dyn. Syst. Meas. Control 2001, 123, 706–711. [Google Scholar] [CrossRef]
- Liu, Y.; Li, A.Q.; Ding, Y.L.; Fei, Q.G. Time Series Analysis with Structural Damage Feature Extraction and Alarming Method. Chin. J. Appl. Mech. 2008, 25, 253–257. [Google Scholar]
- Aswolinskiy, W.; Reinhart, F.; Steil, J. Impact of Regularization on the Model Space for Time Series Classification. In Proceedings of the New Challenges in Neural Computation, Bruges, Belgium, 27–29 April 2015; pp. 49–56. [Google Scholar]
- LI, T.; Tang, L.M.; Shi, S.Y. Regularized time series AR model and its application. J. Transp. Sci. Eng. 2009, 25, 24–28. [Google Scholar]
- Li, A.Q.; Miu, C.Q. Health Monitoring of Bridge Structures; China Communications Press: Beijing, China, 2009. [Google Scholar]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Rissanen, J. A predictive least squares principle. J. Math. Control Inf. 1986, 3, 211–222. [Google Scholar] [CrossRef]
- Schwarz, G. Estimation of the dimension of the model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Wax, M. Order selection for AR models by predictive least squares. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 581–588. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karamousantas, D.C.; Chatzarakis, G.E.; Katsikas, S.K. Electricity demand loads modeling using Auto Regressive Moving Average (ARMA) models. Energy 2008, 33, 1353–1360. [Google Scholar] [CrossRef]
- Hoerl, A.; Kennard, R. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 2000, 42, 80–86. [Google Scholar] [CrossRef]
- Feng, D.M.; Sun, H.; Feng, M.Q. Simultaneous identification of bridge structural parameters and vehicle loads. Comput. Struct. 2015, 157, 76–88. [Google Scholar] [CrossRef]
- Chen, L. What can regularization offer for estimation of dynamical systems? In Proceedings of the 11th IFAC International Workshop on Adaptation and Learning in Control and Signal Processing (ALCOSP13), Caen, France, 3–5 July 2013. [Google Scholar]
- Fang, R.H. Modeling and Application of Theory Based on Time Series ARMA. Sci. Technol. Inf. 2012, 19, 197–199. [Google Scholar]
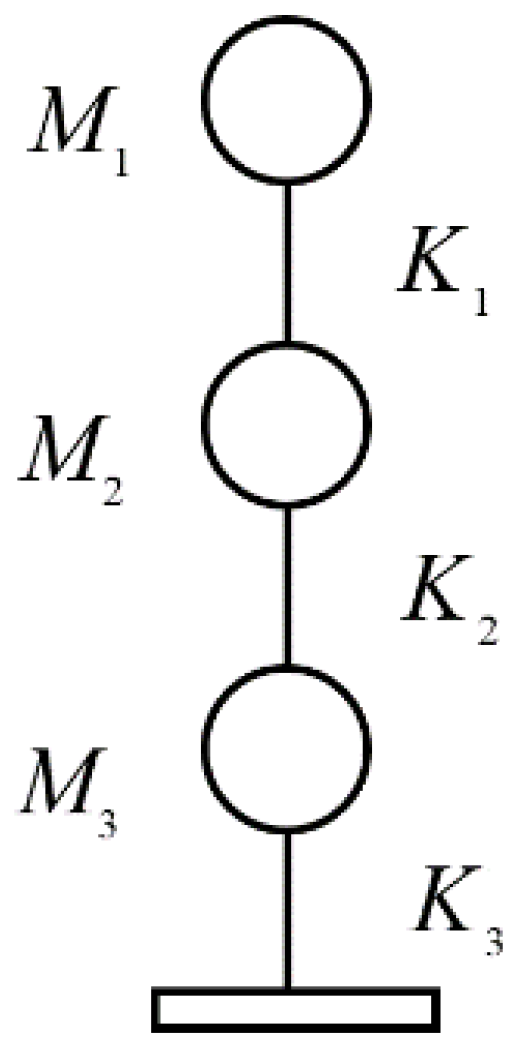

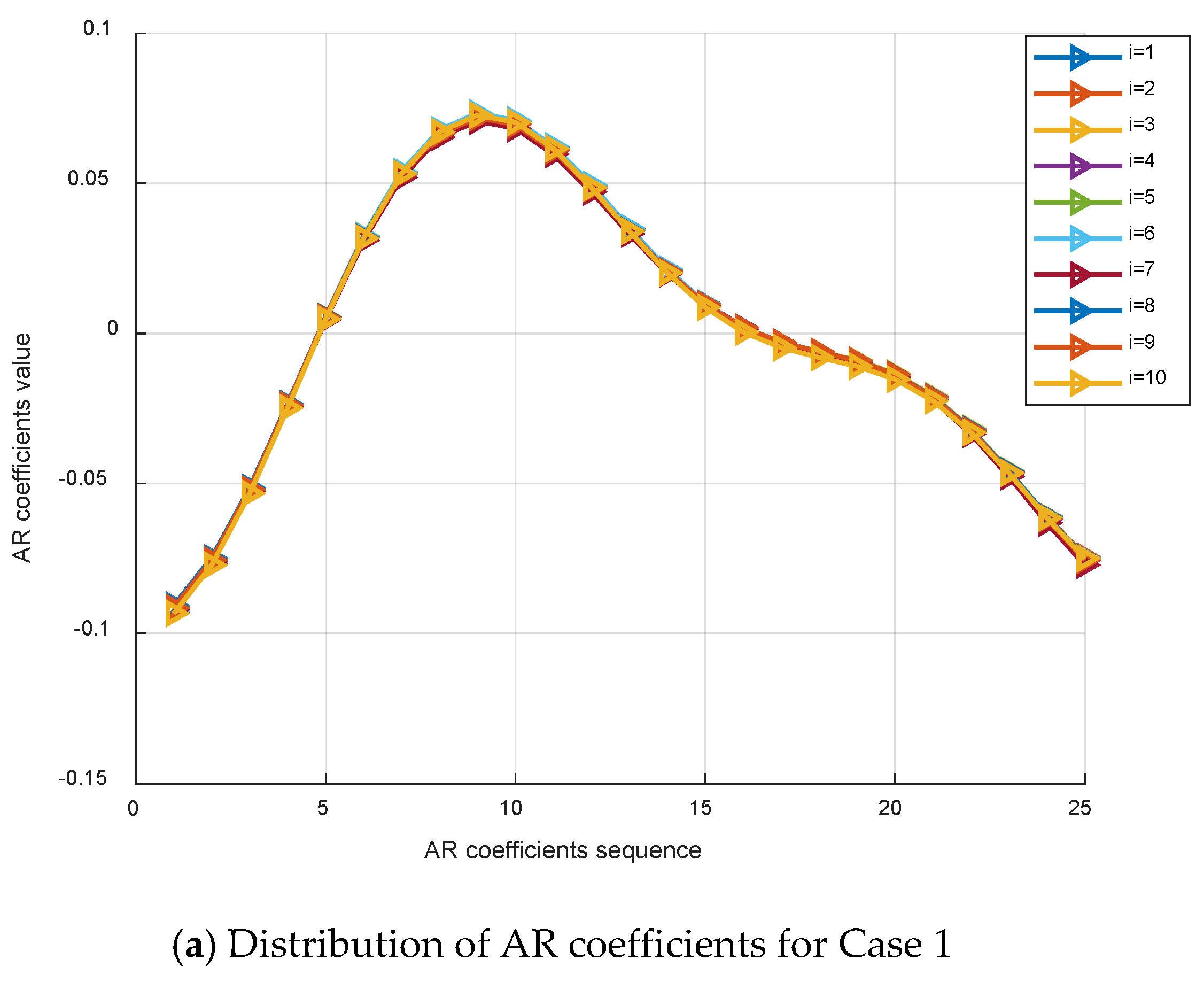
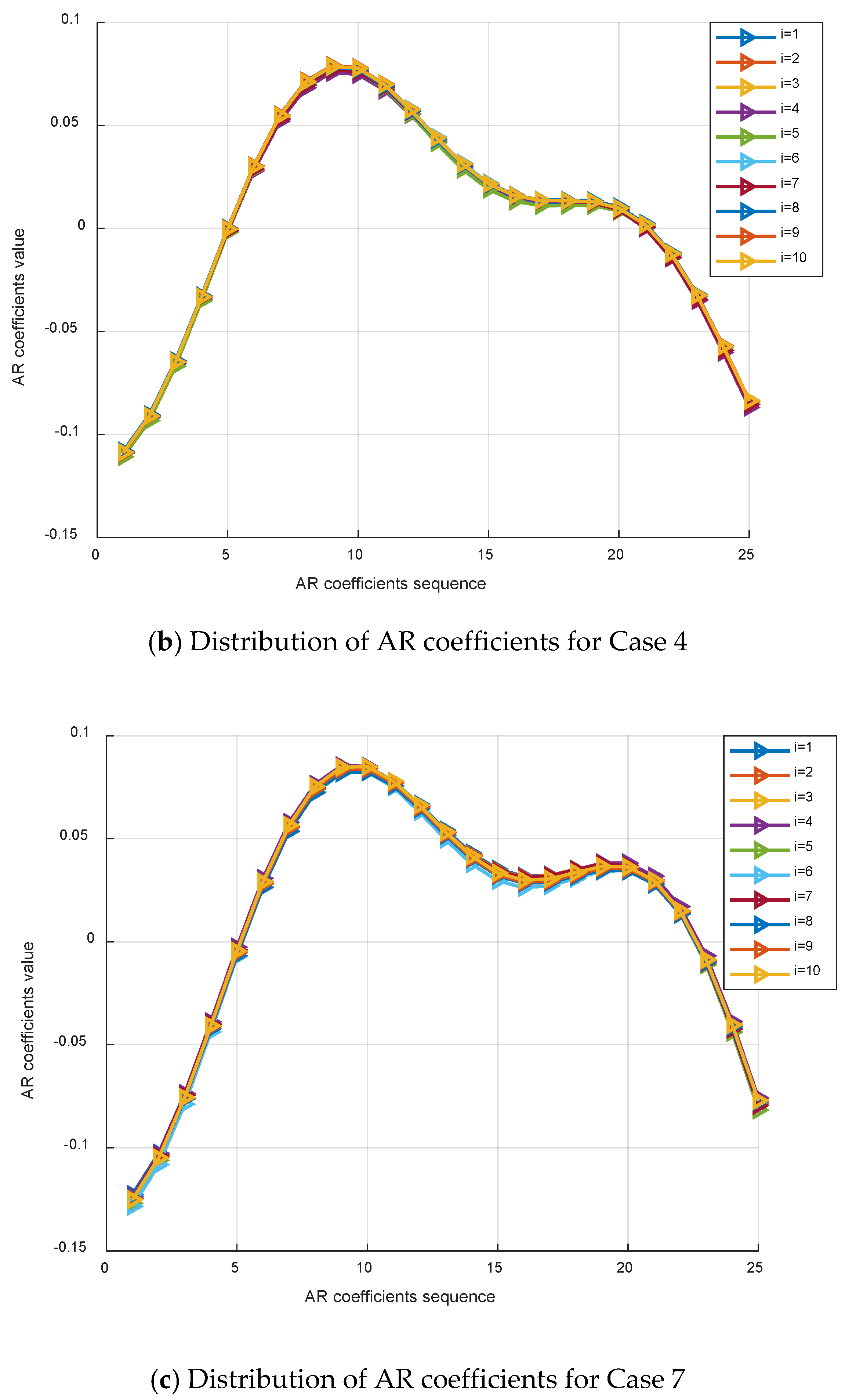



| Cases | Top Floor Stiffness Reduction Percentage |
|---|---|
| Case 1 | 0% |
| Case 2 | 5% |
| Case 3 | 10% |
| Case 4 | 15% |
| Case 5 | 20% |
| Case 6 | 25% |
| Case 7 | 30% |
| Label | State Condition | Description |
|---|---|---|
| State #1 | Undamaged | Baseline condition |
| State #2 | Damaged | 87.5% Stiffness reduction in column 1BD |
| State #3 | Damaged | 87.5% Stiffness reduction in columns 1AD and 1BD |
| State #4 | Damaged | 87.5% Stiffness reduction in column 2BD |
| State #5 | Damaged | 87.5% Stiffness reduction in columns 2AD and 2BD |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, D.; Song, G. Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation. Vibration 2018, 1, 138-156. https://doi.org/10.3390/vibration1010011
Zhang X, Li D, Song G. Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation. Vibration. 2018; 1(1):138-156. https://doi.org/10.3390/vibration1010011
Chicago/Turabian StyleZhang, Xuan, Dongsheng Li, and Gangbing Song. 2018. "Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation" Vibration 1, no. 1: 138-156. https://doi.org/10.3390/vibration1010011
APA StyleZhang, X., Li, D., & Song, G. (2018). Structure Damage Identification Based on Regularized ARMA Time Series Model under Environmental Excitation. Vibration, 1(1), 138-156. https://doi.org/10.3390/vibration1010011





