Abstract
This study investigates the behaviour of plumes from massive fires subjected to crosswinds, focusing on how varying wind profiles and terrain characteristics influence the formation of coherent vortical structures, particularly wake vortices, and the smoke distribution in the near-fire region. Large Eddy Simulations (LES) were employed to model the interaction between the plume, generated by a rectangular fireline with an intensity of , and the crosswind. Upon the consideration of several wind intensities (from 5 to ) and vertical distributions, it was verified that only for relatively low average wind velocities was there significant lateral entrainment to the flame, which promoted the formation of vertical vortical structures. Depending on the vertical distribution of the wind, different mechanisms can play a role in the formation of these structures, with a larger number of mechanisms involved for the cases where there is very low near-wall wind momentum, typical of large vegetation regions. The slope of the terrain (from to ) plays a role in these relations since it affects the fire plume inclination and, consequently, the entrainment process. These structures are more likely to appear in downslope terrains.
1. Introduction
There is a growing interest in the study of large, destructive wildfires, often termed “mega-fires”. Although rare, these events are responsible for the majority of burned areas and fire suppression costs and are characterized by spread rates far exceeding those of conventional wildfires, making them particularly challenging to control [1]. In addition to their devastating impact on ecosystems and human infrastructure, these fires generate large amounts of pollutants—through the incomplete combustion of biomass—that can be carried by wind-blown fire plumes and blanket urban and rural areas in thick layers of smoke [2]. This dispersion of smoke in these regions can create immediate hazards, such as poor visibility on roads or dangerous air quality levels for nearby communities [3].
Studying the movement of smoke in the near-fire region—the area directly influenced by a fire’s heat and emissions—is thus of paramount importance. An increased understanding of the turbulent interactions between heat, smoke, and the local atmosphere in the near-fire zone—which directly influences the fire’s behaviour (intensity and spread)—is crucial for developing accurate fire–atmosphere coupled models, which can enhance the predictability of both fire behaviour and smoke dispersal. Current coupled atmospheric–fire models such as WFDS [4] and WRF-Fire [5] provide essential tools to simulate the interactions between fire, smoke, and the atmosphere, but these models rely heavily on accurate representations of smoke dynamics in the near-fire region [6,7]. A deeper understanding of these dynamics can improve emergency response strategies, which present pressing importance, particularly due to climate change, with rising temperatures and prolonged droughts that are expected to increase the occurrence of these mega-fires.
In fact, the erratic dynamics of these mega-fires can be related to turbulent mixing within the plume, in which the behaviour of several instantaneous coherent flow structures plays an important role [8]. Even though several types of these structures have already been visually identified in large thermal plumes from wildland fires [9,10], to fully understand their dynamics, it is important to consider the simplified geometries of these complex phenomena. Fire plumes in crosswind can theoretically be modelled by the fundamental setup of a flow injecting perpendicularly into a crossflow, which has been widely studied in the literature due to its large number of engineering applications. Some of the most important vortical structures that appear in this type of flow are schematically presented in Figure 1 (see [11]). Their behaviour and characteristics are strongly influenced by factors such as the nozzle cross-section, jet-to-crossflow velocity ratio, and Reynolds number [12].
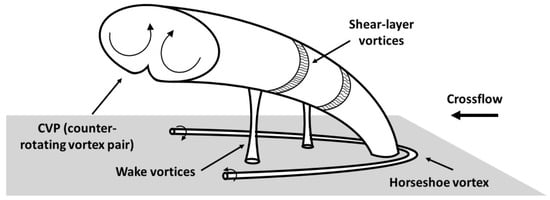
Figure 1.
Visualization of the vortical structures induced by a jet in crossflow.
Briefly, the Kelvin–Helmholtz instabilities in the jet’s shear layer give rise to shear-layer vortices that propagate downstream, enhancing fluid mixing. As these vortices interact with the crossflow, by tilting and folding [13,14], they give rise to a counter-rotating vortex pair (CVP). This structure forms downstream of the jet exit, influenced by the ratio between the jet momentum and the crossflow, producing two counter-rotating streamwise vortices that extend far downstream from the jet. While the time-averaged CVP appears symmetric, its instantaneous behaviour is asymmetric and unsteady [15]. Near the jet’s upstream side, a horseshoe-shaped vortex forms as a result of the crossflow boundary layer separating due to a local adverse pressure gradient. It wraps around the jet and persists downstream [16,17]. Furthermore, wake vortices, resembling upright tornado-like structures, are found downstream of the jet, linking its leeward side to the wall [11]. However, these structures are still the most unknown and are particularly relevant for wildland fires since they can lead to ember transport, spotting, fire-induced winds, firebrand lofting, and, in an extreme case, fire whirls.
Fire whirls represent a distinctive and intense form of flame behaviour, characterized by a rapidly rotating vertical column of hot gases, smoke, and fire. Since fire whirls are characterized by intense heat, high rotational wind speeds, and the ability to spread fire over long distances through spotting, they can be particularly destructive [18,19]. Fire whirls are generally categorized into on-source and off-source types. In on-source fire whirls, the rotating vortex forms directly over the fuel source and remains anchored to the fire itself. Several formation mechanisms have been identified, including fire whirls generated by vorticity formation from an L-shaped heat source [20], inducing rotational flow and subsequent updraft by intense heat, as well as by the lower section of the plume’s CVP [21]. In contrast, off-source fire whirls occur downstream of the primary fire. These fire whirls are periodically shed downwind from the burning area, but their formation mechanisms remain less well understood, making them an area of ongoing research. This type of fire whirl is directly related to the vertical vortices verified in fire plumes subject to crosswind and is potentially more destructive as it is more prone to spread fire to new areas.
Due to this, understanding the mechanisms of formation of these vertical structures is vital to develop effective fire safety measures and perform precise risk assessments. Four distinct mechanisms responsible for the formation of vertical vortices downstream of a flame in a crossflow were experimentally identified by Shinohara and Matsushima [22]. One of the mechanisms is similar to the wake vortex formation suggested by Fric and Roshko [11] where, unlike the vortex shedding observed behind bluff bodies, these wake vortices arise from the separation of the crossflow boundary layer along the sides of the jet induced by the adverse pressure gradient. Another mechanism involves air entrainment into the flame, where the reverse flow interacts with the crossflow passing along the sides of the flame, leading to the formation of vertical vortices. Additionally, these vortices may also develop from the interaction between the crossflow and the V-shaped flame rim or from interactions with the wall vortex pair. However, these different mechanisms have not been numerically identified, as far as the authors are aware, and there is not a clear understanding of what conditions are necessary for each one of these mechanisms to occur. In fact, as pointed out by Ghodrat et al. in their review paper [23], numerical simulation methods have the potential to provide a better understanding of the fundamental mechanisms of fire whirl initiation and stability by considering a large range of temporal and spatial scales of turbulence; however, currently, the literature is scarce in this area.
As can be concluded from the presented literature, one feature that is of extreme importance in this process of the formation of upright vortices is air entrainment. Two very relevant parameters when studying air entrainment are the intensity and vertical distribution of the crosswind as well as the terrain slope. Indeed, wind and topographic slope are widely recognized as key drivers of fire behaviour and continue to be active areas of research [24]. Ambient winds in the atmosphere generate a turbulent boundary layer around the Earth’s surface, with rising average wind velocities as height increases and with considerable velocity fluctuations. The structure of the boundary layer, as well as the inherent turbulent oscillations, is strongly dependent on the landscape [25]. The presence of these turbulent fluctuations in the atmospheric boundary layer (ABL) affects fire spread rates and fire behaviour by altering the entrainment rates and the amount of oxygen available for combustion. In fact, this wildland fire–atmosphere interaction produces complex turbulence patterns with multiple scales, which influence not only the fire spread behaviour but also the firebrand transport and smoke dispersion [26,27]. All of these variations across different ABLs highlight the importance of considering different vertical distributions of the incoming crosswind when studying the formation process of complex turbulent structures such as upright vortices. In fact, as pointed out by Shinohara [28] there is a need to investigate the effects of the boundary layer thickness, i.e., the vertical distribution of the incoming crosswind, on the properties of fire whirls without flames.
On the other side, understanding fire plume behaviour when subject to different slopes as well as the structures that can emerge as a function of the different entrainment patterns is significantly relevant to better investigate complex phenomena such as fire-channelling, an efficient mechanism for spreading a fire across a landscape with an intense fire behaviour [29]. In fact, terrain slope has already been found to significantly impact wildland fire behaviour, primarily by influencing the rate of fire spread and the fire’s intensity. When a fire occurs on an incline, it tends to spread faster uphill compared to downhill. This phenomenon is attributed to the preheating of fuels above the flame, which occurs as the heat and flames rise. The steeper the slope, the more pronounced this effect becomes, leading to a quicker rate of fire progression [30,31]. In addition, topographic features can affect local wind patterns, which can play a role in the formation of vortical structures and further intensify fire behaviour. In fact, recent research highlights the influence of slope on the frequency and height of fire whirls [32].
Large Eddy Simulation (LES) is a powerful tool for resolving these turbulent fire plume dynamics, and numerous studies have examined the influence of crosswinds on plume trajectories and dispersion (e.g., [33,34]). Particular emphasis has been placed on the role of vertical wind structure, drawing on the work of Ong et al. [33] to illustrate how atmospheric boundary-layer and canopy flows shape plume behaviour. The effects of slope are also detailed in the literature [35,36], highlighting the link between increased fire intensity, reduced plume lift-off, and their practical implications for fire management. Comparatively, one of the main gaps in research is understanding the formation of vortical structures in the near-fire region. Thus, this study specifically focuses on the near-fire region of fire plumes generated by massive fires subjected to crosswinds. Its two primary objectives are as follows: first, to examine how varying wind profiles and terrain characteristics influence the formation of coherent vortical structures, particularly moving vertical wake vortices; second, to investigate how these parameters impact smoke distribution in the near-fire region. To this end, this study numerically examines the structure of various fire plumes subjected to different wind intensities and vertical distributions as well as terrain slopes.
The paper is organized as follows: Section 2 presents the physical model and the mathematical and numerical models for fluid flow and combustion, as well as their validation. Following, the results are presented in Section 3, with the influence of the crosswind vertical distribution being investigated in Section 3.1 and the influence of the slope of the terrain in Section 3.2. The key findings of this study are presented in Section 4.
2. Governing Equations and Numerical Method
2.1. Physical Model and Boundary Conditions
A schematic illustration of the computational domain used in this work is shown in Figure 2a. The computational domain’s dimensions were . The fireline was located at from the crosswind inlet and its dimensions were .
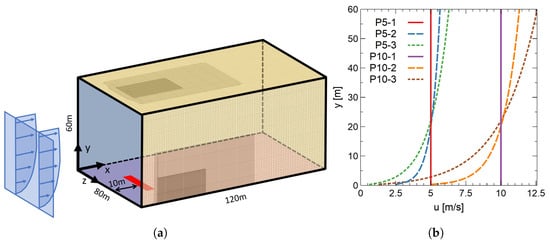
Figure 2.
Schematic representation of the (a) computational domain and (b) velocity profiles at the crosswind entry.
At the burner outlet (red line in Figure 2a), a constant methane mass flow rate was prescribed in order to achieve a very high fireline intensity of . This value was specifically chosen in order to study the behaviour of fire plumes from large-scale fires, such as the Pedrógão Grande 2017 fire during its critical phase [37]. This particular fireline perpendicular arrangement was expected to be critical for the formation of fire whirls (downwind of the fire source) with a large absolute value of circulation and large radius under a low wind speed for large fireline intensities [28].
At the crosswind entry (blue face in Figure 2a), several velocity profiles were imposed. The different velocity profiles are shown in Figure 2b. Two families of velocity profiles were created with the same average velocity along the height of the domain (either 5 or 10 m/s) but with different vertical distributions, with a decreasing velocity in the near-wall region from profiles 1 to 3. The profiles are denoted by P5-1, P5-2, and P5-3 and P10-1, P10-2, and P10-3. These different profiles aim at reproducing different atmospheric boundary layers resulting from different topologies of the terrain and were created based on a logarithmic profile [38], with profiles P5-2 and P10-2 representing a case of open land with grass and the profiles P5-3 and P10-3 representing large vegetation areas with farms and clumps of forest. Table 1 presents the velocity parameters for each profile, including the average velocity, the velocity at a height of 10 m, and the friction velocity. Additionally, the velocity fluctuations at the inlet were produced using the spectral synthesizer method.

Table 1.
Parameters of the imposed velocity profiles at the crosswind entry.
At the solid wall (red face in Figure 2a), an adiabatic no-slip boundary condition was applied; along the sides, top, and outlet areas (yellow faces in Figure 2a), atmospheric pressure was imposed (pressure outlet), allowing a realistic representation of the environment with the entrainment of ambient air into the fire plume. This could not be achieved with periodic or no-slip lateral boundary conditions. Furthermore, the width of the domain was carefully selected in order to allow the usage of this type of boundary condition without creating artificial wind gusts [39]: ten times larger than the length of the fireline.
2.2. Mathematical and Numerical Models
In this study, Large Eddy Simulation (LES) was implemented to model the turbulent flow of the fire plume. LES directly resolves large-scale turbulent structures, whereas the smaller subgrid-scale (SGS) motions are approximated using models. The LES equations were derived by applying a filter to the Navier–Stokes equations to remove eddies smaller than the filter size. The resulting filtered (represented by an overbar) continuity, momentum, and energy equations are represented by Equations (1), (2), and (3), respectively.
In these equations, is the fluid velocity and the index refers to the x-, y-, and z-directions. Additionally, , p, , , , T, and correspond to the fluid density, static pressure, dynamic viscosity, SGS stress, sensible enthalpy, thermal conductivity, and temperature, respectively. The SGS stresses, introduced through the filtering process, were modelled using the Boussinesq approximation, and the SGS enthalpy flux was modelled using the gradient hypothesis. The eddy viscosity was determined through the Dynamic Smagorinsky-Lilly model [40], while radiative heat transfer, which influenced the energy equation, was evaluated using the discrete ordinates (DO) method [41]. To compute the mass fraction of each species, a convection-diffusion equation was solved for each species, with the net production rate of a species due to chemical reactions being calculated using the Eddy dissipation model [42], assuming that the turbulence controlled the reaction rates. More details about these models and their implementation can be found in Reference [43].
The LES computations were carried out using FLUENT 16.2. For spatial discretization, the diffusive terms were computed using a second-order central scheme, whereas a bounded central-difference scheme was applied to the convective terms. Temporal discretization relied on a bounded second-order implicit method, guaranteeing that the Courant–Friedrichs–Lewy (CFL) number remained below 1 across the domain. Statistical analysis was conducted over five crosswind revolutions (large eddy turnovers), which ensured the statistical stationarity of the data of averaged quantities. Convergence was considered reached when the residuals for all the governing equations decreased by three orders of magnitude in each time step. The computational grid consisted of hexahedral cells, divided into three distinct refinement zones, as depicted in Figure 2a. The cell sizes were spatially adjusted, ranging from m near the fireline to 1 m at the domain boundaries. This adaptive refinement ensured high spatial resolution, particularly around the fireline, while maintaining a feasible number of total mesh points. In fact, the total number of cells in the domain was 1.6 million. This number is in agreement with prior studies that used similar numerical methods and is supported by energy spectrum analyses revealing that a portion of the inertial subrange can be captured with this mesh resolution [39].
2.3. Validation
The experimental results reported by Lin et al. [44] of a buoyant diffusion propane flame subject to crossflows were considered for the validation of the numerical model. The size of the computational domain was set as equal to and the burner was a square placed from the crossflow inlet. The domain was meshed using hexahedral cells, with a base size that varied from near the burner to at the domain boundaries. Pressure outlet boundary conditions were set at the top, sides, and outlet of the computation domain, while a velocity inlet boundary condition was applied at the crossflow entry and a non-slip boundary condition at the base. A specified propane mass flow rate was imposed at the burner outlet to maintain a constant heat release rate of . Results were averaged over 5 crossflow revolutions after achieving a quasi-steady state.
Figure 3 presents the predicted flame base extent (or flame attachment region [45,46]) for several crossflow velocities in comparison with the experimental results [44]. The flame base extent was estimated numerically as the distance (from the burner) where the time-averaged equivalence ratio was equal to 1. The experimental results revealed that as the crossflow velocity increased, the flame base extent first increased until it reached a maximum value (increasing regime) and then decreased (declining regime). This decrease in the flame base extent for relatively strong crossflows was explained by the remarkably enhanced air entrainment. With regard to the computational results, LES successfully captured the trend of the flame base extent evolution with the crossflow velocity, particularly capturing both the increasing and decreasing regimes as well as matching the location of the maximum. The slight underprediction of the numerical results in comparison to the experimental measurements could be related to the different approaches to estimating the flame base length and their associated uncertainty.
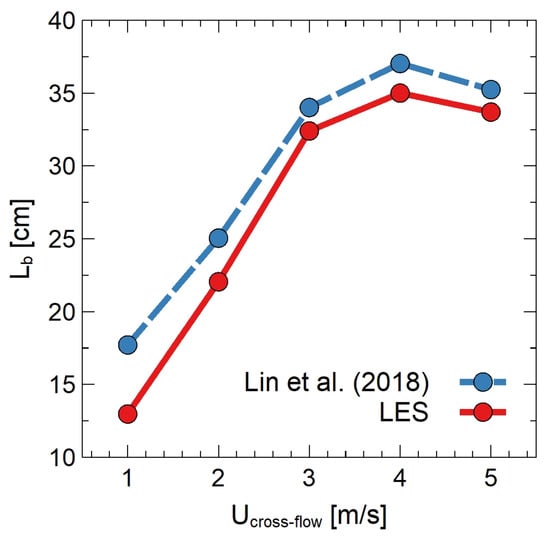
Figure 3.
Validation of the flame base extent of a buoyant diffusion flame subject to crossflow [44].
3. Results and Discussion
The results are divided into two main subsections. Firstly, the impact of the vertical distribution of the crosswind on the fire plume structure and on the development of vertical structures is investigated, and subsequently, the impact of the terrain slope is assessed for the same parameters.
3.1. Influence of Crosswind Vertical Distribution
For the six velocity profiles presented in Figure 2b, Figure 4 presents the side views of instantaneous snapshots depicting the plume structure. More concretely, Figure 4a–f present temperature volume rendering for the velocity profiles P5-1, P5-2, P5-3, P10-1, P10-2, and P10-3, respectively.
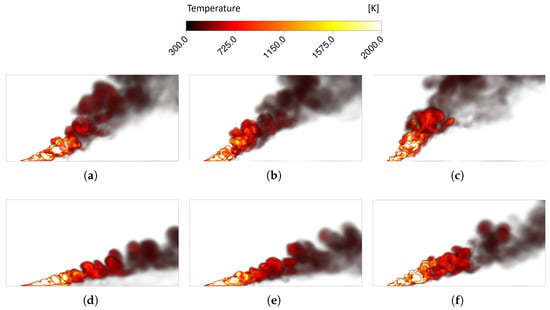
Figure 4.
Side views of the temperature volume rendering for the velocity profile: (a) P5-1, (b) P5-2, (c) P5-3, (d) P10-1, (e) P10-2, (f) P10-3.
Firstly, it is important to note that for all the studied crosswind profiles, the fire plumes were vertically inclined and and exhibited a highly turbulent structure with significant three-dimensional large-scale motions. Additionally, as observed during the validation of the LES model, regardless of the crosswind velocity distribution and intensity, the flame had an attachment zone to the wall in the downwind region near the injection. Further downstream, the flame transitioned to a detached state. This transition occurred earlier for profiles in which the velocity close to the wall was lower. Specifically, the length of the attachment region was smaller for the profiles P5-3 and P10-3, in comparison with the profiles P5-2/1 and P10-2/1, respectively. This variation is governed by the balance between the flame and wind momentum and the combustion-induced buoyancy. In this particular case, the higher momentum in the near-wall region of the fuller profiles explained this evolution. Moreover, due to this deficit of momentum close to the floor, when the fire plume was subject to the crosswind profiles P5-3 and P5-2, in comparison with the flat profile (P5-1), this resulted in a lower fire plume inclination. More concretely, for P5-1, P5-2, and P5-3, the inclination (measured from the vertical position) of the fire plume shifted from 49° to 43° and 37°, respectively. The same trend was visible for the profiles P10-1, P10-2, and P10-3, resulting in fire plume inclinations of 79°, 72°, and 61°. As expected, the direct comparison between the profiles P5-1/2/3 with P10-1/2/3 showed an increased inclination in this near-fire plume region when the average crosswind velocity was higher.
The vertical velocity distribution of the crosswind also affects the smoke propagation from the fire plume in its first metres (studied domain). To investigate this effect, the time-mean CO2 mass fraction was considered a tracer of the evolution of the fire plume. The subfigures (a), (b), and (c) in Figure 5 show the maximum normalized CO2 mass fraction (relative to the maximum value within the domain) along the x-, y-, and z-directions, respectively, for the velocity profiles P5-1, P5-2, and P5-3.
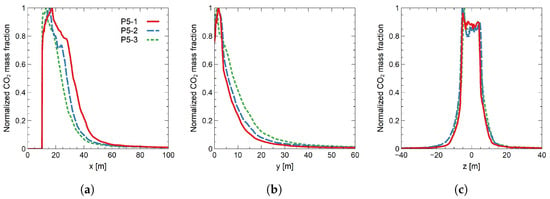
Figure 5.
Time-averaged maximum normalized CO2 mass fraction along the (a) x-, (b) y-, and (c) z-directions.
The vertical distribution of the velocity profile had a relatively negligible effect on the maximum CO2 mass fraction distribution in the z-direction. However, it affected the distribution of the maximum CO2 mass fraction in the y-direction, and it was very significant in the x-direction. As the velocity close to the wall increased, i.e., when moving from the profiles P5-3 to P5-1, there was a noticeable increase in the maximum extent of the concentration of CO2 in the x-direction. Once more, this is associated with the deficit in momentum close to the floor and its balance with the combustion-induced buoyancy, which is also affected by the entrainment velocity. In contrast, as the velocity close to the wall increased, the maximum extent of the CO2 concentration in the y-direction was reduced, in line with the evolution of the plume inclination. Similar trends could be observed for the P10-1, P10-2, and P10-3 profiles but with an overall increase (decrease) in the maximum smoke extent in the x-direction (y-direction).
This variation in the inclination of the fire plume, caused by differences in crosswind momentum, significantly affects the entrainment process near the wall. To illustrate this, Figure 6 and Figure 7 present the velocity vectors and iso-contours of the velocity in the main crosswind direction, highlighting the entrainment process and possible reverse flow regions. More concretely, Figure 6a–c are focused on the near-wall region for the crosswind profiles P5-1, P5-2, and P5-3 respectively, while Figure 6d–f show the same profiles but in a transversal plane located in the middle of the fireline. Figure 7a–f present the same quantities in the same locations mentioned above for the profiles P10-1, P10-2, and P10-3.
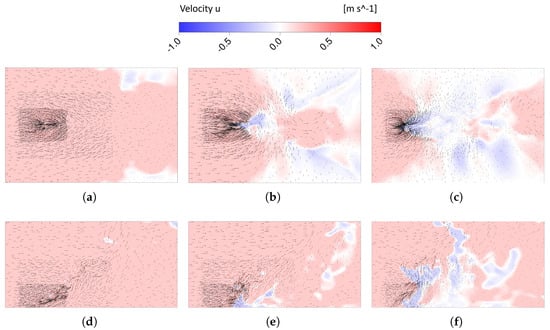
Figure 6.
Velocity vector field and saturated contours of the x-velocity close to the wall for the velocity profiles (a) P5-1, (b) P5-2, and (c) P5-3 as well as in the fireline midspan for the velocity profiles (d) P5-1, (e) P5-2, and (f) P5-3.
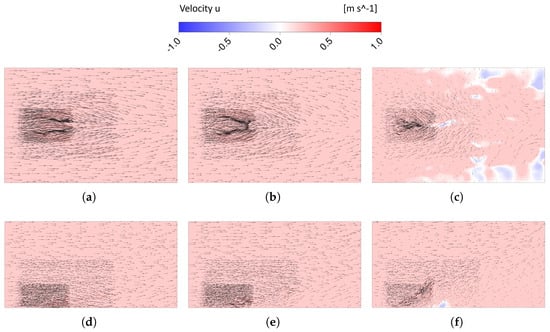
Figure 7.
Velocity vector field and saturated contours of the x-velocity close to the wall for the velocity profiles (a) P10-1, (b) P10-2, and (c) P10-3 as well as in the fireline midspan for the velocity profiles (d) P10-1, (e) P10-2, and (f) P10-3.
Focusing on Figure 6a–c, it is noteworthy that a constant inlet velocity profile resulted in no reverse flow in the near-wall region to the flame. Instead, only a small lateral entrainment, driven by continuity, was observed near the end of the computational domain (a region characterized by negative longitudinal velocity). As the momentum in the near wall region decreased, lateral entrainment started to occur earlier and reverse flow emerged in the vicinity of the flame. This reverse flow region was not confined to the near-wall region; it extended along the initial vertical metres of the fire plume, as shown in Figure 6d–f. The vertical extent of this region increased as the near-wall velocity decreased. Some reverse flow regions were also noteworthy in the upper extent of the fire plume for the velocity profiles studied due to its inherent turbulent motions. Turning to Figure 7a–f, it is possible to note that when the average velocity of the crosswind increased from 5 to 10 , there was a notable decrease in the lateral entrainment rate, attributed to the Coanda effect. Only the case with the P10-3 profile exhibited some lateral entrainment. In all cases, almost no reverse flow close to the flame was verified.
Due to the highly changed flow field in the near-wall region, which included zones where the velocity in the main crosswind direction changed sign, an increased number of vortical regions was expected. This could result in the formation of vertical structures by the fire plume entrainment. In fact, depending on the prescribed inlet velocity profile, several mechanisms for the creation of these vortical structures were identified. Figure 8, Figure 9 and Figure 10 present an instantaneous vortex core region—defined by motion patterns around local centres with a specific swirling strength—along with saturated vertical vorticity contours and 3D streamlines either from the inlet or from the lateral boundaries in the near-wall region. The iso-surface and -contours helped identify vortex regions, while the streamlines provided insight into the driving flow mechanisms and the origins of these structures. Only for the P5-2 and P5-3 profiles were vertical structures detected. For the remaining velocity profiles, there was a negligible reverse flow in the near-wall region and lateral entrainment, decreasing the rate of the formation of vortical structures near the plume. As mentioned, this happened due to the higher velocities and therefore higher momentum of the crosswind in the near-wall region and since the lateral domain size was carefully selected to avoid artificial wind gusts, which are known to generate vertical structures [39].
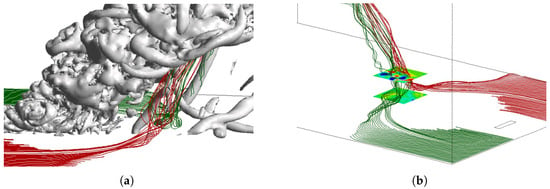
Figure 8.
Three-dimensional streamlines from the inlet for the velocity profile P5-2 as well as the (a) vortex core region with a swirling strength equal to 0.05 and (b) y-vorticity contours.
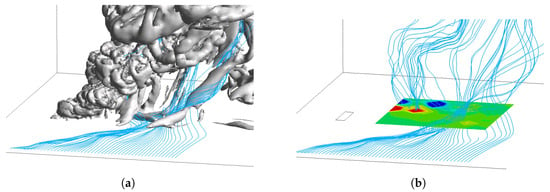
Figure 9.
Three-dimensional streamlines from the lateral domain for the velocity profile P5-3 as well as the (a) vortex core region with a swirling strength equal to and (b) y-vorticity contours.
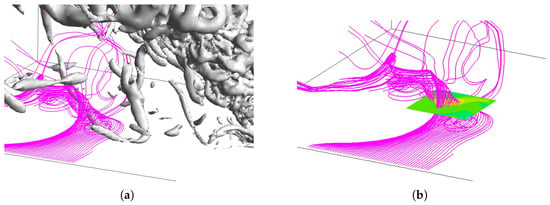
Figure 10.
Three-dimensional streamlines from the end of the lateral domain for the velocity profile P5-3 as well as the (a) vortex core region with a swirling strength equal to and (b) y-vorticity contours.
Figure 8a,b depict the profile P5-2, illustrating the vortex core regions and the vorticity contours, respectively, with streamlines originating from the inlet. Notably, as the lateral entrainment started to flow to the downwind region of the plume, the crosswind coming from the inlet, due to its low momentum, started to roll, moving towards the downwind region and forming vortical structures that stretched and connected to the plume. This mechanism is similar to the process where a separated velocity boundary layer on the ground links to a pair of vertical vortices, as described by Frick and Roshko [11] for a jet in crossflow and by Shinohara and Matsushima [22] for a flame in crossflow. These vortex structures could either remain steady in the downwind region of the plume or be shed downstream, largely depending on erratic fire behaviour. Similar vortex formation was also observed in the P5-3 velocity profile, suggesting that it occurred under conditions of relatively low velocity and vertical distribution.
Figure 9a,b as well as Figure 10a,b present similar data for the profile P5-3, with streamlines originating from the lateral boundaries, and reveal two distinct mechanisms of vertical structure formation for this velocity profile, the one characterized by the lowest velocity near the wall, resulting in the greatest lateral entrainment and reverse flow regions. It is important to note that these mechanisms were not observed in the profile P5-2.
In Figure 9a,b, it can be observed that the lateral entrainment flowed toward the downwind region, very close to the plume, before reversing its direction to flow counter to the crosswind and merging with the additional reverse flow. This abrupt change in the direction of entrainment generated vortical regions that were once again stretched and connected to the lee side of the plume. The primary difference from the previously discussed mechanism lies in the source of the flow that formed the vortices and the flow characteristic responsible for their formation. In the earlier case, vortical regions emerged as the flow rolled due to interaction with the entrainment, whereas here, it was the abrupt change in the lateral flow’s direction caused by strong fire plume entrainment that led to vortex formation.
Differently, Figure 10a,b illustrate a formation mechanism similar to that previously described, where the lateral entrainment flowed toward the downwind region of the plume and interacted with local areas of differing x-velocity, as seen in Figure 6c. In this case, the streamlines began to roll up, generating vortical regions. However, the key difference is that this process occurred further downstream from the fire. This mechanism resembles the one presented by Shinohara and Matsushima, where vertical vortices form at the rim of the V-shaped area downwind of a flame in the absence of crossflow [22]. The strength of these vortices was weaker than that of those formed closer to the fire and did not necessarily connect to the plume.
3.2. Influence of Terrain Slope
In this subsection, the influence of the terrain slope on the fire plume structure and on the development of vertical structures is investigated. Three different slopes (both upslope and downslope) are considered—0°, 10°, and 20°—considering the P5-1 velocity profile. Numerically, the slope was allocated by the prescription of the gravity vector. Figure 11a–c show the side views of the instantaneous temperature volume rendering for the upslopes 0°, 10°, and 20°, respectively. Figure 12a–c present similar results but for the downslope configuration.
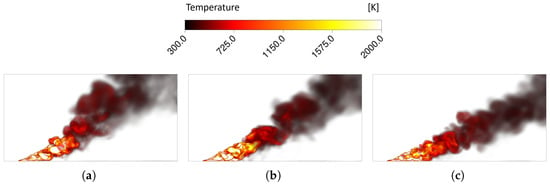
Figure 11.
Side views of the temperature volume rendering for terrains with an upslope angle of (a) 0°, (b) 10°, and (c) 20°.
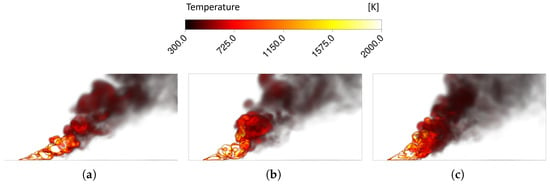
Figure 12.
Side views of the temperature volume rendering for terrains with a downslope angle of (a) 0°, (b) 10°, and (c) 20°.
An immediate impact of the terrain slope was the inclination of the fire plume. As can be seen in Figure 11, an increase in the upslope angle of the terrain resulted in an increased fire plume tilt angle. This behaviour was primarily driven by the Coanda effect, which induced the plume to be more inclined to the floor immediately downstream of the fire source. In fact, as the terrain slope increased, a windward buoyancy force was generated, in addition to the wind force, that further amplified the Coanda effect, resulting in the plume being more closely aligned with the floor. The opposite effect is verified in Figure 12, which shows that an increase in the downslope angle resulted in a decrease in the angle of inclination of the fire plume. More concretely, the fire plume inclination shifted from 49° to 58° and 62° when the upslope shifted from 0° to 10° and 20° and from 49° to 41° and 35° for the same variations in the downslope configuration. These results are in agreement with theory and previous investigations [47,48].
As before, this variation in the fire plume inclination with the slope of the terrain affected the entrainment process close to the wall. To illustrate this, Figure 13a–c present the velocity vectors and iso-contours of the velocity in the main crosswind direction in the near-wall region for the 20° downslope, 0° (flat terrain), and 20° upslope cases, respectively. Figure 13d–f show the same cases but in a transverse plane located in the middle of the fireline.
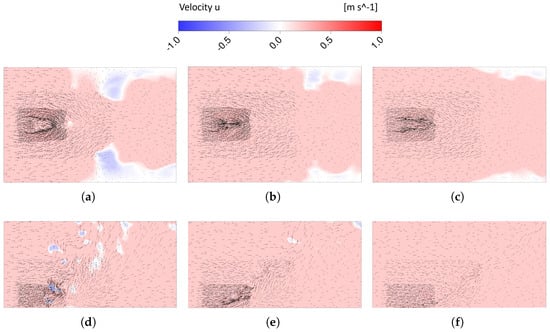
Figure 13.
Velocity vector field and saturated contours of the x-velocity close to the wall for the configurations of (a) 20° downslope, (b) 0°, and (c) 20° upslope as well as in the fireline midspan for the velocity profiles of (d) 20° downslope, (e) 0°, and (f) 20° upslope.
It should be noted that the upslope configuration decreased the lateral entrainment by continuity close to the end of the computational domain. However, as there was an increase in the downslope terrain angle, the lateral entrainment of ambient air started to occur earlier and a small reverse flow region close to the flame started to appear. As discussed before, these flow characteristics are favourable for the creation of vertical vortical structures. For the 20° downslope case, only the formation mechanism shown in Figure 10—which generated weak structures not connected to the plume—was noticeable.
4. Conclusions
In this work, the influence of crosswind and terrain characteristics on the near-fire region of fire plumes from massive fires was studied numerically using Large Eddy Simulations (LES). The case of a purely buoyant diffusion propane flame subject to crossflows was analysed to validate the numerical model. LES effectively captured the trend of the evolution of the flame base extent with the crossflow velocity.
The behaviour of the fire plume and the formation of vortical structures were found to be significantly influenced by the wind’s intensity and vertical distribution; the friction velocity ranged from 0 to for an average velocity of and from 0 to for an average velocity of . Only at relatively low average wind velocities did significant lateral entrainment occur, promoting the development of vertical vortices. These structures were more prone to appear when the wind profiles exhibited low near-wall momentum (higher friction velocity), often observed in regions with large vegetation. In such conditions, different mechanisms for vortex formation could be verified, such as the roll-up of the crosswind coming from the inlet and the reversed direction of the lateral entrainment flow. In contrast, a higher near-wall wind momentum suppressed these entrainment processes, increasing plume inclination (up to ) and reducing the prevalence of vortical structures. Future investigation could target the impact of lower wind velocities (with low near-wall momentum) on the development of vertical vortices. Smoke dispersion patterns also varied, with low near-wall wind momentum leading to greater vertical dispersion, while higher momentum enhanced horizontal propagation.
The slope of the terrain (from to ) further modulated the dynamics of the fire plume by altering the tilt angle of the plume and the entrainment characteristics. The downslope configurations reduced the inclination of the plume (up to ) and facilitated stronger lateral entrainment, creating favourable conditions for the formation of vertical vortices. In contrast, upslope terrains amplified plume inclination (up to ) and suppressed lateral entrainment, limiting vortex formation. Future research could explore the impact of steeper downslope terrains on the vortex formation and its influence on fire spread dynamics.
In summary, this study highlights the complex relation between wind profiles, terrain slopes, and fire dynamics in shaping fire plume behaviour, near-fire turbulence, and smoke dispersion patterns. The findings highlight the critical role of topography—terrain-induced effects combined with variations in wind profiles—on plumes’ entrainment and the formation of vertical structures that generate powerful updrafts capable of lifting burning debris, thereby contributing to fire spread. These insights provide valuable implications for fire–atmosphere coupled modelling and enhance fire behaviour prediction, which is increasingly critical as the risk of wildfires continues to grow.
Author Contributions
Conceptualization, B.A.C.B. and J.C.F.P.; methodology, B.A.C.B. and J.C.F.P.; software, B.A.C.B.; validation, B.A.C.B.; formal analysis, B.A.C.B.; investigation, B.A.C.B.; resources, J.C.F.P.; data curation, B.A.C.B.; writing—original draft preparation, B.A.C.B. and J.C.F.P.; writing—review and editing, B.A.C.B. and J.C.F.P.; visualization, B.A.C.B.; supervision, J.C.F.P.; project administration, J.C.F.P.; funding acquisition, J.C.F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by FCT Fundação para a Ciência e a Tecnologia, through the SmokeStorm project PCIF/MPG/0147/2019 and through IDMEC, under the LAETA project UIDB/50022/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bartlett, T.; Leonard, M.; Morgan, G. The Mega-Fire Phenomenon: Some Australian Perspectives. In Proceedings of the 2007 Institute of Foresters of Australia and New Zealand Institute of Forestry Conference, Coffs Harbour, NSW, Australia, 3–7 June 2007. [Google Scholar]
- Fernandes, A.; Lopes, D.; Sorte, S.; Monteiro, A.; Gama, C.; Reis, J.; Menezes, I.; Osswald, T.; Borrego, C.; Almeida, M.; et al. Smoke emissions from the extreme wildfire events in central Portugal in October 2017. Int. J. Wildland Fire 2022, 31, 989–1001. [Google Scholar] [CrossRef]
- Johnston, F.; Borchers Arriagada, N.; Morgan, G.; Jalaludin, B.; Palmer, A.; Williamson, G.; Bowman, D. Unprecedented health costs of smoke-related PM2.5 from the 2019–20 Australian megafires. Nat. Sustain. 2021, 4, 42–47. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.; Gould, J.; Cheney, P. A Physics-Based Approach to Modeling Grassland Fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Coen, J.; Cameron, M.; Michalakes, J.; Patton, E.; Riggan, P.; Yedinak, K. WRF-Fire: Coupled Weather-Wildland Fire Modeling with the Weather Research and Forecasting Model. J. Appl. Meteorol. Climatol. 2013, 52, 16–38. [Google Scholar] [CrossRef]
- Peterson, D.L.; McCaffrey, S.M.; Patel-Weynand, T. Wildland Fire Smoke in the United States: A Scientific Assessment; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Goodrick, S.; Achtemeier, G.; Larkin, N.; Liu, Y.; Strand, T. Modelling smoke transport from wildland fires: A review. Int. J. Wildland Fire 2013, 22, 83–94. [Google Scholar] [CrossRef]
- Coats, C. Coherent structures in combustion. Prog. Energy Combust. Sci. 1996, 22, 427–509. [Google Scholar] [CrossRef]
- Church, C.; Snow, J.; Dessens, J. Intense Atmospheric Vortices Associated with a 1000 MW Fire. Bull. Am. Meteorol. Soc. 1980, 61, 682–694. [Google Scholar] [CrossRef]
- Haines, D.; Smith, M. Three Types of Horizontal Vortices Observed in Wildland Mass and Crown Fires. J. Appl. Meteorol. 1987, 26, 1624–1637. [Google Scholar] [CrossRef]
- Fric, T.; Roshko, A. Vortical Structure in the Wake of a Transverse Jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Martins, F.; Pereira, J. Numerical Study of Laminar Unsteady Circular and Square Jets in Crossflow in the Low Velocity Ratio Regime. Fluids 2024, 9, 292. [Google Scholar] [CrossRef]
- Cortelezzi, L.; Karagozian, A. On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 2001, 446, 347–373. [Google Scholar] [CrossRef]
- Kelso, R.; Lim, T.; Perry, A. An Experimental Study of Round Jets in Cross-Flow. J. Fluid Mech. 1996, 306, 111–144. [Google Scholar] [CrossRef]
- Mahesh, K. The Interaction of Jets with Crossflow. Annu. Rev. Fluid Mech. 2013, 45, 379–407. [Google Scholar] [CrossRef]
- Kelso, R.; Smits, A. Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 1995, 7, 153–158. [Google Scholar] [CrossRef]
- Krothapalli, A.; Lourenço, L.; Buchlin, J.M. Separated flow upstream of a jet in a crossflow. AIAA J. 1990, 28, 414–420. [Google Scholar] [CrossRef]
- Tohidi, A.; Gollner, M.; Xiao, H. Fire Whirls. Annu. Rev. Fluid Mech. 2018, 50, 187–213. [Google Scholar] [CrossRef]
- Liu, N.; Lei, J.; Wei, G.; Chen, H.; Xie, X. Combustion dynamics of large-scale wildfires. Proc. Combust. Inst. 2021, 38, 157–198. [Google Scholar] [CrossRef]
- Soma, S.; Saito, K. Reconstruction of fire whirls using scale models. Combust. Flame 1991, 86, 269–284. [Google Scholar] [CrossRef]
- Shinohara, M.; Matsushima, S. Flow Visualization Study of Stationary Fire Whirls just Downwind of Meter-Scale Turbulent Flames. Flow Turbul. Combust. 2019, 102, 313–330. [Google Scholar] [CrossRef]
- Shinohara, M.; Matsushima, S. Formation of fire whirls: Experimental verification that a counter-rotating vortex pair is a possible origin of fire whirls. Fire Saf. J. 2012, 54, 144–153. [Google Scholar] [CrossRef]
- Ghodrat, M.; Shakeriaski, F.; Nelson, D.; Simeoni, A. Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review. Fire 2021, 4, 43. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, K. Effect of Slope on the Frequency and Height of Fire Whirls. Fire 2023, 6, 189. [Google Scholar] [CrossRef]
- Pitts, W. Wind effects on fires. Prog. Energy Combust. Sci. 1991, 17, 83–134. [Google Scholar] [CrossRef]
- Heilman, W.; Clements, C.; Seto, D.; Bian, X.; Clark, K.; Skowronski, N.; Hom, J. Observations of fire-induced turbulence regimes during low-intensity wildland fires in forested environments: Implications for smoke dispersion: Observations of fire-induced turbulence regimes. Atmos. Sci. Lett. 2015, 16, 453–460. [Google Scholar] [CrossRef]
- Desai, A.; Guilloteau, C.; Heilman, W.; Charney, J.; Skowronski, N.; Clark, K.; Gallagher, M.; Foufoula-Georgiou, E.; Banerjee, T. Investigating Fire–Atmosphere Interaction in a Forest Canopy Using Wavelets. Bound.-Layer Meteorol. 2024, 190, 21. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, M. Vortex strength and size of fire whirls without flames around a long narrow fire source. Fire Saf. J. 2022, 129, 103561. [Google Scholar] [CrossRef]
- Sharples, J.; McRae, R.; Wilkes, S. Wind-terrain effects on the propagation of wildfires in rugged terrain: Fire channelling. Int. J. Wildland Fire 2012, 21, 282–296. [Google Scholar] [CrossRef]
- Dupuy, J.L.; Maréchal, J. Slope effect on laboratory fire spread: Contribution of radiation and convection to fuel bed preheating. Int. J. Wildland Fire 2011, 20, 289. [Google Scholar] [CrossRef]
- Li, H.; Liu, N.; Xie, X.; Zhang, L.; Yuan, X.; He, Q.; Viegas, D. Effect of Fuel Bed Width on Upslope Fire Spread: An Experimental Study. Fire Technol. 2020, 57, 1063–1076. [Google Scholar] [CrossRef]
- Mehr, R.; Mohammadian, E.; Farhanieh, B.; Afshin, H. Numerical Investigation of the Combined Effect of Terrain Slope and Wind Velocity on Fire Spread Rate in Natural Pastures. Modelling 2025, 6, 15. [Google Scholar] [CrossRef]
- Ong, R.; Patruno, L.; He, Y.; Efthekarian, E.; Zhao, Y.; Hu, G.; Kwok, K. Large-eddy simulation of wind-driven flame in the atmospheric boundary layer. Int. J. Therm. Sci. 2021, 171, 107032. [Google Scholar] [CrossRef]
- Hu, L.; Huo, R.; Yang, D. Large eddy simulation of fire-induced buoyancy driven plume dispersion in an urban street canyon under perpendicular wind flow. J. Hazard. Mater. 2009, 166, 394–406. [Google Scholar] [CrossRef] [PubMed]
- Ghodrat, M.; Edalati-nejad, A.; Simeoni, A. Collective Effects of Fire Intensity and Sloped Terrain on Wind-Driven Surface Fire and Its Impact on a Cubic Structure. Fire 2022, 5, 208. [Google Scholar] [CrossRef]
- Mueller, E.; Mell, W.; Simeoni, A. Large eddy simulation of forest canopy flow for wildland fire modeling. Can. J. For. Res. 2014, 44, 1534–1544. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Oom, D.; Artes, T.; Viegas, D.; Fernandes, P.; Faivre, N.; Freire, S.; Moore, P.; Rego, F.; Castellnou, M. Forest Fires in Portugal in 2017; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Building and Construction Authority. BCA Green Mark for Residential Buildings: Technical Guide and Requirements. 2016. Available online: https://www1.bca.gov.sg/docs/default-source/docs-corp-buildsg/sustainability/gm-rb-2016-technical-guide-_rev010120.pdf (accessed on 8 October 2024).
- Barata, B.; Martins, F.; Pereira, J. LES of fire plumes subjected to crosswind inducing vertical vorticity. Fire Saf. J. 2024, 144, 104112. [Google Scholar] [CrossRef]
- Lilly, D. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633. [Google Scholar] [CrossRef]
- Chui, E.; Raithby, G. Computation of Radiant Heat Transfer on a Non-Orthogonal Mesh Using the Finite-Volume Method. Numer. Heat Transf. Part B-Fundam. 1993, 23, 269–288. [Google Scholar] [CrossRef]
- Magnussen, B.; Hjertager, B. On Mathematical Modeling of Turbulent Combustion with Special Emphasis on Soot Formation and Combustion. Symp. (Int.) Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Ansys. Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Lin, Y.; Xiaolei, Z.; Hu, L. An experimental study and analysis on maximum horizontal extents of buoyant turbulent diffusion flames subject to relative strong cross flows. Fuel 2018, 234, 508–515. [Google Scholar] [CrossRef]
- Gorham, D.; Hakes, R.; Singh, A.; Forthofer, J.; Cohen, J.; Mcallister, S.; Finney, M.; Gollner, M. Studying Wildland Fire Spread Using Stationary Fires. In Proceedings of the VII International Conference on Forest Fire Research, Coimbra, Portugal, 17–20 November 2014; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014. [Google Scholar] [CrossRef]
- Tang, W.; Finney, M.; McAllister, S.; Gollner, M. An Experimental Study of Intermittent Heating Frequencies From Wind-Driven Flames. Front. Mech. Eng. 2019, 5, 34. [Google Scholar] [CrossRef]
- Edalati-nejad, A.; Ghodrat, M.; Simeoni, A. Numerical Investigation of the Effect of Sloped Terrain on Wind-Driven Surface Fire and Its Impact on Idealized Structures. Fire 2021, 4, 94. [Google Scholar] [CrossRef]
- Sharples, J. Review of formal methodologies for wind–slope correction of wildfire rate of spread. Int. J. Wildland Fire 2008, 17, 179–193. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).