Simulation Study and Proper Orthogonal Decomposition Analysis of Buoyant Flame Dynamics and Heat Transfer of Wind-Aided Fires Spreading on Sloped Terrain
Abstract
1. Introduction
2. Computational Methods
2.1. Gas-Phase Governing Equations
2.2. Vegetation Fuel Model
2.3. The Principle of Proper Orthogonal Decomposition
2.4. Experiments and Numerical Setup
3. Results and Discussion
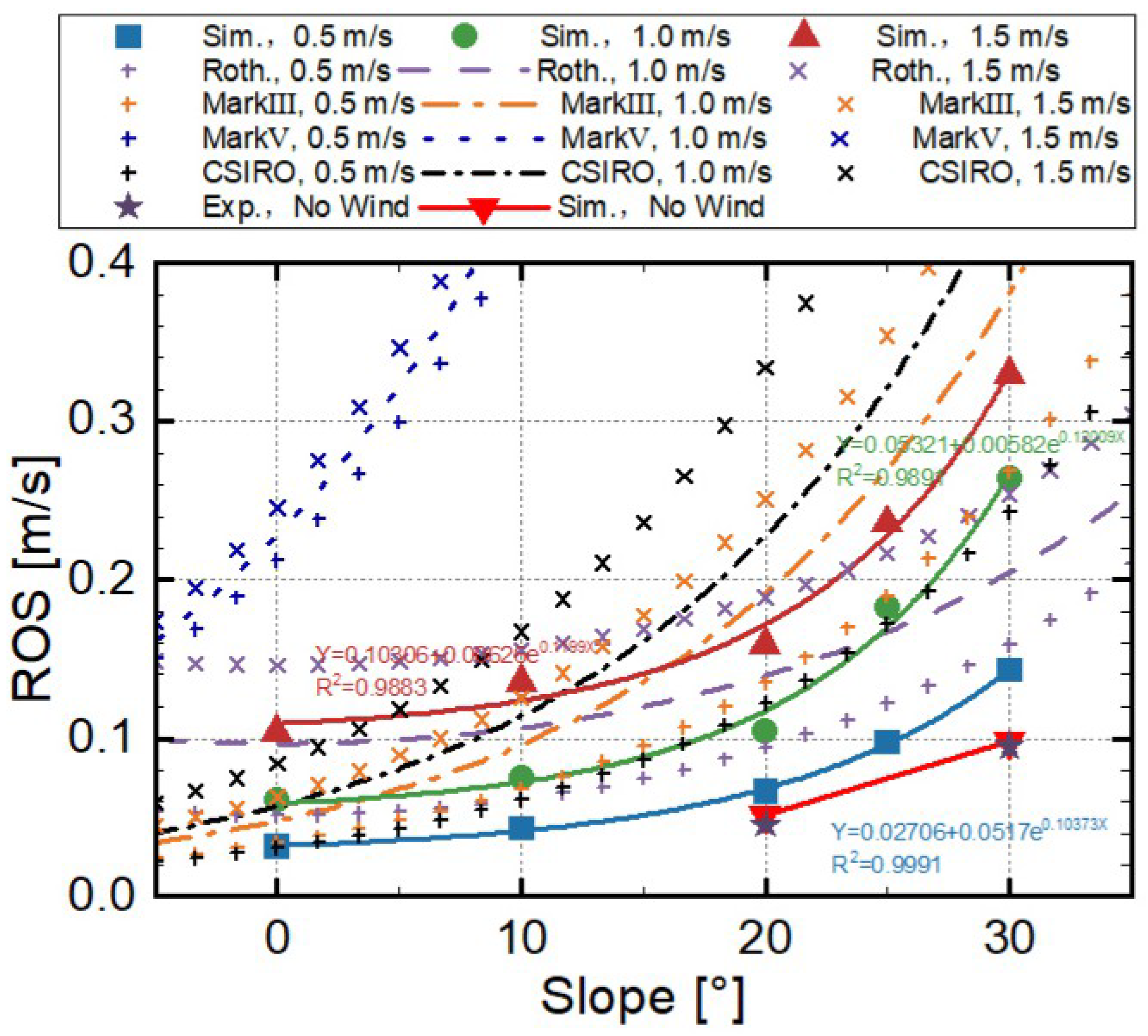
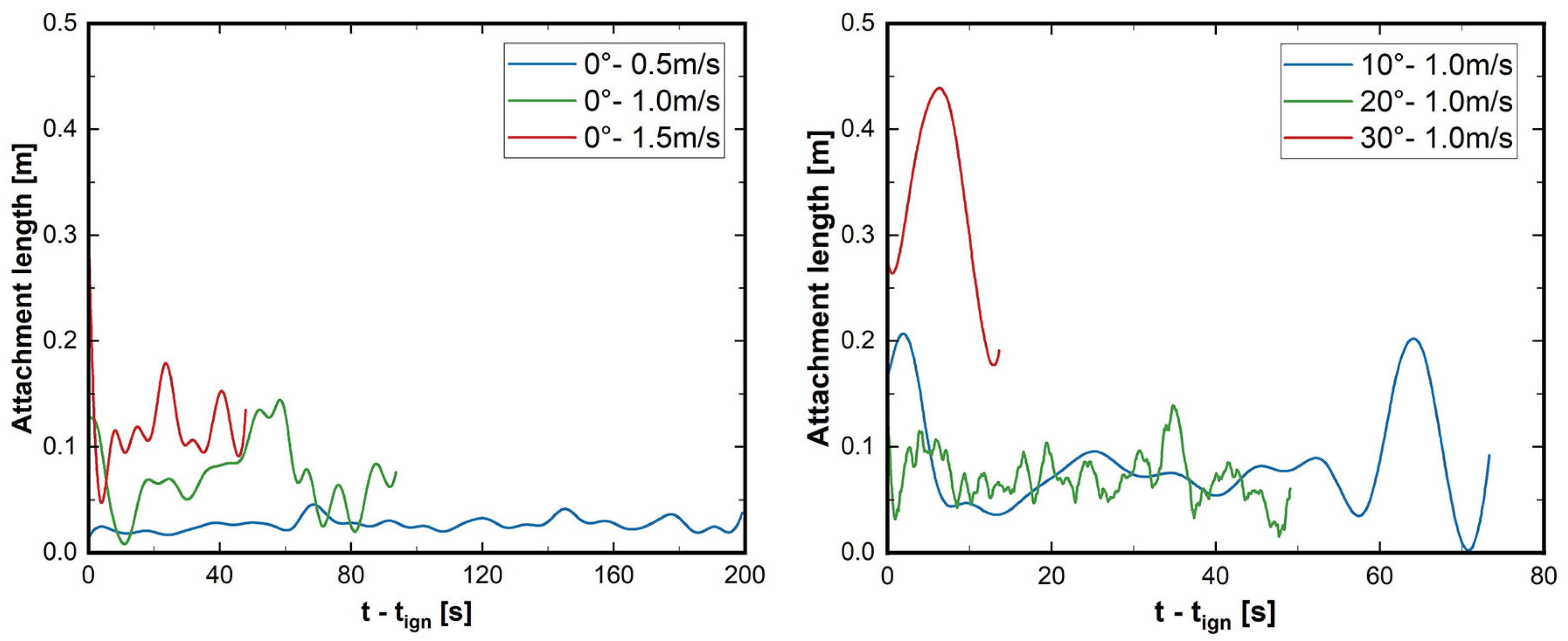
3.1. Fire Perimeter and Rate of Spread (ROS)
3.2. Flow Field and Perturbation Pressure
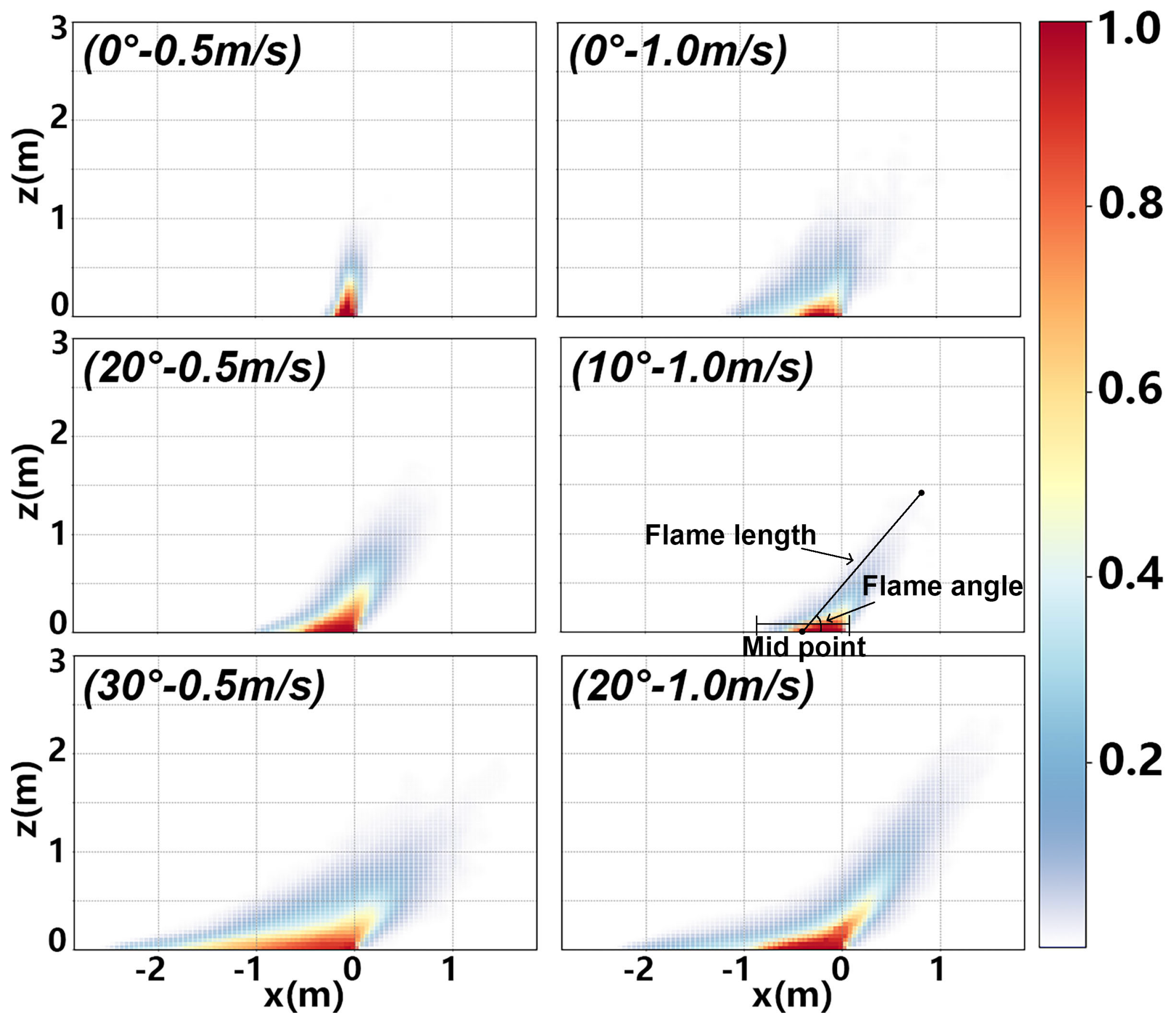
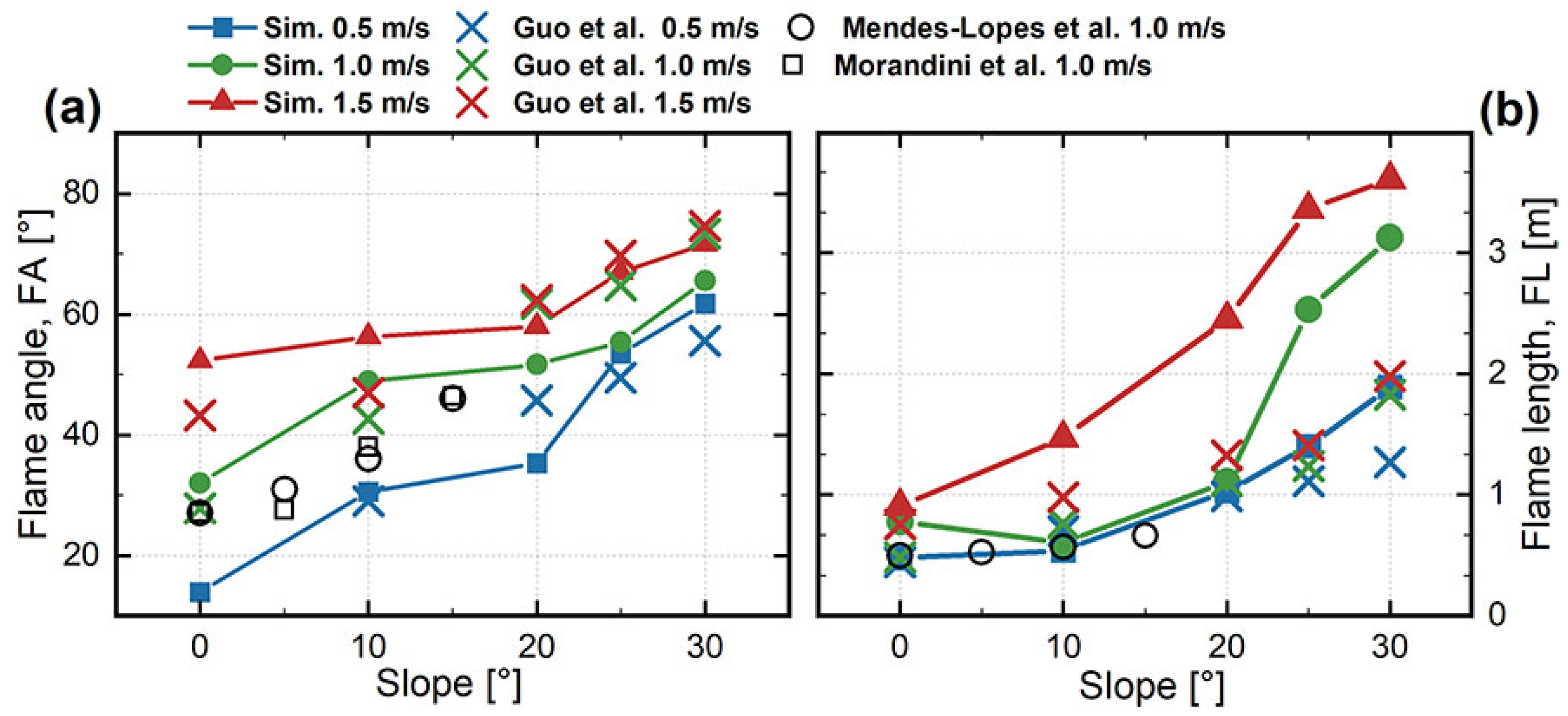
3.3. Flame Morphology
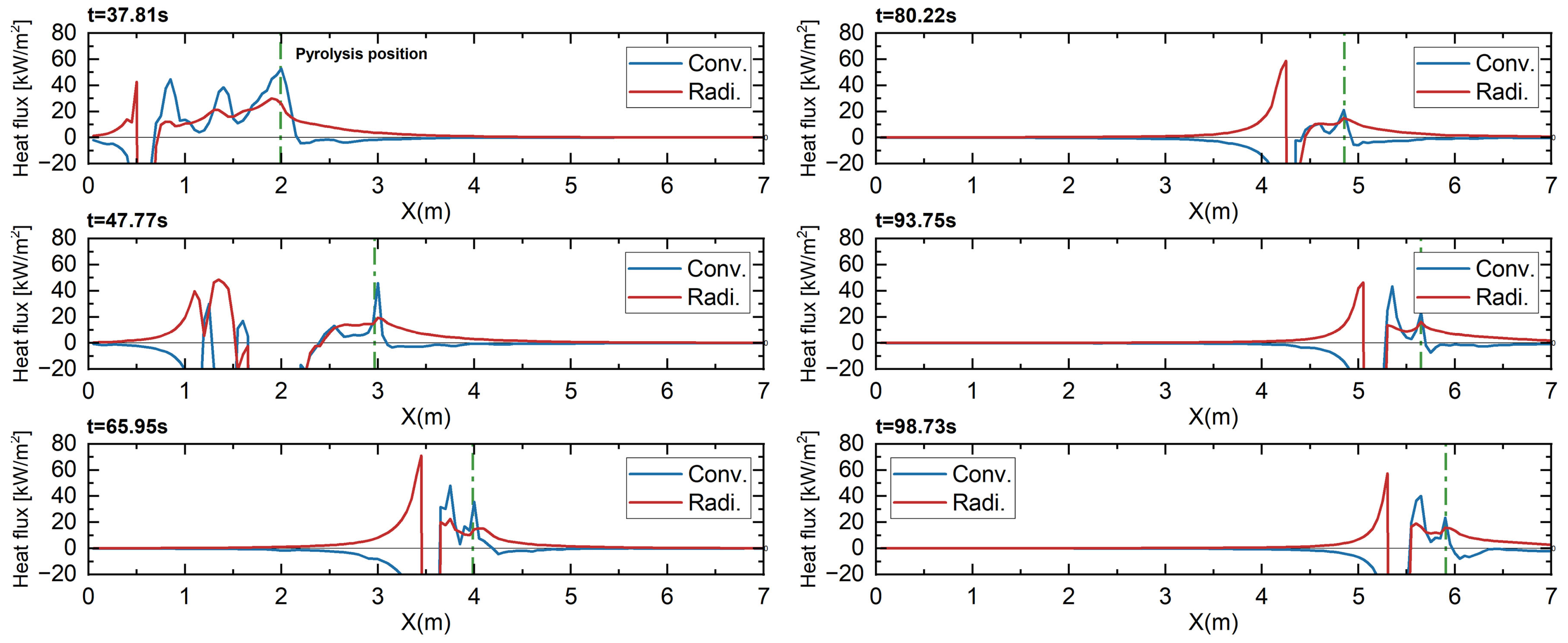
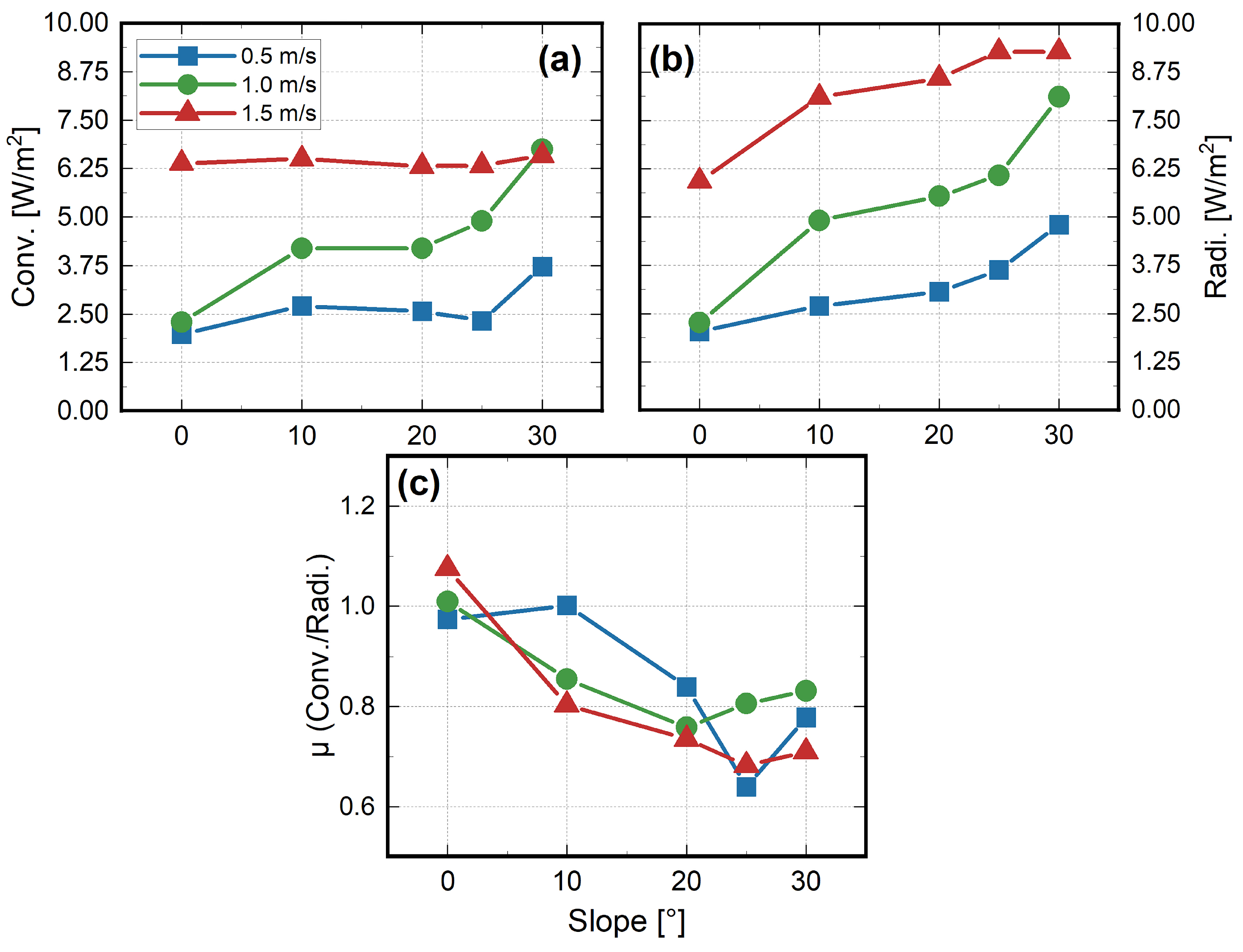
3.4. Radiative and Convective Heat Transfers
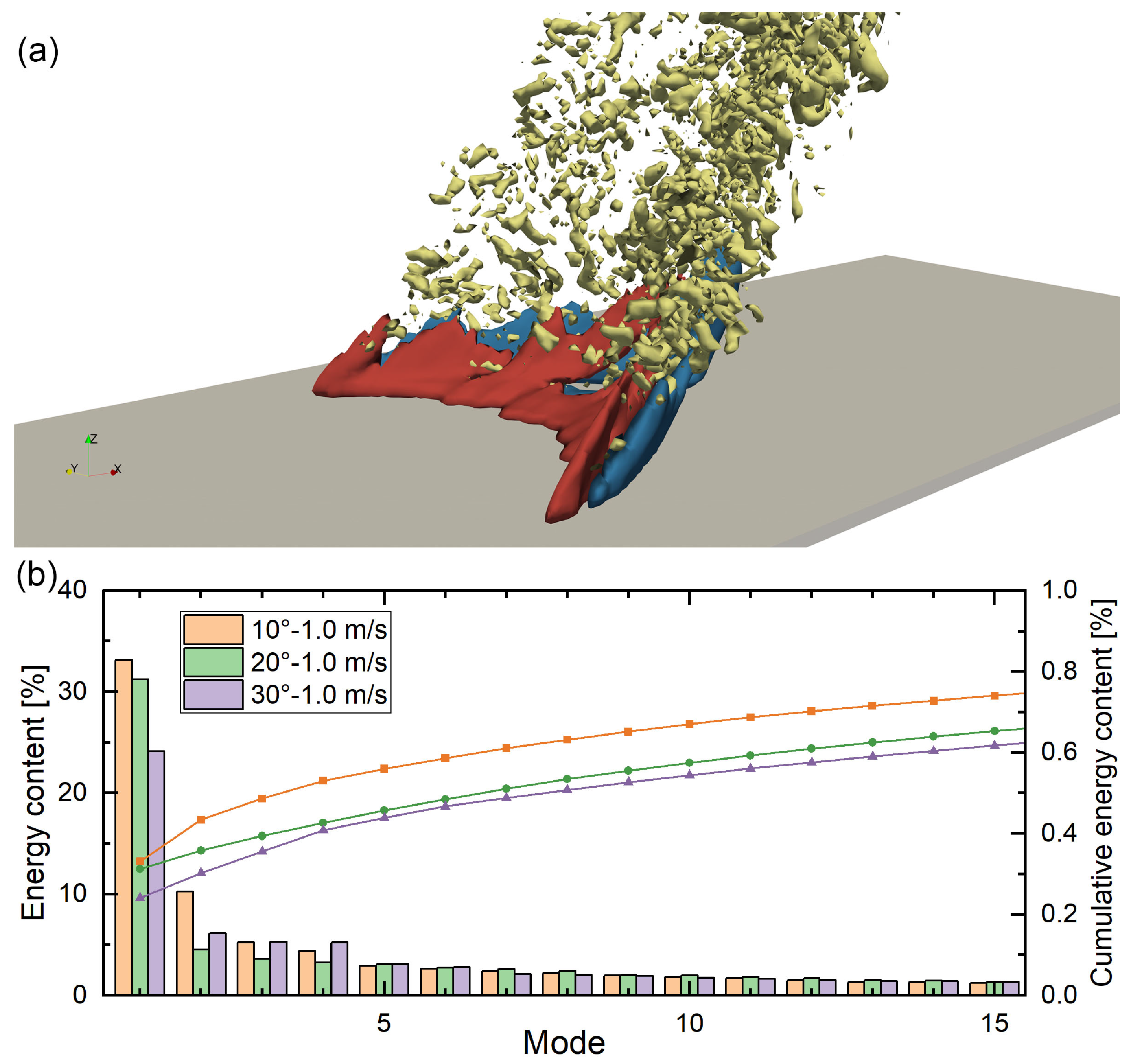
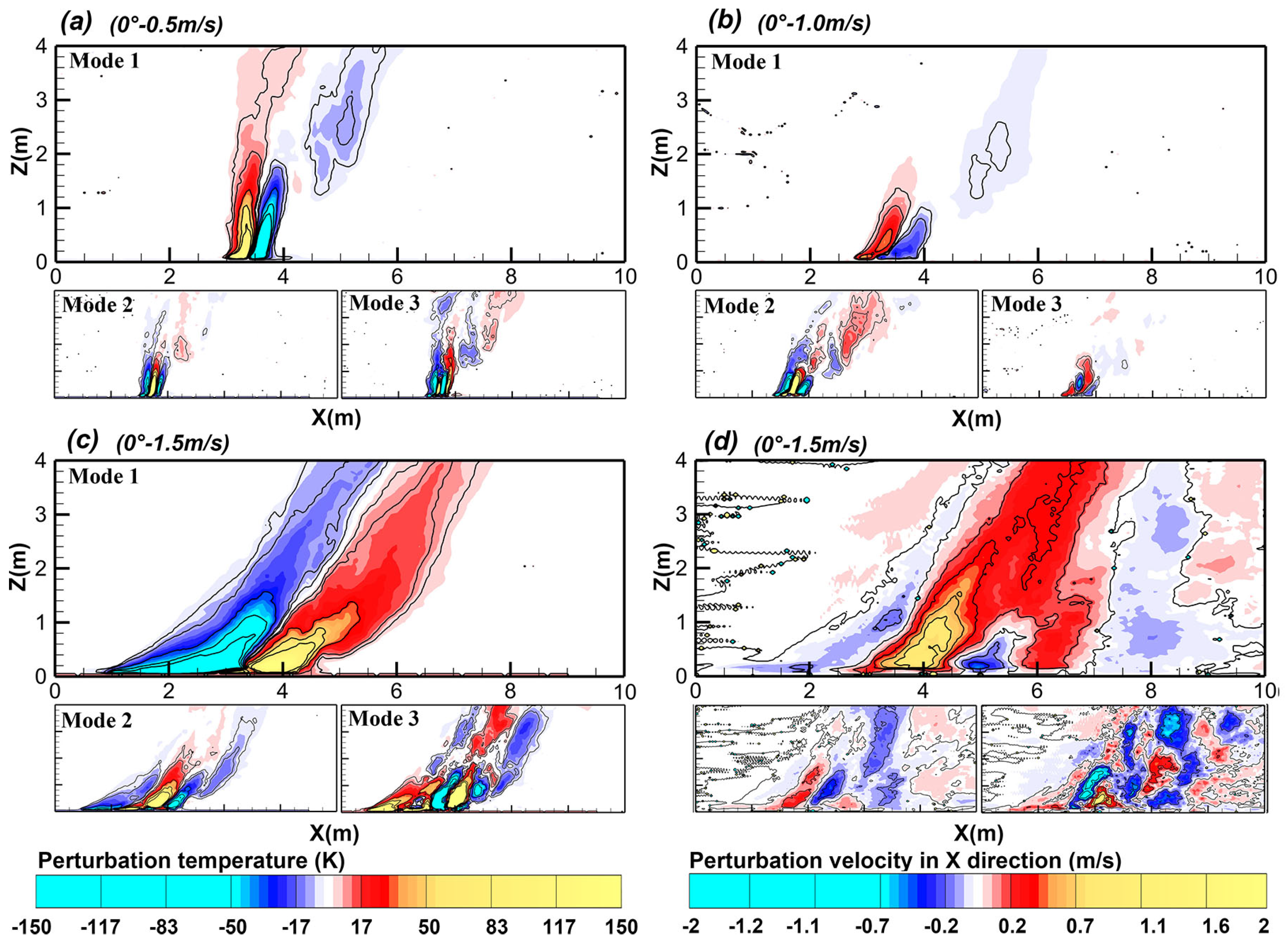
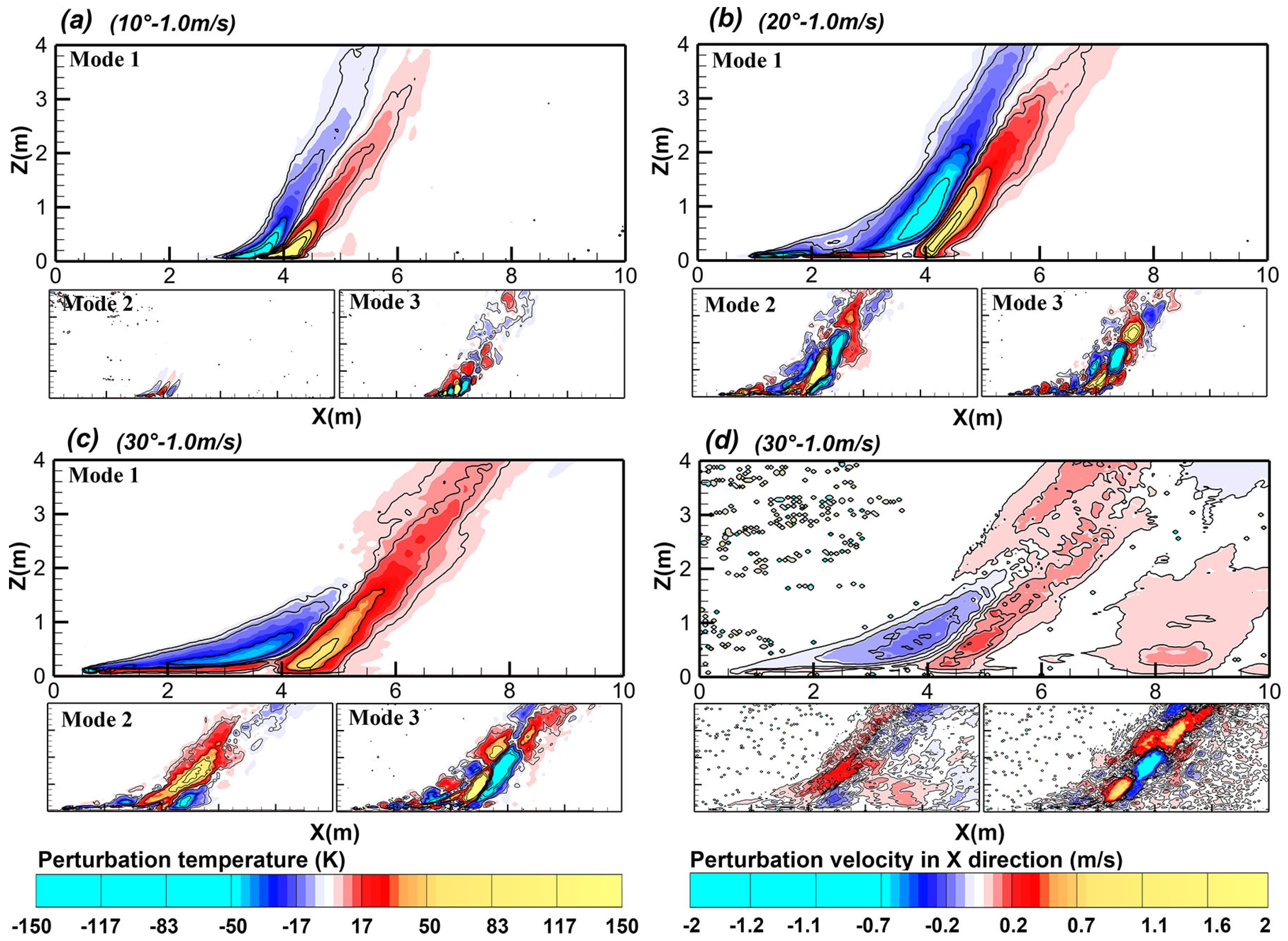
3.5. Proper Orthogonal Decomposition (POD) Analysis
4. Conclusions
- A power-law relationship was found between the ROS and slope angle. It was revealed that in high-slope conditions, the convergence of incoming wind and the weakened indraft air from the frontal area made a significant contribution to the abrupt rise in ROS and the eruptive spread of the head fire. As the slope increased, the flame also approached the combustible material under the action of gravity. As the slope gradually increased, the flame eventually coincided with the combustible material ahead, leading to a rapid increase in convective heat transfer.
- The enlarged volume of the fire plume was deemed to enhance the radiation heat transfer, and in contrast, the higher possibility of flame attachment at higher slopes (especially >20°) led to the prominent role of convective heating. When a flame attached to a wall, convective heat transfer significantly increased compared to radiative heat transfer.
- The investigation into the joint temperature–velocity field utilizing a POD approach revealed an increased forward pulsation of the flame front with the escalating slope, leading to a higher energy density in the pre-combustion zone ahead of the fire line, which further explained the mechanism underlying the accelerated flame propagation.
- For wildfire modeling, the more decent model should distinguish the respective roles of wind and slope, where the slope has a more profound effect in terms of determining flame structures and convective heat; the unsteady feature of flame puffing could be incorporated, considering the dominated mode pattern of backward–forward pulsation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Gas density | |
| Velocity vector | |
| Viscous stress | |
| Drag force by the fuel particles | |
| Vorticity vector | |
| Pressure perturbation | |
| Species diffusion coefficients | |
| Mass increment due to particle degradation | |
| Energy from the chemical reactions | |
| Heat release rate | |
| Energy transferred to particles | |
| Accounts for subgrid heat fluxes of conduction and radiation | |
| M | Fuel moisture content |
| Absorption coefficient | |
| Shape factor | |
| Stefan–Boltzman constant | |
| The endothermic effect of water evaporation | |
| Heats associated with pyrolysis and char oxidation | |
| Surface area to the volume ratio | |
| Packing ratio | |
| h | Convective heat transfer coefficient |
| Fuel mass | |
| Concentration of fuel | |
| A | Pre-exponential factor |
| Activation energy | |
| R | Universal gas constant |
| T | Gas temperature |
Appendix A

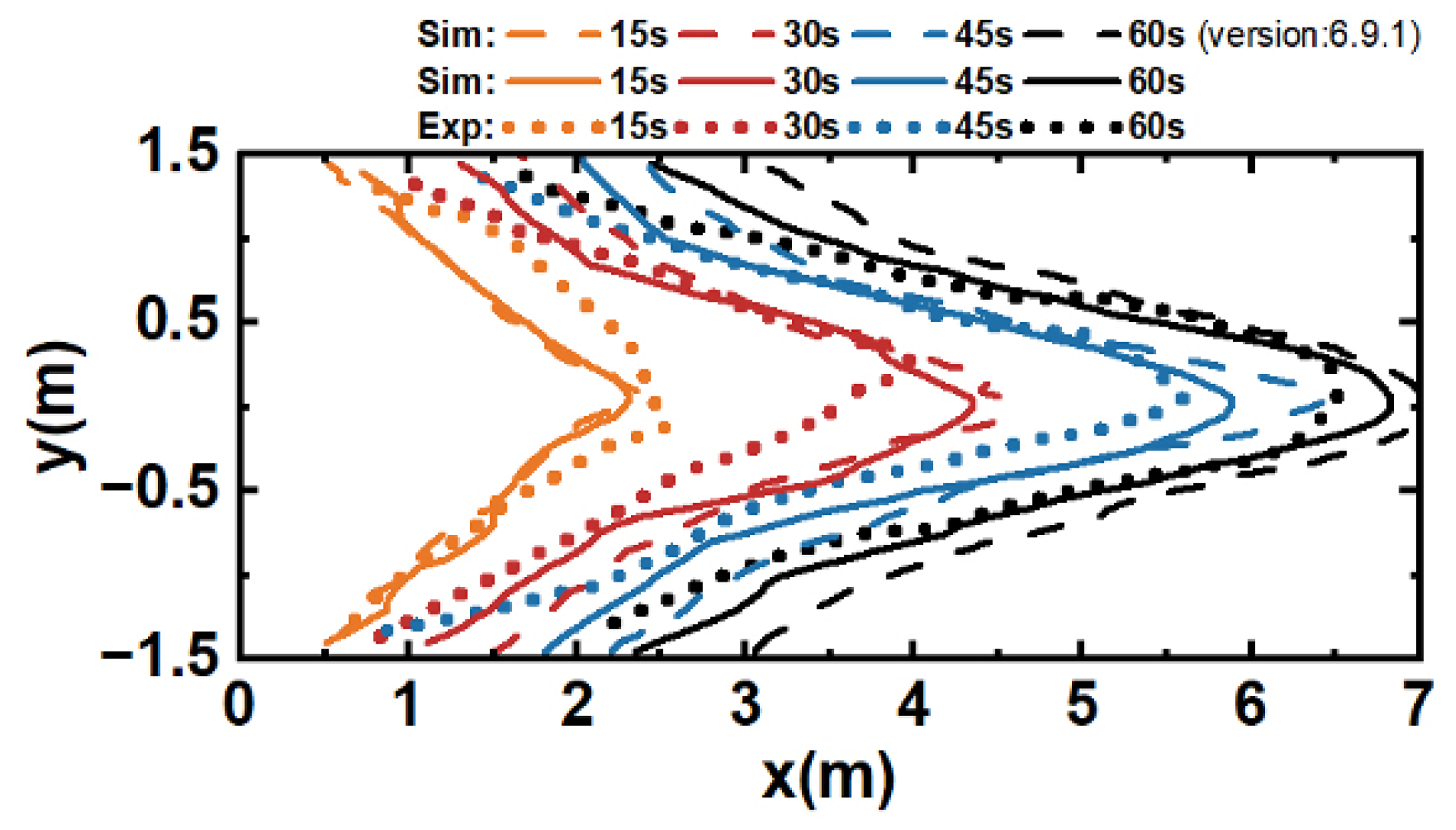
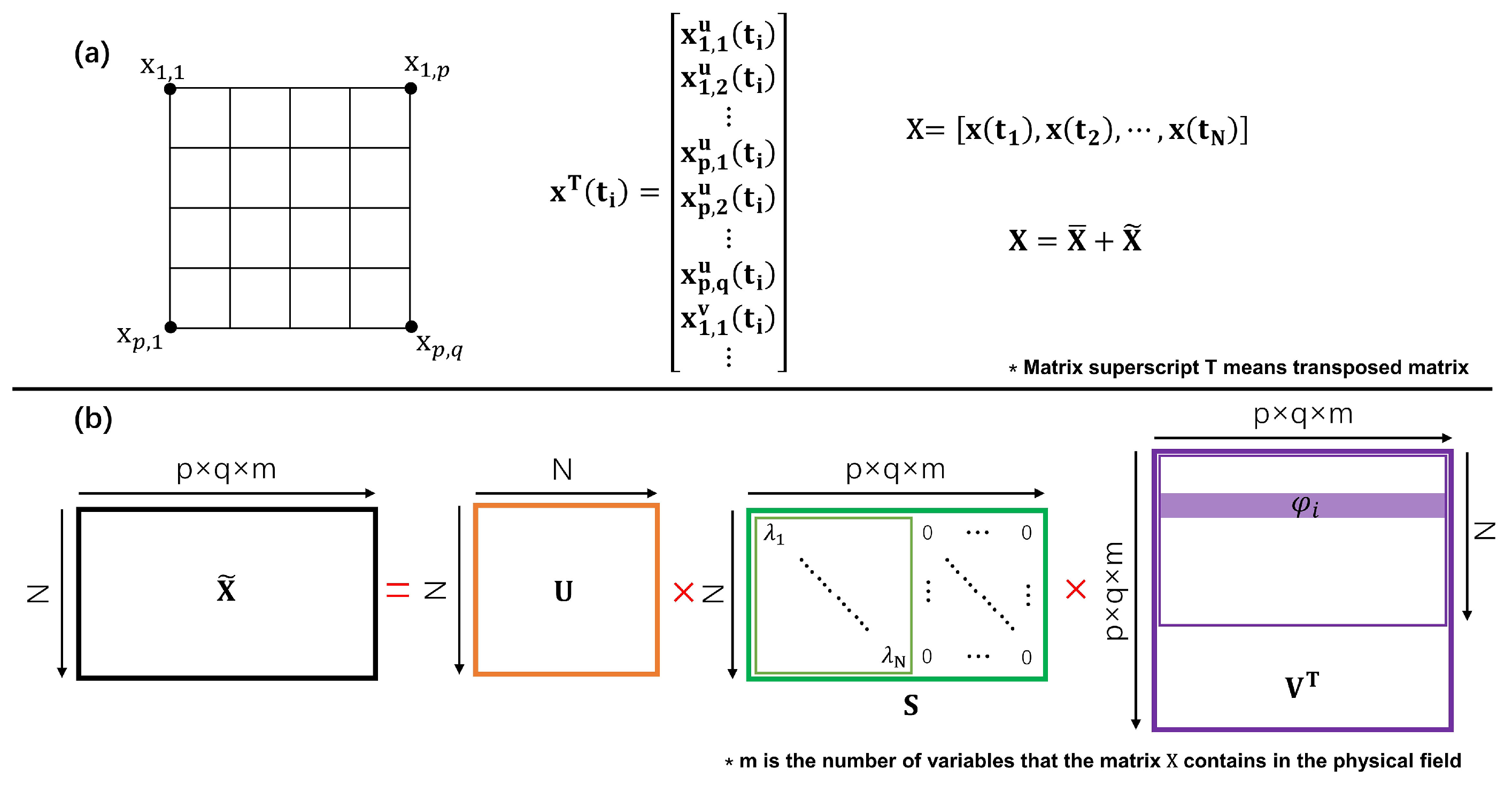
References
- Gajendiran, K.; Kandasamy, S.; Narayanan, M. Influences of wildfire on the forest ecosystem and climate change: A comprehensive study. Environ. Res. 2024, 240, 117537. [Google Scholar] [CrossRef] [PubMed]
- Folharini, S.; Vieira, A.; Bento-Gonçalves, A.; Silva, S.; Marques, T.; Novais, J. Bibliometric Analysis on Wildfires and Protected Areas. Sustainability 2023, 15, 8536. [Google Scholar] [CrossRef]
- Kramer, H.A.; Mockrin, M.H.; Alexandre, P.M.; Radeloff, V.C. High wildfire damage in interface communities in California. Int. J. Wildland Fire 2019, 28, 641–650. [Google Scholar] [CrossRef]
- Or, D.; Furtak-Cole, E.; Berli, M.; Shillito, R.; Ebrahimian, H.; Vahdat-Aboueshagh, H.; McKenna, S. Review of wildfire modeling considering effects on land surfaces. Earth-Sci. Rev. 2023, 245, 104569. [Google Scholar] [CrossRef]
- Sharples, J.J. Review of formal methodologies for wind–slope correction of wildfire rate of spread. Int. J. Wildland Fire 2008, 17, 179–193. [Google Scholar] [CrossRef]
- Clements, C.; Seto, D. Observations of Fire-Atmosphere Interactions and Near-Surface Heat Transport on a Slope. Bound.-Lay. Meteorol. 2015, 154, 409–426. [Google Scholar] [CrossRef]
- Seto, D.; Clements, C.; Heilman, W. Turbulence spectra measured during fire front passage. Agric. For. Meteorol. 2013, 169, 195–210. [Google Scholar] [CrossRef]
- Kochanski, A.; Jenkins, M.A.; Sun, R.; Krueger, S.; Abedi, S.; Charney, J. The importance of low-level environmental vertical wind shear to wildfire propagation: Proof of concept. J. Geophys. Res. Atmos. 2013, 118, 8238–8252. [Google Scholar] [CrossRef]
- Sun, R.; Krueger, S.; Jenkins, M.; Zulauf, M.; Charney, J. The importance of fire-atmosphere coupling and boundary-layer turbulence to wildfire spread. Int. J. Wildland Fire 2009, 18, 50–60. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, L.; Zheng, S. Numerical simulation on the effect of inclination on rectangular buoyancy-driven, turbulent diffusion flame. Phys. Fluids 2022, 34, 117106. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, N.; Gao, W.; Xie, X.; Zhang, L. Experimental study on the combustion characteristics of square fire. Fire Saf. J. 2023, 139, 103839. [Google Scholar] [CrossRef]
- Boboulos, M.; Purvis, M.R.I. Wind and slope effects on ROS during the fire propagation in East-Mediterranean pine forest litter. Fire Saf. J. 2009, 44, 764–769. [Google Scholar] [CrossRef]
- Dupuy, J.L.; Maréchal, J.; Portier, D.; Valette, J.C. The effects of slope and fuel bed width on laboratory fire behaviour. Int. J. Wildland Fire 2011, 20, 272–288. [Google Scholar] [CrossRef]
- Silvani, X.; Morandini, F.; Dupuy, J.L. Effects of slope on fire spread observed through video images and multiple-point thermal measurements. Exp. Therm. Fluid Sci. 2012, 41, 99–111. [Google Scholar] [CrossRef]
- Liu, N.; Yuan, X.; Xie, X.; Lei, J.; Gao, W.; Chen, H.; Zhang, L.; Li, H.; He, Q.; Korobeinichev, O. An experimental study on mechanism of eruptive fire. Combust. Sci. Technol. 2023, 195, 3168–3180. [Google Scholar] [CrossRef]
- Xie, X.; Liu, N.; Lei, J.; Shan, Y.; Zhang, L.; Chen, H.; Yuan, X.; Li, H. Upslope fire spread over a pine needle fuel bed in a trench associated with eruptive fire. Proc. Combust. Inst. 2017, 36, 3037–3044. [Google Scholar] [CrossRef]
- Anderson, W.R.; Catchpole, E.A.; Butler, B.W. Convective heat transfer in fire spread through fine fuel beds. Int. J. Wildland Fire 2010, 19, 284–298. [Google Scholar] [CrossRef]
- Rothermel, R. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Usda Forest Service General Technical Report; U.S. Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972; Volume 115. [Google Scholar]
- Nelson, R. An effective wind speed for models of fire spread. Int. J. Wildland Fire 2002, 11, 153–161. [Google Scholar] [CrossRef]
- Weise, D.R.; Biging, G.S. Effects of wind velocity and slope on flame properties. Can. J. For. Res. 1996, 26, 1849–1858. [Google Scholar] [CrossRef]
- Mell, W.; Jenkins, M.A.; Gould, J.; Cheney, P. A physics-based approach to modelling grassland fires. Int. J. Wildland Fire 2007, 16, 1–22. [Google Scholar] [CrossRef]
- Sánchez-Monroy, X.; Mell, W.; Torres-Arenas, J.; Butler, B.W. Fire spread upslope: Numerical simulation of laboratory experiments. Fire Saf. J. 2019, 108, 102844. [Google Scholar] [CrossRef]
- Moinuddin, K.A.M.; Sutherland, D.; Mell, W. Simulation study of grass fire using a physics-based model: Striving towards numerical rigour and the effect of grass height on the rate of spread. Int. J. Wildland Fire 2018, 27, 800–814. [Google Scholar] [CrossRef]
- Holmes, J.L.L.P.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, 2nd ed.; Cambridge Monographs on Mechanics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Li, W.; Zhao, D.; Zhang, L.; Chen, X. Proper orthogonal and dynamic mode decomposition analyses of nonlinear combustion instabilities in a solid-fuel ramjet combustor. Therm. Sci. Eng. Prog. 2022, 27, 101147. [Google Scholar] [CrossRef]
- Kostas, J.; Soria, J.; Chongo, M.S. A comparison between snapshot POD analysis of PIV velocity and vorticity data. Exp. Fluids 2005, 38, 146–160. [Google Scholar] [CrossRef]
- Podvin, B.; Fraigneau, Y.; Lusseyran, F.; Gougat, P. A reconstruction method for the flow past an open cavity. J. Fluids Eng. 2006, 128, 531–540. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, K.; Duwig, C. Investigation of wet ammonia combustion characteristics using LES with finite-rate chemistry. Fuel 2022, 311, 122422. [Google Scholar] [CrossRef]
- Bhatia, B.; De, A.; Roekaerts, D.; Masri, A.R. Numerical analysis of dilute methanol spray flames in vitiated coflow using extended flamelet generated manifold model. Phys. Fluids 2022, 34, 075111. [Google Scholar] [CrossRef]
- Guelpa, E.; Sciacovelli, A.; Vittorio, V.; Ascoli, D. Faster prediction of wildfire behaviour by physical models through application of proper orthogonal decomposition. Int. J. Wildland Fire 2016, 25, 1181–1192. [Google Scholar] [CrossRef]
- McGrattan, K.B.; McDermott, R.J.; Weinschenk, C.G.; Forney, G.P. Fire Dynamics Simulator, Technical Reference Guide, 6th ed.; Special Publication (NIST SP); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Innocent, J.; Sutherland, D.; Khan, N.; Moinuddin, K. Physics-based simulations of grassfire propagation on sloped terrain at field scale: Motivations, model reliability, rate of spread and fire intensity. Int. J. Wildland Fire 2023, 32, 496–512. [Google Scholar] [CrossRef]
- Porterie, B.; Consalvi, J.; Kaiss, A.; Loraud, J. Predicting wildland fire behavior and emissions using a fine-scale physical model. Numer. Heat Tran. 2005, 47, 571–591. [Google Scholar] [CrossRef]
- Yan, Z.; Gong, J.; Louste, C.; Wu, J.; Fang, J. Modal analysis of EHD jets through the SVD-based POD technique. J. Electrost. 2023, 126, 103858. [Google Scholar] [CrossRef]
- Kapulla, R.; Manohar, K.H.; Paranjape, S.; Paladino, D. Self-similarity for statistical properties in low-order representations of a large-scale turbulent round jet based on the proper orthogonal decomposition. Exp. Therm. Fluid Sci. 2021, 123, 110320. [Google Scholar] [CrossRef]
- Tewarson, A. Prediction of Fire Properties of Materials. Part 1: Aliphatic and Aromatic Hydrocarbons and Related Polymers; Report No. NBS-GCR-86-521; National Institute of Standards and Technology: Gaithersburg. MD, USA, 1986. [Google Scholar]
- Xie, X.; Liu, N.; Raposo, J.R.; Viegas, D.X.; Yuan, X.; Tu, R. An experimental and analytical investigation of canyon fire spread. Combust. Flame 2017, 212, 367–376. [Google Scholar] [CrossRef]
- Li, H.; Liu, N.; Xie, X.; Zhang, L.; Yuan, X.; He, Q.; Viegas, D. Effect of Fuel Bed Width on Upslope Fire Spread: An Experimental Study. Fire Technol. 2021, 57, 1063–1076. [Google Scholar] [CrossRef]
- Porterie, B.; Morvan, D.; Loraud, J.; Larini, M. Firespread through fuel beds: Modeling of wind-aided fires and induced hydrodynamics. Phys. Fluids 2000, 12, 1762–1782. [Google Scholar] [CrossRef]
- Finney, M.A.; Cohen, J.D.; Forthofer, J.M.; McAllister, S.S.; Gollner, M.J.; Gorham, D.J.; Saito, K.; Akafuah, N.K.; Adam, B.A.; English, J.D. Role of buoyant flame dynamics in wildfire spread. Proc. Natl. Acad. Sci. USA 2015, 112, 9833–9838. [Google Scholar] [CrossRef]
- Hassan, A.; Accary, G. Physics-based modelling of wind-driven junction fires. Fire Saf. J. 2024, 142, 104039. [Google Scholar] [CrossRef]
- Balbi, J.H.; Chatelon, F.J.; Morvan, D.; Rossi, J.; Marcelli, T.; Morandini, F. A convective-radiative propagation model for wildland fires. Int. J. Wildland Fire. 2020, 29, 723–738. [Google Scholar] [CrossRef]
- Ma, T.G.; Quintiere, J.G. Numerical simulation of axi-symmetric fire plumes: Accuracy and limitations. Fire Saf. J. 2003, 38, 467–492. [Google Scholar] [CrossRef]
- Guo, H.; Xiang, D.; Kong, L.; Gao, Y.; Zhang, Y. Upslope fire spread and heat transfer mechanism over a pine needle fuel bed with different slopes and winds. Appl. Therm. Eng. 2023, 229, 120605. [Google Scholar] [CrossRef]
- Morandini, F.; Santoni, P.A.; Balbi, J.H. The contribution of radiant heat transfer to laboratory-scale fire spread under the influences of wind and slope. Fire Saf. J. 2001, 36, 519–543. [Google Scholar] [CrossRef]
- Mendes-Lopes, J.M.C.; Ventura, J.M.P.; Amaral, J.M.P. Flame characteristics, temperature-time curves, and rate of spread in fires propagating in a bed of Pinus pinaster needles. Int. J. Wildland Fire 2003, 12, 67–84. [Google Scholar] [CrossRef]
- Nelson, R.M.; Butler, B.W.; Weise, D.R. Entrainment regimes and flame characteristics of wildland fires. Int. J. Wildland Fire 2012, 21, 127–140. [Google Scholar] [CrossRef]
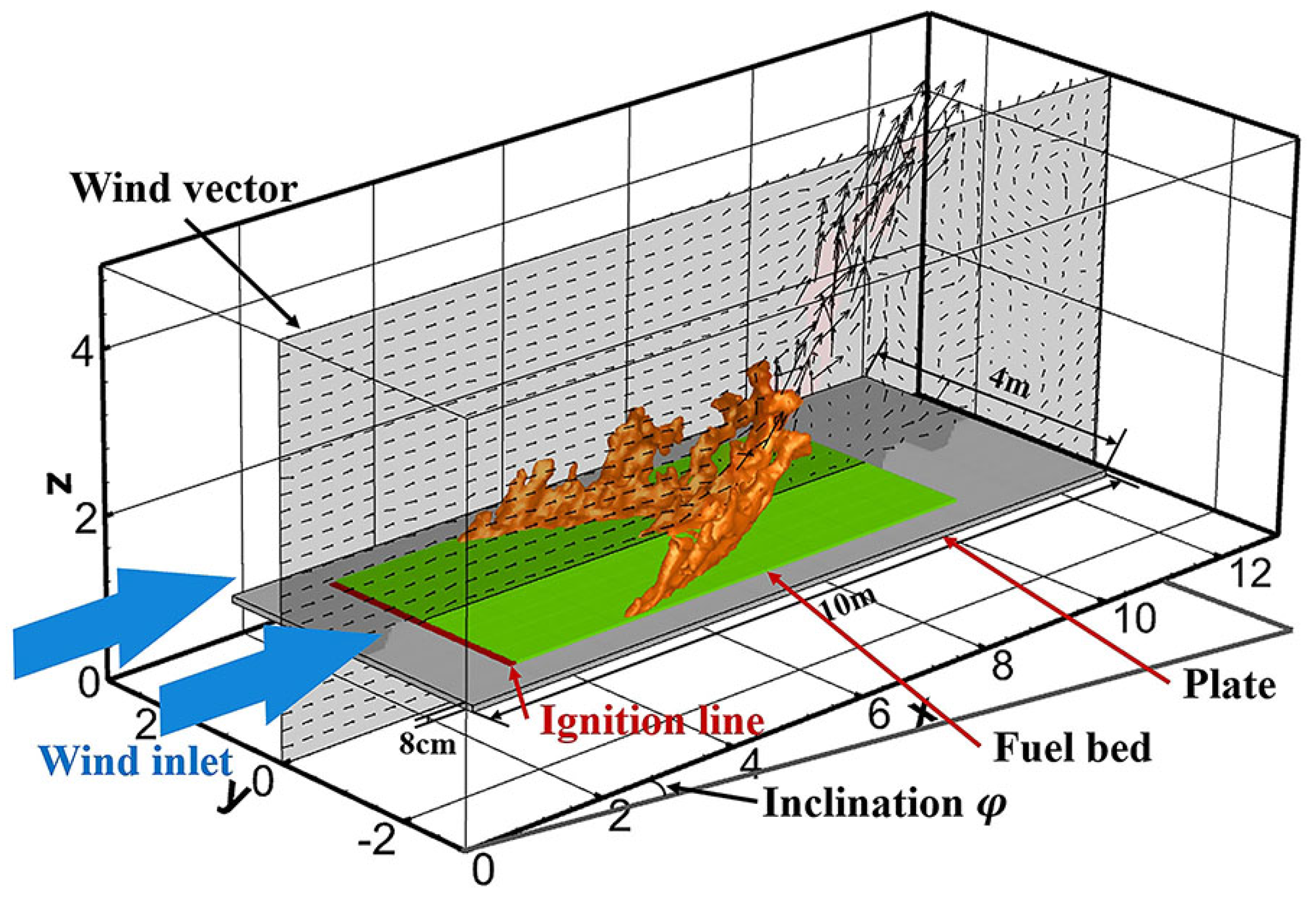

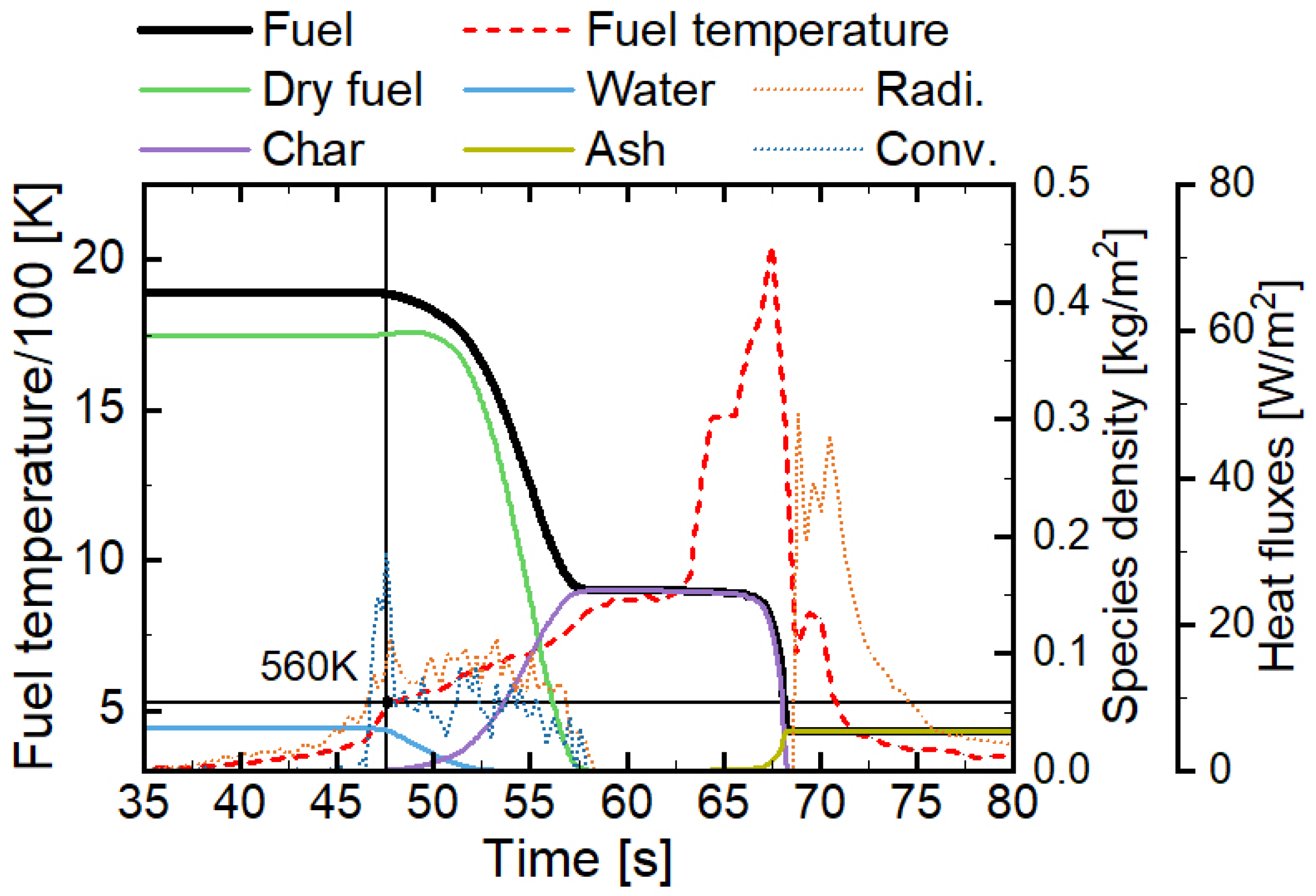
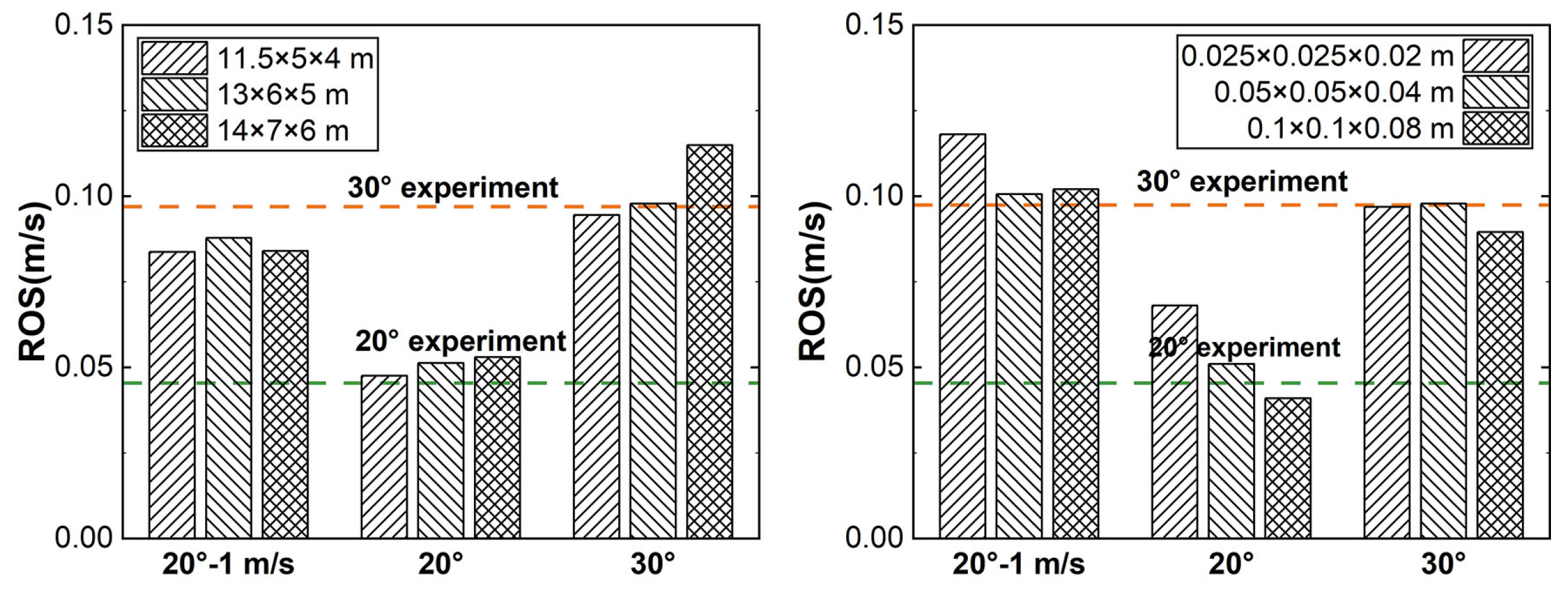
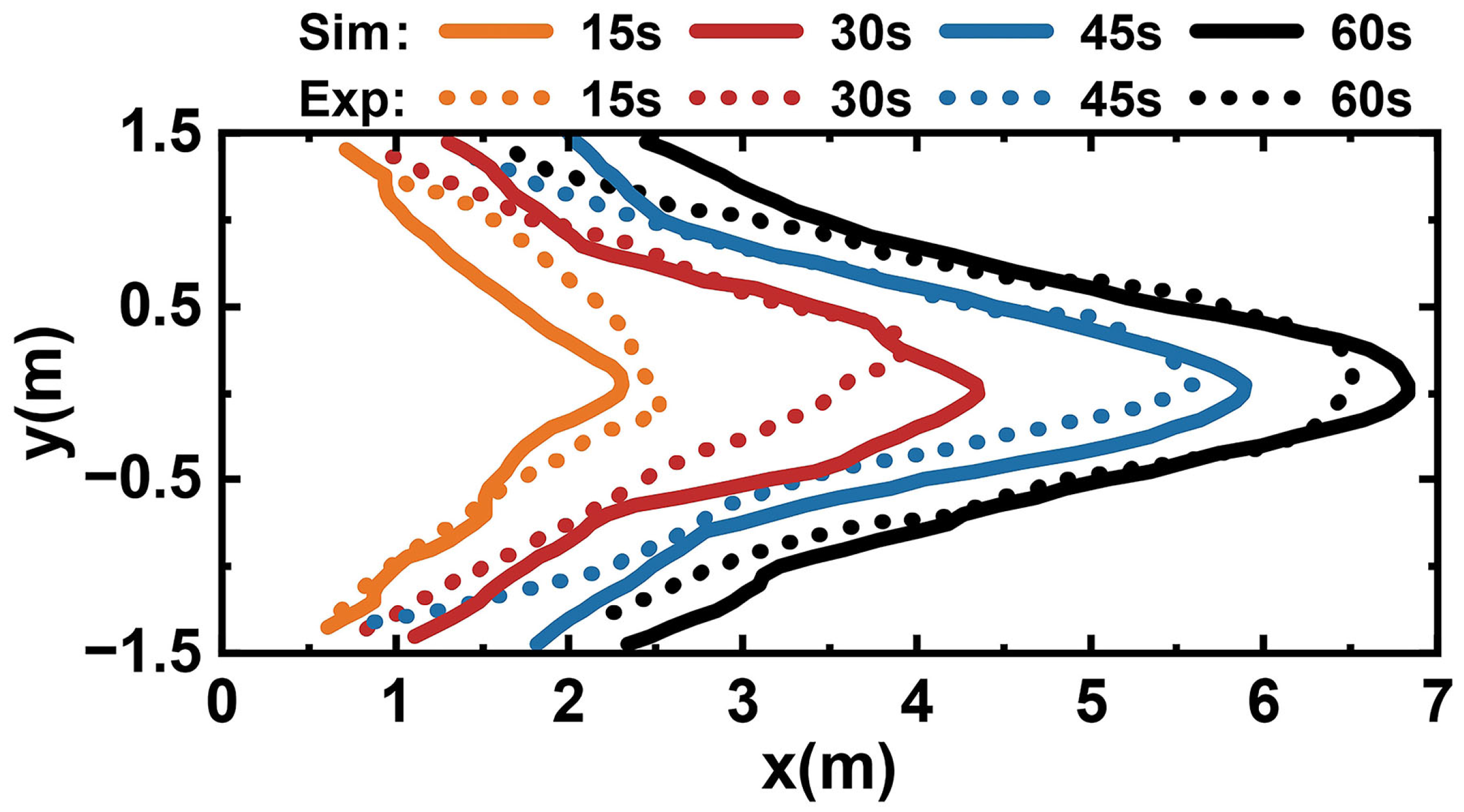
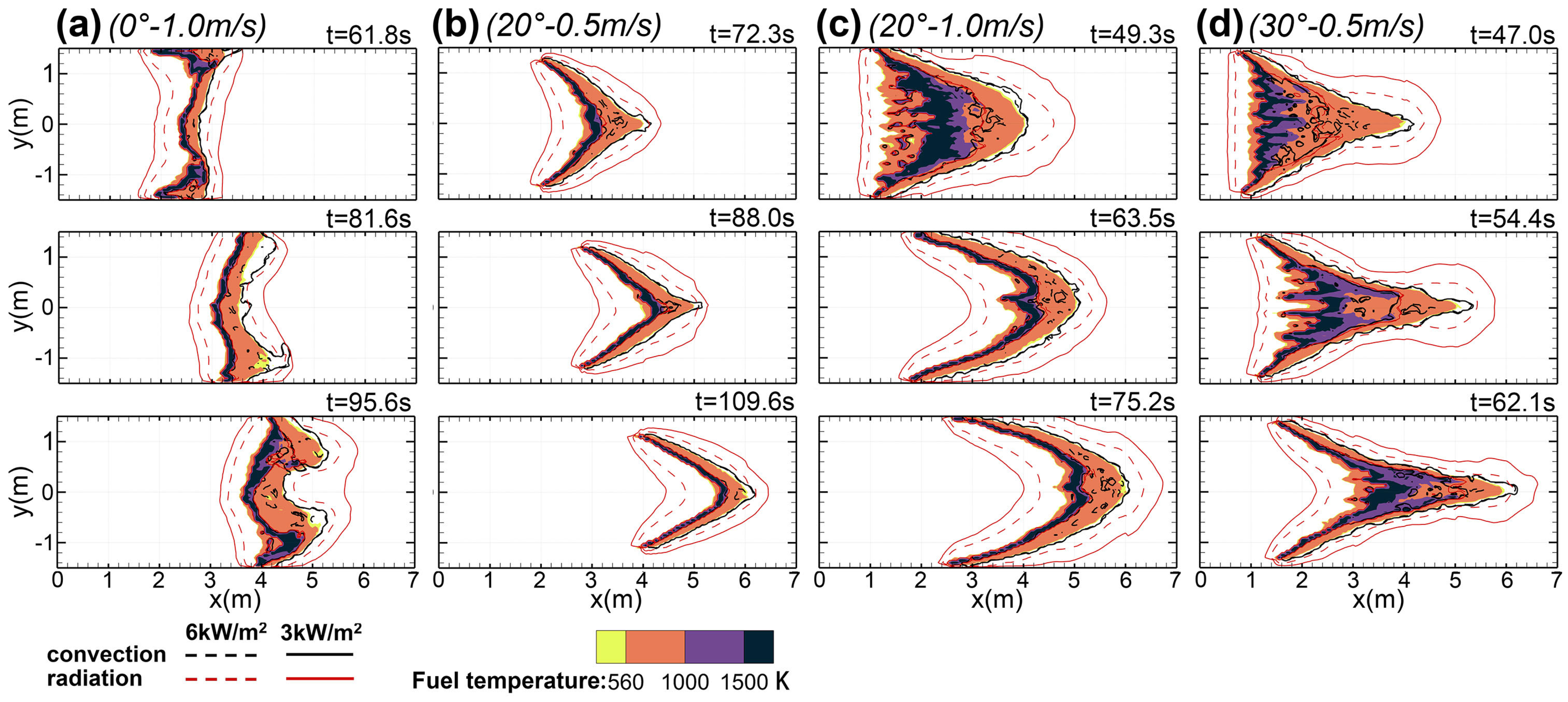


| Fuel Parameter (Units) | Value |
|---|---|
| Fuel density () | 780 [14] |
| Fuel load () | 0.4 [14] |
| Fuel height (m) | 0.08 [14] |
| Surface-to-volume ratio (1/m) | 3800 |
| Fuel moisture (%) | 10 [14] |
| Heat of combustion (kJ/kg) | 17,700 [14] |
| Specific heat (kJ/(kg·K)) | 1.2 |
| Conductivity (W/(m·K)) | 0.1 |
| Ambient temperature (K) | 304 [14] |
| Vegetation char fraction (-) | 0.2 [14] |
| Relative humidity (%) | 40 [14] |
| Radiation fraction (%) | 0.342 [14] |
| 0.5 m/s | ✓ | ✓ | ✓ | ✓ | ✓ |
| 1.0 m/s | ✓ | ✓ | ✓ | ✓ | ✓ |
| 1.5 m/s | ✓ | ✓ | ✓ | ✓ | ✓ |
| 0.5 m/s | 1.0 m/s | 1.5 m/s | |
|---|---|---|---|
| 122.6 | 24.4 | 9.8 | |
| 164.9 | 27.3 | 12.6 | |
| 194.4 | 32.9 | 15.9 | |
| 247.9 | 83.3 | 18.2 | |
| 526.1 | 103.0 | 27.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, C.; Hu, Y.; Ma, Y.; Yang, J. Simulation Study and Proper Orthogonal Decomposition Analysis of Buoyant Flame Dynamics and Heat Transfer of Wind-Aided Fires Spreading on Sloped Terrain. Fire 2025, 8, 139. https://doi.org/10.3390/fire8040139
Su C, Hu Y, Ma Y, Yang J. Simulation Study and Proper Orthogonal Decomposition Analysis of Buoyant Flame Dynamics and Heat Transfer of Wind-Aided Fires Spreading on Sloped Terrain. Fire. 2025; 8(4):139. https://doi.org/10.3390/fire8040139
Chicago/Turabian StyleSu, Chenyao, Yong Hu, Yiwang Ma, and Jiuling Yang. 2025. "Simulation Study and Proper Orthogonal Decomposition Analysis of Buoyant Flame Dynamics and Heat Transfer of Wind-Aided Fires Spreading on Sloped Terrain" Fire 8, no. 4: 139. https://doi.org/10.3390/fire8040139
APA StyleSu, C., Hu, Y., Ma, Y., & Yang, J. (2025). Simulation Study and Proper Orthogonal Decomposition Analysis of Buoyant Flame Dynamics and Heat Transfer of Wind-Aided Fires Spreading on Sloped Terrain. Fire, 8(4), 139. https://doi.org/10.3390/fire8040139






