1. Introduction
Wildfires can have severe environmental, economic, and social consequences. Their frequency and intensity have increased globally in recent decades, driven by climate change, land use change, and extended dry seasons [
1]. As wildfires become more frequent and destructive, the demand for accurate and robust fire spread models has become increasingly urgent.
A central challenge in wildfire modelling is predicting fire spread while accounting for the uncertainties inherent in natural processes. In Canada, widely used systems such as the Canadian Forest Fire Behaviour Prediction (FBP) System [
2] and the Prometheus wildfire growth simulator [
3] are based on deterministic frameworks. While operationally effective, these models rely on a relatively narrow empirical foundation, drawing mainly from controlled field experiments and selected case studies linked to the Canadian Forest Fire Weather Index (FWI) System [
4]. Consequently, they fail to capture the stochastic nature of fire behaviour and environmental variability, leading to discrepancies between predicted and observed fire dynamics, particularly under rapidly changing or extreme conditions. There have been attempts to incorporate stochasticity into fire spread models, such as Burn-P3 [
5], but often the randomness is induced only by randomizing the weather. The papers [
6,
7] suggest that these kinds of models do not adequately capture uncertainty.
Satellite remote sensing provides a valuable supplement to ground-based fire modelling. Instruments such as MODIS and VIIRS enable near-real-time fire detection [
8], while higher-resolution platforms such as Sentinel-2 support detailed burn area mapping [
9]. These tools are especially useful in remote and inaccessible regions. However, they face limitations in continuous fire monitoring. Most Earth observation satellites pass over Canadian latitudes only once or twice per day, typically during late morning or early afternoon, missing the late afternoon to evening period when fire activity peaks [
10]. In addition, the data latency may range from hours to days, and the coarse spatial resolution constrains the ability to capture fine-scale dynamics. These limitations are particularly critical near the wildland–urban interface, where small-scale fire behaviour can disproportionately affect infrastructure, human safety, and evacuation planning [
11].
Given these constraints, our study is motivated by the need for a more granular and temporally responsive approach to measuring fire spread. The main objective of this paper is to complement wildfire science with a computer vision technique that enables the systematic study of the anisotropic spread patterns of fire. We leverage experimental fire videos recorded under controlled conditions to capture the real-time evolution of fire perimeters. Although such burns are necessarily small in scale and cannot replicate the full complexity of wildland fires, they provide a proxy for assessing fire behaviour in a controlled setting. Our contribution forms a proof of concept that anticipates broader application as high-frequency satellite and airborne imagery becomes more available. By segmenting fire perimeters in these controlled burns, we can then characterize the variability in the ROS and subsequently highlight the importance of incorporating stochasticity into fire modelling frameworks.
The remainder of this paper is structured as follows.
Section 2 reviews the background and related work in fire spread modelling, with an emphasis on deterministic frameworks and efforts to integrate uncertainty.
Section 3 describes the experimental and field burn datasets and data collection process.
Section 4 presents the methodology, combining segmentation-based perimeter tracking with statistical models of ROS.
Section 5 reports the results, demonstrating how the approach captures spread variability and reveals the limitations of existing models.
Section 6 concludes the paper with limitations and future directions.
2. Background and Related Work
Wildfire modelling encompasses a wide range of approaches tailored to different objectives, data availability, and computational resources. Below, we summarize the main categories of approaches and highlight their relevance to this study.
2.1. Empirical and Semi-Empirical Models
Empirical and semi-empirical models are among the most widely used, relying on statistical relationships derived from historical fire behaviour and environmental conditions. Systems such as the Fire Weather Index (FWI) [
4] and the Canadian FBP System [
2] use empirical equations from field and laboratory studies to predict fire spread based on the fuel type, weather, and topography. These models provide practical predictions of fire spread and intensity, but their reliance on past patterns limits their adaptability under novel or extreme conditions.
Semi-empirical models, including BEHAVE Plus [
12] and Prometheus [
3], combine statistical relationships with simplified physical principles to improve the balance between accuracy and computational efficiency. Later enhancements, such as bootstrap smoothing in Prometheus [
13], and geometric approaches to stabilize fire-front propagation [
14], introduced limited stochasticity but remain constrained by deterministic assumptions.
2.2. Physical and Deterministic Models
By contrast, physical and deterministic models such as FIRETEC and the Wildland–Urban Interface Fire Dynamics Simulator (WFDS) simulate fire behaviour from fundamental physical principles, offering detailed representations of combustion, heat transfer, and fire–atmosphere interactions [
15]. While these models yield valuable insights into fire physics, their extreme computational demands limit real-time application. Furthermore, their deterministic structure often underrepresents the variability inherent in wildland fire behaviour, leading to overconfident predictions in operational contexts [
16,
17].
2.3. Stochastic and Probabilistic Models
To explicitly represent uncertainty, stochastic and probabilistic models have been developed. Tools such as FlamMap [
18], FSim [
19], and Dionysus [
6] generate ensembles of fire scenarios by sampling input variability. For instance, Dionysus extends Prometheus by producing probability contours around predicted fire fronts through the statistical modelling of input uncertainty. Other approaches incorporate stochasticity directly into fire growth dynamics, capturing not only the mean spread but also variability in spotting and timing [
20]. Validation methods comparing simulated and observed rate-of-spread distributions [
21] further highlight the need for models that reflect real-world variability.
2.4. Data-Driven and Image-Based Approaches
Alongside these approaches, data-driven methods have gained traction. Machine learning techniques including neural networks and random forests are increasingly applied to wildfire susceptibility mapping, real-time detection, and predictive modelling [
22]. Cellular automata models also offer computationally efficient simulations of landscape-scale fire spread by representing terrain as grids with rule-based transitions among neighbouring cells [
23,
24], although they simplify many physical processes. More recently, image-based segmentation has emerged as a complementary direction, enabling fire detection and spread analysis by isolating fire-affected regions in aerial and satellite imagery [
25,
26]. Traditional methods such as thresholding, edge detection, and region growing have been used for perimeter delineation [
27], while deep learning approaches, particularly convolutional neural networks (CNNs), now provide pixel-level classification through more advanced neural network architectures [
28,
29]. Advanced models including YOLOv7 and U-Net variants have shown strong performance under noisy, occluded conditions, supporting near-real-time wildfire monitoring [
30,
31,
32]. Emerging tools such as the Segment Anything Model (SAM) [
33] reduce manual annotation requirements and enable flexible segmentation with minimal supervision. Integrating these techniques into fire spread modelling frameworks offers opportunities to integrate perimeter tracking with fire behaviour modelling.
2.5. Environmental Drivers of Fire Spread
Alongside modelling innovations, environmental drivers remain fundamental to fire behaviour, particularly temperature, fuel moisture, wind, and slope [
34]. Higher temperatures and lower moisture reduce ignition thresholds, while drying times alter flammability. Wind accelerates combustion by enhancing oxygen supply and flame tilt, and slope preheats uphill fuels via convection and radiation, producing faster upslope spread [
35,
36]. In the Canadian FBP System, these drivers are combined into a semi-empirical formulation:
where the rate of spread index (RSI) reflects wind and fine-fuel moisture, the buildup effect (BE) accounts for seasonal fuel buildup and drying, and the slope factor (SF) applies a multiplicative correction for terrain slope. The detailed formulation of RSI and BE is given in
Appendix A. The slope factor on terrain inclined at
degrees follows Van Wagner’s exponential formulation [
37],
with constants
and
; this remains the operational standard, albeit derived from small-scale red pine needle burns. In this study, we treat these parameters as free variables to be re-estimated from experimental data.
2.6. Mixed-Effects Models and Stochastic Variability
Despite these established formulations, fire behaviour exhibits substantial variability and stochasticity due to complex interactions among environmental factors. This uncertainty challenges operational forecasting, particularly under climate change and shifting disturbance regimes [
38]. Mixed-effects models offer a statistical framework for addressing this variability by combining fixed effects (systematic drivers such as slope or fuel moisture) with random effects (unexplained variation across fires or replicates) [
39]. Prior work has applied mixed-effects models to containment probability [
40], fire risk forecasting [
41], and wildfire occurrence data [
42], while experimental studies show their utility in disentangling controlled variables from intrinsic stochastic behaviour [
43]. When coupled with segmentation-based perimeter tracking, mixed-effects models enable the systematic evaluation of both deterministic drivers and stochastic variability, providing a robust foundation for advancements in fire spread prediction.
3. Data Collection
Two datasets were used in this study: (i) controlled laboratory smoulder experiments on inclined fuel beds and (ii) operational field observations of surface fire spread collected by the British Columbia Wildfire Service (BCWS). Together, these datasets enable an examination of fire spread across both experimental and real-world contexts.
3.1. Laboratory Smoulder Experiments on Sloped Surfaces
The laboratory dataset originated from a series of controlled smoulder burns designed to isolate slope effects on fire spread [
44]. The primary objective was to test the slope correction factor prescribed in the FBP System against observed rates of spread. A total of 48 burns were conducted on inclines from
to
in
increments, with all other conditions held constant. This design ensured that differences in spread rate could be attributed solely to slope, minimizing confounding effects.
Fuel beds consisted of single-sided wax paper coated with a 1:10 potassium nitrate (
)–distilled water solution following Thompson et al. [
45]. Sheets were soaked for one hour, air-dried for 24 h, and affixed to shallow trays, allowing airflow beneath the substrate. The nitrate treatment promoted sustained smouldering while suppressing flaming, ensuring clear visibility of the fire perimeter for imaging [
46]. Each burn was recorded with a fixed overhead camera oriented orthogonally to the tray surface. Videos were captured at 15 frames per second and a 320 × 240 pixel resolution, corresponding to a spatial scale of
mm per pixel. Ignition was consistently initiated at the centre using a directed flame. All experiments were conducted inside a fume hood under stable ambient conditions.
Using the experimental fire videos, we constructed a dataset of spread distances. The ignition time () was defined as the first frame exhibiting visible combustion. For each video, we extracted the valid frame range corresponding to active spread prior to the flame front reaching the substrate edge. To ensure comparability across burns, a common analysis interval was defined by taking the maximum lower bound and minimum upper bound of available frames across all videos, yielding a fixed window of 388 frames (≈25 s). This window begins after ignition, excluding highly variable transients, and corresponds to a stable phase of spread; this is consistent with wildfire modelling practice, where the rate of spread is reported during quasi-equilibrium phases (e.g., in the FBP System).
While these experiments offered controlled replication and direct observations of slope effects, several limitations should be noted. The wax paper substrate is a simplified fuel analog and cannot replicate the structural heterogeneity of forest litter. The burns involved smouldering spread only, with combustion dynamics distinct from flaming fires. Moreover, the combustion mechanics and chemistry of wax paper differ from those of natural forest fuels, and further investigation is required to generalize these findings to forest fuels [
47]. Finally, the small experimental scale may have accentuated edge effects; to mitigate this, measurements were taken with margins from tray edges. Despite these limitations, the dataset provides a valuable benchmark for studying slope effects on surface fire spread under controlled conditions.
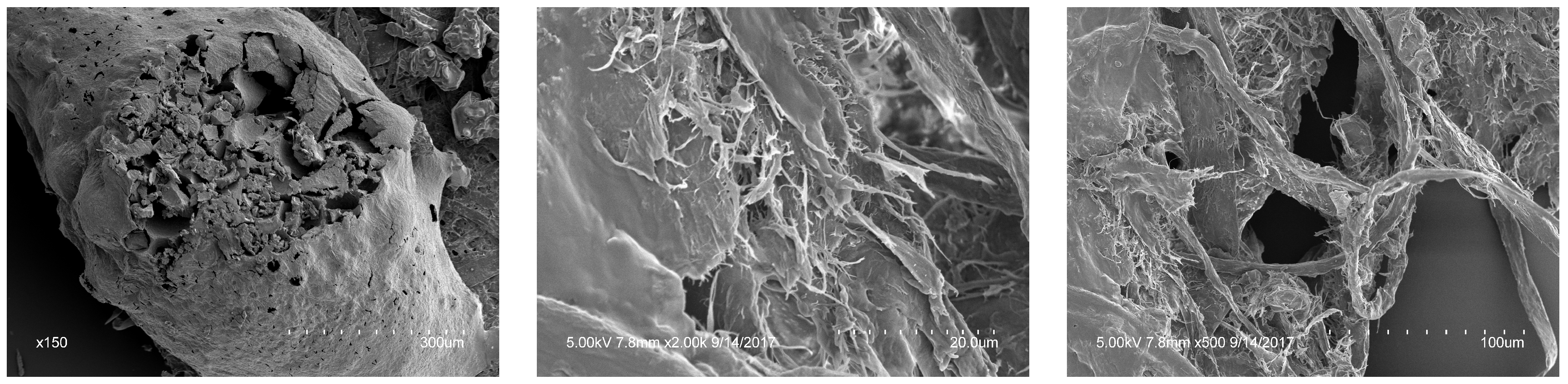
Microstructural Heterogeneity in the Fuel Bed
The treated wax paper served as a standardized analog for natural forest fuels. Scanning electron microscopy (SEM) (
Figure 1) conducted by the original experimenters revealed micro-scale heterogeneity in the treated sheets, including irregular distributions of pores, fibres, and surface textures [
45]. This microstructural complexity is analogous to the heterogeneity in natural forest floors, where fuel beds comprise a mosaic of litter, twigs, organic matter, and mineral particles with distinct thermal properties. Even within a single classified fuel type (e.g., boreal spruce, mixedwood, or grass in the FBP System), substantial within-class variation exists, influencing ignition, heat transfer, and spread rates.
The presence of such heterogeneity, even in a controlled laboratory substrate, highlights a critical limitation of conventional fire behaviour models. Systems such as the FBP System treat the fuel type as homogeneous, implicitly assuming that all instances behave similarly under identical weather and topographic conditions. Our observations challenge this assumption, showing that stochastic variability in the spread rate can emerge even when the fuel type, slope, and ignition are controlled, likely driven by microstructural fuel differences.
3.2. Field Observations in Ponderosa Pine–Douglas Fir (C-7) Fuel
Field data were obtained from 30 experimental burns conducted by BCWS between 2014 and 2019 on crown lands in the Kamloops Fire Centre, British Columbia. Sites were classified as the C-7 fuel type under the FBP System, consisting of Ponderosa pine (Pinus ponderosa) and Douglas fir (Pseudotsuga menziesii) stands with near-continuous litter layers. Burns were primarily conducted during May–July when conditions permitted safe control.
At each site, the temperature, relative humidity, and wind speed/direction were measured at ignition with a sling psychrometer and handheld wind meter. These measurements were used to calculate the fire weather indices, namely the fine-fuel moisture code (FFMC), initial spread index (ISI), and buildup index (BUI), in accordance with the FBP System.
Burns occurred on slopes ranging from 0 to . The slope angle was estimated from the GPS coordinates of the upper and lower plot boundaries using a rise-over-run calculation (elevation difference divided by horizontal distance), rounded to the nearest degree. This averaging introduces potential errors over heterogeneous terrain, similarly to slope estimates from remote sensing, where resolution limits require spatial averaging. The observed spread was quantified by measuring the head, flank, and back distances from a marked ignition point.
Although the ignition protocols varied (match, lighter, or drip torch) and some environmental factors, such as the microclimate and time of day, could not be controlled, these burns represent systematically collected observations of the spread rate in C-7 fuels under documented weather and slope conditions. The data serve as an empirical benchmark for evaluating how fuel-specific variability and site heterogeneity influence spread, even when the fuel type is nominally fixed, while recognizing slope rounding and ignition variability as limitations when interpreting the results.
Together, the laboratory slope experiments and BCWS field burns provide complementary perspectives: the laboratory data isolate slope effects under controlled conditions, whereas the field data capture variability within a single fuel type under operational conditions. The following section outlines the methodology used to analyze these datasets and evaluate FBP formulations against the observed spread dynamics.
4. Methodology
Our methodology followed a three-stage workflow while applying distinct procedures to the laboratory and field datasets. For the laboratory experiments, video data were processed to extract fire perimeters and compute directional rates of spread, allowing an evaluation of the slope correction factor in the Canadian FBP System under controlled conditions. The field dataset, by contrast, already contained spread measurements and was incorporated only at the statistical modelling stage.
4.1. Fire Perimeter Segmentation (Laboratory)
To delineate fire regions from the smouldering video data, we developed a segmentation pipeline structured into three stages: pre-processing, segmentation, and post-processing (
Figure 2).
Pre-processing: For each video, the ignition frame () was identified as the first frame showing visible combustion. Assuming an approximately elliptical spread pattern, the centroid of the fitted ellipse around the ignited region in the ignition frame served as the ignition point. The ignition point was recorded and used as a consistent spatial (point-based) prompt for segmentation across all frames of the video with SAM.
Segmentation: Fire regions were extracted using SAM version 1, a Vision Transformer-based architecture (ViT-H) pre-trained for general-purpose image segmentation. We employed the official release pre-trained weights (sam_vit_h_4b8939.pth) in a GPU-enabled environment. For each laboratory video, frames together with the ignition-point prompt were passed to the model, which returned the mask with the highest confidence score as the final segmentation output for that frame.
Post-processing: The grayscale SAM masks were converted into binary images using a fixed threshold of 127. To reduce noise while preserving edges, a median filter [
48] with a kernel size of 5 was applied. Binary dilation was then used to reinforce regional continuity and suppress small discontinuities. The fire perimeter was delineated by computing the pixel-wise exclusive disjunction (XOR) between the dilated and original binary masks, producing a precise outline of the active fire front, which was used as the basis for quantifying fire growth over time.
4.2. Rate of Spread Calculation from Segmented Fire Boundaries
Rates of spread were derived from binary fire perimeters obtained through segmentation. Conceptually, the fire front is divided into the head, flanks, and rear, corresponding to the fastest advance, lateral spread, and slowest advance, respectively. These regions are central to operational fire behaviour prediction and therefore initially serve as a natural basis for our analysis.
Our method adopts a two-stage hybrid approach: (i) the fire head is identified using a directed Hausdorff distance measure [
49], and (ii) spread distances in the head, rear, and flank directions are then computed using bounding boxes after rotation. This design balances precision and robustness: the Hausdorff step ensures that the head corresponds to the true point of maximum advance, while bounding boxes provide a stable and interpretable frame of reference for directional distances, reducing the sensitivity to pixel-level segmentation noise.
The procedure is summarized in Algorithm 1. First, for each perimeter pixel in the later frame , the minimum distance to all perimeter pixels in the earlier frame is computed. The pixel in with the maximum of these minimum distances defines the fire head, consistent with the directed Hausdorff distance from to . Next, a vector from the ignition point to the identified head is used to rotate both perimeters, aligning the head with the positive x-axis. Finally, axis-aligned bounding boxes are fitted to the rotated perimeters, and directional spread distances are derived from changes in bounding box margins. Dividing by the elapsed time yields directional ROS values. The bounding boxes were selected over convex hulls to reduce the sensitivity to small segmentation irregularities and to facilitate a transparent isotropic comparison of spread in the head, rear, and flank directions.
While the head-based approach aligns with conventional fire behaviour definitions, it implicitly assumes that the head advances in a consistent direction, typically governed by wind or slope. In our small-scale laboratory burns, this assumption was often violated: the head direction shifted laterally or diagonally and did not consistently align with the upslope axis. As a result, head-based ROS estimates were not slope-aware and could not be compared meaningfully across slope treatments. Furthermore, reducing fire growth to a single head fire metric obscures anisotropic spread patterns, particularly along the rear and flanks, which may carry important information about the underlying spread dynamics.
| Algorithm 1: Head-Based ROS Calculation. The fire head is identified via the directed Hausdorff distance; then, bounding box margins are used to compute spread distances in the head, rear, and flank. |
![Fire 08 00384 i001 Fire 08 00384 i001]() |
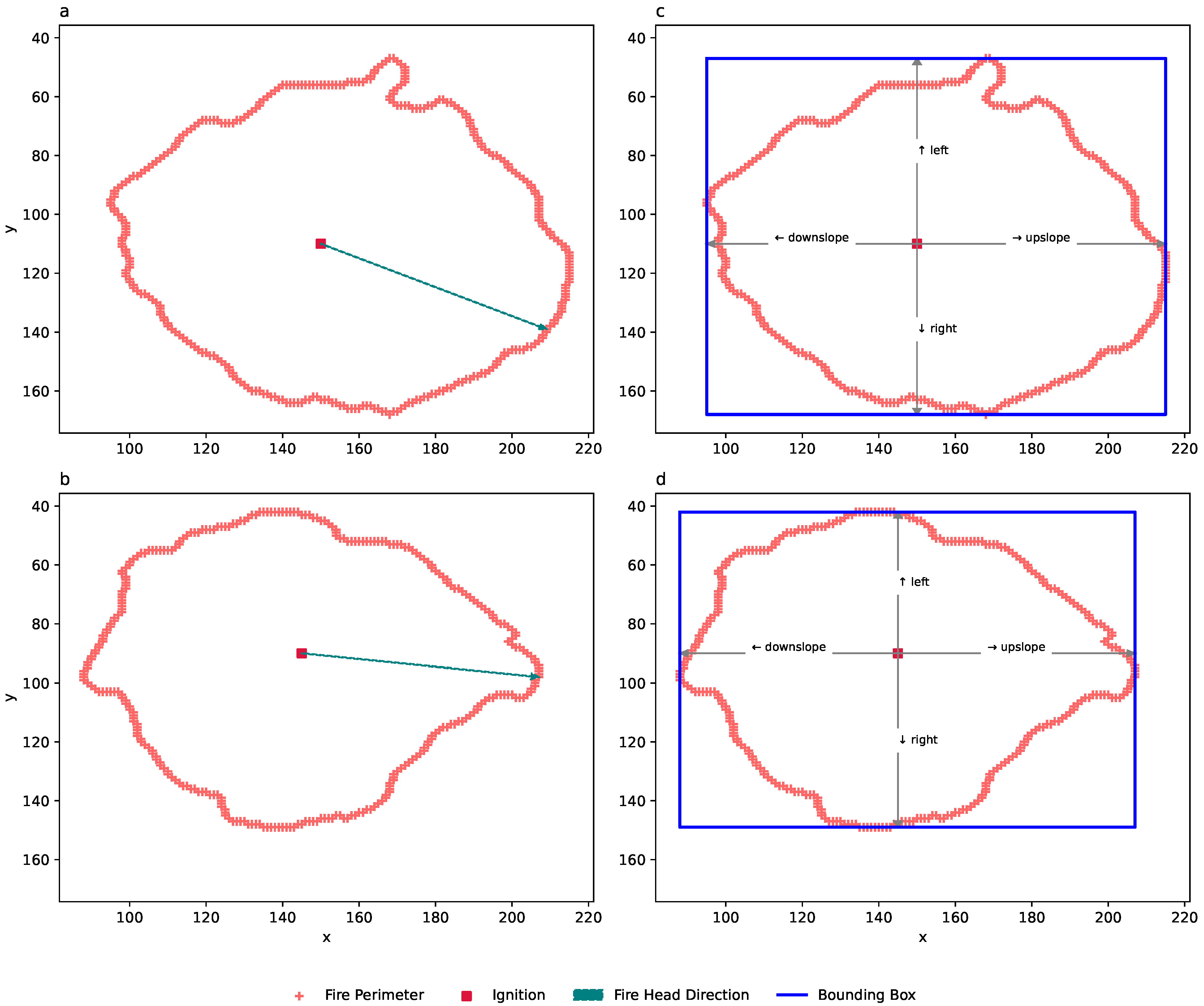
4.3. Ignition-Anchored Bounding Box ROS Calculation
To address the limitations of the head-based ROS calculation, we implemented an ignition-anchored bounding box method. In this formulation, the ROS is quantified along fixed cardinal axes of the image plane (
,
,
,
), corresponding to the upslope, downslope, and lateral spread directions.
Figure 3 illustrates the proposed approach, contrasting conventional head-based ROS estimation with the proposed method. It shows that anchoring the bounding box at the ignition point provides a consistent spatial reference across all burns, enabling the direct comparison of the directional spread under varying slope treatments.
For slope experiments, the ROS was calculated within the fixed analysis window defined in
Section 3.1, ensuring that ignition transients and edge effects were excluded. A bounding box of fixed dimensions (200 pixels in length × 100 pixels in width), centred on the ignition point, was applied consistently across all videos to provide a standardized spatial frame of reference. For each cardinal axis, we recorded the elapsed time until the fire perimeter first intersected the corresponding bounding box margin. The pre-defined travel distances were 75 pixels in the upslope (
) and downslope (
) directions and 50 pixels in the right (
) and left (
) lateral directions. Based on camera calibration (1.2 mm per pixel), these distances corresponded to 12.0 cm along the slope axis and 6.0 cm along the lateral axis. The directional ROS was then computed, consistent with fire behaviour convention, as
This approach yields four independent ROS values per burn (upslope, downslope, right flank, left flank), allowing anisotropy in spread dynamics to be quantified explicitly. By anchoring the measurement window at the ignition point, this method provides comparability across slope treatments and overcomes the directional instability inherent in conventional head-based approaches.
4.4. Statistical Analysis Framework
Our analysis proceeds in two stages. First, controlled laboratory burns on treated wax paper substrates are used to isolate and test the slope correction term, offering mechanistic insights into how the slope influences spread dynamics in simplified fuelbeds, as well as quantifying the variability that remains unexplained by this formulation. Second, we extend the analysis to field observations of the C-7 fuel type using a nonlinear mixed-effects (NLME) model. The NLME formulation embeds the functional structure of the FBP equations while incorporating location-specific random effects. Together, these analyses provide complementary perspectives on both the explanatory power and the predictive limits of deterministic fire behaviour models.
4.4.1. Experimental Test of the Slope–ROS Relationship
In our laboratory experiments, the slope was systematically varied while other conditions were held constant. Since the treated wax paper substrate did not support cumulative buildup, we set
, and replaced the RSI with the baseline ROS under flat conditions,
. From our experimental videos,
was calculated to be 0.027 m/min. Thus, slope dependence was evaluated relative to
using directional ROS values derived from the ignition-anchored bounding box method (
Section 3.1).
To estimate the slope factor, we applied nonlinear regression to the log-transformed form of Equation (
2), yielding
where
is assumed to follow a normal distribution. This formulation implies that the ROS is log-normally distributed on the original scale, consistent with the multiplicative nature of slope effects and with assumptions used in wildfire spread modelling frameworks such as the FBP System.
4.4.2. Hierarchical Field Analysis of Slope–ROS Dynamics
The C-7 fuel type was selected as it represents one of the most widely observed coniferous fuel complexes in Canadian forests. Unlike controlled laboratory experiments, field data capture greater heterogeneity in fuels, topography, and microclimate, which can obscure deterministic slope effects. To address this, we adopted a nonlinear mixed-effects framework that embeds the functional structure of the FBP equations while allowing coefficients to vary across locations. This hierarchical formulation enables us to (i) retain the semi-empirical FBP structure for interpretability, (ii) quantify how the slope sensitivity varies between sites, and (iii) partition variance into deterministic drivers, site-level heterogeneity, and residual stochasticity.
The NLME model is specified as
where
i indexes observations,
ℓ indexes locations,
and
include location-specific random effects, and
represents the within-location residual error. Two key coefficients are estimated, a multiplicative scaling factor (
a) and the slope sensitivity term (
d), both allowed to vary randomly by location. The random effects act as statistical analogues for unmeasured influences such as fuel continuity, fine-scale topography, and the local wind structure, while the residual error captures within-site variability.
5. Results and Discussion
The results are presented in three parts. First, we report the segmentation outcomes and directional ROS estimates from both the head-based and ignition-anchored methods. Second, we test the slope factor using laboratory burns, estimating the parameters of the slope–ROS relationship and assessing the unexplained variability. Finally, we analyze the C-7 field data with a nonlinear mixed-effects model to evaluate site-level variability. Together, these analyses assess the predictive limits of deterministic models and highlight the role of stochastic variability in fire spread.
5.1. Directional ROS Extraction
The segmentation accuracy was first assessed to ensure the reliability of the ROS calculations. Masks were visually cross-checked against original video frames, with the segmentation pipeline successfully delineating fire perimeters for all burns and requiring only minor manual adjustments in fewer than 5% of frames. In addition, a quantitative check was performed by comparing the SAM-generated masks with manually delineated perimeters for two randomly sampled frames per video. Agreement was evaluated using the intersection over union (IoU), which averaged 90.7% across all comparisons, confirming the high fidelity of the automated segmentation.
Using these perimeters, directional ROS values were derived by both the conventional head-based approach and the ignition-anchored bounding box method. The head-based ROS estimates confirmed the expected head–rear anisotropy (
Table 1), with the head advancing faster than the rear. However, this approach provides only a coarse head–rear contrast and does not permit slope-aware comparisons across replicates. Moreover, the relative variability was high even within slope treatments: the coefficients of variation for the head ROS ranged from 8% (
slope) to 47% (
slope), while the rear ROS variability exceeded 50% in some cases. Such variability, despite the controlled conditions, suggests that stochastic microscale processes influence spread beyond deterministic slope effects.
The ignition-anchored bounding box framework provided a more detailed and consistent representation of anisotropy, explicitly separating the upslope, downslope, and lateral spread directions.
Figure 4 presents the calculated directional ROS across slope treatments. The results demonstrate the clear directional dependency of the rate of spread with increasing slope. In the upslope direction, the ROS shows a positive association with the slope, consistent with established fire behaviour theory stating that steeper slopes accelerate fire spread due to the pre-heating of fuels. In contrast, the downslope direction shows a relatively low and weakly varying ROS across slopes, reflecting the limited influence of the slope on fire progression downslope. The flank directions display intermediate behaviour, with modest increases in ROS and higher variability compared to the upslope case.
Importantly, the variability within each directional spread rate highlights the stochasticity of fire spread, even under controlled laboratory conditions. While the overall patterns align with deterministic expectations (fastest upslope, slowest downslope), the scatter around the smoothed trends suggests that small-scale heterogeneities in fuel consumption and ignition dynamics contribute to unpredictable deviations. This finding reinforces the central argument of our study, i.e., that fire spread cannot be fully explained by deterministic slope effects, and probabilistic descriptions are necessary to capture the inherent variability in directional spread.
5.2. Slope Effect on ROS
The laboratory experiments were used to evaluate the slope factor prescribed in the FBP System. We fitted a nonlinear regression model based on the log-transformed slope adjustment (Equation (
4)) for slope angles up to
. Using the bounding box method, the upslope and downslope ROS were analyzed separately to assess directional effects.
5.2.1. Upslope Rate of Spread
On positive slopes, ROS increased significantly with the slope angle.
Table 2 summarizes the estimated parameters for the upslope ROS. Both parameters were statistically significant, confirming the exponential influence of slope on fire spread. However, the estimated coefficients differed from the FBP defaults (
,
). This discrepancy was expected given the different scale of the experiment compared to wildland fires and the fact that our analogue fuel (treated wax paper) differed structurally and chemically from natural forest fuels; it therefore could not be expected to reproduce the FBP coefficients exactly. Despite the significant slope effect, substantial residual variance remained across replicates. Importantly, the residual standard error
corresponds to a multiplicative error of
, indicating substantial unexplained variability in spread rates beyond slope effects, even in such a controlled laboratory environment, suggesting that microscale heterogeneity and stochastic combustion processes play a role.
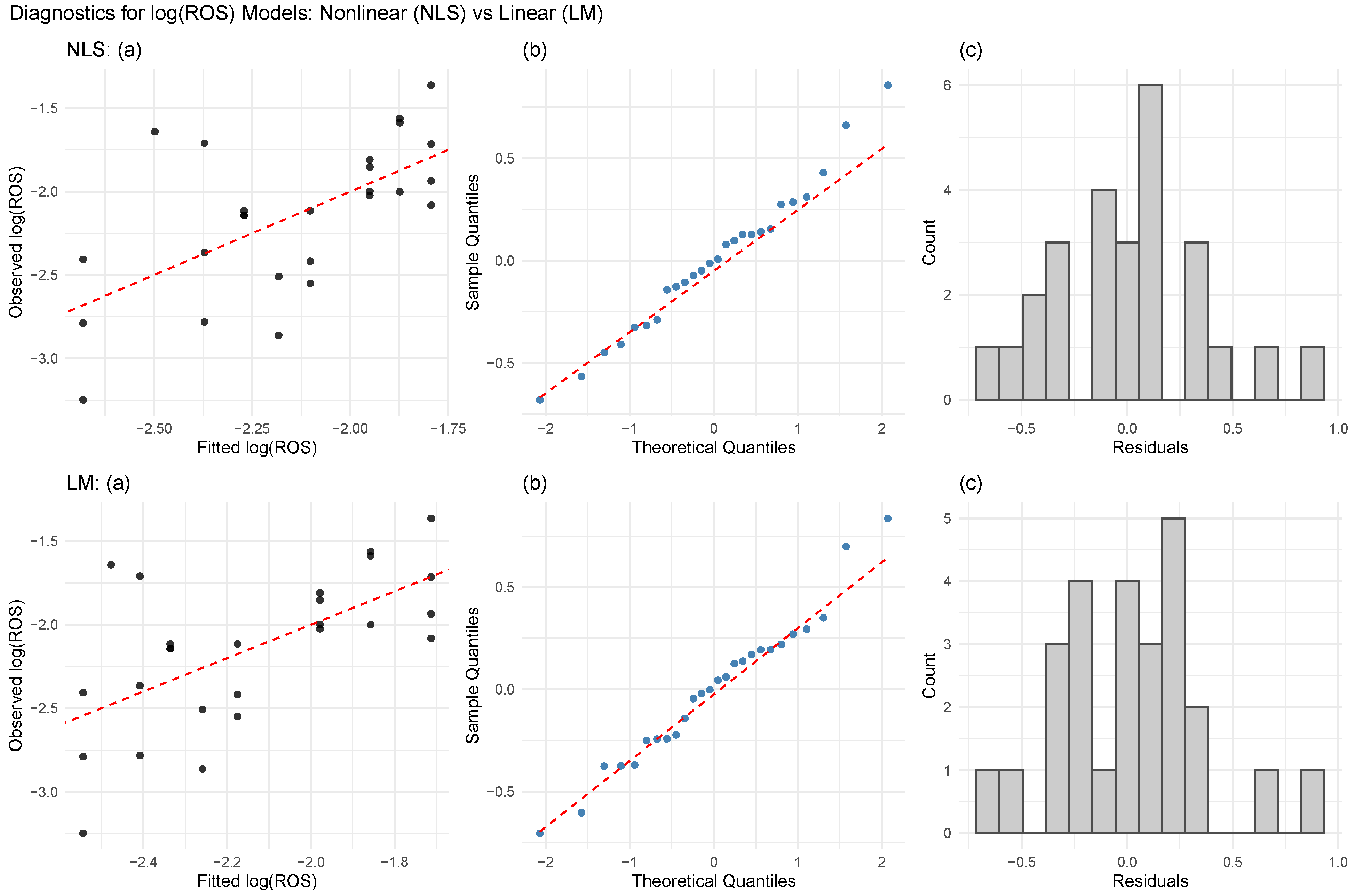
We compared the nonlinear model with a simpler linear model relating
to
. The fitted linear model produced statistically significant coefficients (
,
), confirming the linear dependence between the slope percent and ROS on the log scale, consistent with a simple exponential relationship. This formulation provides a more parsimonious description of the slope effect compared to the nonlinear alternative.
Figure 5 presents diagnostic plots for both models, indicating that the linear specification achieves a slightly better overall fit. Two observations appear as outliers, likely reflecting rapid changes in the head fire direction; while they were retained in the analysis, they may warrant further investigation in future studies.
5.2.2. Downslope Rate of Spread
A parallel model fitted to the downslope ROS (
Table 3) yielded a negative coefficient for the slope, consistent with the expectation of slower spread downslope. However, this effect was not statistically significant. Moreover, in several cases, the observed downslope ROS exceeded the upslope ROS (
Figure 6), a pattern contrary to the expected influence of slope. Close inspection of the videos revealed spotting events in some trials, where new ignition sites appeared downslope from the main fire front (
Figure 7). These events inflated the apparent ROS and introduced discontinuities that are not captured by smooth slope response models, indicating the need for further investigation into the effects of slope on ROS in this direction. These findings underscore the complexity of fire spread dynamics and any attempts to generalize slope effects. Incorporating additional mechanisms may be necessary to improve model accuracy and reliability.
Across both the upslope and downslope models, the residual variance remained high, demonstrating that the slope alone does not explain the full variability in spread rates. The bounding box method, by producing directional ROS values per burn, further revealed anisotropy in spread behaviour that conventional head-based methods obscure. Variability across replicates at the same slope angle indicates that stochastic combustion dynamics and microscale heterogeneity play a significant role.
5.3. Field Data: Inherent Variability in Fire Spread
The nonlinear mixed-effects model (NLME) was fitted by REML to
field observations from eight locations across British Columbia (unbalanced; range 1–10 per location).
Table 4 shows that the fit for C-7 fuels yielded fixed effects
(RSI scale) and
(slope sensitivity). The estimate for
a indicates that, on average across locations, the baseline RSI component in the FBP formulation underpredicts the ROS and requires a
multiplicative adjustment to align with observations. The estimate for
d confirms the strong exponential response to slope and indicates that, when keeping the ISI and BUI fixed, the slope factor increases the ROS by about
at
,
at
,
at
, and
at
. Together, these population-level parameters indicate (i) the systematic upward scaling of wind/moisture effects and (ii) pronounced sensitivity to slope under field conditions, in line with the study’s goal of testing the slope relation observed in the laboratory.
Variance decomposition (
Table 5) indicated negligible between-location variability in
a, suggesting that the influence of wind and fine-fuel moisture (captured by ISI) was consistent across sites. By contrast,
d exhibited
across locations, demonstrating heterogeneity in slope sensitivity that likely reflects differences in fine-scale topography, fuel continuity, and local wind–slope interactions. The pooled within-location residual standard deviation
of
shows that substantial within-location variability remained unexplained after accounting for the ISI, BUI, and slope effects and site-specific slope sensitivity. This residual component is the field-scale analogue of the stochasticity observed in the laboratory experiments. Thus, after accounting for the ISI, BUI, and slope via the semi-empirical FBP structure, most of the remaining variability in the ROS arises within locations (variance share
), with additional but smaller contributions from site-to-site differences in slope sensitivity (variance share
). The random effect for the RSI scale was negligible (<0.001% of unexplained variance), indicating a consistent wind/moisture influence across C-7 sites, whereas slope–ROS coupling varied meaningfully by location. Although the group sizes were unbalanced, REML estimation and partial pooling appropriately shrunk poorly informed site effects toward the population mean, so these conclusions are not caused by sparse groups.
Figure 8 provides a graphical assessment of the fitted NLME model.
Figure 8a highlights the estimated slope sensitivity across different locations, showing that, while a few locations cluster near the population mean, others exhibit marked deviations consistent with the variance component analysis.
Figure 8b compares the predicted and observed ROS values, demonstrating that the model captures the central tendency of the data, with moderate scatter around the 1:1 line; this indicates the good alignment of the semi-empirical FBP structure with field observations, while also reflecting the inherent variability in spread.
Figure 8c shows the residuals plotted against the fitted values, with no systematic trend or curvature evident; however, the residual dispersion underscores the stochastic behaviour of spread within locations, in agreement with the substantial residual variance identified in the variance decomposition.
6. Conclusions, Limitations, and Future Directions
This study introduced the novel integration of computer vision segmentation with statistical modelling to evaluate the stochastic behaviour of directional fire spread. Using the Segment Anything Model, we extracted fire perimeters from laboratory burns and quantified the head, rear, and flank rates of spread, confirming the exponential influence of slope on the upslope ROS but with coefficients differing from the Canadian FBP defaults due to different fuel and environmental properties. Extending the analysis to C-7 field data, we fitted an NLME model that retained the semi-empirical FBP structure while permitting site-specific adjustments. The results showed that the RSI scale required systematic upward correction, slope sensitivity varied across locations, and residual variance remained large, indicating that within-site stochasticity dominates field-scale variability. Together, these findings emphasize the limits of deterministic formulations such as the FBP System in fully capturing real fire spread dynamics.
Our ROS calculation approach, based on bounding box displacements in four directions, enabled anisotropic spread analysis without assuming a dominant axis (head). Establishing a flexible definition of the ROS will become increasingly important as high-resolution perimeter data increase. More broadly, vision-based perimeter extraction provides a scalable means of generating spread data, and mixed-effects models offer a principled framework for partitioning variability into systematic drivers and stochastic components. Importantly, we should highlight that ROS estimates should be accompanied by standard errors, and slope adjustment carries its own uncertainties. Thus, rather than simply multiplying the ROS by the slope factor, both the estimates and their propagated errors should be modelled jointly.
Future work should expand these methods to diverse fuels and conditions and extend them to airborne or satellite video for near-real-time perimeter tracking. Integrating such data streams with probabilistic or machine-learning models capable of representing temporal variability and spotting will support spread forecasts that incorporate uncertainty bounds, providing a more realistic foundation for operational fire management. Ultimately, our goal is to inform the development of probabilistic, data-driven models that better reflect the dynamic and uncertain nature of fire behaviour.
Author Contributions
L.T. led the conceptualization, data analysis, segmentation, and modelling and was the primary author of the manuscript. W.J.B. supervised the project and contributed to methodological development, the interpretation of the results, and manuscript revisions. G.G. provided the slope experiment video dataset and field data. J.R.J.T. conducted the SEM imaging of the fuel substrate. Both J.R.J.T. and G.G. contributed to the original experimental design but were not involved in the modelling or data segmentation in this study. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially support by a Global Centres grant from the Natural Sciences and Engineering Research Council of Canada, grant number F23-02218.
Acknowledgments
The authors thank four anonymous reviewers for comments that have led to an improvement in the manuscript. They also thank Apurva Narayan for suggesting the use of SAM.
Conflicts of Interest
The authors declare no potential conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ROS | Rate of Spread |
| SAM | Segment Anything Model |
| FBP | Fire Behaviour Prediction |
| BCWS | British Columbia Wildfire Service |
| BE | Buildup Effect |
| RSI | Rate of Spread Index |
| SF | Slope Factor |
Appendix A
The detailed FBP formulations for the RSI and BE are as follows:
with the C-7 fuel type corresponding parameters
.
where
is the average buildup index for the fuel type and
q is the dryness factor; for C-7, these indices are
.
References
- Pausas, J.G.; Keeley, J.E. Wildfires and global change. Front. Ecol. Environ. 2021, 19, 387–395. [Google Scholar] [CrossRef]
- Hirsch, K.G. Canadian Forest Fire Behavior Prediction (FBP) System: User’s Guide; Number 7; Forestry Canada, Fire Danger Group: Ottawa, ON, Canada, 1996; x+121p.
- Tymstra, C.; Bryce, R.W.; Wotton, B.M.; Taylor, S.W.; Armitage, O.B. Development and Structure of Prometheus: The Canadian Wildland Fire Growth Simulation Model; Information Report NOR-X-417; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 2010.
- Wagner, C.V. Development and Structure of the Canadian Forest Fire Weather Index System; Number 35; CABI Databases: Delémont, Switzerland, 1987. [Google Scholar]
- Parisien, M.A.; Kafka, V.; Hirsch, K.; Todd, J.; Lavoie, S.; Maczek, P. Mapping Wildfire Susceptibility with the BURN-P3 Simulation Model; Canadian Forest Service Northern Forestry Centre: Edmonton, AB, Canada, 2005.
- Han, L.; Braun, W. Dionysus: A stochastic fire growth scenario generator. Environmetrics 2014, 25, 431–442. [Google Scholar] [CrossRef]
- Beverly, J.L.; McLoughlin, N. Burn probability simulation and subsequent wildland fire activity in Alberta, Canada–Implications for risk assessment and strategic planning. For. Ecol. Manag. 2019, 451, 117490. [Google Scholar] [CrossRef]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375 m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Bastarrika, A.; Rodriguez-Montellano, A.; Roteta, E.; Hantson, S.; Franquesa, M.; Torre, L.; Gonzalez-Ibarzabal, J.; Artano, K.; Martinez-Blanco, P.; Mesanza, A.; et al. An automatic procedure for mapping burned areas globally using Sentinel-2 and VIIRS/MODIS active fires in Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2024, 218, 232–245. [Google Scholar] [CrossRef]
- Barber, Q.E.; Jain, P.; Whitman, E.; Thompson, D.K.; Guindon, L.; Parks, S.A.; Wang, X.; Hethcoat, M.G.; Parisien, M.A. The Canadian fire spread dataset. Sci. Data 2024, 11, 764. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.; Mei, X.; Niu, F.; Fan, X.; Ou, S.; Zhong, S. Fusing social media, remote sensing, and fire dynamics to track wildland-urban interface fire. Remote Sens. 2023, 15, 3842. [Google Scholar] [CrossRef]
- Andrews, P.L. Current status and future needs of the BehavePlus Fire Modeling System. Int. J. Wildland Fire 2013, 23, 21–33. [Google Scholar] [CrossRef]
- Garcia, T.; Braun, J.; Bryce, R.; Tymstra, C. Smoothing and bootstrapping the PROMETHEUS fire growth model. Environmetrics Off. J. Int. Environmetrics Soc. 2008, 19, 836–848. [Google Scholar] [CrossRef]
- Barber, J.; Bose, C.; Bourlioux, A.; Braun, J.; Brunelle, E.; Garcia, T.; Hillen, T.; Ong, B. Burning issues with PROMETHEUS–the Canadian wildland fire growth simulation model. Can. Appl. Math. Q. 2008, 16, 337–378. [Google Scholar]
- Silva, J.; Marques, J.; Gonçalves, I.; Brito, R.; Teixeira, S.; Teixeira, J.; Alvelos, F. A systematic review and bibliometric analysis of wildland fire behavior modeling. Fluids 2022, 7, 374. [Google Scholar] [CrossRef]
- Cui, W.; Perera, A.H. What do we know about forest fire size distribution, and why is this knowledge useful for forest management? Int. J. Wildland Fire 2008, 17, 234–244. [Google Scholar] [CrossRef]
- Taylor, S.W.; Woolford, D.G.; Dean, C.; Martell, D.L. Wildfire prediction to inform fire management: Statistical science challenges. Statist. Sci. 2013, 28, 586–615. [Google Scholar] [CrossRef]
- Finney, M.A. An overview of FlamMap fire modeling capabilities. In Fuels Management-How to Measure Success: Conference Proceedings, Proceedings of the 1st Fire Behavior and Fuels Conference, Oregon, Portland, 28–30 March 2006; Proceedings RMRS-P-41; Andrews Patricia, L., Butler Bret, W., Eds.; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; Volume 41, pp. 213–220. [Google Scholar]
- USDA Forest Service. Fire Simulation (FSim) Project. 2024. Available online: https://research.fs.usda.gov/firelab/projects/fsim (accessed on 4 December 2024).
- Boychuk, D.; Braun, W.J.; Kulperger, R.J.; Krougly, Z.L.; Stanford, D.A. A stochastic forest fire growth model. Environ. Ecol. Stat. 2009, 16, 133–151. [Google Scholar] [CrossRef]
- Braun, W.J.; Woolford, D.G. Assessing a Stochastic Fire Spread Simulator. J. Environ. Inform. 2013, 22, 1–12. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE, Fire Area Simulator—Model Development and Evaluation; Number 4; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 1998.
- Freire, J.G.; DaCamara, C.C. Using cellular automata to simulate wildfire propagation and to assist in fire management. Nat. Hazards Earth Syst. Sci. 2019, 19, 169–179. [Google Scholar] [CrossRef]
- Spiller, D.; Thangavel, K.; Sasidharan, S.T.; Amici, S.; Ansalone, L.; Sabatini, R. Wildfire segmentation analysis from edge computing for on-board real-time alerts using hyperspectral imagery. In Proceedings of the 2022 IEEE International Conference on Metrology for Extended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Rome, Italy, 16–28 October 2022; pp. 725–730. [Google Scholar]
- Jonnalagadda, A.V.; Hashim, H.A. SegNet: A segmented deep learning based Convolutional Neural Network approach for drones wildfire detection. Remote Sens. Appl. Soc. Environ. 2024, 34, 101181. [Google Scholar] [CrossRef]
- Chen, T.H.; Wu, P.H.; Chiou, Y.C. An early fire-detection method based on image processing. In Proceedings of the 2004 International Conference on Image Processing, 2004. ICIP’04, Singapore, 24–27 October 2004; Volume 3, pp. 1707–1710. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; proceedings, part III 18; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Ghali, R.; Akhloufi, M.A.; Mseddi, W.S. Deep learning and transformer approaches for UAV-based wildfire detection and segmentation. Sensors 2022, 22, 1977. [Google Scholar] [CrossRef] [PubMed]
- Ghali, R.; Akhloufi, M.A. Deep learning approaches for wildland fires using satellite remote sensing data: Detection, mapping, and prediction. Fire 2023, 6, 192. [Google Scholar] [CrossRef]
- Ramos, L.; Casas, E.; Bendek, E.; Romero, C.; Rivas-Echeverría, F. Computer vision for wildfire detection: A critical brief review. Multimed. Tools Appl. 2024, 83, 83427–83470. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment Anything. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 3992–4003. [Google Scholar] [CrossRef]
- Morandini, F.; Silvani, X. Experimental investigation of the physical mechanisms governing the spread of wildfires. Int. J. Wildland Fire 2010, 19, 570–582. [Google Scholar] [CrossRef]
- Viegas, D.X. Slope and wind effects on fire propagation. Int. J. Wildland Fire 2004, 13, 143–156. [Google Scholar] [CrossRef]
- Sharples, J.J.; McRae, R.H.; Wilkes, S.R. Wind–terrain effects on the propagation of wildfires in rugged terrain: Fire channelling. Int. J. Wildland Fire 2012, 21, 282–296. [Google Scholar] [CrossRef]
- Wagner, C.V. Effect of slope on fire spread rate. Can. For. Serv.-Bi-Mon. Res. Notes 1977, 33, 7–8. [Google Scholar]
- Thompson, M.P.; Calkin, D.E. Uncertainty and risk in wildland fire management: A review. J. Environ. Manag. 2011, 92, 1895–1909. [Google Scholar] [CrossRef]
- Linear Mixed-Effects Models: Basic Concepts and Examples. In Mixed-Effects Models in Sand S-PLUS; Springer: New York, NY, USA, 2000; pp. 3–56. [CrossRef]
- Finney, M.; Grenfell, I.C.; McHugh, C.W. Modeling containment of large wildfires using generalized linear mixed-model analysis. For. Sci. 2009, 55, 249–255. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, S.; Wang, G.; Wang, W.; Xia, H.; Sun, S.; Guo, F. Evaluation of geographically weighted logistic model and mixed effect model in forest fire prediction in northeast China. Front. For. Glob. Change 2022, 5, 1040408. [Google Scholar]
- Bugallo, M.; Esteban, M.D.; Marey-Pérez, M.F.; Morales, D. Wildfire prediction using zero-inflated negative binomial mixed models: Application to Spain. J. Environ. Manag. 2023, 328, 116788. [Google Scholar] [CrossRef]
- Anderson, W.R.; Cruz, M.G.; Fernandes, P.M.; McCaw, L.; Vega, J.A.; Bradstock, R.A.; Fogarty, L.; Gould, J.; McCarthy, G.; Marsden-Smedley, J.B.; et al. A generic, empirical-based model for predicting rate of fire spread in shrublands. Int. J. Wildland Fire 2015, 24, 443–460. [Google Scholar] [CrossRef]
- Goetz, G.O. A Statistical Investigation of How Slope Affects a Wildfire’s Rate of Spread. Master’s Thesis, University of British Columbia, Kelowna, BC, Canada, 2021. [Google Scholar] [CrossRef]
- Thompson, J.R.J.; Wang, X.J.; Braun, W.J. A mouse-model for studying fire spread rates using experimental micro-fires. J. Environ. Stat. 2020, 9, 1–19. [Google Scholar]
- Johnston, J.M.; Wheatley, M.J.; Wooster, M.J.; Paugam, R.; Davies, G.M.; DeBoer, K.A. Flame-Front Rate of Spread Estimates for Moderate Scale Experimental Fires Are Strongly Influenced by Measurement Approach. Fire 2018, 1, 16. [Google Scholar] [CrossRef]
- Liu, N.; Lei, J.; Gao, W.; Chen, H.; Xie, X. Combustion dynamics of large-scale wildfires. Proc. Combust. Inst. 2021, 38, 157–198. [Google Scholar] [CrossRef]
- Narendra, P.M. A separable median filter for image noise smoothing. IEEE Trans. Pattern Anal. Mach. Intell. 1981, 1, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Borgefors, G. Distance transformations in digital images. Comput. Vision Graph. Image Process. 1986, 34, 344–371. [Google Scholar] [CrossRef]
Figure 1.
Scanningelectron microscopy (SEM) of the treated wax paper used in the laboratory experiments, showing fibre-scale irregularities and pore heterogeneity.
Figure 1.
Scanningelectron microscopy (SEM) of the treated wax paper used in the laboratory experiments, showing fibre-scale irregularities and pore heterogeneity.
Figure 2.
Fire region segmentation pipeline using the Segment Anything Model (SAM). The process consists of three main stages: pre-processing, including frame extraction, resizing, and ignition coordinate extraction; segmentation, where the SAM is applied to isolate fire regions in each frame; and post-processing, which involves smoothing and edge extraction.
Figure 2.
Fire region segmentation pipeline using the Segment Anything Model (SAM). The process consists of three main stages: pre-processing, including frame extraction, resizing, and ignition coordinate extraction; segmentation, where the SAM is applied to isolate fire regions in each frame; and post-processing, which involves smoothing and edge extraction.
Figure 3.
Fire spread direction estimated from head-based ROS for two experimental burns at slopes of (a) and (b), where differences in head orientation reflect in differences in other fire regions and complicate comparison. The proposed bounding box approach (c,d) provides a consistent framework to measure spread systematically in four cardinal directions.
Figure 3.
Fire spread direction estimated from head-based ROS for two experimental burns at slopes of (a) and (b), where differences in head orientation reflect in differences in other fire regions and complicate comparison. The proposed bounding box approach (c,d) provides a consistent framework to measure spread systematically in four cardinal directions.
Figure 4.
Rates of spread for four spread directions using our ignition-anchored bounding box. Facets distinguish upslope, downslope, right-flank, and left-flank spread, with smoothed trend lines illustrating directional differences.
Figure 4.
Rates of spread for four spread directions using our ignition-anchored bounding box. Facets distinguish upslope, downslope, right-flank, and left-flank spread, with smoothed trend lines illustrating directional differences.
Figure 5.
Diagnostic plots for nonlinear (NLS) and linear (LS) models of against slope. Subplots (a–c) in each row show observed vs. fitted values, Q–Q plot of residuals, and residual histogram for the NLS and LS fit. The dashed lines on the left-most plots are 45 degree reference lines. The dashed lines on the middle plots designate the expected locations of the points of the Q–Q plot under the normal distribution assumption.
Figure 5.
Diagnostic plots for nonlinear (NLS) and linear (LS) models of against slope. Subplots (a–c) in each row show observed vs. fitted values, Q–Q plot of residuals, and residual histogram for the NLS and LS fit. The dashed lines on the left-most plots are 45 degree reference lines. The dashed lines on the middle plots designate the expected locations of the points of the Q–Q plot under the normal distribution assumption.
Figure 6.
Comparison of rates of spread of fires in upslope and downslope directions (lab data).
Figure 6.
Comparison of rates of spread of fires in upslope and downslope directions (lab data).
Figure 7.
Spotting for slope degree 25 affecting the downslope rate of spread; upslope is along positive x axis. These images were taken 5 s apart as the burn progressed.
Figure 7.
Spotting for slope degree 25 affecting the downslope rate of spread; upslope is along positive x axis. These images were taken 5 s apart as the burn progressed.
Figure 8.
Model evaluation of directional fire spread in C-7 field burns. Subplot (a) shows random effect for estimates of slope sensitivity. (b) compares predicted versus observed rates of spread (ROS), with the dashed line indicating 1:1 agreement. (c) presents residuals against fitted values, where the dashed line marks zero residuals.
Figure 8.
Model evaluation of directional fire spread in C-7 field burns. Subplot (a) shows random effect for estimates of slope sensitivity. (b) compares predicted versus observed rates of spread (ROS), with the dashed line indicating 1:1 agreement. (c) presents residuals against fitted values, where the dashed line marks zero residuals.
Table 1.
Summary of head fire and rear fire ROS (m/min) from laboratory burns using head-based approach.
Table 1.
Summary of head fire and rear fire ROS (m/min) from laboratory burns using head-based approach.
| Slope (°) | Head Fire | Rear Fire |
|---|
| Average | Std Dev. | Average | Std Dev. |
|---|
| 0 | 0.027 | 0.004 | 0.026 | 0.012 |
| 5 | 0.021 | 0.0064 | 0.018 | 0.0039 |
| 10 | 0.032 | 0.015 | 0.031 | 0.0039 |
| 15 | 0.039 | 0.0095 | 0.026 | 0.0067 |
| 20 | 0.029 | 0.0024 | 0.022 | 0.017 |
| 25 | 0.029 | 0.012 | 0.020 | 0.0040 |
| 30 | 0.0315 | 0.0058 | 0.022 | 0.0047 |
| 40 | 0.045 | 0.0082 | 0.030 | 0.016 |
| 45 | 0.0458 | 0.0091 | 0.025 | 0.0046 |
| 50 | 0.046 | 0.0059 | 0.022 | 0.0069 |
Table 2.
Parameter estimates of slope factor for upslope rate of spread using nonlinear regression model (lab data).
Table 2.
Parameter estimates of slope factor for upslope rate of spread using nonlinear regression model (lab data).
| Parameter | Estimate | Std. Error | t-Value | p-Value |
|---|
| d | 0.017386 | 0.001009 | 22.703 | ≤2 × |
| e | 0.256337 | 0.071923 | 4.319 | 0.000235 |
Table 3.
Parameter estimates for downslope rate of spread using nonlinear regression model (lab data).
Table 3.
Parameter estimates for downslope rate of spread using nonlinear regression model (lab data).
| Parameter | Estimate | Std. Error | t-Value | p-Value |
|---|
| d | 0.019594 | 0.001029 | 19.039 | |
| e | −0.017528 | 0.046828 | −0.374 | 0.711 |
Table 4.
Fixed-effect estimates from the NLME model for C-7 fuels.
Table 4.
Fixed-effect estimates from the NLME model for C-7 fuels.
| Parameter | Interpretation | Estimate |
|---|
| a | RSI scale (population mean) | 2.1004 |
| d | Slope sensitivity (population mean) | 2.3283 |
Table 5.
Variance components from the NLME model for C-7 fuel field data. Standard deviations (SD) are reported for random effects and the residual term; variance shares are computed on the variance scale.
Table 5.
Variance components from the NLME model for C-7 fuel field data. Standard deviations (SD) are reported for random effects and the residual term; variance shares are computed on the variance scale.
| Component | SD | Variance | Variance Share (%) |
|---|
| Between-location, | | | <0.001 |
| Between-location, | 0.6197 | 0.3841 | 37.3 |
| Within-location (residual), | 0.8034 | 0.6455 | 62.7 |
| Total (unexplained) | — | 1.0295 | 100 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).