Abstract
This article focuses on using machine learning to predict the distance at which a chemical storage tank fire reaches a specified thermal radiation intensity. DNV’s Process Hazard Analysis Software Tool (PHAST) is used to simulate different scenarios of tank leakage and to establish a database of tank accidents. Backpropagation (BP) neural networks, random forest models, and the optimized random forest model K-R are used for model training and consequence prediction. The regression performance of the models is evaluated using the mean squared error (MSE) and . The results indicate that the K-R regression prediction model outperforms the other two machine learning algorithms, accurately predicting the distance at which the thermal radiation intensity is reached after a tank fire. Compared with the simulation results, the model demonstrates higher accuracy in predicting the distance of tank fire consequences, proving the effectiveness of machine learning algorithms in predicting the range of consequences of tank storage area fire events.
1. Introduction
In the production process of chemical enterprises, due to their special nature, large quantities of flammable and explosive liquids and gases are stored in the storage tank area. If an oil tank leaks and is exposed to an ignition source, it may lead to a serious fire accident. Once a disaster occurs, personnel exposed to the radiant heat of the fire may suffer serious injuries. In the UK, a significant chemical plant tank leakage and fire incident took place on 11 December 2005 at the Buncefield oil depot, which is situated less than 50 km from London. The explosion and subsequent fire ravaged over 20 substantial oil storage tanks, resulting in injuries to 43 individuals but no fatalities. The direct economic damage amounted to GBP 250 million. This event triggered the most profound ecological crisis in Europe during peacetime, substantially affecting the ecological landscape of London and the entire nation of Great Britain [1].
By collecting and analyzing data on domestic and international chemical incidents from 10 December 2003 to 10 January 2024, we obtained the following findings: domestically, there were 1060 poisoning incidents, 797 fire incidents, 759 explosion incidents, 592 leakage incidents, and 1 other type of incident; internationally, there were 36 poisoning incidents, 285 fire incidents, and 638 explosion incidents, with leakage incidents being the most frequent at 933 occurrences. Based on these data, we conducted a comprehensive analysis of the proportions of each type of incident and visually displayed the proportion of each incident type in Figure 1. This paper conducts a study with a certain oil transfer station as the background, focusing on petroleum products such as gasoline and diesel. These chemicals, when leaked or burned, generate toxic gases or smoke, posing a threat to the surrounding environment and human health, with toxic accidents likely being a consequence of leakage and fire incidents. Among these, explosions are instantaneous reactions that are difficult to intervene in, so this paper does not involve the study of explosions. By combining the frequencies of accident types in Figure 1, this paper mainly focuses on tank leakage and fire accidents.
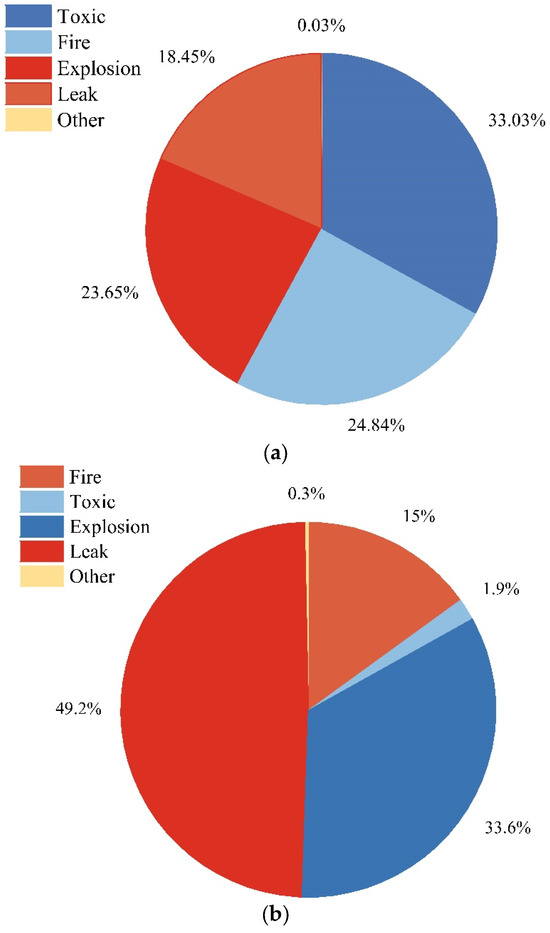
Figure 1.
(a) Data chart of China’s domestic chemical park accidents. (b) Data chart of foreign chemical park accidents.
In existing research, the consequences of leakage and fire accidents in chemical enterprises can be calculated using empirical models, computational fluid dynamics (CFD), and integrated models such as the Process Hazard Analysis Software Tool (PHAST 8.7). Although empirical models provide quick calculations, their accuracy is limited due to factors affecting the overall evaporation rate, such as surface roughness. CFD models like the Fire Dynamics Simulator (FDS) and FLACS can capture these effects, but they come with higher computational costs and longer execution times. The integrated model used in PHAST strikes a balance between accuracy and computational cost while still capturing the effects of surface roughness on propagation, pool evaporation, and mass evaporation—this has been validated by the fire scene experimental results obtained by Henk W.M [2]. Tan Wu et al. [3] used PHAST for a risk analysis and system safety integrity study of enclosed ground flame devices; their findings are useful for designing various types of material windbreaks and flame systems’ strength and for determining the safety distances of surrounding personnel and facilities. Wang Kan et al. [4] studied the impact of leakages of different forms of high-pressure hydrogen storage containers on the scope of consequences after accidental hydrogen leaks or explosions, as well as the variations in environmental temperature differentials and wind conditions. Song Xiaoyan [5] employed the Unified Dispersion Model (UDM) in the PHAST program to conduct numerical simulations of liquefied petroleum gas leakage explosions, analyzing the impact of changes in the wind speed and leak orifice diameter on the consequence range after a leakage.
Although PHAST has significant advantages in process simulation and consequence analysis, with the continuous development of deep learning technology, we can also explore the combination of PHAST and machine learning to achieve more accurate predictions of the consequences in chemical industrial parks. This integrated approach will provide us with more comprehensive and detailed prediction results, helping to further optimize safety management and emergency response strategies. Additionally, machine learning is now widely used in the field of fire decision making. More and more experts and scholars are applying it to the auxiliary decision-making domain. For example, Manuel J. Barros-Daza et al. [6] proposed a data-driven method using artificial neural networks (ANNs) for classification, providing real-time optimal decision making for firefighters in underground coal mine fires. Bilal Umut Ayhan et al. [7] utilized a latent class clustering analysis (LCCA) and artificial neural network (ANN) to develop a new model to predict the outcome of construction accidents and determine the necessary preventive measures. Peng Hu and colleagues [8] performed an analysis and machine learning modeling of the highest roof temperature in the longitudinal ventilation tunnel fire, introducing a new model called the genetic algorithms backpropagation neural network (GABPNN) to predict the highest roof temperature in the ventilation tunnel. Aatif Ali Khan et al. [9] established an intelligent model based on machine learning to predict smoke movement in fires and enhance emergency response procedures through predicting key events for dynamic risk assessment. Mohd Rihan and co-authors [10] conducted an assessment of forest fire susceptibility areas in specific regions using geographic information technology, machine learning algorithms, and uncertainty analysis based on deep learning technology, achieving significant results. Sharma et al. [11] compared eight machine learning algorithms and concluded that the enhanced decision tree model is the most suitable for fire prediction. They also proposed an intelligent fire prediction system based on the site, considering meteorological data and images, and predicted early fires.
Machine learning has made significant progress in the field of fire safety, and we should not overlook the potential advantages of combining PHAST with machine learning. Recent studies have shown that Sun and his team [12] simulated chemical leakage scenarios using PHAST and built causal models of three types of fires using ANN to predict radiation effects on distance. Wang et al. [13] proposed a method for source estimation using ANN, particle swarm optimization (PSO), and simulated annealing (SA). In addition, Yuan et al. [14] established a database of organic compounds with low flammability limits using PHAST, analyzing and predicting the lower flammability limits of organic chemicals. Makhambet Sarbayev et al. [15] proposed a method involving mapping a fault tree (FT) to an ANN and verified the significant progress of combining a numerical simulation software and machine learning to predict the consequences of fire accidents in the chemical industry through the analysis of system failures in the Tassero-Anacortes refinery accident. Jiao et al. [16] used PHAST to establish a toxic diffusion database and developed a model to accurately predict the downwind toxic diffusion distance based on this database. This study aims to accurately estimate the risk level of the oil tank area by utilizing simulated data from the PHAST 8.7 software based on previous research. A comprehensive oil tank leakage fire database was constructed, and machine learning technology was employed to predict the potential impact ranges of accidents. The proposed method seeks to enhance the effectiveness of chemical safety management and risk assessment. However, it is important to note that the created database solely relies on PHAST simulation results and lacks the integration of actual accident data or validation using empirical formulas, consequently limiting its applicability and accuracy. Subsequently, the database is utilized for conducting a predictive analysis of accident consequences through machine learning technology. It is crucial to emphasize that all input data exclusively originated from the PHAST software simulation results, signifying that the database employed for machine learning training is constrained by the scope of PHAST simulation. Hence, this study elucidates the model’s limitations and the restricted application scope of the database, offering valuable insights for future research avenues and data integration.
This paper focuses on the oil storage tank area of a certain oil transfer station as the research object. The station area includes a diesel tank area, gasoline tank area, mixed oil tank area, and mixed oil processing tank area. The main materials involved are gasoline and diesel hydrocarbons. Consequently, the database is constructed based on the PHAST fire consequence simulation results of gasoline and diesel, and it is then used to train the predictive model.
2. Methodology
2.1. Workflow of the Model Design
The main steps of machine learning prediction for the consequence range of storage tank leakage are as follows:
- (1)
- Identify the research subject and scenarios; simulate the consequences of tank leaks and fires using PHAST.
- (2)
- Construct a database of fire consequences based on the simulation results from PHAST.
- (3)
- Develop a quantitative prediction model for the range of consequences based on the database; these include a BP neural network, random forest regression, and K-R regression prediction models.
- (4)
- Tune the prediction models to determine the optimal model.
- (5)
- Evaluate the model’s performance by calculating the mean squared error (MSE) and the R2 coefficient of determination [17].
- (6)
- Apply machine learning algorithms to predict the consequences of fire accidents caused by leaks from storage tanks and draw conclusions by comparing and analyzing actual cases with the predictive results.
The workflow diagram is shown in Figure 2:
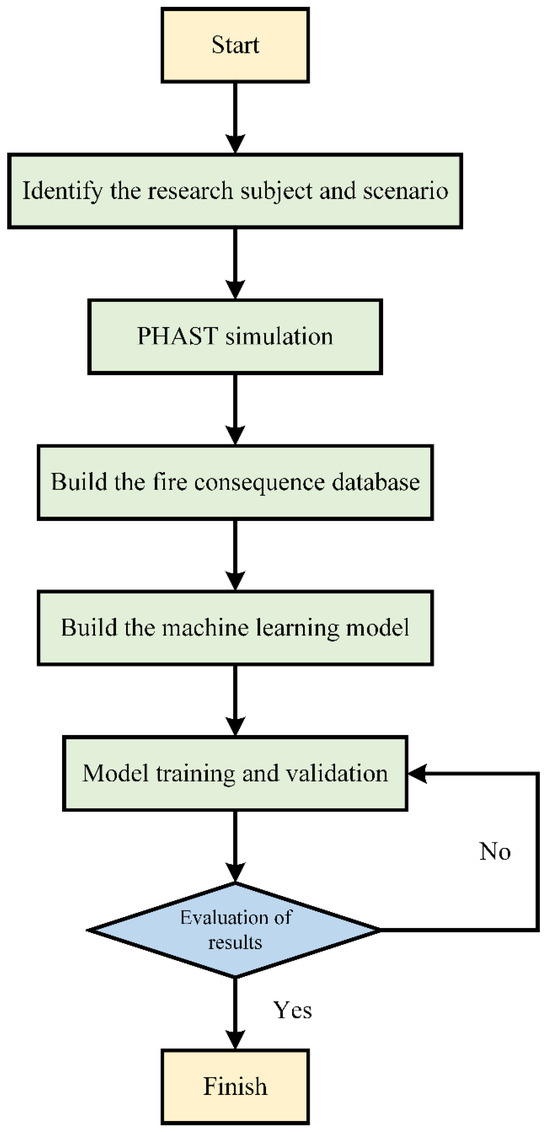
Figure 2.
The workflow diagram.
2.2. PHAST Model
This study is based on the research of a certain oil depot’s storage tanks. The specific distribution of storage tanks in the oil depot is shown in Figure 3 below. The tank area consists of four sections, labeled according to Figure 3, where “1” represents the diesel tank area, “2” represents the gasoline tank area, “3” represents the mixed oil tank area, and “4” represents the mixed oil processing area. The specific specifications of the tank area are shown in Table 1.

Figure 3.
Tank area distribution.

Table 1.
Storage tank sizes in each tank area.
To systematically analyze the impact of the wind speed and direction on the outcomes of fires resulting from tank leakages across varying orifice diameters, this study classifies ten distinct orifice sizes. The sizes range from small (5 mm) to medium (25 mm) and large (100 mm) orifices, extending to scenarios involving catastrophic ruptures. Additionally, this study investigates the influence of environmental temperature on tank leakage outcomes, considering a range of temperatures from −17.9 °C to 42.5 °C, including intermediate conditions at 10 °C, 20 °C, and 25 °C. Moreover, this study evaluates the impact of atmospheric stability on tank leakage outcomes by categorizing atmospheric conditions into ten stability classes labeled A through G. The analysis also explores the effects of preset leak orifice sizes on tank leakages containing diesel, gasoline, and mixed oil. The wind speeds vary from 1 to 16 m/s in 1 m/s increments, resulting in 16 unique meteorological scenarios. These methodological configurations are detailed in Table 2, outlining the foundational settings for the PHAST (Process Hazard Analysis Software Tool) model utilized in this investigation.

Table 2.
PHAST model settings.
Taking the example of a 5 mm leak orifice in a diesel storage tank, the specific configuration parameters are shown in Table 3.

Table 3.
The 5 mm leakage setting parameters of the storage tank.
Based on previous research results, the impact of tank leakage on the surrounding environment mainly depends on its thermal radiation intensity, which varies in its level of harm to the human body. The losses caused by different levels of thermal radiation intensity are shown in Table 4 [18]. According to the results of the literature review, the thermal radiation intensity level for this study is determined to be 4 kW/m2.

Table 4.
Losses caused by different incident intensities of thermal radiation.
2.3. Machine Learning
2.3.1. BP Neural Network
The machine learning algorithm [19] learns and recognizes patterns from historical data and uses these patterns for prediction and decision making. The main machine learning methods include supervised learning, unsupervised learning, and reinforcement learning. This article uses the supervised learning algorithm, employing the BP neural network, random forest regression prediction, and the K-R model, as shown in the neural network architecture diagram in Figure 4. By utilizing PHAST to construct models and perform simulation calculations, this study conducts a comprehensive analysis of the data and organizes them based on the obtained computational results, thereby constructing a dataset. Subsequently, this dataset is used to train algorithmic models, and based on the predictive outcomes of the training process, this study explores and identifies the optimal algorithm.
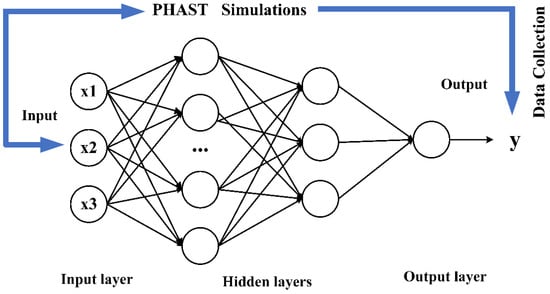
Figure 4.
Neural network architecture diagram.
Regarding the BP neural network model [20], its distinct feature is that signals are propagated forward and errors are propagated backward. Through a certain number of iterations and updates, the network’s predictive results reach the expected accuracy or convergence, yielding the best predictive outcome. The hyperparameters in the neural network also have a significant impact on its predictive outcome. The main hyperparameters include the learning rate, batch size, number of iterations, network structure and layers, activation function, optimizer, and so on. A larger learning rate leads to faster convergence, but there is a risk of skipping the optimal solution. The literature indicates that the batch size is set by considering the memory of the device running the code and the model’s generalization ability [21]. In this model, the device configuration includes a processor of 12th Gen Intel(R) Core(TM) i5-12400F 2.50 GHz and an NVIDIA GeForce RTX 3060 GPU. Considering the dataset size, the batch size is set to 32. The number of iterations and the network structure and layers are mainly found through parameter tuning to seek the optimal results. The number of neurons in each layer of the neural network is calculated based on empirical Formulas (1)–(3) [22] and actual training parameter calculations. The settings are as shown in Table 5.
where h is the number of neurons, n is the number of input neurons, m is the number of output neurons, c is an integer, and .

Table 5.
BP neural network parameter settings.
During the training process of the BP neural network model, a common problem encountered is the vanishing and exploding gradients. The vanishing gradient issue can lead to a slowdown or almost negligible weight updates, while the exploding gradient occurs when the gradient values between network layers exceed 1.0, resulting in an exponential growth of the gradients. This makes the gradients extremely large, causing significant updates to the network weights and thereby making the network unstable. Common activation functions include Sigmoid, Tanh, and ReLU [23], as shown in Figure 5. To address the issues of gradient descent and exploding gradients in the training process mentioned above, the ReLU function is set as the activation function to avoid the vanishing gradient. The final hyperparameter related to the BP neural network is the optimizer [24], with commonly used optimizers such as tochastic gradient descent (SGD), Momentum, Adagrad, and Adam. To avoid becoming stuck in local minima, the optimizer chosen is SGD.
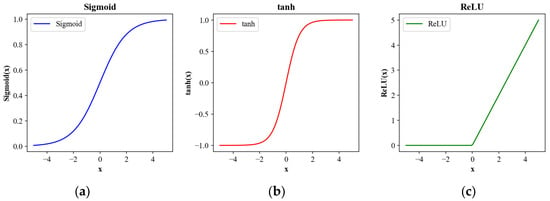
Figure 5.
Illustration of activation functions. (a) Sigmoid activation function graph; (b) tanh activation function graph; (c) ReLU activation function graph.
2.3.2. Random Forest
Random forest [25] is an ensemble model composed of multiple decision trees. It creates multiple subsets by performing sampling with replacement on the training set and builds a decision tree based on each subset. When training each tree, random forest also introduces feature random selection, considering only a random subset of features during the splitting process at each node. During prediction, random forest aggregates the prediction results from multiple trees, commonly using methods such as taking the average (for regression problems) or voting (for classification problems) to obtain the final prediction result. In summary, decision trees split and predict data through a tree-like structure, while random forest utilizes an ensemble strategy of multiple decision trees to enhance predictive performance. Its performance is superior to that of decision tree regression prediction models.
2.3.3. Cross-Validation
Cross-validation is a commonly used model evaluation technique that involves dividing the dataset into training and testing sets. This process is repeated multiple times, allowing for the derivation of various performance metrics for the model. Common cross-validation methods include K-fold cross-validation, leave-one-out cross-validation, and stratified K-fold cross-validation [26], as well as time series cross-validation. The process of K-fold cross-validation, as depicted in Figure 6, involves randomly dividing the dataset into K mutually exclusive subsets, referred to as folds. Then, the model is trained K times, with each training iteration reserving one fold as the testing data and using the remaining K-1 folds as the training data, ensuring different folds are retained for each training iteration. After K iterations of model training, the model with the minimal estimated error on the testing set is selected, and its network architecture and parameters are retained for random forest regression prediction. This article utilizes K-fold cross-validation for model optimization and proposes a new model, the K-R model, by combining K-fold cross-validation with tree models to optimize the tree model’s hyperparameters, thereby improving prediction accuracy.
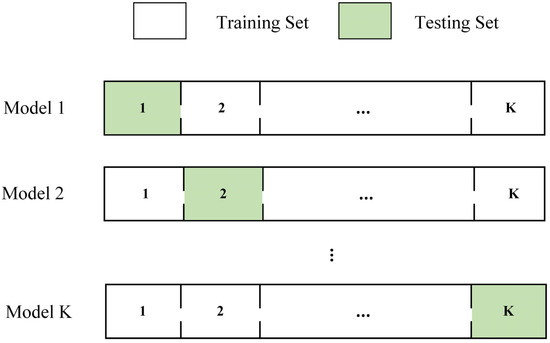
Figure 6.
K-fold cross-validation.
2.4. Model Evaluation
Regarding the performance measurement of the model, the main metrics include accuracy, precision/recall, P-R curve, ROC curve/AUC, , MSE, etc. This article utilizes and MSE to evaluate the model’s performance, with the formulas for and MSE shown as Equations (4) and (5).
where is the predicted output value from the neural network model, is the target value obtained from PHAST, and y is the average of the target values, with n representing the number of scenarios or the quantity of data.
3. Data Preprocessing and Discussion
3.1. Data Preprocessing
In the section regarding data preprocessing and discussion, the initial step involved assessing and cleaning the data for quality. Subsequently, an in-depth exploration of the data’s correlations was undertaken, employing the Pearson correlation coefficient analysis to investigate the linear relationships between variables. Additionally, attention was drawn to the presence of multicollinearity, and corresponding exploration and treatment were carried out. The following will provide a detailed introduction of the specific data analysis methods and results, along with a discussion and explanations of the findings.
3.1.1. Correlation Analysis
The correlation of data within a database is crucial to model training prediction effects; through the Person correlation coefficient [27] analysis for variables—as shown in Formula (6)—we obtain a correlation matrix to eliminate highly correlated variables. As shown in Figure 7, on the right side is a color bar for heat maps; r represents various correlation coefficients. Generally, |r| ≥ 0.8 indicates high correlation between two variables; 0.5 ≤ |r| < 0.8 indicates medium correlation; 0.3 ≤ |r| <0.5 suggests low correlation; and |r| < 0.3 implies little to no correlation between two variables.
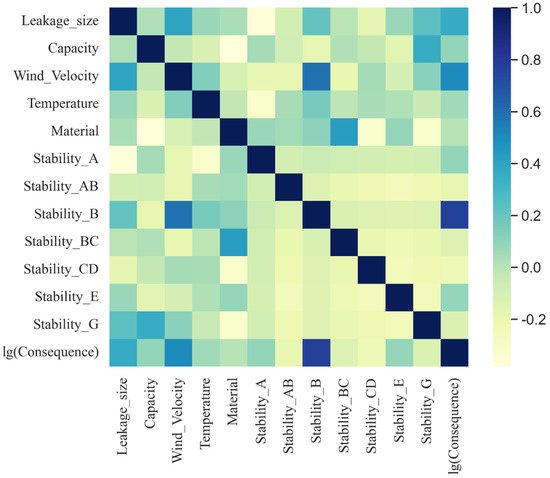
Figure 7.
Thermal map of correlation coefficients in fire aftermath area prediction models.
3.1.2. Multicollinearity
Selecting the right variables is essential to the model’s predictive effectiveness. We determine the input variables for the model based on expert opinions, a search of the literature, and software modeling parameters. Variance Inflation Factor (VIF) and Tolerance (Tol) [28] are widely used indicators for assessing multicollinearity between independent variables in a regression model. VIF represents the variance inflation factor, while Tol represents tolerance.
The VIF value is a measure of the correlation between independent variables. In general, a stronger correlation between independent variables indicates more severe multicollinearity. A VIF value below 10 is generally considered reasonable. Values exceeding 10 indicate strong correlation, necessitating variable screening or transformation. In Table 6, all VIF values are below 10, which is acceptable. Tol represents tolerance and is defined as 1/VIF. Smaller Tol values indicate more severe multicollinearity. Severe multicollinearity is typically indicated when Tol values are below 0.1. Specifically, for this dataset, the minimum Tol value is 0.4827, indicating no multicollinearity.

Table 6.
VIF and Tol of variables.
3.2. Discussion
The PHAST simulation was used to construct a fire database containing over thirty thousand records. This database includes 12,799 sets of jet fire data, 35,998 sets of early pool fire data, and 39,991 sets of late pool fire data. In order to train and validate the model, the training and validation sets were divided in a 7:3 ratio, and predictive analysis was performed. The BP neural network was used for training, and the hyperparameters that minimized prediction errors were selected. The structure of the BP neural network was determined to have two hidden layers, with the first hidden layer comprising 24 neurons and the second hidden layer containing 10 neurons. The learning rate was set to 0.01, the number of iterations was set to 150, and the batch size was 32.
The analysis was conducted on the random forest regression prediction model. Based on the training and debugging results of the model, it was found that the initial parameters of the random forest model with the max depth set to 2 had a large error.
Therefore, in combination with five-fold cross-validation, parameter optimization was carried out, and the K-R model was proposed. The evaluation results of the three models, including MSE and values, are shown in Table 7. It can be observed that the BP neural network model had a large prediction error for the fire dataset, but with a moderate level of accuracy. The random forest model performed well in predicting jet fires and early pool fires but had poor predictions for late pool fires. An analysis indicated that the addition of data related to catastrophic ruptured fire consequence in the late pool fire dataset led to the poor performance of the model. The optimized K-R model outperformed the first two models in predicting jet fires and early pool fires, achieving a high accuracy of 0.99 and optimal predictive performance. The predictive performance of the K-R model for late pool fires improved by approximately 12% compared to the first two algorithms, with an accuracy of 0.99, proving its improved accuracy. This demonstrates that the optimized K-R model has good predictive effects.

Table 7.
MSE values and of three algorithms.
The bar chart shows the MSE and values of the predictions of the three algorithms for the three types of fires. From Figure 8a, it can be seen that the BP neural network, after model training, parameter tuning, and selecting the optimal network structure, outperforms the random forest regression prediction model. However, compared to the K-R model, the prediction results of the BP neural network are slightly inferior. In Figure 8b, the K-R model’s prediction accuracy is at least 0.01 higher than that of the BP neural network, demonstrating a more superior predictive performance.
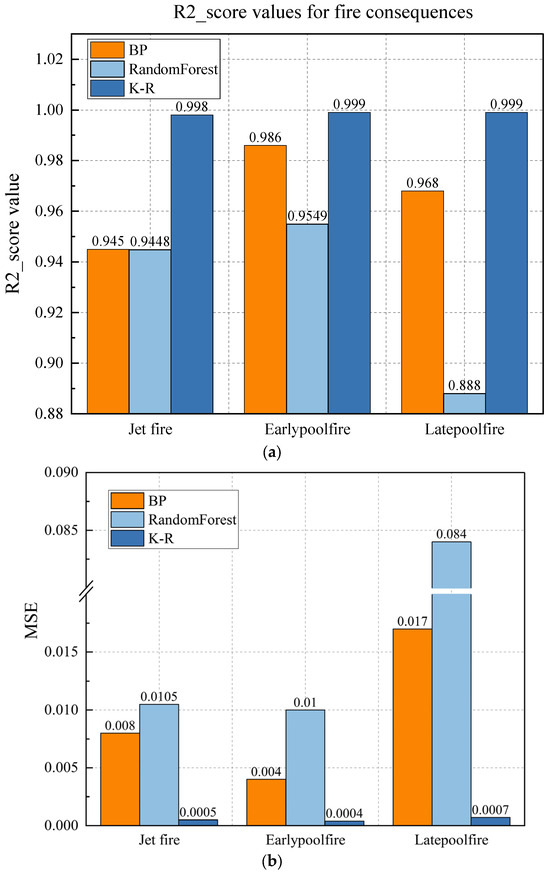
Figure 8.
(a) Bar chart of values for fire prediction outcomes. (b) Bar chart of MSE values for fire prediction outcomes.
We analyzed the predicted values and actual values of three models and plotted the scatter and residual graphs. It is clear from Figure 9 that the data distribution of the K-R model is more concentrated, with a smaller range of fluctuations along the Y = X line, approximately between −0.05 and 0.05, demonstrating a better clustering effect; at the same time, the residuals of this model are relatively small.
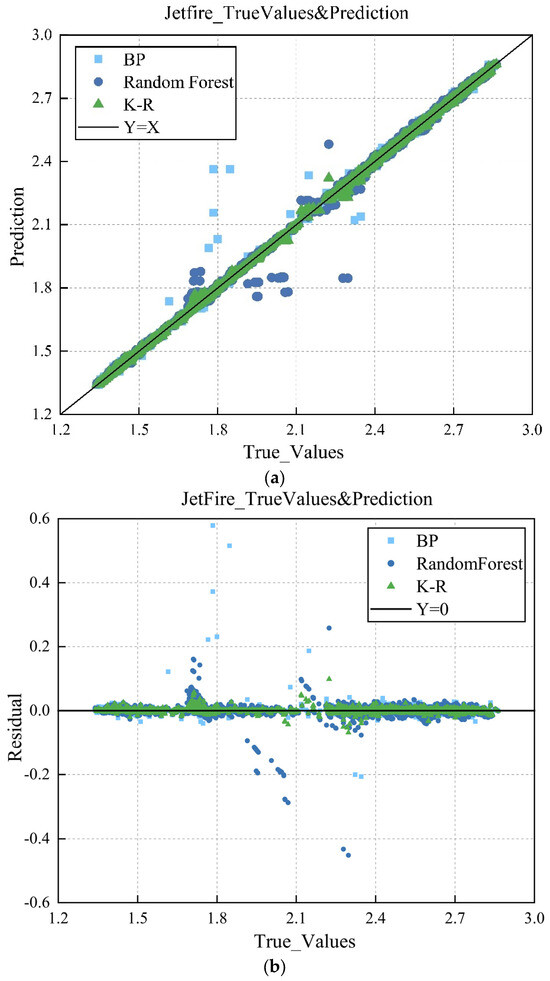
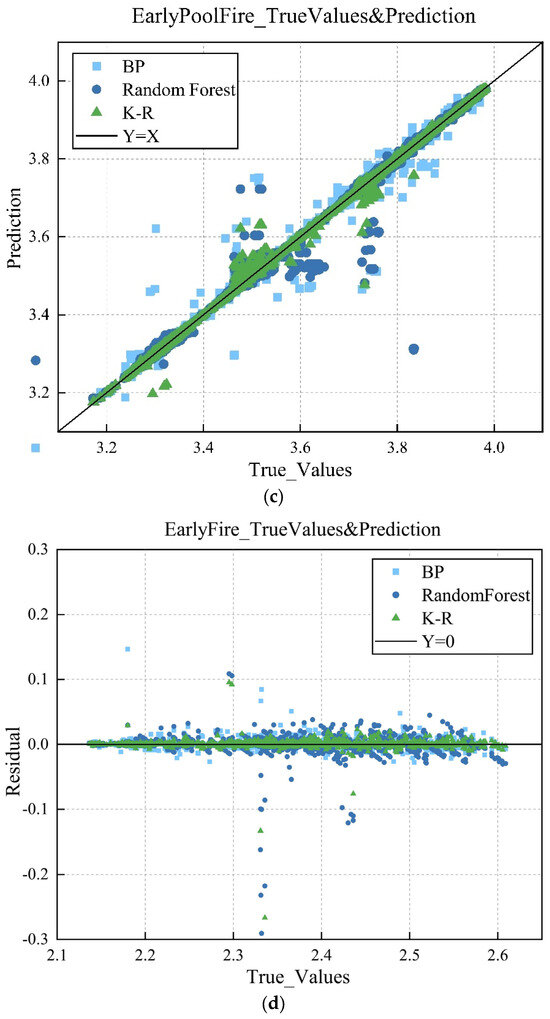
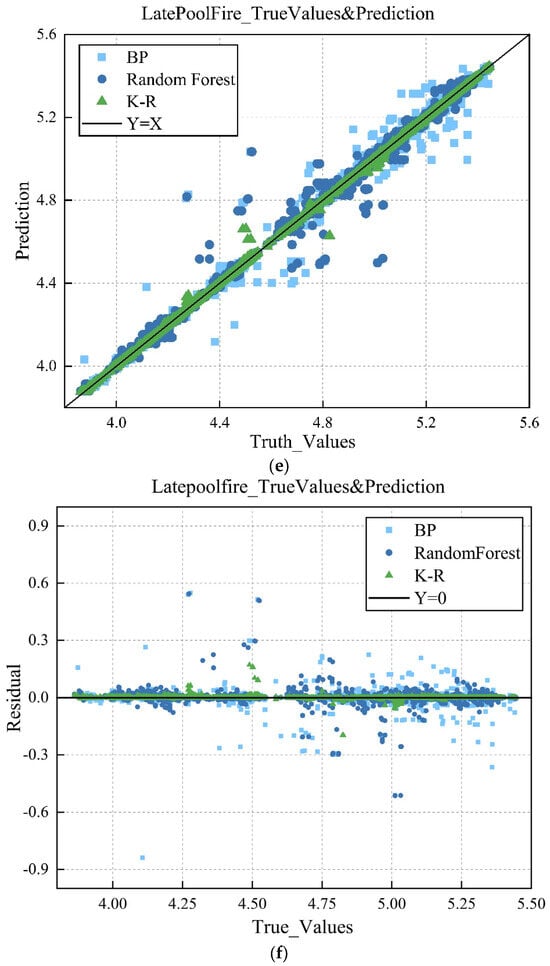
Figure 9.
(a) Scatter plot of predicted outcomes for jet fires. (b) Residual plot of predicted outcomes for jet fires. (c) Scatter plot of predicted outcomes for early pool fires. (d) Residual plot of predicted outcomes for early pool fires. (e) Scatter plot of predicted outcomes for late pool fires. (f) Residual plot of predicted outcomes for late pool fires.
The predicted results of fire consequences were analyzed, and scatter plots and residual plots of the fire consequences were drawn. According to Figure 9a, the predicted values of the three models are evenly distributed along the Y = X line, but it is clear that some points of the BP and random forest models deviate from the Y = X line, indicating a significant error between the predicted and actual values. Based on the residual plot in Figure 9b, the regression effect of the K-R model is relatively better. A comparison of the scatter plots for early pool fires, shown in Figure 9c, and late pool fires, shown in Figure 9d, reveals that, compared to the scatter plot for jet fires, the three models for early pool fires, especially the BP neural network, exhibit a significant error, with many data points distributed outside the Y = X fitting line. In comparison to the three models, the K-R model demonstrates relatively good performance, although there is still room for improvement. From the scatter plots, the residual points of the BP neural network and random forest models are approximately between −0.05 and 0.05, while the absolute error of the K-R model is approximately between −0.02 and 0.02. The data points in the residual plot for late pool fires are more chaotic, with the residual points of the BP neural network and random forest models distributed between −0.03 and 0.03, and the residual points of the K-R model distributed between −0.01 and 0.01. This is attributed to the performances of the first two models.
4. Conclusions
4.1. Case Study
Based on the model database developed through the above analysis and research, a mid-hole leakage incident in a 100,000 internal floating roof gasoline storage tank in a large oil depot was analyzed. The outdoor temperature was 20 °C, the wind speed was 6.5 m/s, and the atmospheric stability was D. Through a PHAST simulation, we derived the thermal radiation intensity of an early pool fire, late pool fire, and jet fire from this oil tank, as well as the corresponding graph (Figure 10) of thermal radiation intensity and downwind distance. From Figure 10a, it can be seen that the downwind distance to 4 for an early pool fire is 35.9504 m; the downwind distance to 12.5 is 28.2839 m; and the downwind distance to 37.5 is 17.8842 m. From Figure 10b, it can be observed that the thermal radiation effect almost disappears at a downwind distance of about 46 m. For a late pool fire, the downwind distance to reach a radiation intensity of 4 is found to be 71.9381 m, and the required downwind distance to reach an intensity level of 12.5 is approximately 48.9713 m, while achieving an intensity level of 37.5 demands a downwind distance of around 40.7759 m, and thermal radiation intensity from late pool fires ceases around at about 100 m downwind. The thermal radiation intensity from jet fires gradually increases with increasing downwind distances—it starts declining when the downwind distance reaches around 2 m, and the rate of decline slows at about the 5 m mark, whereas such thermal radiation effects disappear once the downwind distance reaches approximately 9.2 m.
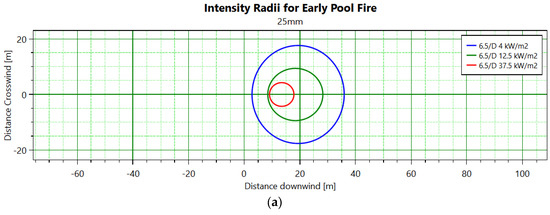
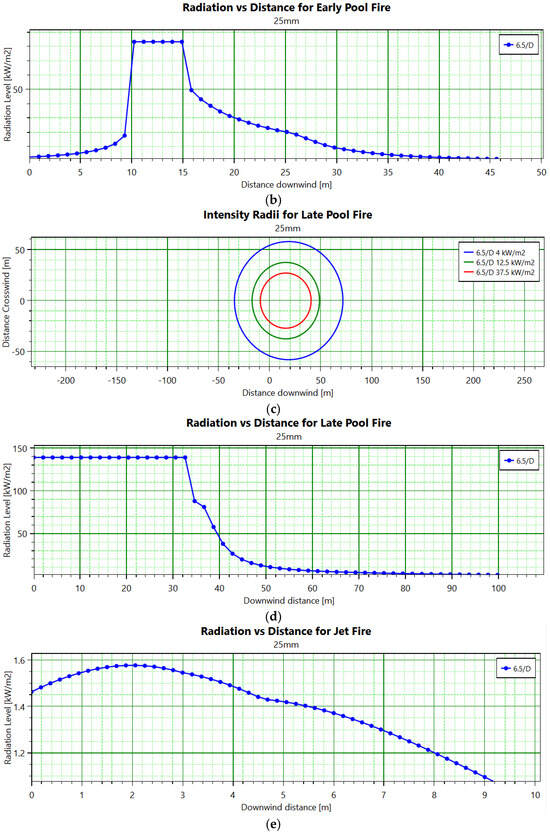
Figure 10.
Related charts for pool and jet fire cases. (a) Early pool fire thermal radiation intensity; (b) Comparison chart of early pool fire thermal radiation intensity and downwind distance; (c) Late pool fire thermal radiation intensity; (d) Comparison chart of late pool fire thermal radiation intensity and downwind distance; (e) Comparison chart of jet fire thermal radiation distance and downwind distance.
The consequences of the tank leakage fire were predicted using the K-R model. The logarithmic value of the consequences was obtained and converted to ascertain the downwind distance of an early pool fire to a specified thermal radiation intensity, which equates to 36.15 m; for a late pool fire, this distance extends to 69.98 m. The early pool fire prediction error is 0.1996 m, and the late pool fire prediction error is 1.9581 m.
4.2. Conclusions
Incorporating case studies into the analysis offered practical insights into the model’s applicability and effectiveness in real-world scenarios, reinforcing the conclusion that machine learning algorithms, notably the K-R model, are essential tools for predicting fire consequences in chemical storage tank areas. This progress signifies a new era in hazard prediction, wherein technology-based solutions have the potential to enhance emergency response planning through more informed decision making, thus potentially saving lives and preventing property damage.
Author Contributions
Data Curation, S.W.; Funding Acquisition, W.Z.; Methodology, W.Z.; Project Administration, X.G.; Software, T.W.; Supervision, T.L.; Validation, X.G.; Writing—Original Draft, S.W.; Writing—Review and Editing, X.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China for the self-extinguishing behavior of tunnel fires under the combined action of longitudinal wind and water fog curtain, grant number [52376130], Engineering Technology Research Centre for Safe and Efficient Coal Mining (Anhui University of Science and Technology), grant number [SECM2206], and the National Supercomputing Center in Zhengzhou.
Data Availability Statement
Due to privacy concerns, data cannot be provided, and this statement is hereby declared.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lonzaga, J.B. Time reversal for localization of sources of infrasound signals in a windy stratified atmosphere. J. Acoust. Soc. Am. 2016, 139, 3053–3062. [Google Scholar] [CrossRef] [PubMed]
- Witlox, H.W.M.; Fernández, M.; Harper, M.; Oke, A.; Stene, J.; Xu, Y. Verification and validation of Phast consequence models for accidental releases of toxic or flammable chemicals to the atmosphere. J. Loss Prev. Process Ind. 2018, 55, 457–470. [Google Scholar] [CrossRef]
- Wu, T.; Wei, X.; Gao, X.; Han, J.; Huang, W. Study on the risk analysis and system safety integrity of enclosed ground flare. Therm. Sci. Eng. Prog. 2019, 10, 208–216. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, M.; Zhang, S.; Ming, Y.; Shi, T.; Yang, F. Study on the Consequences of Accidents of High-Pressure Hydrogen Storage Vessel Groups in Hydrogen Refueling Stations. J. Saf. Environ. 2023, 23, 2024–2032. [Google Scholar] [CrossRef]
- Song, X.; Su, H.; Xie, Z. Numerical Simulation Study on Leakage and Explosion of LPG Tanker [J/OL]. Engineering Blasting:1-7. Available online: http://kns.cnki.net/kcms/detail/11.3675.TD.20231030.1022.002.html (accessed on 1 November 2023).
- Barros-Daza, M.J.; Luxbacher, K.D.; Lattimer, B.Y.; Hodges, J.L. Real time mine fire classification to support firefighter decision making. Fire Technol. 2022, 58, 1545–1578. [Google Scholar] [CrossRef]
- Ayhan, B.U.; Tokdemir, O.B. Accident analysis for construction safety using latent class clustering and artificial neural networks. J. Constr. Eng. Manag. 2020, 146, 04019114. [Google Scholar] [CrossRef]
- Hu, P.; Peng, X.; Tang, F. Prediction of maximum ceiling temperature of rectangular fire against wall in longitudinally ventilation tunnels: Experimental analysis and machine learning modeling. Tunn. Undergr. Space Technol. 2023, 140, 105275. [Google Scholar] [CrossRef]
- Khan, A.A.; Zhang, T.; Huang, X.; Usmani, A. Machine learning driven smart fire safety design of false ceiling and emergency response. Process Saf. Environ. Prot. 2023, 177, 1294–1306. [Google Scholar] [CrossRef]
- Rihan, M.; Bindajam, A.A.; Talukdar, S.; Shahfahad; Naikoo, M.W.; Mallick, J.; Rahman, A. Forest fire susceptibility mapping with sensitivity and uncertainty analysis using machine learning and deep learning algorithms. Adv. Space Res. 2023, 72, 426–443. [Google Scholar] [CrossRef]
- Sharma, R.; Rani, S.; Memon, I. A smart approach for fire prediction under uncertain conditions using machine learning. Multimed. Tools Appl. 2020, 79, 28155–28168. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Zhu, W.; Yuan, S.; Hong, Y.; Mannan, M.S.; Wilhite, B. Development of consequent models for three categories of fire through artificial neural networks. Ind. Eng. Chem. Res. 2019, 59, 464–474. [Google Scholar] [CrossRef]
- Wang, R.; Chen, B.; Qiu, S.; Ma, L.; Zhu, Z.; Wang, Y.; Qiu, X. Hazardous source estimation using an artificial neural network, particle swarm optimization and a simulated annealing algorithm. Atmosphere 2018, 9, 119. [Google Scholar] [CrossRef]
- Yuan, S.; Jiao, Z.; Quddus, N.; Kwon, J.S.-I.; Mashuga, C.V. Developing quantitative structure–property relationship models to predict the upper flammability limit using machine learning. Ind. Eng. Chem. Res. 2019, 58, 3531–3537. [Google Scholar] [CrossRef]
- Sarbayev, M.; Yang, M.; Wang, H. Risk assessment of process systems by mapping fault tree into artificial neural network. J. Loss Prev. Process Ind. 2019, 60, 203–212. [Google Scholar] [CrossRef]
- Jiao, Z.; Ji, C.; Sun, Y.; Hong, Y.; Wang, Q. Deep learning based quantitative property-consequence relationship (QPCR) models for toxic dispersion prediction. Process Saf. Environ. Prot. 2021, 152, 352–360. [Google Scholar] [CrossRef]
- Sathesh, T.; Shih, Y.C. Optimized deep learning-based prediction model for chiller performance prediction. Data Knowl. Eng. 2023, 144, 102120. [Google Scholar] [CrossRef]
- Khodadadi-Mousiri, A.; Yaghoot-Nezhada, A.; Sadeghi-Yarandi, M.; Soltanzadeh, A. Consequence modeling and root cause analysis (RCA) of the real explosion of a methane pressure vessel in a gas refinery. Heliyon 2023, 9, e14628. [Google Scholar] [CrossRef] [PubMed]
- Mahesh, B. Machine learning algorithms-a review. Int. J. Sci. Res. (IJSR) 2020, 9, 381–386. [Google Scholar]
- Sun, B.; Liu, X.; Xu, Z.D.; Xu, D. BP neural network-based adaptive spatial-temporal data generation technology for predicting ceiling temperature in tunnel fire and full-scale experimental verification. Fire Saf. J. 2022, 130, 103577. [Google Scholar] [CrossRef]
- Smith, S.L.; Kindermans, P.J.; Ying, C.; Le, Q.V. Don’t decay the learning rate, increase the batch size. arXiv 2017, arXiv:1711.00489. [Google Scholar]
- Yan, S. Dynamic Adaptive Risk Assessment System for Individual Building Fires Based on Internet of Things and Deep Neural Networks. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2021. [Google Scholar] [CrossRef]
- He, J.; Li, L.; Xu, J.; Zheng, C. ReLU deep neural networks and linear finite elements. arXiv 2018, arXiv:1807.03973. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Pearson correlation coefficient. Noise Reduct. Speech Process. 2009, 2, 1–4. [Google Scholar] [CrossRef]
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).