Indoor Experiments on the Moisture Dynamic Response to Wind Velocity for Fuelbeds with Different Degrees of Compactness
Abstract
1. Introduction
2. Method
2.1. Investigation of Fuelbed Characteristics and Collection of Fuel in the Field
2.2. Constructing of Indoor Fuelbeds with Different Compactness Levels
2.3. Drying Experiment at Different Wind Velocities
3. Data Analysis
3.1. Drying Curve
3.2. Basic Principle of the Drying Coefficient of the Fuelbed
3.3. Calculation of the Drying Coefficient of the Fuelbed
3.4. t Test
3.5. Variance Analysis
3.6. Model
4. Results
4.1. Basic Information
4.2. Drying Process
4.3. Parameter Estimation and T-test
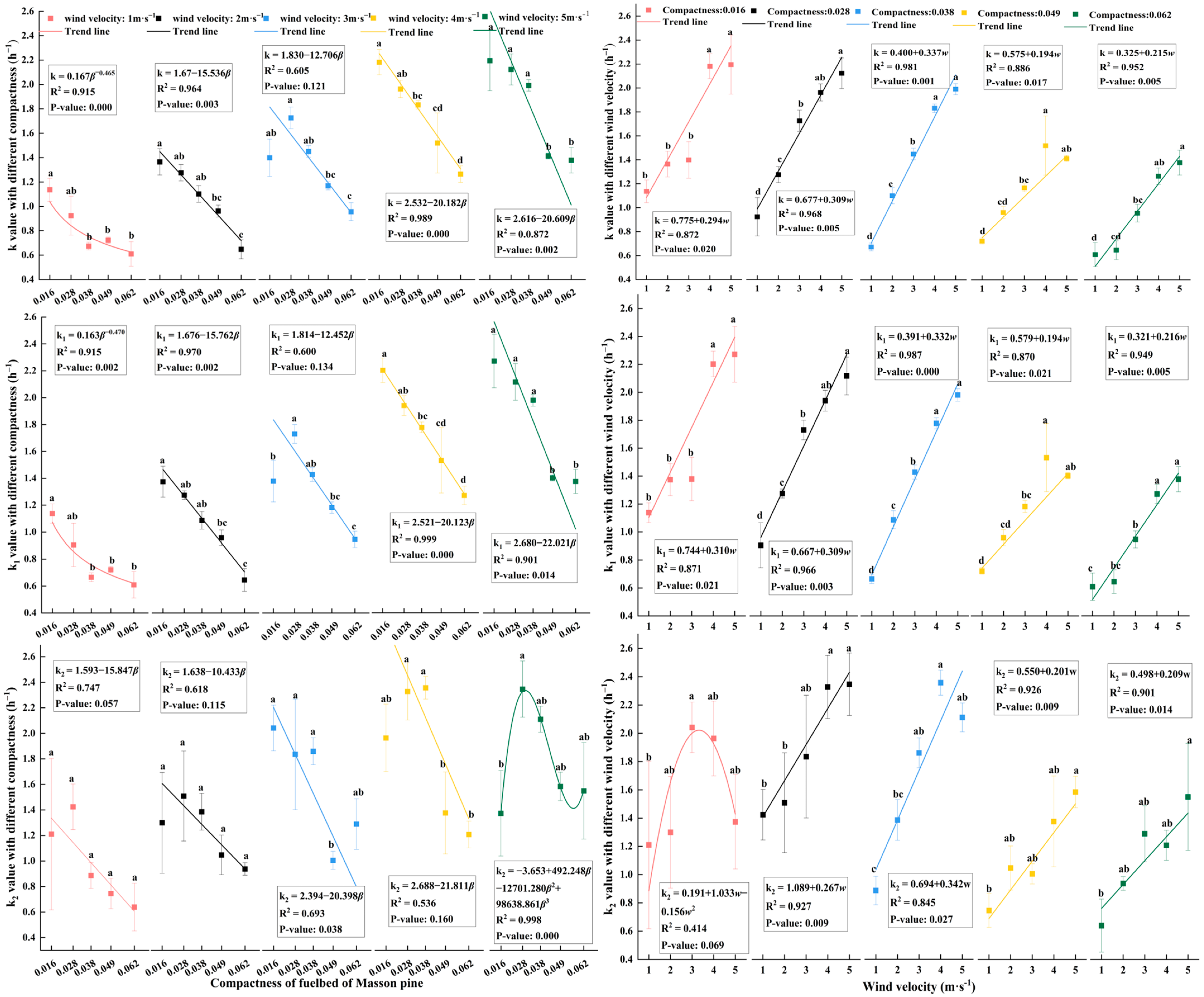
4.4. Effects of Wind Velocity and Compactness on Drying Coefficient
4.5. Model
4.5.1. Parameters of the Model
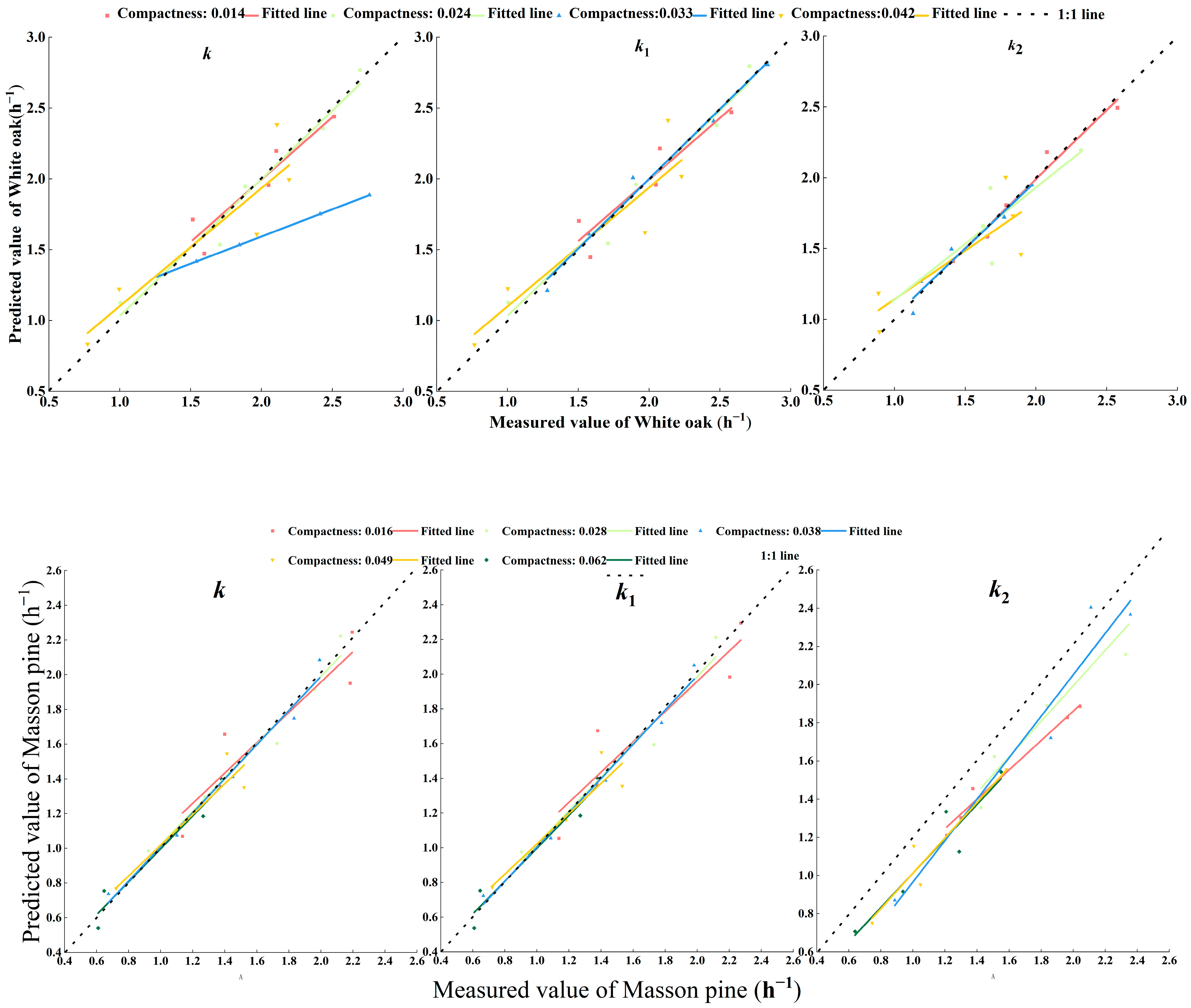
4.5.2. A 1:1 Comparison
5. Discussion
5.1. Basic Information concerning the Drying Coefficient
5.2. Difference Analysis
5.3. Impact Factor Analysis
5.4. Prediction Models
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.L.; Tian, L.L. Dynamic changes in moisture content and applicability analysis of a typical litter prediction model in Yunnan Province. Peer J. 2021, 9, e12206. [Google Scholar] [CrossRef] [PubMed]
- Slijepcevic, A.; Anderson, W.R.; Matthews, S.; Anderson, D.H. An analysis of the effect of aspect and vegetation type on fine fuel moisture content in eucalypt forest. Int. J. Wildland Fire 2018, 27, 190–202. [Google Scholar] [CrossRef]
- Baksic, N.; Baksic, D. Predicting the fine fuel moisture content in Dalmatian black pine needle litter. Int. J. Wildland Fire 2022, 31, 708–719. [Google Scholar] [CrossRef]
- Lei, W.D.; Yu, Y.; Li, X.H.; Xing, J. Estimating dead fine fuel moisture content of forest surface, based on wireless sensor network and back-propagation neural network. Int. J. Wildland Fire 2022, 31, 369–378. [Google Scholar] [CrossRef]
- de Dios, V.R.; Fellows, A.W.; Nolan, R.H.; Boer, M.M.; Bradstock, R.A.; Domingo, F.; Goulden, M.L. A semi-mechanistic model for predicting the moisture content of fine litter. Agric. For. Meteorol. 2015, 203, 64–73. [Google Scholar] [CrossRef]
- Catchpole, E.A.; Catchpole, W.R.; Viney, N.R.; McCaw, W.L.; Marsden-Smedley, J.B. Estimating fuel response time and predicting fuel moisture content from field data. Int. J. Wildland Fire 2001, 10, 215–222. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Sun, P. Study on the Diurnal Dynamic Changes and Prediction Models of the Moisture Contents of Two Litters. Forests 2020, 11, 95. [Google Scholar] [CrossRef]
- Kreye, J.K.; Varner, J.M.; Knapp, E.E. Effects of particle fracturing and moisture content on fire behaviour in masticated fuelbeds burned in a laboratory. Int. J. Wildland Fire 2011, 20, 308–317. [Google Scholar] [CrossRef]
- Sun, P.; Yu, H.Z.; Jin, S. Predicting hourly litter moisture content of larch stands in daxinganling region, China using three vapour-exchange methods. Int. J. Wildland Fire 2015, 24, 114–119. [Google Scholar] [CrossRef]
- Matthews, S. A process-based model of fine fuel moisture. Int. J. Wildland Fire 2006, 15, 155–168. [Google Scholar] [CrossRef]
- Lan, S.X.; Hu, Z.L.; Jin, Y.Q.; Chen, F.F.; Zhang, Y.L. Effect of Compactness of fuelbed on dynamic change of moisture content of litter bed of Pinus massoniana. J. Northeast For. Univ. 2022, 50, 45–50. [Google Scholar]
- Zhang, Y.L. Modeling the drying process of Masson pine needle fuel beds under different packing ratios based on two-phase models in the laboratory. Peer J. 2022, 10, e14484. [Google Scholar] [CrossRef]
- Matthews, S.; Gould, J.; McCaw, L. Simple models for predicting dead fuel moisture in eucalyptus forests. Int. J. Wildland Fire 2010, 19, 459–467. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, L.B.; Yu, H.Z.; Man, Z.Y. Effects of wind speed on two key water loss times of fuelbeds composed of Korean pine needles. J. Cent. South Univ. For. Technol. 2016, 36, 6–10. [Google Scholar]
- Nelson, R.M.; Hiers, J.K. The influence of fuelbed properties on moisture drying rates and timelags of longleaf pine litter. Can. J. For. Res. 2008, 38, 2394–2404. [Google Scholar] [CrossRef]
- Jin, S.; Chen, P.Y. Modelling drying processes of fuelbeds of Scots pine needles with initial moisture content above the fibre saturation point by two-phase models. Int. J. Wildland Fire 2012, 21, 418–427. [Google Scholar] [CrossRef]
- Van Wanger, C.E. Equilibrium Moisture Content of Some Fine Forest Fuels in Eastern Canada; Canadian Forestry Service Information Report PS-X-36 Petawawa Forest Experimental Station: Chalk, ON, Canada, 1972; pp. 1–12. [Google Scholar]
- Anderson, H.E. Moisture diffusivity and response time in fine forest fuels. Can. J. For. Res. 1990, 20, 315–325. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Guo, Y.; Hu, H.Q. Characteristics of forest fire data in Southwest China during 2001–2017. J. Northwest For. Univ. 2021, 36, 179–186. [Google Scholar]
- Wotton, B.M.; Beverly, J.L. Stand-specific litter moisture content calibrations for the Canadian Fine Fuel Moisture Code. Int. J. Wildland Fire 2007, 16, 463–472. [Google Scholar] [CrossRef]
- Sow, M.; Mbow, C.; Hely, C.; Fensholt, R.; Sambou, B. Estimation of Herbaceous Fuel Moisture Content Using Vegetation Indices and Land Surface Temperature from MODIS Data. Remote Sens. 2013, 5, 2617–2638. [Google Scholar] [CrossRef]
- Bradshaw, L.S.; Deeming, J.E.; Burgan, R.E.; Cohen, J.D. The 1978 National Fire-Danger Rating System: Technical Documentation; General Technical Report INT-169; USDA Forest Service, Intermountain Forest and Range Experiment Station Ogden: Ogden, Utah, 1983; p. 84401. [Google Scholar]
- Sun, P.; Zhang, Y.L.; Sun, L.; Hu, H.H.; Guo, F.T.; Wang, G.Y.; Zhang, H. Influence of Fuel Moisture Content, Packing Ratio and Wind Velocity on the Ignition Probability of Fuel Beds Composed of Mongolian Oak Leaves via Cigarette Butts. Forests 2018, 9, 507. [Google Scholar] [CrossRef]
- Byram, G.B. An Analysis of the Drying Process in Forest Fuel Material; Unpublished Report; USDA Forest Service, Southern Forest Fire Laboratory: Macon, GA, USA, 1963. [Google Scholar]
- Pixton, S.W.; Warburton, S. Moisture Content/Relative Humidity Equilibrium of Some Cereal Grains at Different Temperatures. J. Stored Prod. Res. 1971, 6, 283–293. [Google Scholar] [CrossRef]
- Britton, C.M.; Countryman, C.M.; Wright, H.A.; Walvekar, A.G. The Effect of Humidity, Air Temperature, and Wind Speed on Fine Fuel Moisture Content. Fire Technol. 1973, 9, 46–55. [Google Scholar] [CrossRef]
- Simard, A.J. The moisture content of forest fuels-1. In A Review of the Basic Concepts; Information Report FF-X-14; Canadian Department of Forest and Rural Development, Forest Fire Research Institute: Ottawa, ON, Canada, 1968; p. 47. [Google Scholar]
- Anderson, H.E.; Schuette, R.D.; Mutch, R.W. Timelag and Equilibrium Moisture Content of Ponderosa Pine Needles; USDA Interm For and Range Exp Stn: Ogden, Utah, 1978; pp. 8–14. [Google Scholar]
- Nelson, R.M.; Ralph, M. A Method for Describing Equilibrium Moisture Content of Forest Fuels. Can. J. For. Res. 1984, 14, 597–600. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Sun, P.; Liu, F.C. Effects of indoor simulated air temperature and relative humidity on the moisture contents of the needle beds with different compactness of red pine. J. Cent. South Univ. For. Technol. 2020, 40, 18–27, 93. [Google Scholar]
- Luke, R.H.; McArthur, A.G. Bushfires in Australia; Australian Government Publication Service: Canberra, Australia, 1978. [Google Scholar]
- Zhang, L.B.; Sun, P.; Jin, S. Effects of wind speed on drying processes of fuelbeds composed of Mongolian oak broadleaves. Chin. J. Appl. Ecol. 2016, 27, 3463–3468. [Google Scholar]
- Zhang, Y.L. Study on Influencing Factors and Prediction Model of Dynamic Change of Litter Moisture Content of Mongolian Oak and Pinus Koraiensis. Doctoral Dissertation, Northeast Forestry University, Harbin, China, 2019. [Google Scholar]
- Pippen, B.G. Fuel Moisture and Fuel Dynamics in Woodland and Heathland Vegetation of the Sydney Basin; School of Physical, Environmental and Mathematical Sciences, University of New South Wales: Canberra, Australia, 2008. [Google Scholar]
- Yu, M.J.; Zhang, X.J.; Mu, G.L.; Yan, J.S.; Zhang, H.; Shi, Z.L. Research Progress on the Application of Hot Air Drying Technology in China. Agric. Sci. Technol. Equip. 2013, 8, 14–16. [Google Scholar]
- Groot, W.J.D.; Wardati Wang, Y. Calibrating the Fine Fuel Moisture Code for Grass Ignition Potential in Sumatra, Indonesia. Int. J. Wildland Fire 2005, 14, 161–168. [Google Scholar] [CrossRef]
- Mahapatra, A. Influence of Moisture Content and Temperature on Thermal Conductivity and Thermal Diffusivity of rice flours. Int. J. Food Prop. 2011, 14, 675–683. [Google Scholar] [CrossRef]
- Jin, S.; Li, X.Y.; Li, Y.X. The changes of moisture content during drying processes of small fuel. J. Northeast For. Univ. 2000, 28, 35–38. [Google Scholar]
- Jin, S.; Chen, P.Y. Effects of Structure Features of Fuelbed Composed of Scots Pine Needles on Equilibrium Moisture Content Parameters during Desorption Process. Sci. Silvae Sin. 2011, 47, 114–120. [Google Scholar]
- Matthews, S.; Mccaw, W.L.; Neal, J.E.; Neal, J.E.; Smith, R.H. Testing a Process-based Fine Fuel Moisture Model in Two Forest Types. Can. J. For. Res. 2007, 37, 23–35. [Google Scholar] [CrossRef]
- Borujerdi, P.R.; Shotorban, B.; Mahalingam, S.; Weise, D.R. Modeling of water evaporation from a shrinking moist biomass slab subject to heating: Arrhenius approach versus equilibrium approach q. Int. J. Heat Mass Transf. 2019, 145, 118672. [Google Scholar] [CrossRef]
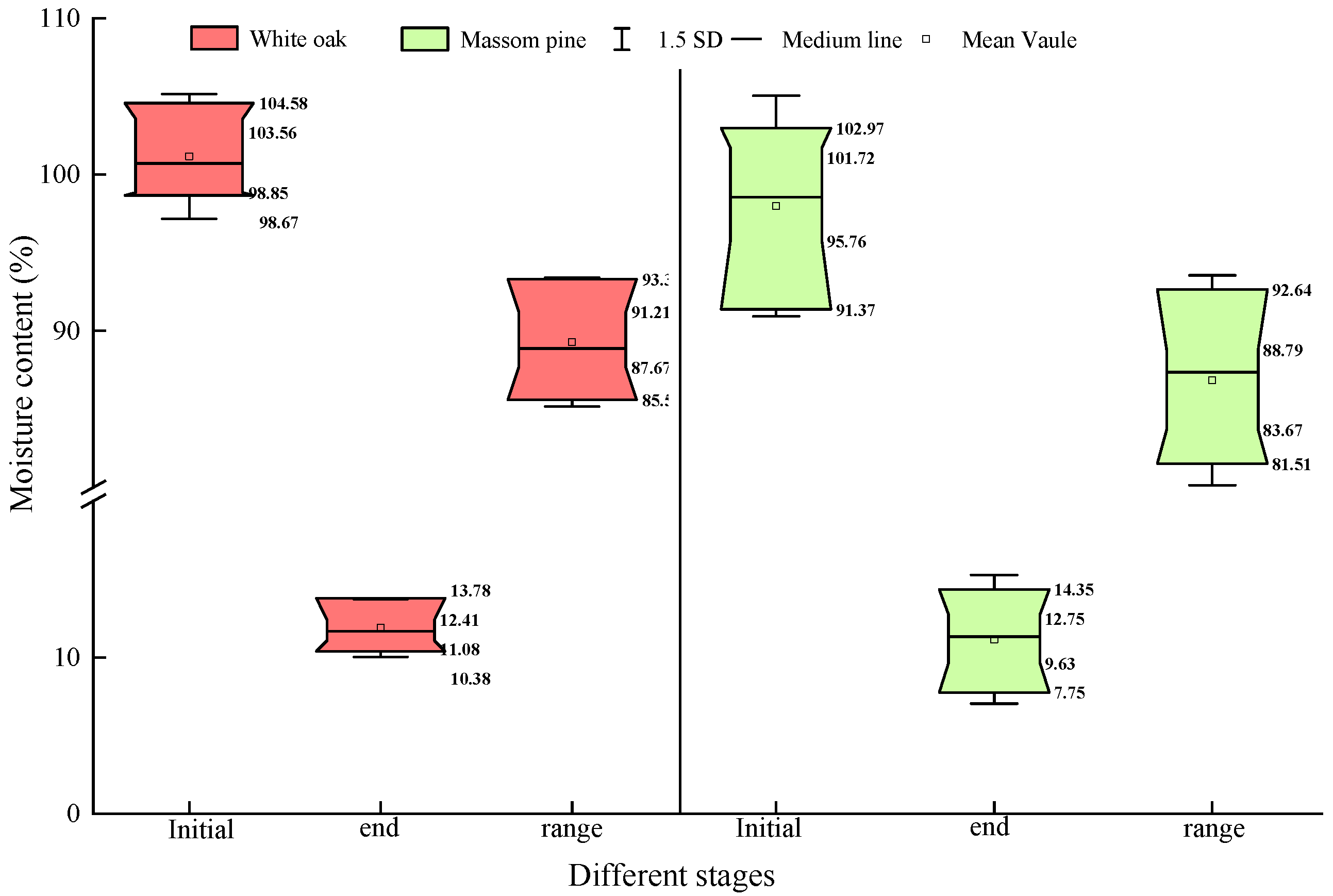
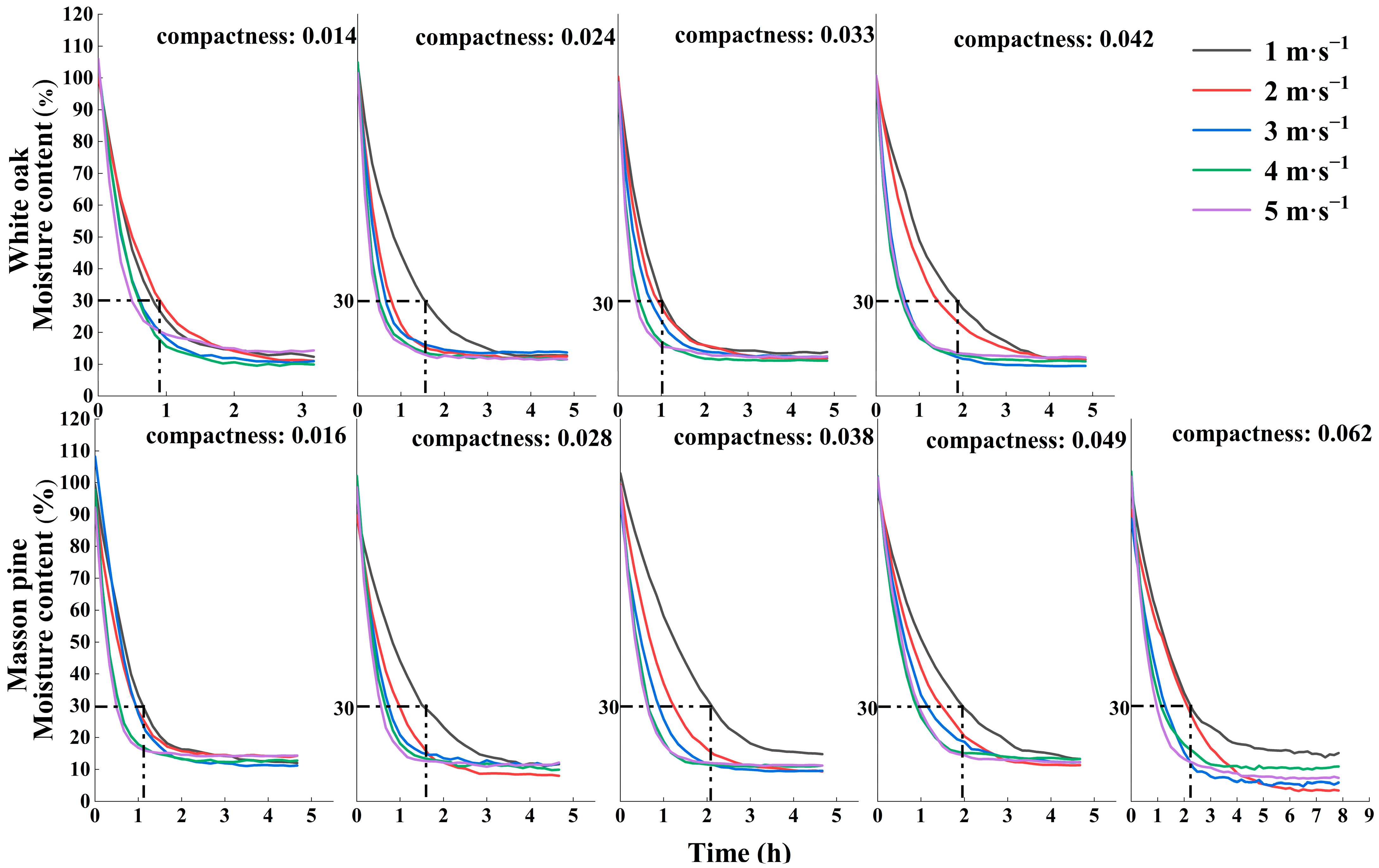
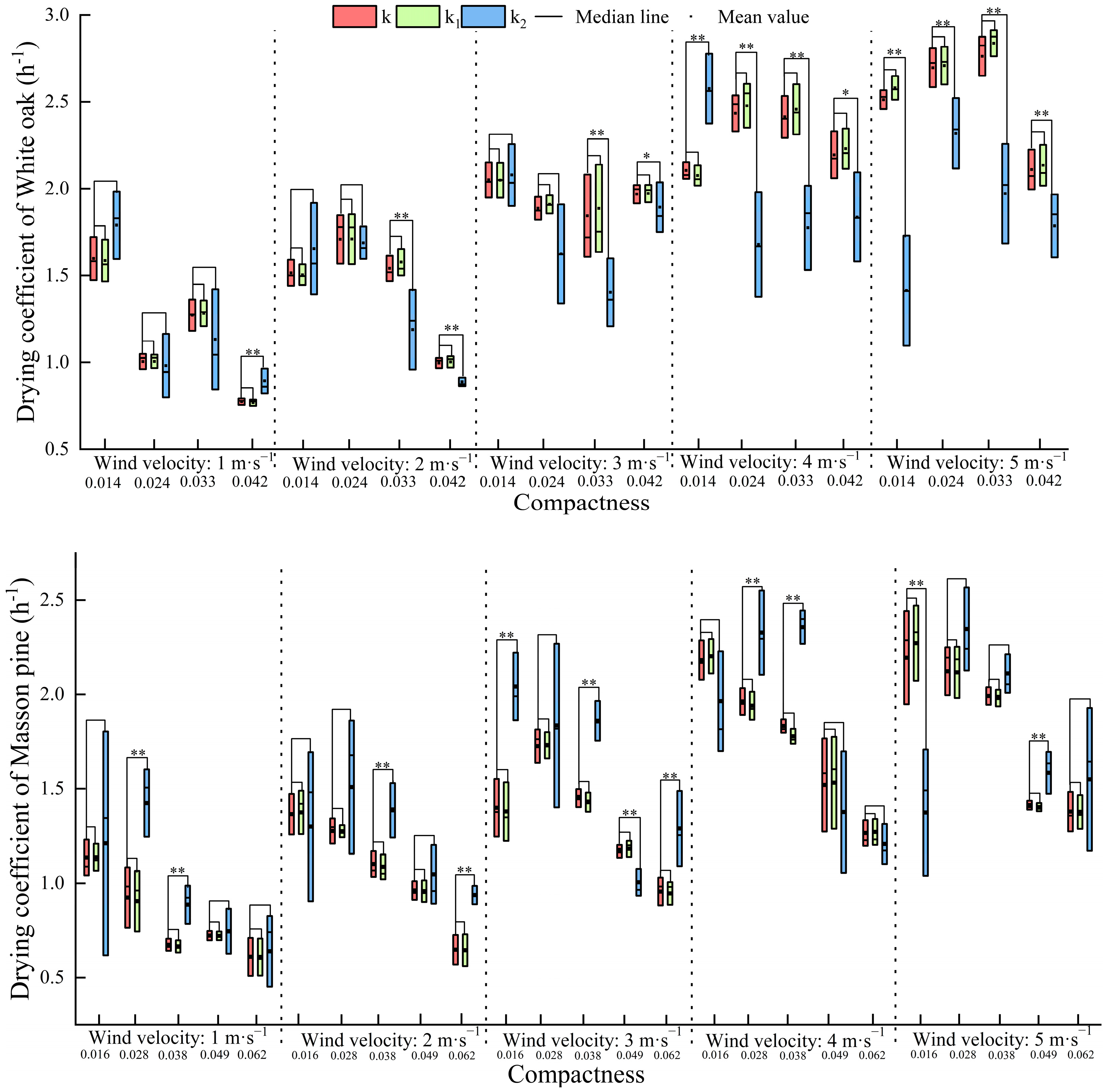
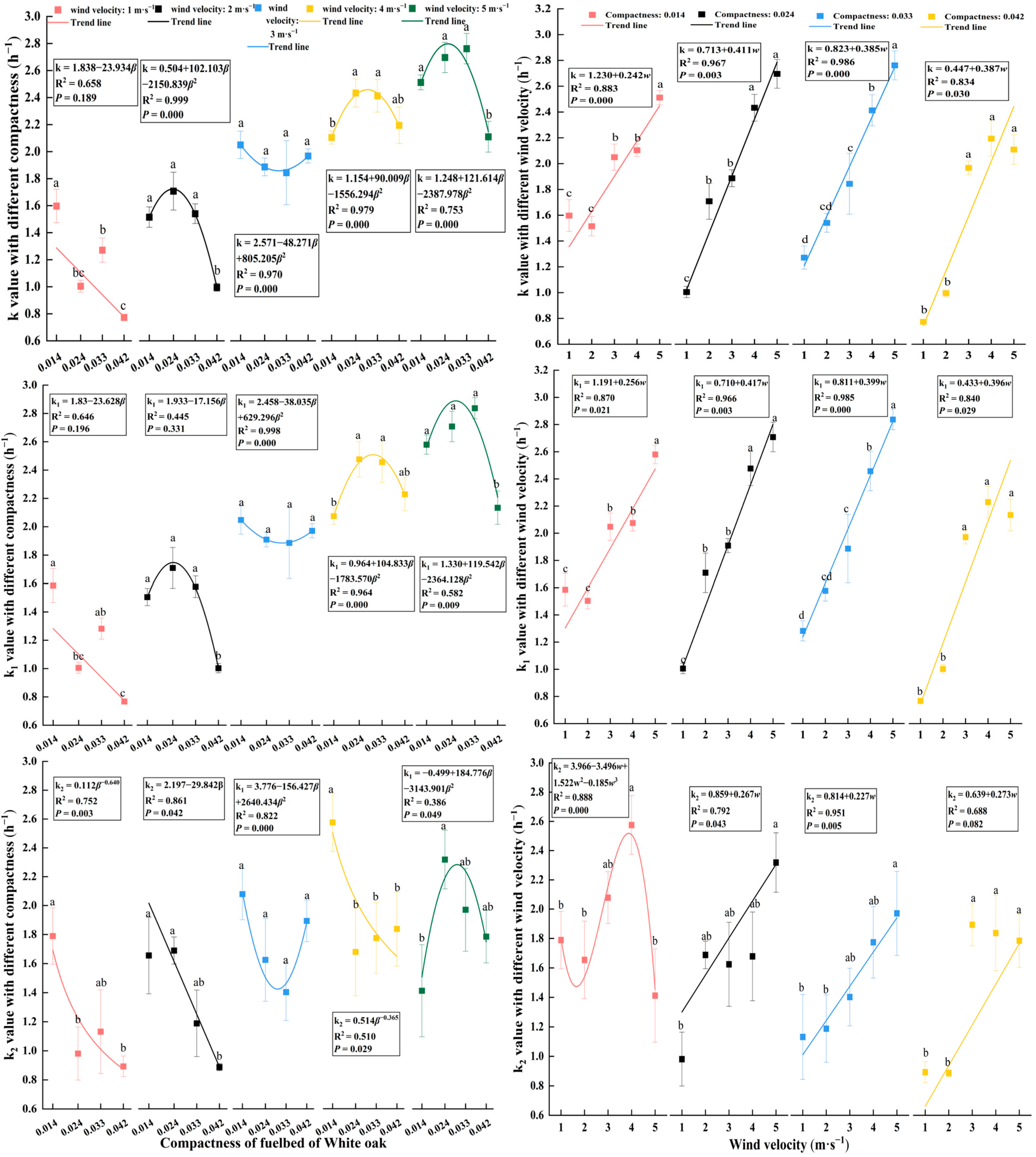
| Forest Type | Mean Diameter at Breast Height (cm) | Mean Height (m) | Canopy | Mean Fuelbed Thickness (cm) | Mean Fuelbed Compactness |
|---|---|---|---|---|---|
| White Oak | 16.7 | 14.1 | 0.73 | 4.6 | 0.033 |
| Masson Pine | 22.7 | 16.9 | 0.89 | 3.0 | 0.038 |
| White Oak | Masson Pine | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Compactness | 0.014 | 0.024 | 0.033 | 0.042 | 0.016 | 0.028 | 0.038 | 0.049 | 0.062 |
| Quantity (g) | 20.73 | 35.80 | 49.62 | 63.98 | 13.52 | 23.34 | 32.36 | 41.73 | 52.37 |
| Fuel Type | Index | df | ||||||
|---|---|---|---|---|---|---|---|---|
| F Value | p | F Value | p | F Value | p | |||
| White oak | Wind | 4 | 355.000 | *** | 370.359 | *** | 27.568 | *** |
| Compactness | 3 | 41.751 | *** | 43.459 | *** | 12.590 | *** | |
| Wind compactness | 12 | 13.094 | *** | 13.285 | *** | 7.843 | *** | |
| Masson pine | Wind | 4 | 242.774 | *** | 277.675 | *** | 32.269 | *** |
| Compactness | 4 | 110.449 | *** | 126.444 | *** | 27.111 | *** | |
| Wind compactness | 16 | 4.760 | *** | 6.071 | *** | 2.638 | ** | |
| Fuel Type | Compactness | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | Mae (h−1) | Mre (%) | Model | R2 | Mae (h−1) | Mre (%) | Model | R2 | Mae (h−1) | Mre (%) | ||
| White oak | 0.014 | = 1.230 + 0.242 | 0.883 | 0.117 | 6.58 | = 1.191 + 0.256 | 0.870 | 0.135 | 7.46 | = 0.185 + 1.522 − 3.496 + 3.966 | 0.888 | 0.055 | 2.72 |
| 0.024 | = 0.713 + 0.411 | 0.967 | 0.100 | 6.20 | = 0.710 + 0.417 | 0.966 | 0.104 | 6.33 | = 0.859 + 0.267 | 0.792 | 0.170 | 10.93 | |
| 0.033 | = 0.823 + 0.385 | 0.986 | 0.403 | 17.46 | = 0.811 + 0.399 | 0.985 | 0.061 | 3.45 | = 0.814 + 0.227 | 0.951 | 0.068 | 5.08 | |
| 0.042 | = 0.447 + 0.387 | 0.834 | 0.224 | 14.16 | = 0.433 + 0.396 | 0.840 | 0.225 | 14.13 | = 0.639 + 0.273 | 0.688 | 0.205 | 14.36 | |
| MRE | 11.10 | 7.84 | 8.27 | ||||||||||
| Masson pine | 0.016 | = 0.775 + 0.294 | 0.857 | 0.122 | 7.47 | = 0.744 + 0.310 | 0.916 | 0.126 | 8.08 | = 0.191 + 1.033 − 0.156 | 0.914 | 0.076 | 4.18 |
| 0.028 | = 0.677 + 0.309 | 0.957 | 0.070 | 4.50 | = 0.667 + 0.309 | 0.633 | 0.070 | 4.50 | = 1.089 + 0.267 | 0.947 | 0.097 | 5.20 | |
| 0.038 | = 0.400 + 0.337 | 0.980 | 0.062 | 4.77 | = 0.391 + 0.332 | 0.354 | 0.052 | 4.27 | = 0.694 + 0.342 | 0.834 | 0.093 | 4.84 | |
| 0.049 | = 0.575 + 0.194 | 0.972 | 0.072 | 5.61 | = 0.579 + 0.194 | 0.574 | 0.081 | 6.36 | = 0.550 + 0.201 | 0.887 | 0.060 | 5.59 | |
| 0.062 | = 0.325 + 0.215 | 0.925 | 0.059 | 7.48 | =0.321 + 0.216 | 0.292 | 0.063 | 7.89 | = 0.498 + 0.209 | 0.866 | 0.078 | 7.32 | |
| MRE | 5.97 | 6.22 | 5.43 | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y. Indoor Experiments on the Moisture Dynamic Response to Wind Velocity for Fuelbeds with Different Degrees of Compactness. Fire 2023, 6, 90. https://doi.org/10.3390/fire6030090
Zhang Y. Indoor Experiments on the Moisture Dynamic Response to Wind Velocity for Fuelbeds with Different Degrees of Compactness. Fire. 2023; 6(3):90. https://doi.org/10.3390/fire6030090
Chicago/Turabian StyleZhang, Yunlin. 2023. "Indoor Experiments on the Moisture Dynamic Response to Wind Velocity for Fuelbeds with Different Degrees of Compactness" Fire 6, no. 3: 90. https://doi.org/10.3390/fire6030090
APA StyleZhang, Y. (2023). Indoor Experiments on the Moisture Dynamic Response to Wind Velocity for Fuelbeds with Different Degrees of Compactness. Fire, 6(3), 90. https://doi.org/10.3390/fire6030090





