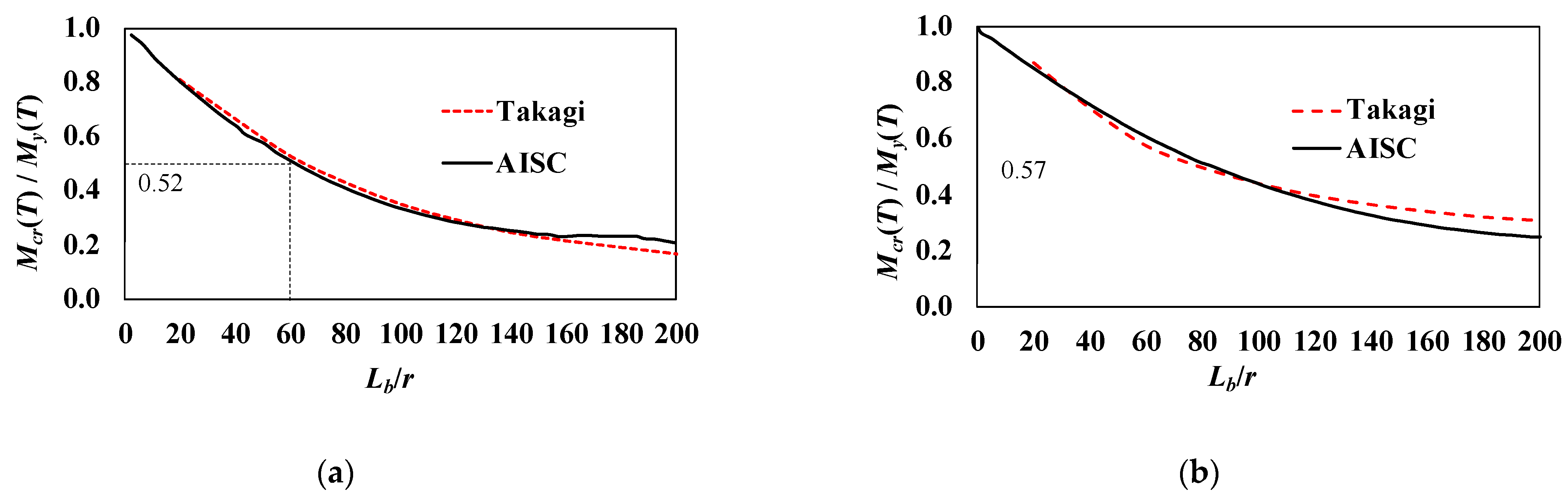Behavior and Capacity of Moment-Frame Members and Connections during Fire
Abstract
1. Introduction
2. Objective and Approach
3. FEM Model Development and Benchmarking
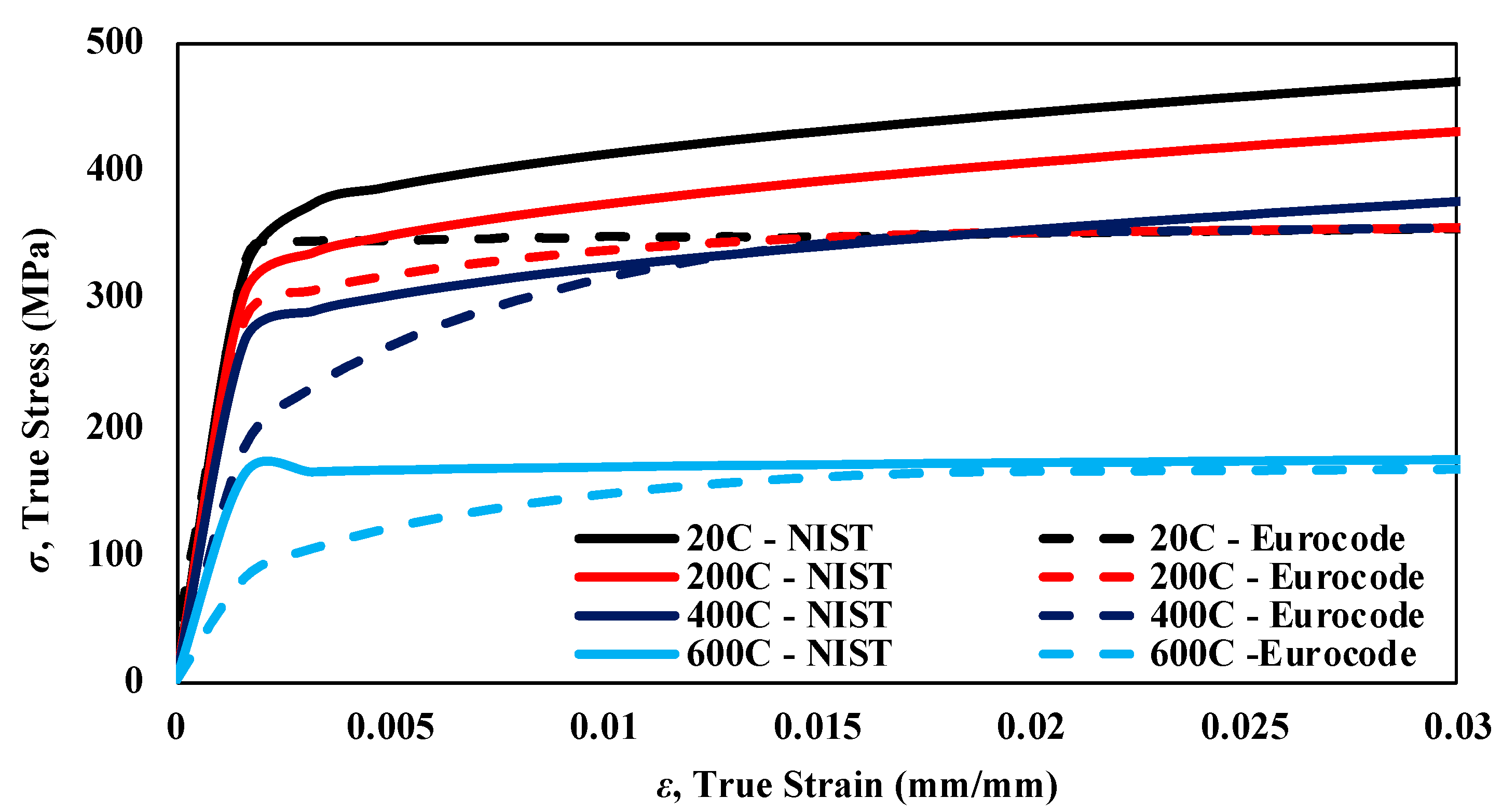
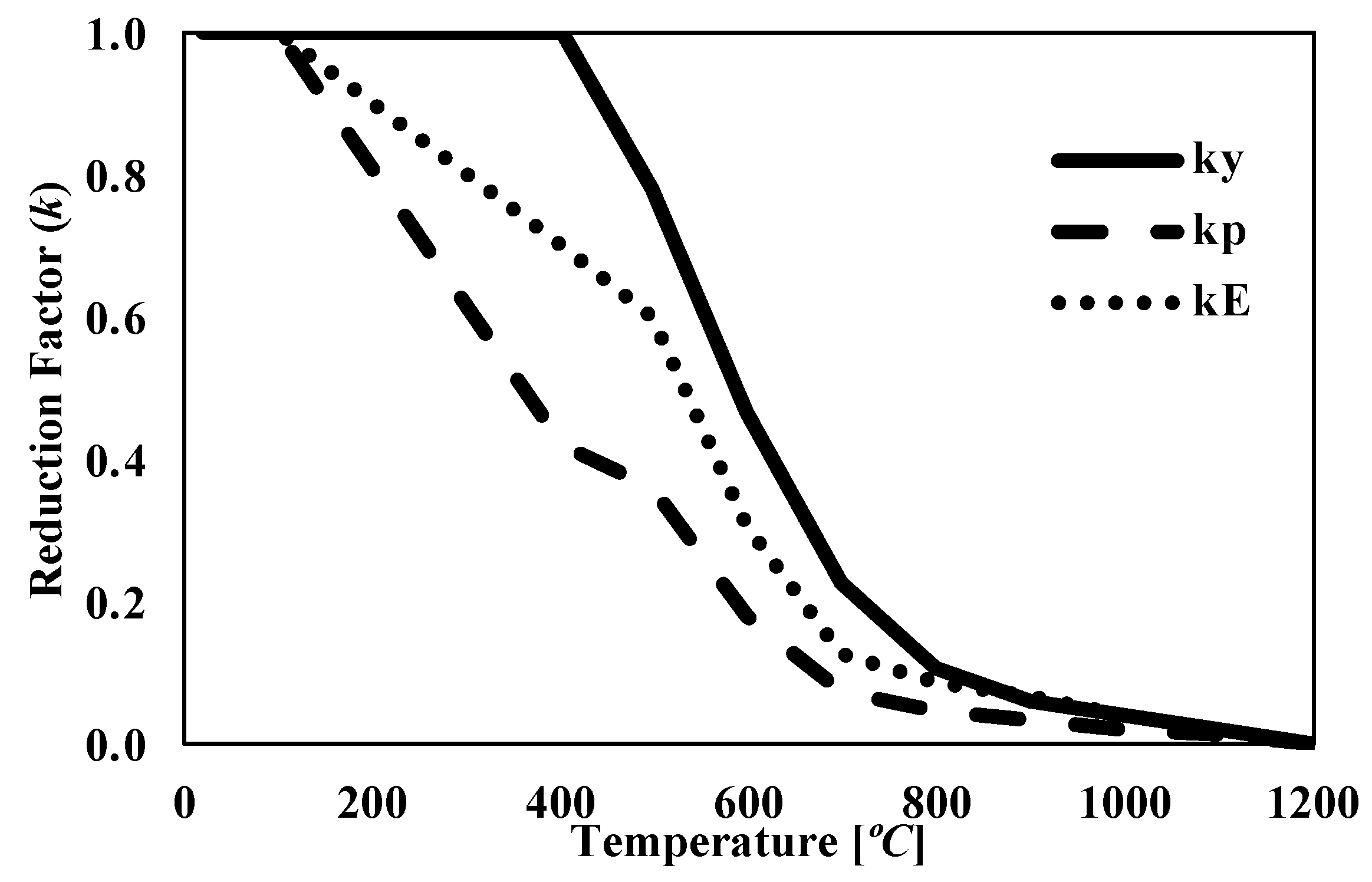
3.1. Temperature-Dependent Material Models for Steel
3.2. Benchmarking of FEM Models
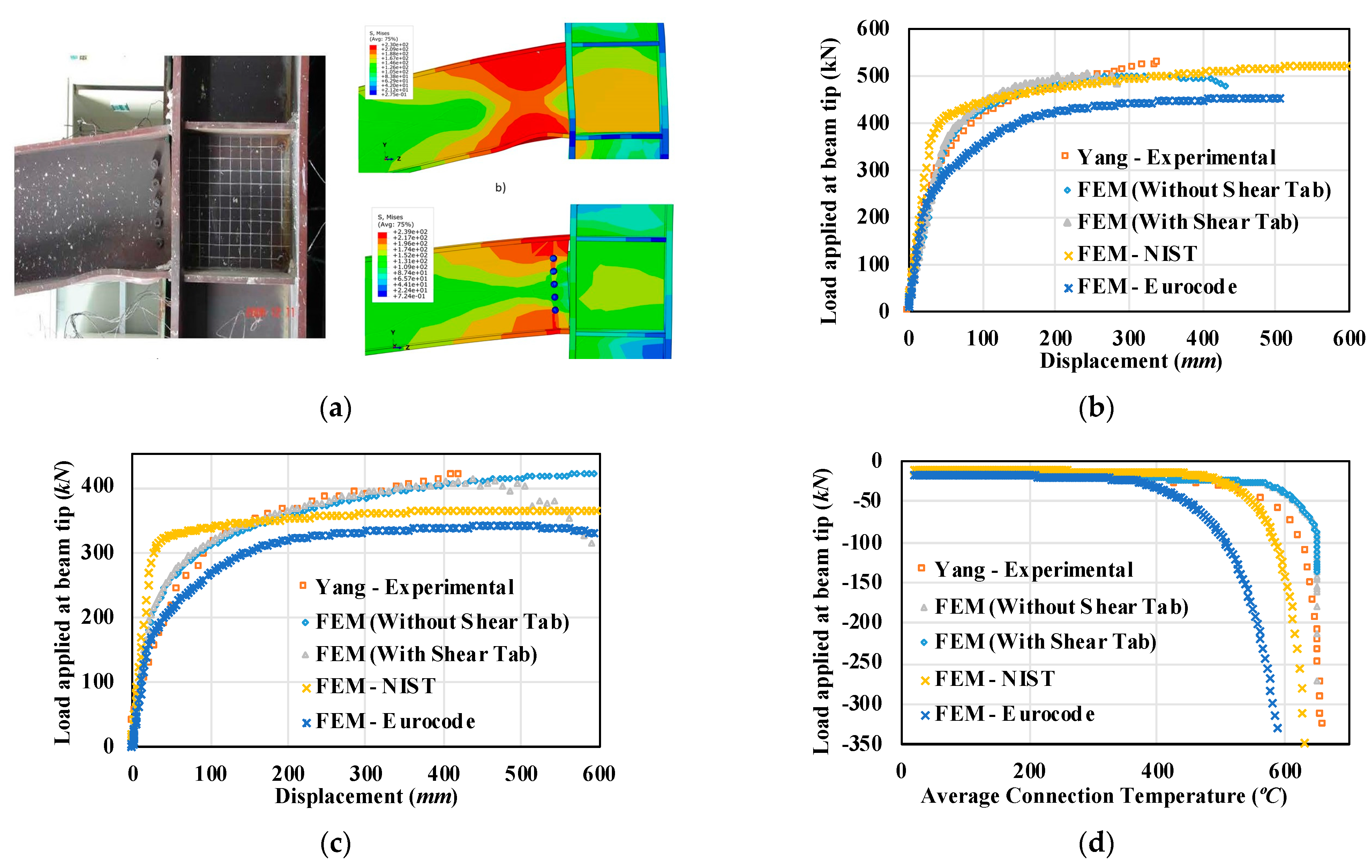
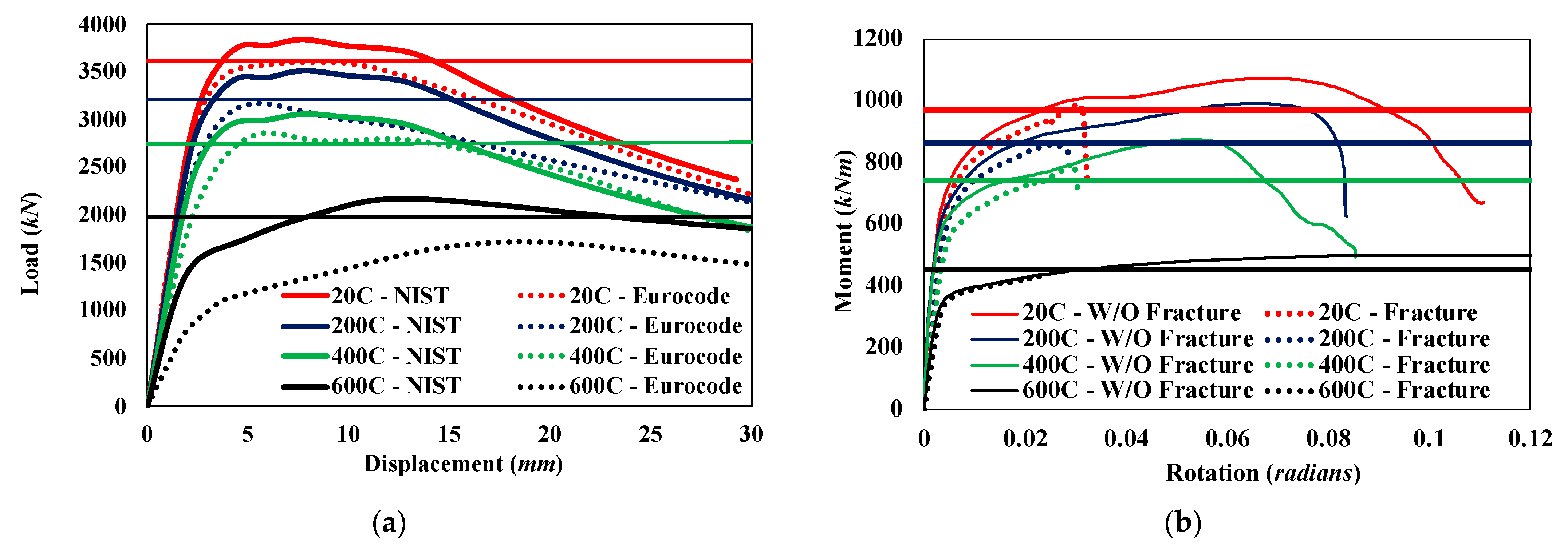
3.2.1. Sub-Frame Tests by Yang et al. (2009)
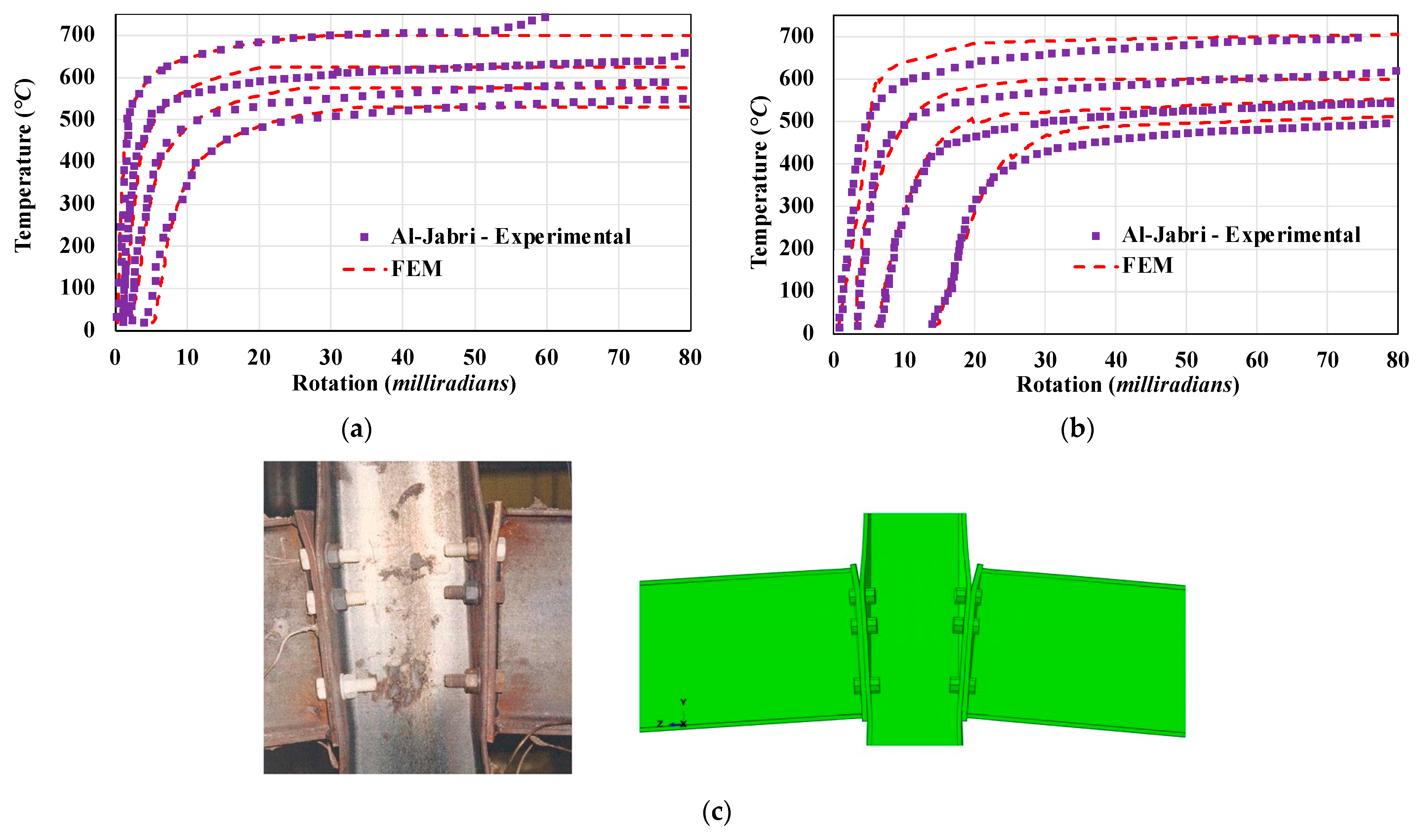
3.2.2. Moment-Frame-Arrangement Tests by Al-Jabri et al. (2006)
4. Member-Strength Assessment at Elevated Temperatures
4.1. AISC—Appendix 4
4.2. Strength Assesment Using Benchmarked Numerical-Modeling Approach
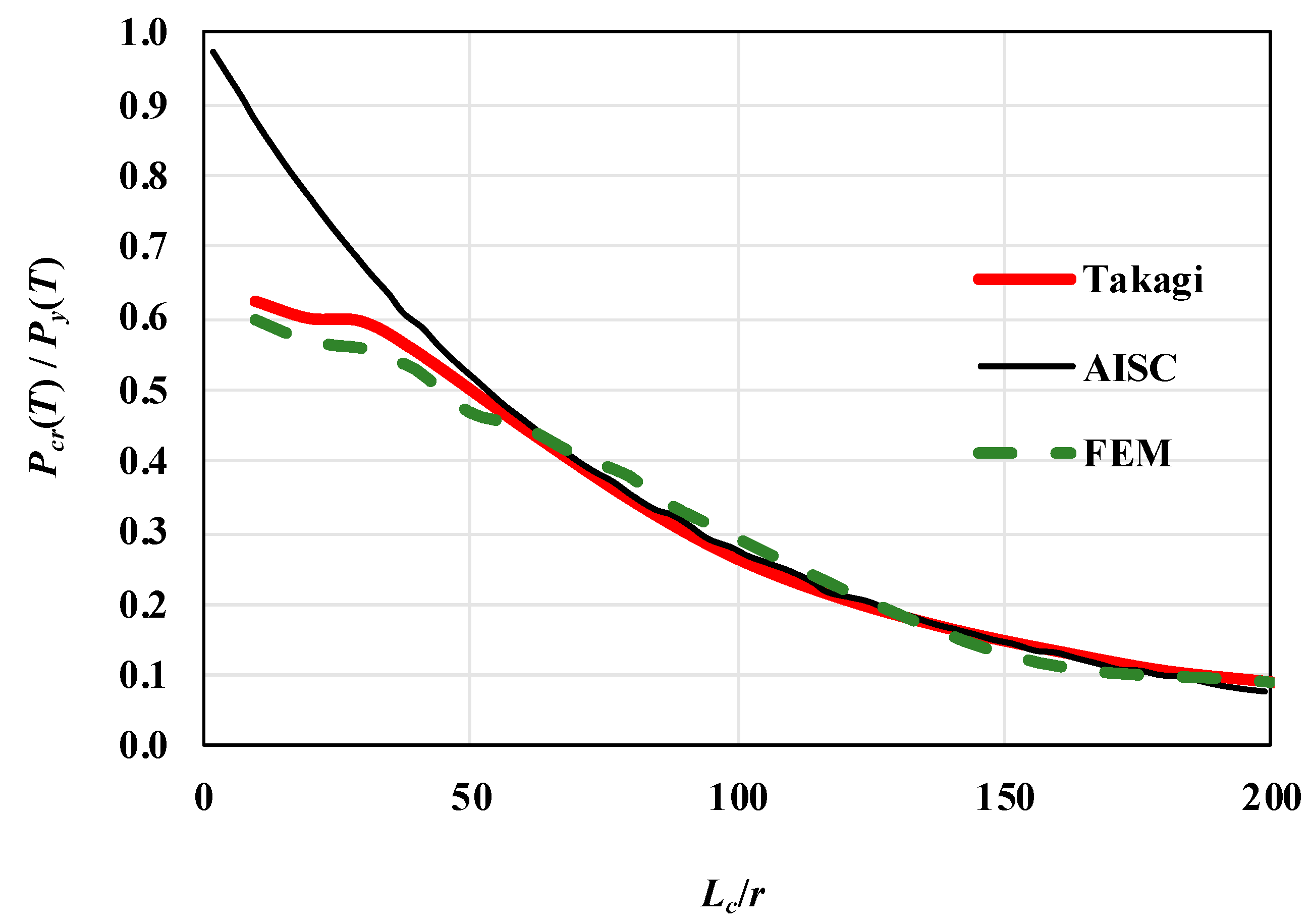
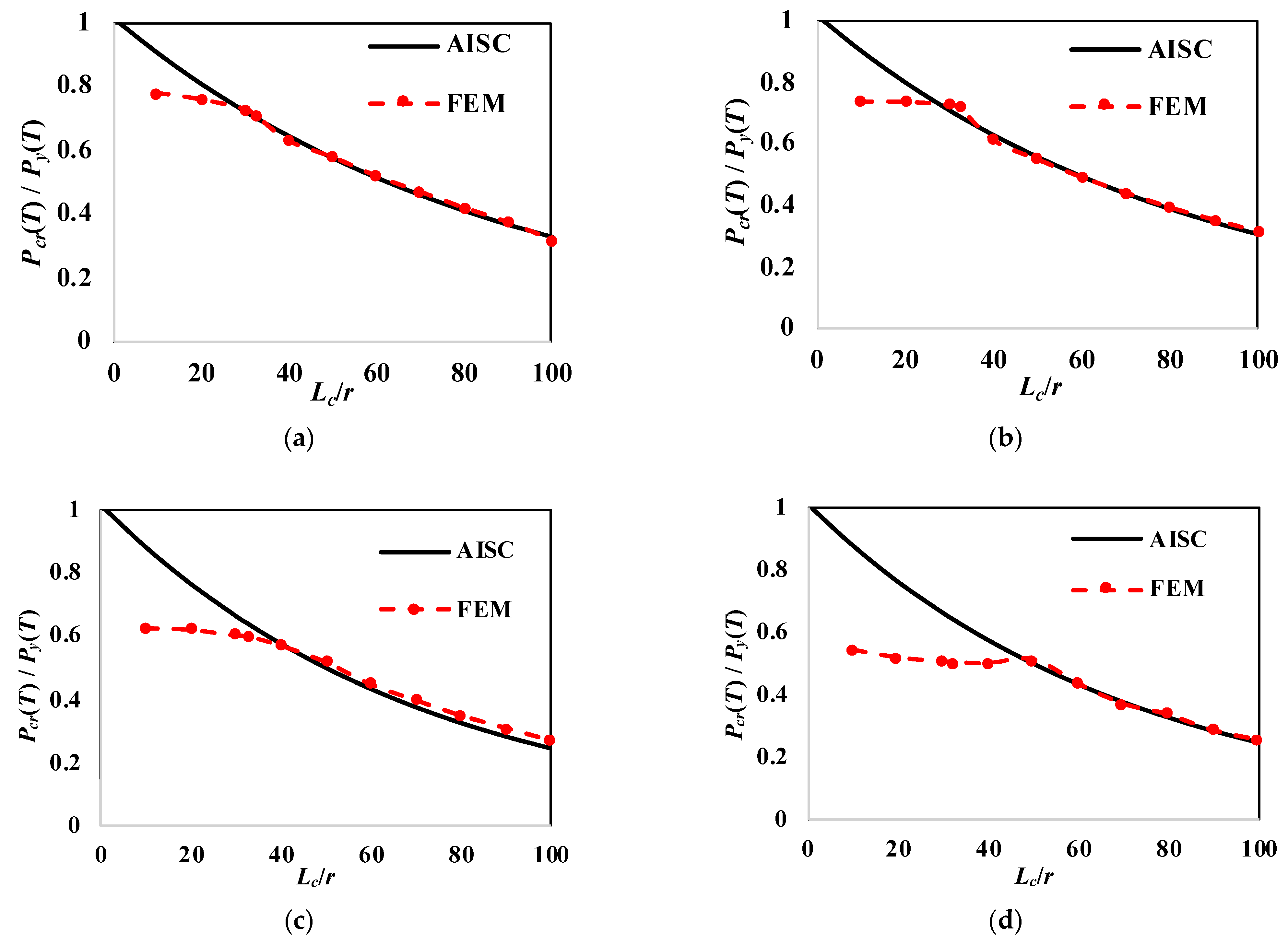
4.2.1. Compressive-Strength Assessment
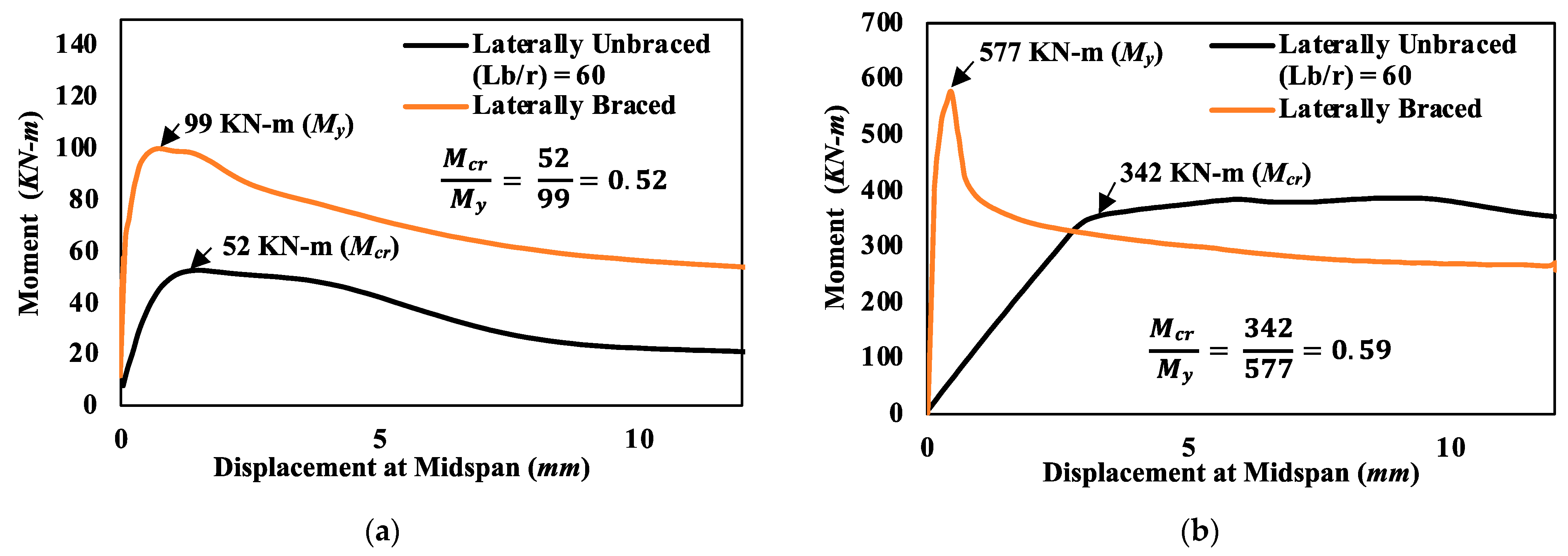
4.2.2. Flexural-Strength Assessment
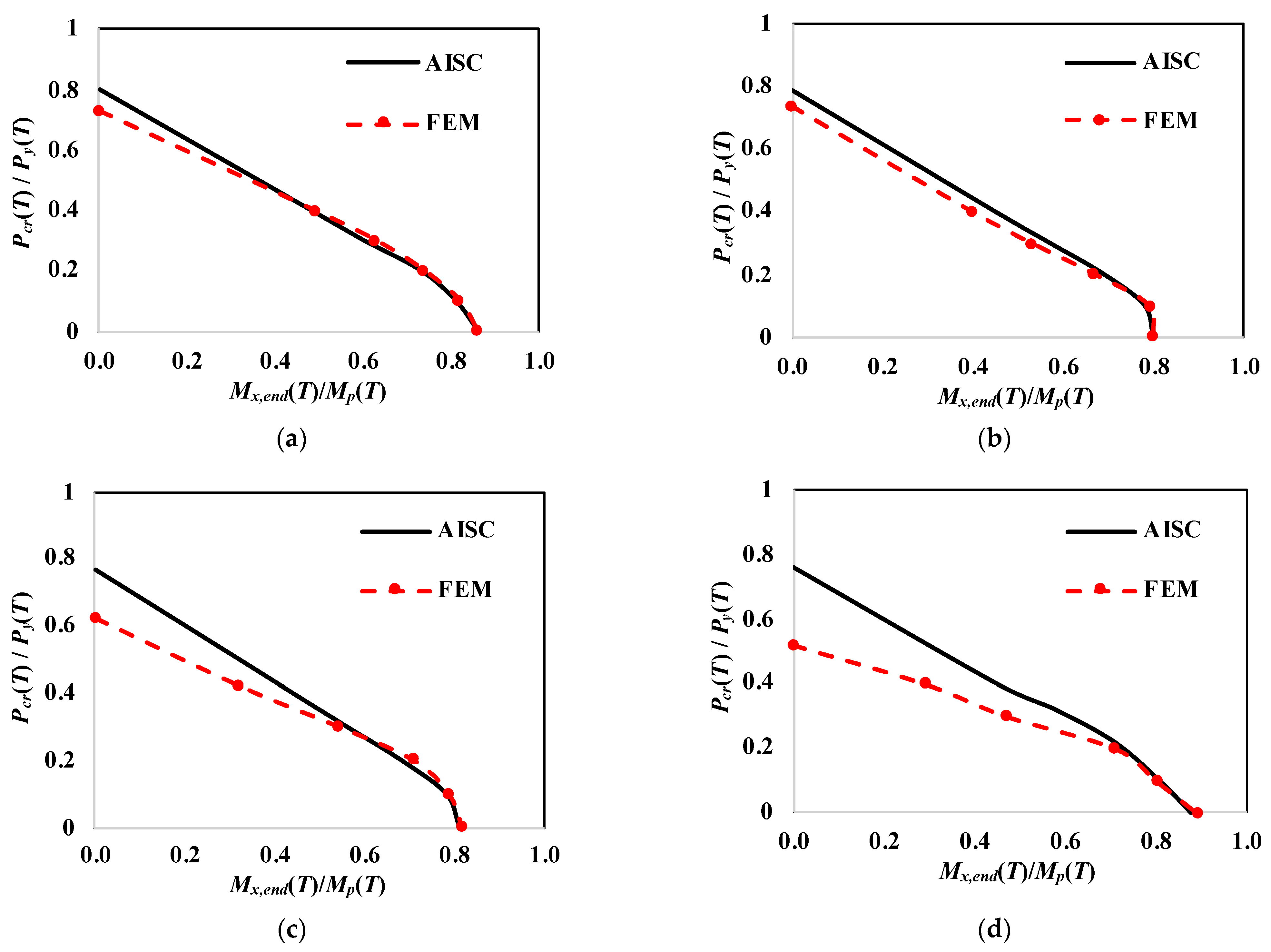
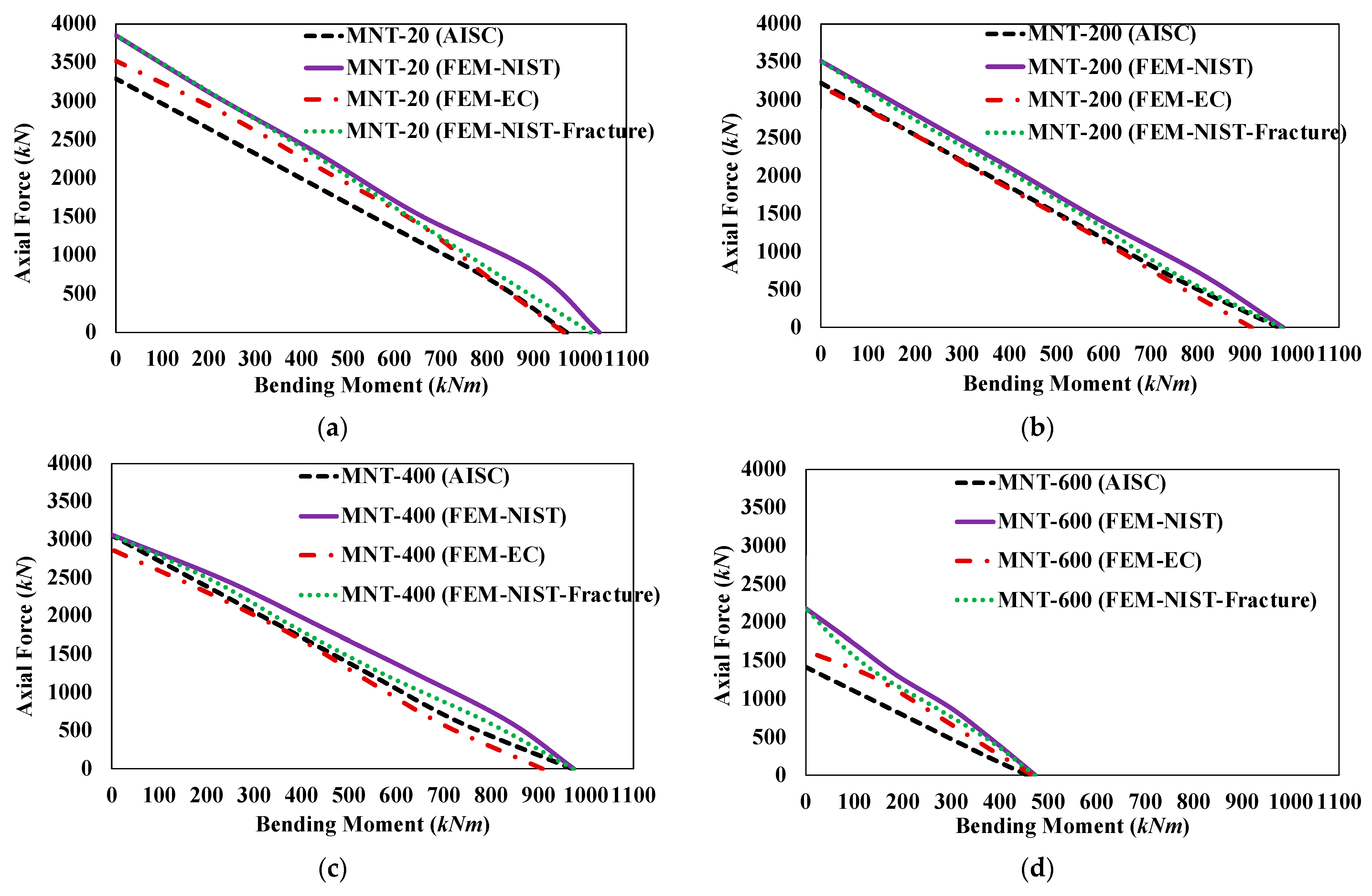
4.2.3. Beam-Column Strength Assessment
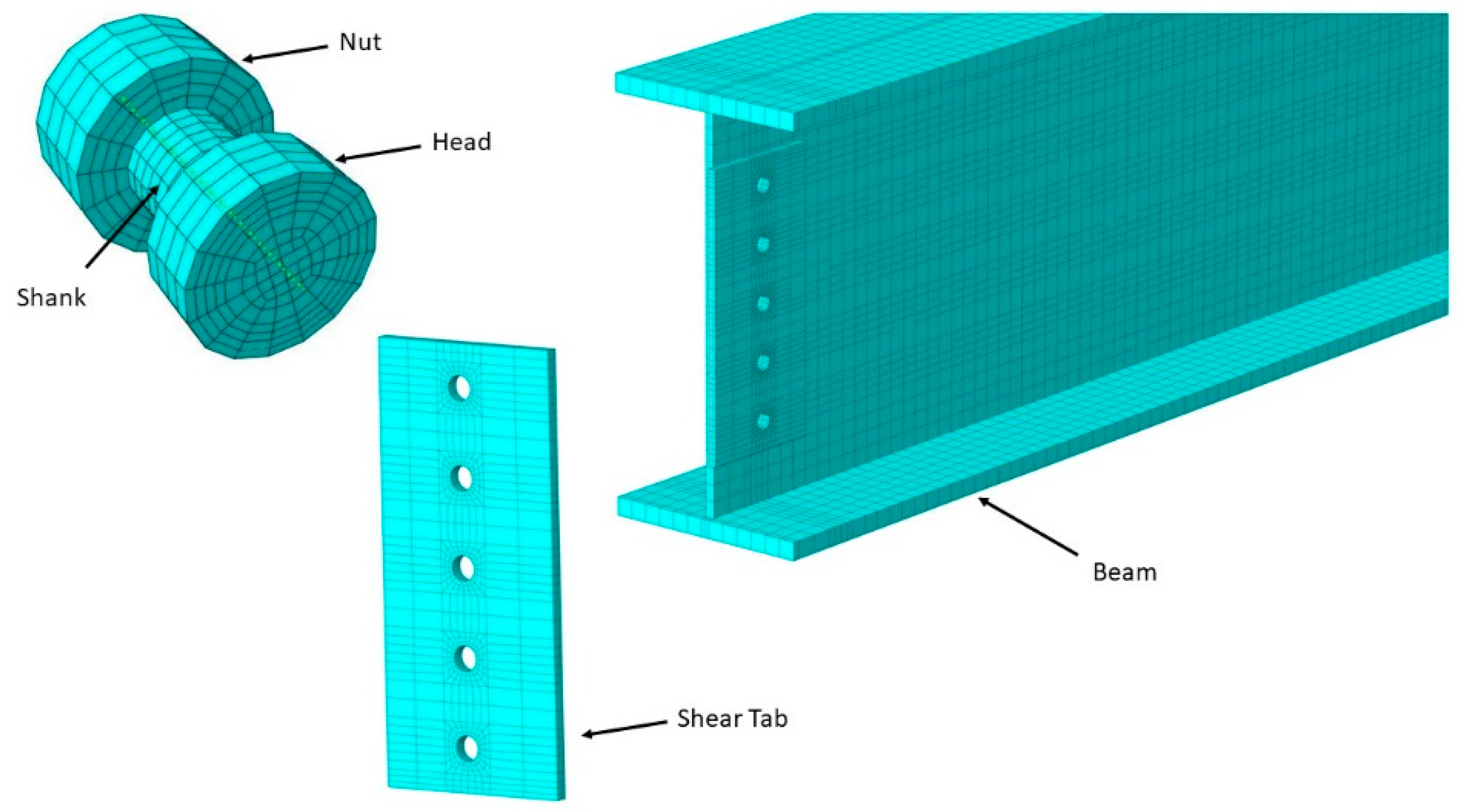
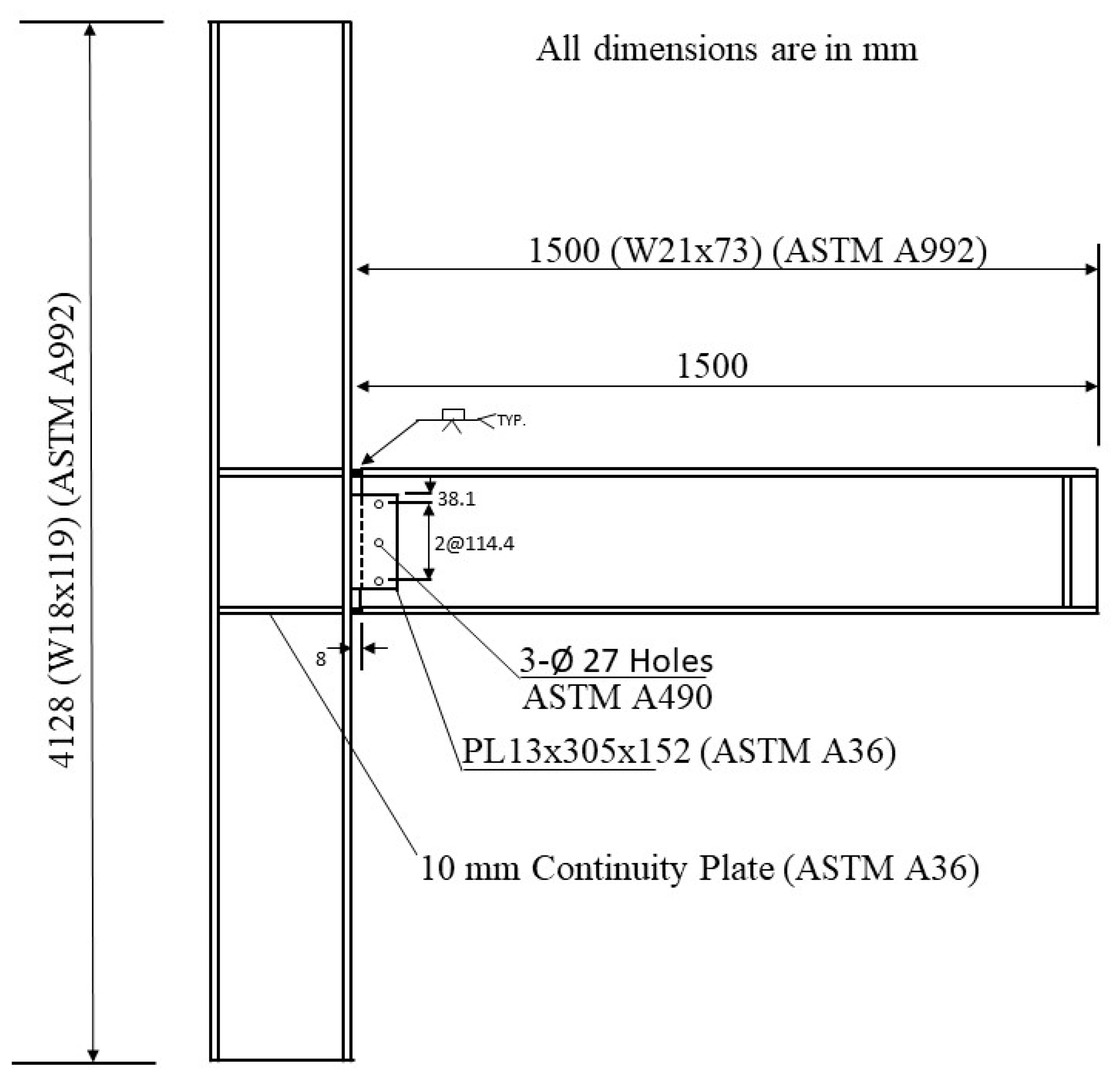
4.2.4. Moment-Connection Capacity Assessment
5. Discussion
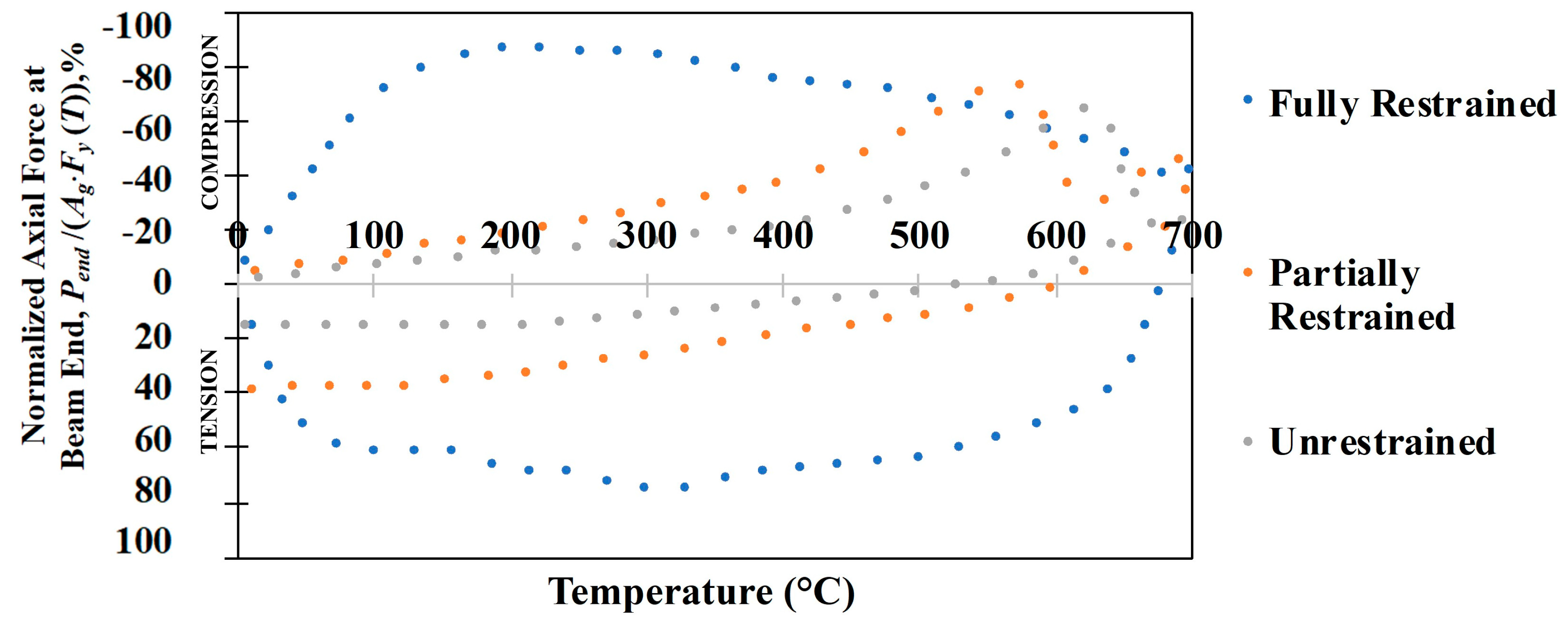
- Additional investigations on the connection behavior under reversing axial loads (from compression to tension) that represent the heating phase followed by the cooling phase.
- The effects of thermal stresses due to expansion (or contraction) on the moment-connection response should be investigated with more realistic modeling of thermal and restraint effects.
- Steel members without a composite slab were considered in this study; therefore, investigations that include the effects of concrete slabs are recommended.
6. Conclusions
- (1)
- The developed numerical models were capable of capturing the behavior and response of beams, columns, and connection elements of typical moment frames. The primary influence on the analysis results were the variations in the temperature-dependent material properties used in the models. Incorporating damage evolution and failure criteria in the material model had a relatively minor impact on the overall moment-connection strength.
- (2)
- The Eurocode 3 material properties, which are the basis for the mechanical properties of steel at elevated temperatures used in the current AISC specification, resulted in more conservative capacity estimates in comparison to the NIST material model. This is mainly because the Eurocode 3 uses elastic-modulus and yield-strength reduction factors that are considerably smaller than those of the NIST models, particularly for temperatures above 400 °C.
- (3)
- The analysis results indicated more accurate comparisons when NIST-developed temperature-dependent material properties were used compared to the Eurocode model. The improvement in the results is credited partly to the NIST models accounting for types of steel such as plates and bolts more accurately, and not accounting for rate-dependent effects such as thermal creep. Therefore, the NIST material models are recommended for detailed analysis of steel members at elevated temperatures.
- (4)
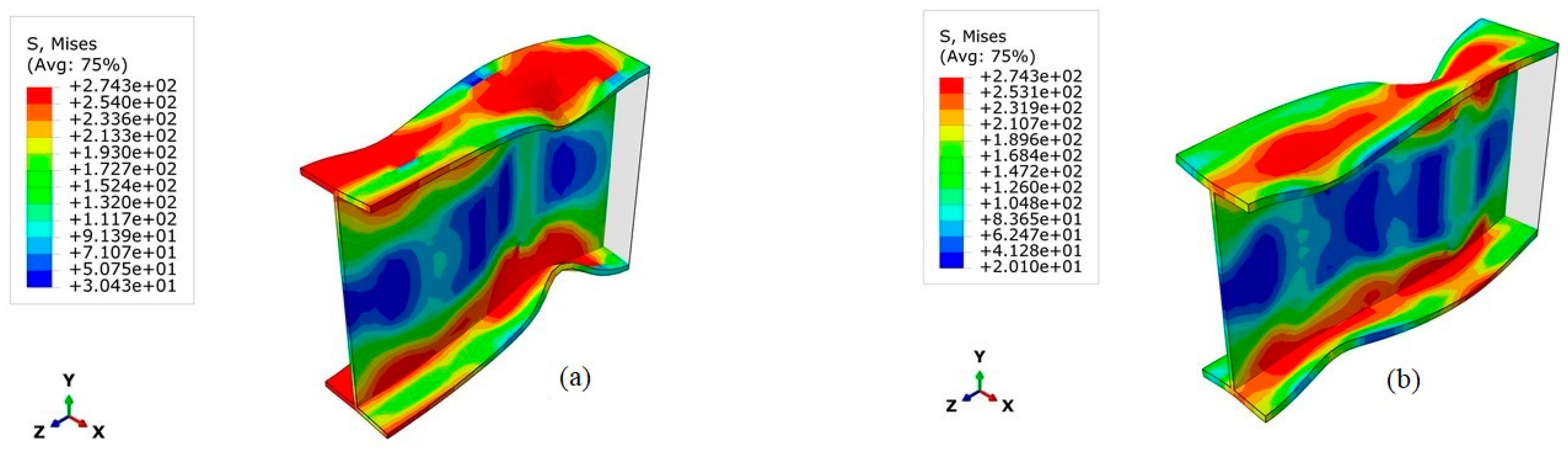
- Failure modes observed for connections of moment frames with slender beam members were typically controlled by buckling of beam members occurring near the connection region and therefore governing the connection strength. Therefore, calculation procedures used for member design were found to be applicable for obtaining moment-connection capacities.
- (5)
- The AISC Appendix 4 equations for compression design provide unconservative results for members with slender beam elements due to neglecting the local buckling-failure modes. Similarly, the beam-column strength equations used for estimating the capacity of members subjected to combined axial force and bending-moment cases in Appendix 4 provided unconservative results for typical beam members at low slenderness ratios. Therefore, the AISC equations are recommended for predicting the capacity of moment-frame members with slenderness ratios greater than 60.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scawthorn, C. Fires following the Northridge and Kobe Earthquakes. In Thirteenth Meeting of the UJNR Panel on Fire Research and Safety; NISTIR 6030; NIST: Gaithersburg, MD, USA, 1996; pp. 325–335. [Google Scholar]
- Himoto, K. Comparative analysis of post-earthquake fires in Japan from 1995 to 2017. Fire Technol. 2019, 55, 935–961. [Google Scholar] [CrossRef]
- Farshadmanesh, P.; Mohammadi, J. A probabilistic methodology for assessing Post-Earthquake Fire Ignition Vulnerability in Residential Buildings. Fire Technol. 2019, 55, 1295–1318. [Google Scholar] [CrossRef]
- Mariappan, T. Recent developments of intumescent fire protection coatings for structural steel: A review. J. Fire Sci. 2016, 34, 120–163. [Google Scholar] [CrossRef]
- Gernay, T.; Khorasani, N.E. Recommendations for performance-based fire design of composite steel buildings using computational analysis. J. Constr. Steel Res. 2020, 166, 105906. [Google Scholar] [CrossRef]
- Al-Jabri, K. The Behavior of Steel and Composite Beam-to-Column Connections in Fire. Ph.D. Thesis, Department of Civil and Structural Engineering, University of Sheffield, Sheffield, UK, 1999. [Google Scholar]
- Robinson, J. New Thinking on Multi-storey Building Fires: The Cardington Fire Test Programme-Initial Conclusions. Fire Saf. Eng. 1997, 4, 25–26. [Google Scholar]
- Steel Construction Institute. Investigation of Broadgate Phase 8 Fire, Structural Fire Engineering; Steel Construction Institute: Ascot, UK, 1991. [Google Scholar]
- Choe, L.; Ramesh, S.; Grosshandler, W.; Hoehler, M.; Seif, M.; Gross, J.; Bundy, M. Behavior and Limit States of Long-Span Composite Floor Beams with Simple Shear Connections Subject to Compartment Fires: Experimental Evaluation. J. Struct. Eng. 2020, 146, 04020088. [Google Scholar] [CrossRef]
- Seif, M.S.; Main, J.A.; Sadek, F.H. Behavior of structural steel moment connections under fire loading. In Proceedings of the Annual Stability Conference Structural Stability Research Council, Nashville, TN, USA, 24–27 March 2015. [Google Scholar]
- Lew, H.S.; Main, J.A.; Robert, S.D.; Sadek, F.; Chiarito, V.P. Performance of steel moment connections under a column removal scenario. I: Experiments. J. Struct. Eng. 2013, 139, 98–107. [Google Scholar] [CrossRef]
- AISC. Specification for Structural Steel Buildings; AISC 360-16; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Qian, Z.H.; Tan, K.H.; Burgess, I.W. Behavior of Steel Beam-to-Column Joints at Elevated Temperature: Experimental Investigation. J. Struct. Eng. 2008, 134, 713–726. [Google Scholar] [CrossRef]
- Abaqus/Standard User’s Manual, version 6.19; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2019.
- Seif, M.; Main, J.; Weigand, J.; Sadek, F.; Choe, L.; Zhang, C.; Gross, J.; Luecke, W.; MeColskey, D. Temperature-Dependent Material Modeling for Structural Steels: Formulation and Application; U.S. Department of Commerce: Washington, DC, USA, 2016.
- European Committee for Standardization (CEN). Eurocode 3: Design of Steel Structures, Part 1.2: General Rules-Structural Fire Design; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Yang, K.-C.; Chen, S.-J.; Ho, M.-C. Behavior of beam-to-column moment connections under fire load. J. Constr. Steel Res. 2009, 6, 1520–1527. [Google Scholar] [CrossRef]
- Al-Jabri, K.; Seibi, A.; Karrech, A. Modelling of unstiffened flush end-plate bolted connections in fire. J. Constr. Steel Res. 2006, 62, 151–159. [Google Scholar] [CrossRef]
- Al-Jabri, K.S.; Al-Jahwari, F. Advances Finite Element Modelling of Flexible End-Plate Beam-to-Column Joints in fire. Adv. Struct. Eng. 2012, 1, 311–324. [Google Scholar]
- ASCE. Standard Calculation Methods for Structural Fire Protections (ASCE/SEI/SFPE 29-05); American Society of Civil Engineers, Society of Fire Prevention Engineers: Reston, VA, USA, 2007. [Google Scholar]
- Leston-Jones, L.; Burgess, I.; Davison, J.; Plank, R. Finite element modelling of steel fin plate connections in fire. Fire Saf. J. 2007, 42, 408–415. [Google Scholar]
- Phan, L.; Gross, J.; McAllister, T. Best Practice Guidlines for Structural Fire Resistance of Concrete and Steel Buildings (NIST-TN-1681); National Institute of Standards and Technology: Gaitherburg, MD, USA, 2010.
- Choe, L.; Zhang, C.; Luecke, W.E.; Gross, J.L.; Varma, A.H. Influence of Material Models on Predicting the Fire Behavior of Steel Columns. Fire Technol. 2017, 53, 375–400. [Google Scholar] [CrossRef] [PubMed]
- International Standard ISO 834; Fire Resistance Tests-Elements of Building Construction. ISO: Geneva, Switzerland, 1975.
- Mao, C.; Chiou, Y.; Hsiao, P.; Ho, M. Fire response of steel semi-rigid beam-column moment connections. J. Constr. Steel Res. 2009, 65, 1290–1303. [Google Scholar] [CrossRef]
- Al-Jabri, K.; Burgess, I.; Lennon, T.; Plank, R. Moment-rotation-temperature curves for semi-rigid joints. J. Constr. Steel Res. 2005, 61, 281–303. [Google Scholar] [CrossRef]
- Takagi, J.; Deierlein, G.G. Strength design criertia for steel members at elevated temperatures. J. Constr. Steel Res. 2007, 63, 1036–1050. [Google Scholar] [CrossRef]
- AISC. Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications; ANSI/AISC 358-16; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Chinivar, S.C. Behavior and Capacity of Thermally Restrained Moment Frame Members during Compartment Fire. Master’s Thesis, Auburn University, Auburn, Alabama, 2021. [Google Scholar]
- Lai, Z. Experimental Databases, Analysis and Design of Noncompact and Slender Concrete-Filled Tube (CFT) Members. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2014. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chinivar, S.N.; Sener, K.C. Behavior and Capacity of Moment-Frame Members and Connections during Fire. Fire 2023, 6, 78. https://doi.org/10.3390/fire6020078
Chinivar SN, Sener KC. Behavior and Capacity of Moment-Frame Members and Connections during Fire. Fire. 2023; 6(2):78. https://doi.org/10.3390/fire6020078
Chicago/Turabian StyleChinivar, Supriya N., and Kadir C. Sener. 2023. "Behavior and Capacity of Moment-Frame Members and Connections during Fire" Fire 6, no. 2: 78. https://doi.org/10.3390/fire6020078
APA StyleChinivar, S. N., & Sener, K. C. (2023). Behavior and Capacity of Moment-Frame Members and Connections during Fire. Fire, 6(2), 78. https://doi.org/10.3390/fire6020078