Effect of Different Smoke Vent Layouts on Smoke and Temperature Distribution in Single-Side Multi-Point Exhaust Tunnel Fires: A Case Study

Abstract

In this paper, a numerical model verified by a 1:10 small-scale model test was used to study the effect of different smoke vent layouts on fire characteristics and smoke exhaust efficiency. The results show that the total smoke spread length is shortest when four smoke vents are opened near the fire source. If there are more than four smoke vents, some of them will only inhale fresh air rather than smoke. More seriously, some smoke vents will promote the spread of toxic smoke farther. Under different smoke vent layout schemes, the maximum temperature shows the same change trend with the increase in smoke exhaust volume (first increasing and then decreasing). When there are four smoke vents, the temperature field is in a good range compared with other schemes. If four smoke vents are opened, the total smoke exhaust efficiency is highest, and exhaust rate has little influence on total exhaust efficiency. Total smoke exhaust efficiency of the tunnel is more than 93.7% under different exhaust volumes, and the maximum difference of total smoke exhaust efficiency is less than 1.5% under different exhaust volume of Case “4”. The exhaust volume has little influence on temperature decay beneath the ceiling, and a temperature attenuation model of a point exhaust tunnel with four smoke vents was proposed. For the single-side point exhaust tunnels, the number of smoke vents near the exhaust fan side shall not be more than that on the other side. Four smoke vents shall be opened in case of fire and the exhaust volume is 220 m³/s with HRR of 30 MW.

1. Introduction

The danger of fire in a long and narrow space refers, mainly, to the damage to the building structure caused by high-temperature and toxic smoke [1,2,3]. Controlling the smoke in a certain area and discharging it out of the buildings in time will help to reduce the fire hazard [4,5,6,7,8,9,10]. Therefore, tunnel ventilation and smoke control are the primary issues in tunnel fire safety research. In recent years, ceiling exhaust ventilation has been widely used in tunnel fire. Ventilation data for underwater tunnels constructed by shield tunnelling machine in southern China were collected through field research, as shown in

Table 1. Ventilation data for underwater tunnels.

City	Tunnel	Length (km)	Number of Smoke Vents Opened	Distance between Smoke Vent (m)
Wuhan	Donghu Tunnel	7.035	4	60
Wuhan	Sanyang Road Tunnel	4.32	6	60
Wuhan	Qingdao Road Yangtze River Tunnel	3.44	4	60
Hangzhou	Qianjiang Tunnel	4.45	6	60
Yangzhou	Shouxihu Tunnel	4.40	6	60
Shanghai	Shanghai Yangtze River Tunnel	8.90	3	60

. Research on the application of point exhaust ventilation in tunnel fire smoke control has been reported extensively. Zhao et al. [11] analyzed the critical smoke exhaust rate and temperature distribution in two-point exhaust tunnels through a 1:20 model test combined with theoretical analysis and obtained the corresponding prediction model. Tang et al. [12] studied the effect of the longitudinal velocity on maximum temperature and found out a calculation model of maximum temperature in a smoke exhaust tunnel. They also explored the influence of smoke exhaust on the transverse temperature profile beneath ceiling, and established a unified temperature calculation model [13]. Tang and other colleagues [14] also studied the effects of longitudinal wind speed and exhaust rate on tunnel fires and proposed a calculation model of smoke distribution considering exhaust volume.

Some scholars have also studied lateral ceiling exhaust tunnel fires. Zhu et al. [15] studied the changes of critical wind speed and maximum temperature when the smoke vent is located on the side wall and put forward some calculation models of maximum temperature and critical wind speed that can guide the tunnel fire ventilation design based on the test results. Wang et al. [16] studied the effect of exhaust volume and smoke vent area on smoke back-layering length through a model test and obtained an empirical formula for calculating the length of smoke back-layering considering in a point exhaust tunnel. He et al. and Jiang et al. investigated the characteristics of smoke entrainment at the vent and found that the HRR and smoke exhaust rate have the greatest influence on smoke entrainment coefficient [17,18]. Tao et al. [19,20] studied the smoke control and temperature distribution of a two-point exhaust tunnel and obtained some conclusions and temperature calculation models that could improve tunnel ventilation design.

The factors, such as smoke and temperature distribution, related to evacuating one- or two-point exhaust tunnels have been widely reported [21,22,23]. A tunnel fire will quickly produce a large amount of toxic smoke. It is difficult to discharge the smoke out of the tunnel by opening only one or two smoke vents. Therefore, the design of tunnel fire ventilation allows for multiple smoke vents to be opened at the same time. More importantly, the traditional smoke exhaust tunnel will discharge the smoke from both sides of the tunnel, which will cause waste for some short tunnels. A separate fan room needs to be built for tunnel ventilation, and the cost is often very expensive. If fan rooms are designed only on one side and the exhaust duct outlet of the tunnel on the other side is closed, it will reduce not only the cost of construction but also the number of axial-flow fans. It will also greatly reduce the maintenance cost of ventilation facilities during operation. This kind of smoke extraction scheme was adopted in the Mawan Tunnel in Shenzhen, China. Unfortunately, the fire characteristics in single-side point exhaust tunnels have not been reported.

To fill this gap, this paper verified the reliability of the numerical model based on the tunnel model. The effects of different smoke vent opening modes and smoke exhaust rate on the smoke distribution, maximum temperature, temperature attenuation, and smoke exhaust efficiency in the tunnel were studied based on the numerical results.

2. Numerical Modeling

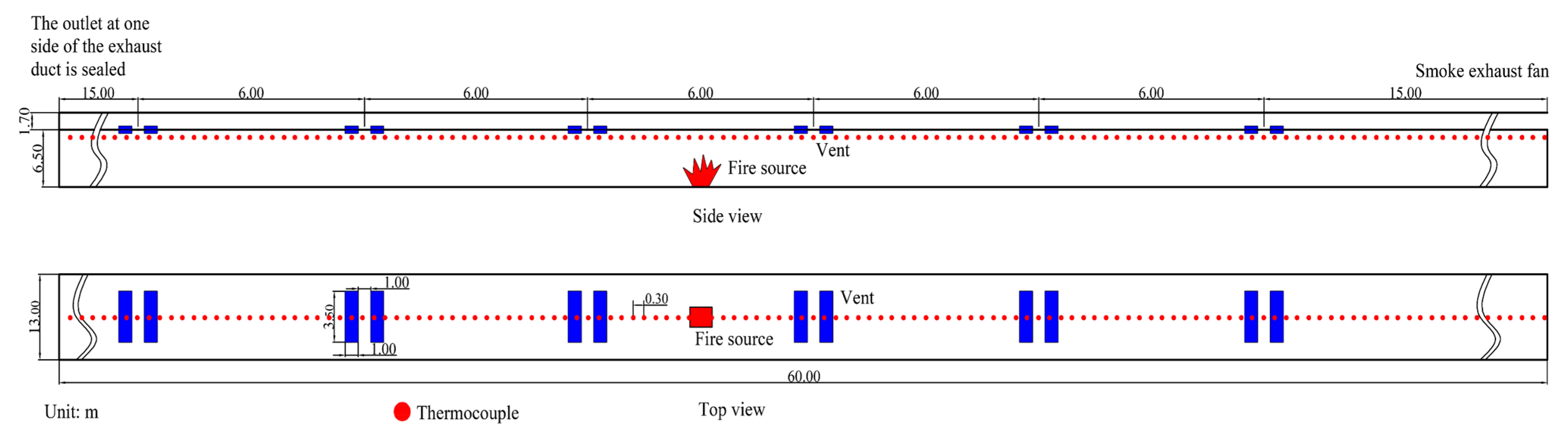
2.1. Model Tunnel

The applicability of FDS (6.7) in tunnel fire calculation has been widely verified [24,25,26,27]. In this paper, the full-scale model tunnel is 600 m long, 13 m wide, and 6.5 m high. The exhaust duct is 1.7 m high and 13 m wide. The area of the exhaust vent is 14.93 m² and the distance between smoke vents is 60 m. The smoke exhaust position consists of two smoke vents with a size of 1 × 3.5 m, and there are six groups of smoke vents, as shown in Figure 1. The two smoke vents in each smoke exhaust position are always in the same state (open or closed). The vault and side walls of the tunnel are made of concrete. During the whole simulation process, the environmental temperature is 20 °C and the mesh boundary condition is “OPEN” [28]. The mass flow of gas and CO mass fraction at the smoke vent should also be measured. In order to monitor the temperature distribution of the tunnel vault, the thermocouple is arranged at 0.20 m below the tunnel ceiling and at intervals of 0.25 m.

Note that the HRR is closely related to the combustibles. The HRR caused by a car is 5–7 MW and that of medium-sized truck or bus is 20–30 MW. The HRR in a tunnel fire may be higher, such as when an oil tank truck is involved [21]. However, tunnel ventilation design must take into account the heat release rate according to the traffic flow and vehicle type after tunnel operation. Therefore, only one heat release rate is generally considered in tunnel fire ventilation design, and it is often much greater than the estimated value. In addition, China’s national regulations (Guidelines for Design of Ventilation of Highway Tunnel, JTG/TD70/2-02-2014) clearly stipulate that the heat release rate of most highway tunnels in ventilation design should be 20 or 30 MW. Therefore, the power of the fire source is 30 MW, and the exhaust volume is 200–280 m³/s in this paper. The fire source (gasoline) is located at the center line of the tunnel floor, and the power of gasoline is controlled by defining the mass loss rate (MLR) in FDS. The mass loss rate of gasoline is 0.055 kg/(m²·s), and the HRR can reach 30 MW when the area of fire source is 12.6 m² [29]. The soot and CO yield are set to 0.1 and 0.05, respectively [30]. A detailed calculation scheme is shown in

Table 2. A summary of the simulation scheme.

Test No.	Smoke Vent Number	HRR (MW)	Smoke Exhaust Rate (m3/s)
1–5	3A	30	200, 220, 240, 260, 280
6–10	3B	30	200, 220, 240, 260, 280
11–15	4	30	200, 220, 240, 260, 280
16–20	5A	30	200, 220, 240, 260, 280
21–25	5B	30	200, 220, 240, 260, 280
26–30	6	30	200, 220, 240, 260, 280

.

Note that a calculation model of temperature decay was also studied in this paper. If only one fire source heat release rate is considered, the temperature calculation model is not rigorous. Therefore, we studied the temperature attenuation beneath the tunnel ceiling with HRR of 10, 20, and 30 MW.

2.2. Mesh Size

Generally, mesh size is the most important aspect for numerical simulation because it determines the reliability of the numerical results. When the grid is less than 0.1$D^{*}$, the numerical results are acceptable to guarantee the reliable operation of FDS [31]. The characteristic diameter $D^{*}$ can be calculated by:

$$D^{*}={\left(\frac{Q}{{\rho }_a{c}_p{T}_a{g}^{1/2}}\right)}^{2/5}$$

(1)

where $T_a$ is the ambient air-temperature (K), ${\rho }_a$ is the ambient air density (kg/m³), $c_p$ is the specific heat capacity of air at constant pressure (kJ/kg·K), $g$ is the gravity acceleration (m²/s), and $Q$ is the heat release rate of fire source (kW). $D^{*}$ is calculated to be 3.74 m when the HRR of fire is 30 MW, thus 0.1$D^{*}$ is approximately 0.374 m. In the previous reports on the use of FDS to study tunnel fires, the selection of mesh size was described in detail, and the mesh size was verified, as shown in

Table 3. Details of previous model tunnel grids.

References	Dimension (m × m) Wide × High	HRR (MW)	Mesh Sizes (m)
Yao [30]	$10 \times$ 5	5–100	0.200
Ji [33]	$10 \times$ 5	5–15	0.200
Liang [36]	$10 \times$ 7	30	0.20
Ji [37]	$10 \times$ 5	3–15	0.167
Guo [38]	$10 \times$ 5	3–10	0.167

. At present, when studying the smoke movement and temperature profile based on FDS, the commonly used grid sizes are 0.1667 and 0.20 m [30,32,33,34,35,36]. Since the tunnel length in this paper is 600 m, we set the mesh size as 0.20 m. Note that the HRR is the main factor affecting the characteristic diameter of the fire source. Since the research scenario in this paper is the same as the existing tunnel fire research based on FDS, we do not repeat the grid sensitivity analysis.

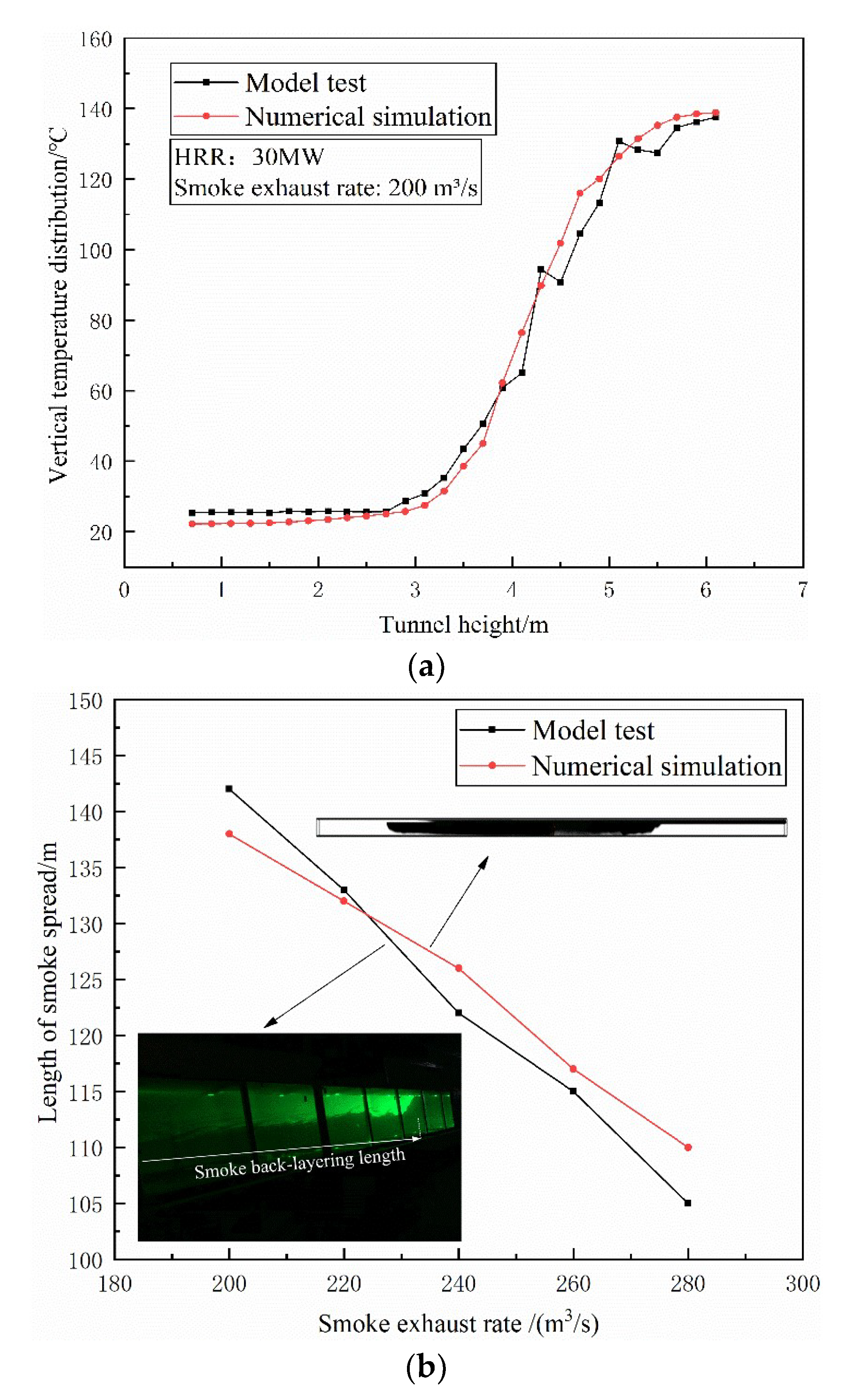
2.3. Experimental Verification

A 1:10 model test with the same tunnel section and length was conducted to verify the reliability of the numerical model. The model tunnel is made of aluminum sheet and fireproof glass, and each smoke vent has a push–pull steel plate to control the opening state of the vent. The outlet on one side of the exhaust duct is connected with the smoke exhaust fan, and the outlet of the exhaust duct on the other side is sealed, as shown in Figure 2. The jet fan in Figure 2 was not installed during the test conditions in this paper. The fire source of the model test is liquefied petroleum gas (LPG), and the HRR of the fire source is controlled by a rotameter [39], as shown in Figure 2. Details of the small-scale model tunnel can be found in the author’s previous research [20,40]. The HRR and smoke exhaust rate are converted by Froude similarity criterion.

In this paper, the numerical model will be verified from the temperature profile and smoke spread. The temperature profile in the tunnel is obtained under the same conditions. The temperature distribution of the numerical results is approximately the same as the model results, as shown in Figure 3a. The temperature difference between the numerical and model results is very small near the tunnel ceiling and floor but relatively large in the middle of the tunnel. The difference between the results of the model test and the numerical simulation is within 10.8 °C under the tunnel ceiling. Under the same condition, the smoke spread length in the numerical calculation is like that in the model test, and the maximum difference is 5.4 m. Maximum errors of temperature and back-layering length are 10.3% and 5.1%, respectively, which can be ignored for tunnel engineering. Therefore, the accuracy of the mesh size of the numerical model can be guaranteed.

3. Results and Discussion

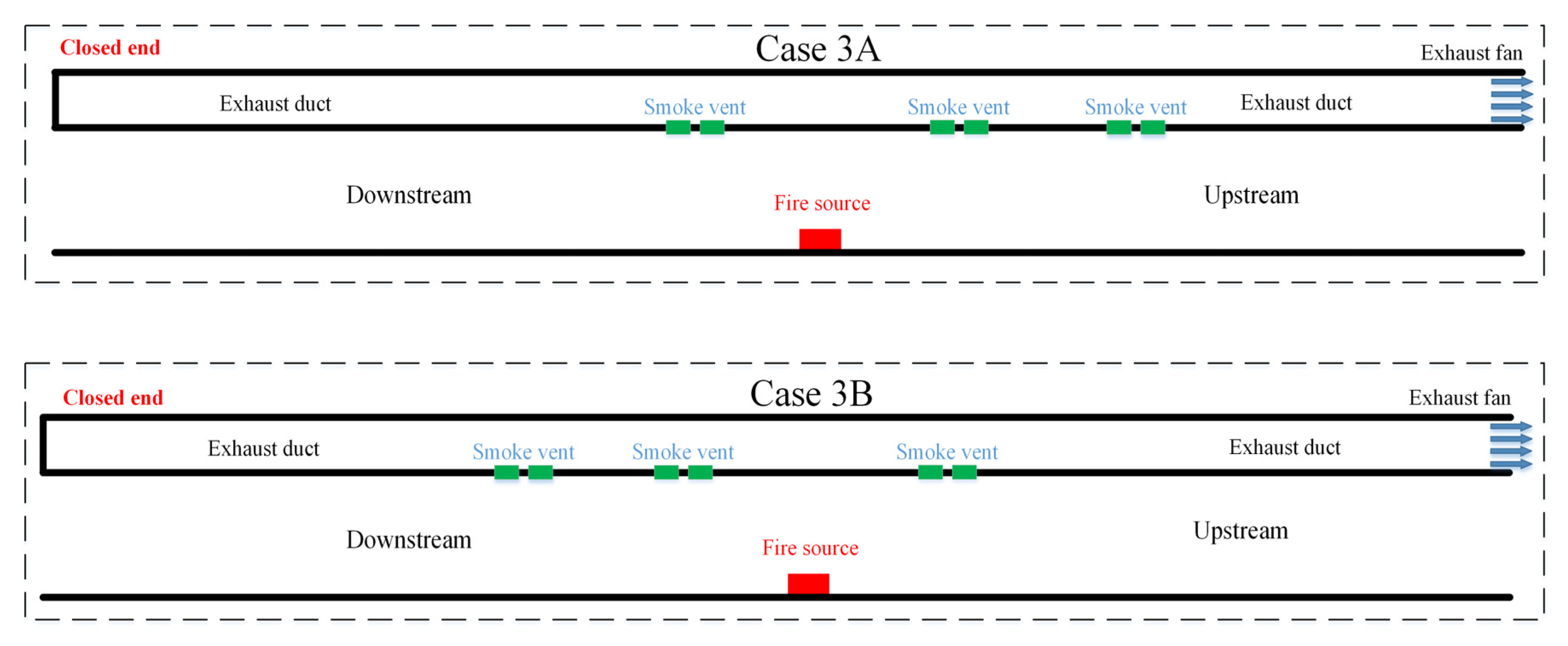
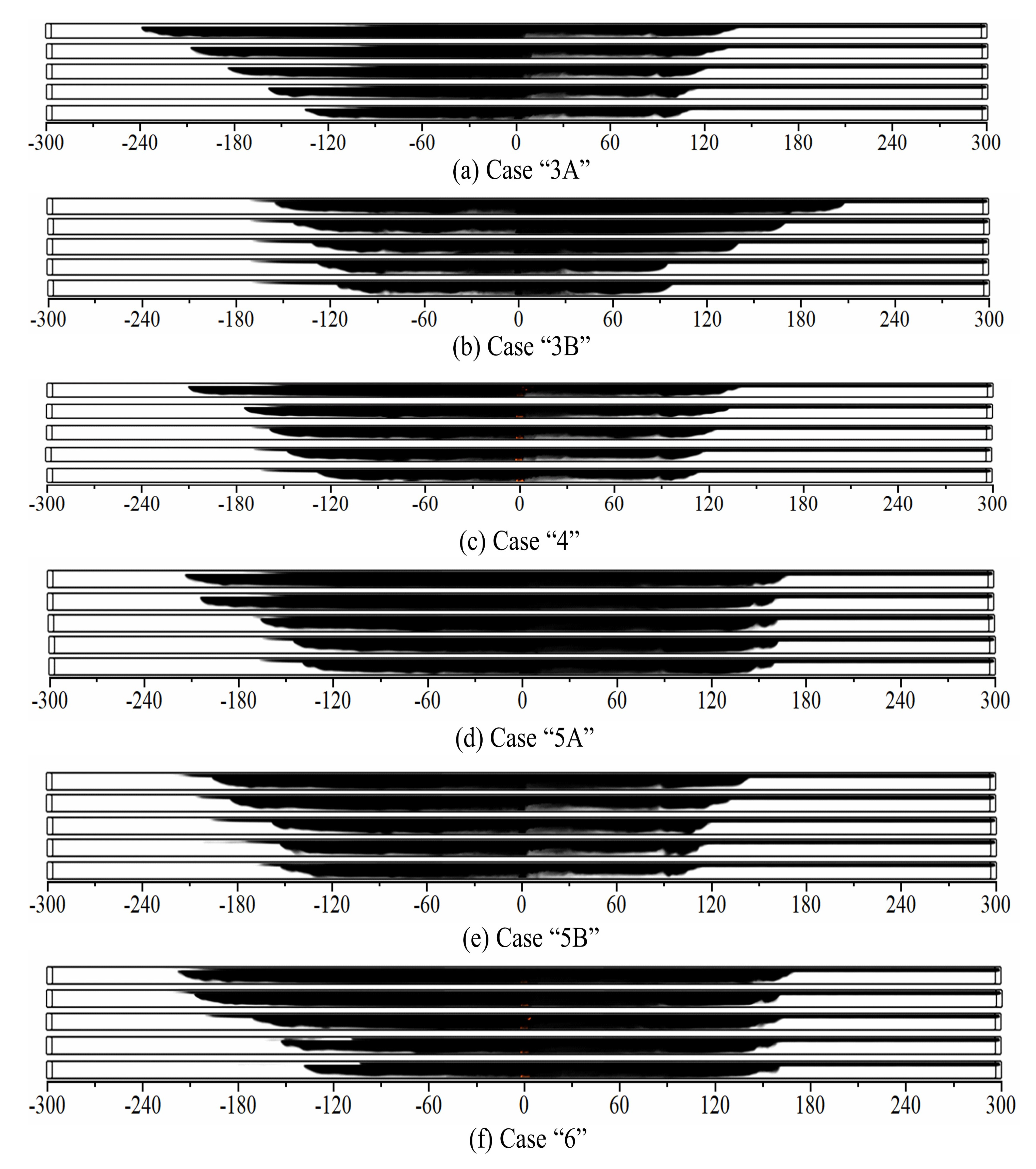
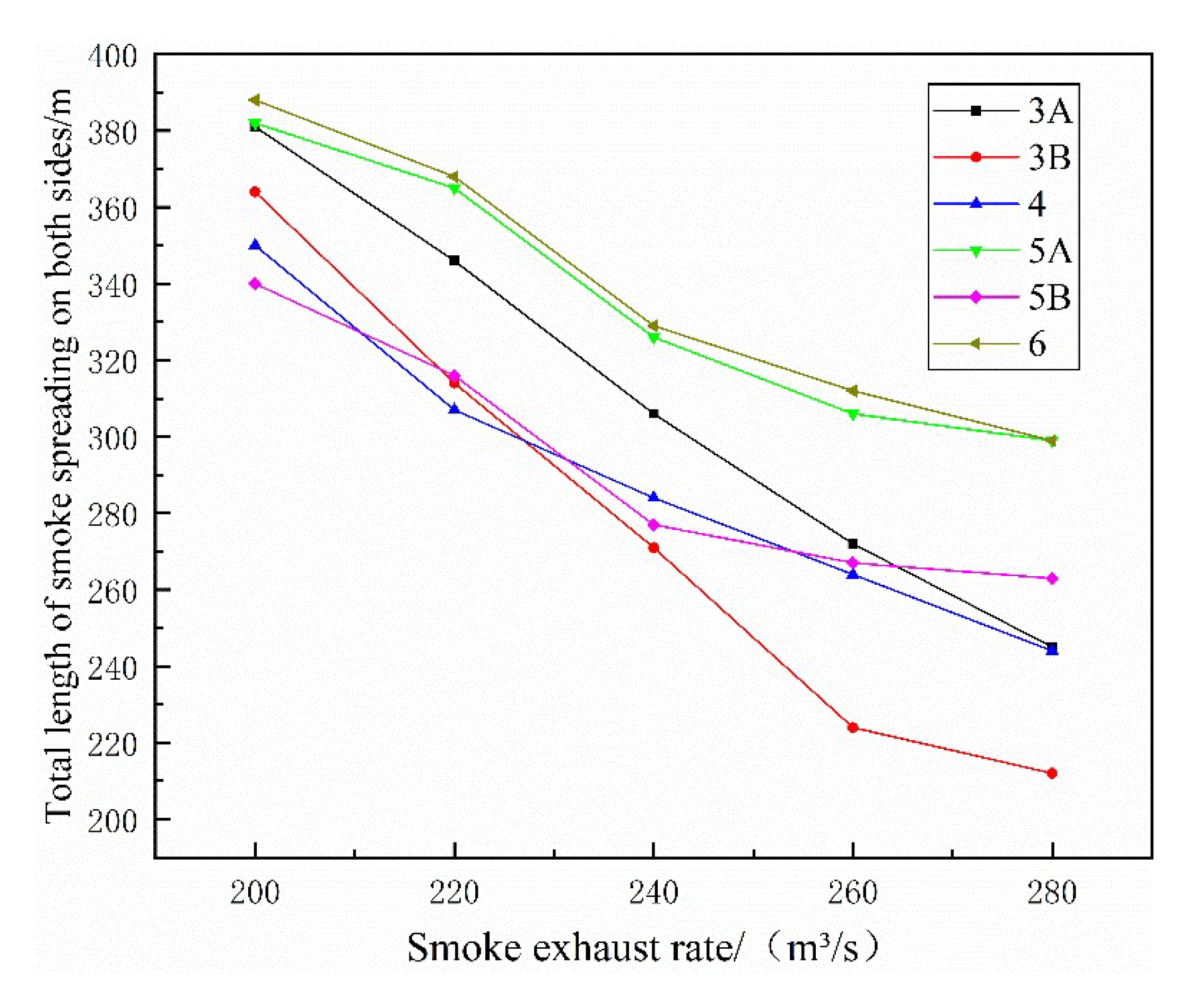
3.1. Smoke Spread

In a tunnel fire, the opening state of the smoke vent is 3, 4, 5, and 6. When opening three smoke vents, there are two situations (Figure 4): (1) Case “3A”: two smoke vents are opened near the axial flow fan (upstream) and one is opened near the closed end (downstream); (2) one smoke vent is opened near the axial flow fan and two are opened near the closed end (Case 3B). There are also two situations when opening five smoke vents: (1) three smoke vents are opened near the axial flow fan (upstream) and two are opened near the closed end (downstream) (Case “5A”); (2) two smoke vents are opened near the axial flow fan and three are opened near the closed end (Case 5B).

When the layout of the exhaust vent is Case “3A”, the smoke upstream can be controlled within 50 m of the last smoke vent; when the exhaust volume exceeds 220 m³/s, the exhaust volume has little effect on smoke spread upstream. However, exhaust volume has a great influence on smoke spread downstream, and the length of the smoke spread decreases with the increase in exhaust rate, as shown in Figure 5a. When the layout of the smoke vent is Case “3B”, the effect of exhaust volume on smoke spread is opposite to that of Case “3A”; the exhaust volume mainly affects the smoke spread upstream, as shown in Figure 5b. Moreover, the total length of the smoke spread (the sum of the spread lengths of both sides of the fire) in the tunnel for Case “3A” is significantly longer than that of Case “3B” at the same exhaust rate, as shown in Figure 6. Therefore, if only three smoke vents near the fire source are opened, the smoke control effect of Case “3B” is better than that of Case “3A”.

When four smoke vents are opened, the smoke distribution on both sides of fire is basically symmetrical. When the exhaust volume is more than 220 m³/s, increasing the exhaust volume has no obvious effect on restraining the smoke spread, especially upstream. The smoke can be controlled within 150 m on both sides of the fire. When there are three smoke vents upstream and two downstream (Case 5A), the smoke spread length upstream increases obviously compared with Case “4”. When the layout of the exhaust vent is Case “5B”, the smoke spread length upstream decreases compared with Case “5A”, as shown in Figure 5d,e. The influence of setting an exhaust fan on one side of the tunnel is highlighted. Due to the single-side point exhaust, the velocity of the third exhaust vent upstream is very high, which will help the smoke to spread to the third smoke vent. The smoke control effect of Case “5B” upstream is better than that of Case “5A”.

When six smoke vents are opened, the smoke spreading length is the longest among all the smoke exhaust opening schemes. Most importantly, when the smoke exhaust rate is greater than 240 m³/s, the smoke downstream cannot spread to the last smoke vent, which will cause serious waste. When three smoke vents are opened upstream, the smoke spread length is much longer than when opening one or two smoke vents upstream, and the total smoke spread length in the tunnel exceeds 300 m (the longest is 388 m) under different exhaust rates. The total length of the smoke spread is more than 200 m in all calculation conditions. From the perspective of smoke diffusion, for a single-side point exhaust tunnel, the best smoke exhaust effect can be obtained when four exhaust vents are opened, especially for a two-way tunnel.

3.2. Temperature Distribution

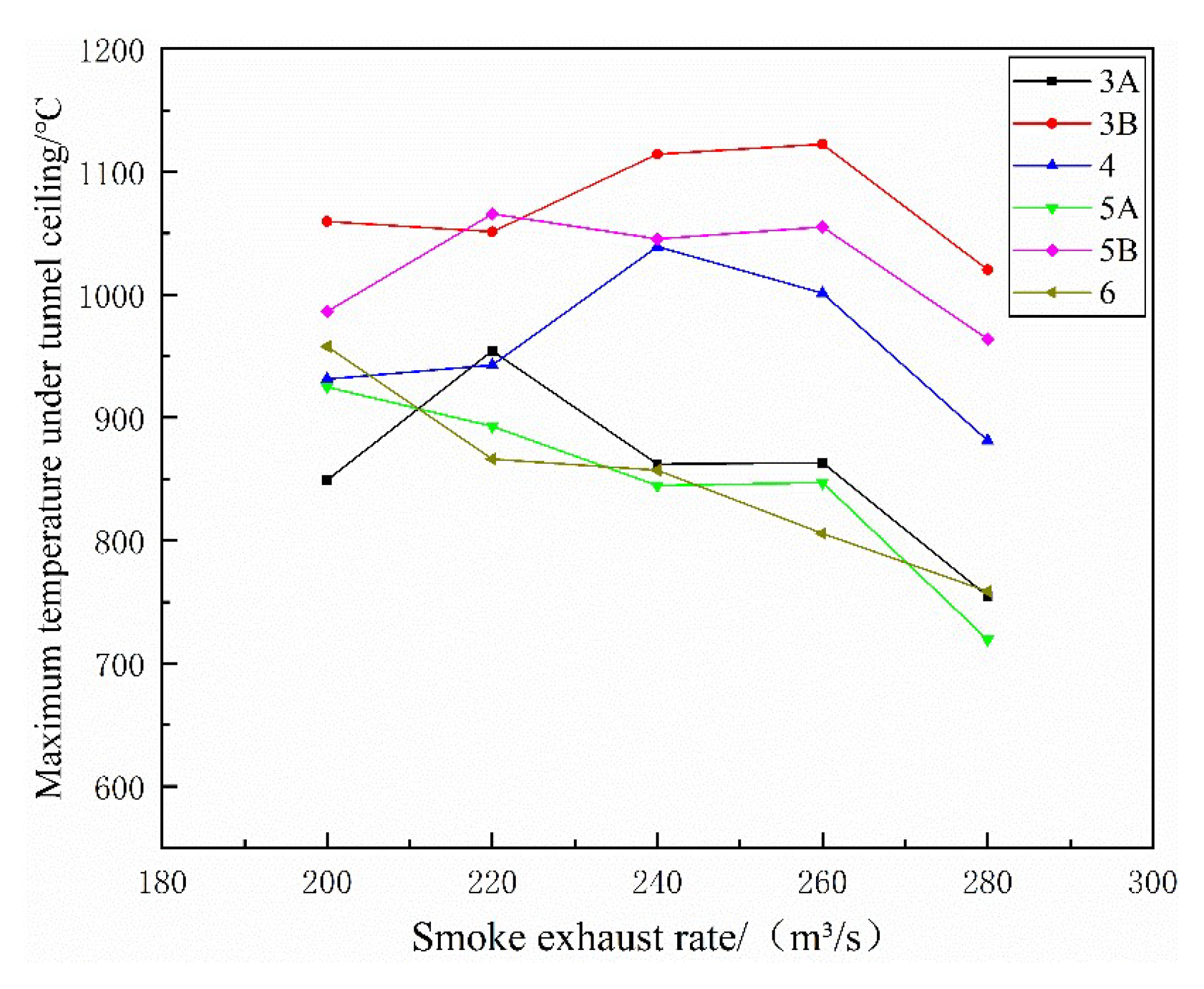
3.2.1. Maximum Temperature

When the layout of the smoke vents is Case “5A” and Case “6”, the maximum temperature decreases with the increase in exhaust volume; the maximum temperature under the tunnel ceiling is 719–918 °C, as shown in Figure 7. When the layout of the exhaust vent is Case “2”, Case “3A”, Case “3B”, Case “4”, and Case “5B”, the maximum temperature first increases and then decreases with the increase in exhaust volume. This is because when the smoke is confined near the fire source and sinks to the bottom of tunnel, the fire is wrapped by the smoke and does not burn sufficiently. Increasing the exhaust volume strengthens the air convection in the tunnel and makes the maximum temperature rise. If the exhaust volume continues to increase, the velocity at the vent nearest to the fire will make the high-temperature smoke unable to gather in the vault, and the smoke vent far away from the fire will restrict air convection, which will reduce the maximum temperature. When the layout of the exhaust vent is Case “5A” and Case “6”, the smoke within the range of the smoke vents will sink to the bottom of the tunnel, as shown in Figure 4. It is difficult for fresh air to reach the fire source with the increase in exhaust volume, so the maximum temperature will not increase suddenly.

When the layout of the exhaust vent is Case “4”, the exhaust volume has a great influence on the maximum temperature. When the exhaust volume increases from 220 m³/s to 240 m³/s, the maximum temperature increases by 97 °C. Although the maximum temperature decreases rapidly with the increase in the exhaust volume, it is still much higher than that of the other schemes. When the exhaust volume is less than 220 m³/s, the maximum temperature is almost the same as that of the other schemes. If only four smoke vents are opened, the exhaust rate should not be more than 220 m³/s.

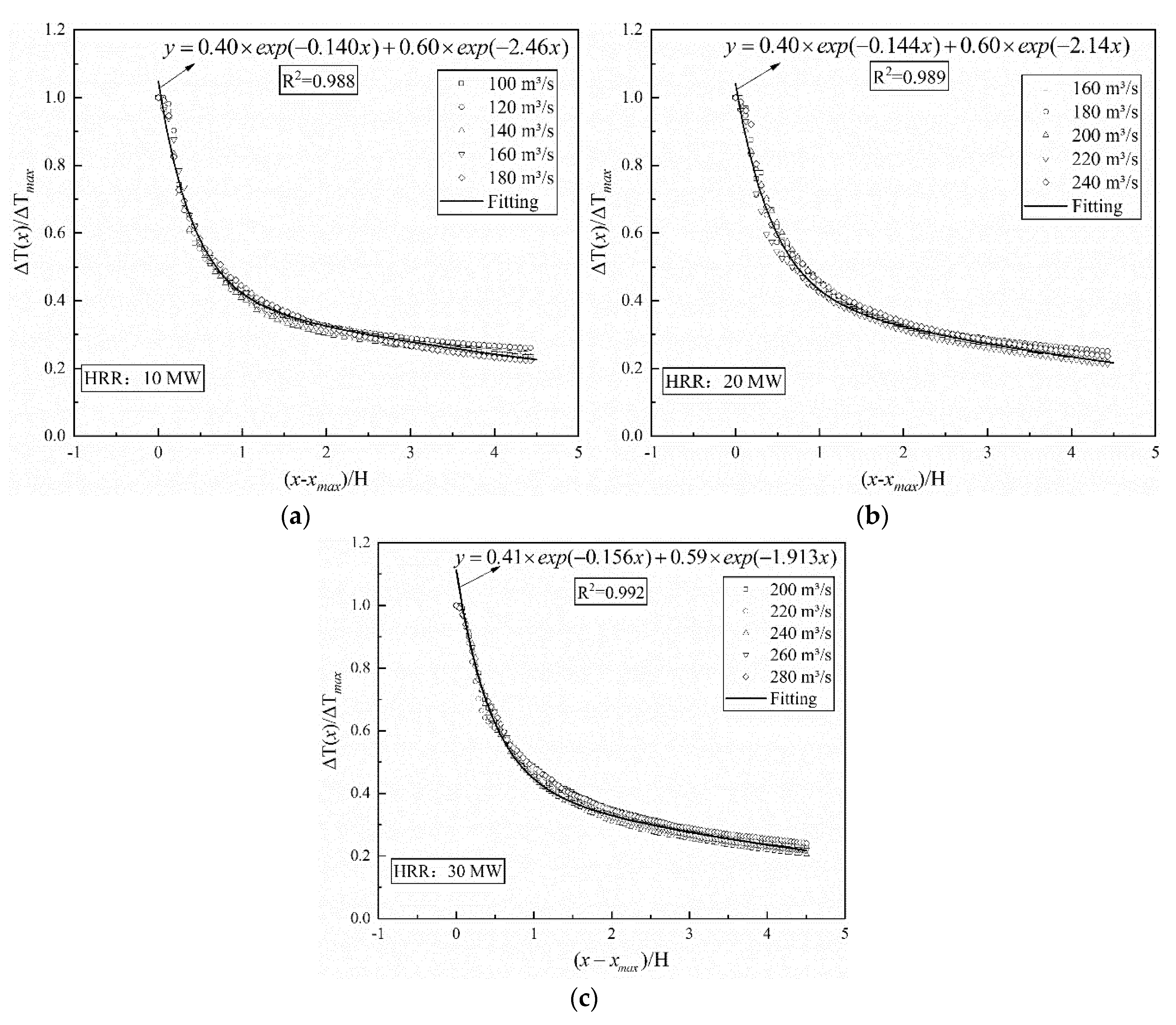
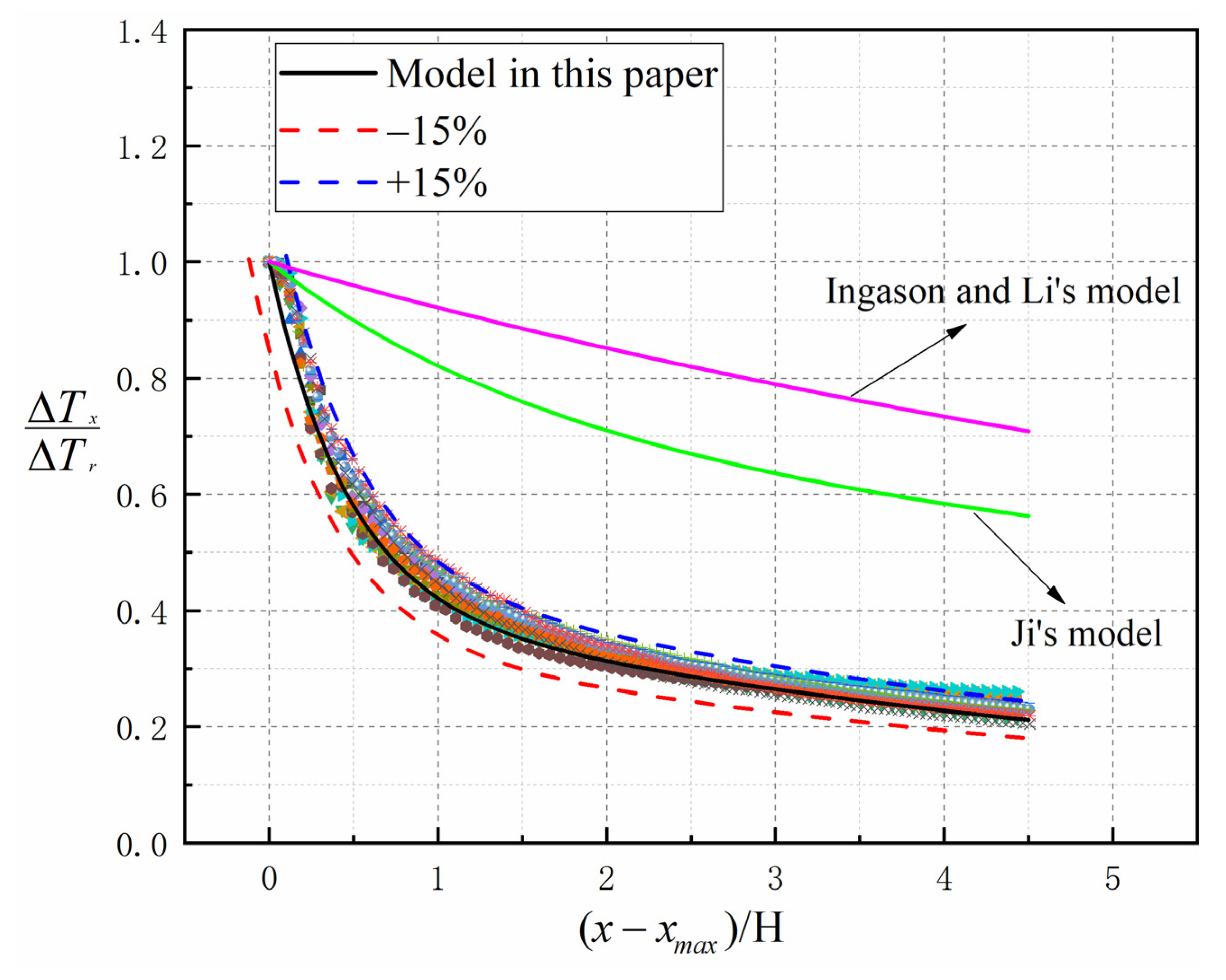
3.2.2. Temperature Decay Model

For the downstream smoke under ceilings far away from fire source:

Mass equation:

$$\frac{\mathrm{d}}{\mathrm{d}x}(\rho uA)={\rho }_{a}W{u}_e$$

(2)

Energy equation:

$$\frac{\mathrm{d}}{\mathrm{d}x}\left(\rho Au{c}_{p}T\right)={\rho }_{a}W{u}_e{c}_p{T}_a-h_t{w}_p\left(T-T_a\right)$$

(3)

The entrainment velocity $u_e$ can be expressed as:

$$u_e=\beta \left(u-u_o\right)$$

(4)

where $\rho$ and $u$ are the density (kg/m³) and velocity (m/s) of smoke; A is the smoke flow section area (m²); W is the width of the tunnel (m); T is the temperature of the smoke (K); $u_e$ is the entrainment velocity of the smoke (m/s); w_p is the wet perimeter of the smoke flow (m); h_t is the total net heat transfer coefficient on the tunnel walls (kW/m²⋅K); $\beta$ is a coefficient measured in the test; and $u_o$ is the velocity of the air (m/s).

In tunnel fires, smoke entrainment velocity is very small [41]. In order to simplify the energy equation, we usually ignore the influence of smoke entrainment on the energy equation. The tunnel wet perimeter can be calculated according to the tunnel design parameters, so the tunnel wet perimeter can be considered a constant. It is assumed that h_t is also a constant. Based on Equations (2)–(4), the temperature attenuation downstream is obtained as:

$$\frac{\mathsf{\Delta }T(x)}{\mathsf{\Delta }{T}_{\max }}=\exp \left(-\frac{h_t{w}_p+{\rho }_a{u}_{e}W{c}_p}{\rho uA{c}_p}x\right)$$

(5)

Because the coefficient $\beta$ (=0.00015) is very small [42], the horizontal entrainment of smoke in the tunnel can be ignored:

$$\frac{\mathsf{\Delta }T(x)}{\mathsf{\Delta }{T}_{\max }}\approx \exp \left(-\frac{h_t{w}_p}{\rho uA{c}_p}x\right)$$

(6)

For a tunnel with a rectangular section, the temperature decay downstream can be expressed as:

$$\frac{\mathsf{\Delta }T(x)}{\mathsf{\Delta }{T}_{\max }}\approx \exp \left(-(\frac{2h}{W}+1)·\frac{h_t}{\rho u{c}_p}·\frac{x}{h}\right)=\exp \left(-\xi ·\frac{x}{h}\right)$$

(7)

$$\xi =(\frac{2h}{W}+1)·\frac{h_t}{\rho u{c}_p}\propto \frac{h_t}{\rho u{c}_p}$$

(8)

Although the coefficient $h_t$ is different in different locations and different fire development stages, when the fire tends to be stable and far enough from fire, the difference of $h_t$ in different locations is very small. In addition, the height of the smoke layer can also be replaced by tunnel height. In view of this, the temperature decay can be approximated using an exponential function [20,40]. Li et al. [43] found that the form of the sum of two exponential functions, that is $\Delta T\left(x\right)/\Delta T_{\max }=a\times \exp \left(b\times \frac{x}{H}\right)+c\times \exp (d\times \frac{x}{H})$, can well describe the decay of temperature under the tunnel ceiling.

Taking the location of the maximum temperature as a reference point, this paper studies the temperature decay from the reference point to the first vent downstream. The smoke control effect is the best in Case “4”, and the decay rate of the temperature is like that of other smoke vent opening schemes. Therefore, this paper only presents the fitting results for the temperature attenuation of Case “4”.

When four smoke vents are opened, the temperature decay rate is the same under different smoke exhaust rates (H is the height of the tunnel, m), as shown in Figure 8. The results of numerical calculation are in good agreement with the fitting curve (R² = 0.992). The constants a, b, c, and d are 0.444, −0.156, 0.598, and −1.913, respectively. The temperature decays the slowest when the layout of the exhaust vent is Case “5B” and decays the fastest when the layout of exhaust vent is Case “3B”. The correlation coefficient (R²) of the fitting curve of the temperature attenuation under different smoke vent opening schemes was greater than 0.976. Except for the smoke vent opening schemes of Case “5B” and Case “3A”, the temperature decays rapidly and the decay rates are similar. Furthermore, the fitting curves of the scheme with fast decay rate are close to the results of temperature for Case “4”. Therefore, we only need to focus on the temperature attenuation of Case “4”.

In order to make the empirical formula for the temperature attenuation more representative, the temperature distributions under different HRRs and exhaust volumes are calculated for Case “4”. The detailed calculation conditions are shown in

Table 4. Calculation condition of 4 smoke vents.

Test No.	Smoke Vent Number	HRR (MW)	Smoke Exhaust Rate (m3/s)
31–35	4	10	100, 120, 140, 160, 180
36–40		20	160, 180, 200, 220, 240

. Under different HRRs, the exhaust volume has little effect on the temperature attenuation, as shown in Figure 9. The influence of the HRR on the attenuation rate is very small. When the HRR of the fire source is 10–30 MW, the temperature decay rate is similar. Taking the average value of each coefficient, the empirical formula of temperature attenuation under the tunnel ceiling with four smoke vents open can be obtained as follows:

$$\Delta T\left(x\right)/\Delta T_{max}={0.40e}^{-0.147(\frac{x-x_{max}}{H})}+{0.60e}^{-2.17(\frac{x-x_{max}}{H})}$$

(9)

To highlight the difference between the single-side multi-point exhaust tunnel and the previous research results, we compared the temperature attenuation model in this paper with some existing temperature attenuation models. Ji et al. [37] studied the effect of pressure and HRR on the temperature decay beneath the ceiling and found that the impact of pressure on temperature decay is very small, and the temperature attenuation conforms to the sum of two exponential attenuations:

$$\Delta T_x/\Delta T_r={0.33e}^{-0.59\frac{\left(x-x_r\right)}{H}}+{0.67e}^{-0.048\frac{\left(x-x_r\right)}{H}}$$

(10)

Ingason and Li [43] concluded that the temperature attenuation beneath the ceiling conforms to the sum of two exponential attenuations:

$$\Delta T_x/\Delta T_r={0.57e}^{-0.13\frac{\left(x-x_r\right)}{H}}+{0.43e}^{-0.021\frac{\left(x-x_r\right)}{H}}$$

(11)

The numerical results are in good agreement with the prediction model proposed in this paper, and the error between the numerical results and the prediction model is basically within 15%, as shown in Figure 10. The closer to the smoke vent, the greater the error between the numerical results and the prediction model, with the numerical calculation results slightly higher than the prediction model. This is because the smoke vent will inhibit the movement of high-temperature smoke and reduce the temperature attenuation rate. Because there are four smoke vents in the tunnel that are continuously discharging high-temperature smoke, the rate of the temperature attenuation model in this paper is faster than that of natural ventilation or longitudinal ventilation tunnel, and the choice of reference points may also be one of the reasons for the large differences.

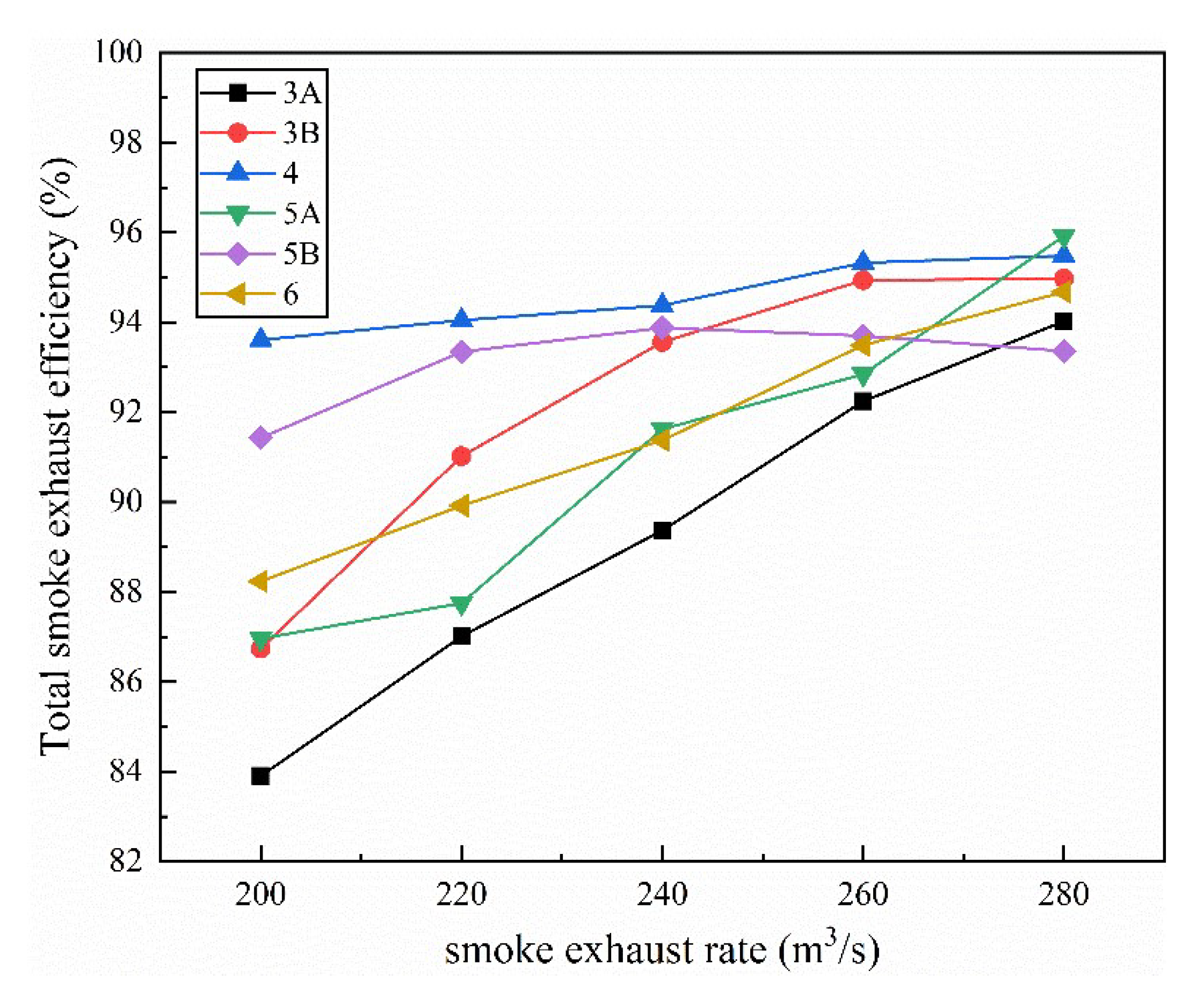
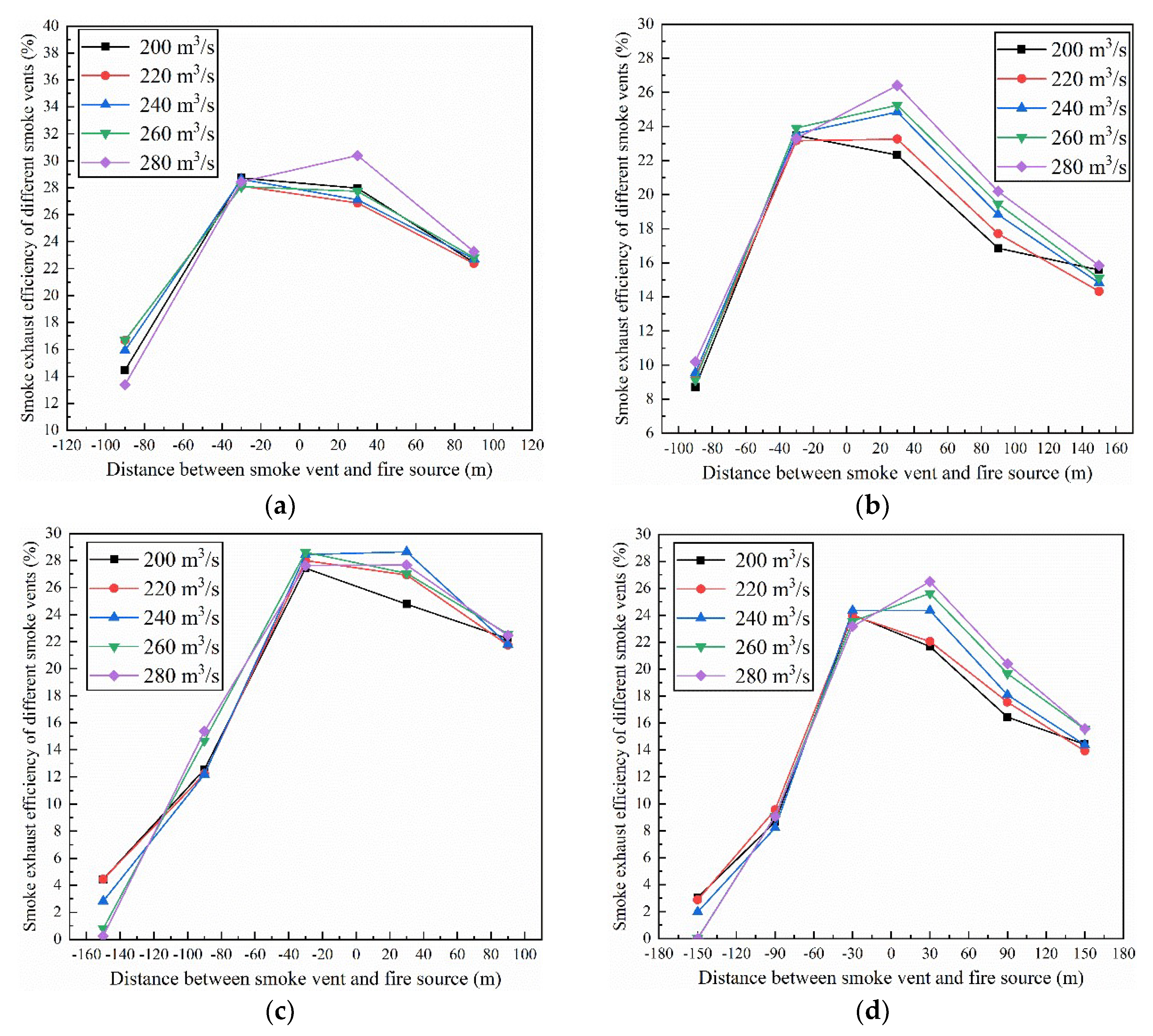
3.3. Exhaust Efficiency

By comparing the mass flow rate of CO in the exhaust duct under different calculation conditions, the efficiency of smoke extraction with different calculation conditions can be judged [30]. When the layout of the smoke vent is Case “4”, the increase in total smoke exhaust efficiency is very small with increasing exhaust volume, and the effect of the exhaust rate on total smoke exhaust efficiency is very small, as shown in Figure 11. Under different exhaust volumes, the total exhaust efficiency is more than 93.7% when the layout of the exhaust vent is Case “4”. The maximum difference of total smoke exhaust efficiency is less than 1.5% under different exhaust volumes in Case “4”. Moreover, the total exhaust efficiency with the same exhaust rate is significantly higher than that of other smoke vent opening schemes. When the layout of the exhaust vent is Case “3A”, the total smoke exhaust efficiency is the lowest compared with other schemes, and the smoke exhaust efficiency is greatly affected by the exhaust rate. When the exhaust volume increases by 20 m³/s, the total smoke exhaust efficiency increases by more than 2.5%.

The trend of total exhaust efficiency under different smoke vent opening states is that the higher the exhaust rate, the greater the total exhaust efficiency. However, if the exhaust rate exceeds 240 m³/s, the total smoke exhaust efficiency decreases with the increase in exhaust volume in Case “5B”. This is because the velocity at the smoke vent downstream is far less than that upstream, and the farther away from the fire, the lower the velocity at the smoke vent. As the exhaust volume increases, the smoke may not spread to the smoke vent, which will result in the intake of fresh air instead of smoke. It can be noticed from Figure 12c,d that when the exhaust volume exceeds 260 m³/s, the exhaust efficiency of the smoke vent farthest downstream from the fire is almost 0%.

With the increase in distance from the fire, the smoke exhaust efficiency of the smoke vent downstream decreases rapidly, as shown in Figure 12. The smoke vent with the highest smoke exhaust efficiency is the nearest one on both sides of the fire. In the process of smoke spreading, the smoke will continuously entrain the fresh air in the tunnel, resulting in the decrease in CO content. Therefore, the CO content near the fire source is the highest. For the smoke vent upstream, the farther away from fire, the higher the exhaust velocity, the lower the exhaust efficiency. Moreover, the exhaust volume has little impact on the exhaust efficiency of the vent closest to the exhaust fan. The smoke exhaust efficiency of the other smoke vents upstream increases with the exhaust rate. The smoke is mainly discharged from the two smoke vents nearest to the fire source, and the exhaust volume has little impact on the exhaust efficiency (the maximum difference of the exhaust efficiency with different exhaust rates is less than 4%). When three smoke vents are opened downstream, the smoke vent 150 m away from the fire makes little contribution to controlling the smoke, and the smoke exhaust efficiency is less than 5% under different smoke exhaust rates.

4. Conclusions

A set of CFD simulations were performed in single-side point exhaust tunnels with different smoke exhaust rates to explore the impact of the number of smoke vents on smoke control, temperature profile, and smoke exhaust efficiency. The main conclusions are as follows:

(1)

When there are more than two smoke vents on one side of the fire source far away from the exhaust fan, some smoke exhaust vents will inhale fresh air rather than toxic smoke. When the layout of the exhaust vent is Case “4”, the total length of the smoke spread in single-side point exhaust tunnels is shortest;

(2)

The maximum temperature decreases with the increase in the smoke exhaust rate. The temperature is much higher than in other smoke exhaust vent opening schemes at the same smoke exhaust volume as Case “6”;

(3)

By analyzing the simulation results of the vault temperature under different HRRs and exhaust rates, an empirical formula of temperature attenuation for Case “4” was proposed: $\Delta T\left(x\right)/\Delta T_{max}={0.40e}^{-0.147(\frac{x-x_{max}}{H})}+{0.60e}^{-2.17(\frac{x-x_{max}}{H})}$. The error of the temperature attenuation model is less than 15%;

(4)

Under the same exhaust volume, the exhaust efficiency is the highest when the layout of the exhaust vent is Case “4”. The total smoke exhaust efficiency of the tunnel is more than 93.7% and the maximum difference of the total smoke exhaust efficiency is less than 1.5% under different smoke exhaust rates;

(5)

For a single-side point exhaust tunnel, the number of smoke vents near the smoke exhaust fan side shall not be more than that on the other side. The proposed smoke control scheme for the Mawan tunnel with a designed HRR of 30 MW is as follows: the layout of the exhaust vent is as shown in Case “4”, and the smoke exhaust rate is 220 m³/s.

This paper mainly studied the smoke and temperature control of a centralized smoke exhaust tunnel, discussed the smoke exhaust effect when there are different numbers of smoke outlets, solved the fire ventilation design of Mawan tunnel, and provided a reference for a similar tunnel fire ventilation design. A study on the temperature field of a single-side point exhaust tunnel fire, especially the maximum temperature, will be carried out in further model tests.