Predicting Wildfire Fuels and Hazard in a Central European Temperate Forest Using Active and Passive Remote Sensing
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
3.1. Field Data
3.1.1. Surface Fuels
3.1.2. Canopy Fuels
3.2. Remote Sensing Data
3.2.1. Sentinel-1 and -2
3.2.2. LiDAR
3.3. Wind
3.4. Fuels Prediction
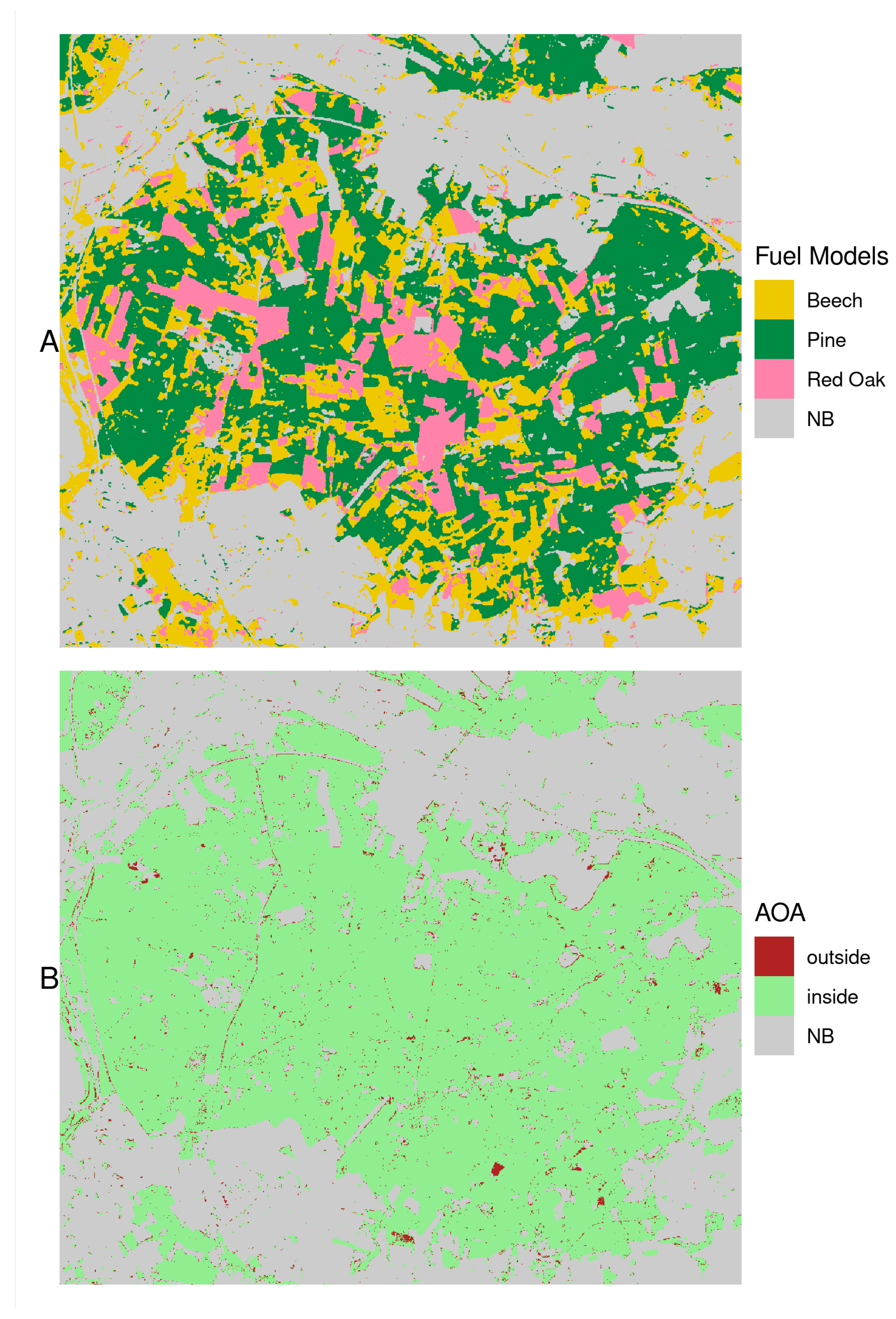
3.4.1. Surface Fuels
3.4.2. Crown Bulk Density
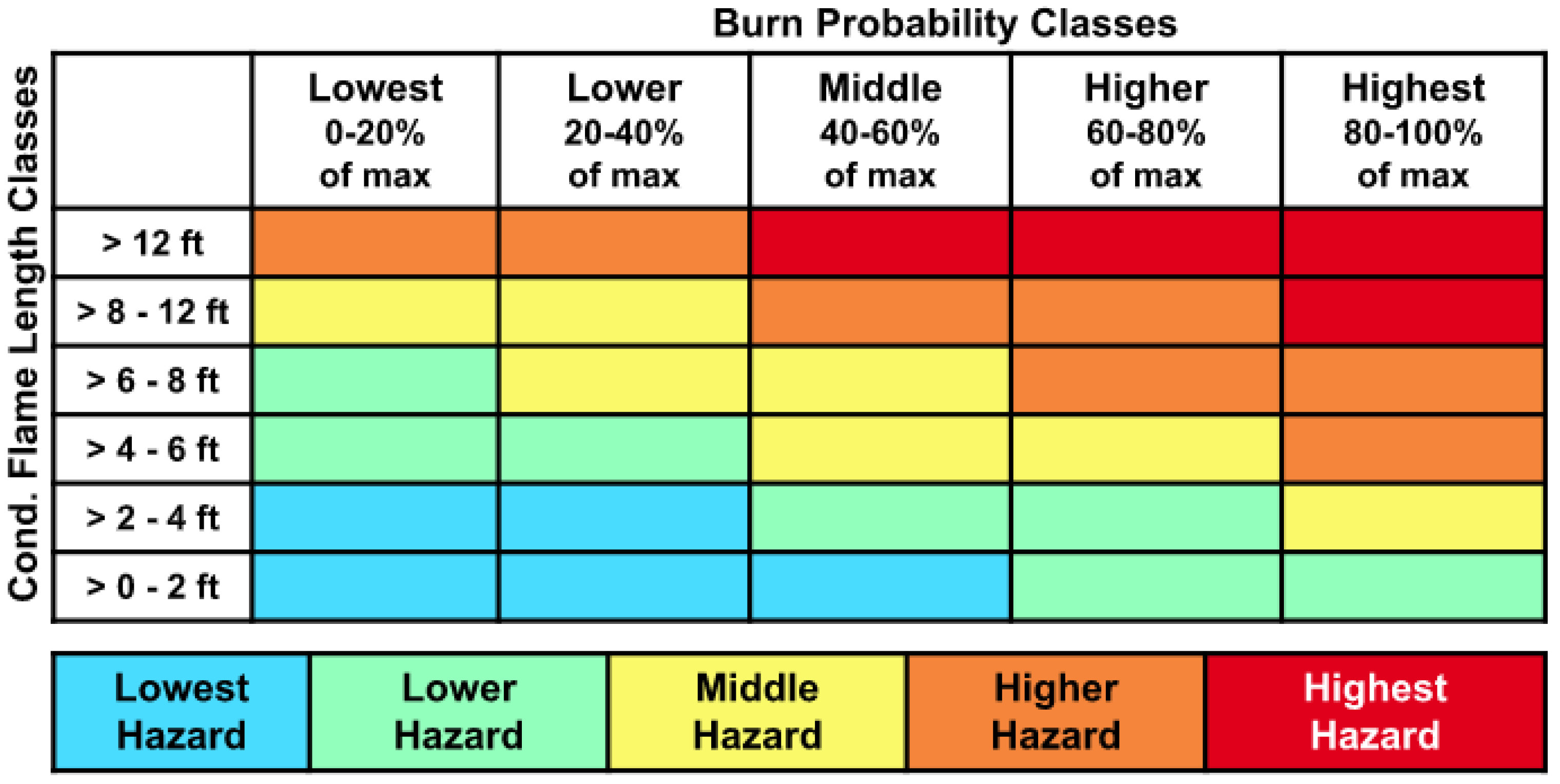
3.5. Fire Behavior and Hazard Modeling
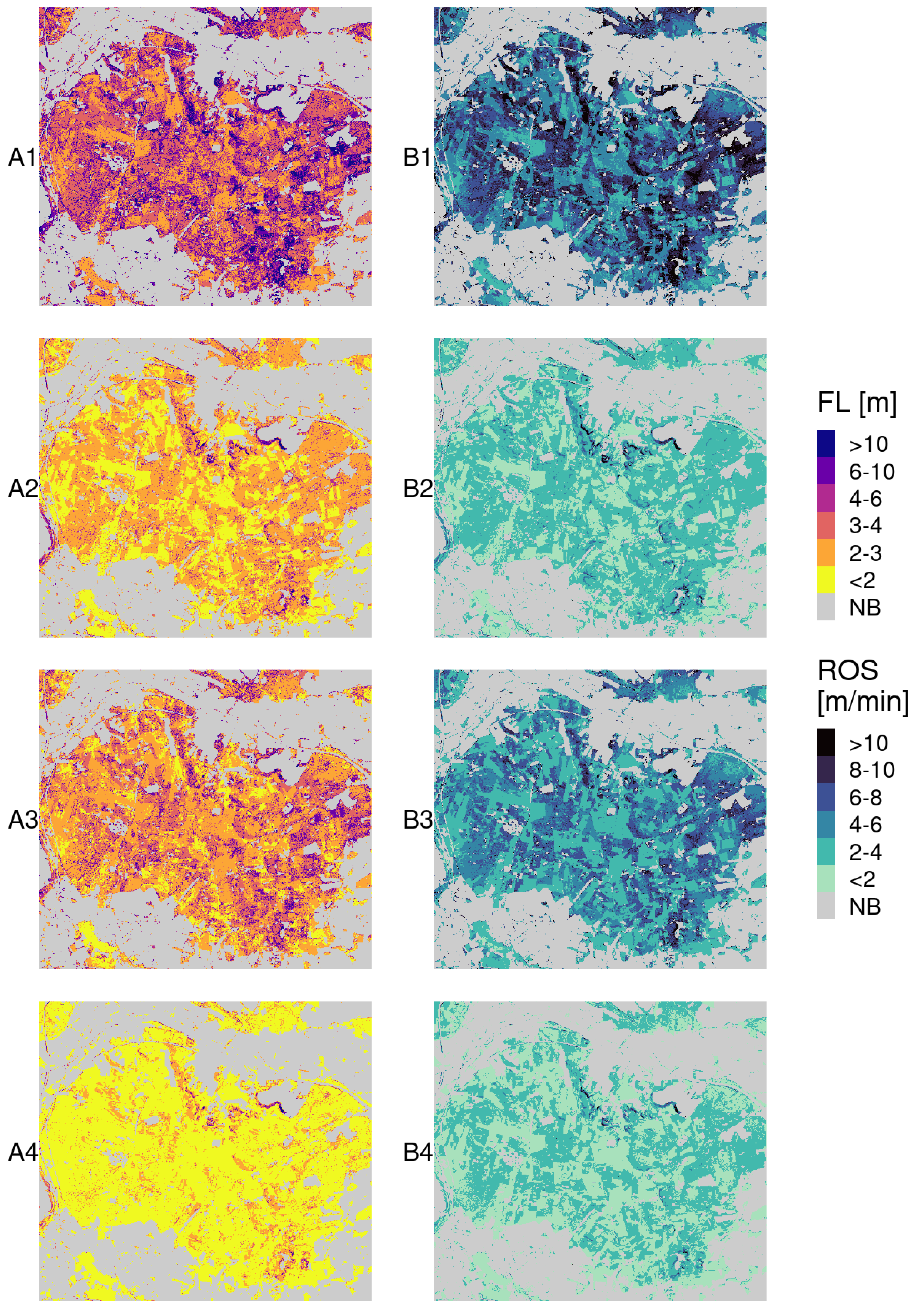
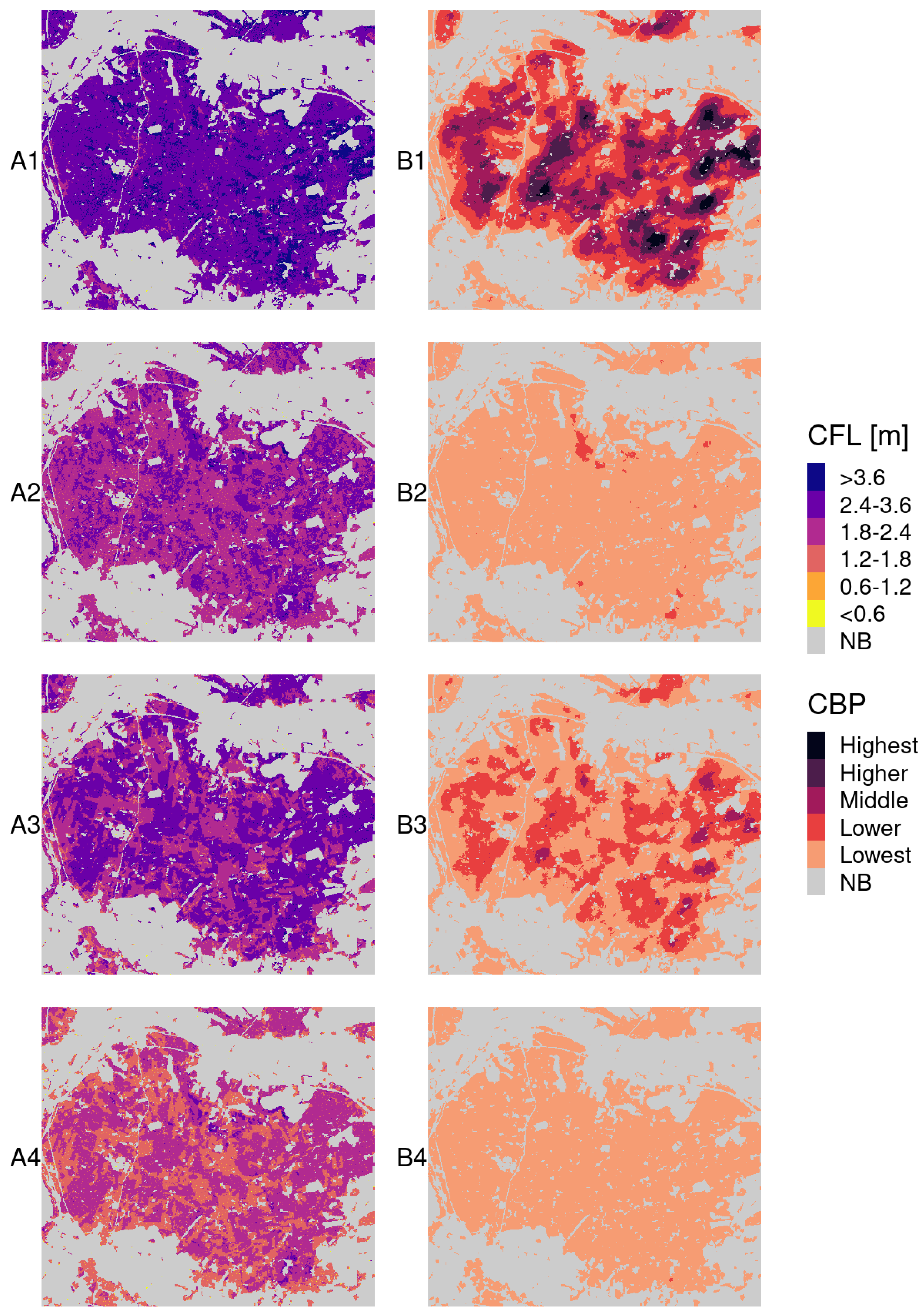
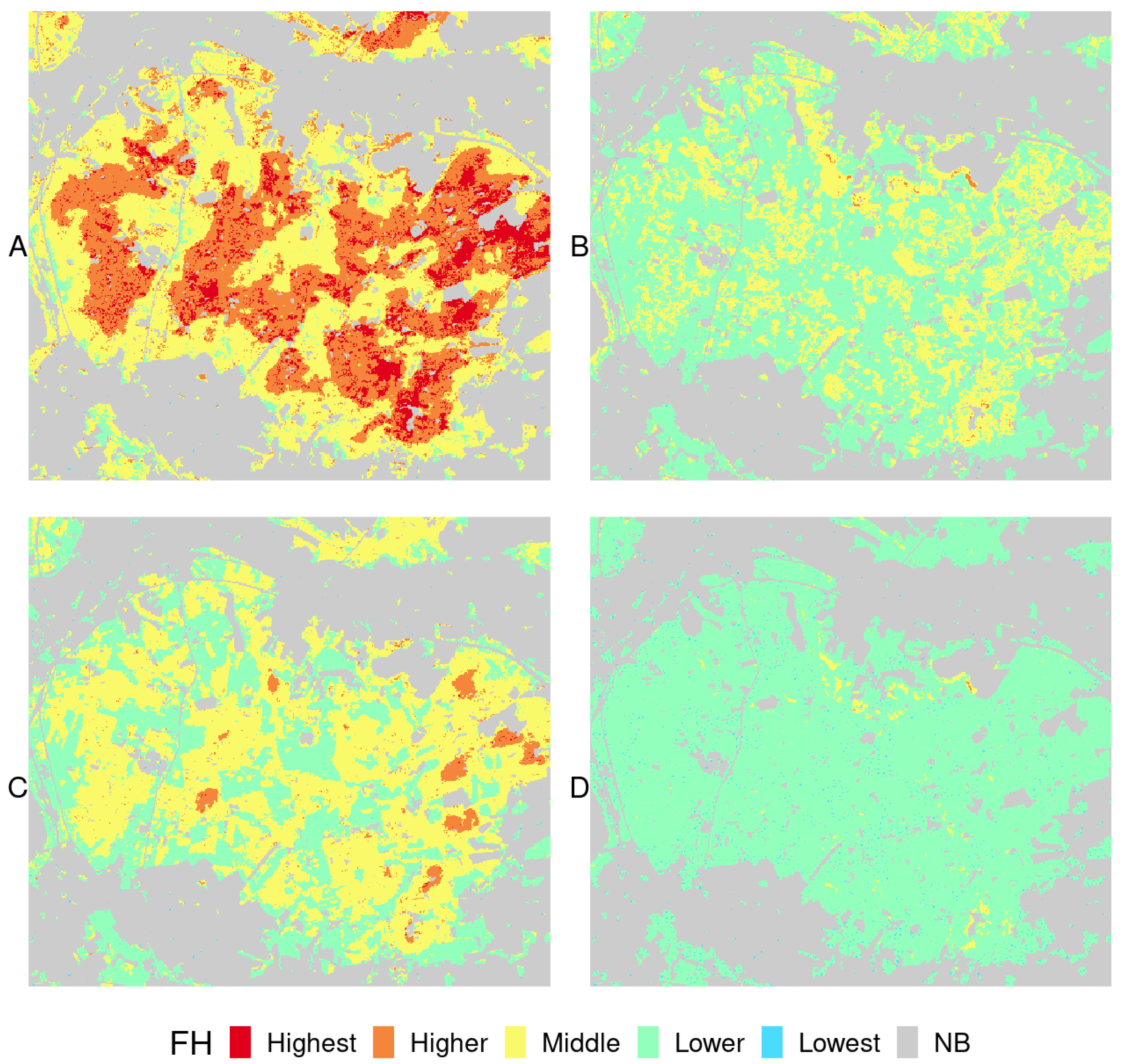
4. Results
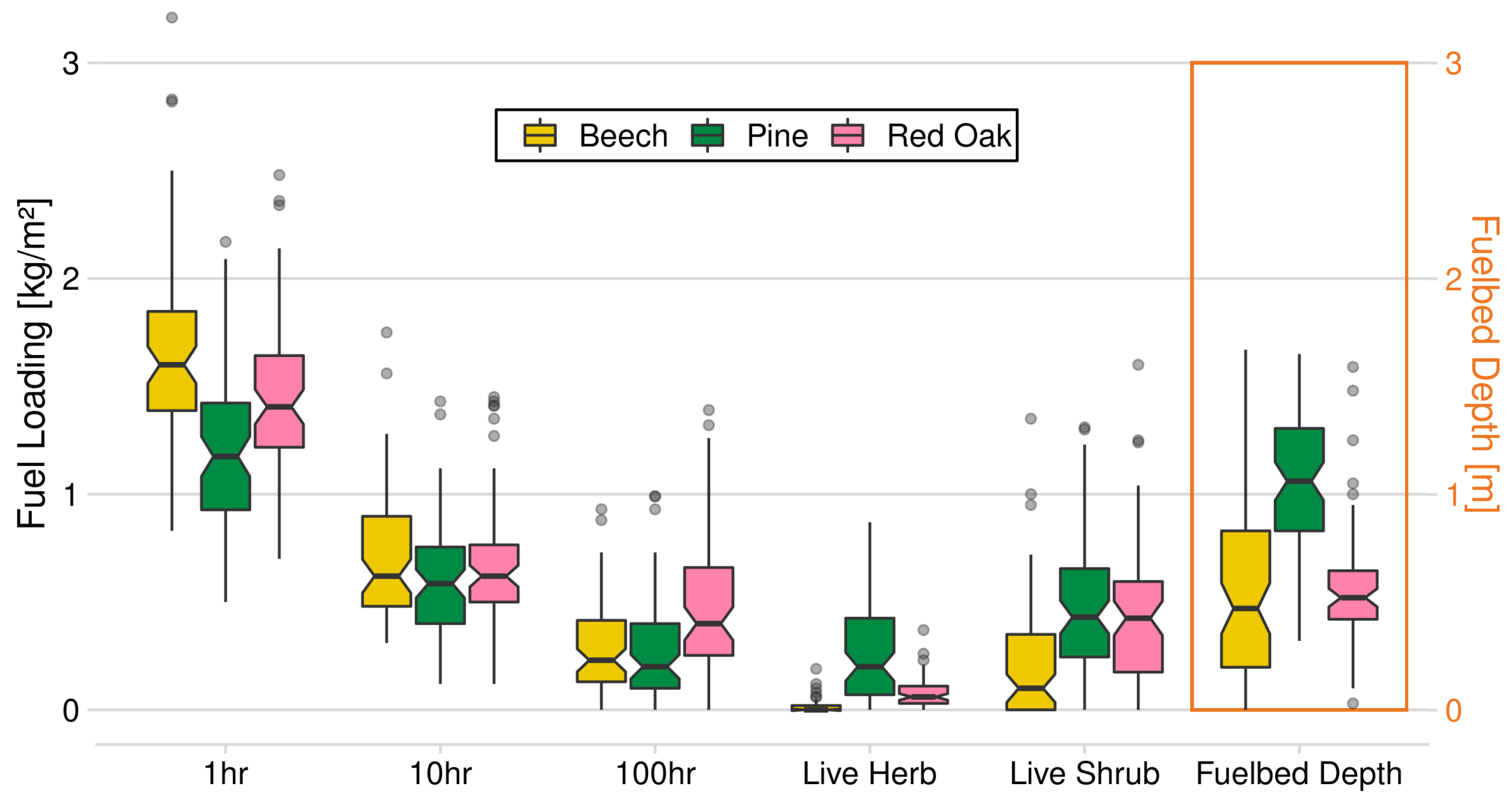
4.1. Surface Fuels
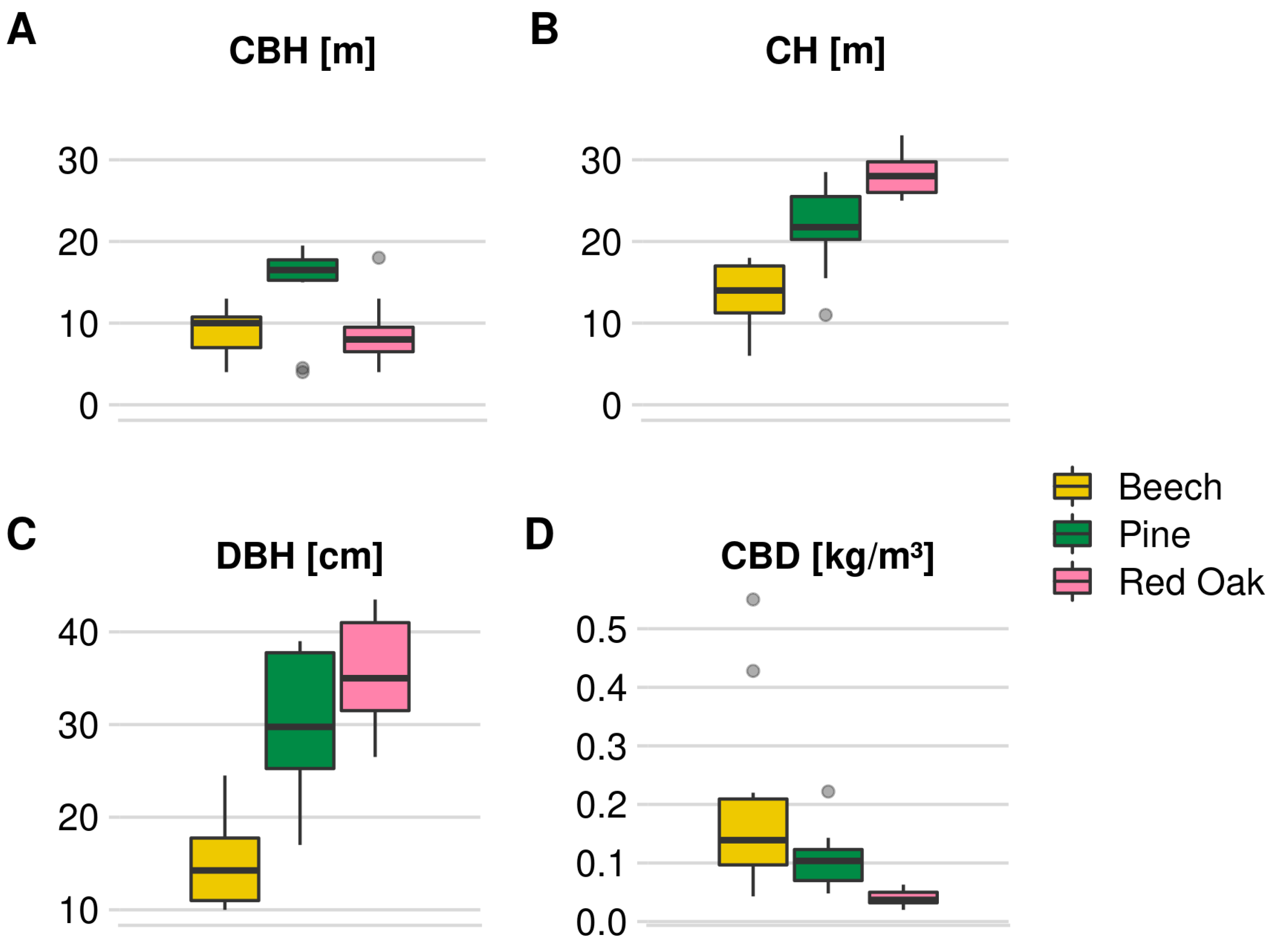
4.2. Crown Bulk Density
4.3. Fire Behavior and Hazard
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; Technical Report; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Cardil, A.; Monedero, S.; Schag, G.; de Miguel, S.; Tapia, M.; Stoof, C.R.; Silva, C.A.; Mohan, M.; Cardil, A.; Ramirez, J. Fire behavior modeling for operational decision-making. Curr. Opin. Environ. Sci. Health 2021, 23, 100291. [Google Scholar] [CrossRef]
- Schuldt, B.; Buras, A.; Arend, M.; Vitasse, Y.; Beierkuhnlein, C.; Damm, A.; Gharun, M.; Grams, T.E.; Hauck, M.; Hajek, P.; et al. A first assessment of the impact of the extreme 2018 summer drought on Central European forests. Basic Appl. Ecol. 2020, 45, 86–103. [Google Scholar] [CrossRef]
- BMEL. Deutschlands Wald im Klimawandel-Eckpunkte und Maßnahmen; Technical Report; Bundesministerium für Ernährung und Landwirtschaft: Bonn, Germany, 2019.
- BMEL. Waldbrandstatistik der Bundesrepublik Deutschland für das Jahr 2019; Technical Report; Bundesministerium für Ernährung und Landwirtschaft: Bonn, Germany, 2019.
- Dillon, G.; Menakis, J.; Fay, F. Wildland Fire Potential: A Tool for Assessing Wildfire Risk and Fuels Management Needs. In Proceedings of the Large Wildland Fires Conference; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Missoula, MT, USA, 2015; pp. 60–76. [Google Scholar]
- Keane, R.E.; Burgan, R.; van Wagtendonk, J. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301. [Google Scholar] [CrossRef]
- Keane, R.E.; Gray, K.; Bacciu, V. Spatial Variability of Wildland Fuel Characteristics in Northern Rocky Mountain Ecosystems; Technical Report RMRS-RP-98; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ft. Collins, CO, USA, 2012. [CrossRef] [Green Version]
- Chuvieco, E.; Aguado, I.; Salas, J.; García, M.; Yebra, M.; Oliva, P. Satellite Remote Sensing Contributions to Wildland Fire Science and Management. Curr. For. Rep. 2020, 6, 81–96. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Vastaranta, M.; Wulder, M.A.; Saarinen, N.; Stepper, C.; Coops, N.C. A Model Development and Application Guide for Generating an Enhanced Forest Inventory Using Airborne Laser Scanning Data and an Area-Based Approach; Technical Report; Natural Resources Canada, Canadian Wood Fibre Center: Ottawa, ON, Canada, 2017. [Google Scholar]
- Finney, M.A.; McHugh, C.W.; Grenfell, I.C.; Riley, K.L.; Short, K. A simulation of probabilistic wildfire risk components for the continental United States. Stoch. Environ. Res. Risk Assess. 2011, 25, 973–1000. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, S.; Rocha, J.; Sá, A. Wildfire risk modeling. Curr. Opin. Environ. Sci. Health 2021, 23, 100274. [Google Scholar] [CrossRef]
- Botequim, B.; Fernandes, P.M.; Garcia-Gonzalo, J.; Silva, A. Coupling fire behaviour modelling and stand characteristics to assess and mitigate fire hazard in a maritime pine landscape in Portugal. Eur. J. Forest Res. 2017, 136, 527–542. [Google Scholar] [CrossRef]
- Taccaliti, F.; Venturini, L.; Marchi, N.; Lingua, E. Forest fuel assessment by LiDAR data. A case study in NE Italy. In Proceedings of the 23rd EGU General Assembly, Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Stockdale, C.; Barber, Q.; Saxena, A.; Parisien, M.A. Examining management scenarios to mitigate wildfire hazard to caribou conservation projects using burn probability modeling. J. Environ. Manag. 2019, 233, 238–248. [Google Scholar] [CrossRef]
- Lutes, D.C.; Keane, R.E. Fuel Load (FL). In FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Sunderland, S., Gangi, L., Eds.; Gen. Tech. Rep. RMRS-GTR-164-CD; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. 1–25. [Google Scholar]
- Brown, J.K. Handbook for Inventorying Downed Woody Material; Technical Report; U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1974. [Google Scholar]
- Keane, R.E.; Reinhardt, E.D.; Scott, J.; Gray, K.; Reardon, J. Estimating forest canopy bulk density using six indirect methods. Can. J. For. Res. 2005, 35, 724–739. [Google Scholar] [CrossRef]
- Lutes, D.C. FuelCalc User’s Guide (Version 1.7); U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Missoula, MT, USA, 2021.
- Reinhardt, E.; Lutes, D.C.; Scott, J.H. FuelCalc: A Method for Estimating Fuel Characteristics. In Proceedings of the Fuels Management-How to Measure Success: Conference Proceedings, Portland, OR, USA, 28–30 March 2006; p. 10. [Google Scholar]
- Erdody, T.L.; Moskal, L.M. Fusion of LiDAR and imagery for estimating forest canopy fuels. Remote Sens. Environ. 2010, 114, 725–737. [Google Scholar] [CrossRef]
- Scott, J.H.; Reinhardt, E.D. Estimating canopy fuels in conifer forests. Fire Manag. Today 2002, 62, 6. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Mullissa, A.; Vollrath, A.; Odongo-Braun, C.; Slagter, B.; Balling, J.; Gou, Y.; Gorelick, N.; Reiche, J. Sentinel-1 SAR Backscatter Analysis Ready Data Preparation in Google Earth Engine. Remote Sens. 2021, 13, 1954. [Google Scholar] [CrossRef]
- Bezirksregierung Köln. Nutzerinformationen für Die 3D-Messdaten aus dem Laserscanning für NRW. 2020. Available online: https://www.bezreg-koeln.nrw.de/brk_internet/geobasis/hoehenmodelle/nutzerinformationen.pdf (accessed on 27 January 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Roussel, J.R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Meador, A.S.; Bourdon, J.F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- Hijmans, R.J. Terra: Spatial Data Analysis. R Package Version 1.3-22. 2021. Available online: https://CRAN.R-project.org/package=terra (accessed on 27 January 2022).
- Andersen, H.E.; McGaughey, R.J.; Reutebuch, S.E. Estimating forest canopy fuel parameters using LIDAR data. Remote Sens. Environ. 2005, 94, 441–449. [Google Scholar] [CrossRef]
- Cameron, H.A.; Schroeder, D.; Beverly, J.L. Predicting black spruce fuel characteristics with Airborne Laser Scanning (ALS). Int. J. Wildland Fire, 2021; in press. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Sánchez Meador, A.J.; Thode, A.E. Airborne lidar provides reliable estimates of canopy base height and canopy bulk density in southwestern ponderosa pine forests. For. Ecol. Manag. 2021, 481, 118695. [Google Scholar] [CrossRef]
- Chuvieco, E.; Riaño, D.; Van Wagtendok, J.; Morsdof, F. Fuel Loads and Fuel Type Mapping. In Wildland Fire Danger Estimation and Mapping—The Role of Remote Sensing; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2003; Volume 4, pp. 119–142. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Riaño, D. Modeling airborne laser scanning data for the spatial generation of critical forest parameters in fire behavior modeling. Remote Sens. Environ. 2003, 86, 177–186. [Google Scholar] [CrossRef]
- Novo, A.; Fariñas-Álvarez, N.; Martínez-Sánchez, J.; González-Jorge, H.; Fernández-Alonso, J.M.; Lorenzo, H. Mapping Forest Fire Risk—A Case Study in Galicia (Spain). Remote Sens. 2020, 12, 3705. [Google Scholar] [CrossRef]
- Parker, G.G.; Harmon, M.E.; Lefsky, M.A.; Chen, J.; Pelt, R.V.; Weis, S.B.; Thomas, S.C.; Winner, W.E.; Shaw, D.C.; Frankling, J.F. Three-dimensional Structure of an Old-growth Pseudotsuga-Tsuga Canopy and Its Implications for Radiation Balance, Microclimate, and Gas Exchange. Ecosystems 2004, 7, 440–453. [Google Scholar] [CrossRef]
- Aber, J.D. Foliage-Height Profiles and Succession in Northern Hardwood Forests. Ecology 1979, 60, 18–23. [Google Scholar] [CrossRef]
- Rouse, J.; Hass, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. Third Earth Resour. Technol. Satell. Symp. 1973, 1, 309–317. [Google Scholar]
- Boessenkool, B. rdwd: Select and Download Climate Data from ’DWD’ (German Weather Service). R Package Version 1.5.0. 2021. Available online: https://CRAN.R-project.org/package=rdwd (accessed on 27 January 2022).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 1620–1633. [Google Scholar] [CrossRef]
- Meyer, H. CAST: `caret’ Applications for Spatial-Temporal Models. R Package Version 0.5.1. 2021. Available online: https://CRAN.R-project.org/package=CAST (accessed on 27 January 2022).
- Kuhn, M. caret: Classification and Regression Training. R Package Version 6.0-88. 2021. Available online: https://CRAN.R-project.org/package=caret (accessed on 27 January 2022).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. (Eds.) An Introduction to Statistical Learning: With Applications in R; Number 103 in Springer Texts in Statistics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Anderson, H.E. Aids to Determining Fuel Models for Estimating Fire Behavior; Technical Report INT-GTR-122; U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1982. [Google Scholar] [CrossRef] [Green Version]
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; Technical Report RMRS-GTR-153; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ft. Collins, CO, USA, 2005. [Google Scholar]
- Finney, M.A. An overview of FlamMap fire modeling capabilities. In Proceedings of the Fuels Management-How to Measure Success: Conference Proceedings, Proceedings RMRS-P-41, Portland, OR, USA, 28–30 March 2006; Andrews Patricia, L., Butler Bret, W., Eds.; US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; Volume 41, pp. 213–220. [Google Scholar]
- Papadopoulos, G.D.; Pavlidou, F.N. A Comparative Review on Wildfire Simulators. IEEE Syst. J. 2011, 5, 233–243. [Google Scholar] [CrossRef]
- Forthofer, J.M.; Butler, B.W.; Wagenbrenner, N.S. A comparison of three approaches for simulating fine-scale surface winds in support of wildland fire management. Part I. Model formulation and comparison against measurements. Int. J. Wildland Fire 2014, 23, 969. [Google Scholar] [CrossRef]
- Finney, M.A. Fire growth using minimum travel time methods. Can. J. For. Res. 2002, 32, 1420–1424. [Google Scholar] [CrossRef]
- US Department of the Interior & US Department of Agriculture. Interagency Fuels Treatment Decision Support System (IFTDSS) (Version 3.4.1.3). 2021. Available online: https://iftdss.firenet.gov/ (accessed on 27 January 2022).
- Calkin, D.E.; Ager, A.A.; Gilbertson-Day, J. Wildfire Risk and Hazard: Procedures for the First Approximation; Technical Report RMRS-GTR-235; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ft. Collins, CO, USA, 2010. [Google Scholar] [CrossRef] [Green Version]




| Variable | Name | Unit | Reference | n |
|---|---|---|---|---|
| LiDAR | ||||
| height | ||||
| canopy height model | m | [27,33] | 1 | |
| crown base height | m | [31] | 1 | |
| maximum height | m | [27] | 1 | |
| mean height | m | [27] | 1 | |
| height standard deviation | m | [27] | 1 | |
| height coefficient of variation | m | [27] | 1 | |
| height inter-quartile range | m | [27] | 1 | |
| height skewness | - | [27] | 1 | |
| height kurtosis | - | [27] | 1 | |
| height entropy | - | [27] | 1 | |
| height percentiles | m | [27] | 18 | |
| cumulative height percentiles | m | [27] | 9 | |
| mean height grass, shrubs, trees | m | [32] | 3 | |
| vertical tree-shrub height gap | m | [32] | 1 | |
| percent of returns above | % | [27] | 1 | |
| percent of returns above 2 m | % | [27] | 1 | |
| cover | ||||
| C | vegetation cover | % | [34] | 1 |
| percent ground returns | % | [27] | 1 | |
| cumulative vertical profile | % | [37] | 21 | |
| cover of grass, shrubs, trees | % | [35] | 3 | |
| density | ||||
| Rumple index | - | [36] | 1 | |
| N | total number of returns | - | [27] | 1 |
| D | density 1st returns in canopy | % | [29] | 1 |
| terrain | ||||
| elevation | m | [27] | 1 | |
| terrain slope | ° | [28] | 1 | |
| terrain aspect | ° | [28] | 1 | |
| Sentinel-1 | ||||
| VV polarization t. c. | dB | [24] | 3 | |
| VH polarization t. c. | dB | [24] | 3 | |
| VV/VH ratio t. c. | - | [24] | 3 | |
| Sentinel-2 | ||||
| ultra blue band t. c. | SR | 3 | ||
| blue band t. c. | SR | 3 | ||
| green band t. c. | SR | 3 | ||
| red band t. c. | SR | 3 | ||
| red edge 1 band t. c. | SR | 3 | ||
| red edge 2 band t. c. | SR | 3 | ||
| red edge 3 band t. c. | SR | 3 | ||
| NIR 1 band t. c. | SR | 3 | ||
| SWIR 1 band t. c. | SR | 3 | ||
| SWIR 3 band t. c. | SR | 3 | ||
| SWIR 4 band t. c. | SR | 3 | ||
| vegetation index t. c. | - | [38] | 3 | |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | |
|---|---|---|---|---|---|---|---|---|
| FMS | D1L1 | D1L1 | D1L1 | D1L1 | D3L1 | D3L1 | D3L1 | D3L1 |
| Wind speed [m/s] | 10 | 10 | 2 | 2 | 10 | 10 | 2 | 2 |
| Air temp. [°C] | 35 | 25 | 35 | 25 | 35 | 25 | 35 | 25 |
| Fuel Loadings [kg/m2] | ||||||
|---|---|---|---|---|---|---|
| Species | 1-h | 10 h | 100 h | Live Herb | Live Shrub | Fuelbed Depth [m] |
| Beech | 1.60 | 0.62 | 0.23 | 0.00 | 0.10 | 0.47 |
| Red Oak | 1.41 | 0.62 | 0.40 | 0.06 | 0.42 | 0.52 |
| Pine | 1.17 | 0.58 | 0.20 | 0.20 | 0.43 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heisig, J.; Olson, E.; Pebesma, E. Predicting Wildfire Fuels and Hazard in a Central European Temperate Forest Using Active and Passive Remote Sensing. Fire 2022, 5, 29. https://doi.org/10.3390/fire5010029
Heisig J, Olson E, Pebesma E. Predicting Wildfire Fuels and Hazard in a Central European Temperate Forest Using Active and Passive Remote Sensing. Fire. 2022; 5(1):29. https://doi.org/10.3390/fire5010029
Chicago/Turabian StyleHeisig, Johannes, Edward Olson, and Edzer Pebesma. 2022. "Predicting Wildfire Fuels and Hazard in a Central European Temperate Forest Using Active and Passive Remote Sensing" Fire 5, no. 1: 29. https://doi.org/10.3390/fire5010029
APA StyleHeisig, J., Olson, E., & Pebesma, E. (2022). Predicting Wildfire Fuels and Hazard in a Central European Temperate Forest Using Active and Passive Remote Sensing. Fire, 5(1), 29. https://doi.org/10.3390/fire5010029






