PIC Modeling of Ionospheric Plasma Diagnostics by Hemispherical Probes: Study of the LAP-CSES at Magnetic Conjugates
Abstract
1. Introduction
2. LAP-CSES Geometry
3. Methodology
4. Results and Discussion
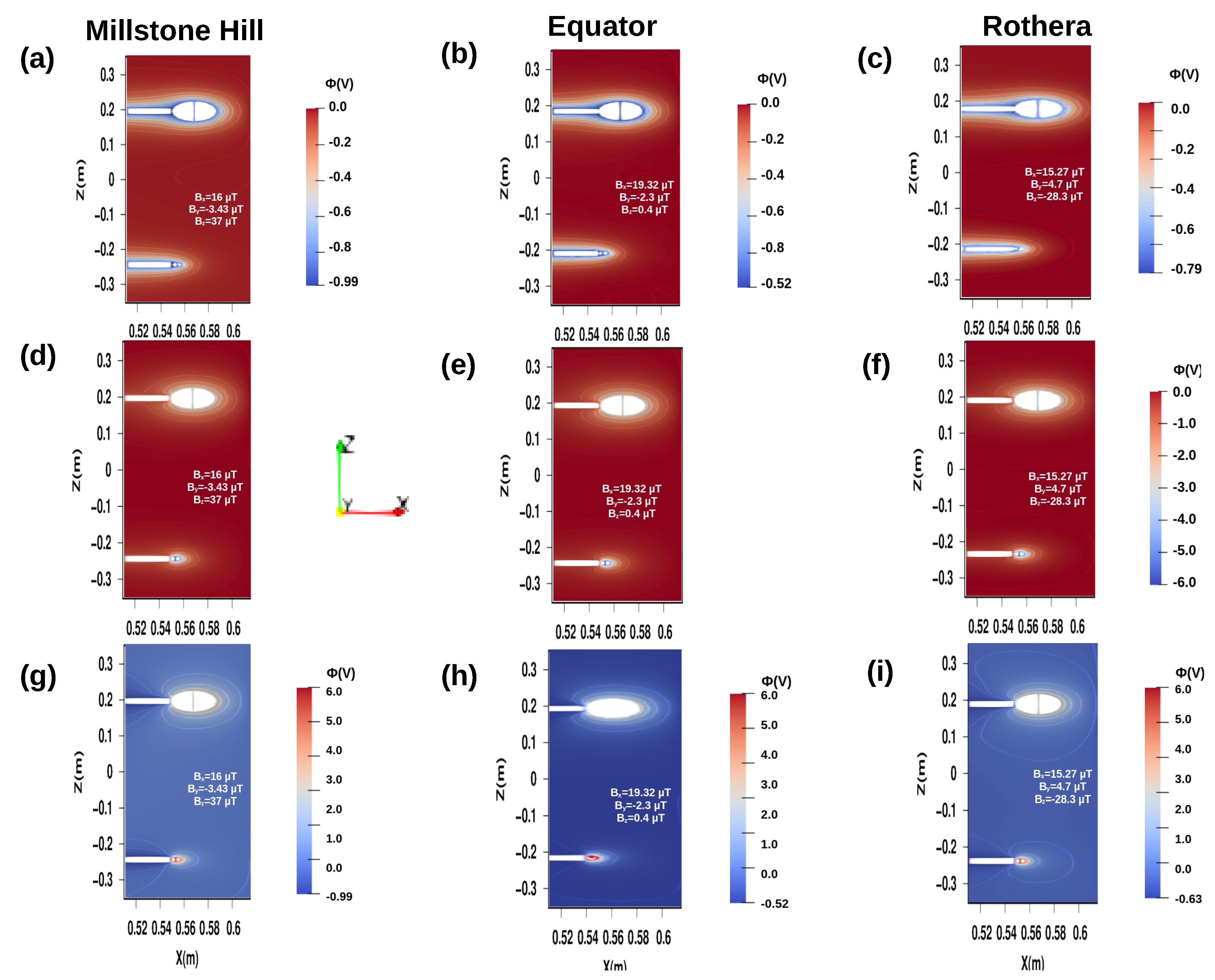
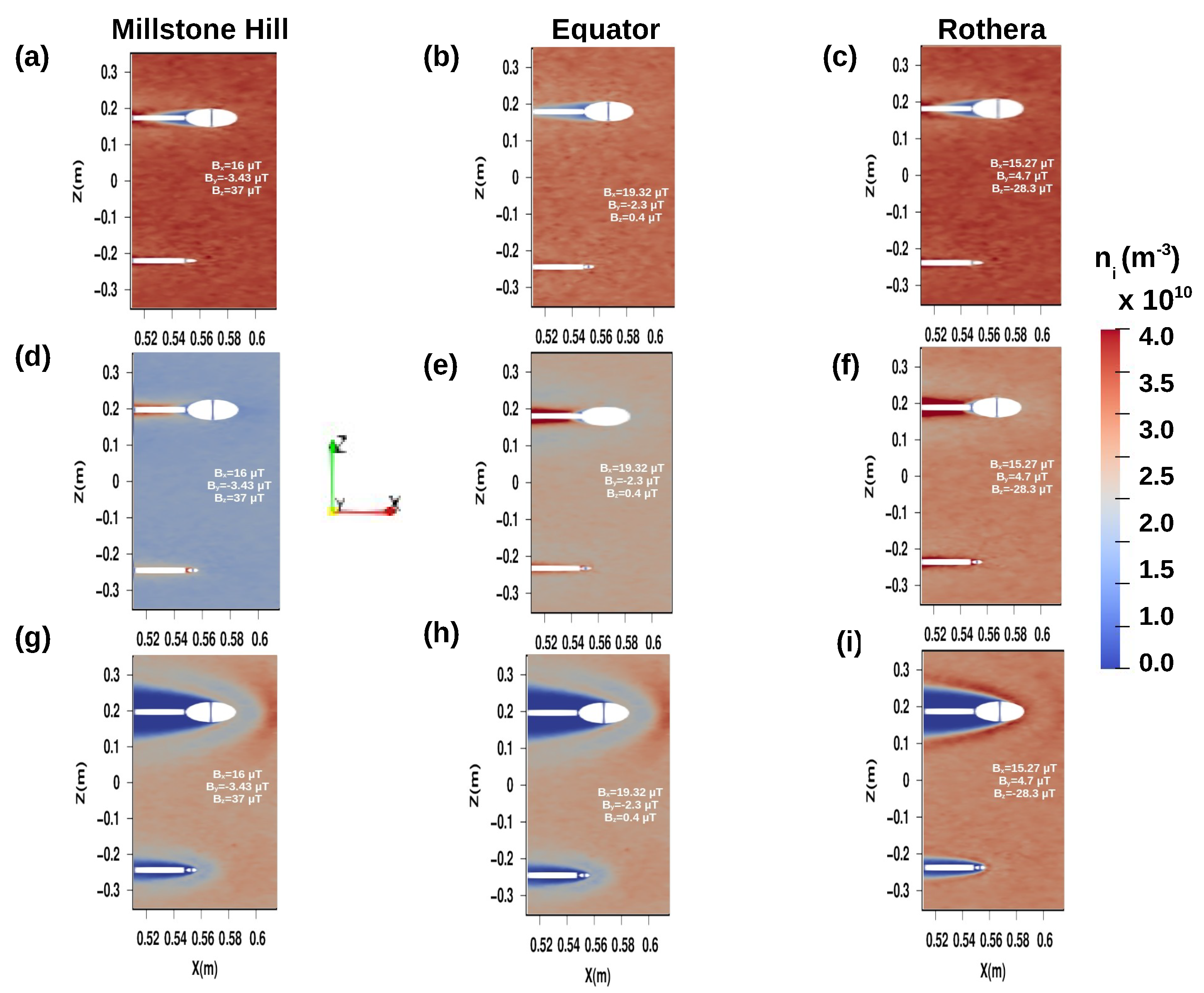
4.1. Electrostatic Sheaths and Probes Wakes
4.2. I-V Characteristics
5. Summary/Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schunk, R.W.; Nagy, A.F. Ionospheres: Physics, Plasma Physics, and Chemistry; Cambridge Atmospheric and Space Science Series; Cambridge University Press: Cambridge, UK, 2000; pp. 464–488. [Google Scholar]
- Velásquez-García, L.F.; Izquierdo-Reyes, J.; Kim, H. Review of in-space plasma diagnostics for studying the Earth’s ionosphere. J. Phys. D Appl. Phys. 2022, 55, 263001. [Google Scholar] [CrossRef]
- Chen, F. Introduction to Plasma Physics, 2nd ed.; Plenum Press: New York, NY, USA, 1984. [Google Scholar]
- Langmuir, I. Positive ion currents from the positive column of mercury arcs. Science 1923, 58, 290. [Google Scholar] [CrossRef]
- Reifman, A.; Dow, W.G. Dynamic probe measurements in the ionosphere. Phys. Rev. 1949, 76, 987. [Google Scholar] [CrossRef]
- Spencer, N.W.; Brace, L.H.; Carignan, G.R.; Taeusch, D.R.; Niemann, H.B. Electron and molecular nitrogen temperature and density in the thermosphere. J. Geophys. Res. 1965, 70, 2665–2698. [Google Scholar] [CrossRef]
- Lebreton, J.P.; Stverak, S.; Travnicek, P.; Maksimovic, M.; Klinge, D.; Merikallio, S.; Lagoutte, D.; Poirier, B.; Blelly, P.L.; Kozacek, Z.; et al. The ISL Langmuir probe experiment processing onboard DEMETER: Scientific objectives, description, and first results. Planet. Space Sci. 2006, 54, 472–486. [Google Scholar] [CrossRef]
- Samaniego, J.I.; Yeo, L.H.; Wang, X. A double hemispherical probe for characterizing and minimizing the self-the wake effects on probe measurements. J. Geophys. Res. Space Phys. 2020, 125. [Google Scholar] [CrossRef]
- Jao, C.S.; Marholm, S.; Spicher, A.; Miloch, W.J. The wake formation behind Langmuir probes in ionospheric plasmas. Adv. Space Res. 2022, 69, 856–868. [Google Scholar] [CrossRef]
- Marchand, R. Ionospheric Langmuir Probe Electron Temperature Asymmetry and Magnetic Field Connectivity. IEEE Trans. Plasma Sci. 2017, 45, 1923–1926. [Google Scholar] [CrossRef]
- Imtiaz, N.; Marchand, R.; Rizvi, H. Effect of magnetic connectivity on CubeSat needle probe measurement. Astrophys. Space Sci. 2022, 367, 49. [Google Scholar] [CrossRef]
- Olowookere, A.; Marchand, R. Density–temperature constraint from fixed-bias spherical Langmuir probes. IEEE Trans. Plasma Sci. 2021, 49, 1997. [Google Scholar] [CrossRef]
- Séran, S.; Berthelier, J.J.; Saouri, F.Z.; Lebreton, J.P. The spherical segmented Langmuir probe in a flowing thermal plasma: Numerical model of the current collection. Ann. Geophys. 2005, 23, 1723–1733. [Google Scholar] [CrossRef]
- Imtiaz, N.; Marchand, R.; Lebreton, J.P. Modeling of current characteristics of segmented Langmuir probe on DEMETER. Phys. Plasmas 2013, 20, 052903. [Google Scholar] [CrossRef]
- Laframboise, J.G. Theory of Spherical and Cylindrical Langmuir Probes in a Collisionless, Maxwellian Plasma at Rest. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1966. [Google Scholar]
- Imtiaz, N.; Marchand, R. Particle-in-cell modeling of dual segmented Langmuir probe on Proba2. Astrophys. Space Sci. 2015, 360, 15. [Google Scholar] [CrossRef]
- Olowookere, A.; Marchand, R. A new technique to infer plasma density, flow velocity, and satellite potential from ion currents collected by a segmented Langmuir probe. IEEE Trans. Plasma Sci. 2022, 50, 3774. [Google Scholar] [CrossRef]
- Hoegy, W.R.; Brace, L.H. Use of Langmuir probes in non-Maxwellian space plasmas. Rev. Sci. Instrum. 1999, 70, 3015. [Google Scholar] [CrossRef]
- Darian, D.; Marholm, S.; Mortensen, M.; Miloch, W.J. Theory and simulations of spherical and cylindrical Langmuir probes in non-Maxwellian plasmas. Plasma Phys. Control. Fusion 2019, 61, 085025. [Google Scholar] [CrossRef]
- Resendiz Lira, P.A.; Marchand, R. Simulation inference of plasma parameters from Langmuir probe measurements. Earth Space Sci. 2021, 8, 795. [Google Scholar] [CrossRef]
- Marchand, R.; Shahsavani, S.; Sanchez-Arriaga, G. Beyond analytic approximations with machine learning inference of plasma parameters and confidence intervals. J. Plasma Phys. 2023, 89, 905890111. [Google Scholar] [CrossRef]
- Brask, S.M.; Marholm, S.; Di Mare, F.; Adhikari, S.; Spicher, A.; Takahashi, T.; Miloch, W.J. Electron–neutral collisions effects on Langmuir probe in the lower E-region ionosphere. Phys. Plasmas 2022, 29, 033511. [Google Scholar] [CrossRef]
- Akasofu, S.I.; Kang, S. Physics of Auroral Arc Formation; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 1981; Volume 25. [Google Scholar]
- Wagner, J.S.; Sydora, R.D.; Tajima, T.; Hallinan, T.; Lee, L.C.; Akasofu, S.I. Small-scale Auroral Arc Deformations. J. Geophys. Res. 2021, 126, e2021JA029999. [Google Scholar] [CrossRef]
- Yan, R.; Guan, Y.; Shen, X.; Huang, J.; Zhang, X.; Liu, C.; Liu, D. The Langmuir probe onboard CSES: Data inversion analysis method and first results. Earth Planet. Phys. 2018, 2, 479. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, C.; Zhang, A.; Piero, D.; Sun, Y. The Technology of Space Plasma In-Situ Measurement on the China Seismo-Electromagnetic Satellite. Sci. China Technol. Sci. 2019, 62, 829–838. [Google Scholar] [CrossRef]
- Guan, Y.b.; Wang, S.j.; Liu, C.; Feng, Y.b. The design of the Langmuir probe onboard a seismo-electromagnetic satellite. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2011: Space Exploration Technologies and Applications, Beijing, China, 24–26 May 2011; Volume 8196, p. 819624. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, C.; Zhang, A.; Zheng, X.; Sun, Y. The Ionosphere Measurement Technology of Langmuir Probe on China Seismo-Electromagnetic Satellite. Acta Phys. Sin. 2016, 65, 189401. (In Chinese) [Google Scholar] [CrossRef]
- Marchand, R. PTetra, a tool to simulate low orbit satellite–plasma interaction. IEEE Trans. Plasma Sci. 2012, 40, 217–229. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. GMSH: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309. [Google Scholar] [CrossRef]
- Whipple, E.C. Potentials of surfaces in space. Rep. Prog. Phys. 1981, 44, 1197–1250. [Google Scholar] [CrossRef]
- Kjølerbakken, K.M.; Miloch, W.J.; Røed, K. Sheath formation time for spherical Langmuir probes. J. Plasma Phys. 2023, 89, 905890102. [Google Scholar] [CrossRef]
- Lafleur, T. Charged aerodynamics: Ionospheric plasma drag on objects in low-earth orbit. Acta Astronaut. 2023, 212, 370. [Google Scholar] [CrossRef]
- Brask, S.M.; Mishra, R.; Holen, G.; Miyake, Y.; Usui, H.; Miloch, W.J. Spherical Langmuir probes in magnetized plasma. A model based on particle-in-cell simulations. Phys. Plasmas 2024, 31, 023506. [Google Scholar] [CrossRef]
- Okada, Y.O.; Matsumoto, M. Computer experiments of spacecraft-plasma interactions in a dilute and high-βe plasma with a fast plasma flow. J. Geophys. Res. 1995, 100, 21549–21559. [Google Scholar] [CrossRef]
- Miloch, W.J. Numerical simulations of dust charging and the wakefield effects. J. Plasma Phys. 2014, 80, 795. [Google Scholar] [CrossRef]
- Marholm, S.; Marchand, R. Finite-length effects on cylindrical Langmuir probes. Phys. Rev. Res. 2020, 2, 023016. [Google Scholar] [CrossRef]
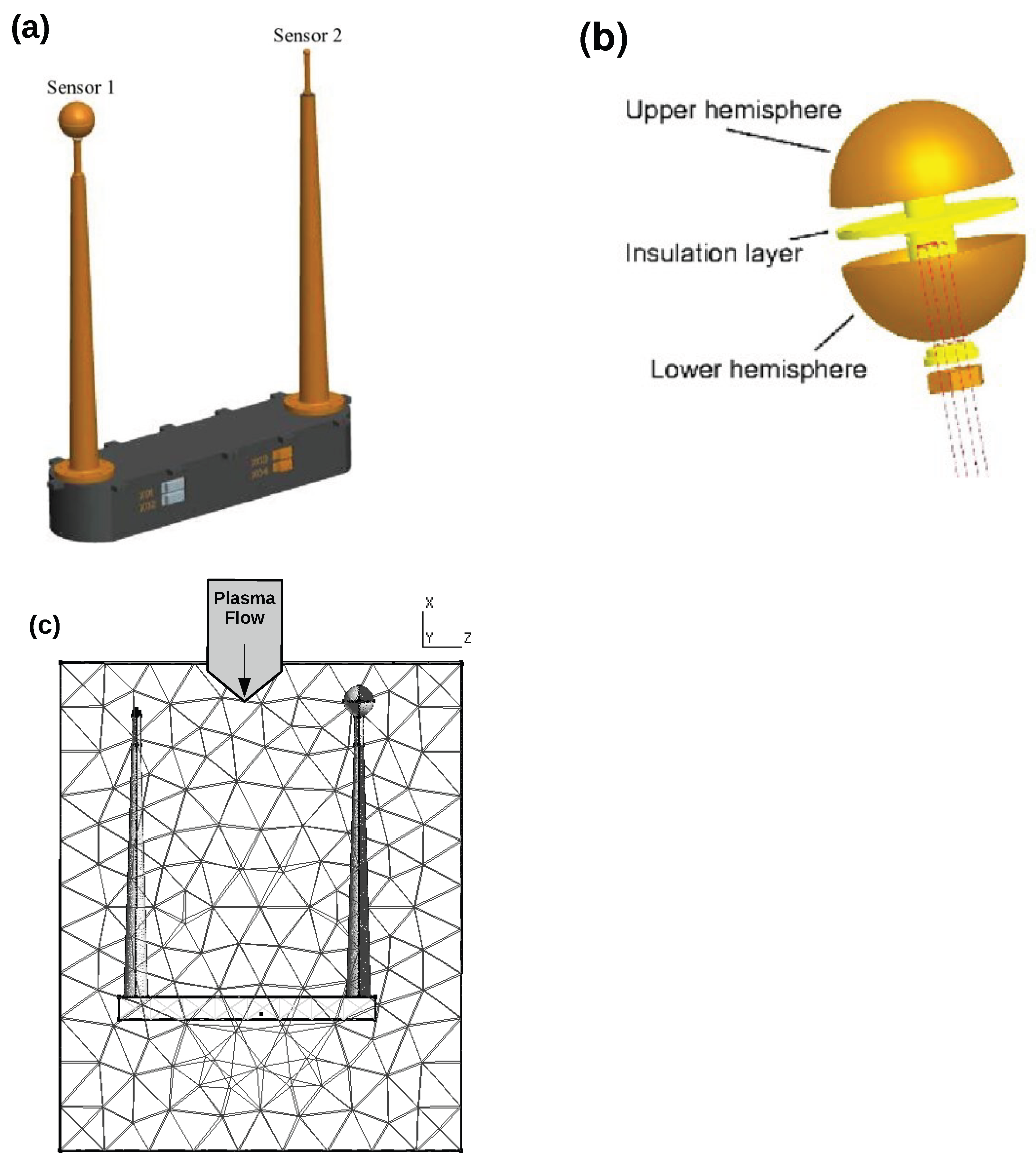


| Structure | Size |
|---|---|
| Diameter of Sensor 1 | |
| Diameter of Sensor 2 | |
| Separation between Sensor 1 and Sensor 2 | |
| Length of extension bars | |
| Material | TiN |
| Site | (T) | ( ) | (K) | (K) | Ion Species | Debye Length (cm) |
|---|---|---|---|---|---|---|
| Millstone Hill | (16, –3.43, 37) | 3133 | 1277 | , | 2.6 | |
| Equator | (19.32, –2.3, 0.4) | 1277 | 1277 | – | 1.6 | |
| Rothera | (15.27, 4.7, –28.3) | 2436 | 1392 | – | 2.3 |
| Physical Quantity | Millstone Hill | The Equator | Rothera |
|---|---|---|---|
| Electric field (V/m) | (0, −0.28, −0.03) | (0, −0.003, −0.02) | (0, 0.22, 0.034) |
| Floating potential (V) | −0.94 | −0.40 | −0.72 |
| Drift velocity (km/s) | 7.6 | 7.6 | 7.6 |
| Electron thermal speed (km/s) | 308 | 206 | 272 |
| Electron gyro-frequency (MHz) | 7.11 | 3.42 | 5.72 |
| Electron gyro-radius (m) | 0.04 | 0.06 | 0.05 |
| Thermal speed (km/s) | 4.59 | 4.59 | 4.56 |
| Thermal speed (km/s) | 1.14 | 1.14 | 1.20 |
| Gyro-frequency (kHz) | 3.88 | 1.95 | 3.11 |
| Gyro-frequency (kHz) | 0.24 | 0.12 | 0.20 |
| Gyro-radius (m) | 1.16 | 2.45 | 1.54 |
| Gyro-radius (m) | 4.80 | 10.3 | 6.20 |
| Mach number | 1.70 | 1.60 | 1.58 |
| Mach number | 6.60 | 6.30 | 6.30 |
| Site | m | r | Correlation Strength | ||
|---|---|---|---|---|---|
| Millstone Hill | 2.6 cm | 0.96 (Thick) | 5.45 | 0.58 | lower positive |
| Equator | 1.6 cm | 1.56 (Thin) | 5.99 | 0.65 | moderate-to-strong positive |
| Rothera | 2.3 cm | 1.09 (Intermediate) | 4.66 | 0.62 | moderate-to-strong positive |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imtiaz, N.; Rehman, S.U.; Chao, L.; Yan, R.; Marchand, R. PIC Modeling of Ionospheric Plasma Diagnostics by Hemispherical Probes: Study of the LAP-CSES at Magnetic Conjugates. Plasma 2025, 8, 39. https://doi.org/10.3390/plasma8040039
Imtiaz N, Rehman SU, Chao L, Yan R, Marchand R. PIC Modeling of Ionospheric Plasma Diagnostics by Hemispherical Probes: Study of the LAP-CSES at Magnetic Conjugates. Plasma. 2025; 8(4):39. https://doi.org/10.3390/plasma8040039
Chicago/Turabian StyleImtiaz, Nadia, Saeed Ur Rehman, Liu Chao, Rui Yan, and Richard Marchand. 2025. "PIC Modeling of Ionospheric Plasma Diagnostics by Hemispherical Probes: Study of the LAP-CSES at Magnetic Conjugates" Plasma 8, no. 4: 39. https://doi.org/10.3390/plasma8040039
APA StyleImtiaz, N., Rehman, S. U., Chao, L., Yan, R., & Marchand, R. (2025). PIC Modeling of Ionospheric Plasma Diagnostics by Hemispherical Probes: Study of the LAP-CSES at Magnetic Conjugates. Plasma, 8(4), 39. https://doi.org/10.3390/plasma8040039







