Abstract
As it turns out, both isotope scaling and density limits are phenomena closely linked to fluid closure. The necessity to include ion viscosity arises for both phenomena. Thus, we have added ion viscosity to our model. The experimental isotope scaling has been successfully recovered in our fluid model through parameter scans. Although ion viscosity typically exerts a small effect, the density limit is manifested by increasing the density by approximately tenfold from the typical experimental density. In our case, this increase originates from the density in the Cyclone base case. Notably, these phenomena would not manifest with a gyro-Landau fluid closure. The isotope scaling is nullified by the addition of a gyro-Landau term, while the density limit results from permitting ion viscosity to become comparable to the gyro-Landau term. The mechanism of zonal flows, demonstrated analytically for the Dimits upshift, yields insights into the isotope scaling observed in experiments. In our approach, ion viscosity is introduced in place of the Landau fluid resonances found in some fluid models. This implies that the mechanism of isotope scaling operates at the level of fluid closure in connection with the generation of zonal flows. The strength of zonal flows in our model has been verified, particularly in connection with the successful simulation of the nonlinear Dimits shift. Consequently, a role is played by our approach in the temperature perturbation part of the Reynolds stress.
1. Introduction
The general problem of tokamak transport has been one of the main issues in fusion research for a long time [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. However, the specific mechanism behind isotope scaling remains undetermined [1,2,3,4]. Similarly, the underlying reason for the density limit has not been clearly understood [11,36,51]. Several other papers [38,39,40,41,42,43] address the density limit. It is commonly associated with increased turbulent transport and collisions, which is also true in our transport model. In some cases (Gates et al. Ref. [40]), the coupling to magnetic perturbations is emphasized. Of course, magnetic field perturbations increase with the turbulence level in our model as well, but we do not see a causal relationship here. However, our model for the L–H transition [28], without ion viscosity, is electromagnetic and agrees very well with the model in Ref. [31]. The density limit in Ref. [31] is associated with collisions (as in our model) and was also discussed by Giacomin et al. Since we obtain the density limit by including ion viscosity, we are consistent with Ref. [31]. In the paper by Giacomin et al., it is also mentioned that the pressure length scale can become significant across the minor radius, as seen in the case of MARFEs (multifaceted asymmetric radiation from the edge).
In this study, we connect both isotopic scaling and density limit phenomena to fluid closure, a mechanism that must also be present in kinetic formulations [10], though it is not always prominently emphasized. In tokamak plasma modeling, fluid closure is a necessary step to simplify the system of equations describing plasma dynamics. “Fluid closure” refers to the fact that fluid models use a finite number of moments (e.g., density, temperature), whereas kinetic theory includes infinitely high moments. Different fluid models handle this limitation using various approaches. One aspect that appears to be important is the effects of classical dissipation [1,3]. As shown numerically in Ref. [6] and analytically in Ref. [7], using the reductive perturbation method [8], the Landau fluid resonance [14] changes the nonlinear Dimits upshift [10] strongly. The Dimits shift refers to a phenomenon observed in plasma turbulence simulations, particularly in the context of ion-temperature-gradient (ITG) driven turbulence. It describes a delay or shift in the onset of strong turbulent transport to higher values of the normalized temperature gradient than predicted by linear instability analysis. Kinetic Cyclone simulations demonstrated stability up to about 50% above the linear threshold, a result attributed to nonlinearly generated zonal flows [6,7]. This upward shift in the threshold has been termed the Dimits upshift. Our fluid model results, in agreement with the kinetic Dimits shift [6,7], show that we have the correct strength of zonal flows. This means that the inverse turbulent cascade [16] is damped out so that there is no pileup of waves at the system size (geometrical size). This also verifies the choice of absorbing boundary for long wavelengths, as used in Ref. [17]. It is intriguing to compare our findings with the resistive drift wave fluid model presented in [9]. In particular, the work in Ref. [18] yielded a kernel transport coefficient that has the same form as the one derived in our study. By ‘kernel’, we refer to a simplified approach in which only the diagonal elements of the transport matrix are retained. These diagonal elements describe direct transport, such as particle flux driven by a density gradient or heat flux driven by a temperature gradient. Here, we refer to the transport matrix for all transport channels related to moments with sources in the experiment, such as density, momentum, temperature, and others. The term ‘moments’ refers to quantities derived from the distribution function of particles in phase space, as used in kinetic theory. In plasma models, the distribution function describes the behavior of particles (such as ions or electrons), and taking ‘moments’ of this function provides macroscopic quantities like density, momentum, energy, and higher-order quantities like heat flux.
The Cyclone Base Case (CBC) referred to above is a widely used benchmark for studying plasma turbulence and transport in tokamaks. It was developed to facilitate comparisons between different simulation codes and their ability to model turbulent transport in magnetically confined plasmas. The CBC provides a standardized test case for simulating ITG-driven turbulence, which is a key driver of transport in tokamak plasmas. Our current approach connects to the Cyclone project conducted in the late 1990s, as published in [10]. The primary motivation for this work was the significant discrepancies in ITER predictions (based on the old ITER design) produced by various fluid models. In the Cyclone project, the ion thermal conductivity for different fluid models was compared to fully nonlinear kinetic models as a function of the temperature gradient. Simulations were conducted over relatively short time scales, up to the point where turbulence saturation occurred. Notably, the differences in ITER predictions produced by the fluid models mirrored their performance in actual experiments from that era, such as DIII-D shot 89499.
In this work, both analytical and numerical methods are used. However, ion viscosity is typically at least an order of magnitude smaller than the Landau fluid resonance [14] and can thus be incorporated into our general approach to fluid closure. As it turns out, usually edge data give a stronger isotope effect (about 20% difference in transport between hydrogen and tritium). A lower temperature at the edge leads to an increase in ion viscosity. Thus, we also have an interest in the L–H transition [28,31,32,33] which is also due to zonal flows. Actually, our fluid model did very well in comparison with local transport simulations as made in Ref. [31]. Our model, as shown in [28], demonstrated good agreement with [31], which, in turn, showed reasonable agreement with Alcator C-Mod results [32]. It was observed that the L–H power threshold increases with ion temperature at the separatrix and with the magnetic field, as also seen in Alcator C-Mod. These findings are influenced by the generation of zonal flows, which are dependent on the fluid closure used. Although our simulations were originally set up for EAST [28], we were able to investigate the same parameter regimes used in Refs. [31,32] for Alcator C-Mod. This allowed us to construct a stability diagram in the magnetohydrodynamic (MHD) parameter and a corresponding diamagnetic resistive parameter , showing good agreement. This type of diagram was suggested in [31]. Our analysis indicates that higher density contributes to instability. As found in Refs. [18,29], a quasilinear approach is quite adequate for studying drift wave turbulence, and in Ref. [29], a fluid approach was found to be accurate. Our scaling of temperature at the separatrix with the magnetic field and the power threshold were also consistent with those reported in Ref. [33]. Thus, we have secured the validity of our simulation of the L–H transition [28,44]. All our new findings are related to the excitation of zonal flows and the associated fluid closure aspects. This connects to our previous work on fast particles [12], where resonance broadening was shown to be important for both fast particle instabilities and drift waves, eliminating wave–particle resonances in the latter case. The foundation of this research lies in our drift wave fluid model [17] (usually referred to as the Weiland model), which still serves as a valid limit of the current model. The motivation behind implementing fluid closure was to incorporate all moments with sources observed in the experiment.
The broadening here refers to the loss of precise wave–particle resonance due to nonlinear frequency shifts induced by turbulence, which weakens or averages out dissipative mechanisms like Landau damping and magnetic drift resonances. The first reference to the use of this term appears in [13], p. 154. Resonance broadening is associated with nonlinear friction in the Fokker–Planck equation for turbulent collisions. It results in nonlinear frequency shifts that move (broaden) the resonance, causing the phase velocity of waves to shift out of resonance with particles. If no source exists in velocity space to counterbalance this effect (as in the case of fast particle instabilities), the resonance can vanish entirely. The model by Mattor and Parker [26], extended by Holod et al. [50], corresponds to the coherent limit of resonance broadening. In this context, nonlinear frequency shifts also cause waves to move out of resonance with particles.
This transport model still has the same normalization as in Ref. [17]. It has never been fitted to any other theoretical model or experiment, yet it consistently yields good agreement with conventional (JET, EAST, KSTAR, and DIII-D) and low aspect ratio tokamak (NSTX) plasma profiles [45,46,47].
As is clear from this introduction, zonal flows play an important role in tokamak transport. We here mention three more papers in this field [20,21,22]. However, none of these include resonance broadening [23,24], which is now the main argument for our fluid closure [12]. Contrary to flattening, which means that particles move out of resonance with waves, resonance broadening means that waves move out of resonance with particles.
The manuscript is structured as follows: Section 2 discusses the inclusion of all moments with sources in the experimental closure approach and the impact of resonance broadening on the fluid model. It concludes that resonance broadening has a stabilizing influence on fast particle instabilities and validates the reactive closure for drift waves, allowing the use of Braginskii’s highest moment for successful modeling. Section 3 outlines the original motivation behind a fluid closure, driven by the aim to encompass all moments with sources and justified by a nonlinear Fokker–Planck equation. It further discusses the implications of the Fokker–Planck equation in understanding turbulence and resonance broadening effects in wave–particle interactions. In Section 4, we explore the incorporation of ion viscosity, emphasize the pivotal role of zonal flows generated by Reynolds stress—specifically, in the form of off-diagonal poloidal momentum flux—and stress the critical consideration of averaged resonances for accurate predictions. Section 5 highlights the relevance of edge data for understanding the H-mode barrier, presenting ion thermal diffusivity against normalized temperature gradients. The observed isotope mass effect leads to a confinement time scaling in agreement with experimental results, along with a global scaling involving heating power. Section 6 explores the strong dependence on system size and the density limit, highlighting the impact of gyro-Landau resonances on rotation dynamics. The interplay with convection is elucidated, emphasizing the need for strong zonal flows to avoid wave pileup and reflections, particularly in finite radial systems. The discussion encompasses stabilizing nonlinearity, showcasing its critical role in preventing an inverse cascade towards longer wavelengths. The importance of such considerations is underscored in reactive systems, as demonstrated in previous works. Section 7 delves into successful applications of the transport model, focusing on isotope scaling and the density limit while acknowledging challenges in the latter. The discussion underlines the importance of ion temperature perturbation resonance in turbulence-rotation balance and tokamak transport dynamics.
2. Fluid Model
The original approach to our fluid closure was to include all moments with sources in the experiment [17], the reason being that moments without sources would die out on the transport time scale. An important mechanism turned out to be resonance broadening [19]. This was applied to our model, with the conclusion that we would obtain a reactive closure with a diagonal part of the same type as in our fluid model [23]. We found that turbulent collisions have the same effect on a fluid description as classical collisions. A generalization to include fast particles verified both the stabilizing trend of resonance broadening on fast particle instabilities [12] and our previous result that our closure is valid for drift waves. Since resonance broadening only shows that we have a reactive closure, we again employed our original rule for the exact point of closure [52]. This closure means that we can take the highest moment at the Braginskii (refers to the collisionless cross-field, or Righi–Leduc ion heat flux, as presented in most of our papers, particularly in [34], Equation (6.137)), and this has been extremely successful in previous studies in cases where the ion viscosity could be ignored. The highest moment typically incorporated in Braginskii’s model is the third moment, which accounts for heat flux. This is particularly significant in collisional plasmas, where higher-order effects beyond simple diffusion become important in describing energy transport. By incorporating the macroscopic quantities (density, momentum, energy, and heat flux), we can more accurately capture the essential transport processes in the plasma. Resonance broadening means that nonlinear frequency shifts change the phase velocity of waves in such a way that waves move out of resonance with particles when we average over turbulent fluctuations. Thus, dissipative wave–particle resonances like Landau damping and magnetic drift resonances are averaged out. Of course, this will be true for all processes, so we can also use the Braginskii derivation for ion viscosity ([13] Equation (1.8)).
3. Formulation
The original motivation for our fluid closure was to include all moments with sources in the experiment. The elimination of higher moments was then motivated by a nonlinear Fokker–Planck equation. The Fokker–Planck equation for turbulent collisions [12,23] can be written as
The index j represents the different wave modes that contribute to the total coefficients () and (), with each mode contributing according to its squared amplitude (). We are here interested in drift waves, so we take . In the given context, W represents the transition probability between states X and over the time interval . The terms , , , and denote the nonlinear turbulent friction, classical friction term due to ion-ion collisions, nonlinear diffusion coefficient in velocity space, and electrostatic potential, respectively. The Fokker–Planck equation leads to the mean square of velocity deviation (velocity dispersion) developing as [23]
This quantity measures the average deviation of particle velocities from their mean due to turbulent collisions over time. It helps in understanding the intensity and impact of turbulence on plasma behavior and illustrates how particles spread over time. A simplified derivation of Equation (3) was given in Ref. [34], Chapter 9, where the Chandrasekhar solution [53] of Equation (1) without viscosity was used as a weight function. Now, the classical collision term just gives the usual classical viscosity, so we will recover Equation (4) since Equation (3) means that we have a reactive closure as discussed in Section 4.
The Fokker–Planck equation can also be applied to fast particles if we add a fast particle source, and then we can recover equations for both fast particles and drift waves within appropriate limits [12]. In both cases, resonance broadening [19,23] reduces the wave–particle interaction. As it turns out, the resonance broadening is due to nonlinear frequency shifts, which would also remain in the coherent limit [26,27].
A solution for coherent explosive instability with a nonlinear frequency shift (Figure 1) was shown already in our book [24]. Similar to our recent work [48], we can explore the coherent three-wave interaction regime as also studied in Refs. [13,54] for drift waves [26,27].
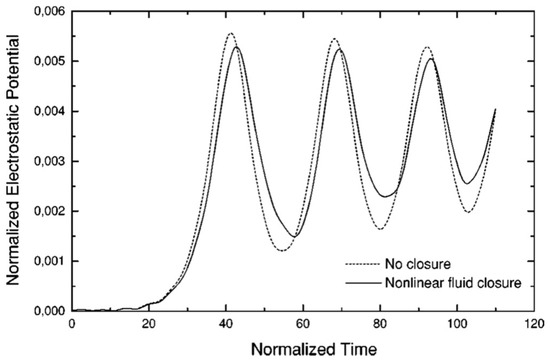
Figure 1.
This figure exhibits similarity to the suppression of explosive instability by a nonlinear frequency shift [27]. Reproduced from [I. Holod, J. Weiland, and A. Zagorodny Physics of Plasmas 9, 1217 (2002)], with the permission of AIP Publishing.
The coherent, unstable three-wave system is stabilized by nonlinear frequency shifts. These work as if the sign of the wave energy is shifted, thus we have alternatively Landau growth and damping. This is the way the effect of waves-particles [23] interaction is averaged out, leading to the absence of energy transfer between waves and particles, as shown by Equation (3) in the turbulent case.
In summary, this section motivates the use of a fluid closure approach, which utilizes a nonlinear Fokker–Planck equation to include all experimental moments and eliminate higher moments. The equation accounts for nonlinear turbulent friction, classical collision friction, and nonlinear diffusion, and can be extended to fast particles and drift waves, leading to resonance broadening and balanced wave–particle interactions. This approach provides a comprehensive framework for understanding turbulent collision dynamics and wave–particle interactions. By incorporating nonlinear effects, it offers a more accurate and robust description of plasma behavior, enabling better predictions and insights in various plasma physics applications.
4. Exploring Ion Viscosity Effects in Drift Wave Turbulence
In order to study isotope scaling, we add ion viscosity to our usual derivation.
As discussed after Equation (3), the model can use ion viscosity from Braginskii’s equations directly. Turbulent viscosity behaves like nonlinear friction (see Ref. [23]) and can be included without changing the model’s final results, where ion viscosity
where A is the isotope mass number and is the electron–electron collision frequency. Our viscosity, however, has been taken from Ref. [13], Equation (1.8). This gives the scaling for the viscosity. Thus, we see that viscosity is smaller for heavier isotopes (favorable scaling) and larger for higher density (unfavorable scaling). Equation (5) leads to the ion temperature perturbation
Note, that the viscosity term enters at the fluid resonance in the ion energy equation, the most sensitive point in our fluid modeling. This sensitivity is the main improvement in our model. Here, is the ion density, is the ion flow velocity, is the diamagnetic ion heat flow, is the electron (ion) temperature, e is the electron charge, is the ion mass, is the electron mass, is the permittivity of free space, , where is the real frequency and is the mode’s growth rate, is the magnetic drift frequency, is the electron diamagnetic drift frequency, and is the ratio of the ion temperature gradient to ion density gradient. It is important to recall that in our usual reactive limit, the linear threshold of Ion Temperature Gradient (ITG) modes appears exactly at the resonance in Equation (6). As it turns out, zonal flows play important roles in both Dimits shifts, the L–H transition, isotope scaling, and finally the density limit. Zonal flows are generated by the Reynolds stress.
We note that Equations (4)–(6) are a generalization of our fluid closure, where the principle is to omit dissipative kinetic resonances, keeping only moments with sources in the experiment. This can be motivated by resonance broadening, as explained in Ref. [12]. Resonance broadening and profile flattening are parallel phenomena that both remove wave particle resonances, although resonance broadening is strongly nonlinear. If you have a particle source that injects particles into the resonant region in phase space, it can balance the flattening so that the resonance survives. The same thing can happen with resonance broadening. Here, we have the source of fast particles, which can balance the resonance broadening so that the resonance remains. In this case, it is the question of waves moving out of resonance with particles. However, as we clarify in our paper on fast particles [12], drift waves lack a source because their frequency is approximately two orders of magnitude lower than the source’s, leading to the averaging of the source. Then, only resonance broadening remains, and the wave particle resonance is cancelled. We have shown this in Ref. [23], and our paper on fast particles [12] just uses this.
In the expression, represents the off-diagonal poloidal momentum flux, denotes the radial component of the drift, signifies the poloidal flow velocity, is defined as where represents the sound speed, stands for the poloidal wavenumber, is defined as , and normalized ion pressure, and is calculated as . In Equation (7), it is noteworthy to observe the dependence on ion temperature through ion pressure (). This dependence is highly sensitive to the fluid closure, as indicated by Equation (6). Here, the last part, the convection of the diamagnetic flow, is often ignored but is, in fact, the most important part. In the Equation (7), “c.c.” denotes the complex conjugate. This means that the complex conjugate of the preceding expression must be added to ensure the result is real, as physical quantities such as fluxes are required to be real-valued.
In the absence of viscosity, marginal stability for the reactive system enters at the resonance in Equation (6). Because of the resonance, we obtain a particularly strong drive of rotation here (see Figure 2). We have used the data from the Cyclone project, specifically: , R = 2.5 m, T = 2.0 keV, a = 0.63 m, q = 1.4, s = 0.78, B = 2.0 T. The data are considered at half the radius. Although ion viscosity is usually small, it can still be of importance here, and it turns out to generate the isotope scaling. We recall from Ref. [7] that the resonance in Equation (6) is completely smeared out by gyro-Landau fluid resonances, giving a significantly smaller rotation. We note that gyro-Landau resonances are averaged out by resonance broadening and are, without this averaging, typically an order of magnitude larger than ion viscosity but added in the same place. We may here add that nonlinear flattening means that particles move out of resonance with waves, while resonance broadening means that waves are moving out of resonance with particles. Thus, there is no way that we could obtain the isotope scaling if we kept the unaveraged gyro-Landau resonances.
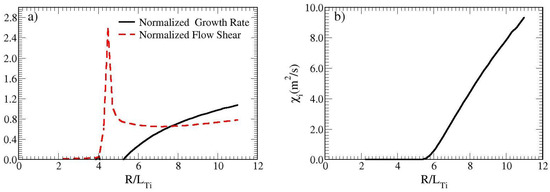
Figure 2.
(a) Normalized growth rate and normalized flow shear (b) transport (ion thermal diffusivity) are derived for Cyclone parameters (, R = 2.5 m, T = 2.0 keV, a = 0.63 m, q = 1.4, s = 0.78, B = 2.0 T) based on the findings in Ref. [7], incorporating ion viscosity corresponding to hydrogen in Equation (6). The data is considered at half the radius. The strong flow shear at marginal stability arises from the fluid resonance described in Equation (6). Waves with wavelengths approaching the system size will inevitably reach marginal stability at some point, leading to strong damping. Consequently, transport is heavily influenced by the fluid closure. The reactive closure results from the detuning of wave–particle resonances due to resonance broadening or nonlinear frequency shifts.
In summary, this section examines the impact of ion viscosity on drift wave turbulence and isotope scaling, utilizing Braginskii’s formulation for ion viscosity and noting that turbulent viscosity behaves similarly to nonlinear friction. The derived equations illustrate the effect of ion viscosity on ion temperature perturbations and validate the fluid closure approach. The study highlights the importance of zonal flows and resonance broadening in achieving isotope scaling and maintaining plasma stability.
5. Isotope Effects on Transport and Confinement: Edge Considerations and Predictive Comparison
As pointed out above, edge data are relevant since the transport flux has to pass the edge. Since the H-mode barrier depends on the same type of zonal flows as the Dimits shift, ion thermal diffusivity as a function of the normalized temperature gradient is shown for the parameters relevant to the plasma edge in Figure 3. Figure 3 directly continues from Figure 2. We are extending the results of Ref. [7] by including ion viscosity.
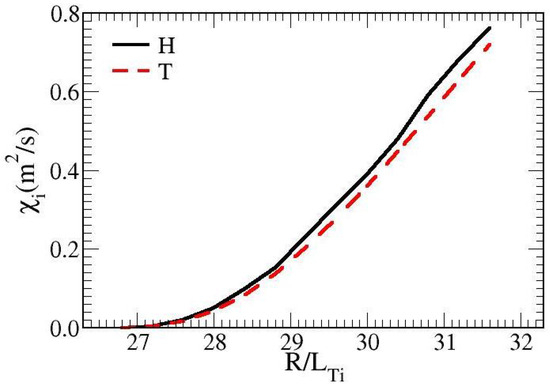
Figure 3.
Transport as a function of normalized ion temperature gradients for both hydrogen and tritium shows a decrease in transport with a higher isotope mass. These results are obtained by adding ion viscosity to the calculations conducted in Ref. [7]. The data here is considered at the edge, where sharper gradients are present.
It is known that the pedestal can be close to force balance, but the L–H transition process involves the creation of zonal flows via poloidal rotation. This allows the use of analytic results from Ref. [7] to determine transport calculations. When switching from the use of hydrogen to tritium, a 6% drop in transport is noted in typical edge data.
Using data from our local code and from Figure 3, the scaling leads to the confinement time () scaling with isotope mass (A),
This result agrees with the experimental result in Ref. [36]. We also recall our result for global scaling with heating power (P) [37] and is also largely consistent with [11]. Additionally, it is important to note the strong FLR stabilization for large gradients (see, e.g., Ref. [34], Equation 6.161).
In summary, these results may be stated as follows:
Now, using our predictive code for ITER simulations of hydrogen and tritium, we instead obtain:
This result was obtained by comparing runs with different isotopes at different temperatures assuming that scales as . The ITER simulations, focusing on ELMY H-mode discharges and employing the Weiland [17,49] and NCLASS [50] neoclassical models for predictive simulation, are shown in Figure 4. The simulations initiate with prescribed sources and an assumed L-mode profile, progressing to the temperature of the L–H transition and pedestal. We do not make any assumptions about the occurrence of an L–H transition or the specific locations of barriers to temperature [44]. We note that these calculations are rather sensitive since we are close to a pole in the fluid equations. Thus, we expect that the difference in these energy confinement scalings (c.f. Ref. [4]) can be due to impurities in the ITER simulations, where . We did not include impurities in the local code.
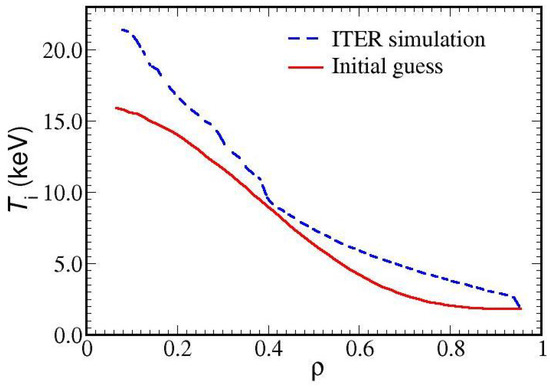
Figure 4.
The ion temperature is depicted by the full line before and after the L–H transition in a simulation of ITER, utilizing the Weiland fluid model along with the neoclassical module. This is a global simulation showing the central ion temperature: keV and the H-mode barrier.
In summary, this section examines isotope effects on transport and confinement at the plasma edge. It highlights the importance of edge data, as transport flux must pass through the edge, and shows that the H-mode barrier depends on zonal flows. Ion thermal diffusivity decreases with higher isotope mass. The L–H transition, driven by poloidal rotation, enables the use of analytic transport calculations. A switch from hydrogen to tritium results in a 6% reduction in transport, with confinement time () scaling as , consistent with experimental data. However, ITER simulations predict a different scaling of , possibly due to impurities not accounted for in local code simulations. The sensitivity of these calculations is noted, particularly near poles in the fluid equations.
6. Density Limit and System Size Dependence: Insights from Gyro-Landau Resonances and E-Cross-B Convection
We now recall from Ref. [7] that there is hardly any rotation if we include the unaveraged gyro-Landau resonances. Then, we obtain a much weaker zonal flow, which could hardly absorb the inverse turbulent cascade. Then, we obtain a pileup of waves at the system size, leading to very strong transport, which is in accordance with the density limit Equation (11). Now, we know that the gyro-Landau resonances are typically about an order of magnitude larger than the ion viscosity. However, ion viscosity will increase with density, so if we increase density by about a factor 10, we reach a density limit [38].
where is the plasma current, and a is the minor radius. Here, we are focusing on processes that may limit the density at the plasma edge, although the average density across the entire plasma volume may well exceed this limit. Our first observation is the strong dependence on the system size, meaning a strong potential dependence on perturbations with radial scale length approaching the system size. Now, the stabilization of an instability due to convection is written:
leading to
where is the radial wavenumber and is the density gradient scale length. Note, that in Equation (13), the diamagnetic drift accounts only for the density gradient. Thus, the density gradient is canceled (see, e.g., Ref. [34]). The saturation level in Equation (13) is in agreement with typical experiments and is used both by us and in other works. A very critical point is whether the nonlinearity in Equation (12) is entirely stabilizing. This is only the case if we are looking at the correlation length (corresponding to the mode number with the largest growth rate as normalized by the drift frequency) and if there are no reflections in k-space. This may be critical for the inverse cascade, leading to cascade towards longer wavelengths, i.e., towards the system size. Clearly, it is very important to take into account that we are here looking at systems with a finite radial size. To avoid obtaining a pileup in waves at the system size with reflections, we need strong zonal flows that absorb the inverse cascade. This is usually only available in reactive systems, as seen in Ref. [18] for only density transport and in Ref. [17] using our reactive fluid closure. We note that in both cases, we obtain a transport kernel of the type
In Ref. [18], we have an exact fluid closure by taking a zero-ion temperature, while in our case, we have no kinetic dissipation because of resonance broadening [7,13]. In our case Equation (12) is applied to ion temperature. In our derivation, we also included pinch terms from a full quasilinear procedure [17]. The quasilinear approach was found in Ref. [29] to be valid within a few percent in the fluid case. We now recall that if the ion density is increased by about a factor of 100, the ion viscosity in Equation (6) becomes comparable to an unnormalized gyro-Landau resonance that was, in fact, displayed in Ref. [7]. The result for the rotation was similar to in Figure 5 below, where the density was only increased by a factor of 10 above the Cyclone case. The result of the Cyclone work was an increase of up to a factor 3 in thermal conductivity for an unnormalized gyro-Landau fluid model. However, recent gyro-Landau fluid models have been normalized to the nonlinear gyrokinetic code [11].
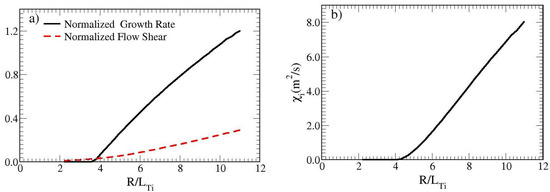
Figure 5.
(a) Normalized growth rates and normalized flow shear (b) transport (ion thermal diffusivity) illustrate similar variations as seen in Figure 2. Both the rotation and Dimits shift exhibit a decreasing trend, consistent with the observations in Ref. [7] for the gyro-Landau fluid model. This particular case corresponds to a density of . It illustrates how thermal diffusivity increases with higher density. The exact density limit depends on when zonal flows become too weak to absorb the inward inverse turbulent cascade.
Consequently, if the density is increased by approximately ten times compared to the density investigated in the Cyclone work [10], it is expected that there will be an increase in thermal transport, a decrease in flow shear, and the disappearance of the Dimits shift. The increase in transport may be associated with a weakening of the H-mode barrier and the emergence of significant turbulence structures, such as MARFEs, which are sometimes observed in experimental studies near the density limit. However, MARFEs can also exist during H-mode without necessarily causing the density limit. Due to the normally larger sizes of MHD modes compared to drift waves, it is anticipated that MHD ballooning, kinetic ballooning modes, resistive ballooning modes, and peeling modes may also be present near the edge.
This section explores the density limit and system size dependence in plasma transport, focusing on gyro-Landau resonances and convection. Including unaveraged gyro-Landau resonances results in weaker zonal flows, leading to increased transport and aligning with the density limit equation. Gyro-Landau resonances are significantly larger than ion viscosity, but ion viscosity increases with density, reaching the density limit when density is increased by about a factor of ten. Stabilization of instabilities due to convection is crucial, with saturation levels matching experimental observation [31]. Strong zonal flows are necessary to prevent wave pileup at system size, which is typically available in reactive systems. Increasing the ion density gradient significantly raises thermal transport, potentially breaking the H-mode barrier and causing substantial turbulence structures, similar to those seen in experiments at the density limit.
7. Summary
In this work, we have achieved two additional successful applications of our transport model: isotope scaling and the density limit. Regarding isotope scaling, we believe it fits perfectly [11]. However, for the density limit [38,39], the evidence is less accurate. We investigated increasing the density in our model and found that exceeding the edge density limit significantly would be required to reach the gyro-Landau limit, which gives viscosity comparable to the gyro-Landau resonance. In comparison, the Greenwald limit can be exceeded by a factor of two when pellet injection (PI) is used, but exceeding the density limit in our case would need even greater increases. We also discuss the implications of encountering MARFEs and ballooning instability in this scenario. MARFEs are very large-scale structures and can, therefore, be torn apart by zonal flows.
We recall the derivation and development of our fluid model, first established in 1988 using theory and simulations with an absorbing boundary for long wavelengths. The original model remains valid within the appropriate limit. The motivation for the absorbing boundary for long wavelengths is now supported by the damping of zonal flows. This first-principles model is not tailored to any other theoretical model or experiment. A notable extension of the model includes the incorporation of fast particles, and applying resonance broadening for fast particle modes—an aspect utilized by other research groups.
From a broader perspective, transport in tokamaks is observed to be governed by a delicate balance between turbulence and rotation. In our model, similar to any fluid model, both turbulence and rotation (resulting from turbulence) originate at the resonance in the ion temperature perturbation. This resonance defines the linear threshold of the ITG and acts as the primary source of rotation. We assert that this interplay fundamentally controls transport. Given that both our isotope scaling and density limit rely predominantly on this resonance, we consider them fundamental. While acknowledging the existence of several other mechanisms contributing to both isotope scaling and density limits, we maintain confidence in the fundamentality of our proposed mechanisms. This confidence arises from their close relation to our fluid closure, previously shown to give excellent agreement [11,31,34,37,45,46,47] with experiment and from their integral role in overall transport control, leading us to expect their dominance.
Author Contributions
J.W.: Writing—original draft (equal); Writing—review and editing (equal). T.R.: Funding acquisition (lead); Writing—original draft (equal); Writing—review and editing (equal). E.S.: Writing—review and editing (support). All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, under Award Numbers DE-SC0013977 and DE-SC0010661.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This task is carried out using our local transport code. The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
One of us (J.W.) wants to express his gratitude to the Bogoliubov Institute of Theoretical Physics, Kiev, Ukraine, for developing the nonlinear kinetic theory on which our main derivations are based. The authors are grateful to HG Gustavsson for assistance with computation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Conner, J.W.; Wilson, H.R. Survey of theories of anomalous transport. Plasma Phys. Control. Fusion 1994, 36, 719. [Google Scholar] [CrossRef]
- Liewer, P.C. Measurements of microturbulence in tokamaks and comparisons with theories of turbulence and anomalous transport. Nucl. Fusion 1985, 25, 543. [Google Scholar] [CrossRef]
- Itoh, S.I.; Itoh, K. Hydrogen isotope effect on the Dimits shift. Nucl. Fusion 2016, 56, 106028. [Google Scholar] [CrossRef]
- Urano, H.; Takizuka, T.; Kikuchi, M.; Nakano, T.; Hayashi, N.; Oyama, N.; Kamada, Y. Publisher’s Note: Small ion-temperature-gradient scale length and reduced heat diffusivity at large hydrogen isotope mass in conventional H-mode plasmas [Phys. Rev. Lett. 109, 125001 (2012)]. Phys. Rev. Lett. 2012, 109, 149901. [Google Scholar] [CrossRef]
- Rosenbluth, M.N.; Hinton, F.L. Poloidal Flow Driven by Ion-Temperature-Gradient Turbulence in Tokamaks. Phys. Rev. Lett. 1998, 80, 724–727. [Google Scholar] [CrossRef]
- Wang, G.Q.; Ma, J.; Weiland, J. Zonal flows near marginal stability in drift wave transport. Phys. Scr. 2015, 90, 065604. [Google Scholar] [CrossRef]
- Weiland, J.; Zagorodny, A. On the normalization of transport from ITG Modes. Phys. Plasmas 2016, 23, 102307. [Google Scholar] [CrossRef]
- Nozaki, K.; Taniuti, T. Plasma Flow and a Soliton in a Theta Pinch. J. Phys. Soc. Jpn. 1979, 46, 970–974. [Google Scholar] [CrossRef]
- Wakatani, M.; Hasegawa, A. A collisional drift wave description of plasma edge turbulence. Phys. Fluids 1984, 27, 611–618. [Google Scholar] [CrossRef]
- Dimits, A.M.; Bateman, G.; Beer, M.A.; Cohen, B.I.; Dorland, W.; Hammett, G.W.; Kim, C.; Kinsey, J.E.; Kotschenreuther, M.; Kritz, A.H.; et al. Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 2000, 7, 969–983. [Google Scholar] [CrossRef]
- Doyle, E.; Houlberg, W.; Kamada, Y.; Mukhovatov, V.; Osborne, T.; Polevoi, A.; Bateman, G.; Connor, J.; Cordey, J.; Fujita, T.; et al. Chapter 2: Plasma confinement and transport. Nucl. Fusion 2007, 47, S18. [Google Scholar] [CrossRef]
- Weiland, J.; Rafiq, T.; Schuster, E. Fast particles in drift wave turbulence. Phys. Plasmas 2023, 30, 042517. [Google Scholar] [CrossRef]
- Hasegawa, A. Plasma Instabilities and Nonlinear Effects; Springer Series on Physics Chemistry Space; Springer: New York, NY, USA, 1975; Volume 8. [Google Scholar]
- Waltz, R.; Dominguez, R.; Hammett, G. Gyro-Landau fluid models for toroidal geometry. Phys. Fluids B Plasma Phys. 1992, 4, 3138–3151. [Google Scholar] [CrossRef]
- Waltz, R.E.; Staebler, G.M.; Dorland, W.; Hammett, G.W.; Kotschenreuther, M.; Konings, J.A. A gyro-Landau-fluid transport model. Phys. Plasmas 1997, 4, 2482–2496. [Google Scholar] [CrossRef]
- Hasegawa, A.; Mima, K. Pseudo-three-dimensional turbulence in magnetized nonuniform plasma. Phys. Fluids 1978, 21, 87–92. [Google Scholar] [CrossRef]
- Weiland, J.; Nordman, H. Transport due to fully toroidal drift waves. Theory of Fusion Plasmas. In Proceedings of the Varenna-Lausanne Workshop, Chexbres, Switzerland, 3–7 October 1988; p. 451. [Google Scholar]
- Connor, J.W.; Pogutse, O.P. On the relationship between mixing length and strong turbulence estimates for transport due to drift turbulence. Plasma Phys. Control. Fusion 2001, 43, 155. [Google Scholar] [CrossRef]
- Dupree, T.H. A Perturbation Theory for Strong Plasma Turbulence. Phys. Fluids 1966, 9, 1773–1782. [Google Scholar] [CrossRef]
- Hahm, T.; Wang, L.; Wang, W.; Yoon, E.; Duthoit, F. Isotopic dependence of residual zonal flows. Nucl. Fusion 2013, 53, 072002. [Google Scholar] [CrossRef]
- Sugama, H.; Watanabe, T.H.; Horton, W. Collisionless kinetic-fluid model of zonal flows in toroidal plasmas. Phys. Plasmas 2007, 14, 022502. [Google Scholar] [CrossRef]
- Kim, S.S.; Jhang, H. A conservative gyrofluid model: Effect of closure on energetics. Phys. Plasmas 2020, 27, 092305. [Google Scholar] [CrossRef]
- Zagorodny, A.; Weiland, J. Statistical theory of turbulent transport (non-Markovian effects). Phys. Plasmas 1999, 6, 2359–2372. [Google Scholar] [CrossRef]
- Weiland, J.; Wilhelmsson, H. Coherent Non-Linear Interaction of Waves in Plasmas; International Series on Natural Philosophy; Pergamon Press: Oxford, UK, 1977; Volume 88. [Google Scholar]
- Weiland, J.; Wilhelmsson, H. Repetitive Explosive Instabilities. Phys. Scr. 1973, 7, 222. [Google Scholar] [CrossRef]
- Mattor, N.; Parker, S.E. Nonlinear Kinetic Fluid Equations. Phys. Rev. Lett. 1997, 79, 3419–3422. [Google Scholar] [CrossRef]
- Holod, I.; Weiland, J.; Zagorodny, A. Nonlinear fluid closure:Three mode slab ion temperature gradient problem with diffusion. Phys. Plasmas 2002, 9, 1217–1220. [Google Scholar] [CrossRef]
- Weiland, J. Simulations of the L–H transition on experimental advanced superconducting Tokamak. Phys. Plasmas 2014, 21, 122501. [Google Scholar] [CrossRef]
- Weiland, J. The role of zonal flows in reactive fluid closures. Plasma Sci. Technol. 2018, 20, 074007. [Google Scholar] [CrossRef]
- Weiland, J.; Zagorodny, J. Drift wave theory for transport in tokamaks. Rev. Mod. Plasma Phys. 2019, 3, 8. [Google Scholar] [CrossRef]
- Rogers, B.N.; Drake, J.F.; Zeiler, A. Phase Space of Tokamak Edge Turbulence, the L–H Transition, and the Formation of the Edge Pedestal. Phys. Rev. Lett. 1998, 81, 4396–4399. [Google Scholar] [CrossRef]
- Hubbard, A.E.; Boivin, R.L.; Drake, J.F.; Greenwald, M.; In, Y.; Irby, J.H.; Rogers, B.N.; Snipes, J.A. Local variables affecting H-mode threshold on Alcator C-Mod. Plasma Phys. Control. Fusion 1998, 40, 689. [Google Scholar] [CrossRef]
- Hubbard, A.E.; Hughes, J.W.; Bespamyatnov, I.O.; Biewer, T.; Cziegler, I.; LaBombard, B.; Lin, Y.; McDermott, R.; Rice, J.E.; Rowan, W.L.; et al. H-mode pedestal and threshold studies over an expanded operating space on Alcator C-Mod. Phys. Plasmas 2007, 14, 056109. [Google Scholar] [CrossRef]
- Weiland, J. Stability and Transport in Magnetic Confinement Systems; Springer: New York, NY, USA; Heidelberg, Germany, 2012. [Google Scholar]
- Snyder, P.; Groebner, R.; Hughes, J.; Osborne, T.; Beurskens, M.; Leonard, A.; Wilson, H.; Xu, X. A first-principles predictive model of the pedestal height and width: Development, testing and ITER optimization with the EPED model. Nucl. Fusion 2011, 51, 103016. [Google Scholar] [CrossRef]
- ITER Physics Expert Group on Confinement and Transport; ITER Physics Expert Group on Confinement Modelling and Database; ITER Physics Basis Editors. Chapter 2: Plasma confinement and transport. Nucl. Fusion 1999, 39, 2175. [Google Scholar] [CrossRef]
- Weiland, J.; Nordman, H. Enhanced confinement regimes in transport code simulations of toroidal drift wave transport. Nucl. Fusion 1991, 31, 390. [Google Scholar] [CrossRef]
- Greenwald, M.; Terry, J.; Wolfe, S.; Ejima, S.; Bell, M.; Kaye, S.; Neilson, G. A new look at density limits in tokamaks. Nucl. Fusion 1988, 28, 2199. [Google Scholar] [CrossRef]
- Borrass, K.; Loarte, A.; Maggi, C.; Mertens, V.; Monier, P.; Monk, R.; Ongena, J.; Rapp, J.; Saibene, G.; Sartori, R.; et al. Recent H-mode density limit studies at JET. Nucl. Fusion 2004, 44, 752. [Google Scholar] [CrossRef]
- Gates, D.A.; Delgado-Aparicio, L. Origin of Tokamak Density Limit Scalings. Phys. Rev. Lett. 2012, 108, 165004. [Google Scholar] [CrossRef]
- Zanca, P.; Sattin, F.; Escande, D.; Pucella, G.; Tudisco, O. A unified model of density limit in fusion plasmas. Nucl. Fusion 2017, 57, 056010. [Google Scholar] [CrossRef]
- Giacomin, M.; Pau, A.; Ricci, P.; Sauter, O.; Eich, T.; the ASDEX Upgrade Team; JET Contributors; the TCV Team. First-Principles Density Limit Scaling in Tokamaks Based on Edge Turbulent Transport and Implications for ITER. Phys. Rev. Lett. 2022, 128, 185003. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Diamond, P.H. Zonal shear layer collapse and the power scaling of the density limit: Old L–H wine in new bottles. Plasma Phys. Control. Fusion 2022, 64, 084004. [Google Scholar] [CrossRef]
- Rafiq, T.; Weiland, J. Self-consistent core-pedestal ITER scenario modeling. Nucl. Fusion 2021, 61, 116005. [Google Scholar] [CrossRef]
- Rafiq, T.; Kritz, A.H.; Tangri, V.; Pankin, A.Y.; Voitsekhovitch, I.; Budny, R.V.; JET EFDA Contributors. Integrated modeling of temperature profiles in L-mode tokamak discharges. Phys. Plasmas 2014, 21, 122505. [Google Scholar] [CrossRef]
- Rafiq, T.; Wang, Z.; Morosohk, S.; Schuster, E.; Weiland, J.; Choi, W.; Kim, H.T. Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios. Plasma 2023, 6, 435–458. [Google Scholar] [CrossRef]
- Rafiq, T.; Wilson, C.; Clauser, C.; Schuster, E.; Weiland, J.; Anderson, J.; Kaye, S.; Pankin, A.; LeBlanc, B.; Bell, R. Predictive modeling of NSTX discharges with the updated multi-mode anomalous transport module. Nucl. Fusion 2024, 64, 076024. [Google Scholar] [CrossRef]
- Weiland, J.; Rafiq, T.; Schuster, E. Nonlinearities in magnetic confinement, ionospheric physics, and population explosion leading to profile resilience. Phys. Plasmas 2024. submitted. [Google Scholar]
- Rafiq, T.; Kritz, A.H.; Weiland, J.; Pankin, A.Y.; Luo, L. Physics basis of Multi-Mode anomalous transport module. Phys. Plasmas 2013, 20, 032506. [Google Scholar] [CrossRef]
- Houlberg, W.A.; Shaing, K.C.; Hirshman, S.P.; Zarnstorff, M.C. Bootstrap current and neoclassical transport in tokamaks of arbitrary collisionality and aspect ratio. Phys. Plasmas 1997, 4, 3230–3242. [Google Scholar] [CrossRef]
- Ding, S.; Garofalo, A.M.; Wang, H.Q.; Weisberg, D.B.; Li, Z.Y.; Jian, X.; Eldon, D.; Victor, B.S.; Marinoni, A.; Hu, Q.M.; et al. A high-density and high-confinement tokamak plasma regime for fusion energy. Nature 2024, 629, 555–560. [Google Scholar] [CrossRef]
- Zagorodny, A.; Weiland, J. Closure at the Irreducible Part of the Fourth Moment for the Case of Constant Coefficients in the Fokker-Planck Equation. AIP Conf. Proc. 2011, 1392, 24–32. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Coppi, B.; Rosenbluth, M.; Sudan, R. Nonlinear interactions of positive and negative energy modes in rarefied plasmas (I). Ann. Phys. 1969, 55, 207–247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).