Abstract
This article provides an up-to-date overview of the problems associated with the detection of hot electrons escaping from laser-produced plasma and corresponding return current flowing from the ground to the target, which neutralises the positive charge occurring on the target due to the escaped electrons. In addition, the target holder system acts as an antenna emitting an electromagnetic pulse (EMP), which is powered by the return target. If the amount of positive charge generated on the target is equal to the amount of charge carried away from the plasma by the escaping electrons, the measurement of the return current makes it possible to determine this charge, and thus also the number of escaped electrons. Methods of return current detection in the mA–10 kA range is presented, and the corresponding charge is compared to the charge determined using calibrated magnetic electron energy analysers. The influence of grounded and insulated targets on the number of escaped electrons and EMP intensity is discussed. In addition to EMP detection, mapping of the electrical potential near the target is mentioned.
1. Introduction
One of the most significant and potential applications of high-power lasers pertains to the generation of plasma by focusing laser radiation on solid, liquid, or gaseous targets [1,2,3,4,5,6,7,8,9,10]. These plasmas have unique and versatile applications, depending on the laser power, focused intensities, and target parameters. For example, microchip lasers possess the capability to drive ion sources required for planetary mass spectrometry [11,12,13], while high-power laser systems can accelerate charged particles to extremely high energies [14] and can initiate fusion reactions [15]. Thus, this allows the laser-produced plasmas to be used as secondary sources of electrons, ions, and various fusion products, as well as optical to gamma-ray radiation. One of their common features is the emission of electromagnetic pulses (EMPs) in the range from radio (MHz) to terahertz (THz) frequencies [10,16,17,18]. These EMPs are considered a threat to electronic equipment, including the computer and detector devices, and have prompted the development of various protective measures [10,17,19]. Detection methods of EMP and mitigation of their adverse effects are also in the forefront of interest.
EMP emission provides additional data on hot electrons accelerated inside a solid target as well as in a filament created in a gas near the geometric focus of a lens or mirror. This emission evidently increases with increasing laser energy, as multiple mechanisms contribute to the acceleration of electrons generating EMP. Although the threshold of laser intensity for the EMP generation has not been clearly established, the closest value can probably be the laser intensity Iλ2 ≥ 1013 W cm−2 μm2. From this intensity, hot electrons can be generated, since part of the energy of the laser pulse is resonantly and parametrically absorbed [20,21].
When a laser beam interacts with a solid target, it is commonly assumed that the most energetic electrons ejected from the target leave a potential behind on the target [22,23] generating a positive accelerating electric field by Larmor law [24,25]. This potential generates an oscillating current flowing through the stalk or target-holder system, which attaches the target to the grounded vacuum chamber and becomes an antenna emitting radio frequency radiation. Another spectral component in the MHz domain is given by the eigenfrequency of the vacuum chamber and the chamber resonant modes that are generated when the expanding plasma hits the chamber walls [26]. By applying the appropriate geometry and material of the target stick, as well as the use of a “birdhouse” that allows the target to be enclosed inside a small Faraday cage (FC), it was possible to greatly reduce the severe damage caused by giant EMP to electrical measurement and equipment when sub-picosecond ultra-high power laser beams interact with solid targets [17,19]. For example, a decrease in EMP emission was achieved with the “birdhouse”, which reduced EMP by a factor of 20 in the frequency range from 100 MHz to 6 GHz and by a factor of 50 in the 1–2 GHz range [19].
In this article, we present the basic concepts and recent development in diagnostics of the target charging and discharging by laser–matter interaction and detection of EMP and wake field. First, the associated methods for low-intensity laser interaction are described, and an experiment estimating the threshold of EMP generation is mentioned. A novel diagnostics method for detection of 10 kA return target currents is then explained. The number of electrons needed to balance the positive charge present on the target, determined by the target current probe, is compared to the number of electrons escaped from the plasma as free particles, determined by the magnetic electron spectrometer. Finally, the main conclusions are presented along with a brief mention of upcoming topics.
2. Diagnostics for Low-Intensity Laser Interaction
2.1. Electric Field near the Target
One of the challenges of laser-produced plasma diagnostics has been to perform a local, time-dependent measurement near the target without disturbing the plasma. For example, the space potential, which can be inferred from the voltage-current characteristics of a Langmuir probe, was measured for the first time by observing the time-dependent deflection of a 10−7 A beam of 22 keV He+ ions by Mendel [27]. Later, the proton radiography method was developed and successfully applied to probe laser–plasma interactions and detect electric and magnetic fields and plasma density gradients with very high temporal and spatial resolution [28]. The proton radiography was successfully utilised to observe target charging and return currents during experiments conducted at the OMEGA laser facility [29]. Here, we mention a high impedance probe used to map the electric potential near the target for plasma produced by laser intensity on a target below 1013 W cm−2 μm2. The plasma was produced utilising a Compex 205 KrF excimer laser operating at 248 nm, which delivered energy up to 56 mJ (i.e., 56 J/cm2) to the aluminium target with a thickness of 1 mm, wherein the laser pulse duration was 23 ns. The laser pulse struck the targets at 70° with respect to the target surface normal. To avoid the effect of plasma particles hitting the probe, a PVC shield was applied. The electric potential was measured in the radial direction at a distance ranging from 4.7 to 6.2 cm relative to the major axis of the target, while the height of the shield from the surface normal to the centre of symmetry of the target was about 3 cm [24]. The time-resolved probe signal consisted of a single peak, as Figure 1 shows. Its duration was about 50 ns, while the rise time in all measurements was stable, ≅25 ns, and all observed potential pulses showed a peak corresponding to the end of the laser pulse and then gradually decreased. To detect the longitudinal electric field, the potential was measured by this probe in two points spaced out horizontally by 1 cm.
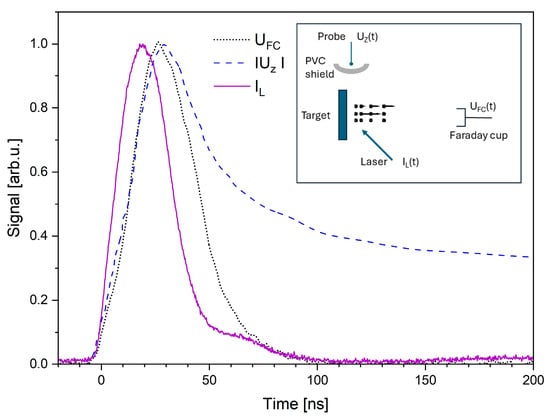
Figure 1.
Comparison of normalized time courses of the photopeak of the Faraday cup signal UFC, potential |Uz| detected by the probe, and the KrF laser pulse, IL, irradiating the Al target. The inset shows schematically the localization of the probe and the Faraday cup relative to the target.
The radial dependence of difference of these potentials was analysed by fitting a power function 1/rn, where n > 0, to the experimental data. It turns out that the decay lies between 1/r and 1/r2. This suggests an interplay between the field resulting from Larmor formula and that coming from Coulomb interaction. Nevertheless, it is also beneficial to clarify this decay using the Larmor’s formula [25]:
where r is the distance, is the acceleration of the charge q, t is the time, and t′ is the retarded time corresponding to t − r/c. If we consider the space charge as a finite charge line, then the dependence of the electric field on the distance:
where r is the distance from the line centre, k = 8.99 × 109 Nm2/C2 is the Coulomb constant, λ is the linear charge density, and L is the length of the charged line. The fit of (1) to the observed radial dependence of U(r) gives the values of both parameters L ≈ 5 cm and λ ≈ 2 × 10−10 C/cm, which correspond with the end of the laser pulse. The electric field was evaluated to be near 5 kV/m. Fitting (2) with the experimental data is equivalent to fitting the power function Ar−δ, which gives δ = 1.845 [24]. This analysis shows that a different kind of field relative to the induced double layer can occur because 1 ≤ δ ≤ 2.
The observed antenna signals suggest that a more consistent explanation could be provided by electron sputtering by the laser pulse. The observed electric field exhibits a direction perpendicular to the target surface and can accelerate positive charges along the target normal. This result is in accordance with measurements of expanding electrons using a positively biased Faraday cup at a voltage of 20 V [30]. Figure 1 shows a comparison of time courses of the normalized signal of antenna |Uz(t)|, laser pulse IL(t), and photopeak recorded by the Faraday cup UFC(t). The pulse of the antenna signal is approximately 50 ns wide, while the rise time in all measurements was stable, near 25 ns. This last value is the same as the laser pulse duration. Electrons that initially reside within the target matrix absorb the laser energy and escape from the target in a vacuum. The escaping electrons impart a net positive charge that creates an electrostatic field. The latter could be responsible for the potential. Moreover, all observed potential pulses detected by the antenna showed a peak corresponding to the end of the laser pulse, as shown in the Figure 2. Although the photopeak observed at negative bias of a Faraday cup could also be partially generated by the scattered laser beam irradiating the FC electrode, a possibility is that it could be caused by electrons escaping from the target by the laser–plasma interaction. Both the duration of the photopeak and the position of its peak correlate with the duration of the potential peak and its position detected by the probe, as shown in Figure 2. The possibility of the acceleration of ions depicted in Figure 1 was confirmed through the analysis of ion currents using a FC signal model based on the Maxwell–Boltzmann distribution {f ≈ exp[−m(v − uCM)2/2kT]} of ions. Fitting the model function to the measured FC signal makes it possible to determine the value of the centre-of-mass velocity, uCM, of the expanding ions accelerated by this potential. The fit also provides a value of thermal energy of ions, kT.
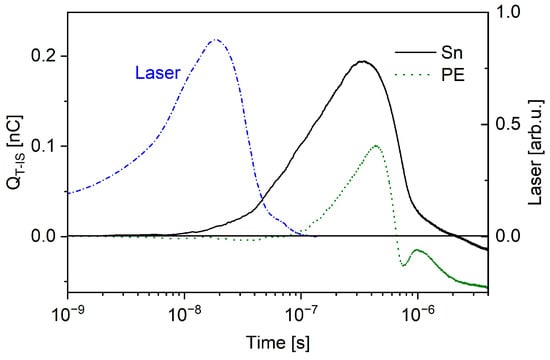
Figure 2.
Polarisation of a target insulated from an interaction chamber with a capacitance of 31 ± 5 pF, and typical waveform of the KrF excimer laser pulse and temporal evolution of the charge on the isolated polyethylene (PE), and Sn targets irradiated with laser pulses of 100 and 64 mJ, respectively.
The contribution of uCM velocity to the total ion expansion velocity is significant because its value is at least comparable with the thermal velocity or can be higher. As the particle release from the surface is thermal in nature, the effect of the uCM velocity on the plasma expansion supports the double layer mechanisms to ion acceleration [31,32,33]. However, the applied fluence of 25 J/cm2, which places this interaction in the region of high fluence interactions (F > 20 J/cm2), should lead to explosive ablation, i.e., explosive boiling, or phase explosion [33,34]. The theory of explosive boiling does not seem to be able to fully explain the experimental results regarding the electric field revealed in [24] and shown in Figure 1. Thus, further complex experiments are obviously needed.
2.2. Return Target Current at Low Laser Intensity
The target polarisation by laser ablation starts when the most energetic electrons escape a potential barrier and leave the target. J.S. Pearlman and G.H. Dahlbacka [35] observed directly, for the first time, voltages on isolated laser-irradiated targets and have inferred substantial electric fields and charge separation. A thick aluminium target isolated from the vacuum chamber was irradiated with 50 ps Nd: glass laser pulses. The peak voltage observed at the target reached a value of 6 kV, and the estimated number of escaping electrons was about 1010. This experiment was conducted in an intensity regime where non-Maxwellian electrons are produced. However, the target polarisation was also observed in experiments with low laser intensity, as shown in Figure 3 for an intensity of 108 W cm−2 μm2. The targets were fixed to a cylindrical metalic holder, electrically insulated from the ground. The total capacitance of the holder together with the target with respect to the vacuum chamber was CT = 31 ± 5 pF. This value was obtained using the chamber as a capacitor within an RC circuit powered with a step voltage source. To obtain the voltage created on the isolated target, the target was connected to the ground by the oscilloscope’s 1 MΩ input connector.
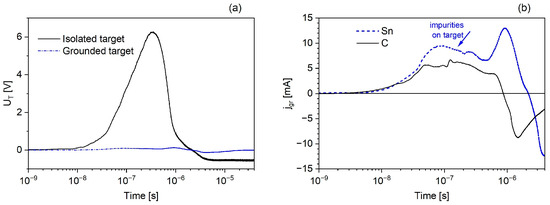
Figure 3.
(a) Time-resolved voltage on an isolated target (solid line) and across the 10 Ω resistor connecting this Sn target to ground (dashed line). Laser delivered energy of 100 mJ on the target. (b) Detail of the current flowing from the Sn and C targets through the 10 Ω resistor to the ground.
The temporal development of the voltage UT (t) on the target isolated from the vacuum chamber by means of an isolator with a capacitance of CT makes it possible to determine the value of the charge captured and thus the current number of escaped electrons: qT(t) = CT UT(t).
Figure 2 shows the large effect of target material on charge generation on isolated targets. Conversely, the effect of laser energy is not so pronounced. Although the total duration of the laser with the targets was about 100 ns, the increase in target charge continued for another 400–700 ns, depending on the target material. This is a non-relativistic interaction where due to the finite transverse size of the beam, a non-linear force acts on electrons along the direction of decreasing laser intensity. A laser beam, propagating through a plasma, pushes electrons away from the axis of the laser beam, creating a space charge in the background of nearly stationary ions. If the laser pulse is sufficiently long, a stationary state is reached wherein the Coulomb force due to the charge separation balances the ponderomotive force on electrons, and a plasma channel is formed [1]. As shown in Figure 3, these conditions are relevant only in the first period of the target polarisation, when the laser pulse heats the target and produces plasma. Charging the target continues until the maximum voltage is reached. At this point, the flow of electrons from the target to the plasma/vacuum stops. This current is defined as
In time tpeak when UT reaches its maximum and j = 0, the escape of electrons from the target stops. The observed maximum charge occurred on the isolated target at tpeak allows for the estimating the number of electrons transferred from the isolated target to the expanding plasma. In the case of the Al target shown in Figure 3, the maximum charge value was 0.22 nC, which corresponds to ne ≈ 1.4 × 109. Because these electrons were moving with velocity, v, allowing them to pass through the potential barrier, i.e., , this number can be expressed as
where e is the electron mass and is the three-dimensional distribution function of electron velocity [36]. Now for t > tpeak, electrons with energy less than eUT−max, where e is the elementary charge, are attracted by the positive potential from the plasma to the target, and the positive volage on the isolated target decreases.
Another electronic circuit, containing a 10 Ω shunt circuit system, made it possible to measure the time course of the target charge neutralisation with the current flowing between the target and the grounded interaction chamber [37]. This 10 Ω short-circuit system was chosen to minimise the voltage generated on this system so as not to affect the plasma expansion. The target holder was connected to the oscilloscope input through an array of eleven 110 Ω resistors. They were equally spaced on the circumference of the flange holding the target to respect the coaxiality of the set-up. One of these was realised through the series of a 60 Ω resistor and a coaxial cable of 50 Ω characteristic impedance. The cable was then connected to the scope’s Rsc = 50 Ω input connector. In one of the branches of this near short-circuit with a total resistance of 10 Ω, we measured only 1/11 of the total short-circuit current. The voltage USC registered on the scope is related to the potential jump on the laser target, UT, through the formula UT = {(Rc + Rsc)/Rsc}·USC, where Rc = 60 Ω. This voltage UT was considerably lower than the voltage across a 1 MΩ resistor isolating the target from the ground, as Figure 3 shows [37,38]. In this case, the mitigation factor of UT exceeded 20. The charging of the isolated target was caused by electrons escaping to the plasma. The waveform of UT significantly differed from the one on the isolated target because two different processes led to the target charging and discharging. In the case of the isolated target, the positive target charge was not balanced by a current flowing from the ground through the target holder system from the beginning of laser interaction but increasing up to a maximum positive charge at ≈230 ns and starting to attract electrons from the plasma, as Figure 3a shows. After the laser interaction, the grounded target acted as a specific probe embedded in the plasma, as shown by other experiments [30]. Figure 3b shows that the grounded target started to conduct a current of electrons from the plasma to the ground at 2.3 μs. At about this time, the voltage on the isolated target also became negative. The peaked structure of the current through the graphite target indicates that the peaks occurring on Sn target currents, jgr(t), up to the time of about 800 ns are caused and affected by ionized impurities bounded to the surface of targets. It is evident that although the number of ionized impurities is much lower than the number of produced target ions, the target currents associated with the ionized impurities are comparable with the balancing currents corresponding with the target ions.
The same phenomenon was reported by Tudisco et al. [39] who used a Langmuir probe as a non-biased TOF detector. The probe was placed in front of the Al target at a distance of 2.5–14.5 mm. Plasma was produced using a 600 mJ, 6ns Quanta System Nd:YAG laser operated at 1064 nm. After reaching the last maximum of about 220 mA, the probe current started to decrease and reached zero at 3.5 μs and minimum at 4.5 μs after the end of the laser–plasma interaction ([39] and Figure 4a therein). Since the values of tzero and tmin, as well as the dimensions of the used vacuum chambers, are comparable in both experiments, it can be assumed that the signals of the probe and the grounded target indicate the effect of the interaction of ions somewhere with the walls of the vacuum chamber. This is apparently the reason why hydrodynamic simulations of the plasma core expansion were unable to reproduce the probe’s negative signal. Electrons produced by the recombination of ions on the metallic walls may be the cause of this qualitative change in the tail of UT(t). Thus, when the secondary electrons from the walls of the chamber enter the plasma, it becomes negatively charged and is neutralised by a circuit that closes the grounded target or probe. Then, the return target current flows in the opposite direction.
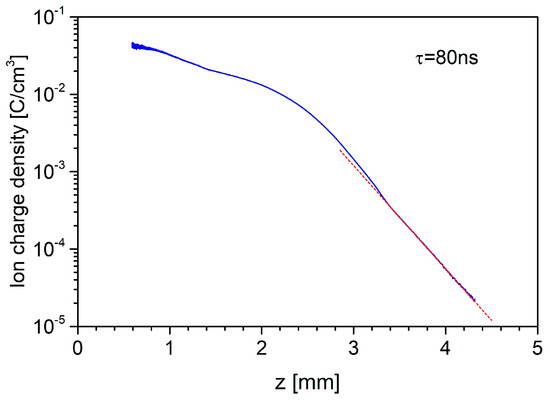
Figure 4.
The ion charge density (DOF spectra) of Cu ions along the target surface normal were determined from the ion detector signal using Equation (5) for a selected time of 80 ns after the laser shot. The dashed line shows the fit of (6) to the data for z ranging from 3.4 to 4.2 mm. The Cu target was irradiated with a 23 ns KrF laser, which delivered an energy of 68 mJ.
Before the ions hit the walls of the chamber, the plasma is rarefied. The effect of the rarefaction on the ion charge density can be estimated transforming the signal of a Faraday cup localised at a distance L from the target to a distance-of-flight spectrum Qi(z,τ) at chosen time τ after the laser–target interaction. The time-of-flight t is transformed to the distance-of-flight (DOF) z using a relationship z = Lτ/t. Values of τ and L are kept fixed. Substituting t by z, the ion current density jFC(L, t) can be transformed to the space-resolved ion charge density at the particular moment of time τ as [38]
Relation (5) exactly corresponds to the expansion of ions in three-dimensional space observed at longer distances from the target, where no recombination of ions takes place and charge states are frozen. Also, in this experiment, the Faraday cup was positioned in a far zone, where the ion density does not decrease due to recombination but due to the rarefaction process. Figure 4 shows characteristic DOF spectrum of an expanded Cu plasma produced by a 68 mJ KrF laser pulse, which was calculated for a time of 80 ns after the laser–target interaction.
The transformation of FC signals to Qi(z,τ) makes it possible to determine the ion sound velocity of the expanding plasma because the ion density should decrease exponentially with distance. This can be expressed in a form ni(z,t) = n0 exp(−v/cs), where ni(z,t) is the density for those ions traveling at velocity v, n0 is the density at the emitting surface, and cs is the ion sound velocity [40]. Substituting v = z/τ gives
where τ is the above-mentioned chosen time and cs = (kTef/mi)1/2 is the ion sound velocity. kTef is generally a function of the charge state q of ions, their temperature Ti, and the temperature of electrons Te. Their values characterise the plasma produced by laser. If Tef does not change during the ion expansion, this curve follows a single exponential decrease over the whole range. Assuming that the mean charge state of ions is , and e is the elementary charge, then the expansion function can be fitted to the DOF spectrum calculated from the FC signal. The distance dependence of depicted in Figure 4 decreased nearly linearly for z > 3.4 mm. The fitting of (6) to this part of the ion charge density allowed for the determining of the cs of the fastest ions formed mainly by H and C ions originating from impurities absorbed on the target surface. Their acoustic speed was cs = 4.1 × 105 cm/s. Cu ions propagated in a vacuum at a lower velocity and with both the ion density and the average charge state changing.
However, DOF spectra show that the rate of decrease varies with distance, and thus only short sections of the DOF spectrum can be considered as a simple exponential decrease, manifesting as linear on a semi-logarithmic scale. It can be assumed that in this short section, the values of and Tef change only slightly. Then, the fitted value of τ cs allows one to calculate the corresponding values of kTef [41]. The step-like decrease in the Qi(z,τ) with increasing distance, z, at a given τ indicates the occurrence of different plasma fronts and, thus, different double layers which gradually dominate during the plasma expansion into the vacuum [37,38]. This could be manifested by the appearance of different maxima in the time-resolved target current. For example, Figure 3b shows two maxima of jgr(t) at time about 200 ns and 1.2 μs.
Due to the similarity of the waveforms at 10–400 ns, it can be concluded that the first maximum shown in Figure 3b corresponded to ionised hydrocarbons and the second to Au ions. Hydrocarbons were chemisorbed on the surface of all targets used, and their ions expanded into the vacuum ahead of the target ions because their expansion rate was greater than that of the ionised elements of the target, mainly due to their smaller mass. This analysis revealed the dependence of tpeak on the mass (A) of the ions and their charge number (Z) in the following form:
This empirical relationship and values of the coefficients α ≈ 100 ns and β ≈ 200 ns were determined from the dependence of the tpeak for a set of mass numbers corresponding to the elements contained in Al, C, Cu, CuBe, AgCu, Sn, Au, and Ta targets irradiated with 34 mJ KrF laser pulses [30]. This relationship indicates that the value of voltage U0 accelerating ions to the kinetic energy of Eions = eZU0 is approximately the same for all the ionised species produced under the same conditions.
The calculated distance dependence of Qi(z,τ) for the chosen time shows that the plasma front containing H and C ions at 100 ns is located a few millimetres–centimetres from the target surface in the dependence on the KrF laser intensity [38]. Within microseconds, these ionised impurities approach the target chamber walls to be neutralised, while the heavier target ions still occupy the chamber and continue to expand. The return flow of electrons to the target continues, that is, the electrons gradually escape from the changing plasma front composed first of the ionised hydrocarbons and, after their disappearance, from the front of the heavier target ions. The different time courses of the target currents reflect the complexity of the plasma production, expansion, and extinction processes, which vary from one target material to another. Target signal waveforms are sensitive to small amounts of impurities in the bulk of the target material as well as the composition of surface impurities [4,37,38], as Figure 3b shows.
The experimental observation of the target current flowing through a shunt circuit system also makes it possible to calculate a total charge needed for target neutralisation, i.e., the number of electrons succeeded to escape the plasma, by the integration of target voltage UT(t): , where t0 is the time for this voltage to drop to zero and then go negative, and RT is the resistance of the target circuit. Assuming the quasi-neutrality of the expanding plasma, the number of slower electrons (i.e., their total charge) moving along with the ions during their expansion into the vacuum chamber can be calculated by integration of ion currents detected with the use of several Faraday cups used for mapping the space distribution of ions. In the case of the isolated target, it is given by the positive peak voltage at tp because this corresponds to the maximum charge captured by the insulated target acting as a capacitor: , where CT is the total capacitance of the holder together with the target with respect to the vacuum chamber, and ϕ is the potential and e is the elementary charge. This allows us to estimate experimentally the throughput of the plasma barrier, ξPB, as similarly presented [36]:
where QTC-P is the total charge needed target neutralisation, and QIONS is the total charge carried by ions trapping the slower electrons which is equal to the charge of remaining electrons. The isolation of the target from a vacuum chamber resulted in a reduction in the number of electrons escaping from the plasma by a factor of 100 relative to the grounded target, as can be deduced from Figure 5. The charge transferred from the ground by the return target current through the 10 Ω resistor was ≈1.5 × 10−8 C, as calculated by integrating the positive part of ITC(t) shown in Figure 5a. ITC(t) became negative around the time the fastest ions hit the Faraday cup. The charge captured by the Faraday cup was of the order of 2.4 × 10−6 C. To measure the total charge carried by the ions, it was necessary to measure the spatial distribution of the ion emission, which requires the use of a system of Faraday cups. Unfortunately, it was not done in the given experiment. The maximum charge value accumulated on the isolated Sn target irradiated with the same 100 mJ KrF laser radiation was ≈2 × 10−10 C. The time-course the target volage is shown in Figure 5b.
ξPB = QTC-P/(QTC-P + QIONS),
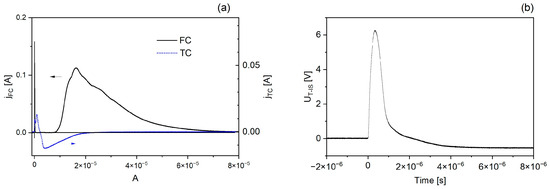
Figure 5.
(a) The time-resolved current of Sn ions detected using a Faraday cup and the return target current flowing through a 10 Ω resistor to ground. (b) Time-resolved voltage on an isolated Sn target. The targets were exposed to 100mJ energy of KrF laser radiation.
The total proportion ξPB depends on the target material and laser–target interaction. ξPB decreases from 10−3 to 10−5, as observed for various targets irradiated with energy of 34–107 mJ delivered by a 23 ns KrF excimer laser [38]. Thus, isolating the target reduces the number of electrons escaping the target and plasma, which is produced by low power lasers. Another interesting result is the fact that electron escape occurs even after the end of the laser–plasma interaction, with the largest number of electrons escaped from the plasma after hundreds of nanoseconds.
The experiments showed how the target voltage on grounded or isolated metal targets reaching only a few volts affects the properties of the plasma. However, complete isolation of the target and the produced plasma from the surroundings can be realised by applying the levitation method [42]. When the plasma is produced by high-power lasers, the removal of the target stalk should lead to an increase in the decay time of the target charge and an increase in the preheating of the target. This is shown by a nonlinear model of electrical discharging of inertial confinement fusion capsules [43]. However, it is stated in [44,45] that a low-intensity KrF laser can also influence the capacitance of targets, namely, plastic ones. It was discovered that the capacitance of plastic discs is dependent on the target material, the thickness, the diameter of the disc, and the laser energy. Variations in bulk conductivity are caused by free electrons released by absorption of 248nm radiation as well as plasma radiation in the target through internal photoemission. It was observed that irradiated ultra-high molecular weight polyethylene (C2H4)n (UHMWPE) and poly(methyl methacrylate) (C5H8O2)n (PMMA) discs differ significantly in both the number of emitted ions and their velocity distribution due to the different microscopic structure that causes a different geometrical dependence through variations in bulk conductivity. Further knowledge of the target charging with nanosecond laser radiation can provide a deeper understanding of the laser–matter interaction physics.
3. Diagnostics of Return Target Current at High Laser Intensity
Systematic efforts to study target charging and the return current balancing this charge began with the advent of megajoule laser devices to mitigate electromagnetic interference, a pervasive problem within and outside of the vacuum target chamber [22,46,47,48,49]. The interaction of nanosecond laser pulses with plasma can produce hot electrons in the 10 to 100 keV range. The ultra-short laser pulses can produce very energetic electrons in the MeV range. In general, it is believed that some of these hot electrons can escape before creating an electrostatic field associated with the escaping electrons, which limits the number of other escaping electrons. Although some important questions have been raised as to how the EMP varies with laser energy, pulse duration, and target size [16], to the best of the authors’ knowledge, there has not been an attempt to experimentally study EMP emission around its threshold. The experiments presented above did not record any EMP emission. To experimentally determine the threshold of EMP generation, it would be appropriate, considering the experiments published so far, to irradiate a metal target with a laser pulse delivering an intensity of 1013 W cm−2 μm2 to the target.
The first comparison of target currents neutralising a massive 5mm × 5mm × 50 mm Cu target exposed to low and high laser intensity of 2 × 108 and 5 × 1013 W cm−2 μm2, respectively, showed that the waveforms of both target currents were similar [50]. These experiments were performed using KrF and PALS lasers. The laser system PALS was operated at a wavelength of 1.315 µm, and the duration of delivered pulses was 350 ns. A loop antenna employed at the high laser intensity experiment did not register any EMP signal up to laser energy of 0.6 J. However, increasing the PALS energy from 0.6 to 1.8 J, the EMP appeared. Figure 6 shows the interference of the EMP with the target probe signal (black line). This signal was measured using a 0.057 Ω shunt circuit system consisting of 44 pieces of 2.5 Ω (4 × 10 Ω) SMD (surface mount device) resistor chips connected in parallel to minimise the voltage on the target.
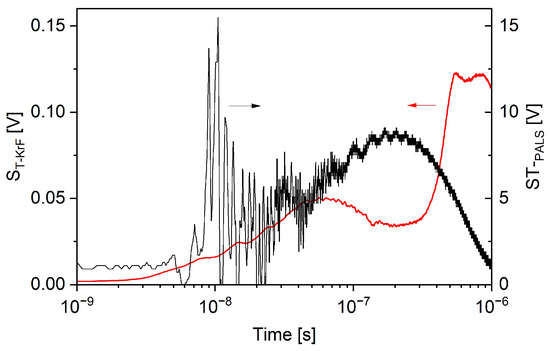
Figure 6.
Time-resolved voltage on massive Cu targets irradiated with the PALS (λ = 1.315 μm, black line) and KrF (λ = 248 nm, red line) lasers, delivering intensities of 1 × 1014 and 1 × 108 W cm−2 μm2, respectively. The EMP interfered with the PALS target probe signal.
It would be very interesting to observe the later negative part of the target voltage induced by the 1.8 J, 350 ps PALS laser pulse. It starts only about 500 ns after the termination of the laser–plasma interaction, while in the case of the KrF laser, it starts about 3 μs, which is about 2.5 μs later. Although the distance of the target from the wall of the PALS chamber is about three times longer than the distance from the wall of the KrF chamber, the fastest ions hit the wall of the PALS chamber at approximately the same time as the ions produced in the KrF chamber. This difference is evidently due to the higher acceleration of ions by the PALS laser, as their expansion velocity is about 10× higher. This allows these ions to hit the walls of the vacuum chamber in a shorter time and accelerate the emission of secondary electrons from these walls. Therefore, the negative signal was detected earlier in the PALS experiment. This correlates with the finding of Pearlman and Dahlbacka [35] that the voltage amplitude and time characteristics of the EMP are dependent on the dimensions of the vacuum chamber and are a consequence of space charge separation.
Figure 6 also demonstrates that in this experiment, the EMP occurs at the laser intensity of 1.5 × 1014 W cm−2 μm2. Since the value of this intensity is at the transition between low and higher intensity, hot electrons should already be produced because ILλ2 ≥ 1013 W cm−2 μm2 [20]. It further shows that the EMP ends when the return target current is decreasing to zero. Further increasing the laser intensity increases the return target current and target voltage, especially during the laser–plasma interaction. By increasing the laser intensity, the waveform of the target current changes significantly as the neutralisation current shortens and the negative tail signal becomes unobservable.
Benjamin et al. [51] measured the current flowing in the target support structure from the chamber ground to the target by mounting a thick Al target on the end of the centre conductor of a 50 Ω coaxial cable and grounding the outer conductor to the target chamber. When this target was irradiated with the Gemini CO2-laser system delivering an intensity of 3.4 × 1017 W cm−2 μm2 (300 J energy in 1.2 ns at 10.6 μm wavelength), the measured peak voltage on the target reached a high value of 175 kV. Due to the generation of a high voltage across the ground resistance, direct observation of kiloampere transient target currents was performed using an inductive target probe developed by J. Cikhardt [52]. The transient return target current IT (t) flowing through the conductive wire from the target to grounded target chamber generates a toroidal magnetic field BT(t) that can be detected with a small inductive loop such as a B-dot probe. This B-dot probe is located near the ground stick inside a hollow copper cylinder (miniature Faraday cage) that protects it from the disruptive EMP produced inside the interaction vacuum chamber. This probe is a part of the target manipulators. The output voltage UT (t) of the B-dot probe is defined by Faraday’s law , where dS is the element of the loop surface. We note that the orientation of the loop antenna relative to the B vector determines the sign of the antenna’s output signal. The magnetic field BT around a ground stick can be expressed in the form , where r is the radius of the magnetic field line. Finally, the target current can be determined by integrating the output voltage on the B-dot probe as , where M is the conversion coefficient representing the mutual inductance given by the geometry of the loop antenna and ground stick arrangement. The used probe has M = 0.6 nH [52]. The major advantage of this probe is that it does not affect the short-circuit current that occurs in the conventional configuration of target holders.
The output signal of this inductive probe is also interesting for the additional information it provides, as it represents the rate of change of the return target current djT/dt. Figure 7a shows the waveform of the time derivative of the target current from an Au target exposed to 1.9 × 1016 W cm−2 μm2 intensity delivered by the PALS laser system. The first three peaks varying from 6 × 1011 to −7 × 1011 A/s indicate that the duration of the return target current is longer than the duration of the laser pulse, which is ≈350 ps. Under these experimental conditions, hot electrons with temperatures around 100 keV [53] are produced and, thus, the highest increase in the target current occurs during the laser–plasma interaction. The target current can reach a maximum value of up to 5 kA. The shot-to-shot fluctuations in the maximum target current depends on the irradiated material and increases with increasing laser energy [52]. The relative error reached of the order of ≈11% at a laser energy of ≈600 J. The time-resolved measurements of the target current indicate that the electron emission continues after the end of the interaction of the nanosecond laser pulse with the expanding plasma.
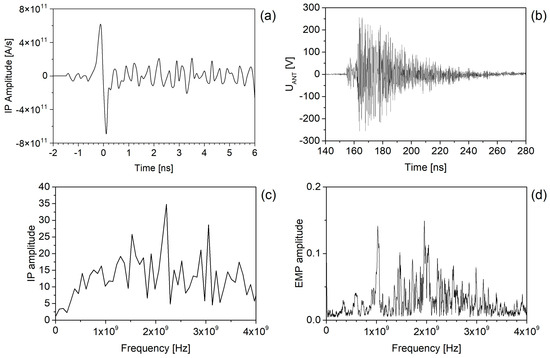
Figure 7.
(a) The typical target probe signal induced by the short-circuit current flowing between the target and ground, where a 1 mm Cu target was exposed to 6 × 1016 W cm−2 μm2 intensity delivered by the PALS laser system. (b) Signal of a H field probe RS H 400-1 (30 MHz–1 GHz) induced by the EMP. (c) Frequency spectrum of the transient return target current, and (d) frequency spectrum of EMP detected inside the interaction chamber.
Return target current and electromagnetic field structure in laser-generated plasmas can be measured using proton deflectometry [29,43]. As being observed, the target potential is generated by the skin plasma around the stalk and drives an ohmic current through it. The magnetic fields generated by this current deflect protons from a backlighter. Variations in proton fluence are detected at different times to obtain information on the temporal evolution of the skin plasma surrounding the stalk. Experiments have shown that after the laser pulse has turned off, a strong positive charge and return current are still prevalent. In addition, some instabilities were observed jetting out from the stalk.
This is also demonstrated by multi-frame complex interferometric experiments, which are devoted to the time-resolved spontaneous magnetic field and the spatial distribution of the electron density in the plasma during the irradiation of surface massive targets [54]. Based on the experimentally obtained spatial–temporal distribution of the spontaneous magnetic field (SMF) B(r, z) in the plasma at the target, the distribution of the electron currents jT (r, z) producing B(r, z) was calculated using Ampere’s law, at different moments of the laser interaction. The experimental result showed that at the end of the laser pulse, the SMF amplitude only decreased from the maximum value of 9 MG to about 2 MG (i.e., after 449 ps the maximum intensity of the laser pulse ≈350 ps) but did not disappear. The currents jT (r, z) were present in the plasma even after the termination of this interaction, and therefore, the plasma was active, as presented above in Section 2.2.
Figure 7b shows that the transient currents of electrons that escaped the plasma generated bursts of broadband EMP. The waveform of the signals coming from the target probe and antenna showed beats (unfixable periods) that could be caused by the interference of two or three frequency bands, which can be identified in frequency spectra shown in Figure 7c,d. Figure 7c shows that the frequency spectrum of the signal of the target inductive probe, which is shielded from EMP, mainly reflects its waveform. Conversely, Figure 7d shows a different spectrum that characterises the signal of the RS H 400-1 antenna induced by EMP inside the interaction chamber. Although the frequency range of the RS H 400-1 antenna is limited, its signal spectrum can be divided into three basic frequency bands: 100–500 MHz, 600–1000 MHz, and 1.2–4 GHz. The first band is related to the eigenfrequency and some resonant frequencies of the target chamber [16,26]. In addition to some resonance frequencies of the target chamber, the second band contains the resonance frequency, fTH, of the target holder, which in the simplest case can be a metal stick, where the value of the lower frequency results fTH ≅ c/4lTH, where c is the light velocity and lTH is the length of this stick [23,38]. Some of the frequency peaks recorded within the target chamber can be identified as resonant modes. However, the number of these resonant peaks above 1 GHz is so high that they form nearly continuous spectrum of microwave radiation in the target chamber [16]. Thus, the peaked spectrum in the 1.2–4 GHz bandwidth could be related to the microwave emission from other sources. A similar distribution of EMP frequencies has been observed in other experiments, such as the interaction of kJ laser pulses with solid targets [55,56] and by a gas jet [18]. Frequencies above 2 GHz were observed by interaction of ultrashort laser pulses with a pre-plasma or solid targets [19,57,58]. Although a significant part of the EMP stems from the bunch of electrons ejected from the target and to the discharge current through the target support, another part can come from the expanding plasma, as can be recognise from the EMP produced by laser interaction with gaseous targets [10,59,60,61]. Although conditions for generation of EMP by interaction of laser pulses with solid and gaseous targets are different, EMP frequency spectrums have a similar range. In the case of gaseous targets, the plasma currents in the filaments are driven by ponderomotive forces associated with the laser pulse [62].
Figure 7b shows the time derivative of the target current which proves the occurrence of the charge of the target generating an electric field. The time varying electric field affects the emission of electrons and ions like the case of the laser–target interaction at low laser intensities (see Figure 3). However, no experiment allows for the measuring of the generation of electrons directly inside the target or plasma, and it can only be characterised from measurements of either escaped electrons into the vacuum or from secondary radiation. The effect of these self-consistent electric fields generated along the target surface on the energy spectrum of the emitted electrons can be estimated via numerical simulations of the measured electron spectra, as presented in the case of the interaction of 70–700 fs laser pulses with 25–250 μm thin targets [63]. These numerical simulations demonstrated that the energy spectrum of the emitted electrons and the simultaneous emission of accelerated surface ions must be accurately accounted for in the original electron distribution function. Link et al. [63] showed that electron emission consists of a phase of rapid target charging and a late phase of long-term plasma expansion with corresponding spectral regions and their coupling to the initial electron distribution. For the electrons produced in the first stage, this target charge is found to be well described by the energetics of a simple time-dependent capacitor. The important conclusion of this work is that the temperature of the low-energy part of the electrons is an artifact of the ion acceleration phase and does not correspond to a similar feature in the original spectrum.
While femtosecond pulses do not interact with the produced plasma, nanosecond pulses interact with it. At high intensities, this interaction is accompanied by nonlinear processes such as stimulated Brillouin scattering, stimulated Raman scattering, two-plasmon decay, and their interplay [64]. This requires the use of advanced diagnostics such as a femtosecond multi-frame polaro-interferometer, a two-dimensional Kα X-ray imaging system, a Bremsstrahlung spectrometer, calorimeters, spectrometers supplemented with a streak camera as well as a multichannel electron spectrometer, and an inductive target probe [64,65,66,67,68,69,70]. It is the multi-channel electron spectrometer and the induction target probe that make it possible to reliably measure the number of electrons escaping from the plasma and the target, as well as to compare the results of both diagnostics. Experiments performed at the PALS facility make it possible to measure the total flux of hot electrons that have escaped from the plasma using the multi-channel magnetic electron spectrometer ranging from 50 keV to 1.5 MeV or from 250 keV to 5 MeV [53,71]. The spectrometers incorporate a plastic electron collimator designed to suppress the secondary radiation by absorbing the wide angle scattered electrons and photons inside the collimator. A total of 12 spectrometers can be placed inside the vacuum chamber around the target at about 30 cm from the target at angles of −39°, −27°, −17°, 0°, 17°, 27°, 39°, 153°, 163°, 180°, 197°, and 207° from the laser axis, as Figure 8 shows.
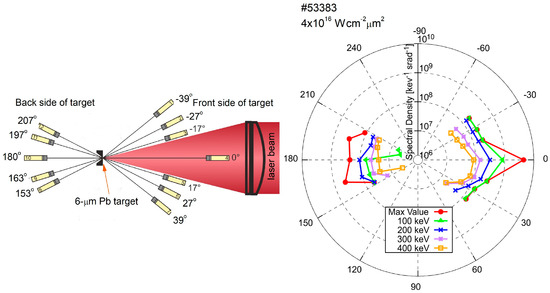
Figure 8.
Schematic layout of 12 magnetic electron spectrometers at different angles from the laser axis on the front and back side of the thin foil target (left). Laser is incident at an angle of 0°. Angular dependence of spectral density of hot electrons for selected energies (right). Results for 12 channel angular arrays were obtained during interaction of the PALS beam (350 ps, 439 J) with a 6 μm thick Pb foil.
In this experiment, hot electrons were produced by focusing an iodine laser beam (IL = 4 × 1016 W cm−2 μm2) on a lead (Pb) target with a thickness of 6 μm. The incoming electrons passing through the collimator of the spectrometer were spectrally resolved by a magnetic field of 95 mT and detected by an image plate (IP) of type BAS-SR. The energy spectrum and temperature of the escaped electrons from a single laser shot (#53383) were determined using measured data from the experiment. Figure 8 shows an angular dependence of spectral density of hot electrons for selected energies (in keV) and the corresponding spectral density (per keV per srad) that characterises the angular dependence of the electron energy distribution function shown in Figure 9. These results conclude that the electron density and energy are maximum along the laser axis, and it decreases with angles in both directions with respect to the laser axis. It should be noted that the total electron flux is calculated by interpolating all distributions measured by spectrometers at different angles in front and back directions with respect to the target position. For the given laser intensity of 4 × 1016 W cm−2 μm2, the total number of escaped electrons was estimated by integrating the measured electron distribution at different angular directions to the entire 4π solid angle. The estimated electron flux for energy greater than 50 keV is ≈5 × 1011, which corresponds to a total charge of the order of 80 nC.
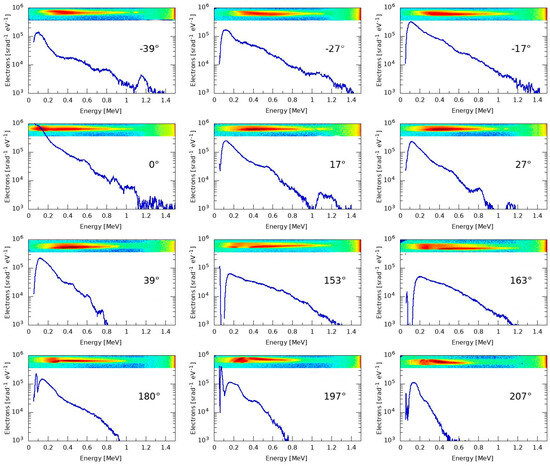
Figure 9.
Energy spectra of electrons emitted at different angles and the images of scanned imaging plate detectors shown at the top of each plot. A 6 μm thin Pb foil was exposed to a laser intensity of 4 × 1016 W cm−2 μm2.
The total charge carried by the escaped electrons can be compared to the charge associated with the target current measured by the current probe during the laser–plasma interaction, which reaches units of μC and is an order of magnitude larger. Since this difference was also observed in experiments with a 5 mm thick Cu target [54], it is obvious that the escape of hot electrons from the plasma detected by magnetic spectrometers does not cause the generation of a positive charge on the target. This suggests that the charging of the target during the interaction with the pico-nanosecond laser pulse and the subsequent process of balancing it with the return current is a more complex process than in the case of the ideal ultrashort laser interaction [1,17,38], and therefore, further experiments focusing on electrons emitted with energy less than 50 keV will be needed to elucidate this difference, not only with sub-nanosecond but also with sub-picosecond lasers.
The raw IP signal and electron energy spectrum data presented in Figure 9 show other interesting features of the hot electron emission. For the typical energy spectrum, the maximum electron energy was observed between 400 keV and 1.4 MeV. However, electron flux varied between 2 × 103 and 1 × 106 srad−1·eV−1. For the thin Pb target, the electron temperature estimated from the slope of the energy distribution varied in the range between 30 keV and 70 keV at different angles with respect to target surface normal.
Of the 12 electron energy spectra shown in Figure 9, only the spectrum measured at an angle of −17° can be characterised by a single electron temperature, Te, estimated from the slope of the energy distribution presented on a semi-logarithmic scale. Figure 9 shows that nanosecond interactions do not show only a single or double exponential property of the electron spectra, but a more complex property. As Figure 10 shows, the energy spectrum of electrons passed through the plasma to the back of the target foil can be characterised by three temperature values of 9.8, 80, and 98 eV. The number of electrons forming these groups decreased with increasing temperature, as in the case of electrons produced by a femtosecond laser [65]. It is evident that electrons reached the back surface and escaped into the vacuum to create an electric field analogous to electrons escaped from the front of the target. This field is itself substantially modified by the simultaneous departure of accelerated surface and plasma ions. Electron and ion emissions are not isotropic, neither in particle abundance nor in energy distribution, as Figure 9 shows. From this angular distribution, it can be estimated that the number of changes in the electric field corresponds to the number of ion bursts, which are the result of a complex non-linear process taking place by the laser–plasma interaction. Some of these changes are not always clear; however, from the spectrum measured at −39 and 0 degrees, it can be concluded that about six changes may have occurred.
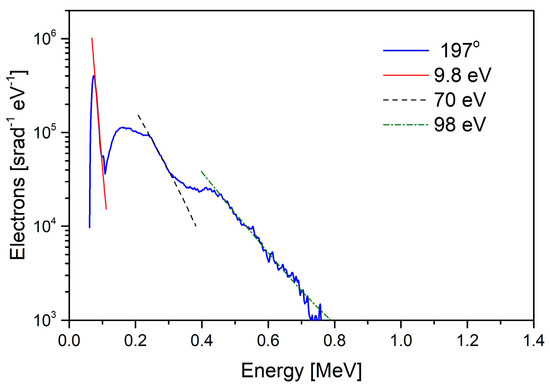
Figure 10.
Energy spectrum of vacuum electrons propagated through the plasma to the back of the target foil at angle of 197° to the laser vector. The 6 μm thin Pb foil was exposed to a laser intensity of 4 × 1016 W cm−2 μm2.
The angular emission characteristic showed a significant directional dependence on the front side of the target, while a weak directional dependence of the electron energy was observed on the back side of the target. The polar plot results led to the conclusion that the electron density and energy were maximum along the laser axis, which was parallel to the normal of the target plane and decreased with angle in both directions relative to the laser axis. However, another important fact can be provided by the angular dependence of electron energy distribution. This may indicate, for example, that hot electrons have not been fully thermalised and are emitted in some directions as electron beams.
4. Conclusions
Increased interest in the origin of the EMP generated during the interaction of laser pulses with matter has stimulated interest in the experimental characterisation of the electron currents that neutralise the charge generated on irradiated targets, as well as its mitigation. The latter is apparently impractical in the case of laser sparks in gases.
This review focused on the detection and characterisation of return target currents produced in laser interaction with solid-state targets in laser experiments from very-low- to high-power laser intensities. Target polarisation and its neutralisation is clearly a rich and complex topic, not only because it continues after the laser interaction, but also due to the newly observed plasma properties in the time after laser–plasma interaction. It has been shown that the threshold between low- and high-power laser interactions (i.e., around 1 × 1014 W cm−2 μm2) can also be related to the occurrence of EMPs, since the generation of EMP is related to nonlinear processes leading to the production of hot electrons. Ablation experiments at low fluences showed that the solid-state target can be used as a specific sensor for monitoring ongoing laser ablation processes. This diagnosis should be supplemented by the observation of the electrostatic field in the target chamber, namely, to complete knowledge about changes in the plasma during its expansion into the vacuum. This specifies the lack of experimental knowledge about the whole plasma expansion process.
The use of a unique inductive probe for measuring the short-circuit return target current induced by the interaction of a high-power laser with the target made it possible to find one of the largest rates of current change at the level of 1012 A/s. This phenomenon is not satisfactorily explained because experiments have not confirmed the assumption that this current only balances the charge carried away by hot electrons from the target since the difference between both measured charges is at least one order of magnitude. The measurement of time-resolved wake fields using broadband antennas can also contribute to the clarification of this phenomenon.
Author Contributions
Conceptualisation, J.K. and V.N.; methodology, J.K., M.K., S.A., V.N., and S.S.; validation, J.K., M.K., and V.N.; formal analysis, S.S.; investigation, M.K. and S.A.; data curation, M.K. and S.A.; writing—original draft preparation, J.K. and V.N.; writing—review and editing, J.K., V.N., and S.S.; visualisation, S.S.; supervision, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Czech Ministry of and Education, Youth Sports (grant no. LM2023068), and the Grant Agency of the Czech Republic (grant no. GM23-05027M).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pathak, V.B.; Lee, S.K.; Pae, K.H.; Hojbota, C.I.; Kim, C.M.; Nam, C.H. Strong field physics pursued with petawatt lasers. AAPPS Bull. 2021, 31, 4. [Google Scholar] [CrossRef]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751–793. [Google Scholar] [CrossRef]
- Tajima, T.; Yan, X.Q.; Ebisuzak, T. Wakefield acceleration. Rev. Mod. Plasma Phys. 2020, 4, 7. [Google Scholar] [CrossRef]
- Tabak, M.; Hammer, J.; Glinsky, M.E.; Kruer, W.L.; Wilks, S.C.; Woodworth, J.; Campbell, E.M.; Perry, M.D.; Mason, R.J. Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1994, 1, 1626–1634. [Google Scholar] [CrossRef]
- Malka, V.; Faure, J.; Marques, J.; Amiranoff, F.; Rousseau, J.-P.; Ranc, S.; Chambaret, J.P.; Walton, B.; Mora, P.; Solodov, A. Characterization of electron beams produced by ultrashort (30 fs) laser pulses. Phys. Plasmas 2001, 8, 2605–2608. [Google Scholar] [CrossRef]
- Lécz, Z.; Polanek, R.; Andreev, A.; Sharma, A.; Papp, D.; Hafz, N.; Kamperidis, C. Hybrid acceleration of compact ion bunches by few-cycle laser pulses in gas jets of two atomic species. Phy. Rev. Res. 2023, 5, 023169. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, M.; Zhang, X.; Lv, C.; Song, J.; Wang, Z.; Yang, G.; Yang, Y.; Wang, J.; Li, Q.; et al. Characteristic diagnosis of supersonic gas jet target for laser wakefield acceleration with high spatial-temporal resolution Nomarski interference system. Front. Phys. 2023, 11, 1203946. [Google Scholar] [CrossRef]
- Bradley, D.; Sheppard, C.G.W.; Suardjaja, I.M.; Woolley, R. Fundamentals of high-energy spark ignition with lasers. Combust. Flame 2004, 138, 55–77. [Google Scholar] [CrossRef]
- Kim, K.Y.; Glownia, J.H.; Taylor, A.J.; Rodriguez, G. Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields. Opt. Express 2007, 15, 4577–4584. [Google Scholar] [CrossRef]
- Englesbe, A.; Elle, J.; Schwartz, R.; Garrett, T.; Woodbury, D.; Jang, D.; Kim, K.-Y.; Milchberg, H.; Reid, R.; Lucero, A.; et al. Ultrabroadband microwave radiation from near- and mid-infrared laser-produced plasmas in air. Phys. Rev. A 2021, 104, 013107. [Google Scholar] [CrossRef]
- Brinckerhoff, W.B.; Managadze, G.G.; McEntire, R.W.; Cheng, A.F.; Green, W.J. Laser time-of-flight mass spectrometry for space. Rev. Sci. Instrum. 2000, 71, 536–545. [Google Scholar] [CrossRef]
- Zayhowski, J.J. Passively Q-switched Nd: YAG microchip lasers and applications. J. Alloys Comp. 2000, 303, 393–400. [Google Scholar] [CrossRef]
- Hahn, D.W.; Omenetto, N. Laser-induced breakdown spectroscopy (LIBS), part II: Review of instrumental and methodological approaches to material analysis and applications to different fields. Appl. Spectrosc. 2012, 66, 347–419. [Google Scholar] [CrossRef]
- Hegelich, B.M.; Albright, B.J.; Cobble, J.; Flippo, K.; Letzring, S.; Paffett, M.; Ruhl, H.; Schreiber, J.; Schulze, R.K.; Fernández, J.C. Laser acceleration of quasi-monoenergetic MeV ion beams. Nature 2006, 439, 441–444. [Google Scholar] [CrossRef]
- Labaune, C.; Baccou, C.; Depierreux, S.; Goyon, C.; Loisel, G.; Yahia, V.; Rafelski, J. Fusion reactions initiated by laser-accelerated particle beams in a laser-produced plasma. Nat. Commun. 2013, 4, 2506. [Google Scholar] [CrossRef]
- Consoli, F.; Tikhonchuk, V.T.; Bardon, M.; Bradford, P.; Carroll, D.C.; Cikhardt, J.; Cipriani, M.; Clarke, R.J.; Cowan, T.E.; Danson, C.N.; et al. Laser produced electromagnetic pulses: Generation, detection, and mitigation. High Power Laser Sci. Eng. 2020, 8, e22. [Google Scholar] [CrossRef]
- Bradford, P.; Woolsey, N.C.; Scott, G.G.; Liao, G.; Liu, H.; Zhang, Y.; Zhu, B.; Armstrong, C.; Astbury, S.; Brenner, C.; et al. EMP control and characterization on high-power laser systems. High Power Laser Sci. Eng. 2018, 6, e21. [Google Scholar] [CrossRef]
- Kugland, N.L.; Aurand, B.; Brown, C.G.; Constantin, C.G.; Everson, E.T.; Glenzer, S.H.; Schaeffer, D.B.; Tauschwitz, A.; Niemann, C. Demonstration of a low electromagnetic pulse laser-driven argon gas jet x-ray source. Appl. Phys. Lett. 2012, 101, 024102. [Google Scholar] [CrossRef]
- Dubois, J.L.; Rączka, P.; Hulin, S.; Rosiński, M.; Ryć, L.; Parys, P.; Zaraś-Szydłowska, A.; Makaruk, D.; Tchórz, P.; Badziak, J.; et al. Experimental demonstration of an electromagnetic pulse mitigation concept for a laser driven proton source. Rev. Sci. Instrum. 2018, 89, 103301. [Google Scholar] [CrossRef]
- Gitomer, S.J.; Jones, R.D.; Begay, F.; Ehler, A.W.; Kephart, J.F.; Kristal, R. Fast ions and hot electrons in the laser–plasma interaction. Phys. Fluids 1986, 29, 2679–2688. [Google Scholar] [CrossRef]
- Courtois, C.; Ash, A.D.; Chambers, D.M.; Grundy, R.A.D.; Woolsey, N.C. Creation of a uniform high magnetic-field strength environment for laser-driven experiments. J. Appl. Phys. 2005, 98, 054913. [Google Scholar] [CrossRef]
- Brown, C.J., Jr.; Throop, A.; Eder, D.; Kimbrough, J. Electromagnetic pulses at short-pulse laser facilities. J. Phys. Conf. Ser. 2008, 112, 032025. [Google Scholar] [CrossRef]
- Dubois, J.L.; Lubrano-Lavaderci, F.; Raffestin, D.; Ribolzi, J.; Gazave, J.; Compant La Fontaine, A.; D’Humières, E.; Hulin, S.; Nicolaï, P.; Poyé, A.; et al. Target charging in short-pulse-laser–plasma experiments. Phys. Rev. E 2014, 89, 013102. [Google Scholar] [CrossRef]
- Nassisi, V.; Delle Side, D.; Monteduro, L.; Giuffreda, E. Mapping of acceleration field in FSA configuration of a LIS. J. Instrum. 2016, 11, C05014. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Mead, M.J.; Neely, D.; Gauoin, J.; Heathcote, R.; Patel, P. Electromagnetic pulse generation within a petawatt laser target chamber. Rev. Sci. Instrum. 2004, 75, 4225. [Google Scholar] [CrossRef]
- Mendel, C.W., Jr. Apparatus for measuring rapidly varying electric fields in plasmas. Rev. Sci. Instrum. 1975, 46, 847–850. [Google Scholar] [CrossRef]
- Borghesi, M.; Sarri, G.; Cecchetti, C.A.; Kourakis, I.; Hoarty, D.; Stevenson, R.M.; James, S.; Brown, C.D.; Hobbs, P.; Lockyear, J.; et al. Progress in proton radiography for diagnosis of ICF-relevant plasmas. Laser Part. Beams 2010, 28, 277–284. [Google Scholar] [CrossRef]
- Manuel, M.E.; Sinenian, N.; Séguin, F.H.; Li, C.K.; Frenje, J.A.; Rinderknecht, H.G.; Casey, D.T.; Zylstra, A.B.; Petrasso, R.D.; Beg, F.N. Mapping return currents in laser-generated Z-pinch plasmas using proton deflectometry. Appl. Phys. Lett. 2012, 100, 203505. [Google Scholar] [CrossRef]
- Krása, J.; Delle Side, D.; Giuffreda, E.; Nassisi, V. Characteristics of target polarization by laser ablation. Laser Part. Beams 2015, 33, 601–605. [Google Scholar] [CrossRef]
- Eliezer, S.; Hora, H. Double layers in laser-produced plasmas. Phys. Rep. 1989, 172, 339–407. [Google Scholar] [CrossRef]
- Eliezer, S.; Nissim, N.; Val, J.M.M.; Mima, K.; Hora, H. Double layer acceleration by laser radiation. Laser Part. Beams 2014, 32, 211–216. [Google Scholar] [CrossRef]
- Bulgakova, N.M.; Bulgakov, A.V. Pulsed laser ablation of solids: Transition from normal vaporization to phase explosion. Appl. Phys. A 2001, 73, 199–208. [Google Scholar] [CrossRef]
- Marla, D.; Bhandarkar, U.V.; Joshi, S.S. A model of laser ablation with temperature-dependent material properties, vaporization, phase explosion and plasma shielding. Appl. Phys. A 2014, 116, 273–285. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Dahlbacka, G.H. Charge separation and target voltages in laser produced plasmas. Appl. Phys. Lett. 1977, 31, 414–417. [Google Scholar] [CrossRef]
- Poyé, A.; Dubois, J.-L.; Lubrano-Lavaderci, F.; D’Humières, E.; Bardon, M.; Hulin, S.; Bailly-Grandvaux, M.; Ribolzi, J.; Raffestin, D.; Santos, J.J.; et al. Dynamic model of target charging by short laser pulse interactions. Phys. Rev. E 2015, 92, 043107. [Google Scholar] [CrossRef] [PubMed]
- Krása, J.; Nassisi, V.; Klír, D. Target holder as a specific sensor for laser-induced plasma ablation. Phys. Lett. A 2021, 385, 126980. [Google Scholar] [CrossRef]
- Krása, J.; Nassisi, V.; Klír, D. Effect of grounding and isolation of the target on the emissive properties of laser-produced plasma. Phys. Plasmas 2021, 28, 092104. [Google Scholar] [CrossRef]
- Tudisco, S.; Mascali, D.; Gambino, N.; Anzalone, A.; Gammino, S.; Musumeci, F.; Scordino, A.; Spitaleri, A. Investigation of laser-produced aluminum plasma. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 653, 47–51. [Google Scholar] [CrossRef]
- Tan, T.H.; McCall, G.H.; Williams, A.H. Determination of laser intensity and hot-electron temperature from fastest ion velocity measurement on laser-produced plasma. Phys. Fluids 1984, 27, 296–301. [Google Scholar] [CrossRef]
- Krása, J.; Burian, T.; Hájková, V.; Chalupský, J.; Jelínek, Š.; Frantálová, K.; Krupka, M.; Kuglerová, Z.; Singh, S.K.; Vozda, V.; et al. Ion emission from warm dense matter produced by irradiation with a soft x-ray free-electron laser. Matter Radiat. Extremes 2024, 9, 016602. [Google Scholar] [CrossRef]
- Price, C.J.; Donnelly, T.D.; Giltrap, S.; Stuart, N.H.; Parker, S.; Patankar, S.; Lowe, H.F.; Drew, D.; Gumbrell, E.T.; Smith, R.A. An in-vacuo optical levitation trap for high-intensity laser interaction experiments with isolated microtargets. Rev. Sci. Instrum. 2015, 86, 033502. [Google Scholar] [CrossRef] [PubMed]
- Sinenian, N.; Manuel, M.J.; Frenje, J.A.; Séguin, F.H.; Li, C.K.; Petrasso, R.D. An empirical target discharging model relevant to hot-electron preheat in direct-drive implosions on OMEGA. Plasma Phys. Control. Fusion 2013, 55, 045001. [Google Scholar] [CrossRef][Green Version]
- Giuffreda, E.; Delle Side, D.; Nassisi, V.; Krása, J. Plasma production in carbon-based materials. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 406, 225. [Google Scholar] [CrossRef]
- Delle Side, D.; Caricato, A.P.; Krása, J.; Nassisi, V. On the origin of negative target currents during laser ablation of polyethylene. EPJ Web Conf. EDP Sci. 2018, 167, 04006. [Google Scholar] [CrossRef][Green Version]
- Raimbourg, J. Electromagnetic compatibility management for fast diagnostic design. Rev. Sci. Instrum. 2004, 75, 4234–4236. [Google Scholar] [CrossRef]
- Stoeckl, C.; Glebov, V.Y.; Jaanimagi, P.A.; Knauer, J.P.; Meyerhofer, D.D.; Sangster, T.C.; Storm, M.; Sublett, S.; Theobald, W.; Key, M.H.; et al. Operation of target diagnostics in a petawatt laser environment. Rev. Sci. Instrum. 2006, 77, 10F506. [Google Scholar] [CrossRef]
- Bourgade, J.L.; Marmoret, R.; Darbon, S.; Rosch, R.; Troussel, P.; Villette, B.; Glebov, V.; Shmayda, W.T.; Gomme, J.C.; Le Tonqueze, Y.; et al. Diagnostics hardening for harsh environment in laser megajoule. Rev. Sci. Instrum. 2008, 79, 10F301. [Google Scholar] [CrossRef] [PubMed]
- Eder, D.C.; Throop, A.; Brown, C.G., Jr.; Kimbrough, J.; Stowell, M.L.; White, D.A.; Song, P.; Back, N.; MacPhee, A.; Chen, H.; et al. Mitigation of Electromagnetic Pulse (EMP) Effects from Short-Pulse Lasers and Fusion Neutrons; Technical Report, LLNL-TR-411183; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2009. [Google Scholar]
- Krása, J.; KlÍr, D.; Řezáč, K.; Cikhardt, J.; Velyhan, A.; Pfeifer, M.; Dostál, J.; Krůs, M.; Dudžák, R.; Buryšková, S.; et al. Target current: An appropriate parameter for characterizing the dynamics of laser-matter interaction. In Proceedings of the XXII International Symposium on High Power Laser Systems and Applications, Frascati, Italy, 9–12 October 2019; Volume 11042. [Google Scholar] [CrossRef]
- Benjamin, R.F.; McCall, G.H.; Ehler, A.W. Measurement of return current in a laser-produced plasma. Phys. Rev. Lett. 1979, 42, 890–893. [Google Scholar] [CrossRef]
- Cikhardt, J.; Krása, J.; De Marco, M.; Pfeifer, M.; Velyhan, A.; Krouský, E.; Cikhardtová, B.; Klír, D.; Rezáč, K.; Ullschmied, J.; et al. Measurement of the target current by inductive probe during laser interaction on terawatt laser system PALS. Rev. Sci. Instrum. 2014, 85, 103507. [Google Scholar] [CrossRef]
- Krupka, M.; Singh, S.; Pisarczyk, T.; Dostal, J.; Kalal, M.; Krasa, J.; Dudzak, R.; Burian, T.; Jelinek, S.; Chodukowski, T.; et al. Design of modular multi-channel electron spectrometers for application in laser matter interaction experiments at Prague Asterix Laser System. Rev. Sci. Instrum. 2021, 92, 023514. [Google Scholar] [CrossRef]
- Pisarczyk, T.; Kalal, M.; Gus’kov, S.Y.; Batani, D.; Renner, O.; Santos, J.; Dudzak, R.; Zaras-Szydłowska, A.; Chodukowski, T.; Rusiniak, Z.; et al. Hot electron retention in laser plasma created under terawatt subnanosecond irradiation of Cu targets. Plasma Phys. Control. Fusion 2020, 62, 115020. [Google Scholar] [CrossRef]
- Yi, T.; Yang, J.; Yang, M.; Wang, C.; Yang, W.; Li, T.; Liu, S.; Jiang, S.; Ding, Y.; Xiao, S. Investigation into the electromagnetic impulses from long pulse laser illuminating solid targets inside a laser facility. Photonic Sens. 2016, 6, 249–255. [Google Scholar] [CrossRef][Green Version]
- Xia, Y.; Li, D.; Zhang, S.; Wu, M.; Yang, T.; Geng, Y.; Zhu, J.; Xu, X.; Li, C.; Wang, C.; et al. Enhancing electromagnetic radiations by a pre-ablation laser during laser interaction with solid target. Phys. Plasmas 2020, 27, 032705. [Google Scholar] [CrossRef]
- Nelissen, K.; Liszi, M.; De Marco, M.; Ospina, V.; Drotár, I.; Gatti, G.; Kamperidis, C.; Volpe, L. Characterisation and modelling of ultrashort laser-driven electromagnetic pulses. Sci. Rep. 2020, 10, 3108. [Google Scholar] [CrossRef]
- Rączka, P.; Nowosielski, L.; Rosinski, M.; Makaruk, D.; Makowski, J.; Zaras-Szydłowska, A.; Tchórz, P.; Badziak, J. Measurement of the electric field strength generated in the experimental chamber by 10 TW femtosecond laser pulse interaction with a solid target. J. Instrum. 2019, 14, P04008. [Google Scholar] [CrossRef]
- Vinoth Kumar, L.; Manikanta, E.; Leela, C.; Prem Kiran, P. Spectral selective radio frequency emissions from laser induced breakdown of target materials. Appl. Phys. Lett. 2014, 105, 064102. [Google Scholar] [CrossRef]
- Ostrovskaya, G.V.; Zaĭdel’, A.N. Laser spark in gases. Sov. Phys. Usp. 1974, 16, 834–855. [Google Scholar] [CrossRef]
- Englesbe, A.; Elle, J.; Reid, R.; Lucero, A.; Pohle, H.; Domonkos, M.; Kalmykov, S.; Krushelnik, K.; Schmitt-Sody, A. Gas pressure dependence of microwave pulses generated by laser-produced filament plasmas. Opt. Lett. 2018, 43, 4953–4956. [Google Scholar] [CrossRef]
- Blair, G.; Sprangle, P. Generation of rf radiation by low-intensity laser pulse trains in air. Phys. Rev. E 2023, 108, 015203. [Google Scholar] [CrossRef]
- Link, A.; Freeman, R.R.; Schumacher, D.W.; Van Woerkom, L.D. Effects of target charging and ion emission on the energy spectrum of emitted electrons. Phys. Plasmas 2011, 18, 053107. [Google Scholar] [CrossRef]
- Cristoforetti, G.; Antonelli, L.; Atzeni, S.; Baffigi, F.; Barbato, F.; Batani, D.; Boutoux, G.; Colaitis, A.; Dostal, J.; Dudzak, R.; et al. Measurements of parametric instabilities at laser intensities relevant to strong shock generation. Phys. Plasmas 2018, 25, 012702. [Google Scholar] [CrossRef]
- Prasad, Y.B.S.R.; Barnwal, S.; Bolkhovitinov, E.A.; Naik, P.A.; Kamath, M.P.; Joshi, A.S.; Kumbhare, S.R.; Rupasov, A.A.; Gupta, P.D. Study of self-generated magnetic fields in laser produced plasmas using a three-channel polaro-interferometer. Rev. Sci. Instrum. 2011, 82, 123506. [Google Scholar] [CrossRef] [PubMed]
- Pisarczyk, T.; Gus’kov, S.Y.; Dudzak, R.; Chodukowski, T.; Dostal, J.; Demchenko, N.N.; Korneev, P.; Kalinowska, Z.; Kalal, M.; Renner, O.; et al. Space-time resolved measurements of spontaneous magnetic fields in laser-produced plasma. Phys. Plasmas 2015, 22, 102706. [Google Scholar] [CrossRef]
- Kalal, M. Complex interferometry: Its principles and applications to fully automated on-line diagnostics. Czech. J. Phys. 1991, 41, 743–748. [Google Scholar] [CrossRef]
- Bolkhovitinov, E.A.; Gospodinov, G.A.; Ivanov, K.A.; Rupasov, A.A.; Savel’ev, A.B. Three-channel polaro-interferometer for laser-produced plasma diagnostics with femtosecond time resolution. Quantum Electron. 2019, 49, 577. [Google Scholar] [CrossRef]
- Singh, S.; Versaci, R.; Laso Garcia, A.; Morejon, L.; Ferrari, A.; Molodtsova, M.; Schwengner, R.; Kumar, D.; Cowan, T. Compact high energy X-ray spectrometer based on forward Compton scattering for high intensity laser plasma experiments. Rev. Sci. Instrum. 2018, 89, 085118. [Google Scholar] [CrossRef] [PubMed]
- Haden, D.; Golovin, G.; Yan, W.; Fruhling, C.; Zhang, P.; Zhao, B.; Banerjee, S.; Umstadter, D. High energy X-ray Compton spectroscopy via iterative reconstruction. Nucl. Instrum. Methods A 2020, 951, 163032. [Google Scholar] [CrossRef]
- Singh, S.; Krupka, M.; Istokskaia, V.; Krasa, J.; Giuffrida, L.; Dudzak, R.; Dostal, J.; Burian, T.; Versaci, R.; Margarone, D.; et al. Hot electron and x-ray generation by sub-ns kJ-class laser-produced tantalum plasma. Plasma Phys. Control. Fusion 2022, 64, 105012. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).