Comparison of Saturation Rules Used for Gyrokinetic Quasilinear Transport Modeling
Abstract
:1. Introduction
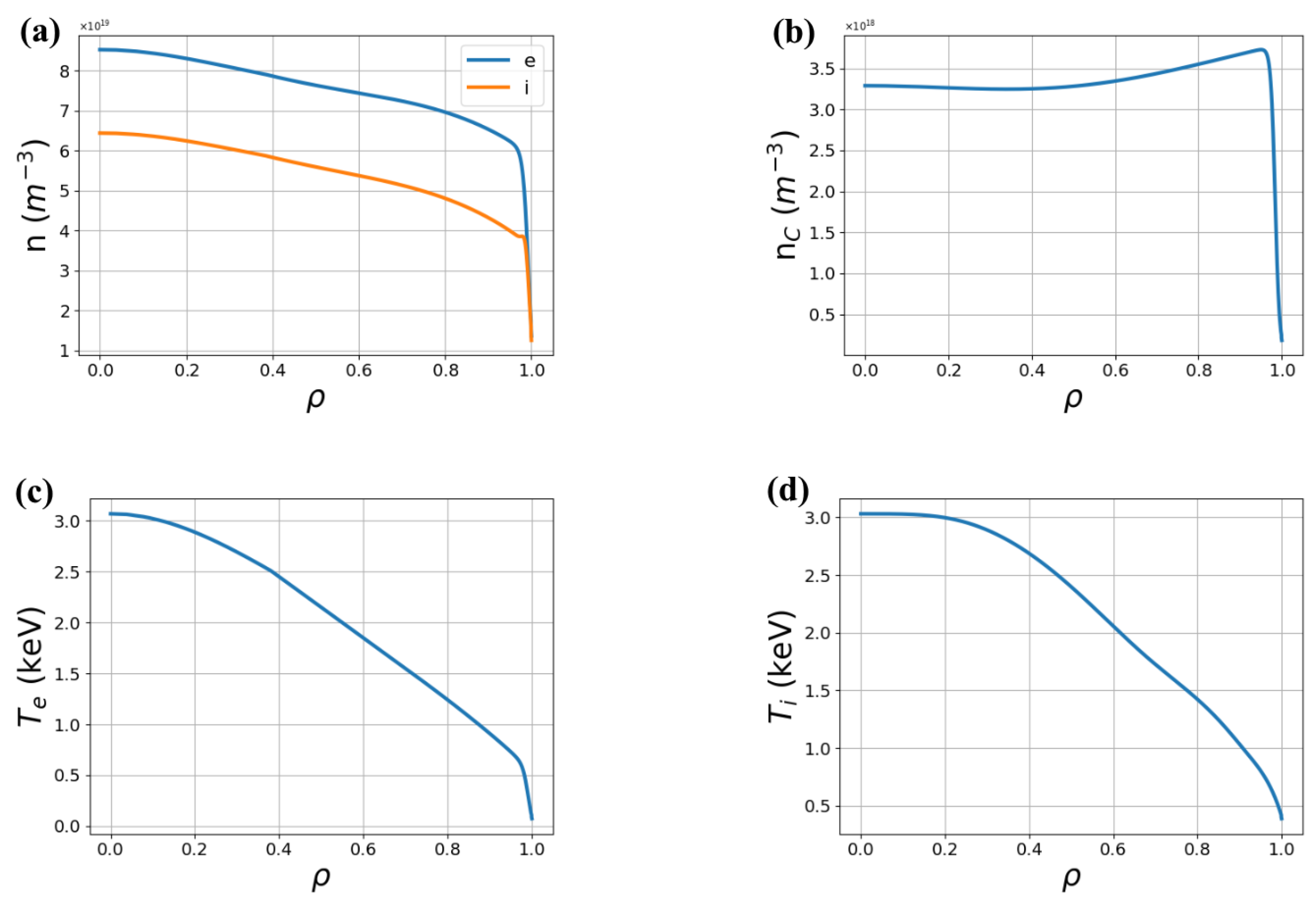
2. Tokamak Plasma Parameters and Assumptions
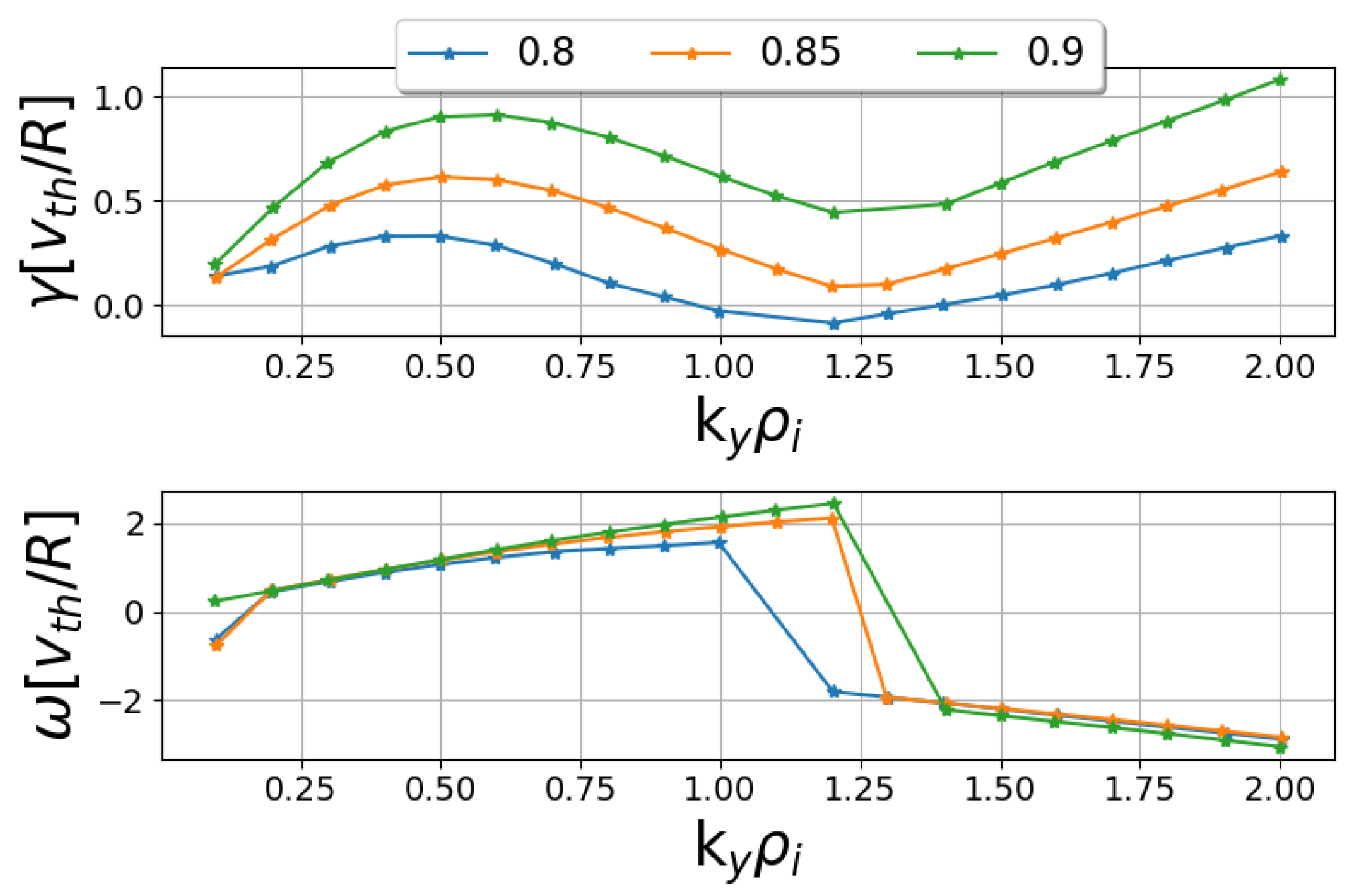
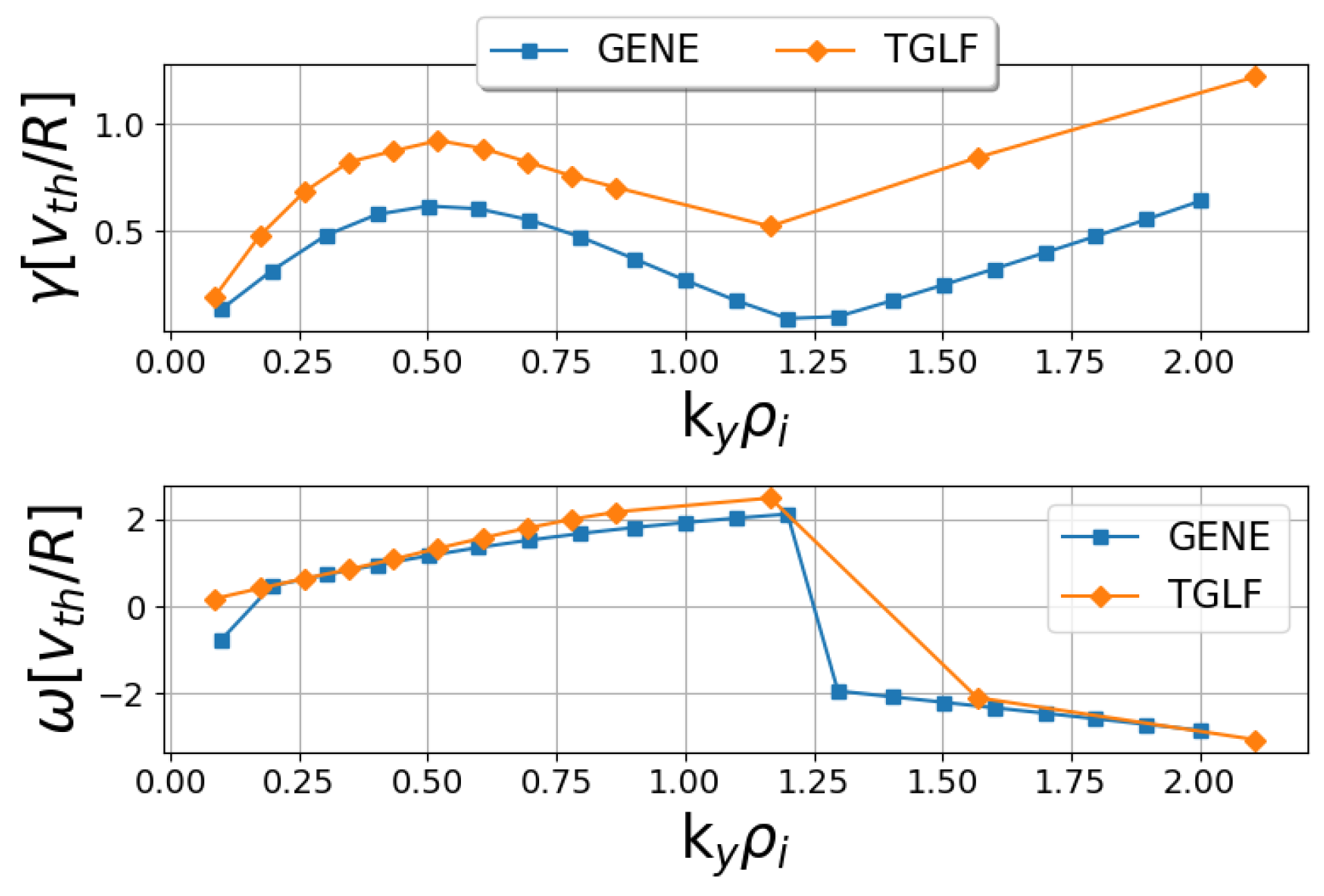
3. Linear Analysis
4. Quasilinear Theory
4.1. Quasilinear Expression of Fluxes Using Linear Gyrokinetic Simulation
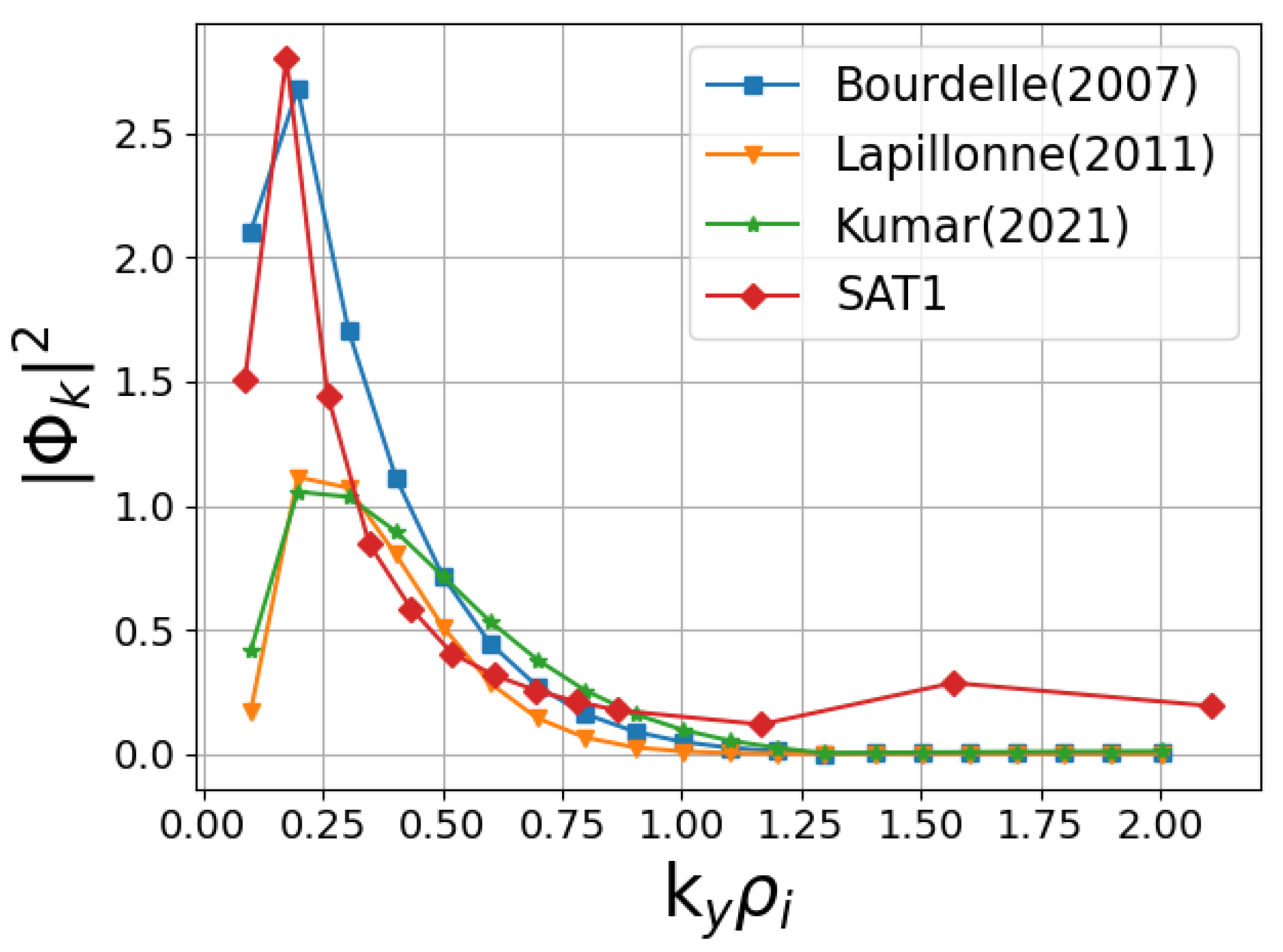
4.2. Saturation Rules
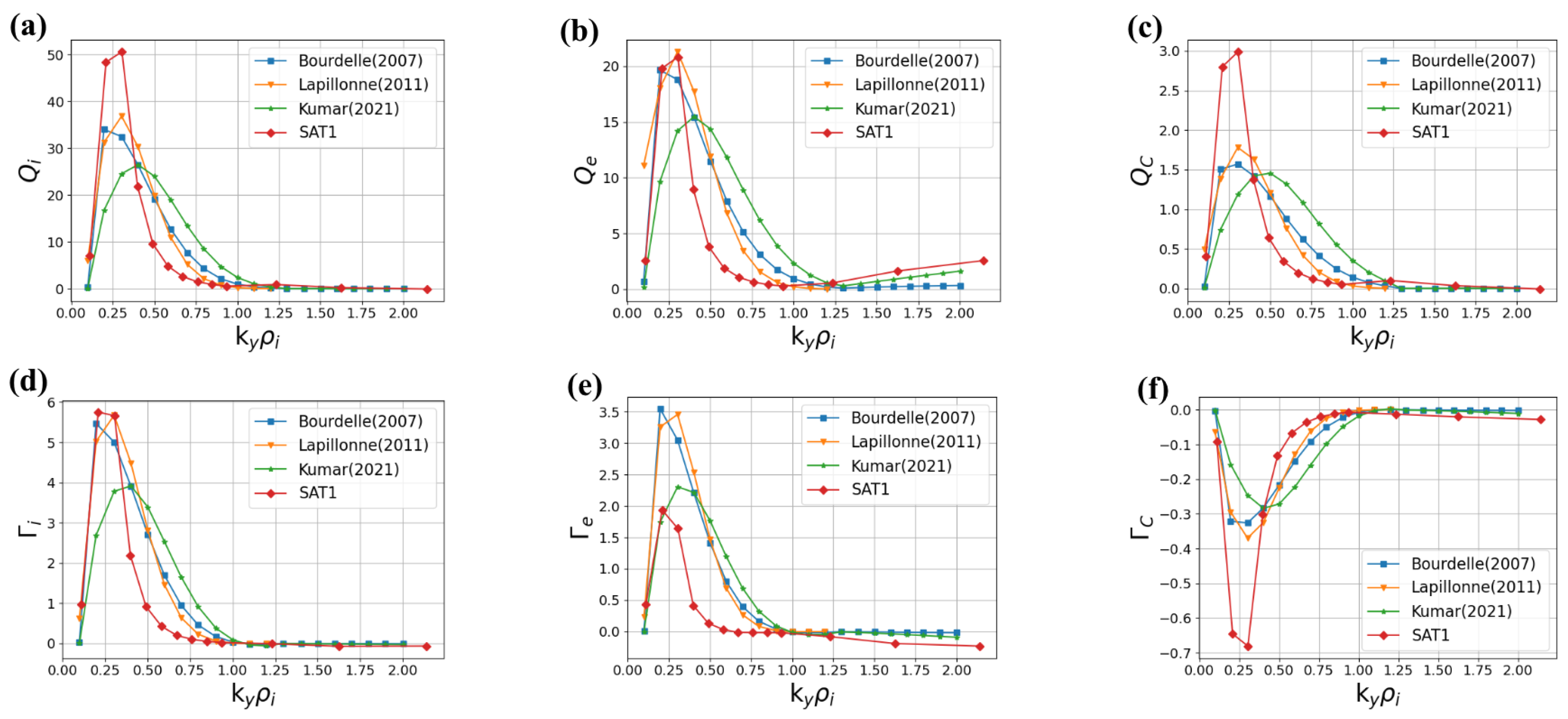
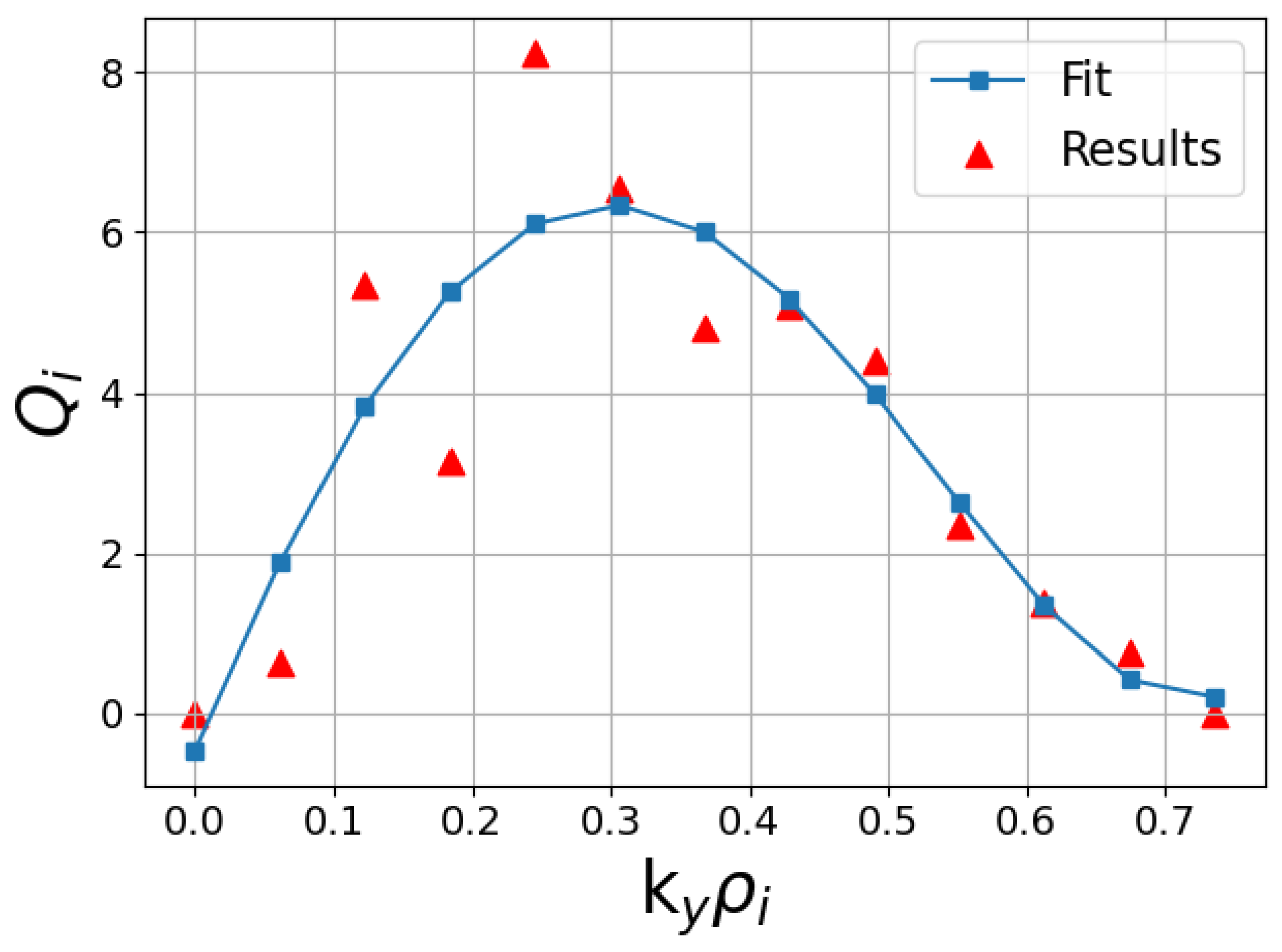
4.3. Saturation Levels and Quasilinear Fluxes
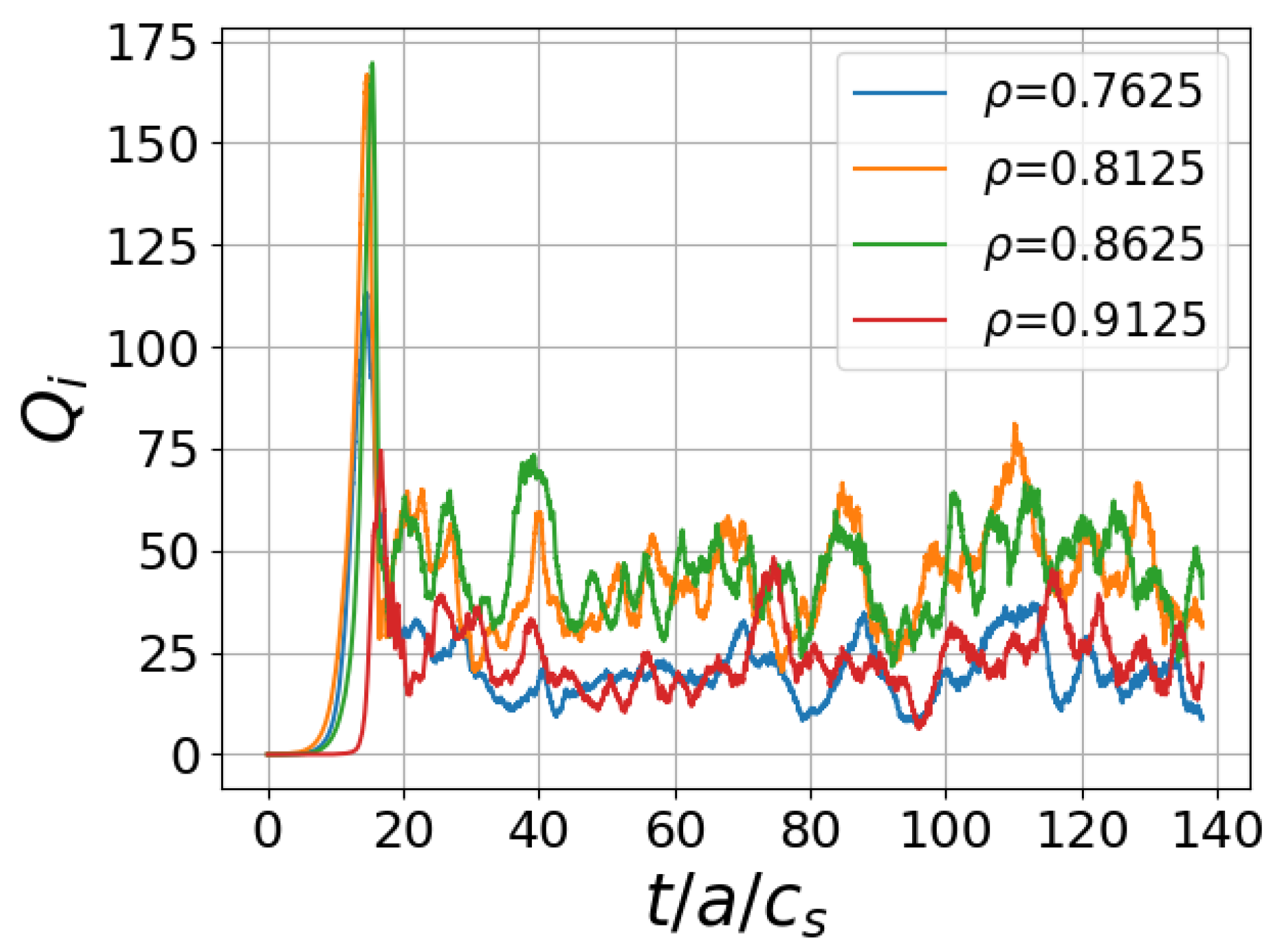
5. Comparison with Nonlinear Gyrokinetic Simulations
6. Discussion and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Staebler, G.; Kinsey, J.; Waltz, R. Gyro-Landau fluid equations for trapped and passing particles. Phys. Plasmas 2005, 12, 102508. [Google Scholar] [CrossRef]
- Staebler, G.; Kinsey, J.; Waltz, R. A theory-based transport model with comprehensive physics. Phys. Plasmas 2007, 14, 055909. [Google Scholar] [CrossRef]
- Kinsey, J.E.; Staebler, G.M.; Candy, J.; Petty, C.C.; Rhodes, T.L.; Waltz, R.E. Predictions of the near edge transport shortfall in DIII-D L-mode plasmas using the trapped gyro-Landau-fluid model. Phys. Plasmas 2015, 22, 012507. [Google Scholar] [CrossRef]
- Staebler, G.; Candy, J.; Howard, N.T.; Holland, C. The role of zonal flows in the saturation of multi-scale gyrokinetic turbulence. Phys. Plasmas 2016, 23, 062518. [Google Scholar] [CrossRef]
- Kinsey, J.; Singer, C.; Cox, D.; Bateman, G. Systematic comparison of a theory-based transport model with a multi-tokamak profile database. Phys. Scr. 1995, 52, 428. [Google Scholar] [CrossRef]
- Bateman, G.; Kritz, A.; Kinsey, J.; Redd, A.; Weiland, J. Predicting temperature and density profiles in tokamaks. Phys. Plasmas 1998, 5, 1793. [Google Scholar] [CrossRef]
- Rafiq, T.; Kritz, A.; Weiland, J.; Pankin, A.; Luo, L. Physics basis of Multi-Mode anomalous transport module. Phys. Plasmas 2013, 20, 032506. [Google Scholar] [CrossRef]
- Weiland, J.; Zagorodny, A.; Rafiq, T. Theory for transport in magnetized plasmas. Phys. Scr. 2020, 95, 105607. [Google Scholar] [CrossRef]
- Bourdelle, C.; Garbet, X.; Imbeaux, F.; Casati, A.; Dubuit, N.; Guirlet, R.; Parisot, T. A new gyrokinetic quasilinear transport model applied to particle transport in tokamak plasmas. Phys. Plasmas 2007, 14, 112501. [Google Scholar] [CrossRef]
- Bourdelle, C.; Citrin, J.; Baiocchi, B.; Casati, A.; Cottier, P.; Garbet, X.; Imbeaux, F.; JET Contributors. Core turbulent transport in tokamak plasmas: Bridging theory and experiment with QuaLiKiz. Plasma Phys. Control Fusion 2016, 58, 014036. [Google Scholar] [CrossRef]
- Citrin, J.; Bourdelle, C.; Casson, F.J.; Angioni, C.; Bonanomi, N.; Camenen, Y.; Garbet, X.; Garzotti, L.; Görler, T.; Gürcan, O.; et al. Tractable flux-driven temperature, density, and rotation profile evolution with the quasilinear gyrokinetic transport model QuaLiKiz. Plasma Phys. Control Fusion 2017, 59, 124005. [Google Scholar] [CrossRef]
- Stephens, C.; Garbet, X.; Citrin, J.; Bourdelle, C.; van de Plassche, K.; Jenko, F. Quasilinear gyrokinetic theory: A derivation of QuaLiKiz. J. Plasma Phys. 2021, 87, 905870409. [Google Scholar] [CrossRef]
- Dannert, T.; Jenko, F. Gyrokinetic simulation of collisionless trapped-electron mode turbulence. Phys. Plasmas 2005, 12, 072309. [Google Scholar] [CrossRef]
- Fable, E.; Angioni, C.; Sauter, O. The role of ion and electron electrostatic turbulence in characterizing stationary particle transport in the core of tokamak plasmas. Plasma Phys. Control Fusion 2010, 52, 015007. [Google Scholar] [CrossRef]
- Lapillonne, X.; Brunner, S.; Sauter, O.; Villard, L.; Fable, E.; Görler, T.; Jenko, F.; Merz, F. Non-linear gyrokinetic simulations of microturbulence in TCV electron internal transport barriers. Plasma Phys. Control Fusion 2011, 53, 054011. [Google Scholar] [CrossRef]
- Tirkas, S.; Chen, H.; Merlo, G.; Jenko, F.; Parker, S. Zonal flow excitation in electron-scale tokamak turbulence. Nucl. Fusion 2023, 63, 026015. [Google Scholar] [CrossRef]
- Angioni, C.; Fable, E.; Greenwald, M.; Maslov, M.; Peeters, A.; Takenaga, H.; Weisen, H. Particle transport in tokamak plasmas, theory and experiment. Plasma Phys. Control Fusion 2009, 51, 124017. [Google Scholar] [CrossRef]
- Howard, N.; Holland, C.; Rhodes, T.; Candy, J.; Rodriguez-Fernandez, P.; Greenwald, M.; White, A.; Sciortino, F. The role of ion and electron-scale turbulence is setting heat and particle transport in the DIII-D ITER baseline scenario. Phys. Plasmas 2021, 28, 072502. [Google Scholar] [CrossRef]
- Loarte, A. Required R & D in Existing Fusion Facilities to Support the ITER Research Plan; Technical Report ITR-20-008; ITER Organization: Saint-Paul-lez-Durance, France, 2020. [Google Scholar]
- Angioni, C.; Bilato, R.; Casson, F.; Fable, E.; Mantica, P.; Odstrcil, T.; Valisa, M.; ASDEX Upgrade Team; JET Contributors. Gyrokinetic study of turbulent convection of heavy impurities in tokamak plasmas at comparable ion and electron heat fluxes. Nucl. Fusion 2017, 57, 022009. [Google Scholar] [CrossRef]
- Kumar, N.; Camenen, Y.; Benkadda, S.; Bourdelle, C.; Loarte, A.; Polevoi, A.; Widmer, F.; JET Contributors. Turbulent transport driven by kinetic ballooning modes in the inner core of JET hybrid H-modes. Nucl. Fusion 2021, 61, 036005. [Google Scholar] [CrossRef]
- Staebler, G.; Belli, E.; Candy, J.; Kinsey, J.; Dudding, H.; Patel, B. Verification of a quasi-linear model for gyrokinetic turbulent transport. Nucl. Fusion 2021, 61, 116007. [Google Scholar] [CrossRef]
- Candy, J.; Belli, E.; Bravenec, R. A high-accuracy Eulerian gyrokinetic solver for collisional plasmas. J. Comput. Phys. 2016, 324, 73. [Google Scholar] [CrossRef]
- Jenko, F.; Dorland, W.; Kotschenreuther, M.; Rogers, B. Electron temperature gradient driven turbulence. Phys. Plasmas 2000, 7, 1904. [Google Scholar] [CrossRef]
- Görler, T.; Lapillonne, X.; Brunner, S.; Dannert, T.; Jenko, F.; Merz, F.; Told, D. The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 2011, 230, 7053. [Google Scholar] [CrossRef]
- Chen, Y.; Parker, S.E. Electromagnetic gyrokinetic delta-f particle-in-cell turbulence simulation with realistic equilibrium profiles and geometry. J. Comput. Phys. 2007, 220, 839. [Google Scholar] [CrossRef]
- Hassan, E.; Hatch, D.; Halfmoon, M.; Curie, M.; Kotchenreuther, M.; Mahajan, S.; Merlo, G.; Groebner, R.; Nelson, A.; Diallo, A. Identifying the microtearing modes in the pedestal of DIII-D H-modes using gyrokinetic simulations. Nucl. Fusion 2021, 62, 026008. [Google Scholar] [CrossRef]
- Curie, M.; Larakers, J.; Hatch, D.; Nelson, A.; Diallo, A.; Hassan, E.; Guttenfelder, W.; Halfmoon, M.; Kotschenreuther, M.; Hazeltine, R.; et al. A survey of pedestal magnetic fluctuations using gyrokinetics and a global reduced model for microtearing stability. Phys. Plasmas 2022, 29, 042503. [Google Scholar] [CrossRef]
- Moser, A.L.; Casali, L.; Covele, B.M.; Leonard, A.W.; McLean, A.G.; Shafer, M.W.; Wang, H.Q.; Watkins, J.G. Separating divertor closure effects on divertor detachment and pedestal shape in DIII-D. Phys. Plasmas 2020, 27, 032506. [Google Scholar] [CrossRef]
- Miller, R.; Chu, M.; Greene, J.; Lin-Liu, Y.; Waltz, R. Noncircular, finite aspect ratio, local equilibrium model. Phys. Plasmas 1998, 5, 973. [Google Scholar] [CrossRef]
- Görler, T.; Tronko, N.; Hornsby, W.A.; Bottino, A.; Kleiber, R.; Norscini, C.; Grandgirard, V.; Jenko, F.; Sonnendrücker, E. Intercode comparison of gyrokinetic global electromagnetic modes. Phys. Plasmas 2016, 23, 072503. [Google Scholar] [CrossRef]
- Rafiq, T.; Kritz, A.H.; Weiland, J.; Luo, L.; Schuster, E. Study of the parametric dependence of linear and nonlinear microtearing modes in conventional tokamak discharges. Phys. Plasmas 2018, 25, 012504. [Google Scholar] [CrossRef]
- Parker, S.E.; Dorland, W.; Santoro, R.A.; Beer, M.A.; Liu, Q.P.; Lee, W.W.; Hammett, G.W. Comparisons of gyrofluid and gyrokinetic simulations. Phys. Plasmas 1994, 1, 1461–1468. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, J.; Parker, S.E. Effects of the heat source on the steady-state transport in gradient-driven global gyrokinetic simulations. Phys. Plasmas 2023, 30, 014502. [Google Scholar] [CrossRef]
- Howard, N.; Greenwald, M.; Mikkelsen, D.; Reinke, M.; White, A.; Ernst, D.; Podpaly, Y.; Candy, J. Quantitative comparison of experimental impurity transport with nonlinear gyrokinetic simulation in an Alcator C-Mod L-mode plasma. Nucl. Fusion 2012, 52, 063002. [Google Scholar] [CrossRef]
- Angioni, C.; Mantica, P.; Pütterich, T.; Valisa, M.; Baruzzo, M.; Belli, E.; Belo, P.; Casson, F.; Challis, C.; Drewelow, P.; et al. Tungsten transport in JET H-mode plasmas in hybrid scenario, experimental observations and modelling. Nucl. Fusion 2014, 54, 083028. [Google Scholar] [CrossRef]

| 0.8 | 6.71 | 7.49 | 0.87 | 1.44 | 2.40 | −0.71 | 5.16 | 2.28 | 1.75 | 1.00 | 1.47 | 0.21 | −0.03 |
| 0.85 | 9.16 | 8.94 | 0.87 | 1.84 | 3.06 | −0.75 | 5.37 | 2.56 | 2.17 | 0.85 | 1.51 | 0.24 | −0.04 |
| 0.9 | 12.49 | 11.17 | 0.88 | 2.36 | 3.98 | −0.79 | 5.65 | 2.97 | 2.94 | 0.67 | 1.55 | 0.28 | −0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, S.E.; Haubrich, C.S.; Tirkas, S.; Cai, Q.; Chen, Y. Comparison of Saturation Rules Used for Gyrokinetic Quasilinear Transport Modeling. Plasma 2023, 6, 611-622. https://doi.org/10.3390/plasma6040042
Parker SE, Haubrich CS, Tirkas S, Cai Q, Chen Y. Comparison of Saturation Rules Used for Gyrokinetic Quasilinear Transport Modeling. Plasma. 2023; 6(4):611-622. https://doi.org/10.3390/plasma6040042
Chicago/Turabian StyleParker, Scott E., Calder S. Haubrich, Stefan Tirkas, Qiheng Cai, and Yang Chen. 2023. "Comparison of Saturation Rules Used for Gyrokinetic Quasilinear Transport Modeling" Plasma 6, no. 4: 611-622. https://doi.org/10.3390/plasma6040042
APA StyleParker, S. E., Haubrich, C. S., Tirkas, S., Cai, Q., & Chen, Y. (2023). Comparison of Saturation Rules Used for Gyrokinetic Quasilinear Transport Modeling. Plasma, 6(4), 611-622. https://doi.org/10.3390/plasma6040042







