Aerosol Charging with a Piezoelectric Plasma Generator
Abstract
:1. Introduction
Aim of This Work
2. Materials and Methods
2.1. Diffusion Charging by Plasma Discharge
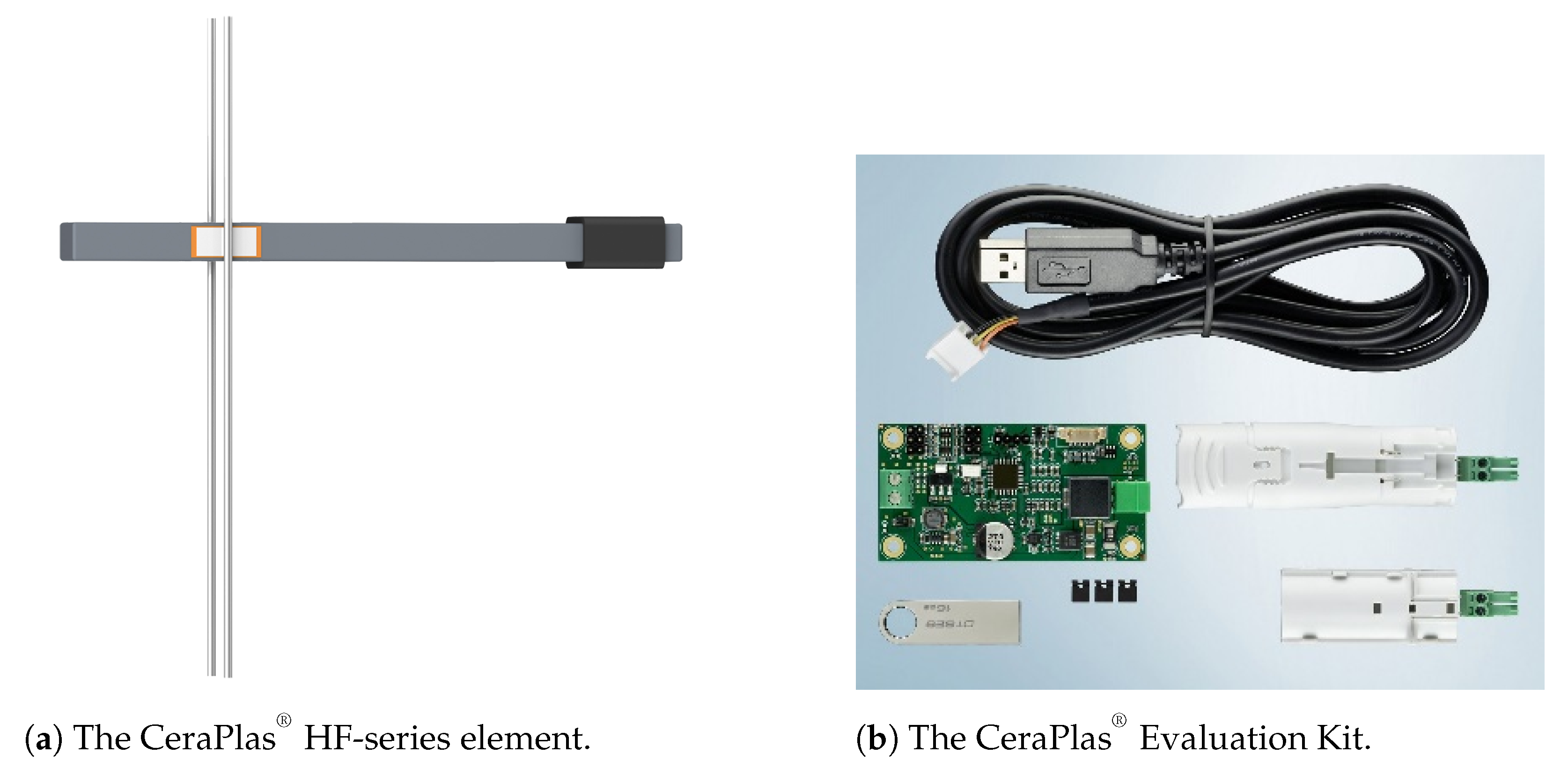
2.2. Description of the Plasma Source
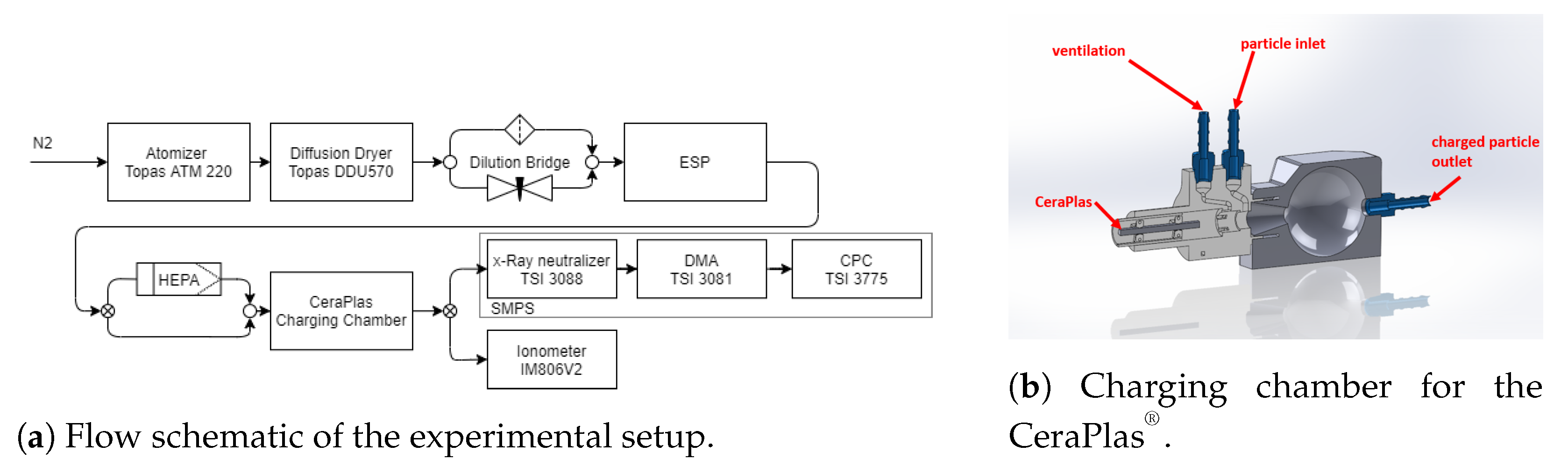
2.3. Feasibility Study Bipolar Charging
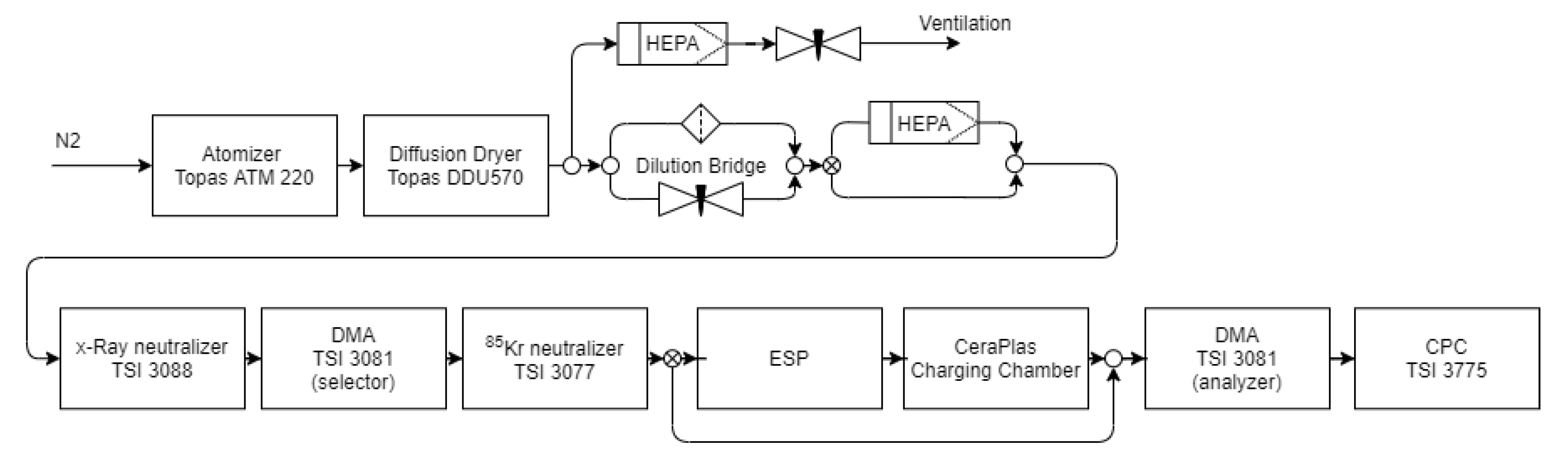
2.4. Charge Distribution Measurements
2.5. Ion Density Measurement
3. Results
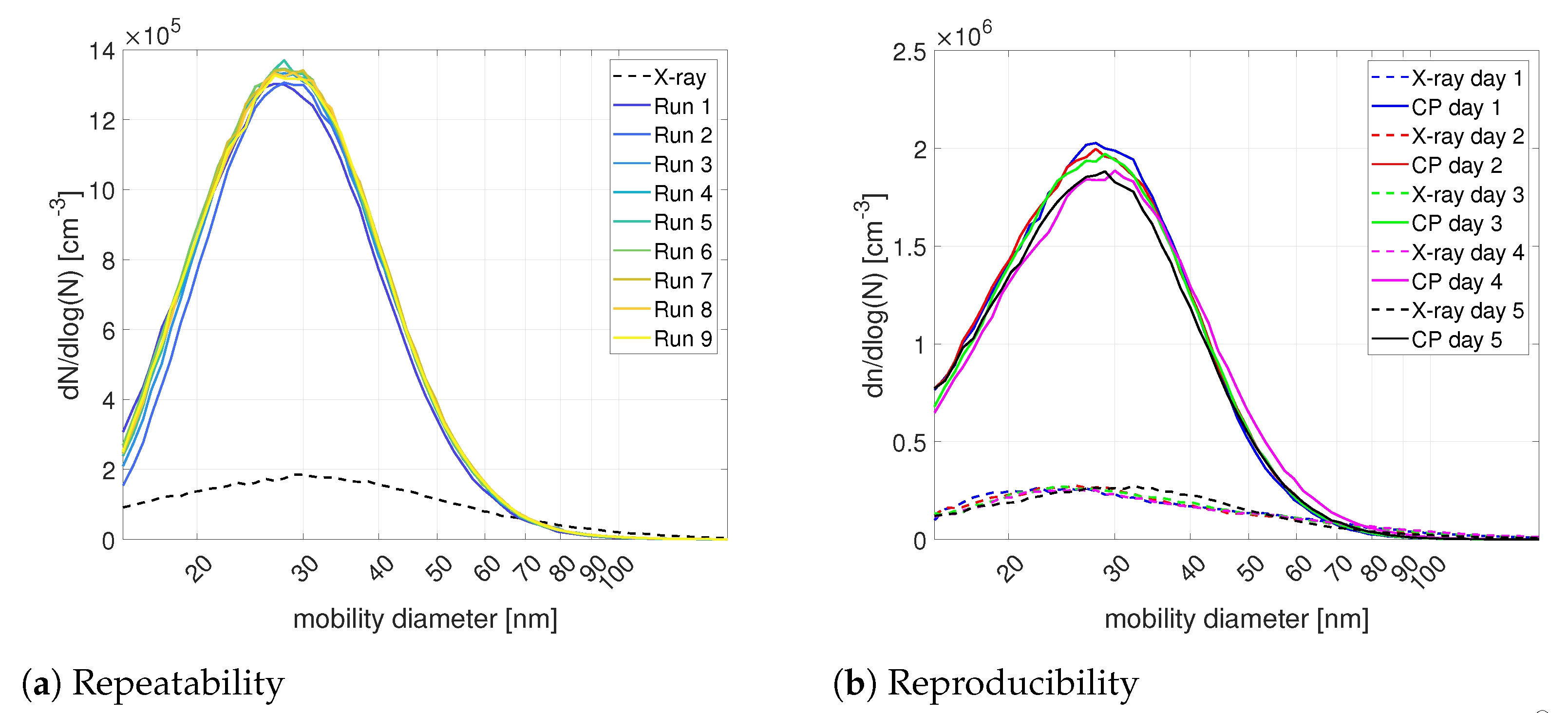
3.1. Feasibility Study Bipolar Charging
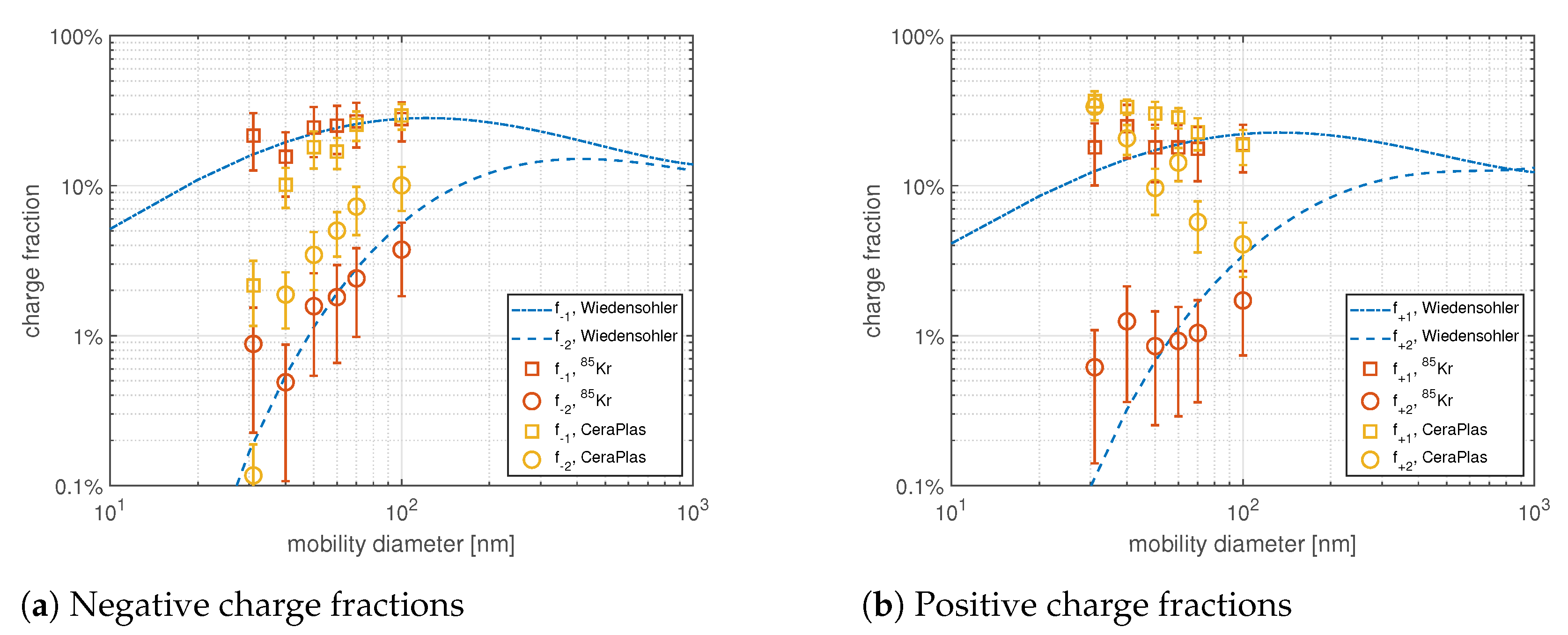
3.2. Charge Distribution Measurements
3.3. Ion Density Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
Abbreviations
| AAC | Aerodynamic Aerosol Classifier |
| AC | Alternating Current |
| CPC | Condensation Particle Counter |
| DBD | Dielectric Barrier Discharge |
| DMA | Differential Mobility Analyzer |
| ESP | Electrostatic Precipitator |
| H | Height |
| HEPA | High Efficiency Particle Air |
| HV | High Voltage |
| L | Length |
| PCPG | Piezoelectric Cold Plasma Generator |
| PDD | Piezoelectric Direct Discharge |
| PN | Particle Number |
| PZT | Lead Ziconite Titanate |
| SMPS | Scanning Mobility Patricle Sizer |
| UV | Ultra Violet |
| W | Width |
Appendix A. Evaluation of Bipolar Charge Distribution Curves
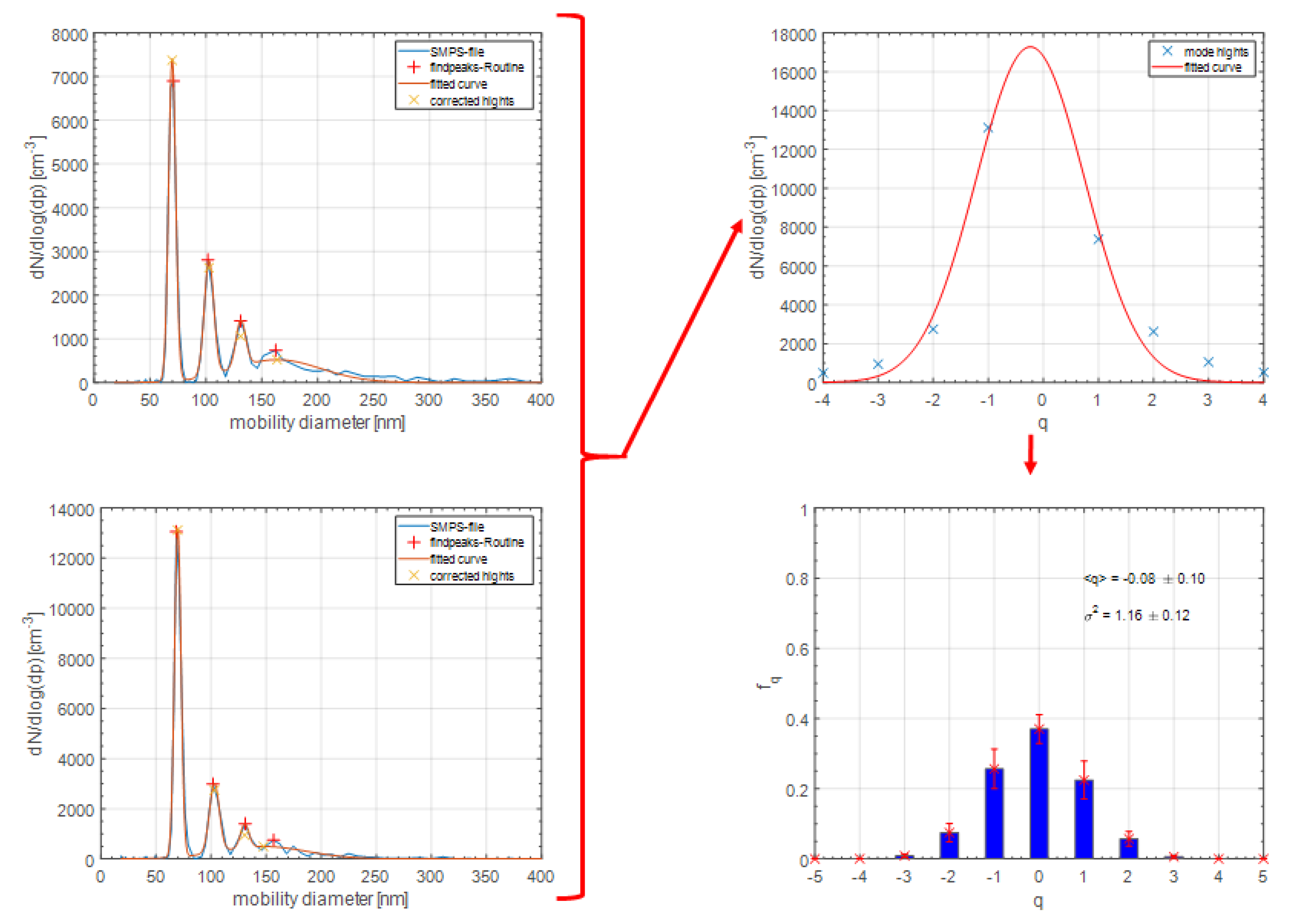
- Determination of the peak heights: Each peak of the mobility spectrum corresponds to a charge fraction. The main peak, which is located at the position of the selected mobility size (set by the selector DMA), corresponds to the singly charged particle fraction. Subsequent peaks correspond to multiply charged particles. Thus, relative peak heights represent the charge fractions. Due to peak overlapping, a multi-modal Gaussian fit is applied to determine the peak heights:with x being the mobility diameter in this case.
- Determination of the charge distribution assuming a Gaussian distribution function: The peak heights from the mobility spectra do not include the uncharged particle fraction. Therefore, the charge distribution is assumed to be Gaussian in shape (see Figure A1) in order to be able to determine the neutral fraction:The logarithmic curve is then fitted with a 2nd-order polynomial with the fitting coefficients , and . Mean and standard deviation of the fitting curve can then be calculated from the fit coefficients as:
- Calculation of uncertainties for the charge bins acc. to [15]:with the assumed uncertainties and .
| i | |||||
|---|---|---|---|---|---|
| 0 | −26.3328 | −2.3197 | 0.0003 | −2.3484 | −44.4756 |
| 1 | 35.9044 | 0.6175 | −0.1014 | 0.6044 | 79.3772 |
| 2 | −21.4608 | 0.6201 | 0.3073 | 0.4800 | −62.8900 |
| 3 | 7.0867 | −0.1105 | −0.3372 | 0.0013 | 26.4492 |
| 4 | −1.3088 | −0.1260 | 0.1203 | −0.1553 | −5.7480 |
| 5 | 0.1501 | 0.0297 | −0.0105 | 0.0320 | 0.5049 |
References
- Baron, P.A.; Willeke, K. Aerosol Measruement, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2001; p. 1063. [Google Scholar]
- Wiedensohler, A. An approximation of the bipolar charge distribution for particles in the submicron size range. J. Aerosol Sci. 1988, 19, 387–389. [Google Scholar] [CrossRef]
- INTERNATIONAL STANDARD ISO 15900 Determination of particle size distribution—Differential electrical mobility analysis for aerosol particles. J. Aerosol Sci. 2009.
- Nishida, R.T.; Johnson, T.J.; Hassim, J.S.; Graves, B.M.; Boies, A.M.; Hochgreb, S. A Simple Method for Measuring Fine-to-Ultrafine Aerosols Using Bipolar Charge Equilibrium. ACS Sens. 2020, 5, 447–453. [Google Scholar] [CrossRef]
- Schriefl, M.A.; Bergmann, A. Design principles for diffusion chargers sensing particle number concentration. Proc. IEEE Sens. 2017, 2–4. [Google Scholar] [CrossRef]
- Adachi, M.; Kousaka, Y.; Okuyama, K. Unipolar and bipolar diffusion charging of ultrafine aerosol particles. J. Aerosol Sci. 1985, 16, 109–123. [Google Scholar] [CrossRef]
- Knoll, M.; Schriefl, M.A.; Nishida, R.T.; Bergmann, A. Impact of pre-charged particles on steady state and pulsed modes of unipolar diffusion chargers. Aerosol Sci. Technol. 2021, 55, 512–525. [Google Scholar] [CrossRef]
- Schriefl, M.A.; Nishida, R.T.; Knoll, M.; Boies, A.M.; Bergmann, A. Characterization of particle number counters based on pulsed-mode diffusion charging. Aerosol Sci. Technol. 2020, 54, 772–789. [Google Scholar] [CrossRef]
- Fuchs, N.A. On the stationary charge distribution on aerosol particles in a bipolar ionic atmosphere. Geofis. Pura E Appl. 1963, 56, 185–193. [Google Scholar] [CrossRef]
- Pui, D.Y.; Fruin, S.; McMurry, P.H. Unipolar diffusion charging of ultrafine aerosols. Aerosol Sci. Technol. 1988, 8, 173–187. [Google Scholar] [CrossRef]
- Gopalakrishnan, R.; Thajudeen, T.; Ouyang, H.; Hogan, C.J. The unipolar diffusion charging of arbitrary shaped aerosol particles. J. Aerosol Sci. 2013, 64, 60–80. [Google Scholar] [CrossRef]
- Li, L.; Gopalakrishnan, R. An experimentally validated model of diffusion charging of arbitrary shaped aerosol particles. J. Aerosol Sci. 2021, 151. [Google Scholar] [CrossRef]
- Boisdron, Y.; Brock, J.R. On the stochastic nature of the acquisition of electrical charge and radioactivity by aerosol particles. Atmos. Environ. (1967) 1970, 4, 35–50. [Google Scholar] [CrossRef]
- Biskos, G.; Reavell, K.; Collings, N. Unipolar diffusion charging of aerosol particles in the transition regime. J. Aerosol Sci. 2005, 36, 247–265. [Google Scholar] [CrossRef]
- Mathon, R.; Jidenko, N.; Borra, J.P. Ozone-free post-DBD aerosol bipolar diffusion charger: Evaluation as neutralizer for SMPS size distribution measurements. Aerosol Sci. Technol. 2017, 51, 282–291. [Google Scholar] [CrossRef] [Green Version]
- de La Verpilliere, J.L.; Swanson, J.J.; Boies, A.M. Unsteady bipolar diffusion charging in aerosol neutralisers: A non-dimensional approach to predict charge distribution equilibrium behaviour. J. Aerosol Sci. 2015, 86, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Nishida, R.T. Measuring Aerosol Nanoparticles by Ultraviolet Photoionisation. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Ye, D.; Gao, D.; Yu, G.; Shen, X.; Gu, F. An investigation of the treatment of particulate matter from gasoline engine exhaust using non-thermal plasma. J. Hazard. Mater. 2005, 127, 149–155. [Google Scholar] [CrossRef]
- Tauber, C.; Schmoll, D.; Gruenwald, J.; Brilke, S.; Wlasits, P.J.; Winkler, P.M.; Wimmer, D. Characterization of a non-thermal plasma source for use as a mass specrometric calibration tool and non-radioactive aerosol charger. Atmos. Meas. Tech. 2020, 13, 5993–6006. [Google Scholar] [CrossRef]
- Fridman, A.; Chirokov, A.; Gutsol, A. Non-thermal atmospheric pressure discharges. J. Phys. D Appl. Phys. 2005, 38. [Google Scholar] [CrossRef]
- TDK CeraPlas® Evaluation Kit Documentation. Available online: https://www.tdk-electronics.tdk.com/inf/130/Cold_Plasma/Z63000Z2910Z1Z69.pdf (accessed on 14 May 2021).
- TDK CeraPlas® Piezoelectric Based Cold Plasma Generator Data Sheet. Available online: https://www.tdk-electronics.tdk.com/inf/130/Cold_Plasma/Z63000Z2910Z1Z66.pdf (accessed on 14 May 2021).
- TDK CeraPlas® Product Homepage. Available online: https://www.tdk-electronics.tdk.com/en/2464638/products/product-catalog/cold-plasma-technology/ceraplas-element (accessed on 14 May 2021).
- Kudela, P.; Puff, M.; Rinner, F. Device for Generating an Atmospheric-Pressure Plasma. US10856399B2, 1 December 2020. [Google Scholar]
- Burger, D.; Hoppenthaler, F.; Kudela, P.; Nettesheim, S.; Puff, M.; Weilguni, M. Plasmagenerator. DE102017105410A1, 20 September 2018. [Google Scholar]
- Sasaki, Y.; Yamamoto, M.; Ochi, A.; Inoue, T.; Takahashi, S. Small Multilayer Piezoelectric Transformers with High Power Density—Characteristics of Second and Third-Mode Rosen-Type Transformers. Jpn. J. Appl. Phys. 1999, 38, 5598–5602. [Google Scholar] [CrossRef]
- Johnson, T.J.; Nishida, R.T.; Irwin, M.; Symonds, J.P.; Olfert, J.S.; Boies, A.M. Measuring the bipolar charge distribution of nanoparticles: Review of methodologies and development using the Aerodynamic Aerosol Classifier. J. Aerosol Sci. 2020, 143, 105526. [Google Scholar] [CrossRef]
- Tigges, L.; Jain, A.; Schmid, H.J. On the bipolar charge distribution used for mobility particle sizing: Theoretical considerations. J. Aerosol Sci. 2015, 88, 119–134. [Google Scholar] [CrossRef]
- Investigation of the bipolar charge distribution at various gas conditions. J. Aerosol Sci. 1986, 17, 413–416. [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasa, H.; Schriefl, M.A.; Kupper, M.; Melischnig, A.; Bergmann, A. Aerosol Charging with a Piezoelectric Plasma Generator. Plasma 2021, 4, 377-388. https://doi.org/10.3390/plasma4030027
Krasa H, Schriefl MA, Kupper M, Melischnig A, Bergmann A. Aerosol Charging with a Piezoelectric Plasma Generator. Plasma. 2021; 4(3):377-388. https://doi.org/10.3390/plasma4030027
Chicago/Turabian StyleKrasa, Helmut, Mario A. Schriefl, Martin Kupper, Alexander Melischnig, and Alexander Bergmann. 2021. "Aerosol Charging with a Piezoelectric Plasma Generator" Plasma 4, no. 3: 377-388. https://doi.org/10.3390/plasma4030027
APA StyleKrasa, H., Schriefl, M. A., Kupper, M., Melischnig, A., & Bergmann, A. (2021). Aerosol Charging with a Piezoelectric Plasma Generator. Plasma, 4(3), 377-388. https://doi.org/10.3390/plasma4030027






