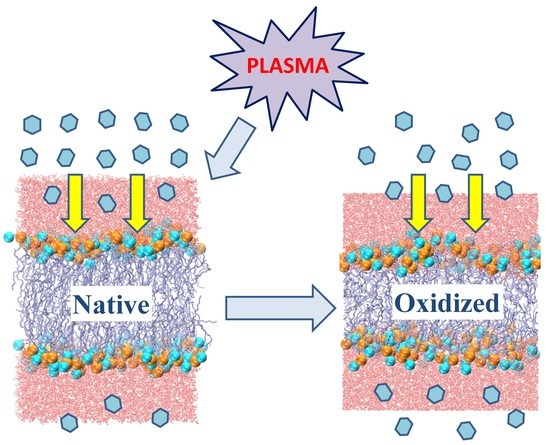
Possible Mechanism of Glucose Uptake Enhanced by Cold Atmospheric Plasma: Atomic Scale Simulations
Abstract
:1. Introduction
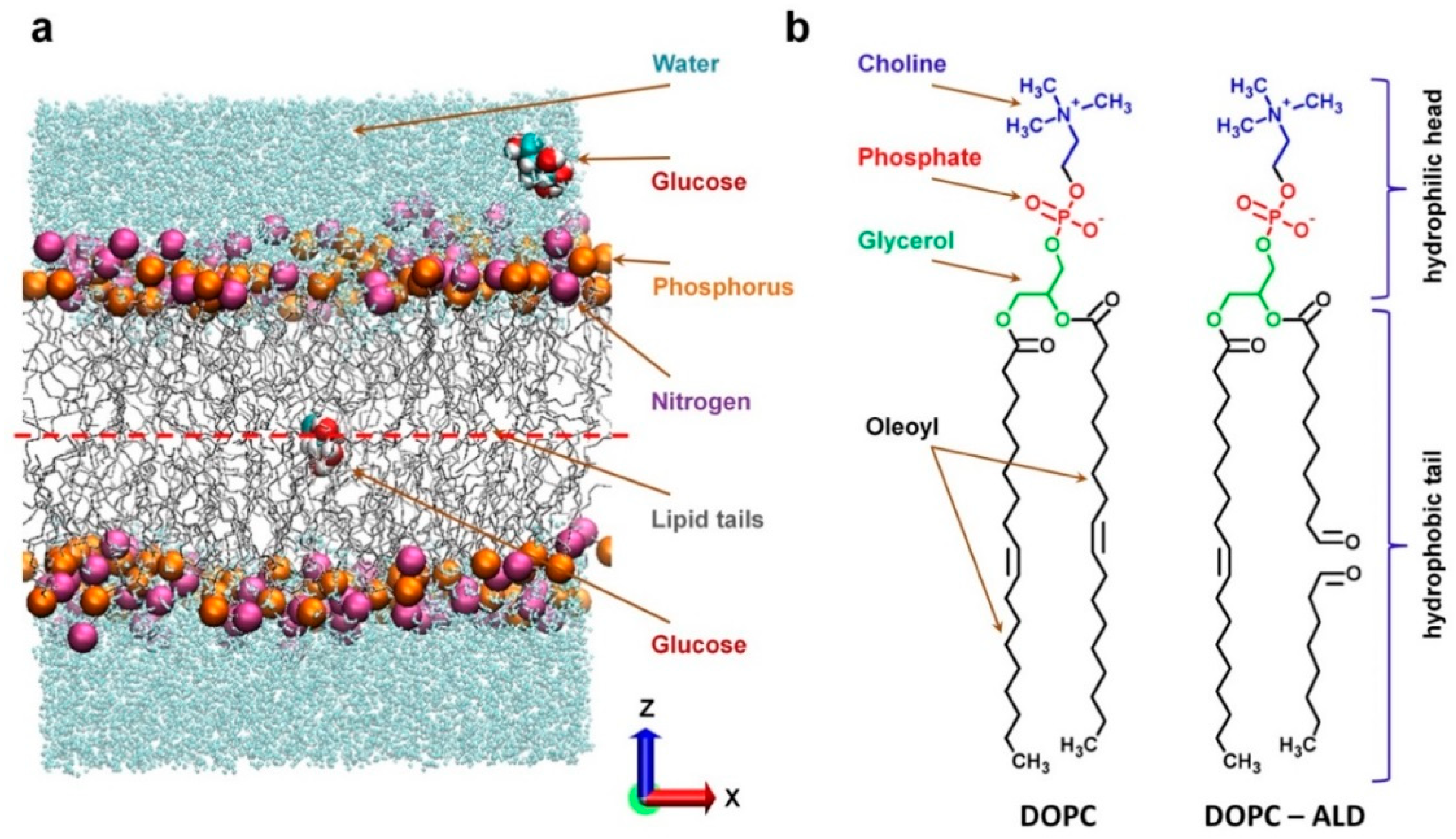
2. Computational Details
2.1. Simulation Setup
2.2. Umbrella Sampling (US) Simulations
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khan, A.; Pessin, J. Insulin regulation of glucose uptake: A complex interplay of intracellular signalling pathways. Diabetologia 2002, 45, 1475–1483. [Google Scholar] [PubMed]
- Saltiel, A.R.; Kahn, C.R. Insulin signalling and the regulation of glucose and lipid metabolism. Nature 2001, 414, 799. [Google Scholar] [CrossRef] [PubMed]
- Kahn, S. The relative contributions of insulin resistance and beta-cell dysfunction to the pathophysiology of type 2 diabetes. Diabetologia 2003, 46, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Cavaghan, M.K.; Ehrmann, D.A.; Polonsky, K.S. Interactions between insulin resistance and insulin secretion in the development of glucose intolerance. J. Clin. Investig. 2000, 106, 329–333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stumvoll, M.; Goldstein, B.J.; van Haeften, T.W. Type 2 diabetes: Principles of pathogenesis and therapy. Lancet 2005, 365, 1333–1346. [Google Scholar] [CrossRef]
- Kumar, N.; Shaw, P.; Razzokov, J.; Yusupov, M.; Attri, P.; Uhm, H.S.; Choi, E.H.; Bogaerts, A. Enhancement of cellular glucose uptake by reactive species: A promising approach for diabetes therapy. RSC Adv. 2018, 8, 9887–9894. [Google Scholar] [CrossRef]
- Fu, A.; Eberhard, C.E.; Screaton, R.A. Role of AMPK in pancreatic beta cell function. Mol. Cell. Endocrinol. 2013, 366, 127–134. [Google Scholar] [CrossRef] [PubMed]
- Higaki, Y.; Mikami, T.; Fujii, N.; Hirshman, M.F.; Koyama, K.; Seino, T.; Tanaka, K.; Goodyear, L.J. Oxidative stress stimulates skeletal muscle glucose uptake through a phosphatidylinositol 3-kinase-dependent pathway. Am. J. Physiol.-Endocrinol. Metab. 2008, 294, E889–E897. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasaki, S.; Hokari, Y.; Kumada, A.; Kanzaki, M.; Kaneko, T. Direct plasma stimuli including electrostimulation and OH radical induce transient increase in intracellular Ca2+ and uptake of a middle-size membrane-impermeable molecule. Plasma Process. Polym. 2018, 15, 1700077. [Google Scholar] [CrossRef]
- Vijayarangan, V.; Delalande, A.; Dozias, S.; Pouvesle, J.-M.; Pichon, C.; Robert, E. Cold atmospheric plasma parameters investigation for efficient drug delivery in HeLa cells. IEEE Trans. Radiat. Plasma Med. Sci. 2018, 2, 109–115. [Google Scholar] [CrossRef]
- Leduc, M.; Guay, D.; Leask, R.; Coulombe, S. Cell permeabilization using a non-thermal plasma. New J. Phys. 2009, 11, 115021. [Google Scholar] [CrossRef]
- Razzokov, J.; Yusupov, M.; Vanuytsel, S.; Neyts, E.C.; Bogaerts, A. Phosphatidylserine flip-flop induced by oxidation of the plasma membrane: A better insight by atomic scale modeling. Plasma Process. Polym. 2017, 14. [Google Scholar] [CrossRef]
- Yusupov, M.; Wende, K.; Kupsch, S.; Neyts, E.; Reuter, S.; Bogaerts, A. Effect of head group and lipid tail oxidation in the cell membrane revealed through integrated simulations and experiments. Sci. Rep. 2017, 7, 5761. [Google Scholar] [CrossRef] [PubMed]
- Yusupov, M.; van der Paal, J.; Neyts, E.; Bogaerts, A. Synergistic effect of electric field and lipid oxidation on the permeability of cell membranes. Biochim. Biophys. Acta 2017, 1861, 839–847. [Google Scholar] [CrossRef] [PubMed]
- Van der Paal, J.; Neyts, E.C.; Verlackt, C.C.; Bogaerts, A. Effect of lipid peroxidation on membrane permeability of cancer and normal cells subjected to oxidative stress. Chem. Sci. 2016, 7, 489–498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van der Paal, J.; Verheyen, C.; Neyts, E.C.; Bogaerts, A. Hampering effect of cholesterol on the permeation of reactive oxygen species through phospholipids bilayer: Possible explanation for plasma cancer selectivity. Sci. Rep. 2017, 7, 39526. [Google Scholar] [CrossRef] [PubMed]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Chiu, S.-W.; Pandit, S.A.; Scott, H.; Jakobsson, E. An improved united atom force field for simulation of mixed lipid bilayers. J. Phys. Chem. B 2009, 113, 2748–2763. [Google Scholar] [CrossRef] [PubMed]
- Reis, A.; Domingues, M.; Amado, F.M.; Ferrer-Correia, A.; Domingues, P. Separation of peroxidation products of diacyl-phosphatidylcholines by reversed-phase liquid chromatography–mass spectrometry. Biomed. Chromatogr. 2005, 19, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Wong-Ekkabut, J.; Xu, Z.; Triampo, W.; Tang, I.-M.; Tieleman, D.P.; Monticelli, L. Effect of lipid peroxidation on the properties of lipid bilayers: A molecular dynamics study. Biophys. J. 2007, 93, 4225–4236. [Google Scholar] [CrossRef] [PubMed]
- Geballe, M.T.; Skillman, A.G.; Nicholls, A.; Guthrie, J.P.; Taylor, P.J. The SAMPL2 blind prediction challenge: Introduction and overview. J. Comput.-Aided Mol. Des. 2010, 24, 259–279. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Neale, C.; Pomès, R. Sampling errors in free energy simulations of small molecules in lipid bilayers. Biochim. Biophys. Acta 2016, 1858, 2539–2548. [Google Scholar] [CrossRef] [PubMed]
- Bresseleers, G.J.; Goderis, H.L.; Tobback, P.P. Measurement of the glucose permeation rate across phospholipid bilayers using small unilamellar vesicles Effect of membrane composition and temperature. Biophys. Acta 1984, 772, 374–382. [Google Scholar] [CrossRef]
- Sweet, C.; Zull, J. Activation of glucose diffusion from egg lecithin liquid crystals by serum albumin. Biophys. Acta 1969, 173, 94–103. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razzokov, J.; Yusupov, M.; Bogaerts, A. Possible Mechanism of Glucose Uptake Enhanced by Cold Atmospheric Plasma: Atomic Scale Simulations. Plasma 2018, 1, 119-125. https://doi.org/10.3390/plasma1010011
Razzokov J, Yusupov M, Bogaerts A. Possible Mechanism of Glucose Uptake Enhanced by Cold Atmospheric Plasma: Atomic Scale Simulations. Plasma. 2018; 1(1):119-125. https://doi.org/10.3390/plasma1010011
Chicago/Turabian StyleRazzokov, Jamoliddin, Maksudbek Yusupov, and Annemie Bogaerts. 2018. "Possible Mechanism of Glucose Uptake Enhanced by Cold Atmospheric Plasma: Atomic Scale Simulations" Plasma 1, no. 1: 119-125. https://doi.org/10.3390/plasma1010011
APA StyleRazzokov, J., Yusupov, M., & Bogaerts, A. (2018). Possible Mechanism of Glucose Uptake Enhanced by Cold Atmospheric Plasma: Atomic Scale Simulations. Plasma, 1(1), 119-125. https://doi.org/10.3390/plasma1010011