Fully Kinetic Simulation of Ion-Temperature-Gradient Instabilities in Tokamaks
Abstract
:1. Introduction
2. Fully Kinetic Ion Model of ITG Instabilities
Electrostatic Limit with Adiabatic Electrons
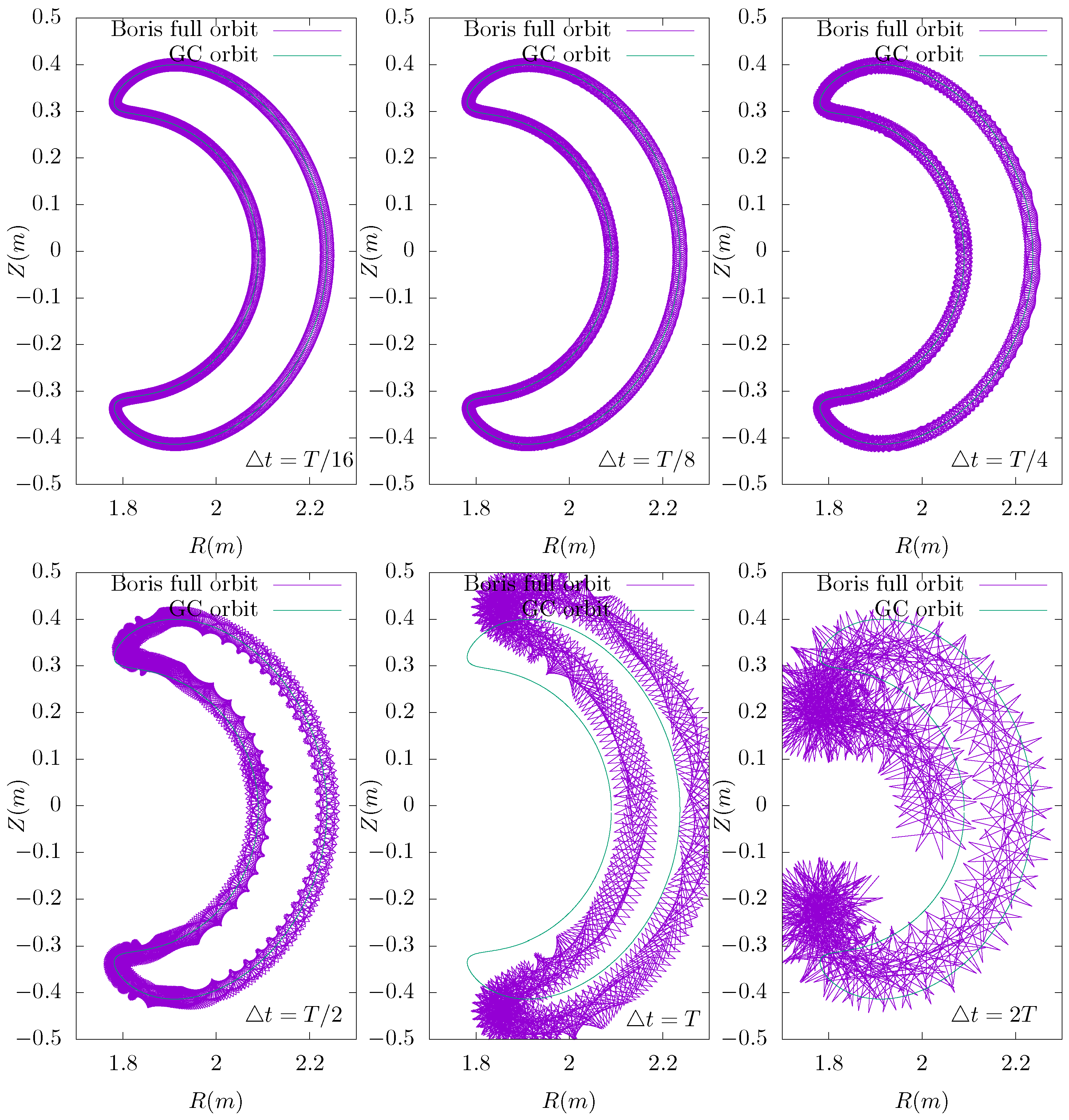
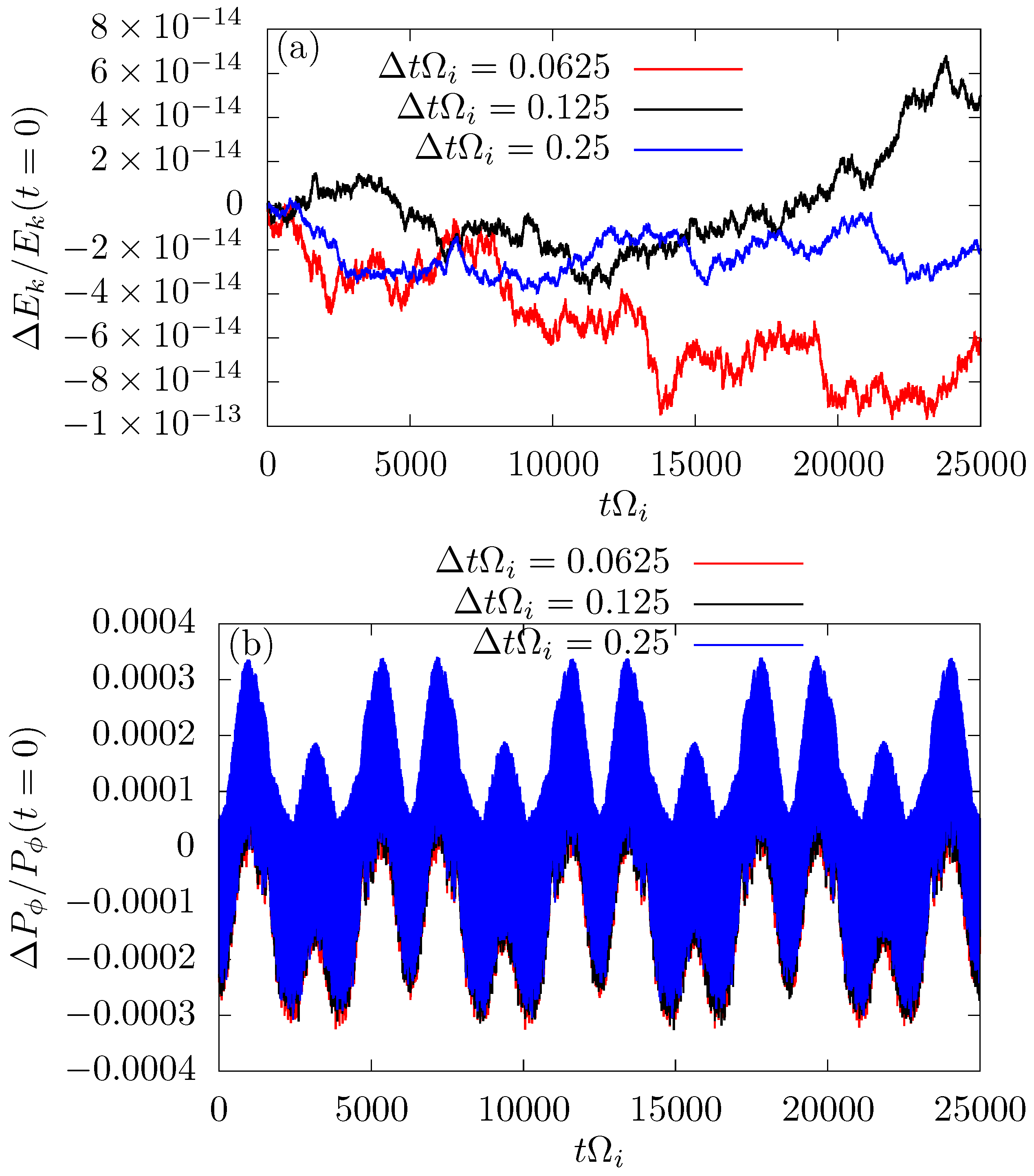
3. Implicit Particle-in-Cell Method and Full Orbit Integrator
4. Magnetic Field Specification and Field-Line-Following Coordinates
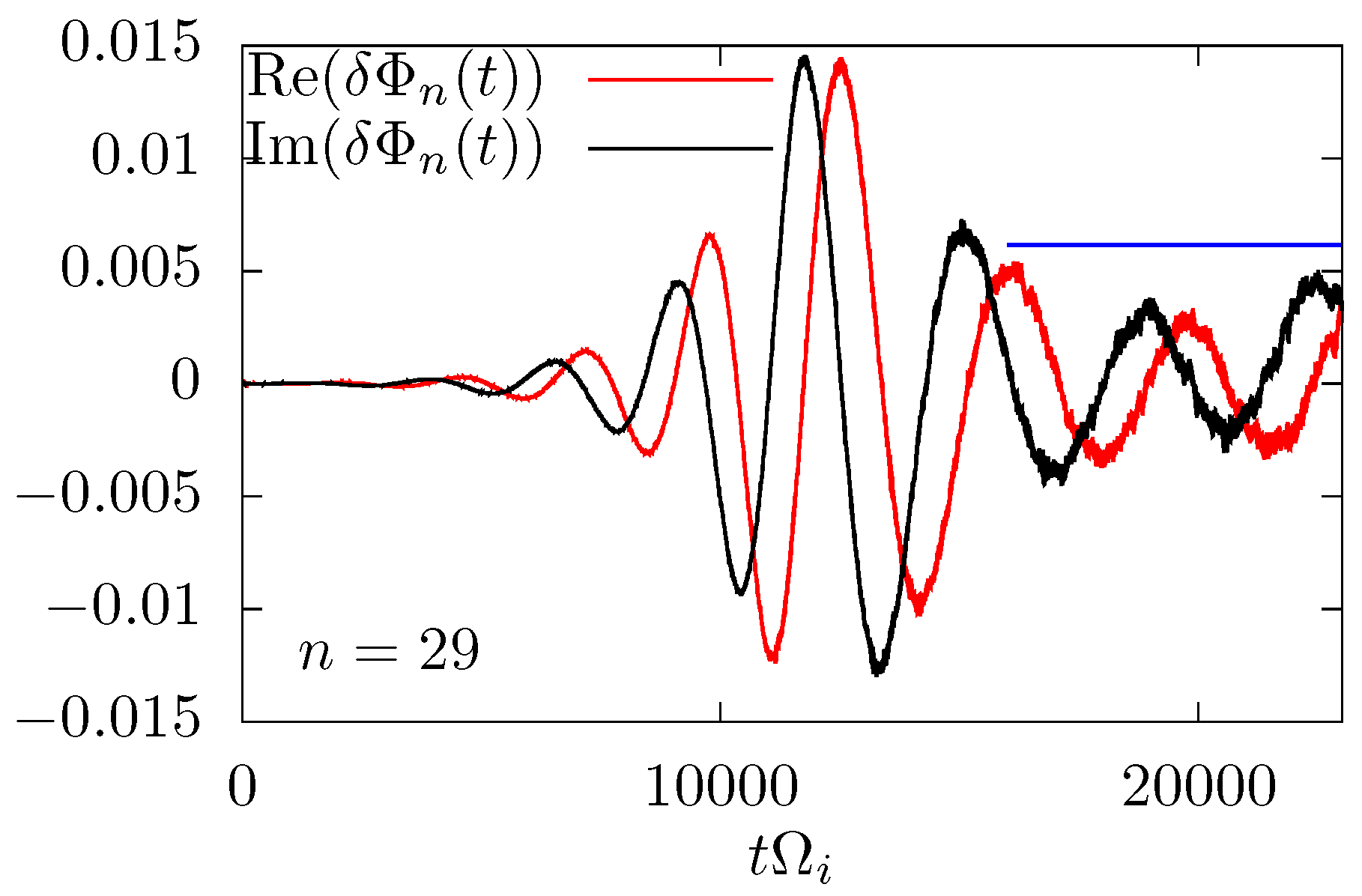
5. Simulation Results of ITG Instabilities
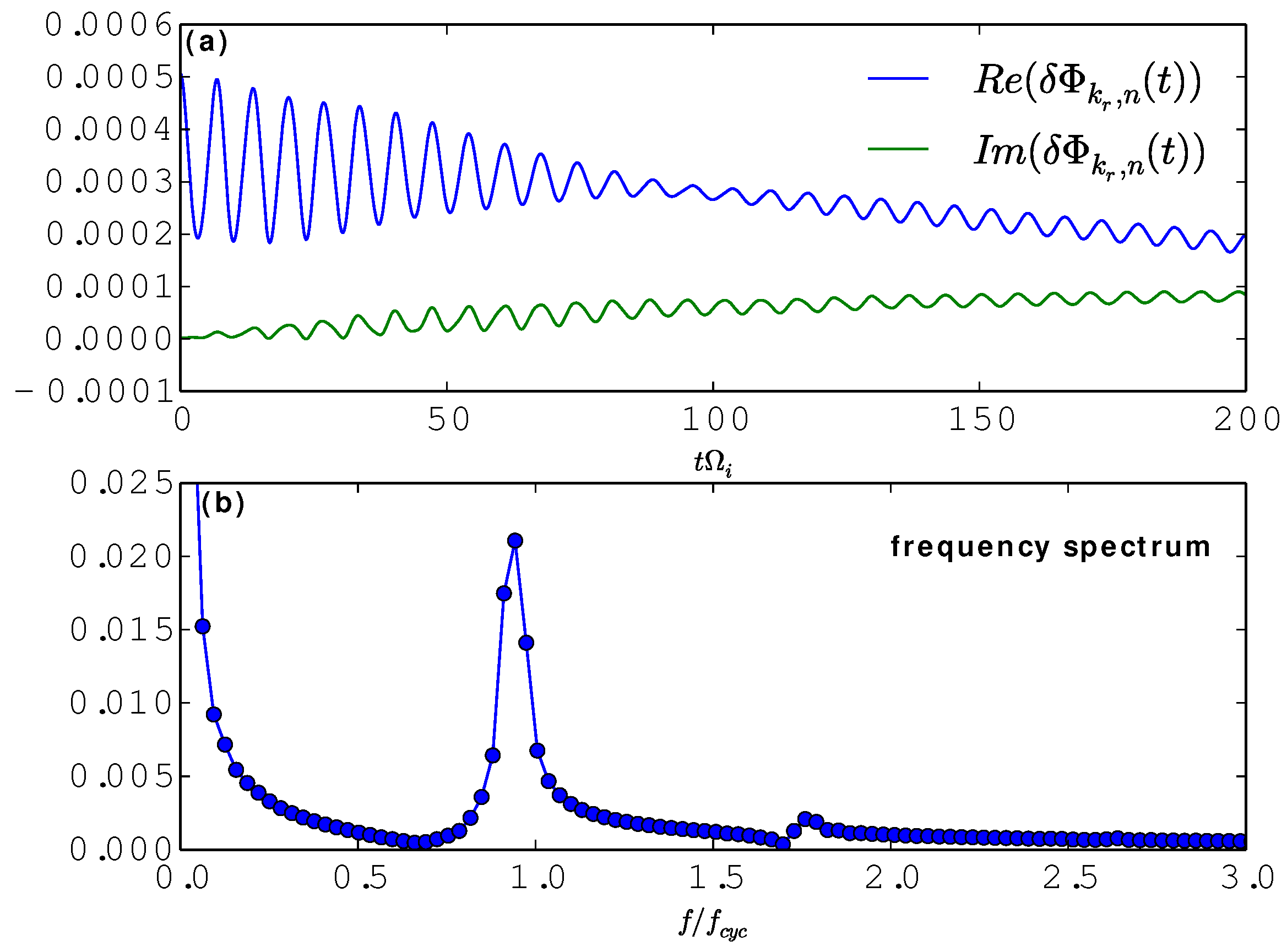
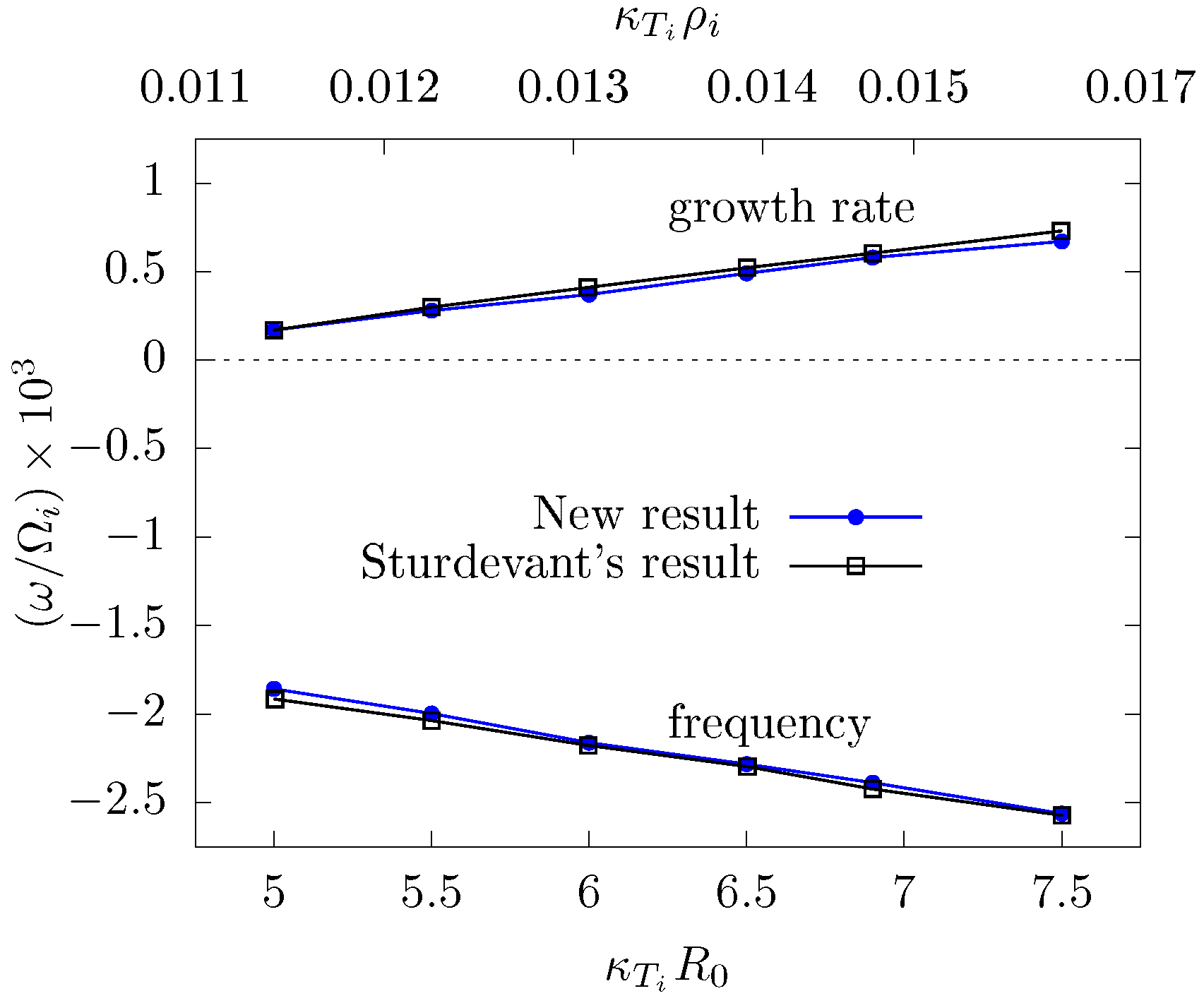
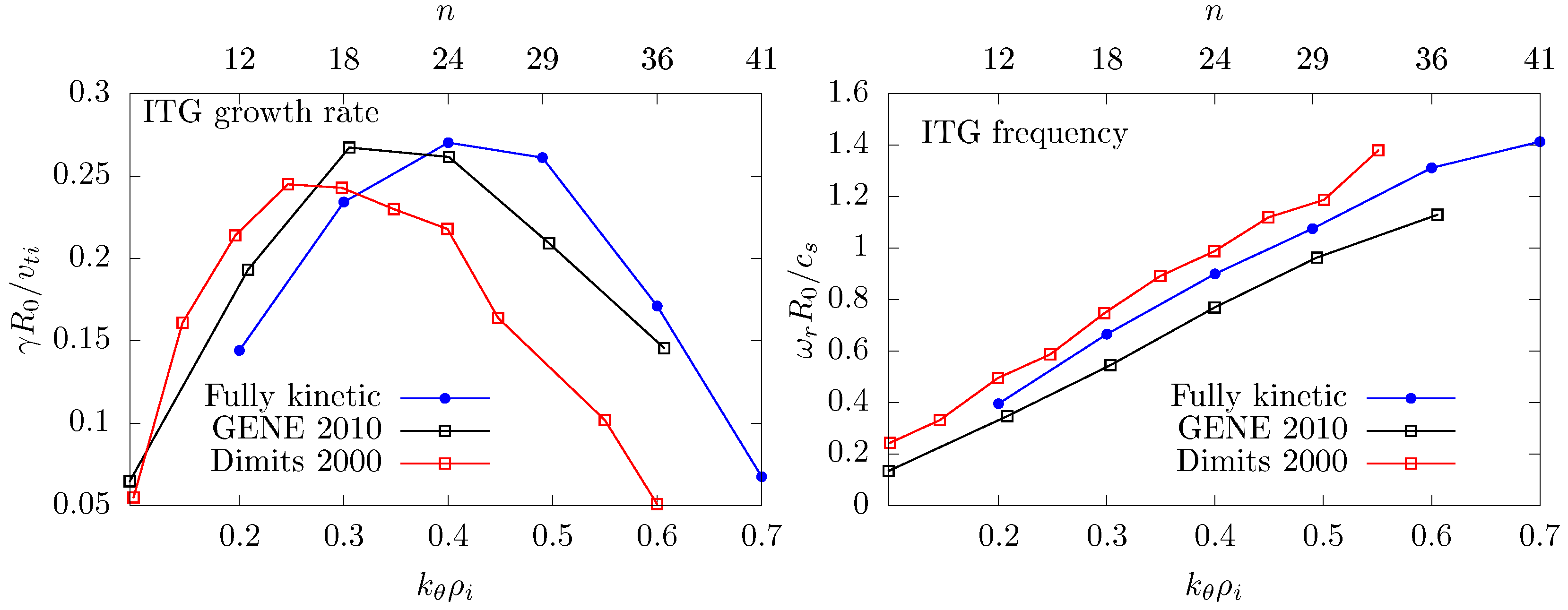
5.1. Linear Results of ITG Instabilities and Benchmarking with Other Codes
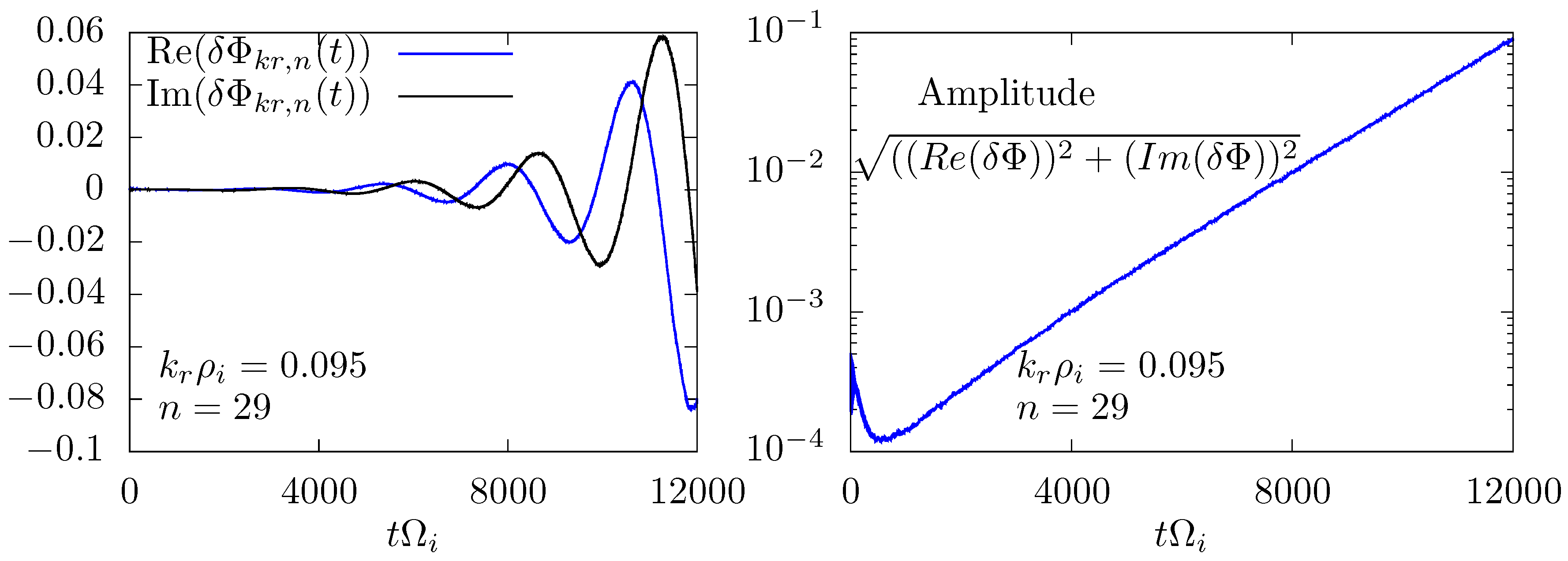
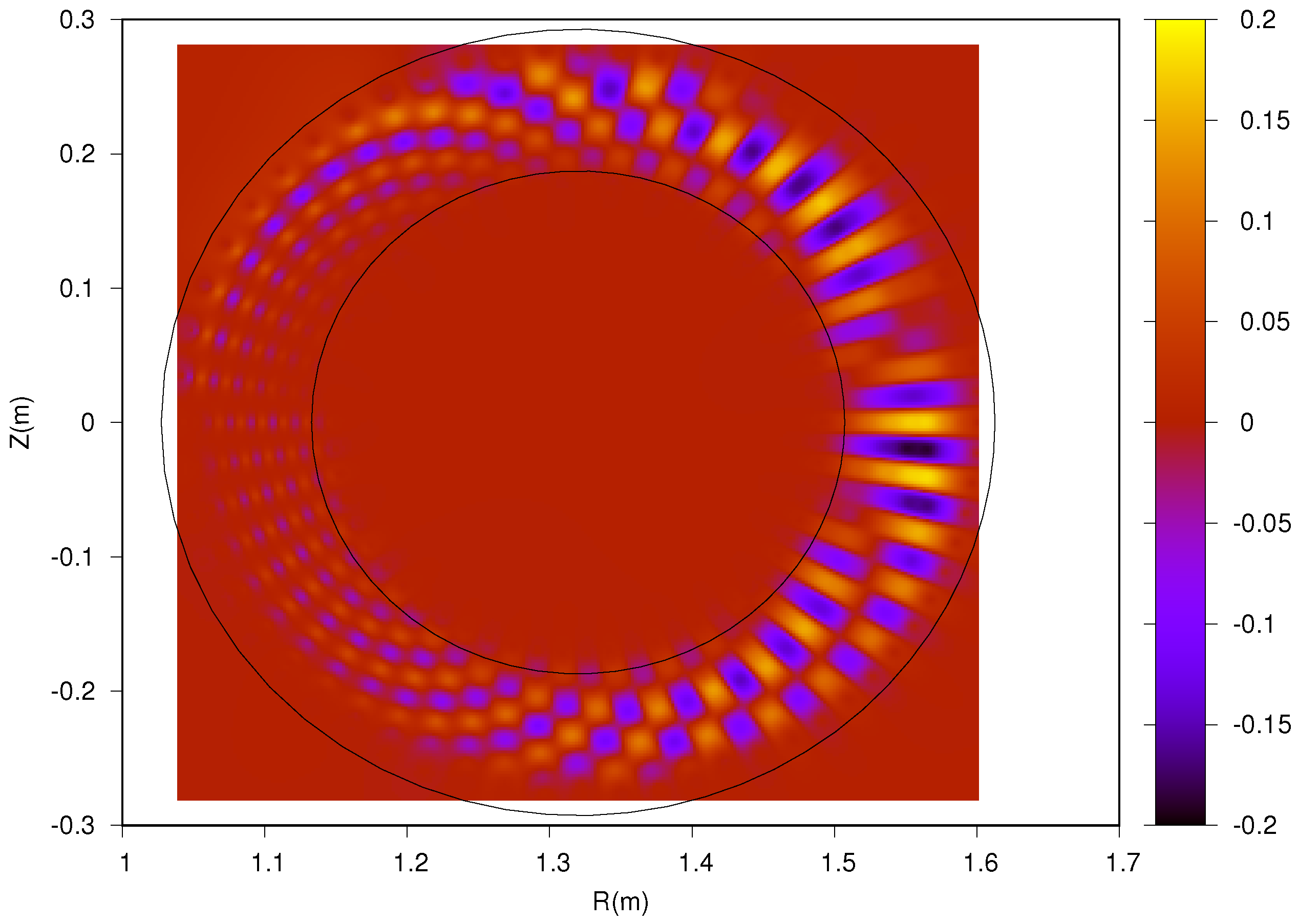
5.2. Nonlinear Results of ITG Instabilities and Analysis of Saturation due to Trapping
6. Summary
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Guzdar, P.N.; Chen, L.; Tang, W.M.; Rutherford, P.H. Ion-temperature-gradient instability in toroidal plasmas. Phys. Fluids 1983, 26, 673–677. [Google Scholar] [CrossRef]
- Rettig, C.L.; Rhodes, T.L.; Leboeuf, J.N.; Peebles, W.A.; Doyle, E.J.; Staebler, G.M.; Burrell, K.H.; Moyer, R.A. Search for the ion temperature gradient mode in a tokamak plasma and comparison with theoretical predictions. Phys. Plasmas 2001, 8, 2232–2237. [Google Scholar] [CrossRef]
- Lin, Z.; Hahm, T.S.; Lee, W.W.; Tang, W.M.; White, R.B. Turbulent Transport Reduction by Zonal Flows: Massively Parallel Simulations. Science 1998, 281, 1835–1837. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.S.; Xiao, Y.; Lin, Z. New Paradigm for Turbulent Transport Across a Steep Gradient in Toroidal Plasmas. Phys. Rev. Lett. 2017, 118, 095001. [Google Scholar] [CrossRef] [PubMed]
- Parker, S.E.; Lee, W.W.; Santoro, R.A. Gyrokinetic simulation of ion temperature gradient driven turbulence in 3D toroidal geometry. Phys. Rev. Lett. 1993, 71, 2042–2045. [Google Scholar] [CrossRef] [PubMed]
- Idomura, Y.; Tokuda, S.; Kishimoto, Y. Global gyrokinetic simulation of ion temperature gradient driven turbulence in plasmas using a canonical Maxwellian distribution. Nucl. Fusion 2003, 43, 234. [Google Scholar] [CrossRef]
- Gao, Z.; Sanuki, H.; Itoh, K.; Dong, J.Q. Short wavelength ion temperature gradient instability in toroidal plasmas. Phys. Plasmas 2005, 12, 022502. [Google Scholar] [CrossRef]
- Chen, Y.; Parker, S.E. Electromagnetic gyrokinetic δf particle-in-cell turbulence simulation with realistic equilibrium profiles and geometry. J. Comput. Phys. 2007, 220, 839–855. [Google Scholar] [CrossRef]
- Ye, L.; Xu, Y.; Xiao, X.; Dai, Z.; Wang, S. A gyrokinetic continuum code based on the numerical Lie transform (NLT) method. J.Comput. Phys. 2016, 316, 180–192. [Google Scholar] [CrossRef]
- Görler, T.; Lapillonne, X.; Brunner, S.; Dannert, T.; Jenko, F.; Merz, F.; Told, D. The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 2011, 230, 7053–7071. [Google Scholar] [CrossRef]
- Ku, S.; Chang, C.; Diamond, P. Full-f gyrokinetic particle simulation of centrally heated global ITG turbulence from magnetic axis to edge pedestal top in a realistic tokamak geometry. Nucl. Fusion 2009, 49, 115021. [Google Scholar] [CrossRef]
- Chang, C.S.; Ku, S.; Tynan, G.R.; Hager, R.; Churchill, R.M.; Cziegler, I.; Greenwald, M.; Hubbard, A.E.; Hughes, J.W. Fast Low-to-High Confinement Mode Bifurcation Dynamics in a Tokamak Edge Plasma Gyrokinetic Simulation. Phys. Rev. Lett. 2017, 118, 175001. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Parker, S.E. Particle-in-cell simulation with Vlasov ions and drift kinetic electrons. Phys. Plasmas 2009, 16, 052305. [Google Scholar] [CrossRef]
- Belova, E.V.; Gorelenkov, N.N.; Cheng, C.Z. Self-consistent equilibrium model of low aspect-ratio toroidal plasma with energetic beam ions. Physics of Plasmas 2003, 10, 3240–3251. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, X.Y.; Chen, L.; Lu, X.; Kong, W. An improved gyrokinetic electron and fully kinetic ion particle simulation scheme: Benchmark with a linear tearing mode. Plasma Phys. Controll. Fusion 2011, 53, 054013. [Google Scholar] [CrossRef]
- Waltz, R.E.; Deng, Z. Nonlinear theory of drift-cyclotron kinetics and the possible breakdown of gyro-kinetics. Phys. Plasmas 2013, 20, 012507. [Google Scholar] [CrossRef]
- Kramer, G.J.; Budny, R.V.; Bortolon, A.; Fredrickson, E.D.; Fu, G.Y.; Heidbrink, W.W.; Nazikian, R.; Valeo, E.; Zeeland, M.A.V. A description of the full-particle-orbit-following SPIRAL code for simulating fast-ion experiments in tokamaks. Plasma Phys. Controll. Fusion 2013, 55, 025013. [Google Scholar] [CrossRef]
- Kuley, A.; Lin, Z.; Bao, J.; Wei, X.S.; Xiao, Y.; Zhang, W.; Sun, G.Y.; Fisch, N.J. Verification of nonlinear particle simulation of radio frequency waves in tokamak. Phys. Plasmas 2015, 22, 102515. [Google Scholar] [CrossRef]
- Sturdevant, B.J.; Parker, S.E.; Chen, Y.; Hause, B.B. An implicit δf particle-in-cell method with sub-cycling and orbit averaging for Lorentz ions. J. Comput. Phys. 2016, 316, 519–533. [Google Scholar] [CrossRef]
- Miecnikowski, M.T.; Sturdevant, B.J.; Chen, Y.; Parker, S.E. Nonlinear saturation of the slab ITG instability and zonal flow generation with fully kinetic ions. Phys. Plasmas 2018, 25, 055901. [Google Scholar] [CrossRef]
- Sturdevant, B.J.; Chen, Y.; Parker, S.E. Low frequency fully kinetic simulation of the toroidal ion temperature gradient instability. Phys. Plasmas 2017, 24, 081207. [Google Scholar] [CrossRef]
- Lapillonne, X.; McMillan, B.F.; Görler, T.; Brunner, S.; Dannert, T.; Jenko, F.; Merz, F.; Villard, L. Nonlinear quasisteady state benchmark of global gyrokinetic codes. Phys. Plasmas 2010, 17, 112321. [Google Scholar] [CrossRef]
- Parker, S.E.; Lee, W.W. A fully nonlinear characteristic method for gyrokinetic simulation. Phys. Fluid. B Plasma Phys. 1993, 5, 77–86. [Google Scholar] [CrossRef]
- Aydemir, A.Y. A unified Monte Carlo interpretation of particle simulations and applications to non-neutral plasmas. Phys. Plasmas 1994, 1, 822–831. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Birdsall, C.; Langdon, A. Plasma Physics via Computer Simulation; CRC Press: Bocaton, FL, USA, 2004. [Google Scholar]
- Qin, H.; Zhang, S.; Xiao, J.; Liu, J.; Sun, Y.; Tang, W.M. Why is Boris algorithm so good? Phys. Plasmas 2013, 20, 084503. [Google Scholar] [CrossRef]
- Parker, S.; Birdsall, C. Numerical error in electron orbits with large ωceΔt. J. Comput. Phys. 1991, 97, 91–102. [Google Scholar] [CrossRef]
- Dimits, A.M.; Bateman, G.; Beer, M.A.; Cohen, B.I.; Dorland, W.; Hammett, G.W.; Kim, C.; Kinsey, J.E.; Kotschenreuther, M.; Kritz, A.H.; et al. Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 2000, 7, 969–983. [Google Scholar] [CrossRef]
- Lao, L.; John, H.S.; Stambaugh, R.; Kellman, A.; Pfeiffer, W. Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 1985, 25, 1611. [Google Scholar] [CrossRef]
- Beer, M.A.; Cowley, S.C.; Hammett, G.W. Field-aligned coordinates for nonlinear simulations of tokamak turbulence. Phys. Plasmas 1995, 2, 2687–2700. [Google Scholar] [CrossRef]
- Chen, Y.; Parker, S.E. A delta-f particle method for gyrokinetic simulations with kinetic electrons and electromagnetic perturbations. J. Comput. Phys. 2003, 189, 463–475. [Google Scholar] [CrossRef]
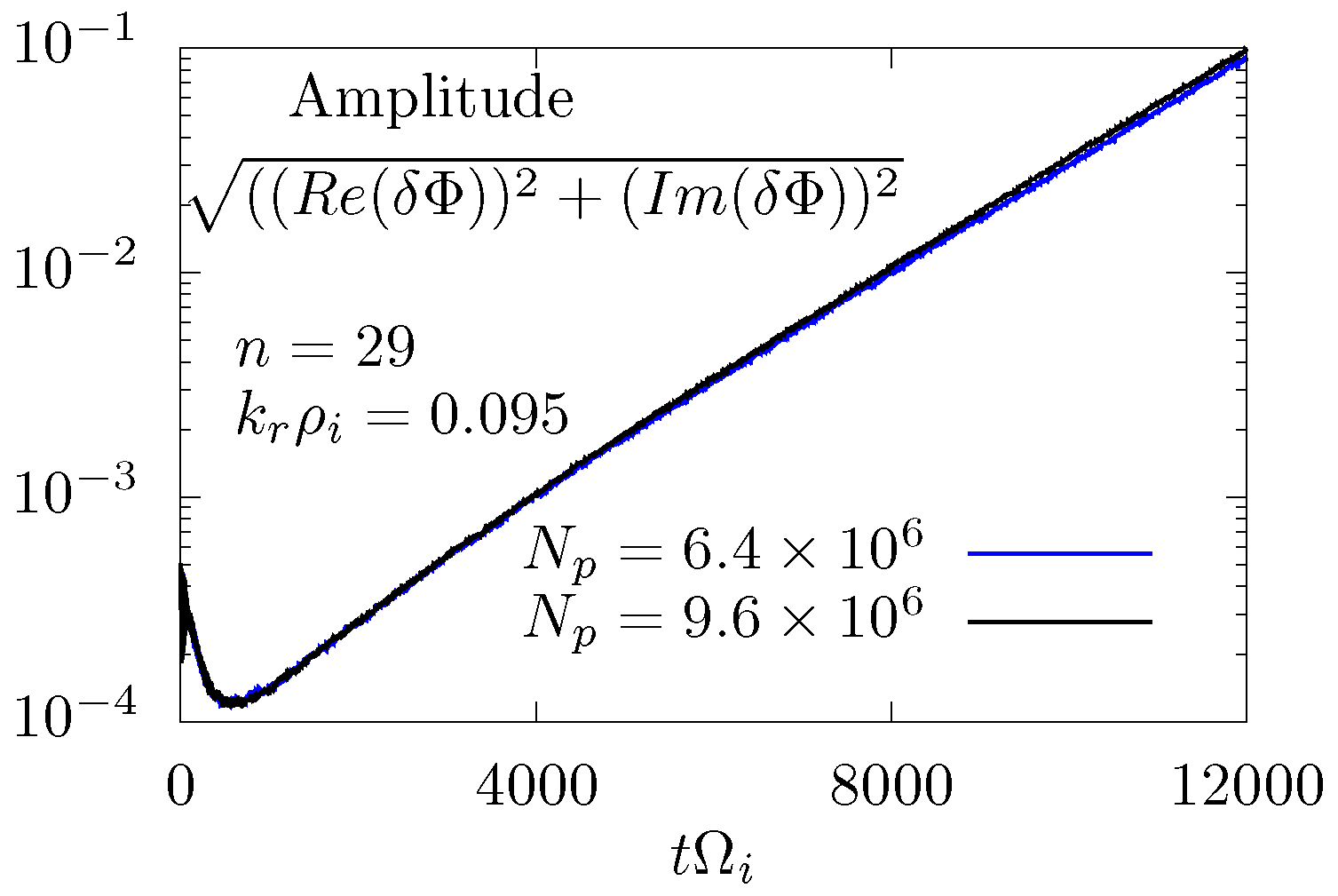

| a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.32 m | 0.48 m | 1.40 | 0.78 | 0.24 m | 6.9 | 2.2 | 1.5 keV | 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Miecnikowski, M.T.; Chen, Y.; Parker, S.E. Fully Kinetic Simulation of Ion-Temperature-Gradient Instabilities in Tokamaks. Plasma 2018, 1, 105-118. https://doi.org/10.3390/plasma1010010
Hu Y, Miecnikowski MT, Chen Y, Parker SE. Fully Kinetic Simulation of Ion-Temperature-Gradient Instabilities in Tokamaks. Plasma. 2018; 1(1):105-118. https://doi.org/10.3390/plasma1010010
Chicago/Turabian StyleHu, Youjun, Matthew T. Miecnikowski, Yang Chen, and Scott E. Parker. 2018. "Fully Kinetic Simulation of Ion-Temperature-Gradient Instabilities in Tokamaks" Plasma 1, no. 1: 105-118. https://doi.org/10.3390/plasma1010010
APA StyleHu, Y., Miecnikowski, M. T., Chen, Y., & Parker, S. E. (2018). Fully Kinetic Simulation of Ion-Temperature-Gradient Instabilities in Tokamaks. Plasma, 1(1), 105-118. https://doi.org/10.3390/plasma1010010






