Abstract
This work presents the design and synthesis of novel high-entropy perovskite oxides (HEPOs) derived from BaCeO3, formulated using the cluster-plus-glue atom model. Particularly, through a carbonate-based co-precipitation technique, we synthesized three novel high-entropy perovskite oxides (HEPOs) derived from barium cerate by substituting cerium with different combinations of five different elements (Ce, Zr, Yb, Sm, La, Gd, Nd) in equal molar ratios, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7. Upon calcination of the as-synthesized samples at different temperatures and subsequent quenching, the formation of an entropy-stabilized single phase was analyzed and assessed. To rationalize the observed differences in phase evolution, a novel set of empirical descriptors, including configurational entropy, Goldschmidt tolerance factor, and B-site size mismatch, was proposed and discussed. With the aim of studying the sinterability of the single-phase samples, the calcination treatment was optimized by reducing its temperature and duration (i.e., 1300 °C for 6 h) so that subsequent densification higher than 95% was achieved by sintering at 1500 °C for 6 h.
1. Introduction
The concept of high-entropy materials first originated in the field of alloys, where systems with five or more principal elements in equimolar or near-equimolar ratios exhibited unique properties due to their high configurational entropy [1,2,3].
The success of this concept in alloys led to its application in oxide systems, firstly including rocksalt [4] and subsequently including many more crystal structures [5,6,7,8,9,10].
The stabilization of single-phase high-entropy oxides (HEOs) is primarily driven by configurational entropy, calculated as:
where ci is the molar fraction of the ith component of a given system, while R is the universal gas constant. For five or more equimolar components, the configurational entropy exceeds the critical threshold of 1.5R [11,12], suppressing phase segregation and favoring an entropy-driven homogeneous single-phase formation when a positive entropy of formation (ΔSf) overcomes a positive enthalpy of formation (ΔHf) at a given temperature, thus leading to a negative free energy of formation (ΔGf):
Perovskite oxides (ABO3) are an essential class of materials with applications ranging from solid oxide fuel cells [13,14,15], catalysts/photocatalysts [16,17,18], photovoltaics [19,20], and dielectric devices [21,22,23]. The flexibility of the perovskite structure, which can accommodate a wide variety of A- and B-site cations, makes it an ideal candidate for the design of novel high-entropy materials. Particularly, high-entropy perovskite oxides (HEPOs) could involve multiple cation substitutions at either or both A- and B-sites, which can lead to entropy-driven stabilization of single-phase perovskites even in much more complex systems [24,25,26,27,28].
Thus, in the context of high-entropy perovskite oxides (HEPOs), the high-entropy design paradigm could offer multiple advantages, particularly in terms of structural stability, functional properties, and processability. In fact, the possible incorporation of multiple cations in either or both A- or B-sites allows for precise control over ionic radii, valence states, and defect chemistry. Furthermore, the heterogeneous electronic structure resulting from the multi-cation environment could enhance catalytic activity or proton conductivity, making HEPOs highly promising for applications in water splitting and CO2 reduction [29,30], as well as low-temperature proton conductors [31,32].
Thus, HEPOs’ potential multifunctionality (thanks to co-existing properties such as ionic conductivity, ferroelectricity, and catalytic activity within a single material) could be achieved through the strategic selection and substitution of involved cations, which allows for the design of materials tailored to specific applications.
Conventional ABO3 systems can exhibit different crystal structures depending on the different cations’ size, predictable through a structural “tolerance factor” introduced by Goldschmidt in 1926 [33]:
where rA, rB, and rO are the radii of A cation, B cation, and oxygen anion, respectively. If t is in the range 0.9 ≤ t ≤ 1.0, the ABO3 structure is cubic; if t > 1.0 (large A and small B), it is either hexagonal or tetragonal; if 0.7 ≤ t ≤ 0.9, the perovskite structure results in either an orthorhombic or rhombohedral phase [34]. However, it has recently been reported that in HEPOs, Goldschmidt’s tolerance factor is not always a sufficient criterion to predict the entropy-stabilized single-phase structure [35]. The three studied systems in this work have been selected considering the average cationic radii in the B-site within the range 0.9 ≤ t ≤ 1.0.
The cluster-plus-glue atom is a chemical model recently proposed to provide a theoretical framework for understanding and predicting the formation and stabilization of high-entropy systems, including HEPOs [36,37,38]. Initially developed for metallic systems [39], this model has been successfully extended to oxides, offering critical insights into their structure and stability [40,41]. According to the cluster-plus-glue atom model, a crystal structure is conceptualized as comprising principal clusters and glue atoms. The principal clusters represent the most strongly bonded and most dense units within the structure, while the glue atoms occupy positions outside the clusters, maintaining charge neutrality and completing the lattice [40]. For high-entropy perovskites with an ABO3 structure, the principal cluster typically corresponds to the octahedral coordination of the B-site cation, such as [BO6]. Conversely, the glue atoms include the A-site cations and additional oxygen atoms that stabilize the lattice [38].
In the study and design of HEPOs, the cluster-plus-glue model could offer significant advantages by providing a predictive tool for determining stable compositions and evaluating the compatibility of clusters and glue atoms among the selected cations.
However, despite its strengths, the cluster-plus-glue model has limitations, particularly in its application to highly complex multinary systems. While it simplifies the conceptualization of novel high-entropy systems, it does not fully account for kinetic barriers to phase formation or the dynamic interactions within the lattice. Nevertheless, we believe that the cluster-plus-glue atom model’s integration with experimental methods and other possible predictors developed for differently structured HEOs [42] could provide a good framework for advancing and accelerating the discovery of novel HEPOs with complex compositions.
Based on the above considerations, this study is focused on the systematic design, synthesis (through a cheap and simple carbonate-based co-precipitation technique), and sintering of three novel HEPOs derived from barium cerate by substituting cerium with different combinations of five different elements (Ce, Zr, Yb, Sm, La, Gd, Nd) in equal molar ratios, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7. Barium cerate and its derivatives have been extensively studied in the literature, mainly for their high proton conductivity [43,44,45,46,47,48], but still, such a class of materials is hindered by severe technological issues such as chemical instability [49], fast performance degradation [50], and sintering challenges [51,52,53]. Thus, within this work, by simultaneously applying the cluster-plus-glue atom model and a standard deviation predictor first introduced by the authors for fluorite/bixbyite-structured HEOs [42], we studied both the entropy stabilization from different starting conditions and the sintering behavior of Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7 systems in order to identify the experimental conditions enabling the formation of structurally stable, gas-tight HEPO pellets for technological applications.
2. Materials and Methods
Cerium (III) nitrate (Ce(NO3)3·6H2O, Carlo Erba, Cornaredo, MI, Italy), zirconyl nitrate (ZrO(NO3)2, Carlo Erba, Cornaredo, Italy), gadolinium (III) nitrate (Gd(NO3)3·6H2O, Carlo Erba, Cornaredo, Italy), lanthanum (III) nitrate (La(NO3)3·6H2O, Sigma Aldrich, Milan, Italy), samarium (III) nitrate (Sm(NO3)3·6H2O, Sigma Aldrich, Milan, Italy), neodymium (III) nitrate (Nd(NO3)3·6H2O, Sigma Aldrich, Milan, Italy), ytterbium (III) nitrate (Yb(NO3)3·5H2O, Sigma Aldrich, Milan, Italy), and ammonium carbonate ((NH4)2CO3, Sigma Aldrich, Milan, Italy) were used as reagents for the three designed HEPOs, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7.
The adopted synthesis method involved dissolving appropriate amounts of differently selected nitrates in deionized water to achieve a total cationic concentration of 0.1 M (Solution A). In parallel, an aqueous solution of ammonium carbonate with a concentration of 0.5 M (Solution B) was prepared. Both solutions were vigorously stirred until complete dissolution and homogenization were achieved. The co-precipitation process was conducted at room temperature by rapidly adding Solution B to Solution A. The volume ratio was adjusted to maintain a molar ratio (R) of 10 between ammonium carbonate and the total cations contained in Solution A.
The resultant suspensions were filtered and dried overnight. Finally, the dried powders were subjected to calcination and quenching in air at different temperatures at two selected temperatures (800 °C and 1300 °C), as detailed in the following sections.
The differently calcined powders were compacted into cylindrical pellets with a diameter of 13 mm by using uniaxial pressing, followed by sintering in air at different temperatures and soaking times.
Both calcination and sintering treatments adopted a constant heating rate of 10 °C/min.
The crystalline structure and phase composition of the different samples were analyzed using X-ray diffraction (XRD) with a Panalytical (Almelo, The Netherlands) X’PERT MPD diffractometer.
The thermal behavior of the as-synthesized powders was examined through differential thermal analysis and thermogravimetric analysis (DTA-TG) using a Netzsch Instruments (Selb, Germany) STA 409 Thermoanalyzer.
The density of the successfully sintered samples was determined by the Archimedes method using a highly sensitive analytical balance (Gibertini, Novate Milanese, Italy) with sensitivity of 0.1 mg.
Microstructural analysis of successfully sintered pellets was conducted through scanning electron microscopy (SEM) using a Philips (Amsterdam, The Netherlands) microscope XL30.
Table 1 summarizes the differently prepared HEPOs, also presenting their labeling according to the thermal cycles (calcination and/or sintering) they were subjected to.

Table 1.
Labeling of the differently studied HEPO systems.
3. Results and Discussion
3.1. Design via the Cluster-Plus-Glue Atom Model
To firstly evaluate the possible formation of high-entropy single-phase perovskite-like structures in the studied systems, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7, a design approach based on the cluster-plus-glue-atom model was employed. This method enables the theoretical representation of complex multi-cationic structures and the rational distribution of cations in the lattice to grant chemical stability and charge compensation. Such a model has already been applied in the recent literature for the prediction of different HEOs [36,37] and compositionally complex systems, and the authors previously applied it for the first time to design a stable single-phase HEPO [38].
In this framework, the chemical formulas for perovskite-structured high-entropy perovskite oxides (HEPOs) can be expressed in terms of clusters and glue atoms, aligning with the general ABO3 structure formula. Particularly, the A-site, occupied by Ba2+ in all three studied systems, acts as a fixed site, while the B-site is populated by multiple equimolar cations, contributing to an increase in the configurational entropy of the whole system.
Thus, according to the cluster-plus-glue atom model [38,40] for granting the octet rule, the B-site clusters could be written as follows:
- [TVO6]Ba2TV;
- [REO6]RE3;
- [REO6]Ba3RE.
- where TV stands for a tetravalent cation (i.e., Ce, Zr in our systems) and RE stands for a generic trivalent rare-earth (i.e., Yb, Sm, La, Gd, Nd in our systems).
Starting from the Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7 system, it consists of a mixture of tetravalent (Ce4+, Zr4+) and trivalent (Yb3+, La3+, Sm3+) cations at the B-site. Thus, the B-site can be “written” as different [BO6] clusters, where the B-site is randomly populated by the five cations (Ce, Zr, Yb, La, Sm) in equimolar proportions. Each [BO6] cluster is influenced by the average charge and ionic radius of its constituent cations, which stabilize the lattice through entropy-driven mixing. The A-site is occupied by Ba2+, which acts as the glue atom for the different [BO6] clusters. Finally, the oxygen sublattice forms the backbone of the octahedral network, with vacancies introduced within the systems to maintain charge neutrality. Definitely, according to the cluster-plus-glue atom model, the Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7 system can be written as:
0.2 [TVO6]Ba2TV + 0.2 [REO6]Ba3RE + 0.05 [REO6]RE3
Similarly, Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7 incorporates a mix of two tetravalent (Ce4+, Zr4+) and three trivalent (Nd3+, La3+, Sm3+) cations at the B-site, thus being possibly written according to the cluster-plus-glue atom model in the same way as (4).
Conversely, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6 features an almost fully trivalent B-site composition (Sm3+, Yb3+, Nd3+, Gd3+), except for Ce4+. Thus, the [BO6] clusters here are differently distributed along the system, resulting in a slightly different local order than the previous systems, being possibly written according to the cluster-plus-glue atom model as follows:
Summarizing, all three systems rely on the entropy-driven stabilization of different kinds of [BO6] clusters, depending on the combination of trivalent and tetravalent cations; Ba2+ ions at the A-site maintain the structural integrity of the lattice acting as glue atoms along with a small percentage of trivalent cations introducing different local environments (on the basis of the various cluster-plus-glue formulae) in samples containing Zr and in sample Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6.
To define a possible predictor for HEPOs based on the cluster-plus-glue atom model, a numerical descriptor highlighting the difference in the A-site to B-site cations ratio for each possible cluster in HEPOs compared to the “standard” [TVO6]Ba2TV cluster in pure ABO3 perovskites (where the A-site-to-B-site cationic ratio is 1 and the only cluster is indeed [TVO6]Ba2TV) have been calculated as follows:
where n is the number of possible clusters containing both A-site and B-site cations in a generic HEPO, ai is the relative abundance of the ith possible cluster, and catA and catB are the numbers of cations occupying A-site and B-site of the HEPO, respectively.
Based on Equation (6), for both Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7 and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7, ΔCG is equal to 0.333, while for Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, ΔCG is equal to 0.278. Thus, it is expected that Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6 is characterized by a short-range order that diverges more from the “unmodified” reference ABO3 perovskite structure than the other two studied systems compared, possibly leading to a much more difficult entropy-driven single-phase stabilization.
3.2. Geometric Descriptors
In addition to the design based on the cluster-plus-glue atom model, inspired by the already consolidated standard deviation predictor for fluorite/bixbyite-structured HEOs [42], the standard deviation of the B-site cationic radii has been calculated for all three studied HEPOs to unravel a possible effect of the “cationic mismatch” in the B-site on the entropy-driven formation of the desired single-phase perovskitic structure in HEPOs. Thus, considering the B-site cations radii (in 6-fold coordination) [54], the three different standard deviations s (alongside their Goldschmidt tolerance factor) of Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7 have been calculated according to:
where ri is the cationic radius of the ith B-site cation and is the mean B-site cationic radius.
Table 2 summarizes, for each studied system, both the standard deviation of the B-site cationic radii (sB) and the Goldschmidt tolerance factor (t).

Table 2.
Standard deviation of the B-site cationic radii, Goldschmidt tolerance factor, and ΔCG descriptor for the differently studied HEPO systems.
3.3. Structural and Thermal Characterization
Subsequent to the co-precipitation-based synthesis route described in Section 2, the three as-prepared systems, i.e., Ba(CSYbNG), Ba(CZYbLS), and Ba(CZNLS), have been characterized both from a structural and thermal point of view to assess the entropy-driven formation of the desired single-phase perovskite-like structure based on both the sB and ΔCG of each studied system.
Figure 1 shows the DTA-TG curves of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c).
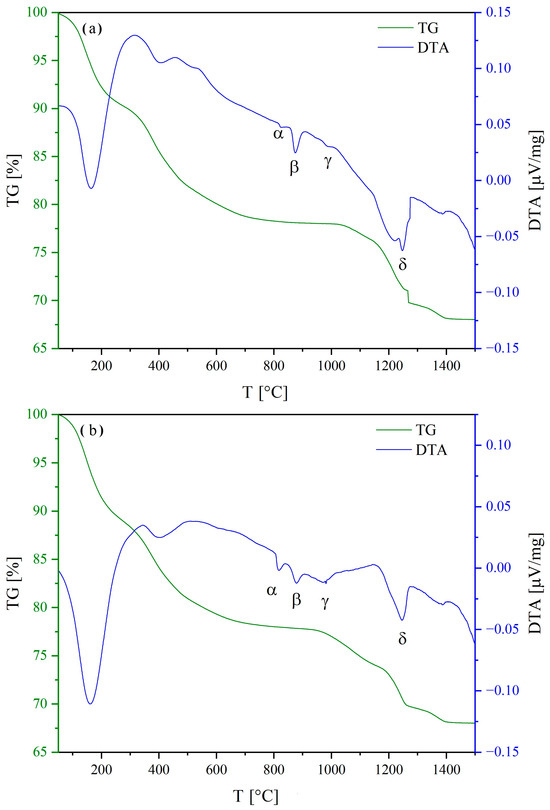
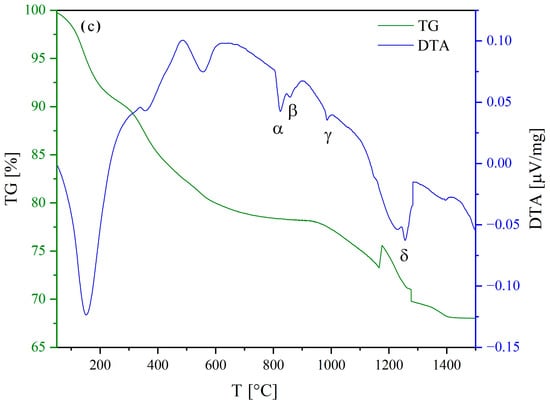
Figure 1.
DTA-DG curves of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c). Irregularities in the TG curves in (a,c) at about 1250° and 1200 °C, respectively, are due to unpredictable instrumental issues.
The DTA and TG curves of the three as-precipitated samples reveal a complex thermal behavior characterized by multiple events, as described in detail below (denoted with Greek letters in Figure 1). The irregularities in the TG curves in Figure 1a,c (at about 1250° and 1200 °C, respectively) are due to unpredictable instrumental issues and do not impair the following discussion.
Carefully analyzing the three TG curves, the thermal evolution of the as-precipitated samples can be divided into two main regions: below and above 700 °C.
Up to 700 °C, the observed weight losses are consistent with the evolution of water and carbon dioxide, resulting from the decomposition of zirconium hydroxide (where present) and rare-earth carbonates formed upon precipitation [55,56]. Based on the exemplary Ba(CZYbLS) composition (containing Zr), the following global reaction can be used to describe this overall decomposition process:
BaCO3 + 0.1 Ce2(CO3)3·xH2O + 0.3 RE2(CO3)3·yH2O + 0.2 ZrO2·zH2O + 0.05 O2 →
BaCO3 + 0.2 CeO2 + 0.3 RE2O3 + 0.2 ZrO2 + (0.1x + 0.3y + 0.2z) H2O↑ + 1.2 CO2↑
BaCO3 + 0.2 CeO2 + 0.3 RE2O3 + 0.2 ZrO2 + (0.1x + 0.3y + 0.2z) H2O↑ + 1.2 CO2↑
Above 700 °C, the registered weight losses are associated with the complex decomposition of barium carbonate [57,58] and the subsequent formation of the entropy-stabilized HEPO. Such overall process can be described by the following global reaction (again referrable to the exemplary Ba(CZYbLS) composition):
BaCO3 + 0.2 ZrO2 + 0.2 CeO2 + 0.3 RE2O3 → Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7 + CO2↑
Such global reaction (9) leads to a theoretical weight loss slightly exceeding 10 wt% (relative to the as-synthesized Ba(CZYbLS) analyzed in the DTA-TG run), which appears in good agreement with both the experimentally measured value and the previously published value for a very similar HEPO [38].
By careful analysis of the DTA curves above 700 °C, it is always possible to distinguish 4 different thermal events, denoted with α, β, γ, and δ in Figure 1, that can be, respectively, explained as follows:
- Endothermic orthorhombic-to-hexagonal polymorphic transformation (around 800 °C) of barium carbonate [57];
- Endothermic hexagonal-to-cubic polymorphic transformation (around 850 °C) of barium carbonate [57];
- Possible formation of the entropy-stabilized fluorite/bixbyite single phase involving the non-Ba cations (around 950 °C);
- Possible formation of the entropy-stabilized perovskite single phase upon completion of barium carbonate decomposition at around 1250 °C (according to reaction (9)).
Thus, based on the thermal characterization results, it is possible to define two different calcination paths for the three analyzed systems, i.e., 800 °C for 12 h and 1300 °C for 12 h. The former calcination temperature (alongside the prolonged treatment duration) was chosen to grant the completion of both rare-earth carbonates and zirconium hydroxide decomposition but not the barium carbonate one, whilst the latter temperature was chosen to grant the completion of all precursors decomposition.
Figure 2 shows the diffraction patterns of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c) after calcination at 800 °C for 12 h.
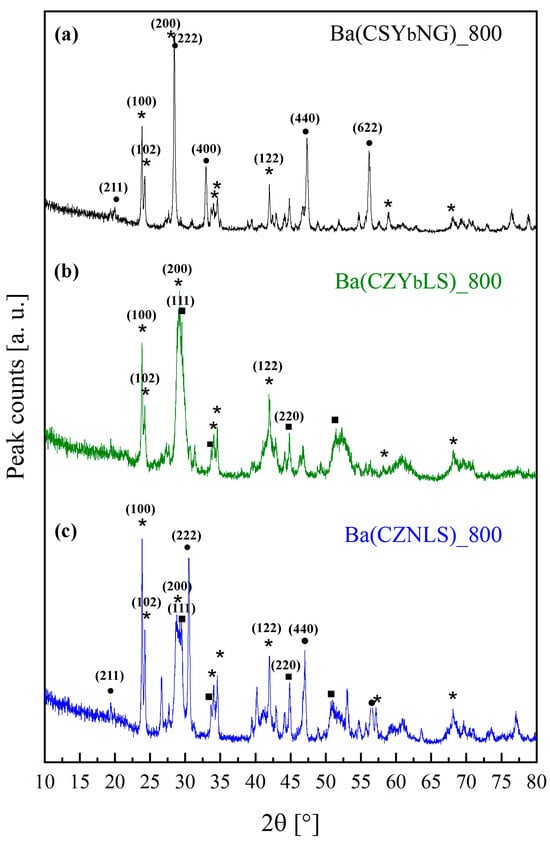
Figure 2.
Diffraction patterns of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c) calcined at 800 °C for 12 h (“*” stands for orthorhombic barium carbonate, “•” for bixbyite-like phases, and “▪” for fluorite-like phases).
All the diffraction patterns in Figure 2 are very complex, being characterized by the presence of at least two crystalline phases, among which orthorhombic barium carbonate (witherite) is mixed with either bixbyite-structured phases, attributable to rare-earth sesquioxides (such as Gd2O3), or fluorite-structured phases, likely corresponding to rare-earths-doped CeO2 and/or Zr-doped CeO2. The reference ICDD cards for these phases are as follows: ICDD card n. 045–1471 for orthorhombic barium carbonate, ICDD card n. 012–0797 for bixbyite-like gadolinium oxide (representative of the rare-earths sesquioxides), and ICDD card n. 034–0394 for fluorite-like cerium oxide. Except for BaCO3, the other present phases are likely solid solutions, given the strong tendency of the differently involved oxides to form them. The identified phases are labeled in Figure 2 with the following symbols: “*” for orthorhombic barium carbonate, “•” for bixbyite-like phases, and “▪” for fluorite-like phases. Therefore, calcination at 800 °C leads to a very similar behavior in the three samples, as revealed by the diffraction patterns in Figure 2; that finding is in perfect agreement with the DTA-TG data.
Conversely, by calcination at 1300 °C for 12 h, very different behavior among the samples arose as revealed by the diffraction patterns of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c), displayed in Figure 3.
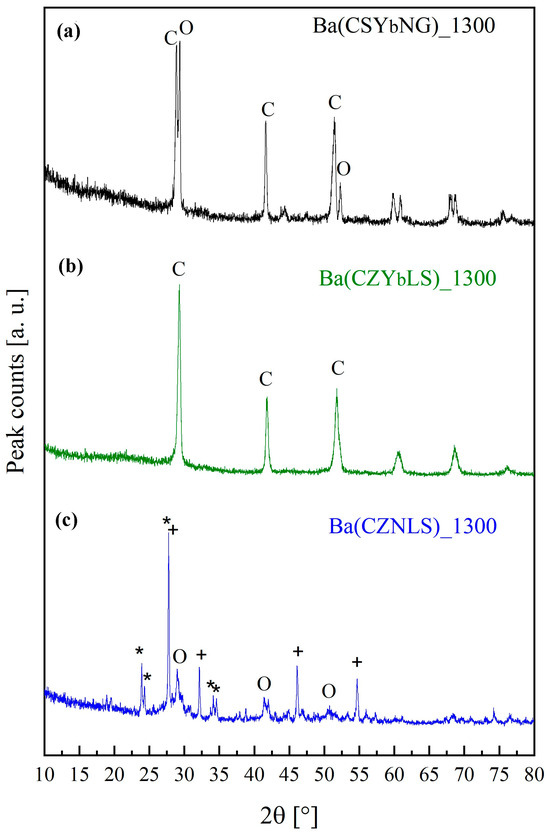
Figure 3.
Diffraction patterns of samples Ba(CSYbNG) (a), Ba(CZYbLS) (b), and Ba(CZNLS) (c) calcined at 1300 °C for 12 h (“O” stands for orthorhombic perovskite, “C” for cubic perovskite, “+” for cubic barium oxide, and “*” for orthorhombic barium carbonate).
Indeed, only the Ba(CZYbLS) sample is monophasic, while the other two systems are pluriphase.
Particularly, sample Ba(CSYbNG) is characterized by the coexistence of two perovskite-like phases, one orthorhombic (ICDD card n. 01-070-3676), labeled with “O” in Figure 3, and one cubic (ICDD card n. 01-075-0431), labeled with “C” in Figure 3. Very likely, the different short-range order suggested by a lower value of ΔCG, along with a lower value of both Goldschmidt tolerance factor and sB predictor, led to two different local “environments” in which the as-formed barium oxide (upon barium carbonate decomposition at around 1250 °C) separately reacted with the surrounding rare-earth oxides to form such differently structured perovskites. Under this hypothesis, as Goldschmidt tolerance factor <0.9 results in the formation of orthorhombic perovskite, the as-formed barium oxide could have separately reacted with smaller rare-earth elements such as Gd and Yb (hypothetically leading to the formation of cubic perovskite), whereas the rest of the as-formed barium oxide separately reacted with larger rare-earth elements like Ce and Nd (hypothetically leading to the formation of orthorhombic perovskite).
Sample Ba(CZYbLS)_1300 is, indeed, monophasic and is characterized by the presence of an entropy-stabilized cubic perovskite (ICDD card n. 01-070-3674).
Finally, sample Ba(CZNLS)_1300 exhibits three different crystal phases: an orthorhombic perovskite (ICDD card n. 01-070-3676), labeled with “O” in Figure 3, along with barium oxide (ICDD card n. 03-065-2923), labeled with “+” in Figure 3, and barium carbonate (ICDD card n. 045-1471), labeled with * in Figure 3. The observed barium oxide could derive from either a partial decomposition (with consequent BaO exsolution) of the entropy-stabilized perovskite-like phase or a local compositional “mismatch” of barium oxide and the (CZNLS) oxide at high temperatures. Conversely, the presence of barium carbonate in the diffraction pattern of Figure 3c is attributable to a partial carbonation of some of the residual observed BaO quickly reacting with atmospheric CO2 to form Ba(CO)3 [59].
To better understand the Ba(CZNLS) chemical stability behavior, an additional thermal treatment at 1500 °C for 12 h on the already-calcined system has been carried out. Figure 4 shows the diffraction patterns of such a system, crushed in powders from a sintered pellet of Ba(CZNLS)_1300_1500, taken after 2 days of atmospheric air exposure.
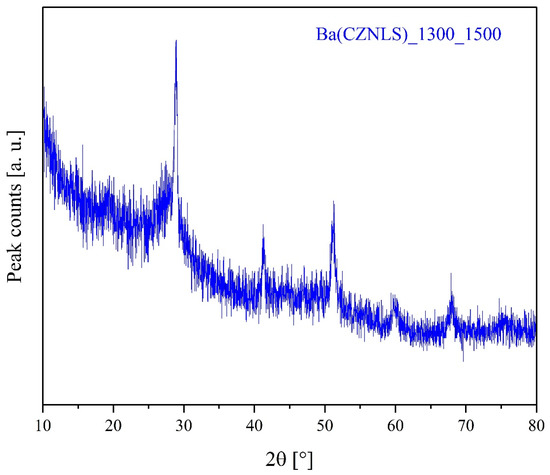
Figure 4.
Diffraction pattern of samples Ba(CZNLS)_1300_1500.
The analysis of the diffraction pattern in Figure 4 mainly reveals a noticeable loss of the sample’s crystallinity, characterized by significantly attenuated and broadened diffraction peaks emerging from an amorphous halo. The few weak peaks observable can be tentatively attributed to a fluorite-structured rare-earth-based HEO and several “hinted” peaks of barium carbonate reflections deriving from the previously formed HEPO that have withstood a significant transformation process. In fact, the pronounced alteration in the structural characteristics of the Ba(CZNLS)_1300_1500 sample is most likely attributable to interactions with the surrounding atmosphere during the post-sintering stages [49,50]. Such interactions could involve moisture absorption, barium oxide carbonation, and consequent structural degradation, leading to the observed predominance of an amorphous phase. Thus, independently of the starting conditions (already-calcined or as-precipitated) and of the extremely severe subsequent thermal treatment, Ba(CZNLS) entropy-stabilized perovskite is not chemically stable over time.
Conversely, the same thermal treatment (1500 °C for 12 h) carried out on sample Ba(CZYbLS)_1300_1500 (crushed into powders from a sintered pellet) led to the results shown in Figure 5, i.e., the entropy-stabilized cubic perovskite (ICDD card n. 01-070-3674) already observed for sample Ba(CZYbLS)_1300. Only a pronounced sharpening of the diffraction peaks due to the noticeable grain growth deriving from the harsh adopted thermal treatment can be observed.
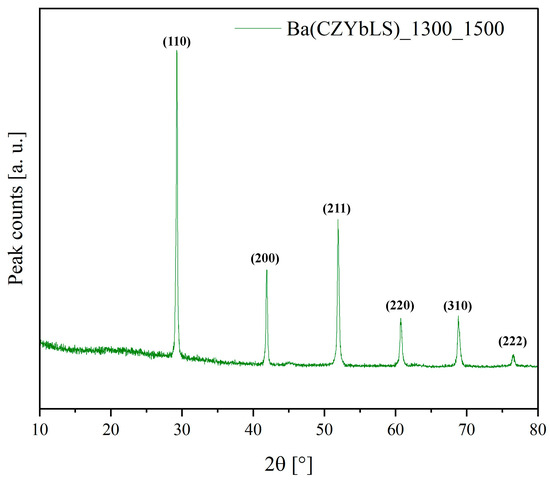
Figure 5.
Diffraction pattern of sample Ba(CZYbLS)_1300_1500.
Finally, Ba(CSYbNG)_1300_1500, whose diffraction pattern is not reported here, is substantially unaltered compared to Ba(CSYbNG)_1300 (see Figure 3a) being a stable biphasic system irrespective of the prolonged and severe thermal treatment at 1500 °C.
Definitely, based on the above-presented results of the three HEPOs structural characterization, it was possible to obtain the desired entropy-stabilized single-phase perovskite only for system Ba(CZYbLS). Thus, it is possible to observe from the used descriptors, by comparing in the following Table 3 Ba(CZYbLS) with another HEPO already demonstrated to be obtainable in a stable form by the authors [38], that high-entropy barium cerate/zirconate derivatives could exist in a very narrow set of conditions that will be further investigated in an upcoming work.

Table 3.
Comparison between Ba(CZYbLS) and a reference system [38] in terms of the three used empirical descriptors for HEPOs.
3.4. Sintering Behavior of System Ba(CZYbLS)
Once having identified the empirical descriptors and the “stability conditions” for barium cerate/zirconate HEPOs derivatives, the Ba(CZYbLS) system was sintered starting from different conditions in order to define a possible fabrication protocol for its use as gas-tight electrolyte for proton conducting fuel cells (PCFCs).
Particularly, a sintering cycle at 1500 °C for 6 h was carried out on both a Ba(CZYbLS) pellet and a Ba(CZYbLS)_1300 one, corresponding to a starting condition of either a mixture of barium carbonate and amorphous rare-earth carbonates and zirconium hydroxide [38] or a fully formed cubic HEPO, respectively.
Figure 6 shows two exemplary micrographs of the Ba(CZYbLS)_1500 sample, obtained by sintering directly the formed as-precipitated Ba(CZYbLS).

Figure 6.
SEM micrographs (taken at different magnifications) of the Ba(CZYbLS)_1500 sample.
The Ba(CZYbLS)_1500 microstructure, even though being rather homogeneous in terms of grain size and distribution, is characterized by a uniform presence of very small (around 1 µm of diameter) pores, possibly derived by the reactions globally described in Equations (8) and (9) concurring with the sintering phenomena at high temperatures, leading to a significant and homogeneous CO2 evolution all over the sintered pellet.
Figure 7 shows two exemplary micrographs of the Ba(CZYbLS)_1300_1500 sample, obtained by sintering the single-phase perovskitic Ba(CZYbLS)_1300 (diffraction pattern of Figure 3b).

Figure 7.
SEM micrographs (taken at different magnifications) of the Ba(CZYbLS)_1300_1500 sample.
The micrographs displayed in Figure 7 reveal a very homogeneous grain structure characterized by a very narrow size distribution. The average grain size of Ba(CZYbLS)_1300_1500, estimated by using the average grain intercept method according to [60] using the ImageJ software, version 1.54k, (reported in Table 4), is equal to around 0.7 μm. Indeed, the Ba(CZYbLS)_1300_1500 microstructure is nearly ideal from the viewpoint of a possible Ba(CZYbLS) use as a solid electrolyte in electrochemical devices [61].

Table 4.
Measured densities of Ba(CZYbLS)_1500 and Ba(CZYbLS)_1300_1500.
Finally, Table 4 reports the measured apparent densities of both sintered Ba(CZYbLS)_1500 and Ba(CZYbLS)_1300_1500, along with their relative densities calculated by using the theoretical density of BCZY27 yttrium-doped barium cerate/zirconate from [62], i.e., 6.210 g/cm3.
4. Conclusions
The present study demonstrates that the cluster-plus-glue atom model provides a robust framework for the design and synthesis of high-entropy perovskite oxides (HEPOs) with different multi-cationic configurations derived from barium cerate (BaCeO3). A detailed structural characterization of three different designed systems, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7, Ba(Ce0.2Sm0.2Yb0.2Nd0.2Gd0.2)O2.6, and Ba(Ce0.2Zr0.2Nd0.2La0.2Sm0.2)O2.7, characterized by different geometrical predictors, highlighted that only one of these, i.e., Ba(Ce0.2Zr0.2Yb0.2La0.2Sm0.2)O2.7–Ba(CZYbLS), resulted in the formation of a stable entropy-stabilized single-phase perovskite. Conversely, the other two systems exhibited the coexistence of multiple phases, including orthorhombic perovskites and residual oxide phases, indicating a lower tendency toward single-phase stabilization.
The three used empirical descriptors, including the Goldschmidt tolerance factor (t), the standard deviation of the B-site cationic radii (sB), and the novel ΔCG descriptor, provided a quantitative framework to predict HEPO stability. Specifically, the Ba(CZYbLS) system exhibited values of t = 0.928, sB = 0.11680, and ΔCG = 0.333, possibly representing a critical range for cubic phase stabilization. In fact, a comparison between Ba(CZYbLS) and a previously established stable HEPO, Ba(CZYLG) [38], further reinforced that the stabilization of high-entropy barium cerate/zirconate perovskites occurs within a narrow set of geometric and chemical conditions. This result suggests that the integration of the cluster-plus-glue model with geometric descriptors may serve as an effective approach for the design and discovery of novel HEPOs.
Having identified Ba(CZYbLS) as the only stable HEPO among the studied systems, a dedicated sintering protocol was developed to fabricate dense pellets in view of Ba(CZYbLS) potential use as a proton-conducting fuel cell electrolyte. Sintering at 1500 °C for 6 h starting from a single-phase perovskitic powder resulted in a densified pellet with a relative density of about 95%. Scanning electron microscopy (SEM) analysis highlighted the obtaining of a homogeneous microstructure characterized by uniform grains whose average size is around 1 μm, being nearly ideal for applications as electrolytes in electrochemical devices.
Definitely, this work validates the cluster-plus-glue atom model as an effective framework for the design and synthesis of high-entropy perovskite oxides (HEPOs) derived from barium cerate, enabling the identification of compositional configurations likely to yield single-phase stability. The successful densification of the stable Ba(CZYbLS) system to 95% relative density, along with the achievement of a fine-grained and homogeneous microstructure, provides a significantly novel contribution in terms of compositional design strategy and process development for its potential application as a proton-conducting electrolyte, even though future research work should be dedicated to a full electrochemical characterization to such system.
Author Contributions
Conceptualization, L.S.; methodology, G.D.; validation, G.D.; formal analysis, L.S., V.M. and A.M.; investigation, L.S. and V.M.; data curation, L.S.; writing—original draft preparation, L.S.; writing—review and editing, G.D.; visualization, A.M. and V.M.; supervision, G.D.; project administration, G.D.; funding acquisition, G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Italian “Ministero dell’Università e della Ricerca” within the “Piano Nazionale di Ripresa e Resilienza (PNRR)” co-financed by the European Union—Next Generation EU—Mission 4 Component 2 Investimento 1.1—2022KWSRSA—CUP H53D23004600006.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar]
- Murty, B.S.; Yeh, J.W.; Ranganathan, S.; Bhattacharjee, P.P. High-Entropy Alloys; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–12. [Google Scholar]
- Otto, F.; Yang, Y.; Bei, H.; George, E.P. Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys. Acta Mater. 2013, 61, 2628–2638. [Google Scholar]
- Rost, C.M.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.C.; Hou, D.; Jones, J.L.; Curtarolo, S.; Maria, J.P. Entropy-stabilized oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar]
- Dąbrowa, J.; Stygar, M.; Mikuła, A.; Knapik, A.; Mroczka, K.; Tejchman, W.; Danielewski, M.; Martin, M. Synthesis and microstructure of the (Co, Cr, Fe, Mn, Ni) 3O4 high entropy oxide characterized by spinel structure. Mater. Lett. 2018, 216, 32–36. [Google Scholar]
- Wang, J.; Cui, Y.; Wang, Q.; Wang, K.; Huang, X.; Stenzel, D.; Sarkar, A.; Azmi, R.; Bergfeldt, T.; Bhattacharya, S.S.; et al. Lithium containing layered high entropy oxide structures. Sci. Rep. 2020, 10, 18430. [Google Scholar]
- Gild, J.; Samiee, M.; Braun, J.L.; Harrington, T.; Vega, H.; Hopkins, P.E.; Vecchio, K.; Luo, J. High-entropy fluorite oxides. J. Eur. Ceram. Soc. 2018, 38, 3578–3584. [Google Scholar]
- Spiridigliozzi, L.; Dell’Agli, G. A novel high-entropy rare-earth hydroxycarbonate synthesized via facile hydrothermal synthesis with superior decomposition temperature. Mater. Lett. 2024, 372, 137090. [Google Scholar]
- Teng, Z.; Zhu, L.; Tan, Y.; Zeng, S.; Xia, Y.; Wang, Y.; Zhang, H. Synthesis and structures of high-entropy pyrochlore oxides. J. Eur. Ceram. Soc. 2020, 40, 1639–1643. [Google Scholar]
- Vinnik, D.A.; Trofimov, E.A.; Zhivulin, V.E.; Zaitseva, O.V.; Gudkova, S.A.; Starikov, A.Y.; Zherebtsov, D.A.; Kirsanova, A.A.; Häßner, M.; Niewa, R. High-entropy oxide phases with magnetoplumbite structure. Ceram. Int. 2019, 45, 12942–12948. [Google Scholar]
- Dippo, O.F.; Vecchio, K.S. A universal configurational entropy metric for high-entropy materials. Scr. Mater. 2021, 201, 113974. [Google Scholar]
- Aamlid, S.S.; Oudah, M.; Rottler, J.; Hallas, A.M. Understanding the role of entropy in high entropy oxides. J. Am. Chem. Soc. 2023, 145, 5991–6006. [Google Scholar] [CrossRef] [PubMed]
- Hanif, M.B.; Motola, M.; Rauf, S.; Li, C.J.; Li, C.X. Recent advancements, doping strategies and the future perspective of perovskite-based solid oxide fuel cells for energy conversion. Chem. Eng. J. 2022, 428, 132603. [Google Scholar] [CrossRef]
- Hanif, M.B.; Rauf, S.; Motola, M.; Babar ZU, D.; Li, C.J.; Li, C.X. Recent progress of perovskite-based electrolyte materials for solid oxide fuel cells and performance optimizing strategies for energy storage applications. Mater. Res. Bull. 2022, 146, 111612. [Google Scholar] [CrossRef]
- Zhang, M.; Du, Z.; Zhang, Y.; Zhao, H. Progress of perovskites as electrodes for symmetrical solid oxide fuel cells. ACS Appl. Energy Mater. 2022, 5, 13081–13095. [Google Scholar] [CrossRef]
- Li, H.; Yu, J.; Gong, Y.; Lin, N.; Yang, Q.; Zhang, X.; Wang, Y. Perovskite catalysts with different dimensionalities for environmental and energy applications: A review. Sep. Purif. Technol. 2023, 307, 122716. [Google Scholar] [CrossRef]
- Bian, Z.; Wang, Z.; Jiang, B.; Hongmanorom, P.; Zhong, W.; Kawi, S. A review on perovskite catalysts for reforming of methane to hydrogen production. Renew. Sustain. Energy Rev. 2020, 134, 110291. [Google Scholar] [CrossRef]
- Ali, S.A.; Ahmad, T. Treasure trove for efficient hydrogen evolution through water splitting using diverse perovskite photocatalysts. Mater. Today Chem. 2023, 29, 101387. [Google Scholar] [CrossRef]
- Zhu, H.; Teale, S.; Lintangpradipto, M.N.; Mahesh, S.; Chen, B.; McGehee, M.D.; Sargent, E.H.; Bakr, O.M. Long-term operating stability in perovskite photovoltaics. Nat. Rev. Mater. 2023, 8, 569–586. [Google Scholar] [CrossRef]
- Liu, X.; Luo, D.; Lu, Z.H.; Yun, J.S.; Saliba, M.; Seok, S.I.; Zhang, W. Stabilization of photoactive phases for perovskite photovoltaics. Nat. Rev. Chem. 2023, 7, 462–479. [Google Scholar] [CrossRef]
- Zhang, L.; Pu, Y.; Chen, M.; Peng, X.; Wang, B.; Shang, J. Design strategies of perovskite energy-storage dielectrics for next-generation capacitors. J. Eur. Ceram. Soc. 2023, 43, 5713–5747. [Google Scholar] [CrossRef]
- Sahoo, L.; Parida, B.N.; Nayak, N.C.; Parida, R.K. Revived BBFTO double perovskite with improved dielectric properties for some possible device applications. J. Mater.Sci. Mater. Electron. 2023, 34, 1019. [Google Scholar]
- Zhang, M.H.; Qi, J.L.; Liu, Y.Q.; Lan, S.; Luo, Z.X.; Pan, H.; Lin, Y.H. High energy storage capability of perovskite relaxor ferroelectrics via hierarchical optimization. Rare Met. 2022, 41, 730–744. [Google Scholar]
- Yang, Q.; Wang, G.; Wu, H.; Beshiwork, B.A.; Tian, D.; Zhu, S.; Yang, Y.; Lu, X.; Ding, Y.; Ling, Y.; et al. A high-entropy perovskite cathode for solid oxide fuel cells. J. Alloys Compd. 2021, 872, 159633. [Google Scholar]
- Zhang, D.; Wang, Y.; Peng, Y.; Luo, Y.; Liu, T.; He, W.; Chen, F.; Ding, M. Novel high-entropy perovskite-type symmetrical electrode for efficient and durable carbon dioxide reduction reaction. Adv. Powder Mater. 2023, 2, 100129. [Google Scholar]
- Guo, M.; Liu, Y.; Zhang, F.; Cheng, F.; Cheng, C.; Miao, Y.; Gao, F.; Yu, J. Inactive Al3+-doped La (CoCrFeMnNiAlx)1/(5+x) O3 high-entropy perovskite oxides as high performance supercapacitor electrodes. J. Adv. Ceram. 2022, 11, 742–753. [Google Scholar]
- Oh, S.; Kim, D.; Ryu, H.J.; Lee, K.T. A Novel High-Entropy Perovskite Electrolyte with Improved Proton Conductivity and Stability for Reversible Protonic Ceramic Electrochemical Cells. Adv. Funct. Mater. 2024, 34, 2311426. [Google Scholar] [CrossRef]
- Ning, Y.; Pu, Y.; Wu, C.; Zhou, S.; Zhang, L.; Zhang, J.; Zhang, X.; Shang, Y. Enhanced capacitive energy storage and dielectric temperature stability of A-site disordered high-entropy perovskite oxides. J. Mater. Sci. Technol. 2023, 145, 66–73. [Google Scholar]
- Zhai, Y.; Ren, X.; Wang, B.; Liu, S. High-Entropy Catalyst—A Novel Platform for Electrochemical Water Splitting. Adv. Funct. Mater. 2022, 32, 2207536. [Google Scholar] [CrossRef]
- Wang, Q.; Xuan, Y.; Gao, K.; Sun, C.; Gao, Y.; Liu, J.; Chang, S.; Liu, X. High-entropy perovskite oxides for direct solar-driven thermochemical CO2 splitting. Ceram. Int. 2024, 50, 1564–1573. [Google Scholar]
- Guo, R.; He, T. High-entropy perovskite electrolyte for protonic ceramic fuel cells operating below 600 °C. ACS Mater. Lett. 2022, 4, 1646–1652. [Google Scholar] [CrossRef]
- Zhou, G.; Li, Y.; Luo, Y.; Wang, X.; Ding, Y. The structure and electrical properties of novel BaSn0.15Ce0.35Hf0.25Y0.1Yb0.1Ho0.05O3-δ high-entropy proton-conducting electrolyte. J. Alloys Compd. 2024, 971, 172668. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Tilley, R.J. Perovskites: Structure-Property Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 1–40. [Google Scholar]
- Wang, Y.; Liu, J.; Song, Y.; Yu, J.; Tian, Y.; Robson, M.J.; Wang, J.; Zhang, Z.; Lin, X.; Zhou, G.; et al. High-entropy perovskites for energy conversion and storage: Design, synthesis, and potential applications. Small Methods 2023, 7, 2201138. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Y.; Li, Z.; Wang, H.; Liu, S.; Yao, T.; Jiang, W.; Wang, N.; Liu, C.; Ding, W.; et al. Composition design, thermodynamic calculation and synthesis of rocksalt structure Mg–Co–Ni–Cu–Zn–O HEOs based on cluster-plus-glue-atom model. Ceram. Int. 2024, 50, 15240–15244. [Google Scholar] [CrossRef]
- Spiridigliozzi, L.; Ferone, C.; Cioffi, R.; Dell’Agli, G. Compositional design of single-phase rare-earth based high-entropy oxides (HEOs) by using the cluster-plus-glue atom model. Ceram. Int. 2023, 49, 7662–7669. [Google Scholar] [CrossRef]
- Spiridigliozzi, L.; Biesuz, M.; Sglavo, V.M.; Dell’Agli, G. Design, synthesis and formation mechanism of a novel entropy-stabilized perovskite oxide derived from barium cerate/zirconate. J. Eur. Ceram. Soc. 2024, 44, 2223–2232. [Google Scholar] [CrossRef]
- Dong, C.; Wang, Q.; Qiang, J.B.; Wang, Y.M.; Jiang, N.; Han, G.; Li, Y.H.; Wu, J.; Xia, J.H. From clusters to phase diagrams: Composition rules of quasicrystals and bulk metallic glasses. J. Phys. D Appl. Phys. 2007, 40, R273. [Google Scholar] [CrossRef]
- Ma, Y.; Dong, D.; Wu, A.; Dong, C. Composition formulas of inorganic compounds in terms of cluster plus glue atom model. Inorg. Chem. 2018, 57, 710–717. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, R.; Yu, C.; He, L.; Ren, H.; Jiang, L. Flexural behavior of simply supported beams consisting of gradient concrete and GFRP bars. Front. Mater. 2021, 8, 693905. [Google Scholar] [CrossRef]
- Spiridigliozzi, L.; Ferone, C.; Cioffi, R.; Dell’Agli, G. A simple and effective predictor to design novel fluorite-structured High Entropy Oxides (HEOs). Acta Mater. 2021, 202, 181–189. [Google Scholar] [CrossRef]
- Reddy, G.S.; Bauri, R. Y and In-doped BaCeO3-BaZrO3 solid solutions: Chemically stable and easily sinterable proton conducting oxides. J. Alloys Compd. 2016, 688, 1039–1046. [Google Scholar]
- Luo, Y.; Li, Y.; Zhang, N.; Ding, Y.; Li, H.; Chen, G. Electrical properties and chemical stability of Br addition in BaCe0.8Gd0.2O3-α proton-conducting electrolyte. Ceram. Int. 2020, 46, 26027–26034. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Cai, X.; Wang, X. Y-Gd-Zn tri-doped BaCeO3-BaZrO3 proton conducting electrolytes with improved electrical and transport properties. J. Mater. Sci. 2024, 59, 20944–20963. [Google Scholar]
- Accardo, G.; Frattini, D.; Yoon, S.P. Enhanced proton conductivity of Gd–Co bi-doped barium cerate perovskites based on structural and microstructural investigations. J. Alloys Compd. 2020, 834, 155114. [Google Scholar] [CrossRef]
- Danilov, N.A.; Starostina, I.A.; Starostin, G.N.; Kasyanova, A.V.; Medvedev, D.A.; Shao, Z. Fundamental understanding and applications of protonic Y-and Yb-coped Ba (Ce, Zr) O3 perovskites: State-of-the-art and perspectives. Adv. Energy Mater. 2023, 13, 2302175. [Google Scholar]
- Spiridigliozzi, L.; Accardo, G.; Audasso, E.; Yoon, S.P.; Dell’Agli, G. On the role of copper as a sintering aid in proton conducting Gd-doped barium cerate (BCGO). J. Alloys Compd. 2023, 960, 170762. [Google Scholar]
- Sonu, B.K.; Sinha, E. Structural, thermal stability and electrical conductivity of zirconium substituted barium cerate ceramics. J. Alloys Compd. 2021, 860, 158471. [Google Scholar]
- Yan, N.; Zeng, Y.; Shalchi, B.; Wang, W.; Gao, T.; Rothenberg, G.; Luo, J.L. Discovery and understanding of the ambient-condition degradation of doped barium cerate proton-conducting perovskite oxide in solid oxide fuel cells. J. Electrochem. Soc. 2015, 162, F1408. [Google Scholar]
- Lin, X.L.; Babar ZU, D.; Gao, Y.; Gao, J.T.; Li, C.X. Influence of triple sintering additives (BaO-CuO-B2O3) on the sintering behavior and conductivity of the proton-conducting BaZr0.1Ce0.7Y0.2O3−δ electrolyte sintered at 1150 °C. ACS Appl. Energy Mater. 2023, 6, 4833–4843. [Google Scholar] [CrossRef]
- Nasani, N.; Shakel, Z.; Loureiro, F.J.; Panigrahi, B.B.; Kale, B.B.; Fagg, D.P. Exploring the impact of sintering additives on the densification and conductivity of BaCe0.3Zr0.55Y0.15O3-δ electrolyte for protonic ceramic fuel cells. J. Alloys Compd. 2021, 862, 158640. [Google Scholar]
- Babar ZU, D.; Hanif, M.B.; Butt, M.K.; Motola, M.; Li, C.X. Towards highly dense electrolytes at lower sintering temperature (∼1200 °C): Optimization strategies for BaCe0.7Zr0.1CuxY0.2-xO3-δ in SOFCs. Ceram. Int. 2024, 50, 40261–40270. [Google Scholar]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Found. Crystallogr. 1976, 32, 751–767. [Google Scholar]
- Accardo, G.; Dell’ Agli, G.; Frattini, D.; Spiridigliozzi, L.; Nam, S.W.; Yoon, S.P. Electrical behaviour and microstructural characterization of magnesia co-doped ScSZ nanopowders synthesized by urea co-precipitation. Chem. Eng. Trans. 2017, 57, 1345–1350. [Google Scholar]
- Turco, R.; Bonelli, B.; Armandi, M.; Spiridigliozzi, L.; Dell’Agli, G.; Deorsola, F.A.; Esposito, S.; Di Serio, M. Active and stable ceria-zirconia supported molybdenum oxide catalysts for cyclooctene epoxidation: Effect of the preparation procedure. Catal. Today 2020, 345, 201–212. [Google Scholar]
- Arvanitidis, I.; Siche, D.; Seetharaman, S. A study of the thermal decomposition of BaCO3. Metall. Mater. Trans. B 1996, 27, 409–416. [Google Scholar]
- Earnest, C.M.; Miller, E.T. An assessment of barium and strontium carbonates as temperature and enthalpy standards. J. Therm. Anal. Calor. 2017, 130, 2277–2282. [Google Scholar]
- Tutuianu, M.; Inderwildi, O.R.; Bessler, W.G.; Warnatz, J. Competitive adsorption of NO, NO2, CO2, and H2O on BaO(100): A quantum chemical study. J. Phys. Chem. B 2006, 110, 17484–17492. [Google Scholar]
- Rahaman, M.N. Ceramic Processing and Sintering; Taylor & Francis: Boca Raton, FL, USA, 2003; pp. 540–619. [Google Scholar]
- Bassano, A.; Buscaglia, V.; Viviani, M.; Bassoli, M.; Buscaglia, M.T.; Sennour, M.; Thorel, A.; Nanni, P. Synthesis of Y-doped BaCeO3 nanopowders by a modified solid-state process and conductivity of dense fine-grained ceramics. Solid State Ion. 2009, 180, 168–174. [Google Scholar]
- Ricote, S.; Bonanos, N.; De Lucas, M.M.; Caboche, G. Structural and conductivity study of the proton conductor BaCe (0.9− x) ZrxY0. 1O (3− δ) at intermediate temperatures. J. Power Sources 2009, 193, 189–193. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).