Abstract
In this study, we used solid-state synthesis to prepare Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 microwave ceramics for mobile communications. Compared with Ba[Zn1/3(Nb0.5Ta0.5)2/3]O3, in the prepared materials, Co2+ substitution with Zn2+ improved the Q × f value and enabled densification and sintering at a lower temperature. We used X-ray diffraction (XRD) and scanning electron microscopy (SEM) to analyze the obtained microstructure. Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 was found to have a 1:2 ordered hexagonal structure, and its Q × f value increased with the increase in sintering temperature. In this work, excellent microwave dielectric properties—τf = −0.7 ppm/°C, εr = 34.5, and Q × f = 110,000 GHz—were obtained by sintering Ba[(Zn0.3Co0.7)1/3(Nb0.5Ta0.5)2/3]O3 at 1400 °C for 5 h.
1. Introduction
Microwave dielectric ceramics have been widely used in the electronics industry because of their near-zero temperature coefficient of resonant frequency and high Q × f value. In this study, we examined the formation of substituent-free, non-stoichiometric, vacancy-containing solid solutions of BZN in the BaO–ZnO–Nb2O5 system. The perovskite structure can accommodate the formation of vacancies at the A position to a considerable extent. However, the extent of vacancy formation at the B site is limited to concentrations below 2% [1]. Relatively large concentrations of B-site vacancies change the stacking of ABO3 layers to form a hexagonal perovskite structure, with vacancies being arranged in an orderly manner in the resulting coplanar octahedral layer. The stoichiometric changes induced by ZnO volatilization can promote the growth of ordered domains, increase the degree of cation ordering and c/a lattice distortion, and improve the dielectric loss characteristics of Ba(Zn1/3Ta2/3)O3 (BZT) [2]. A helpful effect of cation deficiency on loss has been found in other 1:2 composite perovskites, such as BaMg1/3Ta2/3O3 (BMT) and BaMg1/3Nb2/3O3 (BMN). A variety of different mechanisms and even contradictory results on non-stoichiometric effects on cation ordering [3] have been reported in the literature [3]. It has been pointed out in previous studies that BZT increases the degree of ordering and c/a distortion due to the partial substitution of Zn with the cationic part of the A site of Ba. The reduction of Zn and the associated reduction in the Zn–Nb ratio increase under these conditions [4]. According to the literature, the reduction of ZnO due to cation diffusion is enhanced by the formation of zinc ion vacancies; a higher degree of cation ordering has been observed in free BZT powders compared with the bulk [5]. Two BZT phases with slightly different unit cell parameters and c/a ratios were reported, and a solid explanation for the formation of zinc-deficient BZT phase was obtained by using high-resolution X-ray scattering analysis. This observation has been explained in terms of vacancy formation during the partial melting of the phases, which has been claimed to increase the degree of anti-site disorder [6,7]. There are also conflicting reports on the effects of non-stoichiometry on grain growth and densification in these systems. According to research, the volatilization of ZnO induces the formation of a second phase, and densification has a negative impact on BZT. However, according to other works, the lack of Mg2+ in BMN increases density, while excess Mg2+ hinders grain growth and densification. Regarding A-site elements, there are also conflicting data on the effect of non-stoichiometry on microstructure and densification [8]. However, no evidence of liquid-phase sintering was found in another study on BaO-deficient BMT, where the samples were prepared with (MgCO3)4·Mg(OH)2·5H2O instead of MgO [9]. In high-Ba2+-content BNN, abnormal grain growth resulted in density differences, but uniform grain size was also observed.
In previous studies, various conflicting findings in these systems have been reported, highlighting the difficulties that can be encountered during the above-mentioned processes. It can be confirmed that perovskite materials are closely related to the current trend of extending the operating frequency range of MW wireless communications in microwave-operating frequency bands, for example, 26–38 GHz in PtP Radiolinks, 20–30 GHz in VSATs, 28–40 GHz in local multi-point distribution systems (LMDSs), and even up to 60 GHz in some applications.
Low-noise modules (LNBs) are used in various microwave dielectric components, such as local multi-point distribution system (LMDS), module upconverters (BUCs), and very-small-aperture terminals (VSATs). For various microwave system requirements, in addition to the high quality of materials, it is also important to consider the price. Therefore, considering that the dielectric loss is extremely low, new low-cost dielectric materials with appropriate dielectric constants are needed [10,11,12,13,14,15,16].
Perovskite ceramics have good microwave dielectric properties and can be applied to dielectric resonators. In particular, the chemical ordering of B-site cations and the tilt of the oxygen octahedron are the main factors affecting the Q and τf values in these ceramics. The dielectric properties of these materials are largely influenced by their perovskite structure. According to research, Ba(Ni1/3Nb2/3)O3 and Ba(Zn1/3Nb2/3)O3 ceramics have negative temperature coefficients of resonant frequency (τf), while Ba(Co1/3Nb2/3)O3 [17,18,19,20] has a positive temperature coefficient of resonant frequency (τf). Therefore, a (1 − x)Ba(Co1/3(Nb0.5Ta0.5)2/3)O3–xBa(Zn1/3(Nb0.5Ta0.5)2/3)O3 solid solution was studied, and the obtained materials showed novel τf values close to zero. Ba(Zn1/3(Nb0.5Ta0.5)2/3), specifically, has a high dielectric constant and a high Q value, while Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 solid solutions are expected to have excellent microwave dielectric properties. Researchers have studied Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 microwave ceramics for a long time, but (1 − x)Ba(Co1/3(Nb0.5Ta0.5)2/3)O3–xBa(Zn1/3(Nb0.5Ta0.5)2/3)O3 microwave ceramics have not been studied yet.
In this study, we used Zn2+ substitution content in Ba(Co1/3(Nb0.5Ta0.5)2/3)O3 to form Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3, which was possible because Zn2+ (0.74 Å) has an ionic radius close to that of Co2+ (0.745 Å) [14]. This research method greatly improved Q × f, allowing it to reach a very high value, and ensured an extremely reliable temperature drift coefficient for materials with stable dielectric properties. In addition, the correlations between microstructure and microwave dielectric constant/Q × f value were also studied.
2. Experimental Procedures
2.1. Synthesis of the Samples
Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 (x = 0.1–1) samples were prepared by using solid-state mixed oxides; the starting materials were high-purity oxide powders (>99.9%), namely, BaO, ZnO, CoO, Nb2O5, and Ta2O5, all of which were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd., Shanghai, China. Initially, the raw materials were meticulously weighed and mixed by using agate ball-milling in distilled water for 24 h. Subsequently, the resulting mixtures underwent a process of drying and calcination at 1100 °C for 5 h. Following this, the prepared powders were subjected to another round of drying and ball-milling, this time for 24 h, in the presence of a binder—5 wt% of 10% PVA solution. The resulting mixture was granulated by passing it through a 100-mesh sieve and then molded into pellets with dimensions of 11 mm in diameter and 5 mm in thickness using an automatic uniaxial hydraulic press at a pressure of 200 MPA. Finally, the pellets were sintered in air at temperatures ranging from 1325 °C to 1475 °C for 5 h.
2.2. Characterization of the Samples
Cu K radiation (at 30 KV and 20 mA) and a graphite monochromator were employed to collect both powder and bulk X-ray diffraction spectra in the 2θ range of 10° to 60°. The crystalline phases in the sintered ceramics were determined with XRD analysis using Cu Kα (λ = 0.15406 nm) radiation, which was generated with a Siemens D5000 diffractometer (Munich, Germany) operating at 40 kV and 40 mA. Lattice constant calculations were carried out using GSAS software by applying the Rietveld method to fit the XRD patterns [21]. To examine the microstructure and morphology of the sintered surface, a scanning electron microscope (Philips XL40FEG, Netherlands) was utilized.
Furthermore, the Archimedes method was employed to determine the bulk density of the sintered pellets. Microwave dielectric properties, including the dielectric constant and unloaded Q, were measured in the frequency range of 6–12 GHz using the post-resonant method, as recommended by Hakki and Coleman [22]. This technique involves the use of parallel conducting plates and coaxial probes operating in TE011 mode, where “TE” signifies transverse electric waves. In TE011, the first two subscript integers indicate the waveguide mode, and the third integer indicates the order of resonance within a progressively increasing set of discrete resonant lengths. The measurement of the temperature coefficient of resonant frequency was conducted over a temperature range spanning from 20 °C to 80 °C. Additionally, for the measurement, we employed an HP8757D network analyzer and an HP8350B sweep oscillator (HP, Palo Alto, CA, USA) in combination.
3. Results and Discussion
Figure 1 shows the XRD patterns of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics (with x values from 0.1 to 0.9) sintered at 1400 °C for 5 h. The 1:2 ordered structure was found in Ba(Zn1/3Nb2/3)O3 ceramics sintered at lower temperatures that presented x values from 0.1 to 0.5, but this structure disappeared in BZN ceramics sintered above 1400 °C due to the evaporation of Zn2+. Therefore, the disturbance of the 1:2 ordering occurring in Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics with an x value below 0.7 could be attributed to higher Zn2+ content and Zn2+ evaporation during the sintering process. Furthermore, the XRD patterns revealed the absence of a secondary phase, and all identified peaks successfully matched the simple perovskite unit cell. The negligible shift in the diffraction peaks with the increase in the value of x can be attributed to the nearly identical ionic diameters of Zn2+ and Co2+. This suggests that the substitution of Co2+ with Zn2+ across the entire composition range does not significantly alter the lattice parameters.
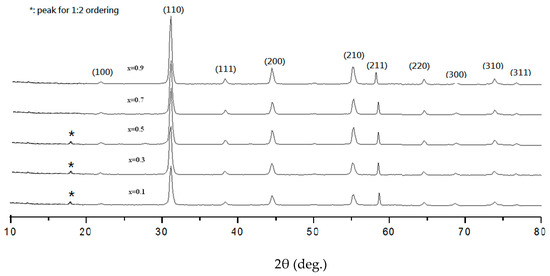
Figure 1.
X-ray diffraction patterns of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at 1400 °C for 5 h.
Figure 2 shows the SEM micrographs of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at 1400 °C for 5 h. With the increase in Zn2+ content in Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics, the average grain size increased and the shape became more square. At the sintering temperature of 1400 °C, with the increase in Co2+ content, the observed grain size was smaller than at the relatively low sintering temperature, resulting in higher porosity. Poor grain growth leads to smaller grain size, resulting in more pores and reducing bulk density.

Figure 2.
SEM photographs of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at 1400 °C for 5 h.
Figure 3 shows the relative density of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics as a function of their sintering temperature. It is important to observe that the relative density exhibited an initial increase with the increase in sintering temperature, reaching a peak at 1400 °C. However, a subsequent decrease in relative density occurred at sintering temperatures beyond 1400 °C, although this was not notably significant. Furthermore, it is worth noting that the relative density consistently exceeded 95.5% of the theoretical density for all specimens. The sintering temperature exhibited a decrease with the increase in Zn2+ content (x = 0.5), enabling the sintering of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 at 1400 °C.
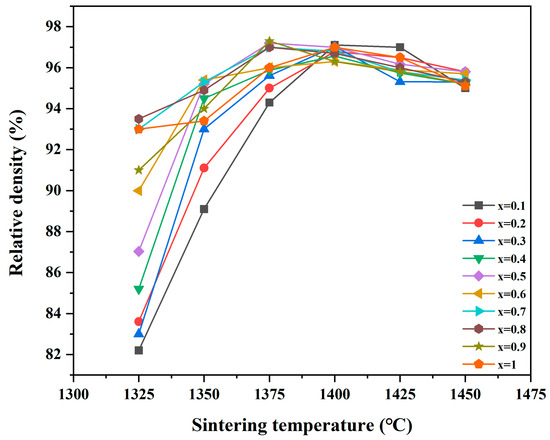
Figure 3.
Relative density of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at different temperatures.
The dielectric property of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at various temperatures was a function of their x value, as illustrated in Figure 4. The correlations observed between εr value and sintering temperature mirrored the trends observed in the relationship between relative density and sintering temperature. The dielectric constant exhibited a slight increase with the increase in sintering temperature. It is important to note that the dielectric constant of a microwave dielectric ceramic is influenced by ionic polarizability [23], that is, the εr values of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 increase with the Co2+ substitution with Zn2+, as mentioned above. The ionic polarizability (αobs) of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 samples was estimated in order to clarify the effects of Co2+ substitution with Zn2+ on the dielectric constant by using the following equation [24]:
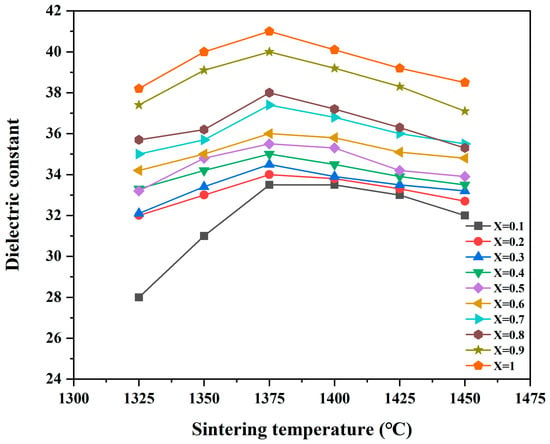
Figure 4.
εrvalues of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at different temperatures.
In Equation (1), εr, Vm, and αm are the relative permittivity, molar volume, and macroscopic polarizability, respectively. The macroscopic polarizability (αm) was calculated by using the experimental relative permittivity and unit cell volume data. The data reported in Table 1 reveal an almost sigmoidal increase in theoretical polarizability with Zn2+ content, whereas the unit cell volume increased with x. The relative permittivity increased with αm, and this increase was very rapid as the value of αm approached 3Vm/4π. It has previously been reported that the macroscopic polarizability of a complex system with ideal symmetry can be determined by the sum of the polarizability values of the constituent cations [25], i.e.,
αm = Σ α (ions)

Table 1.
Lattice parameters, cell volume, ionic polarizability, and εr data of sintered Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 samples.
The theoretical polarizability (αm(theoretical)) calculated according to Equation (2) was compared with the experimental polarizability (αm(exp.)) determined with Equation (1), as shown in Table 1. It is worth noting that the αm (exp.) of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 end-member was larger than its αm (theoretical) value. Shannon [25] noted that deviations from the additivity of ion polarizability can occur when the cation size changes and cation compression or vibration occurs at structural sites. Therefore, the lower αm(exp.) value of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 may have been due to the compression effect caused by the large difference in ion polarizability between Co2+ and Zn2+, which is consistent with the harmonic oscillator model. Consequently, in the studied Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics, the polarizability increased with the Zn2+ content, and so did the dielectric constant, according to Equation (1).
Figure 5 shows the Q × f values of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at various temperatures; it can be seen that the Q × f value was a function of the x value. For the samples with x < 0.3, the Q × f value was high, above 90,000 GHz, similar to that of Ba(Co1/3(Nb0.5Ta0.5)2/3)O3. On the contrary, for the specimens with x > 0.5, their Q × f value was below 90,000 GHz, similar to that of Ba(Zn1/3(Nb0.5Ta0.5)2/3)O3.
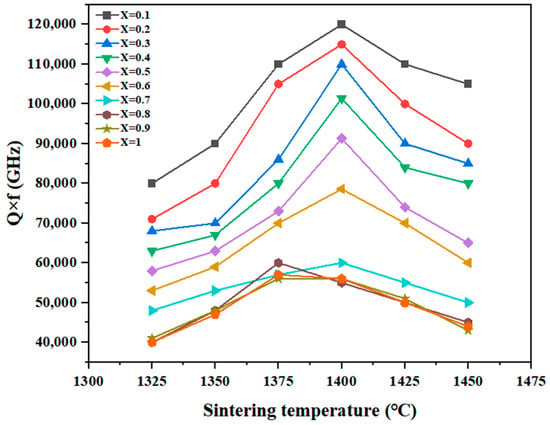
Figure 5.
Q × f values of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at different temperatures.
Since the microstructures of the specimens with x < 0.5 and x > 0.5 were similar to those of Ba(Co1/3(Nb0.5Ta0.5)2/3)O3 and BZN ceramics, respectively, it is considered that the Q-values of these Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics are closely related to the microstructures of the specimens. With the increase in sintering temperature, the Q × f value increased to a maximum value but subsequently decreased. A maximum Q × f value of 120,000 GHz was obtained for a Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 (x = 0.1) ceramic sample at 1400 °C. Microwave dielectric losses are mainly caused by lattice vibration modes, pores, second phases, impurities, and lattice defects [26]. Moreover, the relative density also increases the dielectric loss, as has been shown in other microwave dielectric materials. It is well known that the Q value of a dielectric material is influenced by intrinsic and extrinsic factors, where one factor is the interaction between polar phonon vibration and the microwave electric field in crystals while the other depends on order–disorder transition, pore density, grain size, oxygen vacancies, and impurity phases in ceramics. The intrinsic Q value sets an upper limit for pure and defect-free single crystals and can be quantitatively described by the well-known classical damped oscillator model in the microwave frequency range. In this model, when using one-phonon absorption approximation, the roughly reciprocal relationship between Q × f and permittivity (ε) can be expressed as
where the frequency (f) should be restricted to the vicinity of the phonon engine frequency of 1012 Hz at room temperature for the estimate to be valid. However, a series of experiments at room temperature demonstrated that the extrapolation of Equation (3) from microwave frequencies down to a few megahertz, that is, one to four orders of magnitude lower than optical phonon engine frequencies, can also be used to obtain a satisfactory dielectric Q order for well-processed ceramics. The experimental results, however, revealed that the dependence of Q × f on εr only generated Q × f α εr−0.6, indicating that the rate of increase in the Q × f value with εr is very smooth compared with Equation (3). The most likely cause of this phenomenon may have exogenous origins. On the other hand, the porosity of dielectric materials has an adverse effect on the Q × f value, and different dielectric materials present different degrees of influence. For ceramics with low dielectric Q × f values of the order of 103 GHz, the effect of porosity on the dielectric Q value can be illustrated as [27]
where Qo is the intrinsic quality factor measured by using microwave reflectance spectroscopy and P is the porosity. For ceramics with high Q × f values of the order of 105–106 GHz, such as polycrystalline Al2O3 ceramics, even a small amount of porosity can significantly reduce the dielectric Q value as [28]
where Qo is the full-density quality factor (1.565 × 10−5), A′ is a constant with value 9.277 × 10−3, and P is the porosity. According to Equations (4) and (5), the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 end-component in the present study presented 8% porosity. The Q × f value was high for the specimens with , but it decreased when x exceeded 0.5. The Q × f value of the specimens was greatly affected by the microstructure, as shown in Figure 1. The 1:2 ordering structure only appeared in the specimens with x values from 0.1 to 0.5, while this structure does not exist in Ba(Zn1/3(Nb0.5Ta0.5)2/3)O3 ceramics.
Q = Qo(1 − 1.5P)
Figure 6 shows that the τf value of Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at various temperatures was a function of the Zn2+ content. The τf linearly increased with the x value, and it was close to zero when x = 0.3. The remarkable variations in the τf values of the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics were obtained by replacing Co2+ with Zn2+, and these values ranged from −7.2 to 20 ppm/°C. Therefore, it is believed that for high-frequency dielectric resonator applications, the τ_f value needs to be further increased.
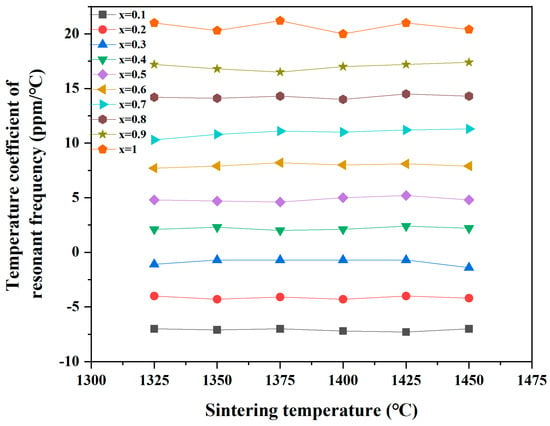
Figure 6.
Temperature coefficients of resonant frequency of Ba[(ZnxCo1-x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics sintered at different temperatures.
The temperature coefficient () of resonant frequency is defined as follows:
where αl is the linear thermal expansion coefficient and τε is the temperature coefficient of permittivity. Because the αl of a microwave dielectric material is known to be in the range of 0 to 10 ppm/°C and assuming that the αl of a Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramic is independent of the x value, τ_f mainly depends on τε. Moreover, by plotting the trend of τf values versus permittivity for the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics, it was found that the τf values increased from −7.2 to 20 ppm/°C and linearly depended on the x values increasing from 0.1 to 1. It can be seen that the τf value has a linear relationship with the x value.
4. Conclusions
The phase stability of Ba(B1/3′2+ B2/3′′5+)O3 microwave media with complex perovskite structures was studied by using first-principles calculations. The experiment showed that many Ba(B1/3′2+ B2/3′′5+)O3 (B1/3′2+ = Co, Mg; B″5+ = Nb, Ta) compounds should be completely ordered in equilibrium in the 1:2 B-site structure of the space group . Our calculations are not consistent with the experimental results on Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 but with many experimental results on other Ba(B1/3′2+ B2/3′′5+)O3 components. We found that the greater the stability of the ordered 1:2 structure relative to the disordered phase was, the higher the measured microwave quality factor was. The results show that the difference in the ionic radius and electronegativity of B′ and B” ions exhibited no relationship with phase stability. The results show that aberrations were induced by B-site cations or ordering and were enhanced by more stable and ordered structural phases.
In the Ba[(ZnxCo1−x)1/3(Nb0.5Ta0.5)2/3]O3 ceramics, a 1:2 ordered hexagonal structure was observed in samples with x ≤ 0.5. τf increased with the increase in x, and the τf of the sample with x = 0.3 was close to zero. When x ≤ 0.5, the Q × f value was higher, but it decreased when x exceeded 0.5. The Q × f value of a sample was greatly influenced by the microstructure. In this work, Ba[(Zn0.3Co0.7)1/3(Nb0.5Ta0.5)2/3]O3 ceramics were sintered at 1400 °C for 5 h to obtain τf = −0.7 ppm/°C and excellent microwave dielectric performance, with εr = 34.5 and Q × f = 110,000 GHz. The proposed dielectric material has extremely low losses and shows promise for microwave and millimeter-wave applications.
Author Contributions
Y.-B.C.: preparation of materials; methodology; software; writing—original draft preparation; S.-H.C., Y.F. and S.S.: data curation; writing—review and editing; theoretical calculation; and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by grant number 612-22010501.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this study.
References
- Millet, J.M.; Roth, R.S.; Ettlinger, L.D.; Parker, H.S. Phase Equilibria and Crystal Chemistry in the Ternary Systems BaO-TiO2-Nb2. J. Solid State Chem. 1987, 67, 259–270. [Google Scholar] [CrossRef]
- Liu, F.; Cheng, L.-J.; Li, H.; Liu, S.-J. Ordering-induced domains in sub-micron-sized Ba(Zn1/3Ta2/3)O3–BaZrO3 microwave ceramics. J. Mater. Sci. Mater. Electron. 2021, 32, 26126–26136. [Google Scholar] [CrossRef]
- Siny, I.G.; Tao, R.; Katiyar, R.S.; Guo, R.; Bhalla, A.S. Raman spectroscopy of Mg-Ta order-disorder in BaMg1/3Ta2/3O3. J. Phys. Chem. Solids 1998, 59, 181–195. [Google Scholar] [CrossRef]
- Ioachim, A. Effect of the sintering temperature on the Ba(Zn1/3Ta2/3)O3 dielectric properties. J. Eur. Ceram. Soc. 2007, 27, 1117–1122. [Google Scholar] [CrossRef]
- Moussa, S.M.; Ibberson, R.M.; Bieringer, M.; Fitch, A.N.; Rosseinsky, M.R. In situ Measurement of Cation Order and Domain Growth in an Electroceramic. Chem. Mater. 2003, 15, 2527–2533. [Google Scholar] [CrossRef]
- Bensemma, N.; Trefalt, G.; Glinsek, S.; Kosec, M.; Taibi, K.; Abbaci, M. Investigation of the BaTiO3-BaMg1/3Nb2/3 system: Structural, dielectric, ferroelectric and electromechanical studies. J. Electroceram. 2013, 30, 206–212. [Google Scholar] [CrossRef]
- Kim, I.-T. Effects of non-stoichiometry and chemical inhomogeneity on the order-disorder phase formation in the complex perovskite compounds, Ba(Ni1/3Nb2/3)O3and Ba(Zn1/3Nb2/3)O3. J. Mater. Sci. 1995, 30, 514–521. [Google Scholar] [CrossRef]
- Fan, Y.; Zhou, Z.; Liang, R.; Zhou, M.; Dong, X. The effect of A-site nonstoichiometry on the microstructure, electric properties, and phase stability of NaNbO3 polycrystalline ceramics. J. Eur. Ceram. Soc. 2019, 39, 4712–4718. [Google Scholar] [CrossRef]
- Surendran, K.P.; Sebastian, M.T.; Mohanan, P.; Moreira, R.L.; Dias, A. Effect of Nonstoichiometry on the Structure and Microwave Dielectric Properties of Ba(Mg0.33Ta0.67)O3. Chem. Mater. 2005, 17, 142–151. [Google Scholar] [CrossRef]
- Storr, B.; Kodali, D.; Chakrabarty, K.; Baker, P.A.; Rangari, V.; Catledge, S.A. Single-Step Synthesis Process for High-Entropy Transition Metal Boride Powders Using Microwave Plasma. Ceramics 2021, 4, 257–264. [Google Scholar] [CrossRef]
- Yang, H. The latest process and challenges of microwave dielectric ceramics based on pseudo phase diagrams. J. Adv. Ceram. 2021, 10, 885–932. [Google Scholar] [CrossRef]
- Dernovsek, O.; Dernovsek, M.O.; Eberstein, M.; Schiller, W.A. LTCC glass-ceramic composites for microwave application. J. Eur. Ceram. Soc. 2001, 21, 1693–1697. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Feng, Z.; Wu, H.; Zhang, X. Crystal structure; infrared spectra, and microwave dielectric properties of the EuNbO4 ceramic. Ceram. Int. 2021, 47, 4321–4326. [Google Scholar] [CrossRef]
- Ji, Y.; Song, K.; Zhang, S.; Lu, Z.; Wang, G.; Li, L.; Zhou, D.; Wang, D.; Reaney, I.M. Cold sintered, temperature-stable CaSnSiO5-K2MoO4 composite microwave ceramics and its prototype microstrip patch antenna. J. Eur. Ceram. Soc. 2021, 41, 424–429. [Google Scholar] [CrossRef]
- Chen, C.; Peng, Z.; Xie, L.; Bi, K.; Fu, X. Microwave dielectric properties of novel (1 − x)MgTiO3–xCa0.5Sr0.5TiO3 ceramics. J. Mater. Sci. Mater. Electron. 2020, 31, 13696–13703. [Google Scholar] [CrossRef]
- Zaman, A.; Uddin, S. Nasir Mehboob and Asad Ali, Structural investigation and improvement of microwave dielectric properties in Ca(HfxTi1−x)O3 ceramics. Phys. Scr. 2021, 96, 025701. [Google Scholar] [CrossRef]
- Bao, J.; Du, J.; Liu, L.; Wu, H.; Zhou, Y.; Yue, Z. A new type of microwave dielectric ceramic based on K2O–SrO–P2O5 composition with high quality factor and low sintering temperature. Ceram. Int. 2022, 48, 784–794. [Google Scholar] [CrossRef]
- Nomura, S.; Kaneta, K. Ba(Mg1/3Ta2/3)O3 Ceramics with Temperature-Stable High Dielectric Constant and Low Microwave Loss. Jpn. J. Appl. Phys. 1982, 21, L624. [Google Scholar] [CrossRef]
- Kawashima, S.; Nishida, M.; Ueda, I.; Ouchi, H. Dielectric properties of Ba(Zn,Ta)O-Ba(Zn,Nb)O ceramic. Proc. Ferroelectr. Mater. 1977, 1, 293. [Google Scholar]
- Desu, S.B.; O’Bryan, H.M. Microwave Loss Quality of BaZn1/3Ta2/3O3 Ceramics. J. Am. Ceram. Soc. 1985, 68, 546. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. Los Alamos National Laboratory Report LAUR-86-748. 1987. Available online: https://11bm.xray.aps.anl.gov/documents/GSASManual.pdf (accessed on 25 January 2024).
- Hakki, B.W.; Coleman, P.D. A Dielectric Resonator Method of Measuring Inductive Capacities in the Millimeter Range. IRE Trans. Microw. Theory Tech. 1960, 8, 402. [Google Scholar] [CrossRef]
- Belous, A.; Ovchar, O.; Durilin, D.; Krzmanc, M.M.; Valant, M.; Suvorov, D. High-Q Microwave Dielectric Materials Based on the Spinel Mg2TiO4. J. Am. Ceram. Soc. 2006, 89, 3441. [Google Scholar] [CrossRef]
- Hannay, J.H. Constantino Grosse. DIBORIDE MICROPATTERNED SURFACES FOR CELL CULTURE. Ferroelectrics 1988, 86, 171–179. (United States Patent Application 20230133393). Available online: https://www.zhangqiaokeyan.com/patent-detail/06130502846548.html (accessed on 25 January 2024).
- Shannon, S.R.D. Dielectric polarizabilities of ions in oxides and fluorides. J. Appl. Phys. 1993, 73, 348–366. [Google Scholar] [CrossRef]
- Lichtenecker, K. Dielectric constant of natural and synthetic mixtures. Phys. Z. 1926, 27, 115. [Google Scholar]
- Chen, Y.-B. Dielectric properties and crystal structure of (Mg0.9Zn0.05Co0.05)4(Nb(1−x)Tax)2O9 ceramics. J. Alloys Compd. 2012, 541, 283–287. [Google Scholar] [CrossRef]
- Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M. Michael Reece and Kevin Schrapel. Am. Ceram. Soc. 1997, 80, 1885–1888. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).