Coupled Photonic Crystal Nanocavities as a Tool to Tailor and Control Photon Emission
Abstract
1. Introduction
2. Material and Methods
3. Results
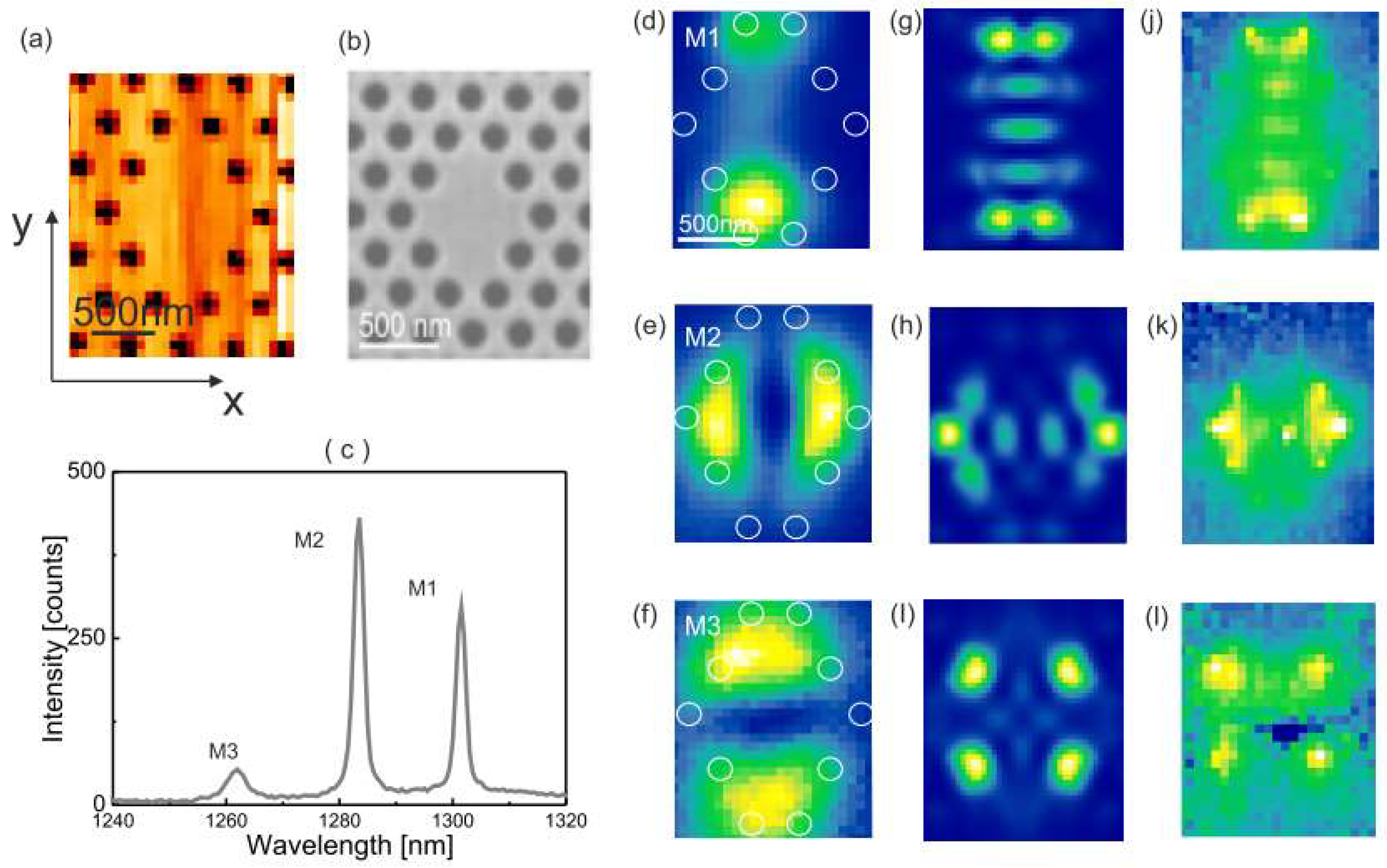
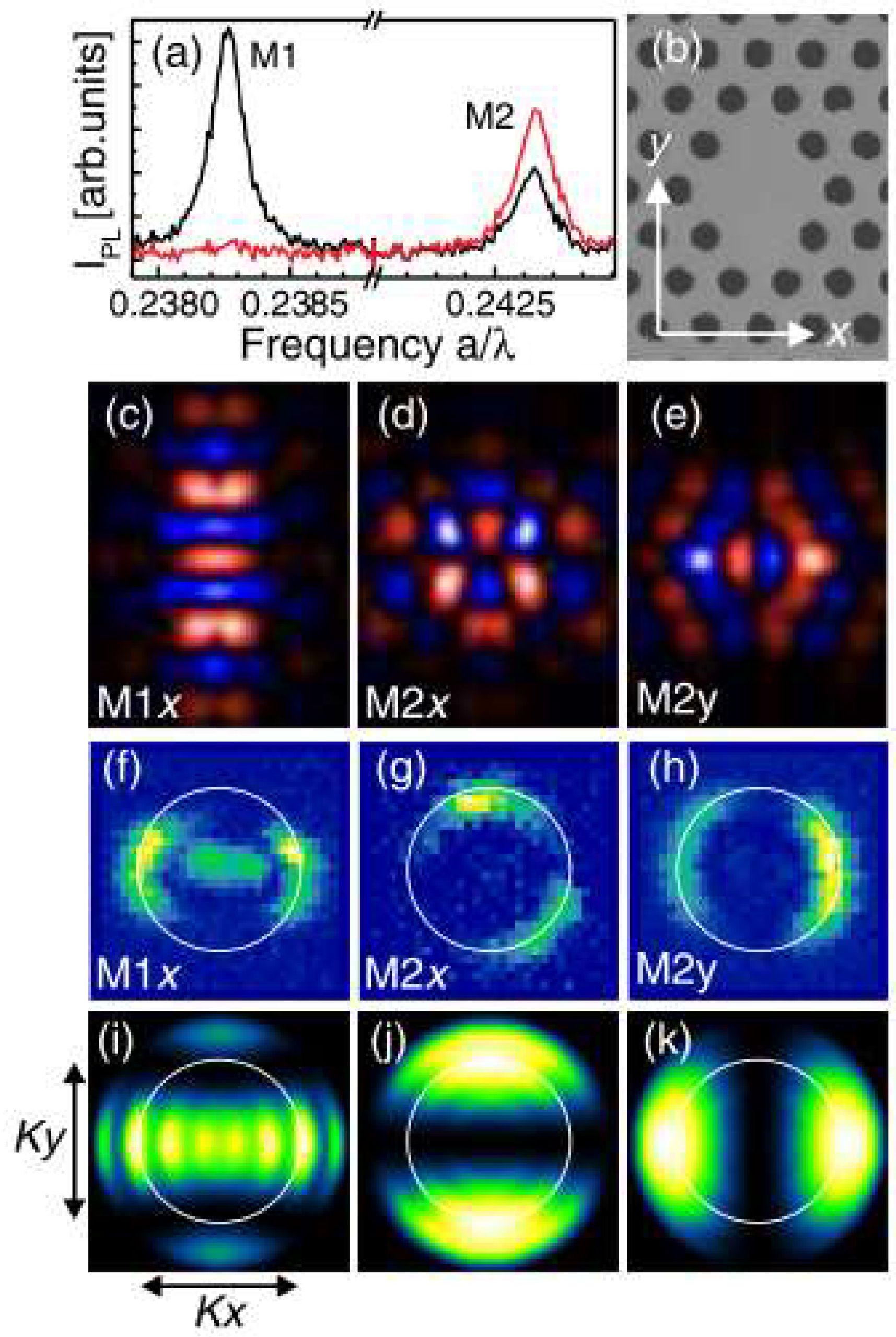
3.1. Photonic Crystal Molecules: Two Nanocavities Case
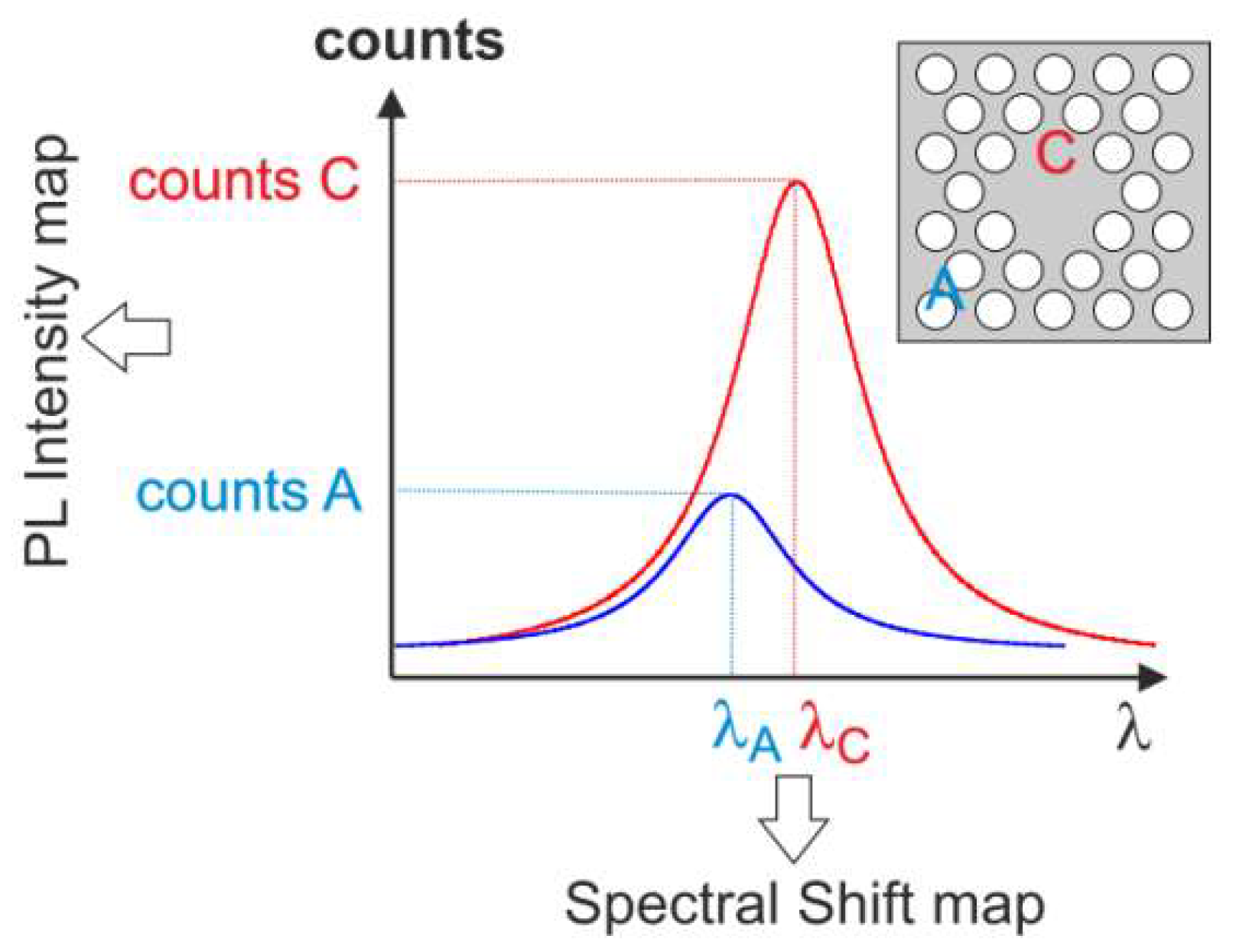
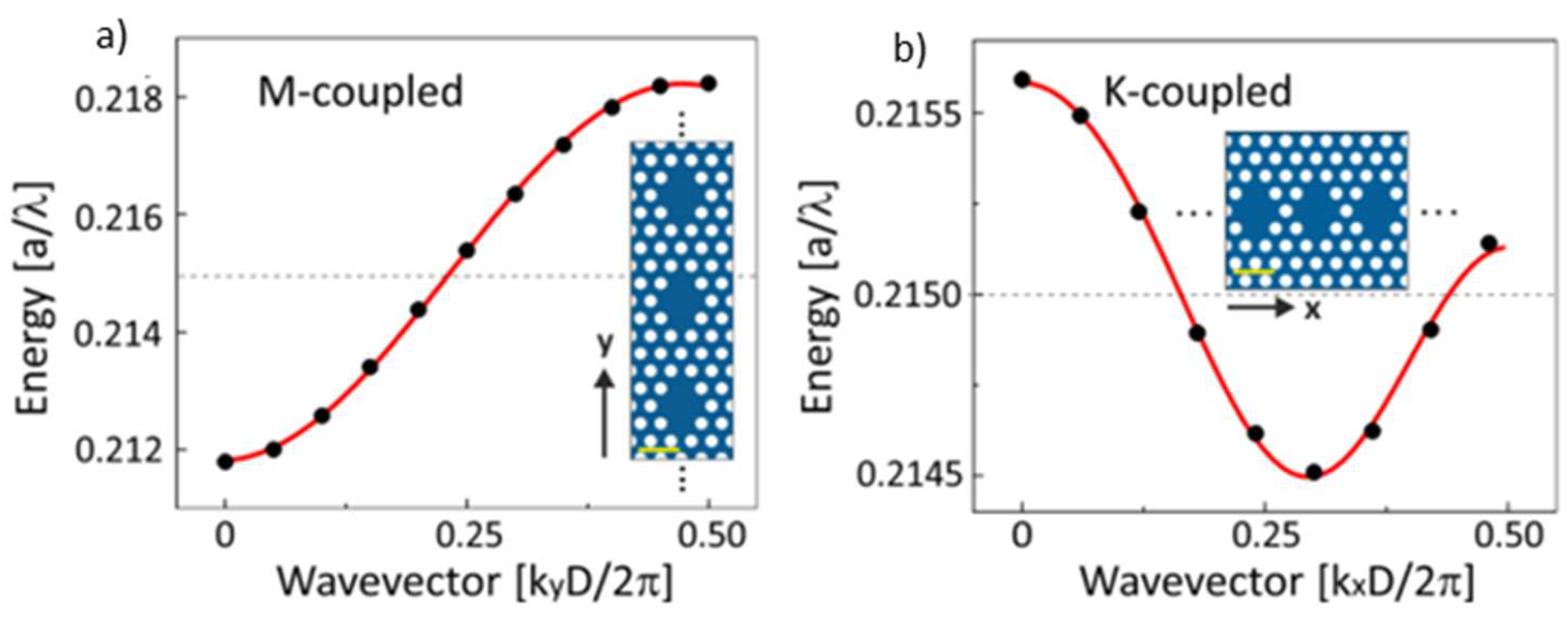
3.1.1. Mode Symmetry
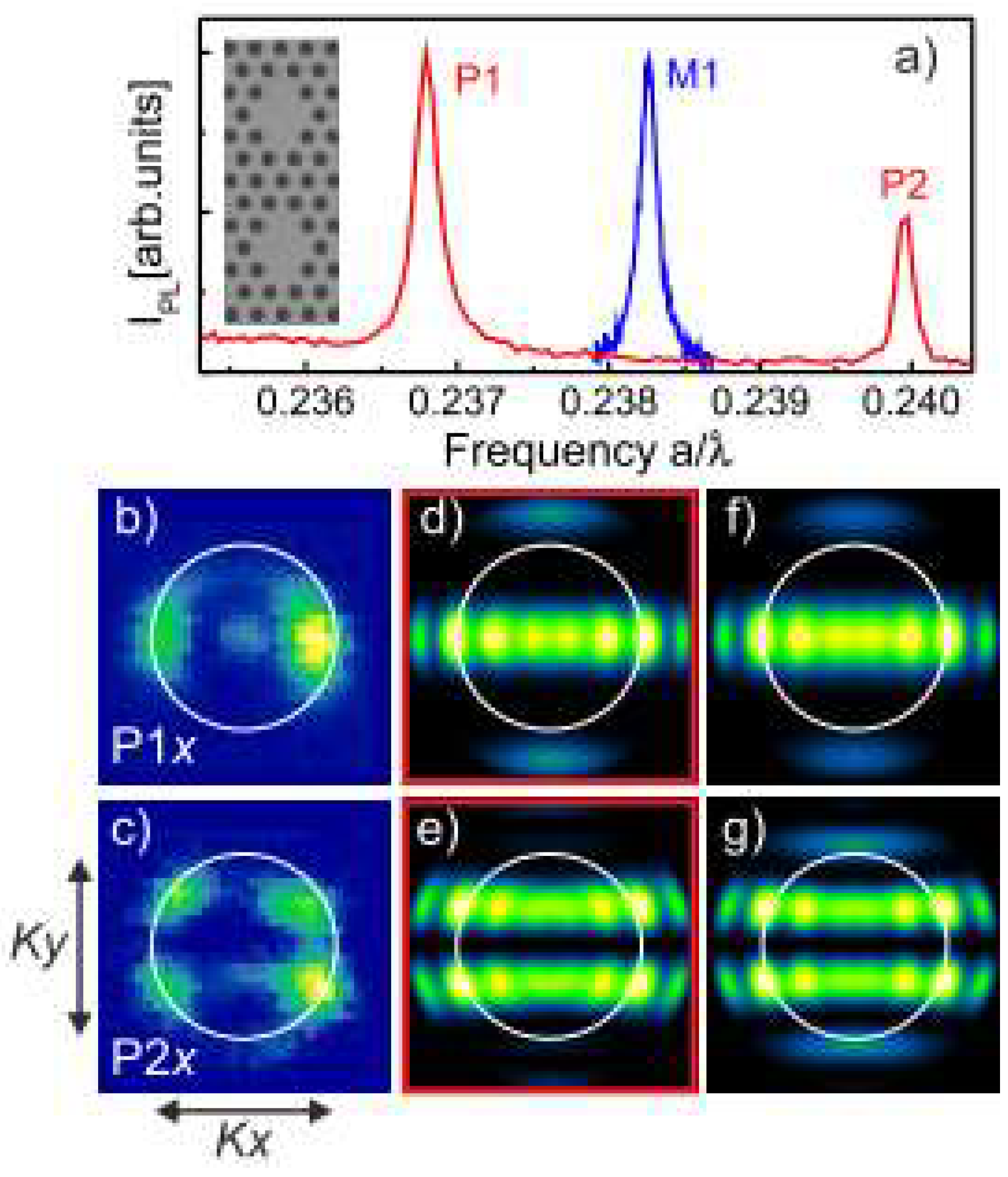
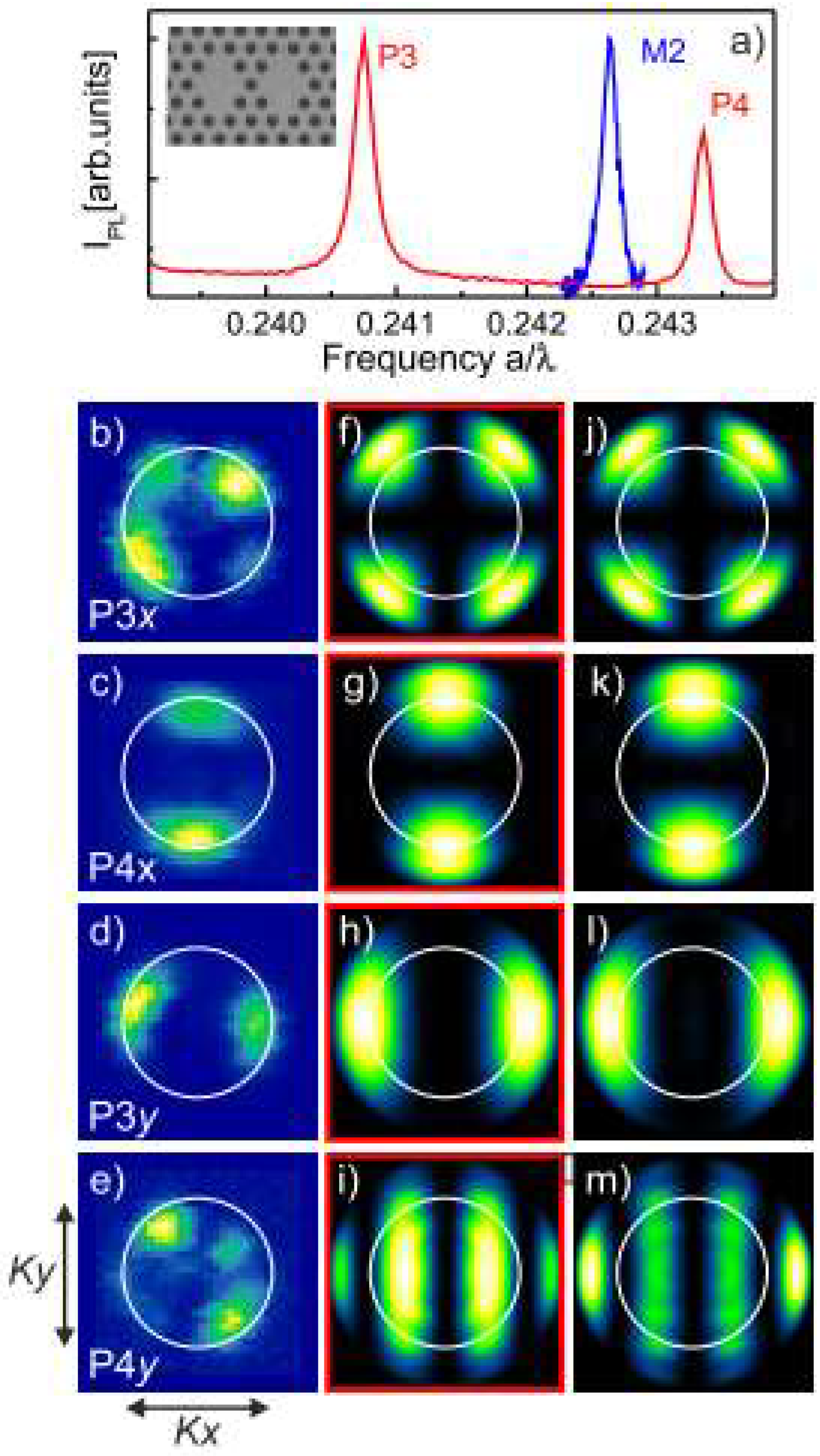
3.1.2. Controlling Bonding and Antibonding Ground State
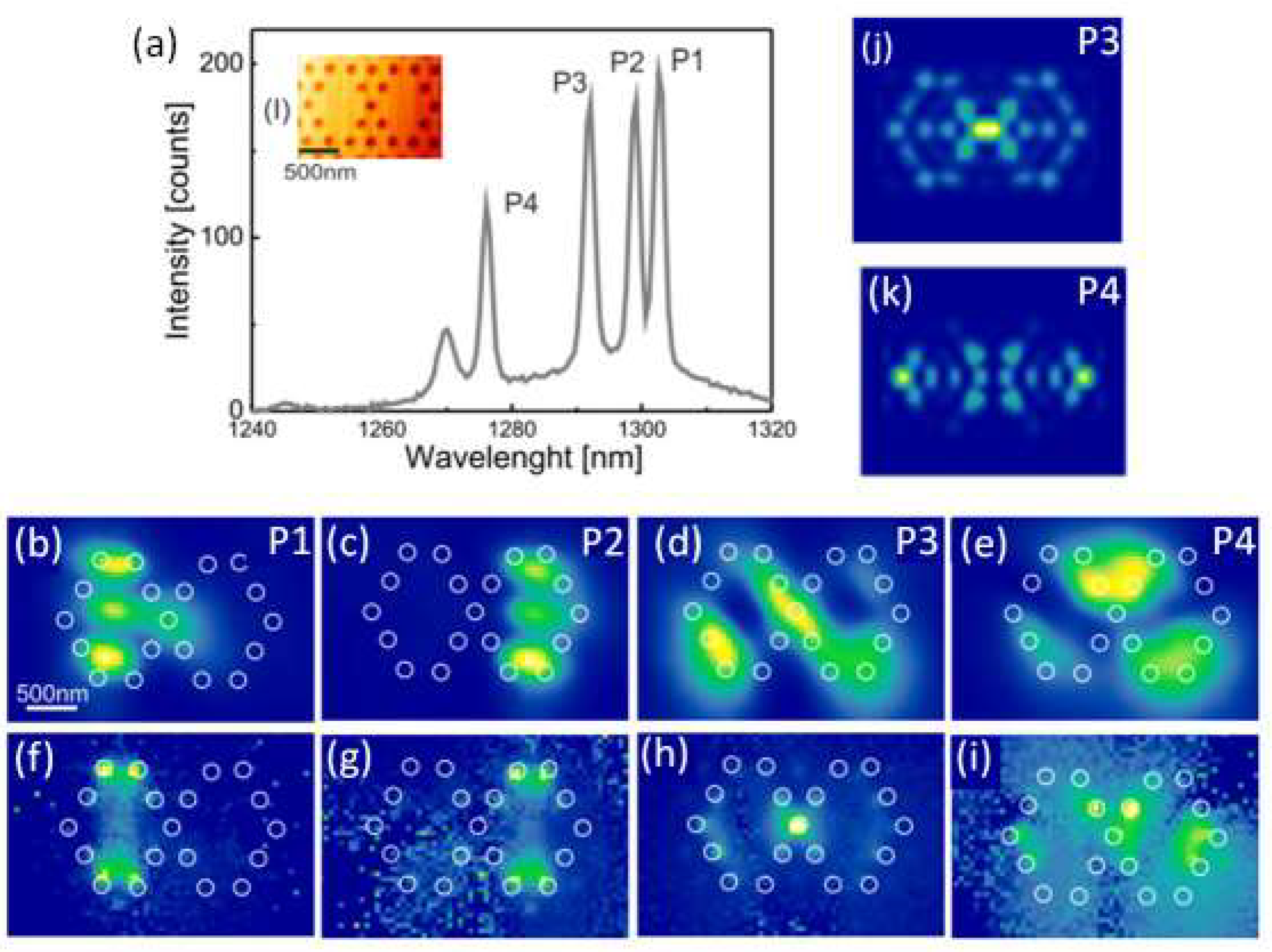
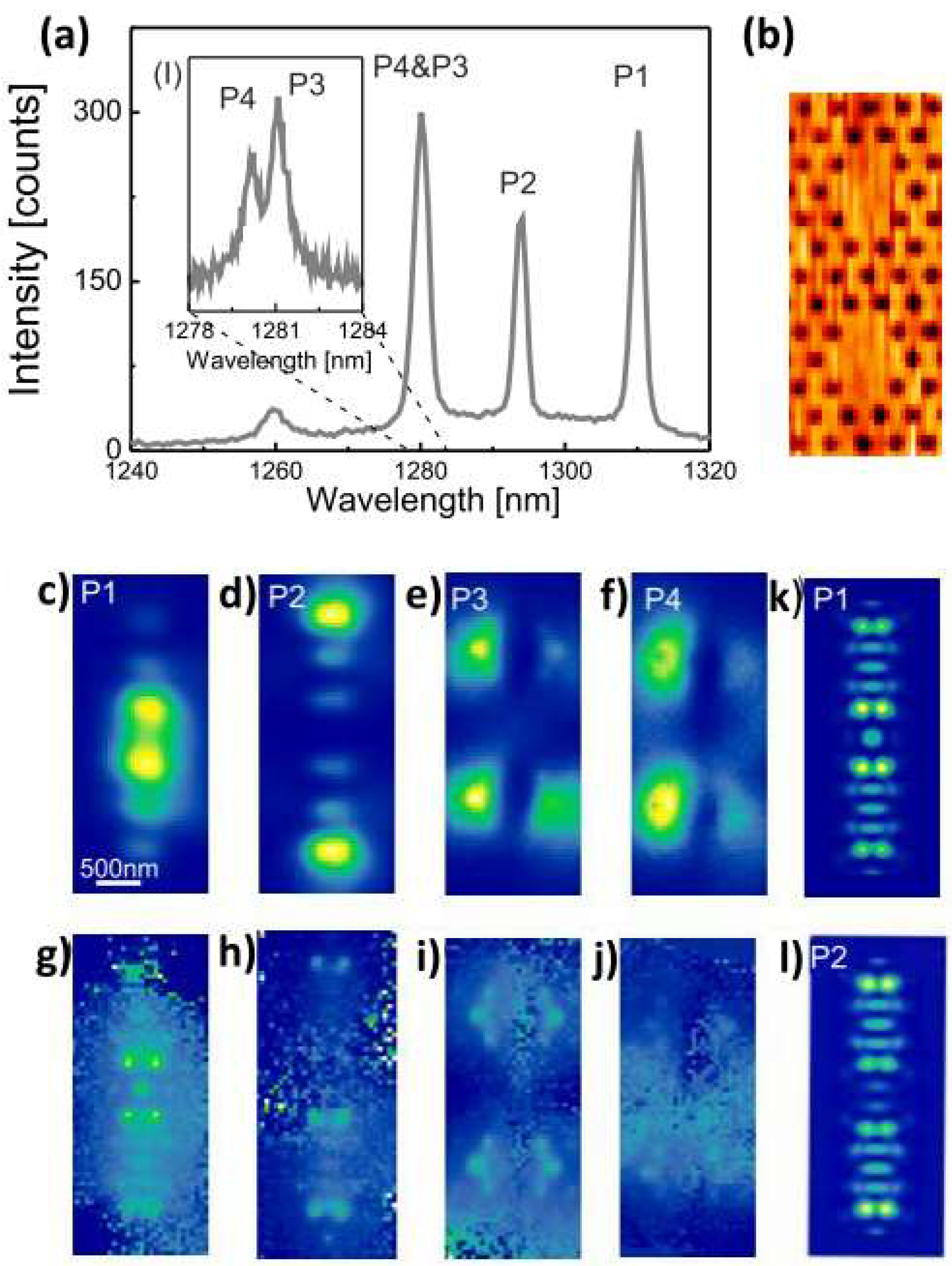
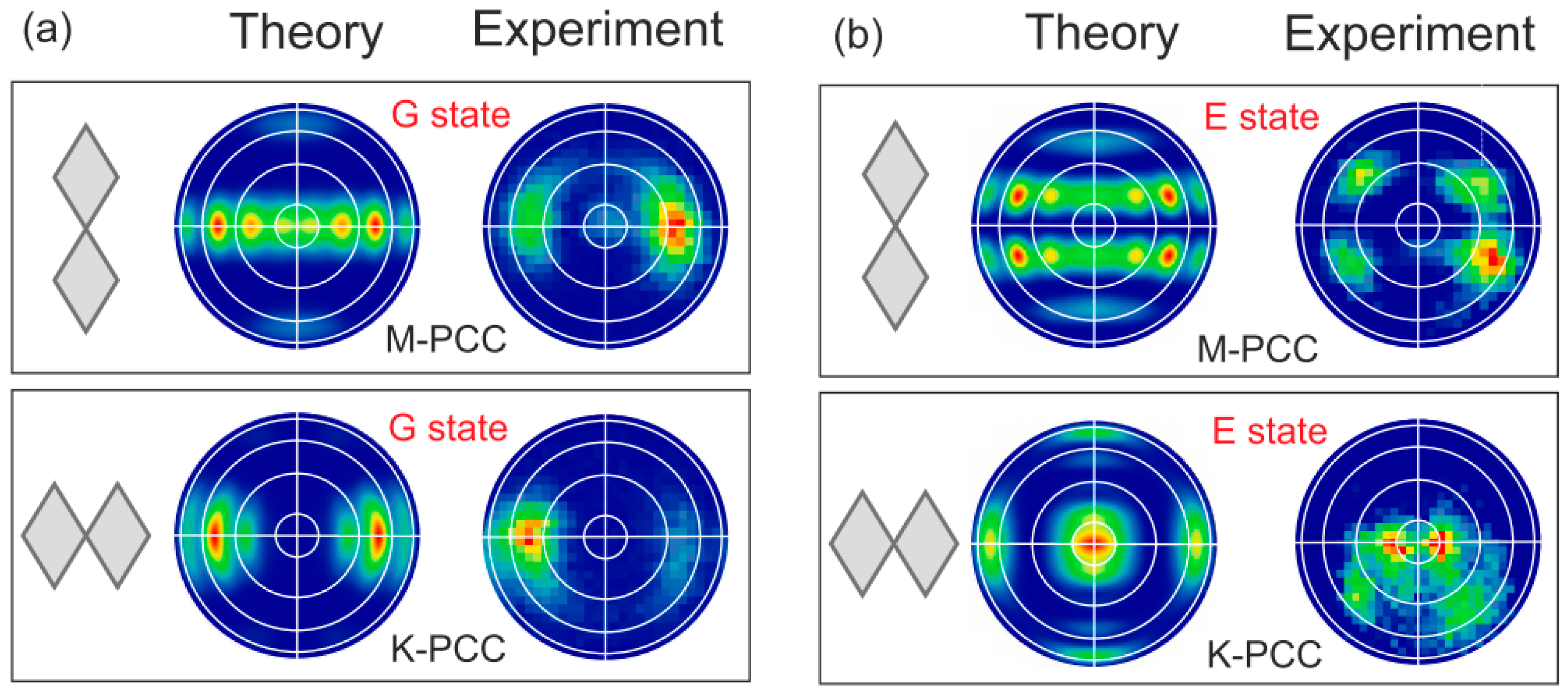
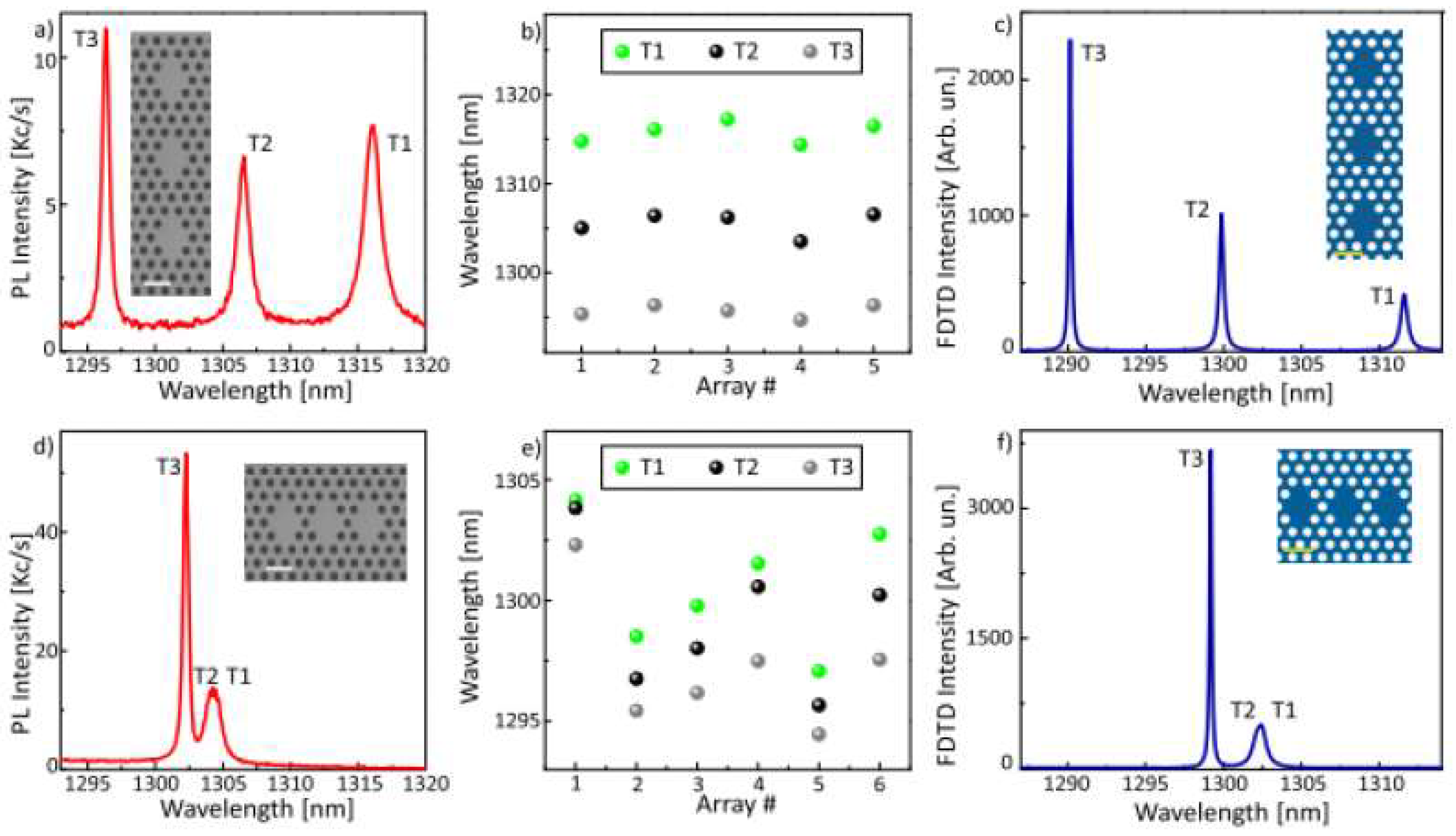
3.2. Photonic Crystal Molecules: Three Nanocavities Case
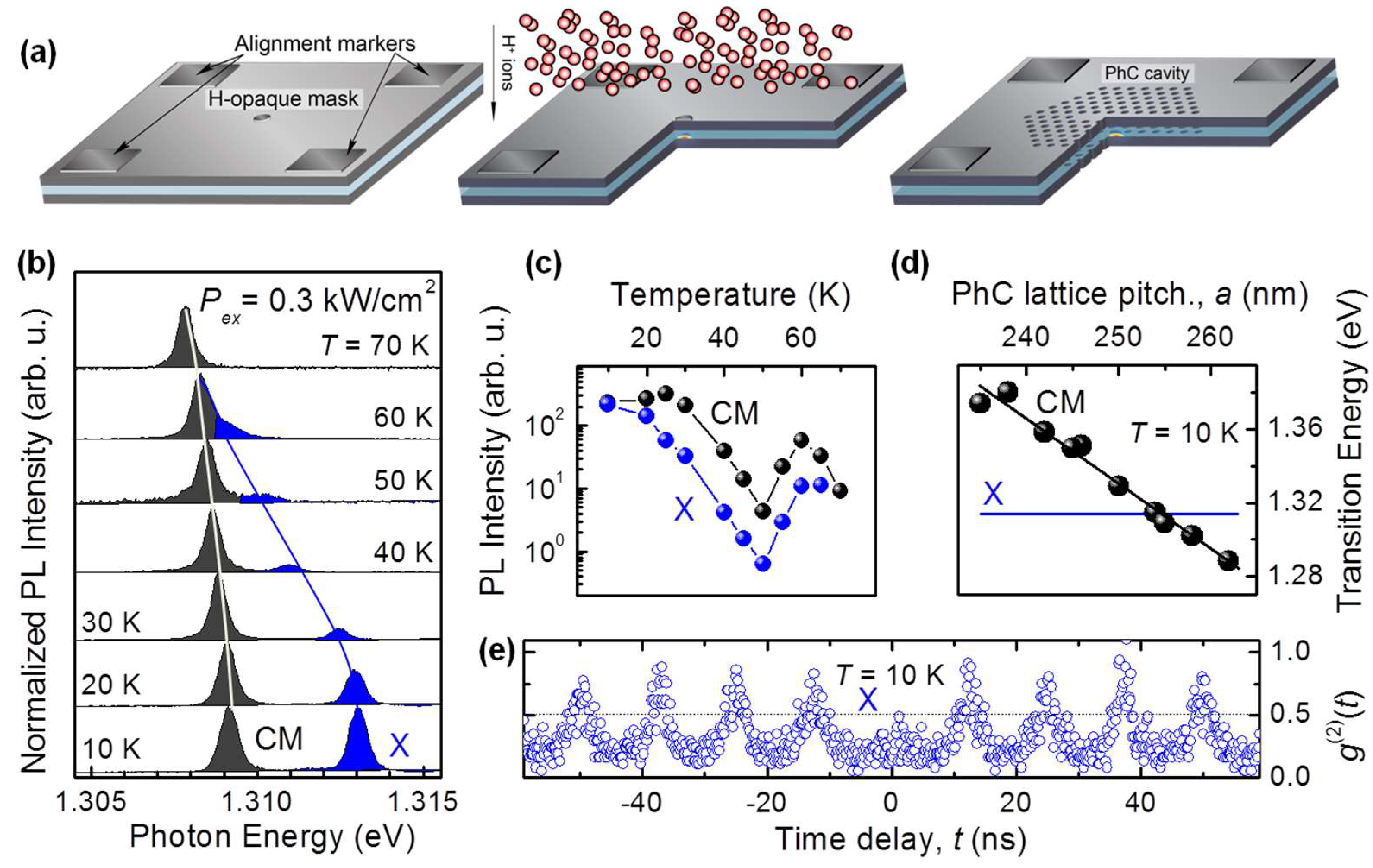
3.3. All Lithographic Approach to PCC and QD Coupled Systems
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prasad, P. Nanophotonics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 0-471-64988-0. [Google Scholar]
- Brodie, I.; Muray, J.J. The Physics of Micro/Nano-Fabrication; Springer: New York, NY, USA, 1992; ISBN 978-1-4757-6775-9. [Google Scholar]
- Yablonovitch, E. Inhibited spontaneous emission in solid state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 9780691124568. [Google Scholar]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamogu, A. Quantum nature of a strongly coupled single quantum dot-cavity system. Nature 2007, 445, 896. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Manga Rao, V.S.C.; Hughes, S. On-chip single photon sources using planar photonic crystals and single quantum dots. Laser Photonics Rev. 2010, 4, 499–516. [Google Scholar] [CrossRef]
- Chang, W.H.; Chen, W.Y.; Chang, H.S.; Hsieh, T.P.; Chyi, J.I.; Hsu, T.M. Efficient single-photon sources based on low-density quantum dots in photonic-crystal nanocavities. Phys. Rev. Lett. 2006, 96, 117401. [Google Scholar] [CrossRef]
- Dousse, A.; Suffczynski, J.; Beveratos, A.; Krebs, O.; Lemaıtre, A.; Sagnes, I.; Bloch, J.; Voisin, P.; Senellart, P. Ultrabright source of entangled photon pairs. Nature 2010, 466, 217. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical Microcavities. Nature 2003, 424, 839. [Google Scholar] [CrossRef]
- Ellis, B.; Mayer, M.A.; Shambat, G.; Sarmiento, T.; Harris, J.; Haller, E.E.; Vučković, J. Ultralow-threshold electrically pumped quantum-dot photonic-crystal nanocavity laser. Nat. Photonics 2011, 5, 297–300. [Google Scholar] [CrossRef]
- Park, H.-G.; Kim, S.-H.; Kwon, S.-H.; Ju, Y.-G.; Yang, J.-K.; Baek, J.-H.; Kim, S.-B.; Lee, Y.-H. Electrically driven single-cell photonic crystal laser. Science 2004, 305, 1444–1447. [Google Scholar] [CrossRef]
- Song, B.S.; Noda, S.; Asano, T. High-Q photonic nanocavity in a two-dimensional photonic crystal. Science 2003, 300, 944–947. [Google Scholar] [CrossRef]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.M.; Rupper, G.; Ell, C.; Shchekin, O.B.; Deppe, D.G. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 2015, 87, 347. [Google Scholar] [CrossRef]
- Michler, P.; Kiraz, A.; Becher, C.; Schoenfeld, W.V.; Petroff, P.M.; Zhang, L.D.; Hu, E.; Imamoğlu, A. A quantum dot single-photon turnstile device. Science 2000, 290, 2282–2285. [Google Scholar] [CrossRef] [PubMed]
- Salter, C.L.; Stevenson, R.M.; Farrer, I.; Nicoll, C.A.; Ritchie, D.A.; Shields, A.J. An entangled-light emitting diode. Nature 2010, 465, 594–597. [Google Scholar] [CrossRef]
- Boriskina, S.V. Photonic Molecules and Spectral Engineering. In Photonic Microresonator Research and Applications; Chremmos, I., Uzunoglu, N., Schwelb, O., Eds.; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-1744-7. [Google Scholar]
- Zhukovsky, S.V.; Chigrin, D.N.; Lavrinenko, A.V.; Kroha, J. Switchable Lasing in Multimode Microcavities. Phys. Rev. Lett. 2007, 99, 073902. [Google Scholar] [CrossRef] [PubMed]
- Mookherjea, S.; Yariv, A. Coupled resonator optical waveguides. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 448–456. [Google Scholar] [CrossRef]
- Hill, M.T.; Dorren, H.S.J.; De Vries, T.; Leijtens, X.J.M.; DenBesten, J.H.; Smalbrugge, B.; Oel, Y.S.; Binsma, H.; Khoe, G.D.; Smit, M.K. A fast low-power optical memory based on coupled micro-ring lasers. Nature 2004, 432, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Vignolini, S.; Intonti, F.; Zani, M.; Riboli, F.; Wiersma, D.S.; Li, L.H.; Balet, L.; Francardi, M.; Gerardino, A.; Fiore, A.; Gurioli, M. Near-field imaging of coupled photonic-crystal microcavities. Appl. Phys. Lett. 2009, 94, 151103. [Google Scholar] [CrossRef]
- Kuramochi, E.; Nozaki, K.; Shinya, A.; Takeda, K.; Sato, T.; Matsuo, S.; Taniyama, H.; Sumikura, H.; Notomi, M. Large-scale integration of wavelength-addressable all-optical memories on a photonic crystal chip. Nat. Photonics 2014, 8, 474–481. [Google Scholar] [CrossRef]
- Schweickert, L.; Jöns, K.D.; Zeuner, K.D.; Covre da Silva, S.F.; Huang, H.; Lettner, T.; Reindl, M.; Zichi, J.; Trotta, R.; Rastelli, A.; Zwiller, V. On-demand generation of background-free single photons from a solid-state source. Appl. Phys. Lett. 2018, 112, 093106. [Google Scholar] [CrossRef]
- Dalacu, D.; Reimer, M.E.; Fréderick, S.; Kim, D.; Lapointe, J.; Poole, P.J.; Aers, G.C.; Williams, R.L.; Ross McKinnon, W.; Korkusinski, M.; Hawrylak, P. Directed self-assembly of single quantum dots for telecommunication wavelength optical devices. Laser Photonics Rev. 2009, 4, 283–299. [Google Scholar] [CrossRef]
- Francardi, M.; Balet, L.; Gerardino, A.; Monat, C.; Zinoni, C.; Li, L.H.; Alloing, B.; Le Thomas, N.; Houdré, R.; Fiore, A. Quantum dot photonic crystal nanocavities at 1300 nm for telecom-wavelength single-photon sources. Phys. Status Solidi C 2006, 3, 3693. [Google Scholar] [CrossRef]
- Painter, O.; Husain, A.; Scherer, A.; Lee, P.T.; Kim, I.; O’Brien, J.D.; Dapkus, P.D. Lithographic Tuning of a Two-Dimensional Photonic Crystal Laser Array. IEEE Photonics Technol. Lett. 2000, 12, 1126–1128. [Google Scholar] [CrossRef]
- Intonti, F.; Vignolini, S.; Riboli, F.; Vinattieri, A.; Wiersma, D.S.; Colocci, M.; Balet, L.; Monat, C.; Zinoni, C.; Li, L.H.; et al. Spectral tuning and near-field imaging of photonic crystal microcavities. Phys. Rev. B 2008, 78, 041401. [Google Scholar] [CrossRef]
- Koenderink, A.F.; Kafesaki, M.; Buchler, B.C.; Sandoghdar, V. Controlling the Resonance of a Photonic Crystal Microcavity by a Near-Field Probe. Phys. Rev. Lett. 2005, 95, 153904. [Google Scholar] [CrossRef] [PubMed]
- Cognée, K.G.; Yan, W.; La China, F.; Balestri, D.; Intonti, F.; Gurioli, M.; Koenderink, A.F.; Lalanne, P. Mapping Complex Mode Volumes with Cavity Perturbation Theory; Cornell University: Ithaca, NY, USA, 2018. [Google Scholar]
- Vignolini, S.; Intonti, F.; Riboli, F.; Wiersma, D.S.; Balet, L.; Li, L.H.; Francardi, M.; Gerardino, A.; Fiore, A.; Gurioli, M. Polarization-sensitive near-field investigation of photonic crystal microcavities. Appl. Phys. Lett. 2009, 94, 163102. [Google Scholar] [CrossRef]
- Bayer, M.; Gutbrod, T.; Reithmaier, J.P.; Forchel, A.; Reinecke, T.L.; Knipp, P.A.; Dremin, A.A.; Kulakovskii, V.D. Optical Modes in Photonic Molecules. Phys. Rev. Lett. 1998, 81, 2582. [Google Scholar] [CrossRef]
- Atlasov, K.A.; Karlsson, K.F.; Rudra, A.; Dwir, B.; Kapon, E. Wavelength and loss splitting in directly coupled photonic-crystal defect microcavities. Opt. Express 2008, 16, 16255. [Google Scholar] [CrossRef]
- Intonti, F.; Riboli, F.; Caselli, N.; Abbarchi, M.; Vignolini, S.; Wiersma, D.S.; Vinattieri, A.; Gerace, D.; Balet, L.; Li, L.H.; et al. Young’s Type Interference for Probing the Mode Symmetry in Photonic Structures. Phys. Rev. Lett. 2011, 106, 143901. [Google Scholar] [CrossRef]
- Balistreri, M.L.M.; Gersen, H.; Korterik, J.P.; Kuipers, L.; van Hulst, N.F. Tracking femtosecond laser pulses in space and time. Science 2001, 294, 1080. [Google Scholar] [CrossRef]
- Le Thomas, N.; Houdré, R.; Kotlyar, M.V.; Krauss, T.F. Phase-sensitive Fourier space imaging of optical Bloch modes. Phys. Rev. B 2008, 77, 245323. [Google Scholar] [CrossRef]
- Kee, C.S.; Lim, H.; Lee, J. Coupling characteristics of localized photons in two-dimensional photonic crystals. Phys. Rev. B 2003, 67, 073103. [Google Scholar] [CrossRef]
- Chalcraft, A.R.A.; Lam, S.; Jones, B.D.; Szymanski, D.; Oulton, R.; Thijssen, A.C.T.; Skolnick, M.S.; Whittaker, D.M.; Krauss, T.F.; Fox, A.M. Mode structure of coupled L3 photonic crystal cavities. Opt. Express 2011, 19, 5670. [Google Scholar] [CrossRef]
- Caselli, N.; Intonti, F.; Riboli, F.; Vinattieri, A.; Gerace, D.; Balet, L.; Li, L.H.; Francardi, M.; Gerardino, A.; Fiore, A.; Gurioli, M. Antibonding ground state in photonic crystal molecules. Phys. Rev. B 2012, 86, 035133. [Google Scholar] [CrossRef]
- Leonard, S.W.; Mondia, J.P.; van Driel, H.M.; Toader, O.; John, S.; Busch, K.; Birner, A.; Gösele, U.; Lehmann, V. Tunable two-dimensional photonic crystals using liquid crystal infiltration. Phys. Rev. B 2000, 61, R2389. [Google Scholar] [CrossRef]
- Hennessy, K.; Högerle, C.; Hu, E.; Badolato, A.; Imamoglu, A. Tuning photonic nanocavities by atomic force microscope nano-oxidation. Appl. Phys. Lett. 2006, 89, 041118. [Google Scholar] [CrossRef]
- Lee, H.S.; Kiravittaya, S.; Kuma, S.; Plumhof, J.D.; Balet, L.; Li, L.H.; Francardi, M.; Gerardino, A.; Fiore, A.; Rastelli, A.; et al. Local tuning of photonic crystal nanocavity modes by laser-assisted oxidation. Appl. Phys. Lett. 2009, 95, 191109. [Google Scholar] [CrossRef]
- Intonti, F.; Caselli, N.; Vignolini, S.; Riboli, F.; Kumar, S.; Rastelli, A.; Schmidt, O.G.; Francardi, M.; Gerardino, A.; Balet, L.; et al. Mode tuning of photonic crystal nanocavities by photoinduced non-thermal oxidation. Appl. Phys. Lett. 2012, 100, 033116. [Google Scholar] [CrossRef]
- Hecht, E. Interference, Chapter 9. In Optics, 5th ed.; Addison-Wesley Reading: Boston, MA, USA, 1998; ISBN 10: 1-292-09693-4. [Google Scholar]
- Caselli, N.; Riboli, F.; La China, F.; Gerardino, A.; Li, L.H.; Linfield, E.H.; Pagliano, F.; Fiore, A.; Intonti, F.; Gurioli, M. Tailoring the Photon Hopping by Nearest-Neighbor and Next-Nearest-Neighbor Interaction in Photonic Arrays. ACS Photonics 2015, 2, 565–571. [Google Scholar] [CrossRef]
- Bayindir, M.; Temelkuran, B.; Ozbay, E. Propagation of photons by hopping: A waveguiding mechanism through localized coupled cavities in three-dimensional photonic crystals. Phys. Rev. B 2000, 61, R11855. [Google Scholar] [CrossRef]
- Matsuda, N.; Kuramochi, E.; Takesue, H.; Notomi, M. Dispersion and light transport characteristics of large-scale photonic- crystal coupled nanocavity arrays. Opt. Lett. 2014, 39, 2290–2293. [Google Scholar] [CrossRef] [PubMed]
- Imamoglu, A.; Awschalom, D.; Burkard, G.; di Vincenzo, D.; Loss, D.; Sherwin, M.; Small, A. Quantum information processing using quantum dot spins and cavity QED. Phys. Rev. Lett. 1999, 83, 4204–4207. [Google Scholar] [CrossRef]
- Hartmann, M.; Brandao, F.; Plenio, M. Quantum many-body phenomena in coupled cavity arrays. Laser Photonics Rev. 2008, 2, 527–556. [Google Scholar] [CrossRef]
- Senellart, P.; Solomon, G.; White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 2017, 12, 1026–1039. [Google Scholar] [CrossRef] [PubMed]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Felici, M.; Gallo, P.; Mohan, A.; Dwir, B.; Rudra, A.; Kapon, E. Site-controlled InGaAs quantum dots with tunable emission energy. Small 2009, 5, 938–943. [Google Scholar] [CrossRef]
- Trotta, R.; Polimeni, A.; Martelli, F.; Pettinari, G.; Capizzi, M.; Felisari, L.; Rubini, S.; Francardi, M.; Gerardino, A.; Christianen, P.C.M.; Maan, J.C. Fabrication of site-controlled quantum dots by spatially selective incorporation of hydrogen in Ga (AsN)/GaAs heterostructures. Adv. Mater. 2011, 23, 2706–2710. [Google Scholar] [CrossRef]
- Biccari, F.; Boschetti, A.; Pettinari, G.; La China, F.; Gurioli, M.; Intonti, F.; Vinattieri, A.; Sharma, M.; Capizzi, M.; Gerardino, A.; et al. Site-controlled single photon emitters fabricated by near field illumination. Adv. Mater. 2018, 30, 1705450. [Google Scholar] [CrossRef]
- Pettinari, G.; Felici, M.; Trotta, R.; Capizzi, M.; Polimeni, A. Hydrogen effects in dilute III-N-V alloys: From defect engineering to nanostructuring. J. Appl. Phys. 2014, 115, 012011. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Pettinari, G.; Makarovsky, O.; Turyanska, L.; Fay, M.W.; De Luca, M.; Polimeni, A.; Capizzi, M.; Martelli, F.; Rubini, S. Band-gap profiling by laser writing of hydrogen-containing III-N.-Vs. Phys. Rev. B 2012, 86, 155307. [Google Scholar] [CrossRef]
- Pettinari, G.; Gerardino, A.; Businaro, L.; Polimeni, A.; Capizzi, M.; Hopkinson, M.; Rubini, S.; Biccari, F.; Intonti, F.; Vinattieri, A.; et al. A lithographic approach for quantum dot-photonic crystal nanocavity coupling in dilute nitrides. Microelectron. Eng. 2017, 174, 16–19. [Google Scholar] [CrossRef]
- Akahane, Y.; Mochizuki, M.; Asano, T.; Tanaka, Y. Design of a channel drop filter by using a donor-type cavity with high-quality factor in a two-dimensional photonic crystal slab. Appl. Phys. Lett. 2003, 82, 1341–1343. [Google Scholar] [CrossRef]
- Polimeni, A.; Bissiri, M.; Augieri, A.; Baldassarri Hoger von Högersthal, G.; Capizzi, M.; Gollub, D.; Fischer, M.; Reinhardt, M.; Forchel, A. Reduced temperature dependence of the band gap in GaAs1−yNy investigated with photoluminescence. Phys. Rev. B 2002, 65, 235325. [Google Scholar] [CrossRef]
- Gevaux, D.G.; Bennett, A.J.; Stevenson, R.M.; Shields, A.J.; Atkinson, P.; Griffiths, J.; Anderson, D.; Jones, G.A.C.; Ritchie, D.A. Enhancement and suppression of spontaneous emission by temperature tuning InAs quantum dots to photonic crystal cavities. Appl. Phys. Lett. 2006, 88, 131101. [Google Scholar] [CrossRef]
- Pankove, J. Optical Processes in Semiconductors; Dover: New York, NY, USA, 1975; ISBN 10 0486602753. [Google Scholar]
- Felici, M.; Pettinari, G.; Biccari, F.; Boschetti, A.; Birindelli, S.; Younis, S.; Gurioli, M.; Vinattieri, A.; Gerardino, A.; Businaro, L.; et al. Broadband enhancement of light-matter interaction in photonic crystal cavities integrating site-controlled Ga (AsN)/Ga (AsN):H. quantum dots. Phys. Rev. X 2018. under review. [Google Scholar]
- Caselli, N.; Intonti, F.; La China, F.; Riboli, F.; Gerardino, A.; Bao, W.; Bargioni, A.W.; Li, L.; Linfield, E.H.; Pagliano, F.; et al. Ultra-subwavelength phase-sensitive Fano-imaging of localized photonic modes. Light Sci. Appl. 2015, 4, e326. [Google Scholar] [CrossRef]
- Caselli, N.; Intonti, F.; Bianchi, C.; Riboli, F.; Vignolini, S.; Balet, L.; Li, L.H.; Francardi, M.; Gerardino, A.; Fiore, A.; Gurioli, M. Post-fabrication control of evanescent tunnelling in photonic crystal molecules. Appl. Phys. Lett. 2012, 101, 211108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerardino, A.; Pettinari, G.; Caselli, N.; Vignolini, S.; Riboli, F.; Biccari, F.; Felici, M.; Polimeni, A.; Fiore, A.; Gurioli, M.; et al. Coupled Photonic Crystal Nanocavities as a Tool to Tailor and Control Photon Emission. Ceramics 2019, 2, 34-55. https://doi.org/10.3390/ceramics2010004
Gerardino A, Pettinari G, Caselli N, Vignolini S, Riboli F, Biccari F, Felici M, Polimeni A, Fiore A, Gurioli M, et al. Coupled Photonic Crystal Nanocavities as a Tool to Tailor and Control Photon Emission. Ceramics. 2019; 2(1):34-55. https://doi.org/10.3390/ceramics2010004
Chicago/Turabian StyleGerardino, Annamaria, Giorgio Pettinari, Niccolò Caselli, Silvia Vignolini, Francesco Riboli, Francesco Biccari, Marco Felici, Antonio Polimeni, Andrea Fiore, Massimo Gurioli, and et al. 2019. "Coupled Photonic Crystal Nanocavities as a Tool to Tailor and Control Photon Emission" Ceramics 2, no. 1: 34-55. https://doi.org/10.3390/ceramics2010004
APA StyleGerardino, A., Pettinari, G., Caselli, N., Vignolini, S., Riboli, F., Biccari, F., Felici, M., Polimeni, A., Fiore, A., Gurioli, M., & Intonti, F. (2019). Coupled Photonic Crystal Nanocavities as a Tool to Tailor and Control Photon Emission. Ceramics, 2(1), 34-55. https://doi.org/10.3390/ceramics2010004









