Radial-Concentric Freeze Casting Inspired by Porcupine Fish Spines
Abstract
1. Introduction
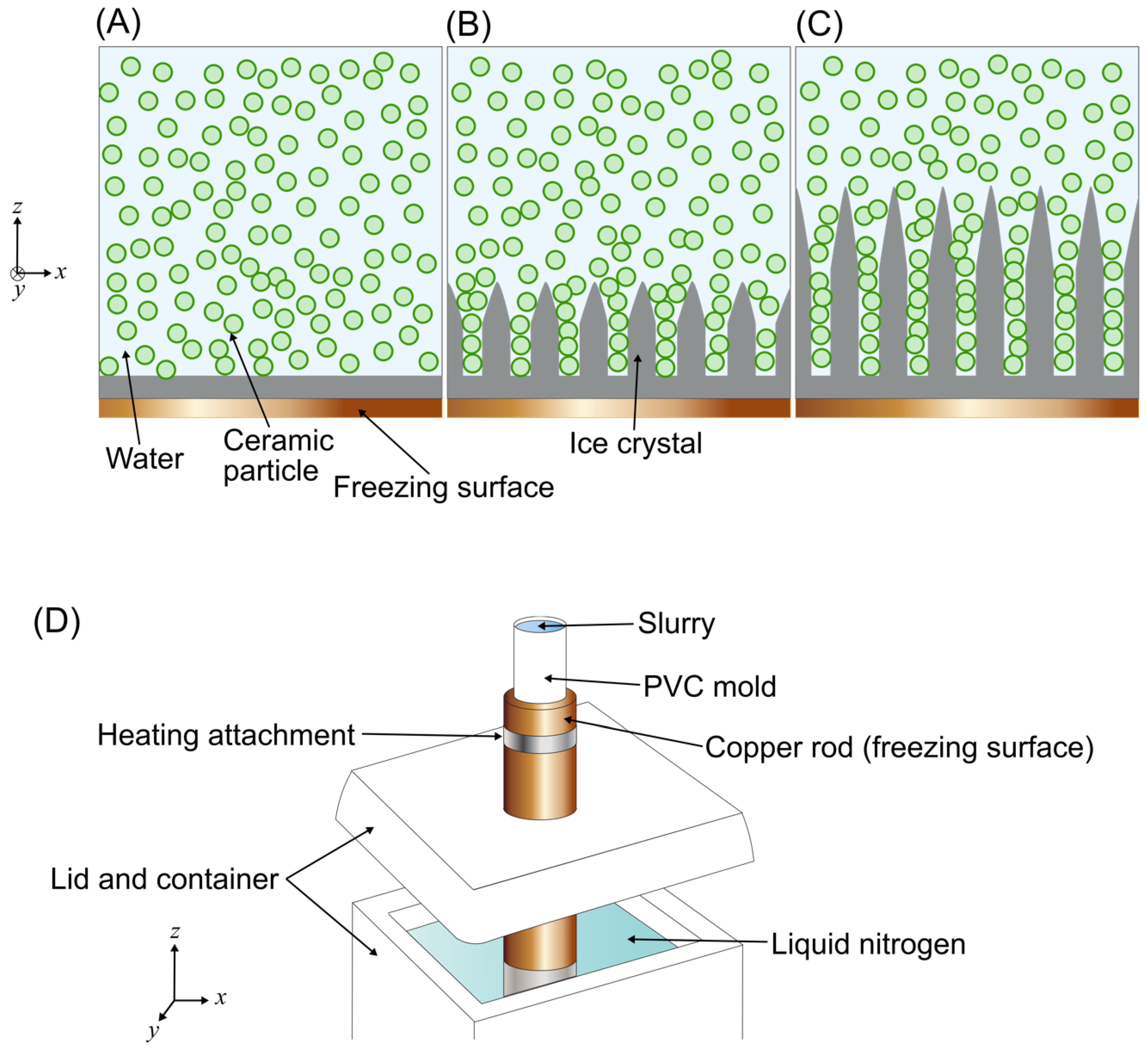
1.1. Microstructural Control in Freeze Casting for Bioinspired Materials
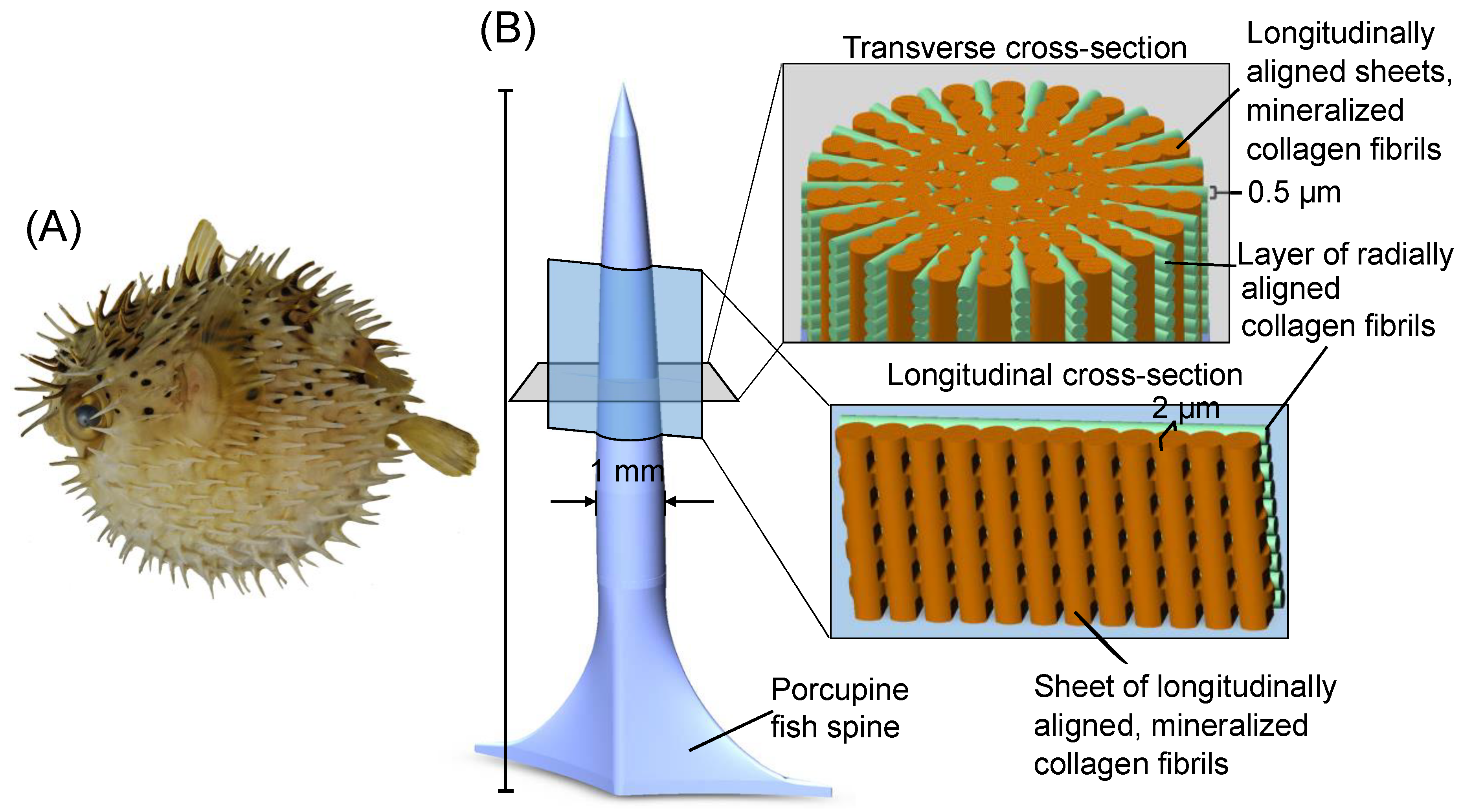
1.2. Bioinspiration from the Porcupine Fish Spine
2. Materials and Methods
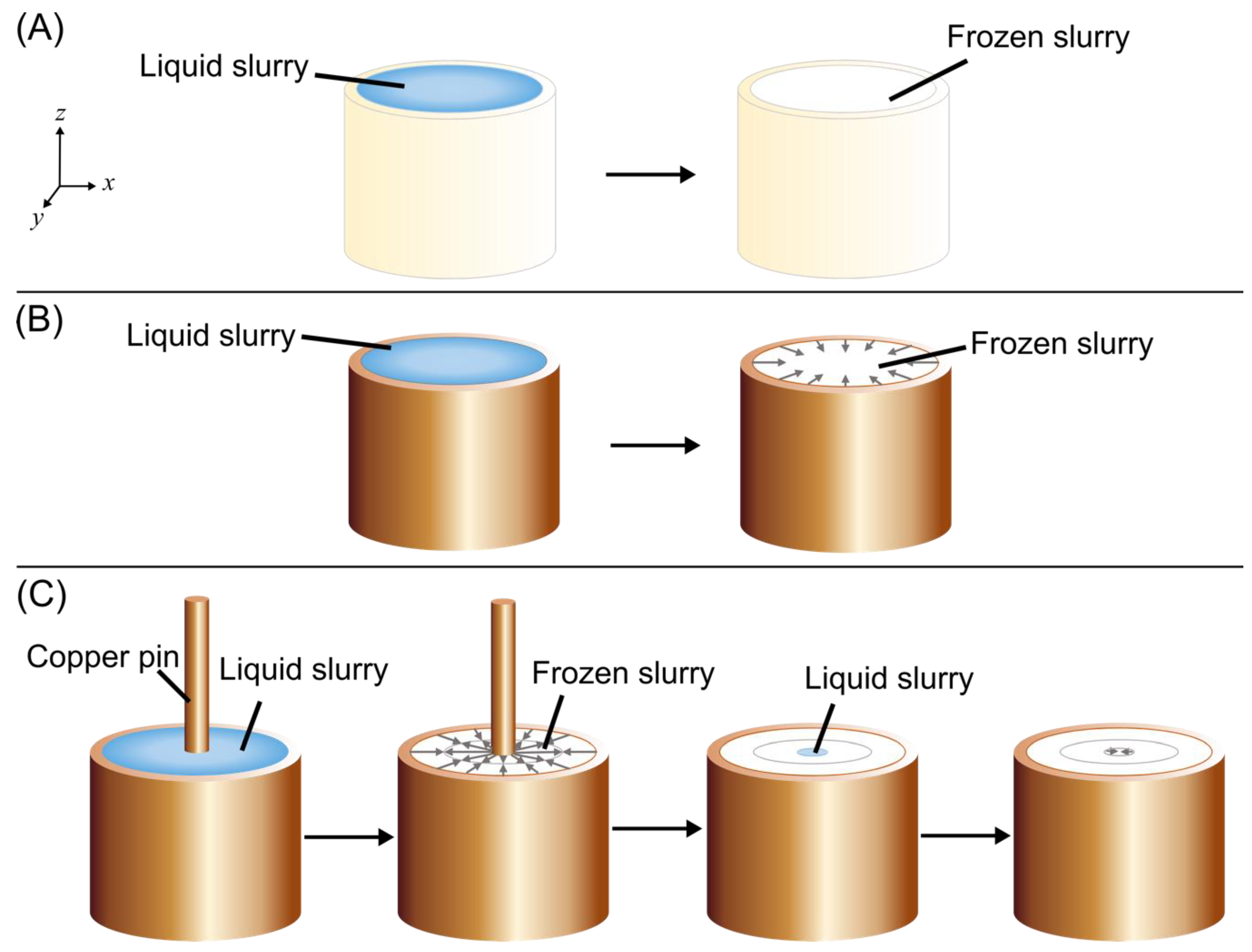
2.1. Freeze Casting
2.2. Microstructural Characterization
2.3. Mechanical Testing
3. Results and Discussion
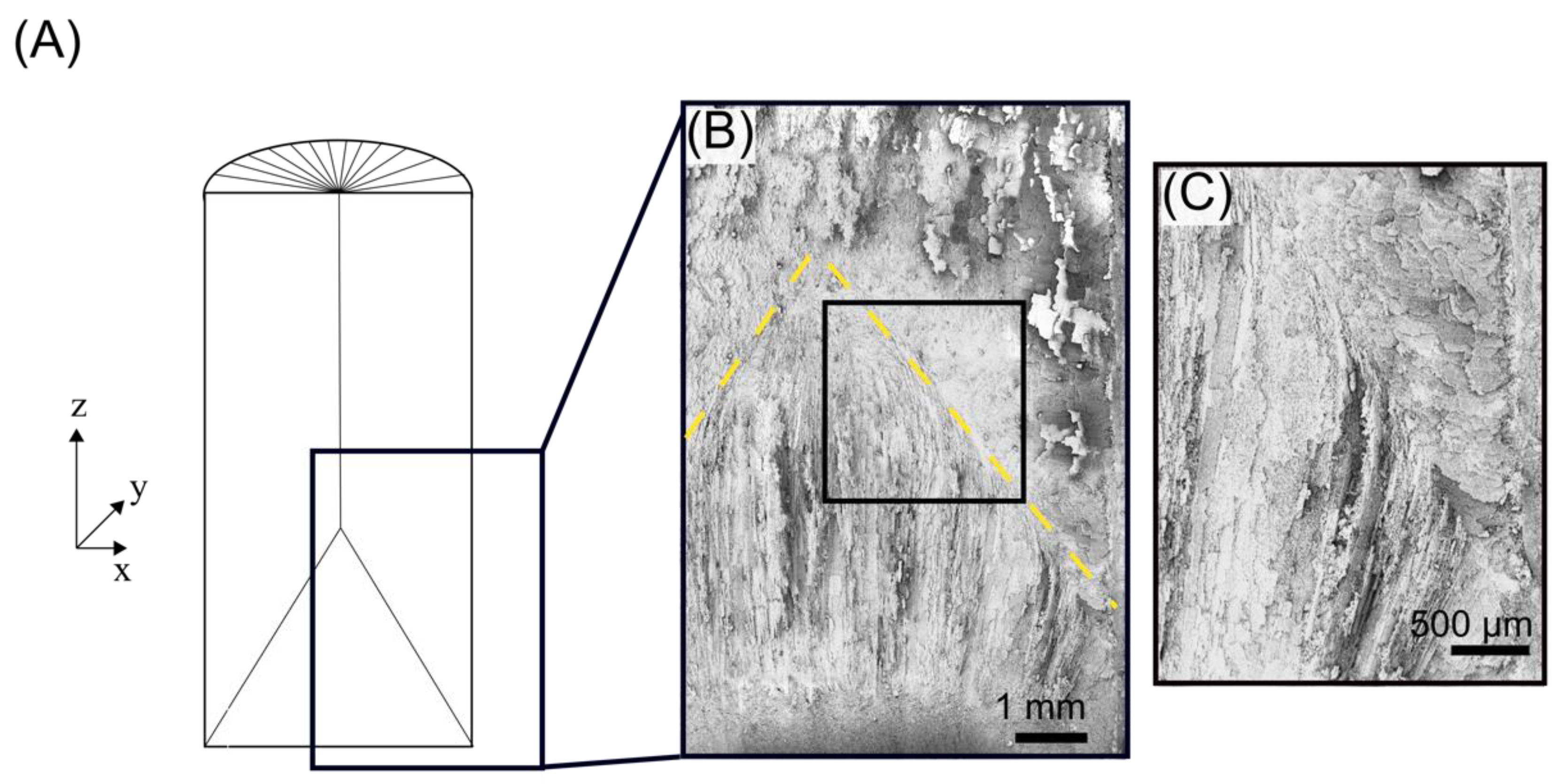
3.1. Radial and Radial-Concentric Freeze Casts: Axial Cross Sections
3.2. Radial Freeze Cast: Longitudinal Cross Section
3.3. Radial Concentric Freeze Casts: Outer Interface
3.4. Radial Concentric Freeze Casts: Inner Interface
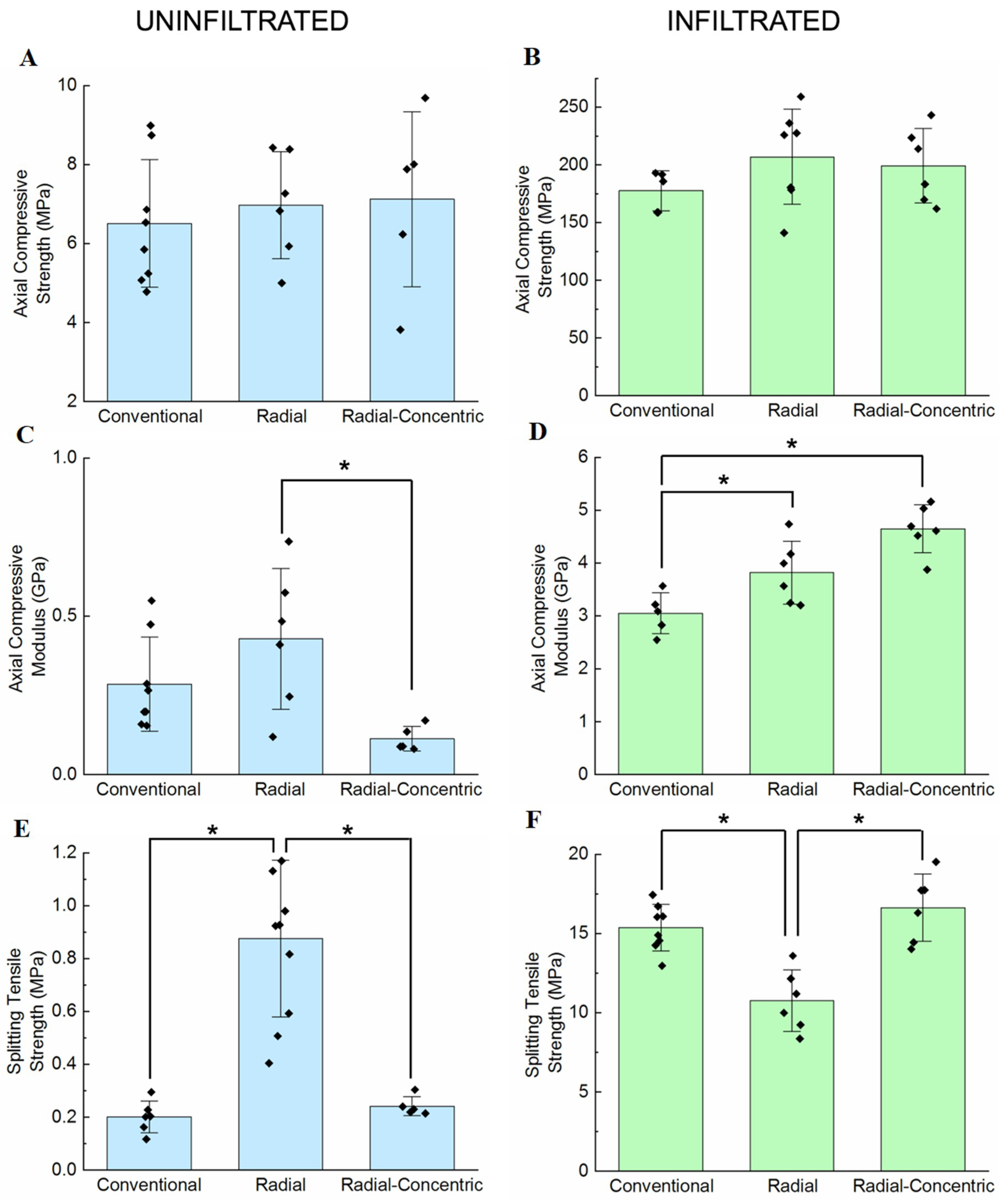
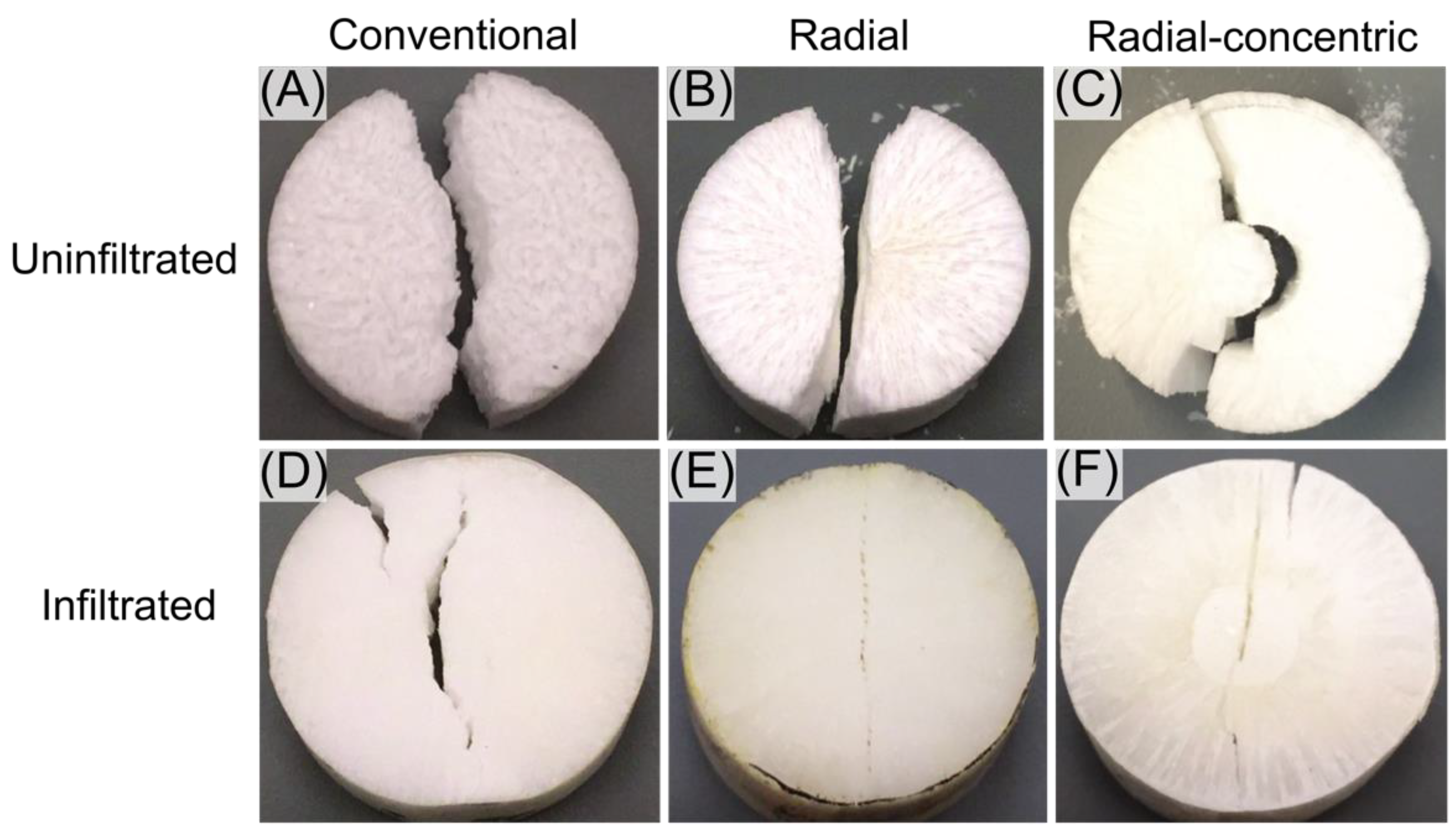
3.5. Mechanical Test Results
4. Conclusions
- Radial-concentric freeze cast samples from our two-step freeze casting process had three layers. The outer two layers resulted from the first step in the process, in which two freezing fronts met to form an interface. The inner core layer resulted from the second step in the process, where another interface could be seen between this core layer and the layer formed in the first step of the freeze cast method.
- When infiltrated with epoxy, radial-concentric freeze cast ceramics had improved axial compressive modulus over uninfiltrated radial-concentric freeze casts, especially when compared against the effects of infiltration in conventional or radial freeze cast ceramics.
- Amongst uninfiltrated samples, radial-concentric freeze cast ceramics had one of the lowest splitting tensile strengths. With infiltration, radial-concentric freeze casts improved significantly to having the highest splitting tensile strength.
- In comparison, uninfiltrated radial freeze casts initially had the highest splitting tensile strength. Upon infiltration, the splitting tensile strength of radial freeze casts only improved moderately.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Maxwell, W.; Gurnick, R.; Francisco, A. Preliminary Investigation of the “Freeze-Casting” Method for Forming Refractory Powders; National Advisory Committee for Aeronautics (NACA): Washington, DC, USA, 1954.
- Chino, Y.; Dunand, D.C. Directionally freeze-cast titanium foam with aligned, elongated pores. Acta Mater. 2008, 56, 105–113. [Google Scholar] [CrossRef]
- Yook, S.-W.; Yoon, B.-H.; Kim, H.-E.; Koh, Y.-H.; Kim, Y.-S. Porous titanium (Ti) scaffolds by freezing TiH2/camphene slurries. Mater. Lett. 2008, 62, 4506–4508. [Google Scholar] [CrossRef]
- Li, J.C.; Dunand, D.C. Mechanical properties of directionally freeze-cast titanium foams. Acta Mater. 2011, 59, 146–158. [Google Scholar] [CrossRef]
- Ramos, A.I.; Dunand, D.C. Preparation and characterization of directionally freeze-cast copper foams. Metals 2012, 2, 265–273. [Google Scholar] [CrossRef]
- Dash, R.; Li, Y.; Ragauskas, A.J. Cellulose nanowhisker foams by freeze casting. Carbohydr. Polym. 2012, 88, 789–792. [Google Scholar] [CrossRef]
- Zhou, Y.; Fu, S.; Pu, Y.; Pan, S.; Ragauskas, A.J. Preparation of aligned porous chitin nanowhisker foams by directional freeze–casting technique. Carbohydr. Polym. 2014, 112, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Fu, S.; Pu, Y.; Pan, S.; Levit, M.V.; Ragauskas, A.J. Freeze-casting of cellulose nanowhisker foams prepared from a water-dimethylsulfoxide (DMSO) binary mixture at low DMSO concentrations. RSC Adv. 2013, 3, 19272–19277. [Google Scholar] [CrossRef]
- Donius, A.E.; Liu, A.; Berglund, L.A.; Wegst, U.G. Superior mechanical performance of highly porous, anisotropic nanocellulose–montmorillonite aerogels prepared by freeze casting. J. Mech. Behav. Biomed. Mater. 2014, 37, 88–99. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Liu, J.Z.; Chang, S.L.; Wu, Y.; Li, D. Biomimetic superelastic graphene-based cellular monoliths. Nat. Commun. 2012, 3, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Antink, M.M.H.; Röpke, L.; Bartels, J.; Soltmann, C.; Kunzmann, A.; Rezwan, K.; Kroll, S. Porous ceramics with tailored pore size and morphology as substrates for coral larval settlement. Ceram. Int. 2018, 44, 16561–16571. [Google Scholar] [CrossRef]
- Moon, J.-W.; Hwang, H.-J.; Awano, M.; Maeda, K. Preparation of NiO–YSZ tubular support with radially aligned pore channels. Mater. Lett. 2003, 57, 1428–1434. [Google Scholar] [CrossRef]
- Deville, S. Freeze-casting of porous biomaterials: Structure, properties and opportunities. Materials 2010, 3, 1913–1927. [Google Scholar] [CrossRef]
- Yoon, B.H.; Koh, Y.H.; Park, C.S.; Kim, H.E. Generation of large pore channels for bone tissue engineering using camphene-based freeze casting. J. Am. Ceram. Soc. 2007, 90, 1744–1752. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, K.; Zeng, Y.-P. Effects of gelatin addition on the microstructure of freeze-cast porous hydroxyapatite ceramics. Ceram. Int. 2009, 35, 2151–2154. [Google Scholar] [CrossRef]
- Fu, Q.; Rahaman, M.N.; Bal, B.S.; Brown, R.F. Proliferation and function of MC3T3-E1 cells on freeze-cast hydroxyapatite scaffolds with oriented pore architectures. J. Mater. Sci. Mater. Med. 2009, 20, 1159–1165. [Google Scholar] [CrossRef] [PubMed]
- Deville, S.; Saiz, E.; Tomsia, A.P. Freeze casting of hydroxyapatite scaffolds for bone tissue engineering. Biomaterials 2006, 27, 5480–5489. [Google Scholar] [CrossRef] [PubMed]
- Suetsugu, Y.; Hotta, Y.; Iwasashi, M.; Sakane, M.; Kikuchi, M.; Ikoma, T.; Higaki, T.; Ochiai, N.; Tanaka, M. Structural and tissue reaction properties of novel hydroxyapatite ceramics with unidirectional pores. Key Eng. Mater. 2007, 330–332, 1003–1006. [Google Scholar] [CrossRef]
- Yoon, B.-H.; Choi, W.-Y.; Kim, H.-E.; Kim, J.-H.; Koh, Y.-H. Aligned porous alumina ceramics with high compressive strengths for bone tissue engineering. Scr. Mater. 2008, 58, 537–540. [Google Scholar] [CrossRef]
- Hong, C.; Zhang, X.; Han, J.; Du, J.; Han, W. Ultra-high-porosity zirconia ceramics fabricated by novel room-temperature freeze-casting. Scr. Mater. 2009, 60, 563–566. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Meille, S.; Van de Moortèle, B.; Stevenson, A.J.; Deville, S. Strong, tough and stiff bioinspired ceramics from brittle constituents. Nat. Mater. 2014, 13, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.M.; Yeh, M.; Strawson, J.; Goehring, T.; Lujan, S.; Siripasopsotorn, P.; Meyers, M.A.; McKittrick, J. Magnetic freeze casting inspired by nature. Mater. Sci. Eng. A 2012, 556, 741–750. [Google Scholar] [CrossRef]
- Porter, M.M.; Meraz, L.; Calderon, A.; Choi, H.; Chouhan, A.; Wang, L.; Meyers, M.A.; McKittrick, J. Torsional properties of helix-reinforced composites fabricated by magnetic freeze casting. Compos. Struct. 2015, 119, 174–184. [Google Scholar] [CrossRef]
- Frank, M.B.; Naleway, S.E.; Haroush, T.; Liu, C.-H.; Siu, S.H.; Ng, J.; Torres, I.; Ismail, A.; Karandikar, K.; Porter, M.M. Stiff, porous scaffolds from magnetized alumina particles aligned by magnetic freeze casting. Mater. Sci. Eng. C 2017, 77, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Uhlmann, D.R.; Chalmers, B.; Jackson, K.A. Interaction between particles and a solid-liquid interface. J. Appl. Phys. 1964, 35, 2986–2993. [Google Scholar] [CrossRef]
- Araki, K.; Halloran, J.W. Porous ceramic bodies with interconnected pore channels by a novel freeze casting technique. J. Am. Ceram. Soc. 2005, 88, 1108–1114. [Google Scholar] [CrossRef]
- Peppin, S.S.; Worster, M.G.; Wettlaufer, J. Morphological instability in freezing colloidal suspensions. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2006, 463, 723–733. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Wettlaufer, J.S.; Worster, M.G. Experimental verification of morphological instability in freezing aqueous colloidal suspensions. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Deville, S.; Maire, E.; Lasalle, A.; Bogner, A.; Gauthier, C.; Leloup, J.; Guizard, C. In Situ X-Ray Radiography and Tomography Observations of the Solidification of Aqueous Alumina Particles Suspensions. Part II: Steady State. J. Am. Ceram. Soc. 2009, 92, 2497–2503. [Google Scholar] [CrossRef]
- Naleway, S.E.; Christopher, F.Y.; Hsiong, R.L.; Sengupta, A.; Iovine, P.M.; Hildebrand, J.A.; Meyers, M.A.; McKittrick, J. Bioinspired intrinsic control of freeze cast composites: Harnessing hydrophobic hydration and clathrate hydrates. Acta Mater. 2016, 114, 67–79. [Google Scholar] [CrossRef]
- Porter, M.M.; McKittrick, J.; Meyers, M.A. Biomimetic materials by freeze casting. JOM 2013, 65, 720–727. [Google Scholar] [CrossRef]
- Mukai, S.R.; Nishihara, H.; Tamon, H. Formation of monolithic silica gel microhoneycombs (SMHs) using pseudosteady state growth of microstructural ice crystals. Chem. Commun. 2004, 874–875. [Google Scholar] [CrossRef] [PubMed]
- Koh, Y.H.; Lee, E.J.; Yoon, B.H.; Song, J.H.; Kim, H.E.; Kim, H.W. Effect of polystyrene addition on freeze casting of ceramic/camphene slurry for ultra-high porosity ceramics with aligned pore channels. J. Am. Ceram. Soc. 2006, 89, 3646–3653. [Google Scholar] [CrossRef]
- Shanti, N.O.; Araki, K.; Halloran, J.W. Particle redistribution during dendritic solidification of particle suspensions. J. Am. Ceram. Soc. 2006, 89, 2444–2447. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Tomsia, A.P. Ice-templated porous alumina structures. Acta Mater. 2007, 55, 1965–1974. [Google Scholar] [CrossRef]
- Fukasawa, T.; Ando, M.; Ohji, T.; Kanzaki, S. Synthesis of porous ceramics with complex pore structure by freeze-dry processing. J. Am. Ceram. Soc. 2001, 84, 230–232. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Nalla, R.K.; Tomsia, A.P. Freezing as a path to build complex composites. Science 2006, 311, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Nakata, M.; Tanihata, K.; Yamaguchi, S.; Suganuma, K. Fabrication of porous alumina sintered bodies by a gelate-freezing method. J. Ceram. Soc. Jpn. 2005, 113, 712–715. [Google Scholar] [CrossRef]
- Zhang, H.; Hussain, I.; Brust, M.; Butler, M.F.; Rannard, S.P.; Cooper, A.I. Aligned two-and three-dimensional structures by directional freezing of polymers and nanoparticles. Nat. Mater. 2005, 4, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Deville, S. Freeze-casting of porous ceramics: A review of current achievements and issues. Adv. Eng. Mater. 2008, 10, 155–169. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, K.; Hu, L.; Wu, Z. Two-step freeze casting fabrication of hydroxyapatite porous scaffolds with bionic bone graded structure. Ceram. Int. 2013, 39, 9703–9707. [Google Scholar] [CrossRef]
- Tang, Y.; Miao, Q.; Qiu, S.; Zhao, K.; Hu, L. Novel freeze-casting fabrication of aligned lamellar porous alumina with a centrosymmetric structure. J. Eur. Ceram. Soc. 2014, 34, 4077–4082. [Google Scholar] [CrossRef]
- Leis, J.M. Nomenclature and distribution of the species of the porcupinefish family Diodontidae (Pisces, Teleostei). Mem. Mus. Vic. 2006, 63, 77–90. [Google Scholar] [CrossRef]
- Brainerd, E.L. Pufferfish inflation: Functional morphology of postcranial structures in Diodon holocanthus (Tetraodontiformes). J. Morphol. 1994, 220, 243–261. [Google Scholar] [CrossRef] [PubMed]
- Su, F.Y.; Bushong, E.A.; Deerinck, T.J.; Seo, K.; Herrera, S.; Graeve, O.A.; Kisailus, D.; Lubarda, V.A.; McKittrick, J. Spines of the porcupine fish: Structure, composition, and mechanical properties. J. Mech. Behav. Biomed. Mater. 2017, 73, 38–49. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Ortega, C.F.; Motamedi, R.; Szewciw, L.; Vernerey, F.; Barthelat, F. Structure and mechanical performance of a “modern” fish scale. Adv. Eng. Mater. 2012, 14, B185–B194. [Google Scholar] [CrossRef]
- Yu, Z.B.; Krstic, V.D. Fabrication and characterization of laminated SiC ceramics with self-sealed ring structure. J. Mater. Sci. 2003, 38, 4735–4738. [Google Scholar] [CrossRef]
- Marshall, D.B.; Ratto, J.J.; Lange, F.F. Enhanced fracture toughness in layered microcomposites of Ce-ZrO2 and Al2O3. J. Am. Ceram. Soc. 1991, 74, 2979–2987. [Google Scholar] [CrossRef]
- Williams, J.T.; Carpenter, K.E.; Van Tassell, J.L.; Hoetjes, P.; Toller, W.; Etnoyer, P.; Smith, M. Biodiversity assessment of the fishes of Saba Bank Atoll, Netherlands Antilles. PLoS ONE 2010, 5, 1–37. [Google Scholar] [CrossRef]
- ASTM International. ASTM C39/C39M-18, Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 1921. [Google Scholar]
- ASTM International. ASTM D3967-16, Standard Test Method for Splitting Tensile Strength of Intact Rock Core Specimens; ASTM International: West Conshohocken, PA, USA, 1981. [Google Scholar]
- Deville, S.; Meille, S.; Seuba, J. A meta-analysis of the mechanical properties of ice-templated ceramics and metals. Sci. Tech. Adv. Mater. 2015, 16, 043501. [Google Scholar] [CrossRef] [PubMed]
- Deville, S.; Maire, E.; Lasalle, A.; Bogner, A.; Gauthier, C.; Leloup, J.; Guizard, C. In Situ X-Ray Radiography and Tomography Observations of the Solidification of Aqueous Alumina Particle Suspensions—Part I: Initial Instants. J. Am. Ceram. Soc. 2009, 92, 2489–2496. [Google Scholar] [CrossRef]
- Waschkies, T.; Oberacker, R.; Hoffmann, M.J. Control of lamellae spacing during freeze casting of ceramics using double-side cooling as a novel processing route. J. Am. Ceram. Soc. 2009, 92, S79–S84. [Google Scholar] [CrossRef]
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Sabet, F.A.; Su, F.Y.; McKittrick, J.; Jasiuk, I. Mechanical Properties of Model Two-Phase Composites with Continuous Compared to Discontinuous Phases. Adv. Eng. Mater. 2018, 20, 1–6. [Google Scholar] [CrossRef]
- Nalla, R.K.; Kinney, J.H.; Ritchie, R.O. Mechanistic fracture criteria for the failure of human cortical bone. Nat. Mater. 2003, 2, 164–168. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Wong, L.N.Y. The Brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]



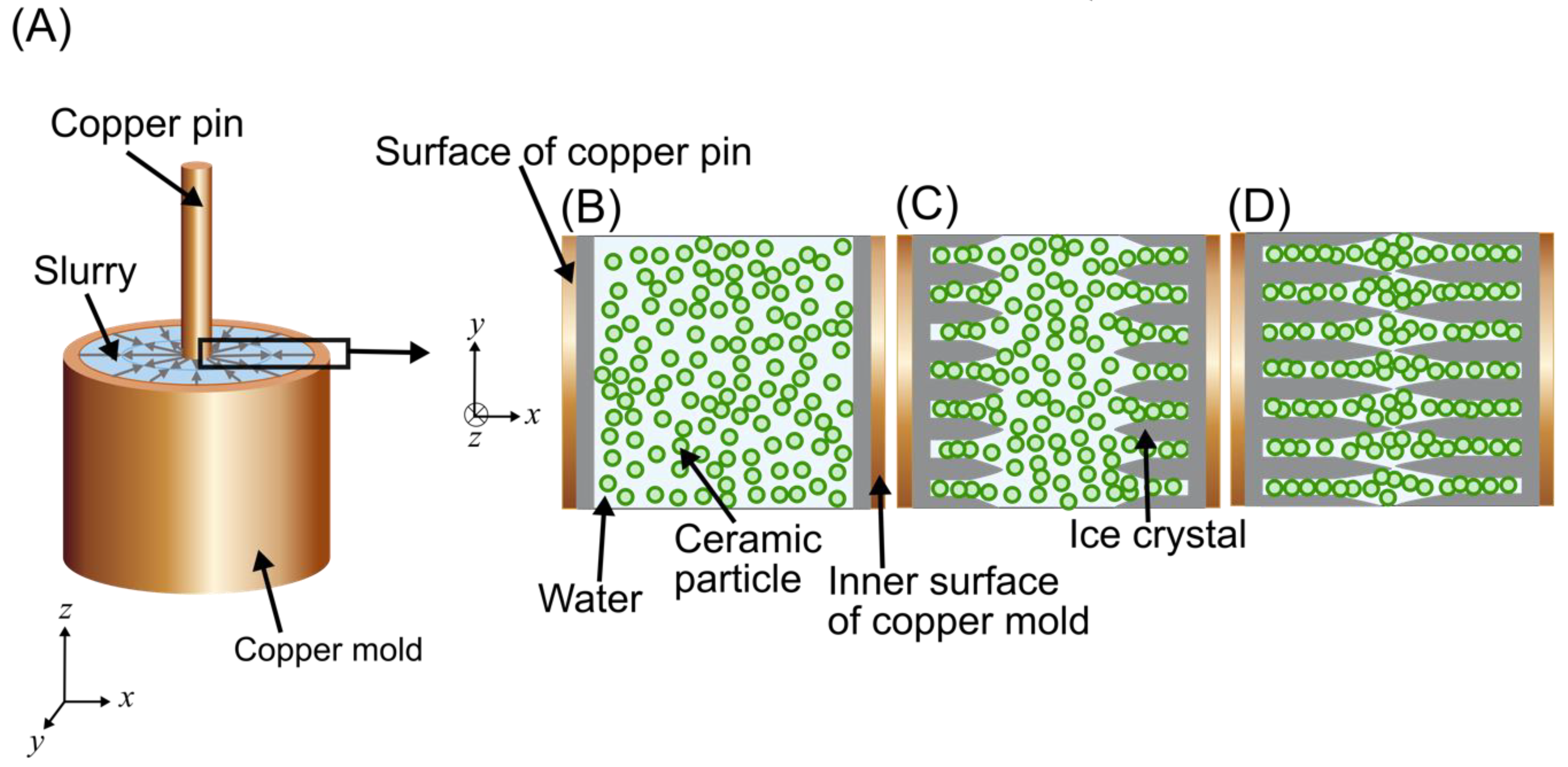
| Freeze Cast Type | Zone | Region | Nm | Thickness ± SD (µm) | Porosity ± SD (%) |
|---|---|---|---|---|---|
| Conventional | N/A | N/A | 50 | 46 ± 15 | 52.6% ± 0.9% |
| Radial | N/A | Outer | 50 | 14 ± 4 | 51.9% ± 2.7% |
| Radial | N/A | Inner | 50 | 8 ± 2 | |
| Radial-concentric | Outer layer | Outer | 53 | 19 ± 6 | 56.2% ± 2.9% |
| Radial-concentric | Outer layer | Inner | 51 | 17 ± 3 | |
| Radial-concentric | Core layer | Outer | 53 | 21 ± 6 | |
| Radial-concentric | Core layer | Inner | 50 | 12 ± 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, F.Y.; Mok, J.R.; McKittrick, J. Radial-Concentric Freeze Casting Inspired by Porcupine Fish Spines. Ceramics 2019, 2, 161-179. https://doi.org/10.3390/ceramics2010015
Su FY, Mok JR, McKittrick J. Radial-Concentric Freeze Casting Inspired by Porcupine Fish Spines. Ceramics. 2019; 2(1):161-179. https://doi.org/10.3390/ceramics2010015
Chicago/Turabian StyleSu, Frances Y., Joyce R. Mok, and Joanna McKittrick. 2019. "Radial-Concentric Freeze Casting Inspired by Porcupine Fish Spines" Ceramics 2, no. 1: 161-179. https://doi.org/10.3390/ceramics2010015
APA StyleSu, F. Y., Mok, J. R., & McKittrick, J. (2019). Radial-Concentric Freeze Casting Inspired by Porcupine Fish Spines. Ceramics, 2(1), 161-179. https://doi.org/10.3390/ceramics2010015





