Design of Hydrogen-Powered Mobile Emergency Power Vehicle with Soft Open Point and Appropriate Energy Management Strategy

Abstract

Mobile emergency power supply vehicles (MEPSVs), powered by diesel engines or lithium-ion batteries (LIBs), have become a viable tool for emergency power supply. However, diesel-powered MEPSVs generate noise and environmental pollution, while LIB-powered vehicles suffer from limited power supply duration. To overcome these limitations, a hydrogen-powered MEPSV incorporating a soft open point (SOP) was developed in this study. We analyzed widely used operating scenarios for the SOP-equipped MEPSV and determined important parameters, including vehicle body structure, load capacity, driving speed, and power generation capability for the driving motor, hydrogen fuel cell (FC) module, auxiliary LIB module, and SOP equipment. Subsequently, we constructed an energy management strategy for the model for MEPSV, which uses multiple energy sources of hydrogen fuel cells and lithium-ion batteries. Through simulations, an optimal hydrogen consumption rate in various control strategies was validated using a predefined load curve to optimize the energy consumption minimization strategy and achieve the highest efficiency.

1. Introduction

Emergency power supply systems are essential during natural disasters and temporary power outages. Additionally, demand for specialized power solutions to support critical events such as high-level meetings and temporary capacity expansions is increasing. Mobile emergency power supply vehicles (MEPSVs), traditionally powered by diesel engines or lithium-ion batteries (LIBs), have become vital in providing such emergency power [1]. However, diesel-powered MEPSVs produce excessive noise and environmental pollution, while LIB-powered vehicles are limited by short operational durations. Consequently, there is an urgent need for a more sustainable, stable, and long-lasting emergency power solution [2].

Modern power distribution networks have integrated renewable energy to accommodate diverse loads. However, the networks face challenges such as unexpected stochastic behavior, reverse power flows, and insufficient supply capacity. To address the challenges, the soft open point (SOP), a novel power electronic device, has been developed to replace conventional open tie switches. It comprises a back-to-back AC-DC-AC converter built upon high-power, fully controlled electronic components with symmetrical converters at each end. SOPs enable the modularity, diverse connection configurations, and flexible closed-loop operation of distribution networks. When an energy storage system is integrated into the SOP’s DC link, it precisely regulates feeder power flows and mitigates random fluctuations, thereby enhancing the safety and performance of networks on dynamic loads with renewable energy sources [3].

We developed a hybrid MEPSV that integrates LIB and a fuel cell system (FCS), coupled with an SOP device. Hydrogen energy, characterized by high energy density and conversion efficiency, has been applied to future energy systems. By adopting FCS, the developed MEPSV delivers zero emissions, low noise, and extended power supply capabilities during emergencies. MEPSV connects to the distribution network via the SOP device, effectively embedding an energy storage system in the DC link. Its mobility diversifies its application to an uninterruptible power supply (UPS) to support temporary power flow regulation and fluctuation suppression in power distribution networks.

To enhance operational flexibility, the MEPSV developed is equipped with two FCS units and three LIB modules. Given the limited dynamic response, the FCS units are designated to supply base load power, while LIBs manage peak shaving and valley filling. An energy management strategy (EMS) is employed in MEPSV to coordinate power distribution among sources, maintain the LIB’s state of charge (SOC), and ensure FCS operation within its peak efficiency range.

2. Literature Review

EMS is categorized into rule-based and optimization-based strategies. Due to the nonlinear nature of hybrid power systems, rule-based EMS incorporates fuzzy logic to address problems caused by the system complexity. Optimization-based EMS adopts global optimization through dynamic programming (DP), local optimization through equivalent fuel consumption minimization strategy (ECMS), model predictive control (MPC), or reinforcement learning-based optimization through data-driven deep reinforcement learning (D3RL). Global optimization strategies rely on static data and prior knowledge but are not appropriate for real-time implementation. Local optimization strategies operate online based on the real-time system states, achieving instantaneous optimality. In reinforcement learning-based optimization strategies, optimal policies are autonomously learned through trial-and-error, enabling near-global performance without requiring precise models [4,5].

The rule-based EMS has been developed by many researchers. Fu et al. [6] developed a durability-oriented strategy that extended fuel cell lifespan by 9.47% compared with the previous strategies, though it lacked the real-time validation and optimization of fuel cell and battery aging. Mazouzi et al. [7] applied genetic algorithms to optimize fuzzy logic controller parameters, enhancing system economy and durability. Liu et al. [8] proposed a rule-based EMS that extracts real-time parameters, applies DP to determine optimal driving cycle solutions. They used deep learning to construct a rule for a real-time application.

Guo et al. [9] introduced a hierarchical adaptive EMS to reduce hydrogen consumption and improve system longevity and responsiveness for local optimization EMS. Wu et al. [10] proposed an MPC-based rolling optimization strategy that minimizes the costs of hydrogen usage and fuel cell degradation, while suppressing system constraints. Song et al. [11] developed a real-time EMS using a nonlinear MPC strategy by integrating Markov Chain Monte Carlo-based speed prediction, DP rolling optimization, and computational reduction techniques to enhance fuel economy and reduce powertrain losses.

In the reinforcement learning-based EMS, Huang et al. [12] improved training efficiency and fuel economy using a modified twin delayed deep deterministic policy gradient algorithm. Peng et al. [13] combined imitation learning with deep reinforcement learning (DRL) for global optimization with online learning capabilities to reduce driving costs. Xu et al. [14] proposed a hierarchical DRL method that integrates macroscopic traffic flow and microscopic powertrain dynamics using graph neural networks for coordinated ecological driving and energy allocation.

Wang et al. [15] proposed an automated multidimensional dynamic programming algorithm for a globally optimized EMS and modeled the multidimensional state space using adaptive grid technology. The algorithm addresses penalty function tuning and discretization errors, and dependency constraints, which are inherent challenges in traditional DP. The grid support strategy for fuel cell electric vehicles (FCEVs) enables bidirectional energy flow, allowing vehicles to both charge from and supply power to the grid. It uses a dynamic planning algorithm that considers real-time grid conditions, vehicle status, and user behavior to optimize energy exchange. The system respects operational constraints to maintain vehicle performance and longevity. Predictive scheduling helps anticipate grid needs and vehicle availability. Additionally, thermal and purge management ensure fuel cell readiness and efficiency during grid interactions. Chen et al. [16] combined improved DP and air supply optimization to improve system hydrogen economy and reliability EMS.

A comparative analysis reveals that rule-based EMS relies on heuristic rules, enabling low computational overhead. However, the rule-based EMS has limited adaptability and suboptimal performance. The optimization-based EMS employs mathematical programming to ensure global (DP) or local (ECMS) optimality but demands accurate models and incurs high computational costs. Reinforcement learning-based EMS is model-free, highly adaptable, and capable of near-global optimization, but requires extensive offline training data. Existing studies have been conducted to enhance economic efficiency, equipment durability, or real-time performance when applying EMS to various types of vehicles.

MEPSV is used in complex application scenarios that require active and reactive power management strategies within distribution networks. Therefore, sufficient training data for reinforcement learning is not easy to obtain. Similarly, global optimization strategies are inappropriate for the real-time deployment of MEPSV. Therefore, we selected rule-based and local optimization EMS for the simulation and validation of the state machine control, rule-based fuzzy logic control, classical proportional-integral (PI) control, frequency decoupling with fuzzy logic, and rule-based ECMS.

In the rule-based ECMS, operational rules were defined for initiating or shutting down FCS units based on load demand and alternating LIB groups between charging, discharging, and standby to prevent frequent switching and extend battery life. These rules are applied based on LIB SOC thresholds. Using the ECMS, instantaneous power distribution was optimized to enhance performance and powertrain durability.

3. MEPSV Design

The developed MEPSV adopts a SAIC Maxus truck chassis. The design parameters of the vehicle body are presented in

Table 1. Parameters of MEPSV developed in this study.

Parameter (Abbreviation, Unit)	Value
Full load vehicle mass (m) (kg)	18,000
Max speed (v) (km/h)	80
Maximum gradient at 10 km/h (a) (%)	30
Frontal area (A) (m2)	9.1
Aerodynamic drag coefficient (CD)	0.7
Rolling resistance coefficient (f)	0.03
Coefficient of rotational mass (δ)	1.01
Transmission efficiency (ηT)	90

.

The driving power required for vehicle driving was calculated using the following automotive driving power balance equation.

$$P=v\left(mgf+{\displaystyle \frac{C_{D}A{v}^2}{21.15}}+mg\alpha +\delta m{\displaystyle \frac{dv}{dt}}\right)/\left(3600{\eta }_T\right)$$

(1)

where $\alpha$ is the grade angle.

We used a permanent magnet synchronous motor (Suzhou Green Control Transmission Technology Co., Ltd., Suzhou, China) with a rated power of 100 kW and a peak power of 185 kW as the drive motor of MEPSV. The motor torque was calculated separately based on its transmission configuration and gradeability/speed indicators.

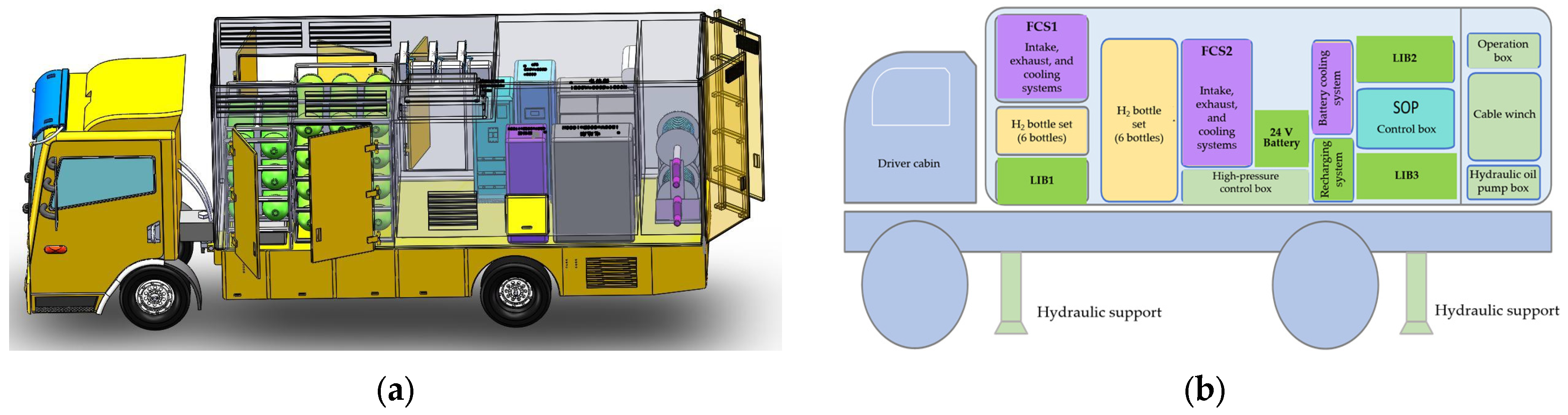
Based on the power requirements and considering various conditions such as driving and power generation, we designed MEPSV, which has three sets of hydrogen storage bottles, two sets of FCS, and three sets of lithium iron phosphate (LFP) batteries. The parameters of the components of the MEPSV developed are listed in

Table 2. Parameters of MPESV components.

Component	Parameter (Unit)	Value
Driving motor	Rated peak power (kW)	100/185
	Rated peak torque (Nm)	750/1300
Battery	Nominal capacity (Ah)	173
	Cell voltage rated voltage (V)	3.22/521
	Total nominal energy (kWh)	90 × 3
	Bidirectional DC-DC converter (BDCC) rated peak power (kW)	110/130
	BDCC efficiency (ηDC) (%)	97
Hydrogen storage bottle	Nominal hydrogen quality (kg)	3.7
	Nominal water volume (L)	166
FCS	Rated peak power (PFC) (kW)	110/136
	Unidirectional DC-DC converter (UDCC) rated peak power (PFCS) (kW)	110/150
	UDCC efficiency (ηUDCC) (%)	97
SOP	Single-port rated capacity (kW)	250

. The MEPSV also has a cable winch, a centralized monitoring system, and SOP inside the compartment (Figure 1).

The International Organization for Standardization (ISO) 17268 connection standard [17] is applied to the hydrogen storage bottles to ensure a quick connection. ISO 17268 applies to gaseous hydrogen land vehicle refuelling connection devices, formulated by the Technical Committee: ISO/TC 197—Hydrogen technologies. Replacing an individual bottle requires approximately 20 min; however, the entire set can be refueled directly by a mobile refueling vehicle. This vehicle is equipped with a hydrogen compressor and dispenser compliant (Guangdong Hongli Hydrogen Power Technology Co., Ltd., Zhaoqing, China) which follows the Society of Automotive Engineers (SAE) J2601 standard [18], enabling a refueling rate of 1.5–5.0 kg/min. Each set of bottles contains 22.2 kg of hydrogen, making mobile refueling time-efficient. The SAE J2601 standard is fueling protocols for light-duty gaseous hydrogen surface vehicles to ensure safe, fast, and consistent refueling.

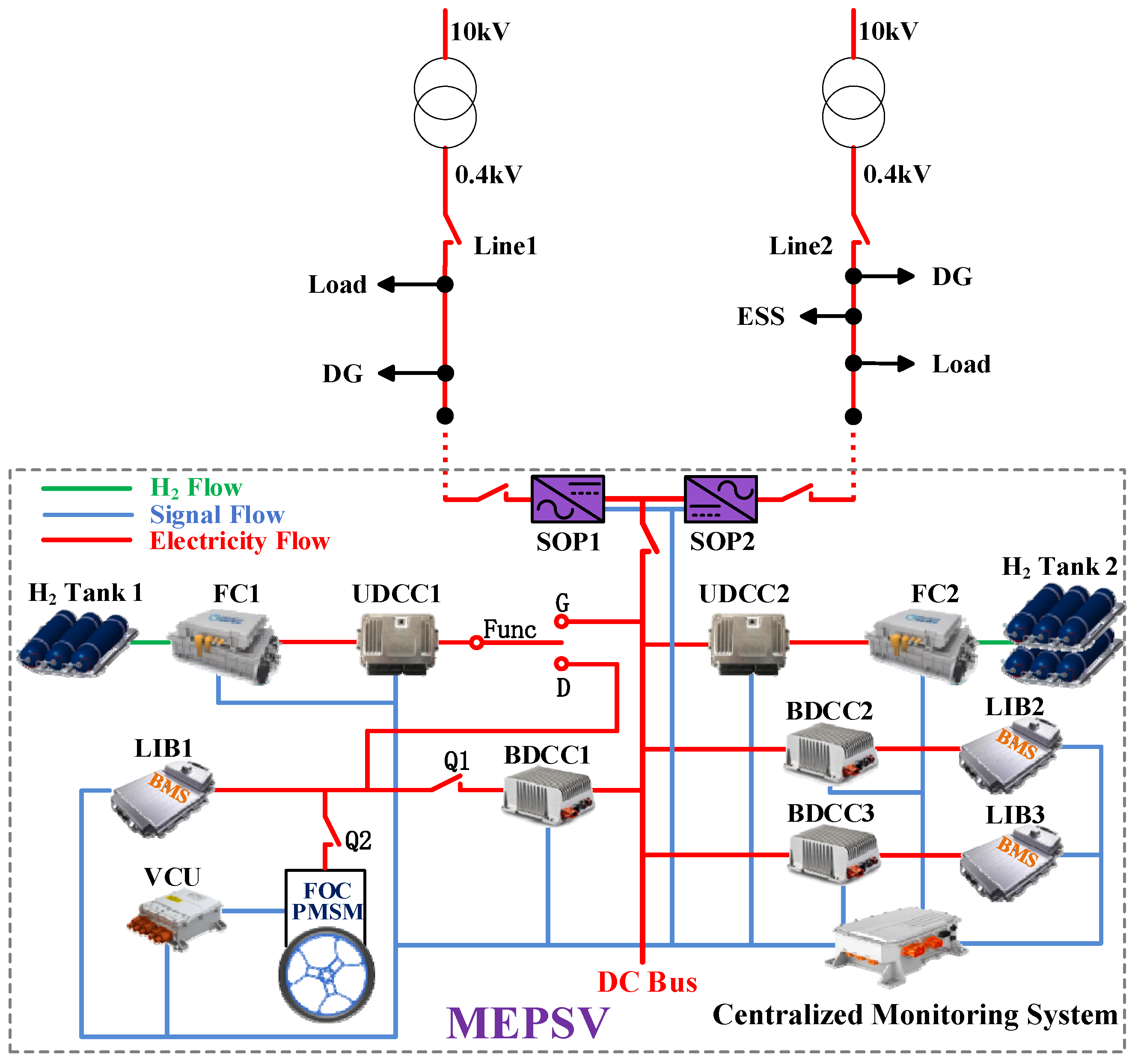
Since one set of hydrogen storage bottles can be refueled while the remaining two continue supplying power, the MEPSV sustains uninterrupted power generation over extended durations. The onboard SOP connects two 0.4 kV feeders (onboard 8-groove winch with 8 × 25 m wear-resistant flexible cables). It provides a conventional active power transmission mode as well as an operating mode. The SOP control powers in both modes and makes the interactive power sum zero. Then, power flow becomes flexible, improving equipment utilization.

From a power electronics perspective, MEPSV is a multi-input, multi-output DC microgrid system that requires advanced power conversion to manage energy flow and voltage levels. The components include DC-DC converters and a DC-AC inverter. Specifically, bidirectional DC-DC converters are essential for connecting the three LIB units to the common DC bus, enabling controlled charging/discharging and voltage matching, as the LIB’s voltage varies with its SOC. The FCS stack, with its inherently low and variable output voltage, is connected through a high-efficiency boost DC-DC converter to elevate its voltage to the DC bus level. Finally, a high-power DC-AC inverter is required at the output stage to convert the DC bus voltage into the required AC output voltage for emergency load supply or grid connection through SOP. The efficiency, stability, and control bandwidth of these converters are critical, as they directly impact the system’s overall fuel economy, dynamic response, and ECMS control [19]. The specification of FCS used in this study is presented in

Table 3. The steady-state characteristic data of FCS used in this study (from Guangdong Hongli Hydrogen Power Technology Co., Ltd.).

Test Number	Current (A)	Voltage (V)	Power (kW)	Total Power Consumption (kW)	Power Consumed by Auxiliary Components (kW)	Rate of H2 Consumption (g/min)	Efficiency of the Fuel Cell (FC) (%)	Efficiency of the FCS (%)
1	438.34	302.20	132.47	109.89	22.58	134.71	49.17	40.79
2	409.28	308.17	126.13	105.73	20.40	126.32	49.92	41.85
3	383.44	312.08	119.66	101.74	17.92	118.94	50.30	42.77
4	354.17	316.88	112.23	96.60	15.63	110.23	50.91	43.82
5	328.41	319.95	105.07	91.68	13.39	102.51	51.25	44.72
6	299.35	325.51	97.44	86.14	11.30	93.46	52.13	46.08
7	245.03	331.24	81.16	73.85	7.31	76.20	53.25	48.46
8	188.67	341.65	64.46	60.01	4.45	59.06	54.57	50.80
9	163.05	346.00	56.42	53.13	3.29	51.07	55.24	52.02
10	133.86	351.17	47.01	44.34	2.67	42.07	55.87	52.70
11	106.63	356.27	37.99	36.39	1.60	33.66	56.43	54.06
12	79.48	365.22	29.03	27.51	1.52	25.19	57.62	54.61
13	46.80	384.90	18.01	16.49	1.52	15.20	59.24	54.24

.

4. Operation of MEPSV

The developed MEPSV operates flexibly under six different driving conditions (

Table 4. Typical Operating Conditions.

Driving Condition	Func Switch Position	Q1	Q2	FCS1	FCS2	LIB1	LIB2	LIB3	SOP1	SOP2	Property
1	D	OFF	ON	ON	OFF	ON	OFF	OFF	OFF	OFF	Motion, SOCFCS1 > 10%
2	D	OFF	ON	OFF	OFF	ON	OFF	OFF	OFF	OFF	Motion, SOCFCS1 ≤ 10%, SOCLIB1 > 0.3
3	D	ON	ON	OFF	ON	ON	ON/ OFF	ON/ OFF	OFF	OFF	Motion, SOCFCS1 ≤ 10%, SOCLIB1 ≤ 0.3
4	G	ON	OFF	OFF	OFF	ON	ON	ON	OFF	OFF	Stop, LIB charge, hydrogen filling
5	G	ON	OFF	OFF	OFF	ON	ON	ON	ON/ OFF	ON/ OFF	Parking, improve power quality
6	G	ON	OFF	ON	ON	ON	ON	ON	ON/ OFF	ON/ OFF	Parking, emergency power supply

). The architecture of MEPSV is presented in Figure 2.

We set three driving conditions as follows.

• Driving Condition 1: 80 km/h, grade 0%, P₁ = 178.26 kW.
• Driving Condition 2: 10 km/h, grade 30%, P₂ = 179.76 kW.
• Driving Condition 3: P₃ ≈ 56.51 kW in China Heavy-Duty Commercial Vehicle Test Cycle—Heavy Truck (CHTC-HT) [20]
• Driving Condition 4–6: Stationary MEPSV

MEPSV is built upon a single-link DC-coupled hybrid architecture that employs three distinct bus categories to manage energy flow between power sources and loads. First, the central energy aggregation point is the high-voltage DC (HVDC) bus, clearly illustrated as the main horizontal line in Figure 2. This bus maintains a regulated voltage of 590 V and serves as the electrical backbone, linking the DC/DC outputs of all power sources to the input of the primary DC/AC inverter. Second, the system includes low-voltage DC (LVDC) buses, located at the terminals of the main power sources. The raw DC output from the FC1 and FC2 stacks qualifies as LVDC, with a variable voltage range of 265 V to 480 V. This output is conditioned by boost DC/DC converters before integration into the stable HVDC bus. The system incorporates an AC Bus located downstream of the main DC/AC inverter. Operating at a standard three-phase 400 V/50 Hz grid voltage, the AC bus connects to external emergency loads and enables power exchange with the grid through SOP. The SOP controller actively regulates voltage and frequency on the AC Bus to ensure high-quality power delivery to connected loads.

• Driving Conditions 1–3

These three driving conditions correspond to driving scenarios of the CHTC-HT cycle. In Driving Condition 1, the vehicle operates in a standard driving mode when the state of charge of Fuel Cell System 1 (SOC_FCS1), representing the remaining hydrogen capacity in hydrogen storage bottle set 1, exceeds 10% of its volume. FCS1 includes the hydrogen bottles, FC1, and UDCC1In this mode, switch “Func” is set to the driving position “D”, switch “Q2” is closed, and switch “Q1” is open. Fuel Cell 1 (FC1) is activated to generate power within the range of 265–480 V, which is then boosted through the unidirectional DC-DC converter (UDCC1) and connected in parallel with LIB1 to drive the permanent magnet synchronous motor (PMSM). The motor output is transmitted to the drive wheels through the vehicle’s transmission system.

The output from FCS1 is sufficient to support constant-speed driving. In vehicle start-up, uphill driving, acceleration, deceleration, and downhill movement, LIB1 compensates for rapid load variations. LIB1 supports a discharge rate of up to 3 C (a measure of the charge or discharge current relative to the battery’s nominal capacity), which is adequate to meet peak power demands. LIB1 is charged at 2C during braking, leading to efficient energy recovery. When hydrogen consumption increases and SOC_FCS1 falls below 10%, SOC_LIB1 remains above 0.3, and the MEPSV transitions to Driving Condition 2.

In this condition, FC1 is deactivated, and LIB1 solely supplies power. Under full hydrogen and battery charge, the combined driving range with FCS1 and LIB1 reaches 240 km. In exceptional cases where this range is exceeded and SOC_LIB1 drops to less than 0.3, the EMS enters Driving Condition 3. In this case, switch “Q1” is closed, and power is drawn from the 580 V DC bus via BDCC1 to drive the motor. The DC bus is powered by FCS2. In extreme scenarios, LIB2 and LIB3 are engaged to jointly supply power, extending the driving range to 450 km. When FCS and LIB systems operate concurrently, their power output must be optimally distributed, as outlined in Driving Condition 6.

2.

Driving Conditions 4

Driving Condition 4 pertains to stationary MEPSV for refueling and recharging. In this condition, switch “Func” is set to the generation position “G”, switch “Q1” is closed, and switch “Q2” is open. Fuel cells are turned off, and all hydrogen storage bottles are refueled to full capacity. The onboard charging port connects to an external charging station through the DC bus to recharge all three LIB units. Each LIB is embedded with a battery management system (BMS) to monitor voltage, current, and temperature and conduct charge/discharge operations, balance management, and safety protocols based on sensor data and commands from the centralized monitoring system. In Driving Condition 4, BMS autonomously manages the charging process and maintains SOC_LIB1 at 0.8 and SOC_LIB2 and SOC_LIB3 within the range of 0.5–0.8.

3.

Driving Conditions 5

In Driving Condition 5, the MEPSV functions as a solid-state power controller (SOPC) with energy storage. After parking, the MEPSV stabilizes itself using four hydraulic supports, and one or both SOP port cables are connected to the feeders of the power distribution network. Switch “Func” is set to generation position “G”, switch “Q1” is closed, and switch “Q2” is open. Fuel cells remain off. SOP, enhanced with energy storage and the Internet of Things connection, performs voltage monitoring with an online feeder, acting as an uninterruptible power supply (UPS). The fuel cells are remotely dispatched to balance loads across feeders and phases, provide reactive power compensation, and suppress voltage fluctuations.

For example, if Feeder 1 is heavily loaded while Feeder 2 is lightly loaded, SOP2 can be configured as a load for Feeder 2 and SOP1 as a source for Feeder 1, balancing inter-feeder loads. In cases of intra-feeder imbalance, such as FCS1 being significantly more loaded than FCS2, SOP1 can transfer current from FCS2 to FCS1 to balance the phase loads and stabilize the transformer-side output, thus preventing short-term load shedding.

To mitigate frequent charge/discharge cycles that accelerate battery aging and underutilize storage capacity, the LIB system is divided into three groups assigned to different states: charging, discharging, and standby. During charging, the SOC threshold is set at 0.8; during discharging, it is set at 0.2. When a battery unit reaches its threshold, the units are assigned to different states. In Driving Condition 5, no algorithmic optimization is required. The centralized monitoring system issues commands, and SOP and BMS execute the designated functions automatically.

4.

Driving Conditions 6

Driving Condition 6 is triggered when MEPSV, acting as a UPS, detects a sudden power outage in the connected feeder or is temporarily supplying power to a de-energized feeder. The vehicle remains parked with SOP port cables connected. Switch “Func” is set to generation position “G”, switch “Q1” is closed, and switch “Q2” is open. When all five onboard power sources operate simultaneously, the system delivers power of over 500 kW, sufficient to support full-load operation of both SOP ports.

Due to the limited response of fuel cells, the three LIB groups alternate states between charging, discharging, and standby, while each LIB handles peak shaving and valley filling. Once the load stabilizes, the centralized monitoring system calculates the optimal power distribution strategy, sends commands to the two FCS units, and uses LIBs to maintain DC bus voltage stability. Such coordinated control ensures balanced power delivery among the power sources and the connected load.

The LIB system is architecturally designed for longevity and reliability. This architecture is essential for implementing a flexible rule-based grouping strategy that manages SOC and mitigates accelerated aging. Such physical separation helps EMS dynamically assign each unit to charging, discharging, or standby states in the stationary operation (Driving Conditions 4–6). While the real-time operational rules are simplified based on SOC to maintain computational efficiency, this three-unit modularity enables more advanced, durability-oriented optimization. Such enhancements incorporate SOH, cumulative energy throughput, and temperature monitoring to manage the rotation schedule and ensure equitable usage across the fleet. In stationary operation under Driving Conditions 5 and 6, the function of LIBs is activated using a rule-based grouping strategy to meet the high power demand and safeguard the batteries from detrimental operation. The current strategy rotates LIB units (e.g., one discharging, one charging, one standby) based on pre-defined SOC thresholds (e.g., 0.2 and 0.8) to prevent deep discharge and overcharge, which are major contributors to capacity degradation. This rule-based approach leads to a real-time, lightweight application. Although effective in avoiding worst-case aging scenarios, the strategy contributes to multi-objective optimization, where durability metrics such as cumulative energy throughput and unit temperature are incorporated into the rotation logic to balance the SOH of the LIB units.

5. Multi-Source Control Strategy

When FCS and LIB operate cooperatively under specific power demand conditions, it is essential to establish an optimal power distribution strategy to minimize hydrogen consumption while prioritizing the extension of both systems’ service life.

The state of health (SOH) of FC is defined as the voltage drop rate (%) observed under rated current conditions. At the end of its operational life, a fuel cell exhibits a maximum permissible voltage drop of up to 10% below its rated output. Frequent start-stop cycles, frequent power fluctuations, extended idle periods, and sustained high-load operation accelerate SOH degradation. Although the two fuel cells of the MPESV developed have identical specifications, they diverge in degradation profiles over time. To prolong system longevity, the fuel cell with the higher SOH needs to be used first, thereby mitigating accelerated wear on the more degraded unit.

The integration of LIBs further mitigates such wear. System longevity can also be extended using a grouping strategy in which three LIB units alternate between charging, discharging, and standby modes.

The rule-based ECMS employed in this study fosters the operational health of FCS and LIB. Therefore, in the rule-based ECMS, the optimization of hydrogen consumption is required, which is defined as Equations (2)–(4).

$$C_{\mathit{total}}=C_{\mathit{FCS}1}\left(P_{\mathit{FCS}1}\right)+C_{\mathit{FCS}2}\left(P_{\mathit{FCS}2}\right)+\alpha \cdot C_{\mathit{LIB}}\left(P_{\mathit{LIB}}\right)$$

(2)

where $C_{\mathit{total}}$ is the sum of the equivalent hydrogen consumption rates (hydrogen consumption at sampling) of FCS1, FCS2, and LIB, $C_{\mathit{FCS}1}$ is the hydrogen consumption rate of FCS1, $C_{\mathit{FCS}2}$ is the hydrogen consumption rate of FCS2, $C_{\mathit{LIB}}$ is the equivalent hydrogen consumption rate of LIB, and $\alpha$ is a penalty coefficient.

$$P_{\mathit{Load}}=P_{\mathit{FCS}1}+P_{\mathit{FCS}2}+P_{\mathit{LIB}}$$

(3)

where $P_{\mathit{Load}}$ is the load power at the current sampling instant, $P_{\mathit{FCS}1} \mathrm{a}\mathrm{n}\mathrm{d} P_{\mathit{FCS}2}$ are the net output power of FCS1 and FCS2 at the current sampling instant, and $P_{\mathit{LIB}}$ is the discharge power of the LIB at the current sampling instant.

$$\left\{\begin{array}{c}{P}_{\mathit{FCS}1, \mathit{min}}\le P_{\mathit{FCS}1}\le P_{\mathit{FCS}1, \mathit{max}}\hfill \\ P_{\mathit{FCS}2, \mathit{min}}\le P_{\mathit{FCS}2}\le P_{\mathit{FCS}2, \mathit{max}}\\ \Delta P_{\mathit{down}}\le P_{\mathit{FCS}1}-P_{\mathit{FCS}1\_\mathit{Pre}}\le \Delta P_{\mathit{up}} \\ \Delta P_{\mathit{down}}\le P_{\mathit{FCS}2}-P_{\mathit{FCS}2\_\mathit{Pre}}\le \Delta P_{\mathit{up}}\end{array}\right.$$

(4)

where $P_{\mathit{FCS}1, \mathit{min}},P_{\mathit{FCS}2, \mathit{min}},P_{\mathit{FCS}1, \mathit{max}},{ \mathrm{a}\mathrm{n}\mathrm{d} P}_{\mathit{FCS}2, \mathit{max}}$ are the minimum and maximum load powers at the current sampling instant FCS1 and FCS2, respectively. $P_{\mathit{FCS}1\_\mathit{Pre}} \mathrm{a}\mathrm{n}\mathrm{d} P_{\mathit{FCS}2\_\mathit{Pre}}$ are the net output power of FCS1 and FCS2 at sampling, $\Delta P_{\mathit{up}}$ is the maximum allowed increase in net output power for the FCS within one sampling interval, and $\Delta P_{\mathit{down}}$ is the maximum allowed decrease in net output power for the FCS within one sampling interval.

The penalty coefficient $\alpha$ presents the additional hydrogen consumption rate caused by LIB charge/discharge losses. It is a function of SOC (Equation (5)).

$$\alpha =1-2\mu {\displaystyle \frac{SOC-0.5\left(SO{C}_{max}+SO{C}_{min}\right)}{SO{C}_{max}-SO{C}_{min}}}$$

(5)

where $\mu$ is the SOC balance coefficient of LIB, taken as 0.6 in this study, $SO{C}_{max}$ is the upper working threshold for LIB, taken as 0.8, and $SO{C}_{min}$ is the lower working threshold for LIB, taken as 0.2.

Simplifying the calculation of the penalty coefficient $\alpha$, the objective function transforms into Equation (6).

$$C_{\mathit{total}}=C_{\mathit{FCS}1}\left(P_{\mathit{FCS}1}\right)+C_{\mathit{FCS}2}\left(P_{\mathit{FCS}2}\right)+\left(2-2SOC\right)\cdot C_{\mathit{LIB}}\left(P_{\mathit{LIB}}\right)$$

(6)

The objective function and its constraints require two real-time data points: SOC obtained in real-time from the system as an average of the SOC in charging and discharging LIB units, and the load power $P_{\mathit{Load}}$ at the current sampling instant. There are three decision variables, $P_{\mathit{FCS}1},P_{\mathit{FCS}2},{ \mathrm{a}\mathrm{n}\mathrm{d} P}_{\mathit{LIB}}$, which minimizes $C_{\mathit{total}}$.

To solve the optimization problem, the FCS degradation calculation model was established based on the relationship curve of the full lifecycle of $P_{\mathit{FCS}}-{\eta }_{\mathit{FCS}}-C_{\mathit{FCS}}$ which was obtained from experimental data provided by the FCS manufacturer. That is, the $P_{\mathit{FCS}}-C_{\mathit{FCS}}$ relationship curve varies with SOH. Second, the LIB-equivalent hydrogen consumption rate calculation model was constructed based on the simplified Rint model of the LIB, that is, the $P_{\mathit{LIB}}-C_{\mathit{LIB}}$ relationship curve. Finally, the optimal solution was determined for the objective function.

5.1. FCS Degradation Calculation Model

The efficiency of FCS is determined using Equation (7) [21,22].

$${\eta }_{\mathit{FCS}}={\eta }_{\mathit{fuel}}\cdot {\eta }_{\mathit{FC}}\cdot {\eta }_{\mathit{elec}}$$

(7)

where ${\eta }_{\mathit{fuel}}$ is the hydrogen fuel utilization rate, approximately 1, due to the equipped hydrogen recirculation system, ${\eta }_{\mathit{FC}}$ is the FC conversion efficiency, defined as the ratio between the electrical energy generated by the FC and the chemical energy of the hydrogen consumed by the FC, and ${\eta }_{\mathit{elec}}$ is the electrical efficiency, determined by the UDCC efficiency and the power of various auxiliary machines.

From Equation (7), the degraded efficiency of the FCS is calculated as follows.

$${\eta }_{\mathit{FCS}\_d}={\eta }_{\mathit{FC}\_d}\cdot {\eta }_{\mathit{elec}\_d}$$

(8)

where ${\eta }_{\mathit{FCS}\_d},{\eta }_{\mathit{FC}\_d}, \mathrm{a}\mathrm{n}\mathrm{d} {\eta }_{\mathit{elec}\_d}$ denotes the FCS efficiency, FC conversion efficiency, and electrical efficiency after performance degradation, respectively.

The simplified calculation of FC conversion efficiency is conducted using Equation (9).

$${\eta }_{\mathit{FC}}={\displaystyle \frac{E_{\mathit{FC}}}{E_{H_2\_\mathit{consumed}}}}={\displaystyle \frac{V_{\mathit{mean}}}{1.254}}$$

(9)

where $E_{\mathit{FC}}$ is the electrical energy output by the FC, $E_{H_2\_\mathit{consumed}}$ is the chemical energy produced by the hydrogen consumed by the FC, $V_{\mathit{mean}}$ is the average single-cell FC voltage. 1.254 V is the theoretical equivalent voltage corresponding to the Lower Heating Value (LHV) of hydrogen.

${\eta }_{\mathit{FC}}$ decreases as FCS performance degrades, and its degree of reduction is estimated by using the degradation coefficient ${\xi }_{\mathit{FC}\_d}$ from Equation (10).

$${\xi }_{\mathit{FC}\_d}={\displaystyle \frac{{\eta }_{\mathit{FC}\_d}}{{\eta }_{\mathit{FC}}}}={\displaystyle \frac{V_{\mathit{mean}\_d}}{V_{\mathit{mean}}}}=0.9+0.1\times SOH$$

(10)

The electrical efficiency is calculated using Equation (11).

$${\eta }_{\mathit{elec}}={\displaystyle \frac{E_{\mathit{FCS}}}{E_{\mathit{FC}}}}={\displaystyle \frac{E_{\mathit{FC}}\cdot {\eta }_{\mathit{UDCC}}-E_{\mathit{aux}}}{E_{\mathit{FC}}}}={\eta }_{\mathit{UDCC}}-{\displaystyle \frac{E_{\mathit{aux}}}{E_{\mathit{FC}}}}$$

(11)

where $E_{\mathit{FCS}}$ is the net output energy of the FCS, $E_{\mathit{aux}}$ is the energy consumed by auxiliaries, and ${\eta }_{\mathit{UDCC}}$ is the UDCC conversion efficiency.

From Equations (7) and (11), the following relationship is derived.

$${\epsilon }_{\mathit{aux}\_\mathit{FC}}={\displaystyle \frac{E_{\mathit{aux}}}{E_{\mathit{FC}}}}={\eta }_{\mathit{UDCC}}-{\eta }_{\mathit{elec}}={\eta }_{\mathit{UDCC}}-{\displaystyle \frac{{\eta }_{\mathit{FCS}}}{{\eta }_{\mathit{FC}}}}$$

(12)

where ${\epsilon }_{\mathit{aux}\_\mathit{FC}}$ is the percentage of auxiliary energy consumption relative to FC power generation; ${\eta }_{\mathit{UDCC}}$ is 97%.

Based on the relationship curves of $P_{\mathit{FCS}}-{\eta }_{\mathit{FCS}}$ and $P_{\mathit{FCS}}-{\eta }_{\mathit{FC}}$ provided by the manufacturer, the $P_{\mathit{FCS}}-{\epsilon }_{\mathit{aux}\_\mathit{FC}}$ relationship curve is drasn using Equation (12).

The electrical efficiency ${\eta }_{\mathit{elec}\_d}$ after fuel cell performance degradation is derived from Equation (11) as follows.

$${\eta }_{\mathit{elec}\_d}={\eta }_{\mathit{UDCC}}-{\displaystyle \frac{E_{\mathit{aux}\_d}}{E_{\mathit{FC}\_d}}}={\eta }_{\mathit{UDCC}}-{\displaystyle \frac{E_{\mathit{aux}}}{{\xi }_{\mathit{FC}\_d}^2{E}_{\mathit{FC}}}}={\eta }_{\mathit{UDCC}}-{\displaystyle \frac{{\epsilon }_{\mathit{aux}\_\mathit{FC}}}{{\xi }_{\mathit{FC}\_d}^2}}$$

(13)

where $E_{\mathit{aux}\_d}$ is the energy consumed by auxiliaries after performance degradation, and $E_{\mathit{FC}\_d}$ is the electrical energy output by the FC after performance degradation.

The performance of UDCC is considered non-degrading throughout the lifecycle in the calculation. Therefore, the degraded efficiency of the FCS is determined as Equation (14) based on Equations (8), (10) and (13).

$${\eta }_{\mathit{FCS}\_d}={\eta }_{\mathit{FC}\_d}\cdot {\eta }_{\mathit{elec}\_d}={\xi }_{\mathit{FC}\_d}\cdot {\eta }_{\mathit{FC}}\cdot {\eta }_{\mathit{elec}\_d}={\xi }_{\mathit{FC}\_d}\cdot {\eta }_{\mathit{FC}}\cdot ({\eta }_{\mathit{UDCC}}-{\displaystyle \frac{{\epsilon }_{\mathit{aux}\_\mathit{FC}}}{{\xi }_{\mathit{FC}\_d}^2}})$$

(14)

Since ${\xi }_{\mathit{FC}\_d}$ and ${\xi }_{\mathit{FC}\_d}^2$ are approximately equal, the degraded efficiency of FCS is further simplified based on Equations (7)–(14) as follows.

$$\begin{array}{cc}\hfill {\eta }_{\mathit{FCS}\_d}& ={\xi }_{\mathit{FC}\_d}\cdot {\eta }_{\mathit{UDCC}}\cdot {\eta }_{\mathit{FC}}+{\eta }_{\mathit{FCS}}-{\eta }_{\mathit{UDCC}}\cdot {\eta }_{\mathit{FC}}\hfill \\ & ={\eta }_{\mathit{FCS}}-\left(1-{\xi }_{\mathit{FC}\_d}\right)\cdot {\eta }_{\mathit{UDCC}}\cdot {\eta }_{\mathit{FC}}\hfill \\ & ={\eta }_{\mathit{FCS}}-0.1\times \left(1-SOH\right)\cdot {\eta }_{\mathit{UDCC}}\cdot {\eta }_{\mathit{FC}}\hfill \end{array}$$

(15)

The hydrogen consumption rate of FCS is related to the net output power and the degradation efficiency, so is defined as follows.

$$C_{\mathit{FCS}}={\displaystyle \frac{P_{\mathit{FCS}}}{\mathit{LHV}\cdot {\eta }_{\mathit{FCS}\_d}}}={\displaystyle \frac{P_{\mathit{FCS}}}{{\eta }_{\mathit{FCS}\_d}}}\times 0.00834$$

(16)

where the unit of $C_{\mathit{FCS}}$ is g/s, LHV denotes the lower heating value of hydrogen, taken as 119.9 MJ/kg, and the unit of $P_{\mathit{FCS}}$ is kW.

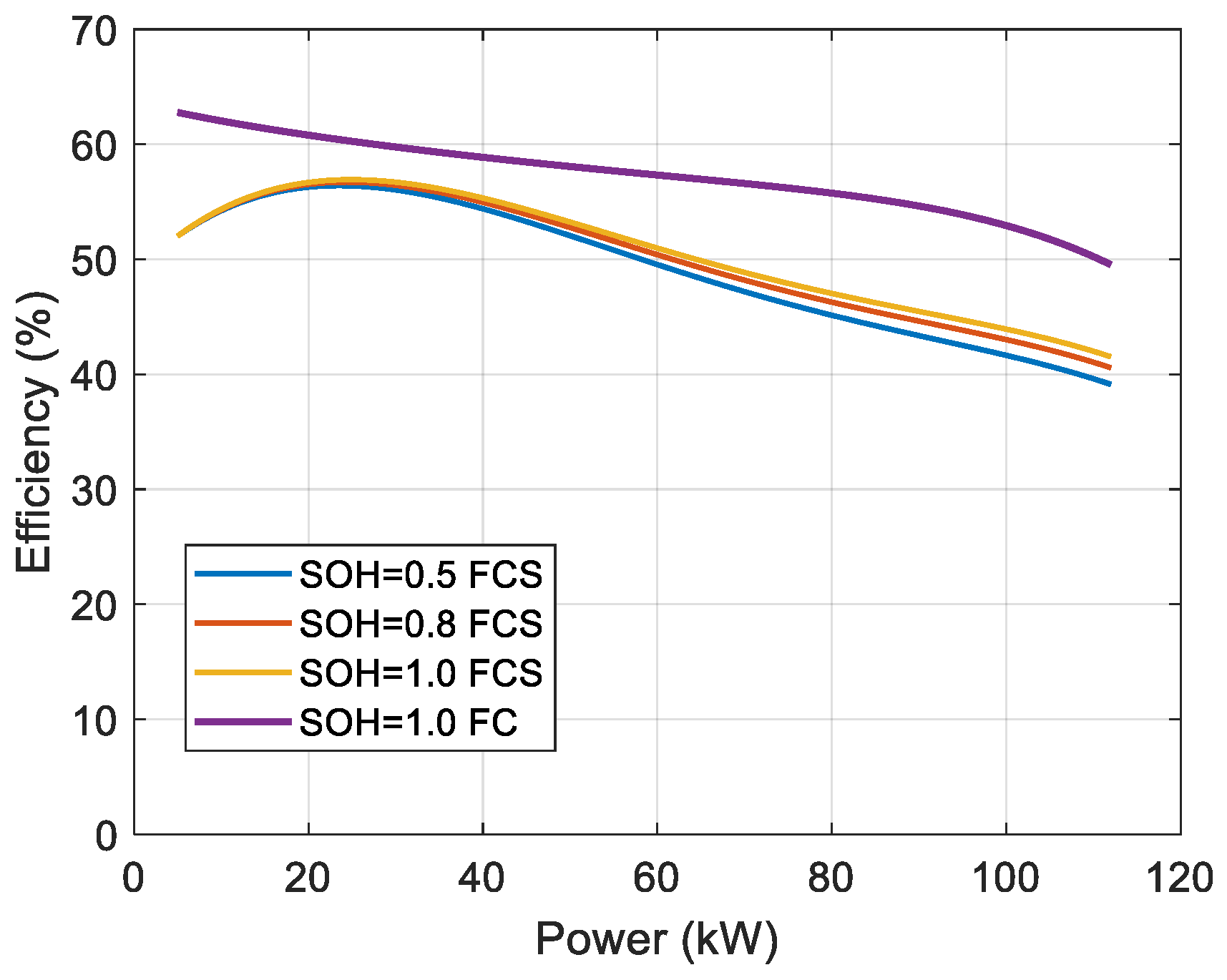
Based on the $P_{\mathit{FCS}}-{\eta }_{\mathit{FCS}}$ and $P_{\mathit{FCS}}-{\eta }_{\mathit{FC}}$ relationship curves, the FCS degradation calculation model that varies with SOH is obtained from Equations (15) and (16) (Figure 3 and Figure 4). The figures present the $P_{\mathit{FCS}}-{\eta }_{\mathit{FCS}\_d}$ curves and $P_{\mathit{FCS}}-C_{\mathit{FCS}}$ curves for SOH values of 0.5, 0.8, and 1.0, respectively.

5.2. LIB-Equivalent Hydrogen Consumption Rate

When the entire system operates in power generation mode, the electrical energy in LIB is generated by FCS, which consumes hydrogen. When the system load is lower than the power output of FCS, the surplus energy is used to charge LIB. Conversely, when the FCS output is insufficient to meet the load demand, the LIB discharges to compensate for the deficit. In calculating total hydrogen consumption, energy used to charge LIB is subtracted, as it represents stored energy for future use. In contrast, energy discharged from LIB to support the load is included in the total hydrogen consumption. The energy loss incurred during a complete LIB charge–discharge cycle is defined as the LIB’s equivalent hydrogen consumption.

Therefore, the electrical energy used for LIB charging is treated as negative hydrogen consumption, while LIB discharging is considered positive hydrogen consumption. The hydrogen consumption rate and corresponding power are estimated only at data sampling. During LIB charging, the hydrogen consumption rate associated with the LIB’s future power output is converted into an equivalent hydrogen consumption rate, which shows a negative value as shown in Equation (17).

$$C_{\mathrm{LIB}}={\displaystyle \frac{2\left(P_{\mathrm{LIB}}{\eta }_{\mathit{charge}}{\eta }_{\mathit{discharge}, \mathit{avg}}\right)}{P_{\mathit{FCS}1, \mathit{avg}}+P_{\mathit{FCS}2, \mathit{avg}}}}\cdot {\displaystyle \frac{C_{\mathit{FCS}1, \mathit{avg}}+C_{\mathit{FCS}2, \mathit{avg}}}{2}}$$

(17)

When $P_{\mathrm{LIB}}<0$,

$$\sigma ={\eta }_{\mathit{discharge}, \mathit{avg}}{\eta }_{\mathit{charge}}$$

(18)

From Equation (16), the following is derived.

$${\displaystyle \frac{C_{\mathit{FCS}1, \mathit{avg}}+C_{\mathit{FCS}2, \mathit{avg}}}{P_{\mathit{FCS}1, \mathit{avg}}+P_{\mathit{FCS}2, \mathit{avg}}}}={\displaystyle \frac{1}{\mathit{LHV}\cdot {\eta }_{\mathit{MulFCS}, \mathit{avg}}}}$$

(19)

From Equations (17)–(19), we derived Equation (20) to estimate the equivalent hydrogen consumption rate during LIB charging.

$$C_{\mathrm{LIB}}={\displaystyle \frac{P_{\mathrm{LIB}}\cdot \sigma }{\mathit{LHV}\cdot {\eta }_{\mathit{MulFCS}, \mathit{avg}}}}$$

(20)

In the equations, ${\eta }_{\mathit{discharge}, \mathit{avg}}$ denotes the average efficiency during LIB discharge, $C_{\mathit{FCS}, \mathit{avg}}$ denotes the average hydrogen consumption rate of FCS power generation, $P_{\mathit{FCS}, \mathit{avg}}$ denotes the average FCS power generation, and ${\eta }_{\mathit{MulFCS}, \mathit{avg}}$ denotes the average efficiency of the multi-fuel cell system.

When the LIB discharges, its output power is translated into an equivalent hydrogen consumption rate, corresponding to the power that otherwise, is generated by the fuel cell system (FCS). This equivalent hydrogen consumption rate for LIB discharge is treated as a positive value.

$$C_{\mathrm{LIB}}={\displaystyle \frac{\frac{P_{\mathrm{LIB}}}{{\eta }_{\mathit{discharge}}\cdot {\eta }_{\mathit{charge}, \mathit{avg}}}}{\frac{P_{\mathit{FCS}1, \mathit{avg}}+P_{\mathit{FCS}2, \mathit{avg}}}{2}}}\cdot {\displaystyle \frac{C_{\mathit{FCS}1, \mathit{avg}}+C_{\mathit{FCS}2, \mathit{avg}}}{2}}$$

(21)

When $P_{\mathrm{LIB}}\ge 0$,

$$\sigma ={\displaystyle \frac{1}{{\eta }_{\mathit{discharge}}{\eta }_{\mathit{charge}, \mathit{avg}}}}$$

(22)

Based on Equations (19)–(22), the equivalent hydrogen consumption rate during LIB discharging is derived and presented in Equation (23).

$$C_{\mathrm{LIB}}={\displaystyle \frac{P_{\mathrm{LIB}}\cdot \sigma }{\mathit{LHV}\cdot {\eta }_{\mathit{MulFCS}, \mathit{avg}}}}$$

(23)

A combined equation for the equivalent hydrogen consumption rate during LIB charging and discharging is derived from Equations (18)–(23).

$$\left\{\begin{array}{c}{C}_{\mathrm{LIB}}={\displaystyle \frac{P_{\mathrm{LIB}}\cdot \sigma }{\mathit{LHV}\cdot {\eta }_{\mathit{MulFCS}, \mathit{avg}}}}\\ \sigma =\left\{\begin{array}{c}{\displaystyle \frac{1}{{\eta }_{\mathit{charge}, \mathit{avg}}{\eta }_{\mathit{discharge}}}}, P_{\mathrm{LIB}}\ge 0\\ {\eta }_{\mathit{discharge}, \mathit{avg}}{\eta }_{\mathit{charge}}, P_{\mathrm{LIB}}<0\end{array}\right.\end{array}\right.$$

(24)

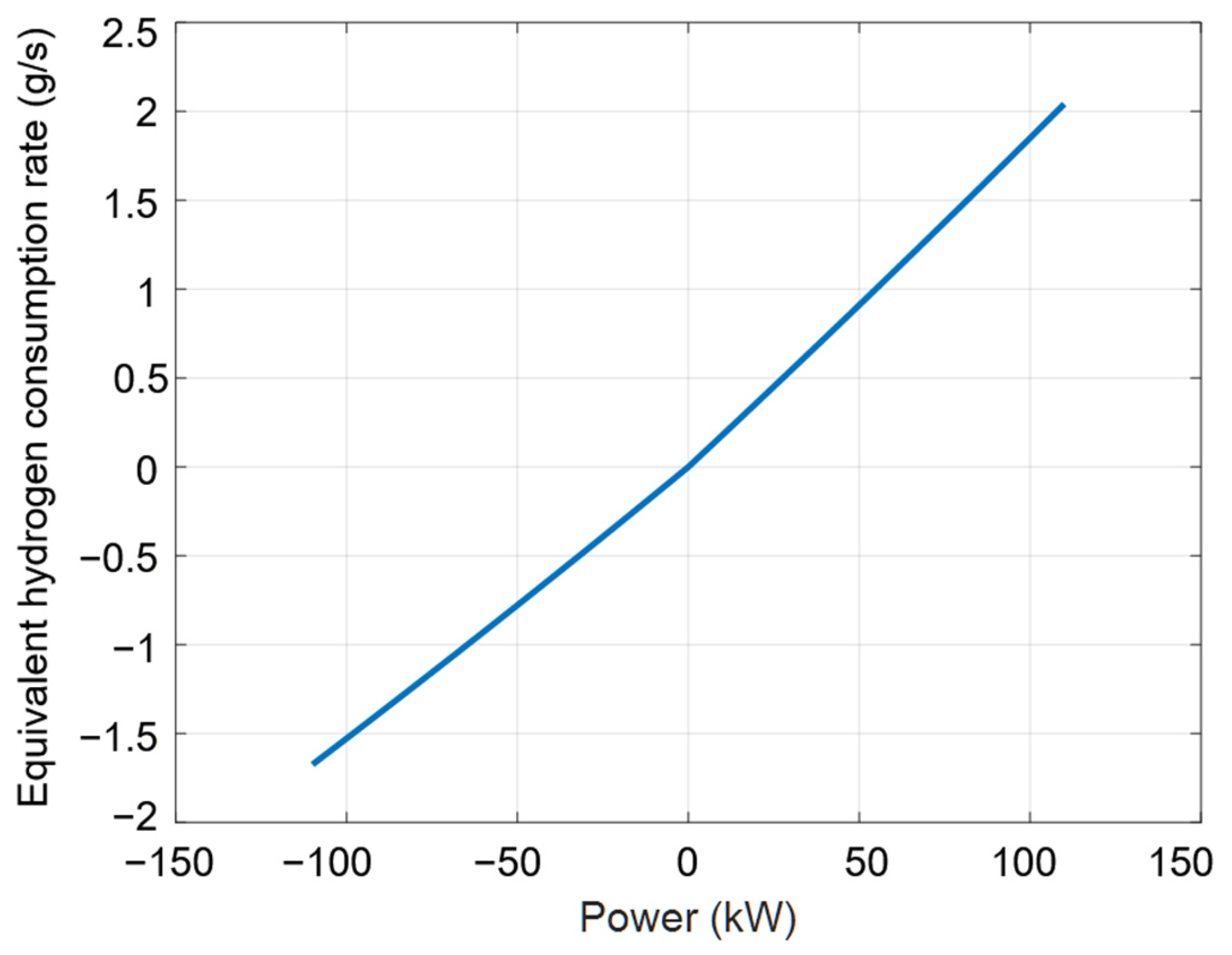
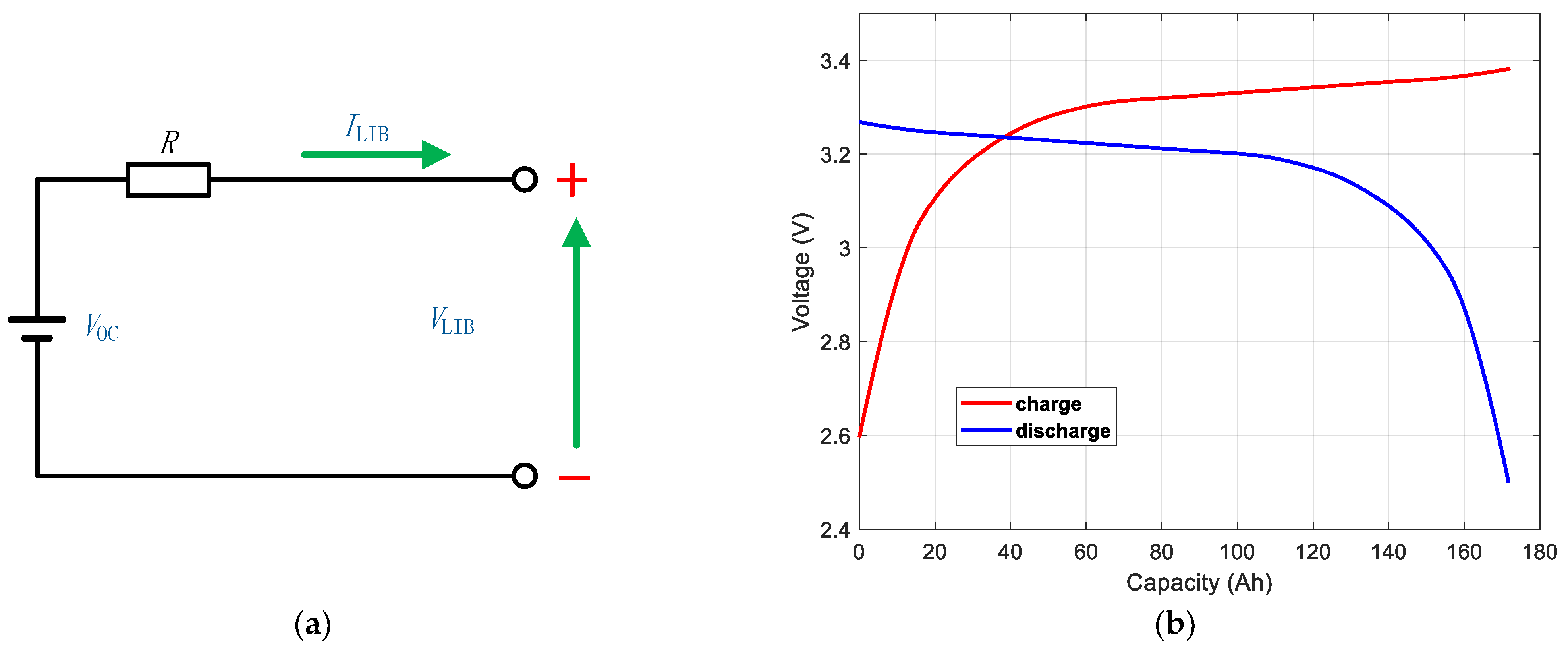
$C_{\mathrm{LIB}}$, the equivalent hydrogen consumption rate of the LIB, is determined by the corresponding charge/discharge power $P_{\mathrm{LIB}}$ and the associated charge/discharge efficiency. In this study, we used the Rint model (Figure 5) to derive the LIB charge/discharge efficiency calculation equation. Although the Rint model does not account for battery polarization and ignores dynamic processes, it offers a simplified structure with minimal computational overhead. Since the equivalent hydrogen consumption of the LIB reflects the energy loss during a complete charge–discharge cycle and represents a relatively small fraction of the total energy exchange, the Rint model yields results that closely approximate those obtained from more sophisticated models, such as the first-order or second-order resistance-capacitance (RC) models.

According to the battery Rint model 5, we determined the following relationship.

$$\left\{\begin{array}{c}{V}_{\mathrm{LIB}}=V_{\mathit{OC}}-I_{\mathrm{LIB}}R\\ P_{\mathrm{LIB}}=V_{\mathrm{LIB}}{I}_{\mathrm{LIB}}\\ R=\left\{\begin{array}{c}{R}_{\mathit{discharge}}\\ R_{\mathit{charge}}\end{array}\right.\hspace{1em}\hspace{1em}\hspace{1em}\begin{array}{c}{P}_{\mathrm{LIB}}\ge 0\\ P_{\mathrm{LIB}}<0\end{array}\\ {\eta }_{\mathit{discharge}}={\displaystyle \frac{V_{\mathrm{LIB}}}{V_{\mathit{OC}}}}\\ {\eta }_{\mathit{charge}}={\displaystyle \frac{V_{\mathit{OC}}}{V_{\mathrm{LIB}}}}\end{array}\right.$$

(25)

where $V_{\mathrm{LIB}}$ is the terminal voltage of a single LIB cell, $V_{\mathit{OC}}$ is the open-circuit voltage of a single LIB cell, $I_{\mathrm{LIB}}$ is the LIB cell current, $R_{\mathit{charge}}$ is the internal resistance of a single LIB cell during charging, and $R_{\mathit{discharge}}$ is the internal resistance of a single LIB cell during discharging.

From Equation (25), we finally formulated the following equation.

$$\begin{gathered} I_{\mathrm{LIB}}={\displaystyle \frac{V_{\mathit{OC}}-\sqrt{V_{\mathit{OC}}^2-4R{P}_{\mathrm{LIB}}}}{2R}} \\ \left\{\begin{array}{c}{\eta }_{\mathit{discharge}}={\displaystyle \frac{1+\sqrt{1-\frac{4R_{\mathit{discharge}}{P}_{\mathrm{LIB}}}{V_{\mathit{OC}}^2}}}{2}}, P_{\mathrm{LIB}}\ge 0\\ \\ {\eta }_{\mathit{charge}}={\displaystyle \frac{2}{1+\sqrt{1-\frac{4R_{\mathit{charge}}{P}_{\mathrm{LIB}}}{V_{\mathit{OC}}^2}}}}{, P}_{\mathrm{LIB}}<0\end{array}\right. \end{gathered}$$

(26)

Using Equations (24)–(26) and incorporating the following manufacturer-provided parameters, the equivalent hydrogen consumption rate $C_{\mathrm{LIB}}$ is computed as a function of P_LIB: ${\eta }_{\mathit{MulFCS}, \mathit{avg}}$ as 50%, ${\eta }_{\mathit{charge}, \mathit{avg}}$ as 93%, ${\eta }_{\mathit{discharge}, \mathit{avg}}$ as 95%, and a constant $V_{\mathit{OC}}$ in the SOC plateau region (3.22 V). $R_{\mathit{discharge}}$ is taken as 0.3 mΩ, and the charging internal resistance is assumed to be 20% higher, consistent with the typical 15–30% range observed in lithium iron phosphate batteries (Figure 6).

5.3. ECMS Simulation

In the ECMS used in this study, the objective function employs the FCS hydrogen consumption rate and the LIB equivalent hydrogen consumption rate. To reduce the computational load of the optimization algorithm and facilitate the real-time control system feedback, the FCS hydrogen consumption rate $P_{\mathit{FCS}}-C_{\mathit{FCS}}$ degradation and the LIB equivalent hydrogen consumption rate $P_{\mathrm{LIB}}-C_{\mathrm{LIB}}$ curves are fitted using fifth-order polynomial approximations.

In the objective function defined by Equations (3), (4) and (6), SOC and $P_{\mathit{Load}}$ are sampled from the system at one-second intervals. SOH is updated by sampling the fuel cell voltage each time the cell reaches its rated current output, enabling dynamic updates of the $P_{\mathit{FCS}}-C_{\mathit{FCS}}$ degradation curve. To prevent FCS from operating in low-efficiency regions and reduce drastic power fluctuations of FCs, Equation (4) is used to set boundary constraints on the FCS output power range and the maximum permissible ramp rates for loading and unloading. These constraints are used in the power allocation process to obtain optimal solutions. Additionally, the control strategy is employed to enforce SOC boundaries for LIB in the range of 0.2 to 0.8 to prevent overcharging and over-discharging. If SOC exceeds these limits, the battery operating mode is adjusted accordingly.

The objective function is formulated as the sum of fifth-order polynomials concerning a smooth, nonlinear, and non-convex function, with equality and boundary constraints. The sequential quadratic programming (SQP) algorithm is used to optimize the objective function and minimize $C_{\mathit{total}}$, with $P_{\mathit{FCS}1},P_{\mathit{FCS}2},{ \mathrm{a}\mathrm{n}\mathrm{d} P}_{\mathrm{LIB}}$ (decision variables), and constraints given by Equations (3) and (4). The SQP algorithm is recognized for its effectiveness in solving constrained nonlinear problems, particularly in small to medium-scale systems.

In the simulation, $P_{\mathit{FCS}1, \mathit{min}}$ and $P_{\mathit{FCS}2, \mathit{min}}$ were set to 5 kW, $P_{\mathit{FCS}1, \mathit{max}}$ and $P_{\mathit{FCS}2, \mathit{max}}$ to 110 kW, $\Delta P_{\mathit{up}}$ to 5.5 kW/s, and $\Delta P_{\mathit{down}}$ to −10.5 kW/s. The initial SOC of the three LIB units was assumed to be 0.5, while the SOH of FCS1 and FCS2 were set to 0.5 and 0.8, and the state maintenance judgment duration $T_{\mathit{keep}}$ was set to 5 s.

To validate the control strategy’s ability to allocate power according to predefined rules under varying load conditions, the MEPSV developed in this study was operated under four states.

• Idle state: Load power was 0 kW, while all power sources were shut down.
• Low load state: Load remained below than $P_{\mathit{FCS}, \mathit{min}}$ for longer than $T_{\mathit{keep}}$; only the LIB operated, and both FCSs were shut down.
• Moderate load state: Load was between $P_{\mathit{FCS}, \mathit{min}}$ and 2$P_{\mathit{FCS}, \mathit{min}}$ for longer than $T_{\mathit{keep}}$, the LIB, and the healthier FCS2 with higher SOH were operated, while FCS1 was shut down.
• Load exceeded 2$P_{\mathit{FCS}, \mathit{min}}$ for longer than $T_{\mathit{keep}}$, and FCS1, FCS2, and LIB were activated
• The manually defined load profile for the test was as follows: 0 kW for 8 s, 4 kW for 7 s, 8 kW for 10 s, 4 kW for 3 s, 7 kW for 3 s, 14 kW for 3 s, 16 kW for 3 s, followed by a drop to 3 kW for 9 s, and finally 0 kW for the remaining duration. The total simulation time was 60 s.

When the load power was 0 kW, LIB continuously output approximately 1 kW despite losses incurred by various converter components. When the load power stabilized at 4 kW, it was fully supplied by LIB. At 17 s, the load increased to 8 kW, exceeding the minimum output threshold of FCS. After this condition persisted for 5 s, the system initiated FCS. Since FCS2 exhibited a higher SOH than FCS1, FCS2 was activated. Its output power increased at the maximum permitted ramp-up rate of 5.5 kW/s. Subsequently, LIB transitioned to a charging state until FCS2’s output reached 29 kW, where it was stabilized. This coincided with the optimization result obtained from the ECMS algorithm, which predicted that the combined equivalent hydrogen consumption rates of FCS2 and the LIB were minimized at this operating point. Thereafter, FCS2 maintained stable output with minimal variation despite load fluctuations. During the rapid load drop between 28 and 31 s, FCS2’s operating state did not significantly change. At 36 s, the load exceeded 10 kW. After 5 s, FCS1 was activated to enable parallel power supply. FCS1’s output increased rapidly at the maximum allowed rate of 5.5 kW/s. Although the load decreased rapidly below 5 kW at 43 s, the power allocation among FCS1, FCS2, and LIB remained optimal, being dynamically adjusted according to the load demand. At 48 s, FCS was shut down, and only LIB supplied power. Consequently, FCS1 and FCS2 reduced their output at the maximum permitted unloading rate of 10.5 kW/s. The simulation results in Figure 7 confirmed that the load distribution and system response aligned with predicted results.

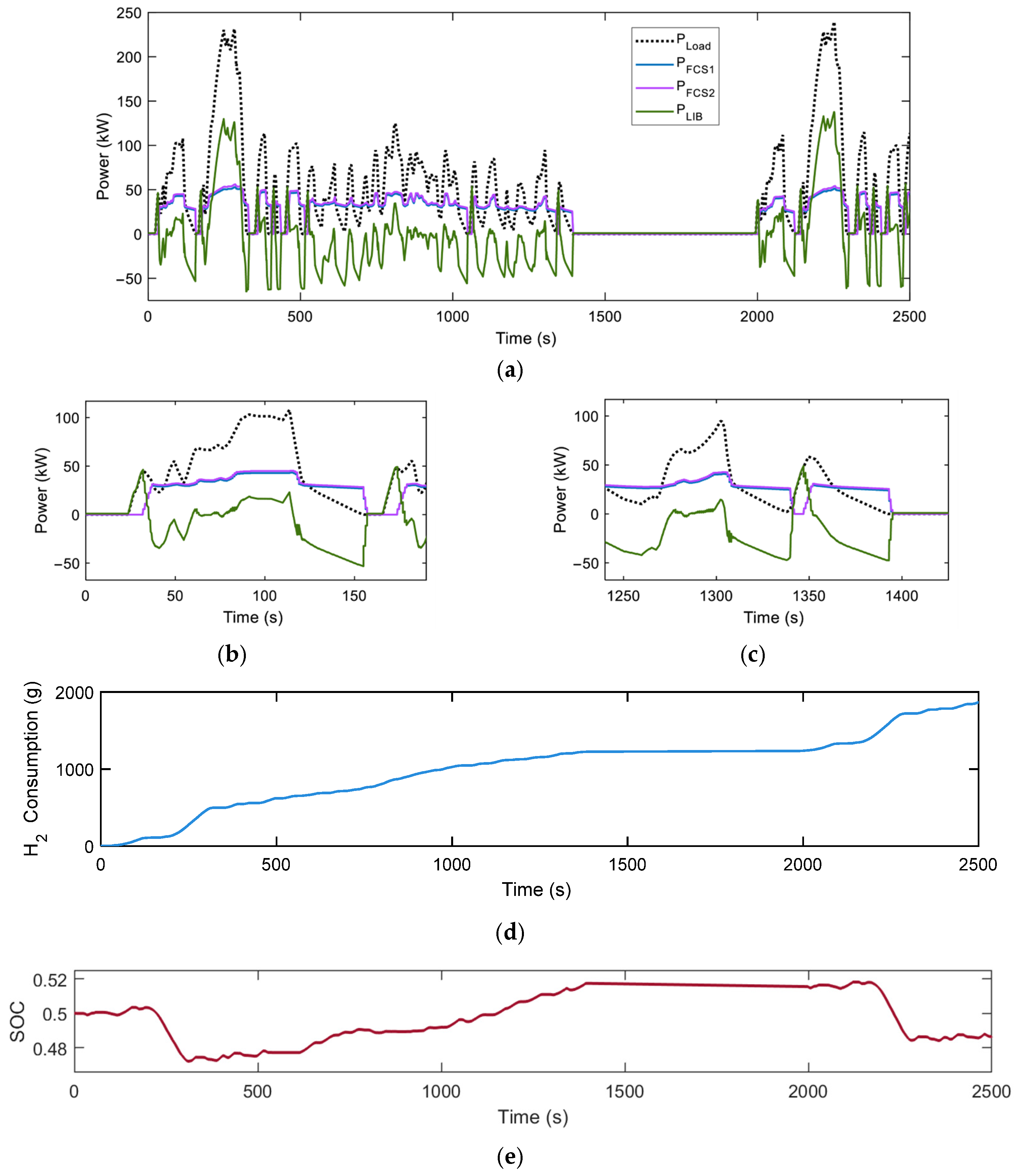
In a subsequent simulation, the power allocation and dynamic response of each power source were evaluated under complex, high-power load variations. Based on the operational characteristics of the MEPSV developed, a 2500-s load profile was extracted from the CHTC-HT driving cycle for heavy-duty trucks. This profile was adjusted in scale so that the peak load approached 250 kW and was applied as the electrical load for the simulation (Figure 8).

When the load power exceeded 200 kW, FCS1 and FCS2 contributed approximately 50 kW each, with the remaining demand supplied by LIB. The FCS efficiency was high in the 10–50 kW output range (Figure 3). Figure 8e indicates that the LIB’s SOC was increased during this period. Due to the influence of the penalty factor estimated from the penalty coefficient in Equation (6), LIB served as the primary power source to minimize hydrogen consumption.

Figure 8b,c presents the enlarged segments of the power allocation simulation results. Despite significant fluctuations in load power, LIB performed peak shaving and valley filling, resulting in stable output from both fuel cells and contributing to extending FCS service life. In the large power scale, the outputs of FCS1 and FCS2 overlapped; however, the difference exceeded 2 kW, consistent with their respective SOH values, indicating they could supply more power.

Both fuel cells automatically shut down after the load was not exerted for the specified duration. The total hydrogen consumption throughout the simulation was approximately 2 kg. Overall, the load distribution results and system response were consistent with expected performance.

5.4. Testing Results

To evaluate the effectiveness of the rule-based multi-source system cooperative control ECMS developed in this study, a test was conducted under Driving Condition 6. We utilized a 380 V/250 kW programmable RLC load bank in the test. The SOC of LIBs was initialized to 0.5, and FCS was assumed to be in a new condition, with a SOH of 1. Scaled 2500-s load data obtained from the CHTC-HT driving cycle was used in the test. The hydrogen consumption rate was measured and compared with the simulation results (Figure 8d and Figure 9).

The simulation results obtained using ECMS agreed with the measured data in short-term operation. The maximum cumulative error in hydrogen consumption at 2500 s was 46.3 g with a relative error of 2.4%. Considering the simplifying assumption of equal SOH across fuel cells, the actual error is expected to be smaller than 2.4%. This result validates the accuracy of the system developed in this study and confirms its appropriateness for evaluating alternative optimization control strategies.

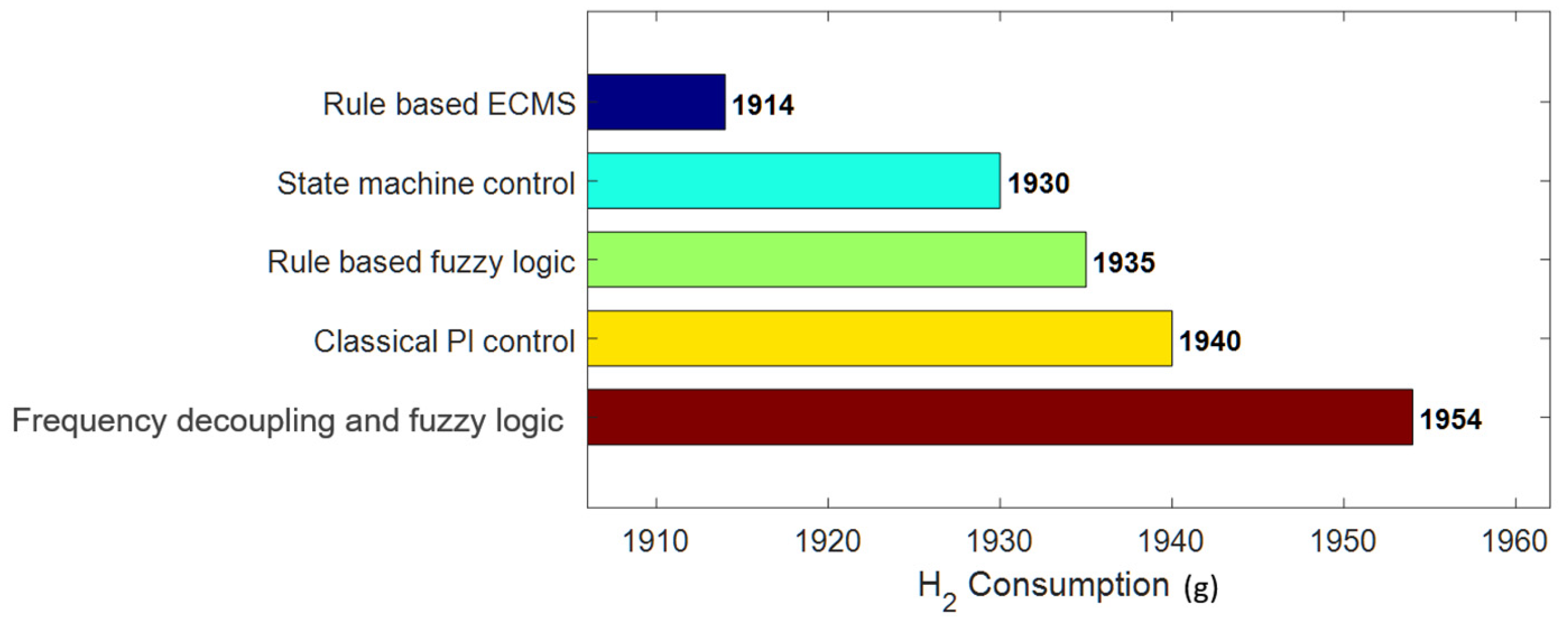
To evaluate the performance of the MEPSV developed, we simulated optimization control programs based on five strategies [22,23]: the rule-based ECMS, state machine control strategy, rule-based fuzzy logic control strategy, classical PI control strategy, and frequency decoupling and fuzzy logic strategy. Each strategy has different optimization priorities. When fuel consumption minimization was the primary purpose, the rule-based ECMS outperformed the other strategies. Under identical software and hardware testing conditions, hydrogen consumption for each strategy was compared as shown in Figure 10.

• Enhancing FCS efficiency and stability

ECMS employed in this study incorporates $P_{\mathit{FCS}}-C_{\mathit{FCS}}$ relationship curve with SOH to operate FCS within its high-efficiency range. As shown in Figure 7 and Figure 8, when LIB energy is available, FCS avoids maximum output and maintains operation within the optimal efficiency band. Additionally, LIB and an adjustable delay mechanism (approximating frequency decoupling) reduce power fluctuations, enhancing the stability and extending the service life of FCS.

2.

Constraining ramp rates for reliability

ECMS applies maximum loading and unloading rates of 5.5 and 10.5 kW/s, respectively, based on manufacturer specifications and constraints for safety. These constraints reflect the time required for uniform and stable distribution of hydrogen, oxygen, and water within the fuel cell, as well as the dynamics of electrochemical reactions, ensuring operation within safe limits and reducing the risk of failure.

3.

Optimizing multi-FCS efficiency and LIB longevity

ECMS enhances overall system efficiency by balancing power distribution across multiple FCS units while accounting for LIB service life. By minimizing excessive cycling and avoiding operation outside safe SOC boundaries, the strategy reduces the likelihood of LIB degradation and failure.

The key performance indicator for H₂ utilization efficiency in MEPSV is the total hydrogen consumption (kg), which directly impacts both operational cost and driving range. This metric is derived cumulatively from the hydrogen flow rate of FCS, calculated using a model that correlates instantaneous electrical power output with the required hydrogen mass flow rate using the FCS efficiency curve. System-wide effectiveness is evaluated based on energy conversion efficiency, defined as the ratio of total energy delivered to the load (integrated load power) to the total energy consumed (integrated hydrogen energy input). ECMS enhances performance by operating FCS predominantly within its optimal efficiency range (typically 45–55%) and suppressing high-flow transients. This leads to a measurable reduction in average hydrogen flow compared with rule-based strategies. In the tested scenarios, ECMS achieved a hydrogen consumption of 1914 g, outperforming the benchmark PI-based control, which recorded 1940 g.

The rule-based ECMS pertains to the SOP operation, which is responsible for transient power quality and grid stability, not overall fuel economy. The advantage of the fuzzy logic control over the conventional PI controller is enhanced dynamic performance and robustness against system non-linearities and disturbances inherent in connecting to a variable emergency load. While ECMS provides the optimal power reference, the fuzzy logic-based SOP controller ensures that MEPSV maintains a superior speed and minimal overshoot, especially during rapid load changes or grid integration. This robustness is critical for an emergency power system, guaranteeing faster isolation/reconnection and higher-quality power supply for sensitive loads. Therefore, the consumption difference is secondary to improving the transient stability and power quality of the SOP connection.

To achieve superior transient performance and system-wide economy, fuzzy logic and ECMS can be used to fine-tune all control layers. For the local SOP control, the conventional PI controller requires precise calibration of its proportional and integral gains. These are determined using the Ziegler-Nichols method to ensure optimal damping and fast settling time for the current and voltage loops. The fuzzy logic control provides robustness and replaces fixed gains with a calibrated set of membership functions and a fuzzy rule matrix. The critical tuning steps for fuzzy logic control involve setting the shape and range of membership functions and calibrating the input/output gain factors based on iterative simulation and expert knowledge to create the necessary non-linear control surface. Finally, at the global ECMS layer, the most critical tuning element is the equivalent factor. This value dictates the instantaneous power split and is carefully determined through an offline optimization sweep over the defined duty cycle, ensuring the long-term LIB SOC is optimally maintained (typically between 0.4 and 0.8 to guarantee global hydrogen economy and component durability [21,24]).

While the reduction in total hydrogen consumption provides a compelling economic metric for ECMS, its superiority over simpler strategies is rooted in component durability and operational quality. Specifically, ECMS quantitatively minimizes the hydrogen consumption rate by applying a dynamic equivalence factor. This approach helps the control system avoid operation in regions detrimental to FCS and LIB units. For FCS, ECMS results in the low-power starvation region (typically below 10% of rated power) and the high-load/high-temperature region (near peak power), which are known to accelerate membrane and catalyst degradation. For LIBs, ECMS penalizes rapid or deep discharge/charge cycles due to the weighting effect, leading to lower power fluctuations and a quantifiable increase in time spent within the optimal SOC range (0.4–0.8). Therefore, ECMS enables a lower final consumption number and a quantitatively less stressful load profile for all core components compared to strategies lacking this dynamic cost function.

The current rule-based battery grouping strategy, which alternates the three LIB units between charging, discharging, and standby based on SOC thresholds of 0.8 and 0.2, was designed to prevent frequent switching and excessive cycling to extend battery life. However, as an area for future enhancement, a more formalized and durable strategy must employ SOH estimates, cumulative energy throughput, or temperature data to optimize unit rotation. This advances the battery grouping strategy from a simple rule-based switch to a more adaptive, durability-oriented layer, similar to existing multi-objective optimization strategies for hybrid systems.

5.5. Limitations

The FCS model can be enhanced to better support the dynamic performance analysis of ECMS. The current model employs a steady-state empirical formulation to estimate the instantaneous hydrogen consumption rate and efficiency map for ECMS. For a more comprehensive representation of transient dynamic effects for system stability and fast load changes, it is necessary to incorporate ECM, comprising RC branches in the anode and cathode circuits that model gas concentration overpotentials and membrane capacitance effects, reflecting the actual physical limitations of the gas flow and electrochemical reactions. The polarization curve (I–V curve) of the FCS stack must be drawn to plot the output voltage against the current density. This curve is critical for visually defining the three operating regions (activation, ohmic, and concentration losses) and quantitatively confirming the system’s high-efficiency operating window, which ECMS is designed to target and maintain. In the following study, the dynamic performance analysis results and the polarization curve will be obtained through the application of the developed strategy in this study [21,22].

6. Conclusions

We developed MEPSV that integrates a hybrid power system, consisting of two FCSs and three LIB units with an SOP device. This configuration addresses the limitations of traditional diesel- or LIB-powered MEPSVs by offering zero emissions, low noise, and extended power supply capabilities. The integration of SOP enables the MEPSV to function flexibly as an emergency power source and a solid-state power controller with energy storage for load balancing and power quality improvement in distribution networks. ECMS was employed to optimally coordinate the power distribution among the multiple sources. The rule-based ECMS employed minimized the total equivalent hydrogen consumption while prioritizing the maximization of the operational lifespan for FCS and LIB systems. The optimization problem was formulated using an objective function that includes the hydrogen consumption rate of FCS and the equivalent hydrogen consumption rate of LIB units, which is converted based on the LIB’s charge/discharge efficiency using the simplified Rint model and a penalty coefficient related to SOC. The ECMS employed in this study prevents FCS degradation by dynamically updating the power-hydrogen consumption rate curve based on the SOH of FCs and applies constraints such as power range limits and maximum ramp rates for FCS loading and unloading to ensure system safety and durability. An SQP algorithm was used for real-time optimization of the power allocation.

The current strategy divides the LIB system into three groups (charging, discharging, and standby) that alternate states based on SOC thresholds (0.8 for charging, 0.2 for discharging). This is a rule-based approach, chosen for its low computational overhead and suitability for real-time deployment in complex Mobile Emergency Power Vehicle (MEPSV) scenarios where extensive training data for reinforcement learning is difficult to obtain, and global optimization is inappropriate. While the rule-based approach provides a foundation for extending battery life by avoiding overcharging and over-discharging and frequent switching, it has limited adaptability and suboptimal performance compared with optimization-based strategies. Therefore, relying only on the current SOC-based state switch is a simplification for real-time computational efficiency, but it may not be optimally durable.

However, the simulation and experimental test results confirmed the effectiveness of the proposed ECMS. ECMS successfully distributed power, allowing LIBs to perform peak shaving and valley filling to manage rapid load changes. This resulted in stable, high-efficiency operation for the FCS units, which helps to extend their service life by minimizing power fluctuations and avoiding low-efficiency regions. Five different control strategies were compared, and the results demonstrated that the rule-based ECMS delivered superior performance in minimizing hydrogen consumption. The ECMS simulation results for hydrogen consumption were almost identical to the measured data under the CHTC-HT profile, with a low maximum cumulative relative error of 2.4% over 2500 s. The strategy contributes to extending the lifespan of the components by utilizing the healthier FCS unit first, setting constraints on the FCS power ramp rates for safe operation, and maintaining the LIB’s SOC within a safe operational range (0.2 to 0.8) to prevent degradation. The rule-based ECMS for the SOP-equipped hybrid MEPSV enables optimal multi-source power allocation by simultaneously minimizing hydrogen consumption and maximizing the operational lifespan of the fuel cell and battery systems. The results validate its appropriateness as a control strategy for the deployment of MEPSV in complex power distribution network scenarios.