Detecting Anomalous Non-Cooperative Satellites Based on Satellite Tracking Data and Bi-Minimal GRU with Attention Mechanisms
Abstract
1. Introduction
- (1)
- We propose a method for detecting anomalies in cataloged non-cooperative satellites using low-cost satellite observation resources, thereby providing a decision-making basis for the scheduling and allocation of high-value and high-precision satellite observation resources during tracking and observation of non-cooperative satellites. This experiment accounts for limitations inherent in satellite tracking data from low-cost satellite observation resources, such as relatively high data noise and fewer data categories. To ensure sufficient observation time for subsequent precision tracking, we imposed constraints on the experimental scenario: shorter observation durations and the need for lightweight models. Based on the aforementioned conditions, this paper constructs a deep learning anomaly detection model for cataloged non-cooperative satellites. The objective is to rapidly determine whether anomalies exist during the initial phase when cataloged non-cooperative satellites enter the observable range.
- (2)
- We propose a Bi-Directional Minimal GRU deep learning network model incorporating an attention mechanism to detect anomalies in cataloged non-cooperative satellites. First, to significantly reduce the number of parameters and computational complexity without substantially compromising model expressiveness, we adopted the Minimal GRU model as the foundational architecture for the entire network framework. Next, to capture the full contextual information at each time step, we enhanced the Minimal GRU, creating the Bi-Directional Minimal GRU. Finally, to enable the model to autonomously learn weights across different time steps and enhance detection performance, we incorporated an attention mechanism into the Bi-Directional Minimal GRU, ultimately forming the Attention-based Bi-Directional Minimal GRU model. This model enables rapid and effective anomaly detection for cataloged non-cooperative satellites.
- (3)
- We designed simulation experiments and validated the model’s effectiveness by analyzing the simulation results. Through comparative experiments between our Attention-based Bi-Directional Minimal GRU deep learning model and other lightweight algorithms, we demonstrated that our designed algorithm outperforms others in terms of efficiency and performance.
2. Literature Review
2.1. Satellite Observation Data
2.2. Algorithms for Mining Multivariate Time Series Data
3. Problem Description and Modeling
3.1. Experiment Scenario Description
3.2. Model Construction
3.2.1. Data Preprocessing
3.2.2. Symbol Settings
3.2.3. Model Establishment
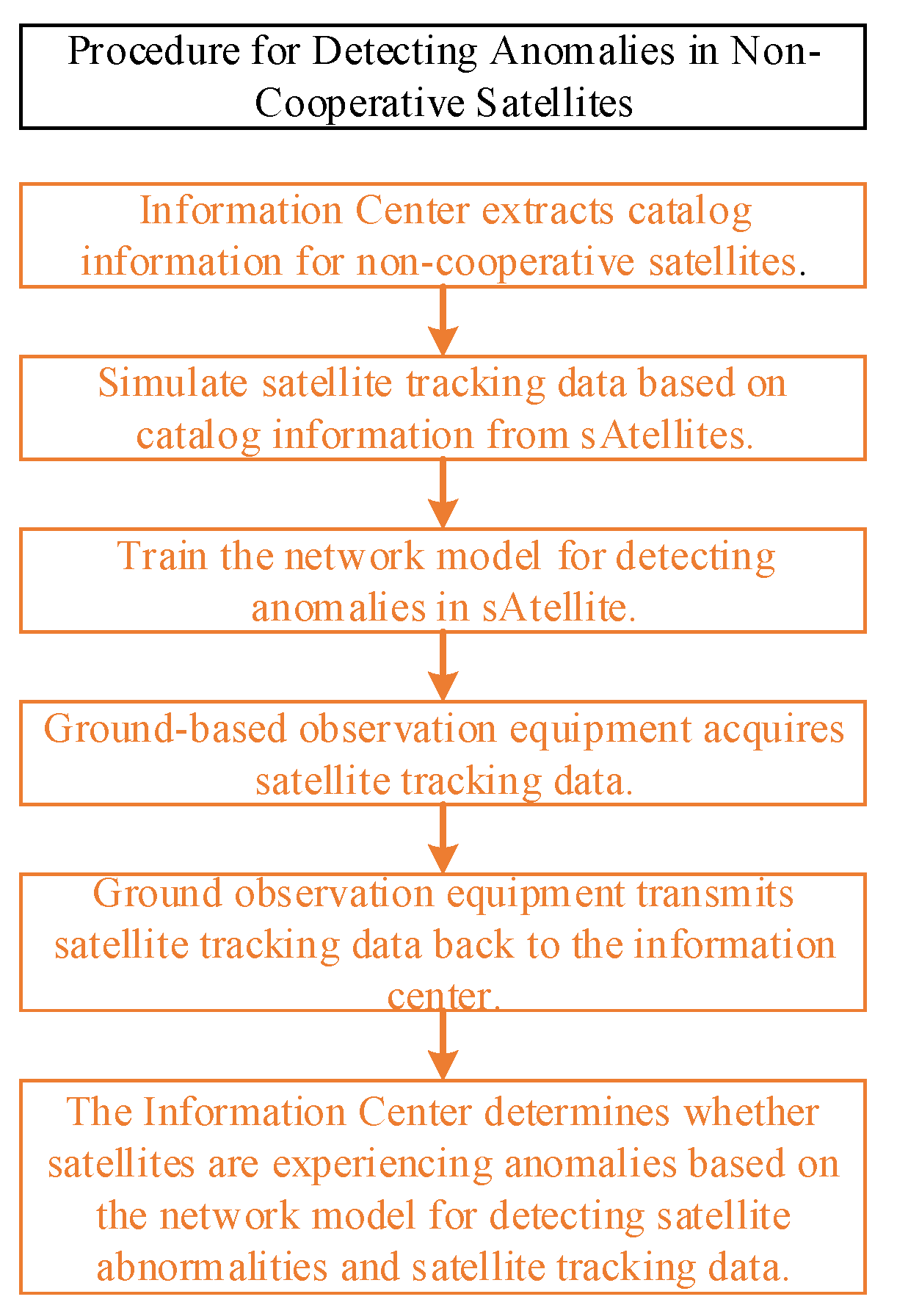
3.3. Procedure for Detecting Anomalies in Non-Cooperative Satellites
4. Experiments and Analysis
4.1. Experimental Design
4.2. Hyperparameter Settings
4.3. Model Complexity Analysis
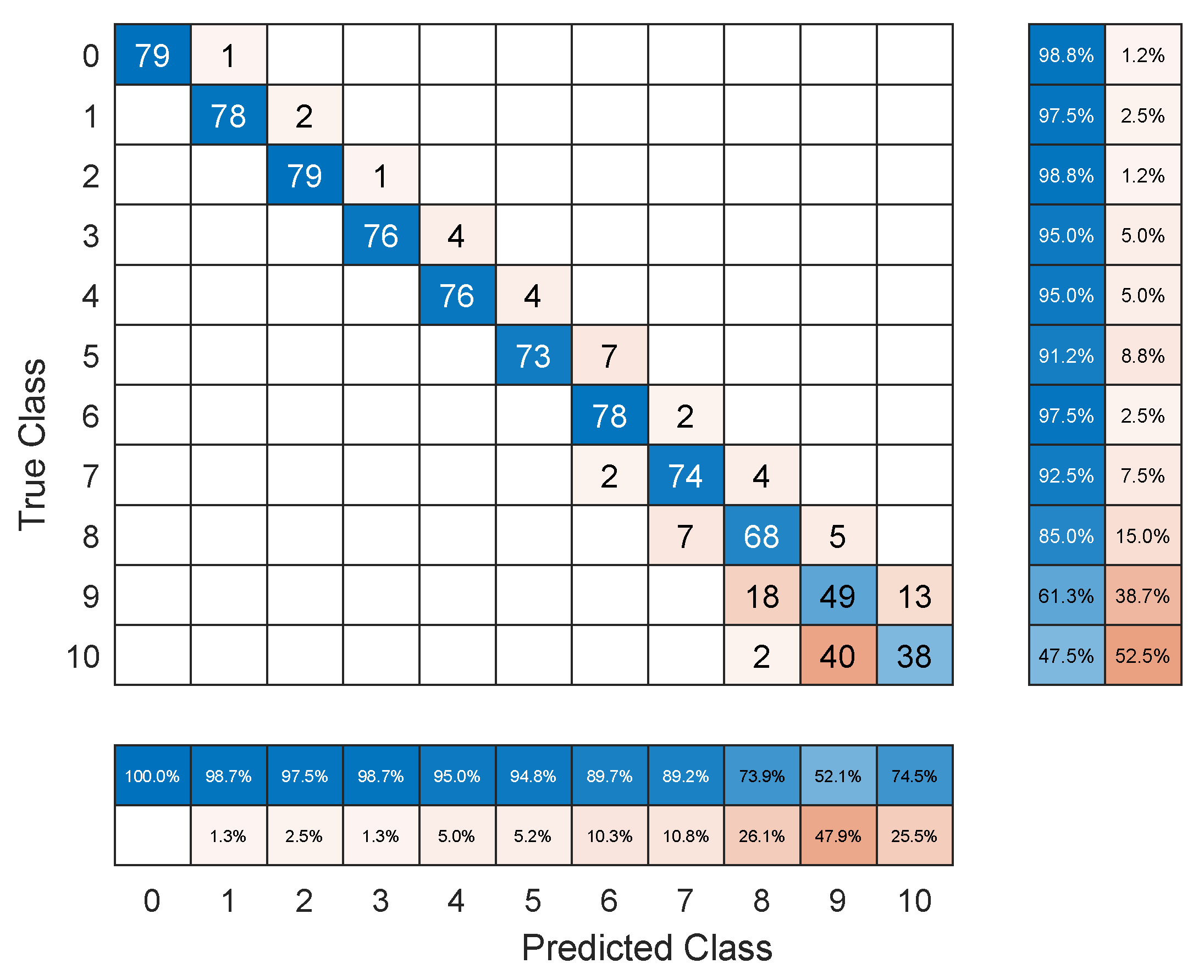
4.4. Experimental Results and Analysis
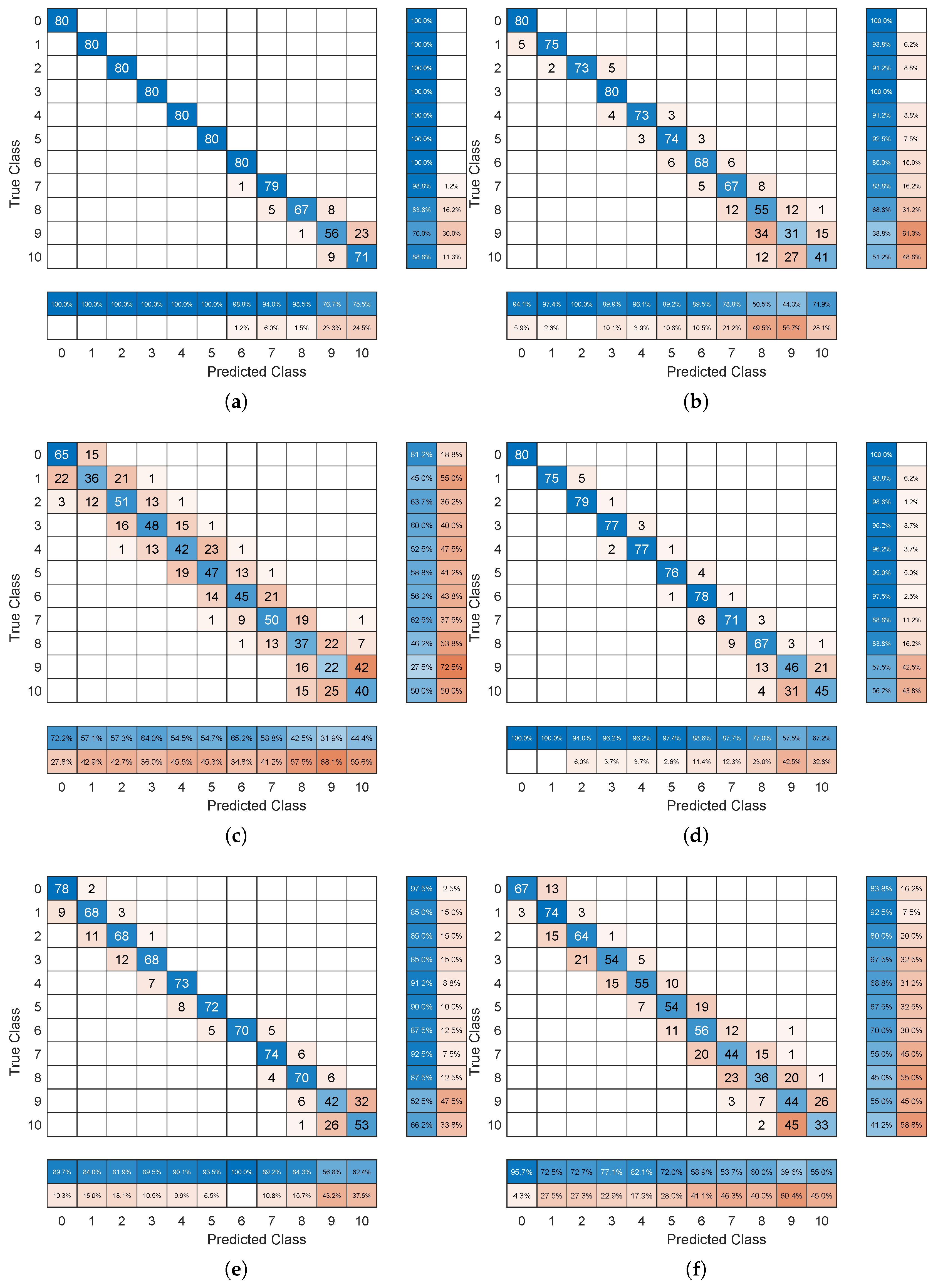
4.5. Verification of the General Applicability of ABMGRU and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AR | Autoregression |
| MA | Moving Average |
| ARMA | Auto-Regression and Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| VAR | Vector Autoregression |
| VARMA | Vector Autoregressive Moving Average |
| VARIMA | Vector Autoregressive Integrated Moving Average |
| BPnetwork | Back Propagation Neural Networks |
| LSSVM | Least Squares Support Vector Machines |
| RNN | Recurrent Neural Networks |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| GCN | Graph Convolutional Networks |
| GAT | Graph Attention Networks |
| BGRU | Bi-Directional Gated Recurrent Unit |
| BMGRU | Bi-Directional Minimal Gated Recurrent Unit |
| ABMGRU | Attention-based Bi-Directional Minimal Gated Recurrent Unit |
| STK | Satellite Tool Kit |
| M | million |
| NaN | Not a Number |
References
- Xiao, J.; Fu, X. Space Security:A Shared Responsibility. Beijing Rev. 2025, 17, 28–29. [Google Scholar]
- Jia, Q.; Xiao, J.; Bai, L.; Zhang, Y.; Zhang, R.; Feroskhan, M. Space situational awareness systems: Bridging traditional methods and artificial intelligence. Acta Astronaut. 2025, 228, 321–330. [Google Scholar] [CrossRef]
- Kazemi, S.; Azad, N.; Scott, K.; Oqab, H.; Dietrich, G. Orbit determination for space situational awareness: A survey. Acta Astronaut. 2024, 222, 272–295. [Google Scholar] [CrossRef]
- Hu, Y.; Li, K.; Liang, Y.; Chen, L. Review on strategies of space-based optical space situational awareness. J. Syst. Eng. Electron. 2021, 32, 1152–1166. [Google Scholar] [CrossRef]
- Zhong, J. Space Strategic Competition and Rivalry are Intensifying. Renming Luntan·Xueshu Qianyan 2020, 16, 22–28. [Google Scholar]
- Albrecht, M.; Graziani, P. Congested Space. Space News Int. 2016, 27, 22–23. [Google Scholar]
- Marcussen, E. Congested and Contested Spaces. Acts Aid 2023, 1, 248–301. [Google Scholar]
- Laura, S. Is the Security Space too Congested. Secur. Distrib. Mark. 2016, 46, 58–66. [Google Scholar]
- Han, H.; Dang, Z. Threat assessment of non-cooperative satellites in interception scenarios: A transfer window perspective. Defence Technol. 2025. [Google Scholar] [CrossRef]
- Yuan, W.; Xia, Q.; Qian, H.; Qiao, B.; Xu, J.; Xiao, B. An intelligent hierarchical recognition method for long-term orbital maneuvering intention of non-cooperative satellites. Adv. Space Res. 2025, 75, 5037–5050. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Pedrycz, W.; Li, H.; Wang, L. Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy. Comput. Ind. Eng. 2017, 113, 576–588. [Google Scholar] [CrossRef]
- Chahal, A.; Addula, S.; Jain, A.; Gulia, P.; Gill, N.; Bala, V. Systematic Analysis based on Conflux of Machine Learning and Internet of Things using Bibliometric analysis. J. Intell. Syst. Internet Things 2024, 13, 196–224. [Google Scholar]
- Shawn, M.; Marco, C.; Marcello, R. Simulations of Multiple Spacecraft Maneuvering with MATLAB/Simulink and Satellite Tool Kit. J. Aerosp. Inf. Syst. 2013, 10, 348–358. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, Y.; Wu, L.; Liu, P.; Lv, R.; Ullah, H. Lightweight micro-motion gesture recognition based on MIMO millimeter wave radar using Bidirectional-GRU network. Neural Comput. Appl. 2023, 35, 23537–23550. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Li, A.; Zhang, J. Earth observation satellite data receiving, processing system and data sharing. Int. J. Digit. Earth 2012, 3, 241–250. [Google Scholar] [CrossRef]
- Schefels, C.; Schlag, L.; Helmsauer, K. Synthetic satellite telemetry data for machine learning. CEAS Space J. 2025, 17, 863–875. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhang, K.; Fu, Y.; Zhang, W. Precise orbit determination for LEO constellation based on onboard GNSS observations, inter-satellite links and ground tracking data. GPS Solut. 2025, 29, 107. [Google Scholar] [CrossRef]
- Kaseris, M.; Kostavelis, I.; Malassiotis, S. A Comprehensive Survey on Deep Learning Methods in Human Activity Recognition. Mach. Learn. Knowl. Extr. 2024, 6, 842–876. [Google Scholar] [CrossRef]
- Barandas, M.; Folgado, D.; Fernandes, L. TSFEL: Time series feature extraction library. SoftwareX 2020, 11, 100456. [Google Scholar] [CrossRef]
- Kini, B.; Sekhar, C. Large margin mixture of AR models for time series classification. Appl. Soft Comput. 2013, 13, 361–371. [Google Scholar] [CrossRef]
- Zhuang, Y.; Li, D.; Yu, P.; Li, W. On buffered moving average models. J. Time Ser. Anal. 2025, 46, 599–622. [Google Scholar] [CrossRef]
- Raza, S.; Majid, A. Maximum likelihood estimation of the change point in stationary state of auto regressive moving average (ARMA) models, using SVD-based smoothing. Commun. Stat.-Theory Methods 2022, 51, 7801–7818. [Google Scholar]
- Sayed Rahmi, K.; Athar Ali, K. A Bayesian Prediction for the Total Fertility Rate of Afghanistan Using the Auto-regressive Integrated Moving Average (ARIMA) Model. Reliab. Theory Appl. 2023, 18, 980–997. [Google Scholar]
- Yang, H.; Pan, Z.; Tao, Q. Online learning for vector auto-regressive moving-average time series prediction. Neurocomputing 2018, 315, 9–17. [Google Scholar] [CrossRef]
- Gong, X.; Liu, X.; Xiong, X. Non-Gaussian VARMA model with stochastic volatility and applications in stock market bubbles. Chaos Solitons Fractals 2019, 121, 129–136. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, C.; Cao, R. Multivariate probabilistic forecasting and its performance’s impacts on long-term dispatch of hydro-wind hybrid systems. Appl. Energy 2021, 283, 116243. [Google Scholar] [CrossRef]
- Davesh, M.; Shen, J.; Yin, Q. Perverse filtrations and Fourier transforms. Acta Math. 2025, 234, 1–69. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wei, X.; Li, M. Back Propagation Neural Network-Enhanced Generative Model for Drying Process Control. Informatica 2025, 49, 63–76. [Google Scholar] [CrossRef]
- Wang, M.; Zhong, C.; Yue, K.; Zheng, Y.; Jiang, W.; Wang, J. Modified MF-DFA Model Based on LSSVM Fitting. Fractal Fract. 2024, 8, 320. [Google Scholar] [CrossRef]
- Gupta, M.; Chandra, P. A comprehensive survey of data mining. Int. J. Inf. Technol. 2020, 12, 1243–1257. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, M.; Zhang, Y.; Weng, S. Stability of Stochastic Delayed Recurrent Neural Networks. Mathematics 2025, 13, 2310. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tjandra, A.; Sakti, S.; Manurung, R.; Adriani, M.; Nakamura, S. Gated Recurrent Neural Tensor Network. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F. A comprehensive survey on graph neural networks. lEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Latif-Martínez, H.; Suárez-Varela, J.; Cabellos-Aparicio, A.; Barlet-Ros, P. GAT-AD: Graph Attention Networks for contextual anomaly detection in network monitoring. Comput. Ind. Eng. 2025, 200, 110830. [Google Scholar] [CrossRef]
- Håkon, G.; Håkon, T. Ensemble Kalman filter with precision localization. Comput. Stat. 2025, 40, 2781–2805. [Google Scholar]
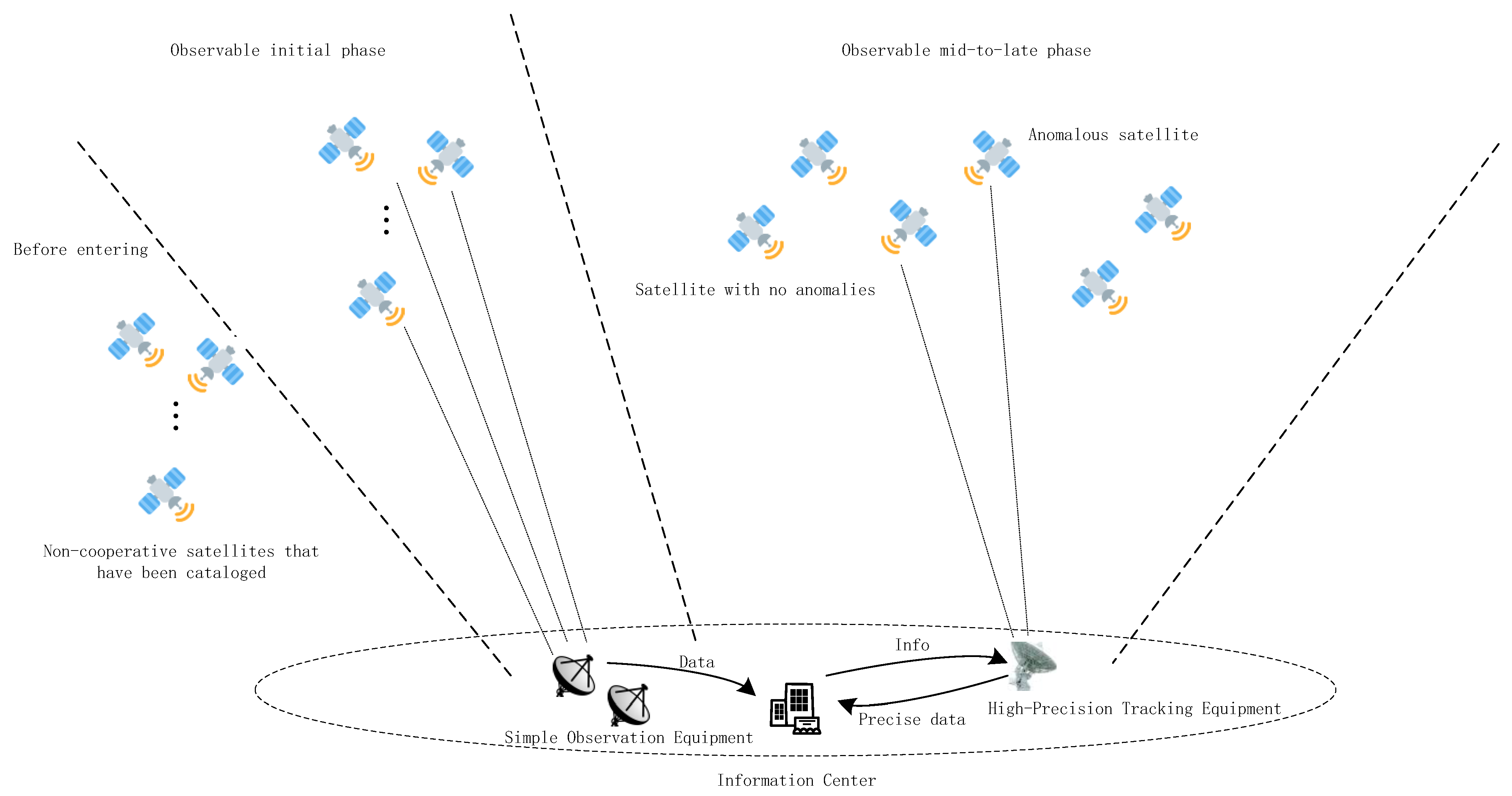



| Core Elements | Definition |
|---|---|
| Timestamp | Precisely record the moment data is captured. |
| Satellite Identifier | Clearly indicate which satellite the data originates from. |
| Ground Station Identifier | Record which ground station received this data. |
| Telemetry data [16] | A “health check report” reflecting the satellite platform and payload’s operational status and performance parameters. |
| Tracking Data [17] | Core raw measurement data used for precisely determining satellite position and velocity. |
| Key Characteristics | Definition |
|---|---|
| Time dependence | Also known as autocorrelation or temporal dependence, it refers to a statistically significant correlation between the current observation in a time series and its past observation (s) at one or more preceding time points. In a multivariate context, this dependency exists both within individual variables (univariate autocorrelation) and between different variables (cross-correlation). |
| Spatial dependence | Spatial dependence specifically refers to the interdependent relationship between observations of different variables (dimensions) at the same or different time points within a multivariate time series. It describes the “lateral” interactions or influences between variables. |
| Spectral characteristics | Spectral characteristics describe the properties of a time series in the frequency domain. They decompose the time series into sinusoidal and cosine wave components of different frequencies and analyze the intensity of these frequency components. |
| Noise characteristics | Noise characteristics refer to the unpredictable, randomly fluctuating components within a time series. They represent the portion of the data that cannot be explained by the model and are typically regarded as “error” or “disturbance”. |
| Shape characteristics | Shape characteristics focus on the morphology, contours, and structure of local segments within a time series. They provide an intuitive description of sub-sequences, such as ascending, descending, peaks, troughs, plateaus, and so forth. |
| Similarity features | Similarity features are used to quantify the degree of similarity in overall or local patterns between two time series (or two subsequences). |
| Model | Brief Principle | Advantage | Defect |
|---|---|---|---|
| BPnetwork | Flatten the input multivariate time series into a one-dimensional vector. Subsequent operations follow the same procedure as classic BPnetwork. | Strong nonlinear fitting capability. High flexibility. | Flattening operations disrupt the temporal relationships within the data. Input length must be fixed. |
| LSSVM | Flatten the input data. Manually extract features to form feature vectors. | High computational efficiency. Few parameters. | Sensitive to outliers. Overly reliant on feature engineering, making it difficult to extract features directly from raw time series data. |
| RNN | Process time step data sequentially. Errors propagate backward through time. | Natural sequence modeling capability. Does not require fixed input data length. | It is prone to issues such as vanishing gradients or exploding gradients. The theoretical advantages of RNN are almost entirely realized through its variant algorithms. |
| LSTM | Variant algorithms of RNNs. Utilizing unique mechanisms to selectively remember or forget information. | Exceptional long-term modeling capabilities. Mitigates the issues of vanishing gradients or exploding gradients in RNN. | Computational costs are high. Model training is time-consuming. |
| GRU | A variant of LSTM with a simpler structure. | Faster training and inference speeds. | May not perform as well as LSTM when handling complex tasks. |
| CNN | Treating multivariate time series as pseudo-images for processing. | Strong local pattern extraction capability. Flexible and efficient architecture. | Long-term dependency extraction capability is weak. |
| Transformer | Modeling global dependencies through self-attention mechanisms. | Powerful global modeling capabilities. Fully parallelized computation significantly accelerates training speed. | Extremely high computational complexity. High memory requirements. |
| GCN | Model multi-dimensional time series as graphs. Graph convolution operations aggregate neighboring information. | A fresh perspective. Applicable to non-Euclidean data. Explicitly model relationships between variables. | Performance is highly dependent on the quality of adjacency matrix. Graph structure in standard GCN is static. |
| GAT | Dynamically learn the strength of relationships between variables through the Graph Attention Mechanism. | GAT represents a revolutionary evolution of GCN, freeing it from dependence on a predefined adjacency matrix. Attention coefficient calculations can be parallelized, resulting in significantly faster training speeds. | Similar to GCN, it requires relatively complex interrelationships among variables in multivariable time series; otherwise, its performance may be inferior to traditional models. |
| Symbol | Description |
|---|---|
| t | Time step t, . |
| D | The size D of the input dimension for each time step, . |
| Update Gate Vector at time step t, . | |
| Reset Gate Vector at time step t, . | |
| Hidden State Vector at time step t, , (In Bi-Directional Minimal GRU, ). | |
| Hidden State Vector of the forward GRU at time step t, . | |
| Hidden State Vector of the backward GRU at time step t, . | |
| h | h is the hidden state sequence containing all time step information. , . |
| H | The dimension size of the hidden layer . |
| is the dimension of the attention network and is a hyperparameter. | |
| Candidate Hidden State Vector at time step t, . | |
| represents the sigmoid function. | |
| X | X is the input sequence, , . |
| Raw data vector at time step t, . | |
| Weight Matrix of Update Gate, . | |
| Weight Matrix of Reset Gate, . | |
| Weight Matrix of Candidate Hidden State, . | |
| Weight Matrix of Attention Mechanism, . | |
| Weight Matrix of Classifier, . | |
| Bias of Update Gate, . | |
| Bias of Reset Gate, . | |
| Bias of Candidate Hidden State, . | |
| Bias of Attention Mechanism, . | |
| Bias of Classifier, . | |
| converted from . It can be regarded as “energy” at time step t, . | |
| The context vector can be regarded as a “query” vector used to identify significant hidden states, . | |
| is the attention weight at time step t, . | |
| c | A fixed-size Context Vector focused on key information, . |
| C | Total number of categories for satellite tracking observation data. |
| The final probability distribution obtained through the model. . | |
| L | Input Sequence Length. |
| Hidden Feature Dimensions of Transformer. |
| Item | Description |
|---|---|
| Processor * | 11th Gen Intel(R) Core(TM) i5-11400H @ 2.70 GHz (2.69 GHz) |
| RAM * | 16.0 GB |
| OS * | Windows11 (64-bit) |
| Python version | Python 3.9 |
| Classification | Key Members |
|---|---|
| Data-related hyperparameters | The Length of the Sequence, Number of Features, Number of Classes |
| Model structure hyperparameters | Hidden Layer Size, Number of Layers, Attention Hidden Layer Size |
| Training hyperparameters | Batch size, Learning rate, Number of Epochs |
| Regularization hyperparameters | Dropout Rate, Weight Decay |
| Parameter | Value | Description |
|---|---|---|
| Learning Rate | 0.001 | Learning rate for the Adam optimizer |
| Number of Epochs | 25 | Total number of iterations in model training |
| Optimizer | Adam | The type of optimizer used by the model |
| Loss Function | Categorical crossentropy | the type of loss function used in the model |
| Batch Size | 128 | The total number of samples drawn during each iteration of model training |
| Dropout Rate | 0.3 | The ratio of parameters discarded during output at each network layer |
| Weight Decay | 0.0001 | L2 regularization coefficient |
| Number of Layers | 2 | Total number of layers in the GRU network |
| Hidden Layer Size | 64 | Dimension of the GRU Hidden Layer |
| Attention Hidden Layer size | 32 | Dimension of the hidden layer in the attention mechanism |
| Model | Computational Complexity | Number of Network Parameters | Total per Layer (Approx.) |
|---|---|---|---|
| Transformer | 1 M | ||
| LSTM | 0.066 M | ||
| GRU | 0.05 M | ||
| BGRU | 0.05 M | ||
| BMGRU | 0.033 M | ||
| ABMGRU | 0.043 M |
| Model | Accuracy | Precision | Recall | F1 | Time (s) |
|---|---|---|---|---|---|
| BPnetwork | 0.668 ± 0.013 | 0.669 ± 0.014 | 0.668 ± 0.013 | 0.665 ± 0.015 | 3.355 ± 0.694 |
| LSSVM | 0.16 ± 0.012 | 0.151 ± 0.014 | 0.16 ± 0.011 | 0.15 ± 0.010 | 1.066 ± 0.127 |
| GAT | 0.599 ± 0.019 | 0.568 ± 0.053 | 0.599 ± 0.020 | 0.569 ± 0.014 | 27.745 ± 2.834 |
| Transformer | 0.829 ± 0.018 | 0.831 ± 0.015 | 0.829 ± 0.019 | 0.82 ± 0.013 | 101.689 ± 6.142 |
| LSTM | 0.847 ± 0.009 | 0.851 ± 0.014 | 0.847 ± 0.011 | 0.844 ± 0.011 | 148.12 ± 6.137 |
| CNN | 0.784 ± 0.015 | 0.783 ± 0.015 | 0.784 ± 0.016 | 0.781 ± 0.012 | 19.026 ± 0.283 |
| GRU | 0.837 ± 0.033 | 0.848 ± 0.021 | 0.837 ± 0.032 | 0.839 ± 0.026 | 23.538 ± 2.363 |
| BGRU | 0.866 ± 0.027 | 0.878 ± 0.023 | 0.877 ± 0.025 | 0.874 ± 0.017 | 91.776 ± 6.756 |
| BMGRU | 0.874 ± 0.023 | 0.884 ± 0.017 | 0.874 ± 0.022 | 0.878 ± 0.015 | 45.016 ± 2.353 |
| ABMGRU | 0.903 ± 0.019 | 0.904 ± 0.018 | 0.903 ± 0.022 | 0.902 ± 0.017 | 86.083 ± 4.874 |
| Model | Difference in Means | t-Statistic | p-Value | Significance |
|---|---|---|---|---|
| ABMGRU vs. Transformer | 7.4% | 6.98 | significant | |
| ABMGRU vs. LSTM | 5.6% | 6.24 | significant | |
| ABMGRU vs. CNN | 11.9% | 11.97 | significant | |
| ABMGRU vs. GRU | 6.6% | 4.37 | significant | |
| ABMGRU vs. BGRU | 3.7% | 2.88 | significant | |
| ABMGRU vs. BMGRU | 2.9% | 2.35 | significant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Jiao, Y.; Pan, X.; Wang, X.; Sun, B. Detecting Anomalous Non-Cooperative Satellites Based on Satellite Tracking Data and Bi-Minimal GRU with Attention Mechanisms. Appl. Syst. Innov. 2025, 8, 163. https://doi.org/10.3390/asi8060163
Li P, Jiao Y, Pan X, Wang X, Sun B. Detecting Anomalous Non-Cooperative Satellites Based on Satellite Tracking Data and Bi-Minimal GRU with Attention Mechanisms. Applied System Innovation. 2025; 8(6):163. https://doi.org/10.3390/asi8060163
Chicago/Turabian StyleLi, Peilin, Yuanyuan Jiao, Xiaogang Pan, Xiao Wang, and Bowen Sun. 2025. "Detecting Anomalous Non-Cooperative Satellites Based on Satellite Tracking Data and Bi-Minimal GRU with Attention Mechanisms" Applied System Innovation 8, no. 6: 163. https://doi.org/10.3390/asi8060163
APA StyleLi, P., Jiao, Y., Pan, X., Wang, X., & Sun, B. (2025). Detecting Anomalous Non-Cooperative Satellites Based on Satellite Tracking Data and Bi-Minimal GRU with Attention Mechanisms. Applied System Innovation, 8(6), 163. https://doi.org/10.3390/asi8060163






