Assessment of Airport Pavement Condition Index (PCI) Using Machine Learning
Abstract
1. Introduction
1.1. Framework
1.2. Pavement Condition Index (PCI)
1.3. Machine Learning: Concepts, Algorithms, and PCI Prediction
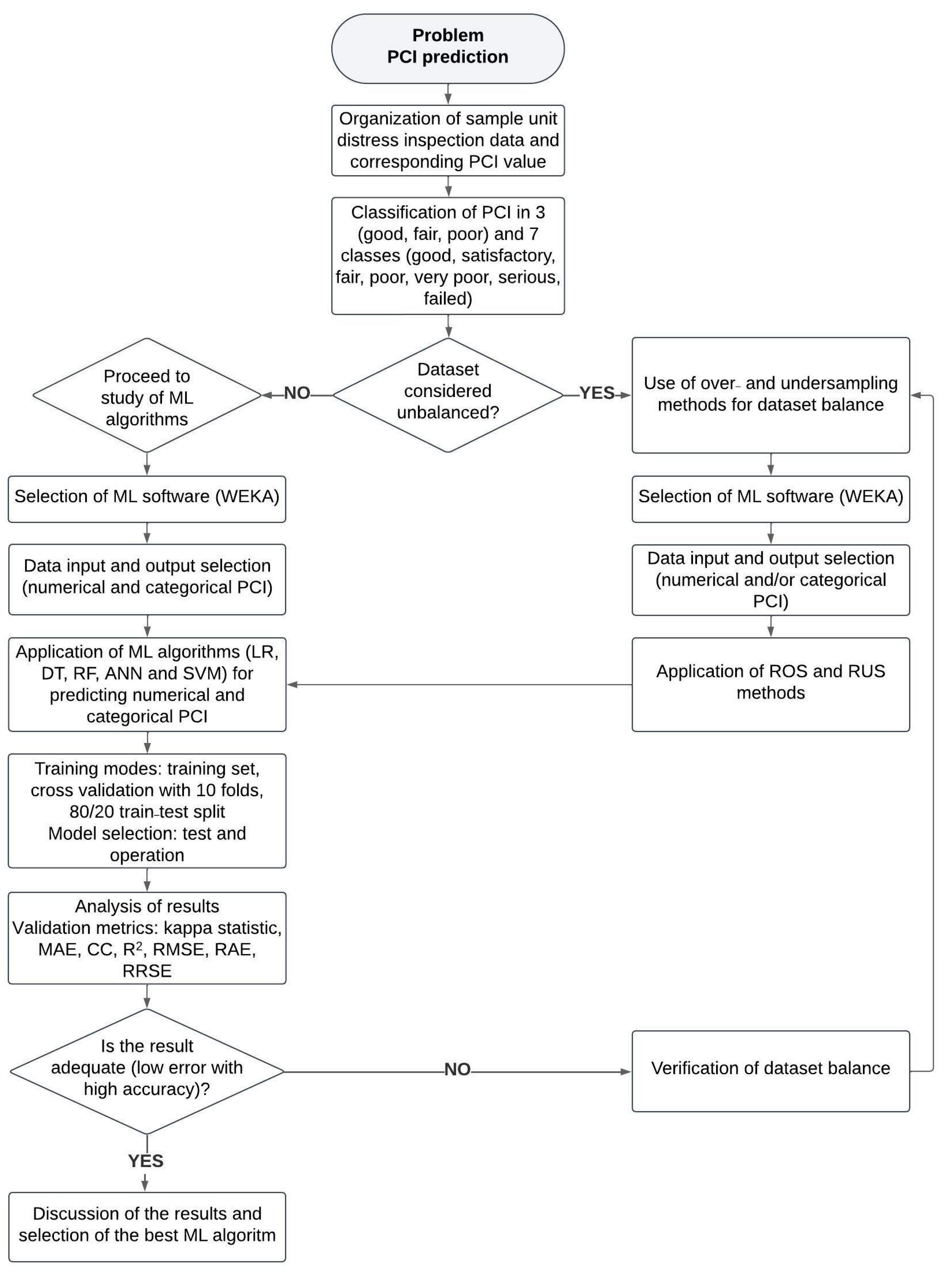
2. Materials and Methods
| Correlation Coefficient | |
|---|---|
| Range | Correlation |
| ±0.00–0.10 | Negligible |
| ±0.10–0.39 | Weak |
| ±0.40–0.69 | Moderate |
| ±0.70–0.89 | Strong |
| ±0.90–1.00 | Very strong |
| Kappa statistic | |
| Range | Correlation |
| <0 | Worse than expected |
| 0–0.20 | None |
| 0.21–0.39 | Minimal |
| 0.40–0.59 | Weak |
| 0.60–0.79 | Moderate |
| 0.80–0.90 | Strong |
| >0.90 | Almost perfect |
| ROC area | |
| Range | Model discriminative ability |
| 0.50 | No discriminative ability |
| 0.51–0.70 | Discrimination is weak |
| 0.71–0.80 | Discrimination is acceptable |
| 0.81–0.90 | Discrimination is good |
| >0.90 | Discrimination is exceptional |
3. Case Study
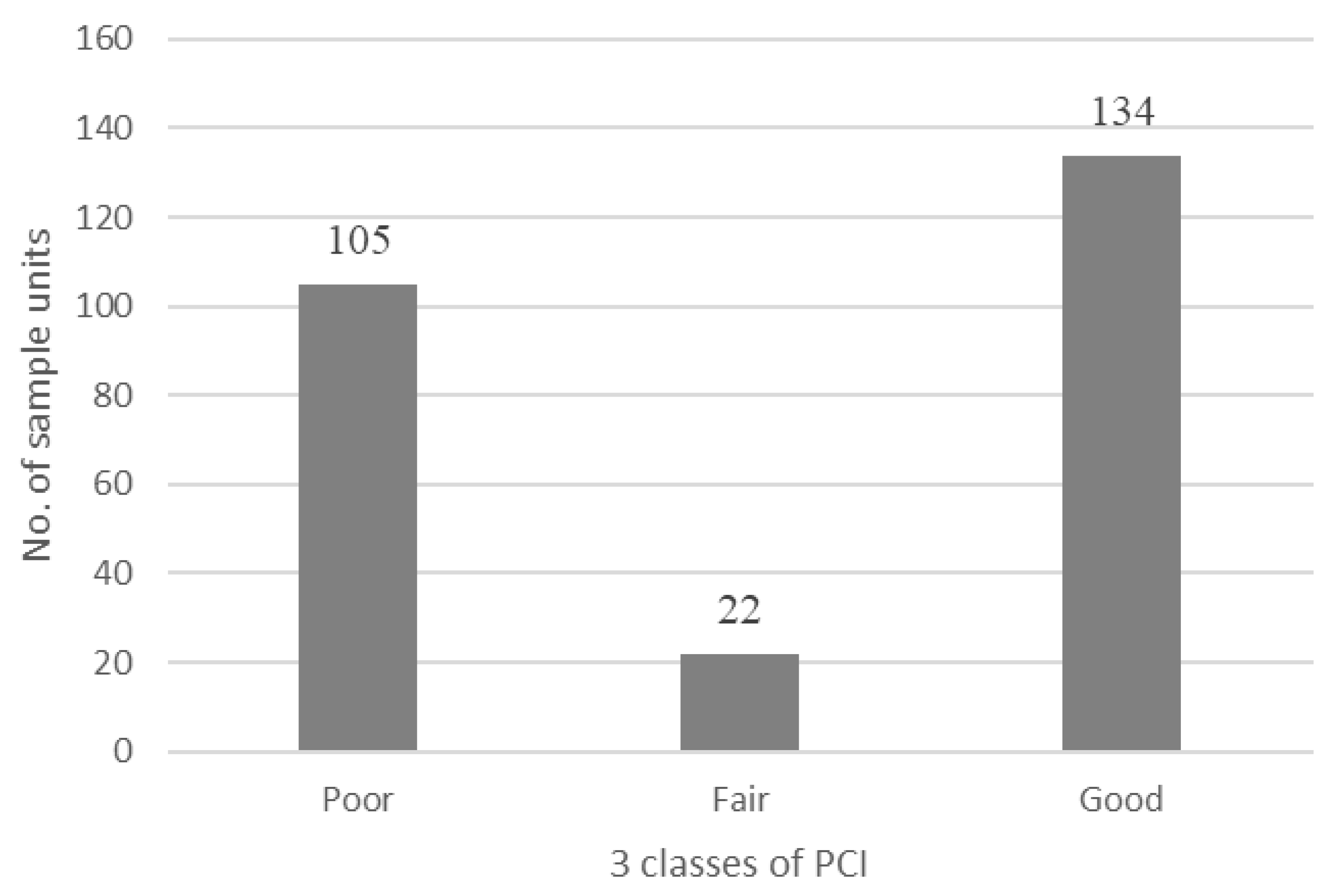
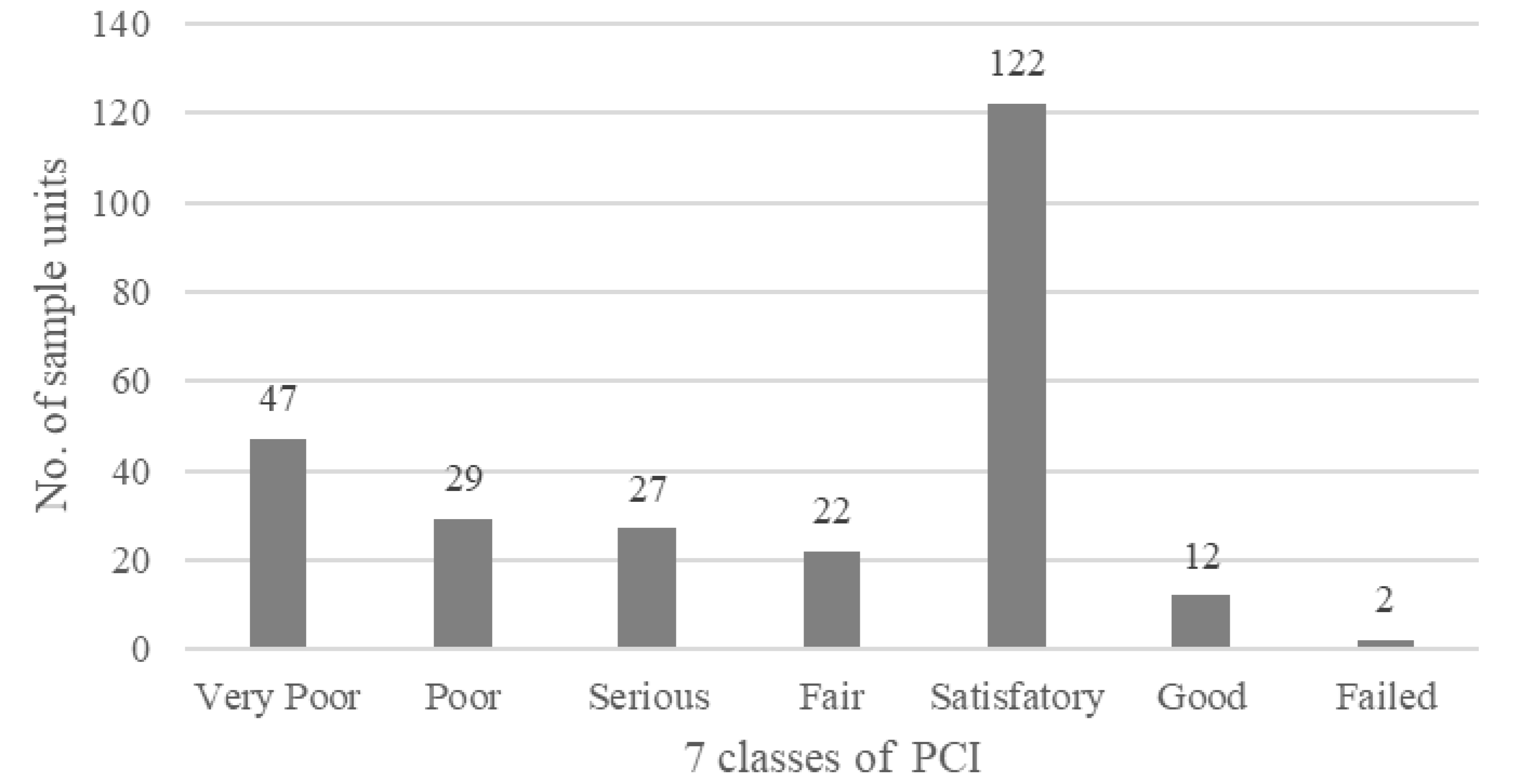
3.1. Data Description
3.2. Algorithms
3.3. Results and Discussion
3.3.1. Numerical PCI
3.3.2. Three- and Seven-Class PCI
4. Conclusions
- The ‘training set’ option on the chosen software is not recommended as it reveals overfitting tendencies due to the output calculation being based on the same trained database.
- Random Forest with 10-fold cross-validation was the most efficient and reliable algorithm for both numeric and categorical PCI, with Kappa statistic values between 0.88 and 0.93, error <7.17%, and a ROC area >0.93. Statistical comparison and ranking analysis consistently identified the RF model as the best-performing algorithm. This was evidenced by the highest mean correlation coefficient (0.93) for the numerical PCI, and superior Kappa statistics for both the three-class (0.88) and seven-class (0.92) classifications.
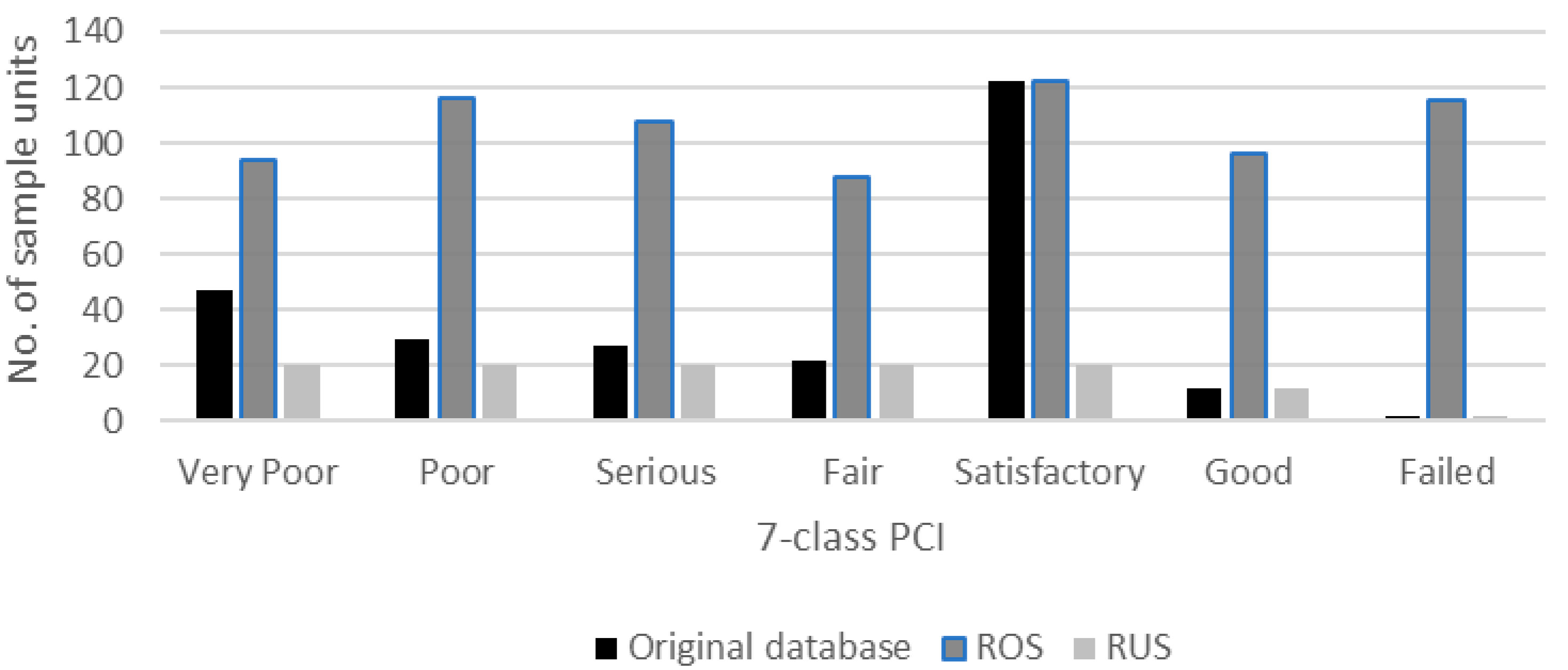
- The success of ROS (SMOTE) in the seven-class PCI prediction was marked by a significant increase in the Kappa statistical value (from 0.58 to 0.91). Conversely, RUS proved unsuccessful, likely due to the resulting reduction of an already limited database. However, the limited number of initial instances in certain classes (e.g., ‘failed’, ‘good’, and ‘fair’) might have constrained the SMOTE technique’s effectiveness in generating meaningful synthetic cases.
- The database must contain sufficient information in both quantity and distress variety, as insufficient data will negatively impact the model’s overall performance. However, database imbalance can also significantly impact the training of ML algorithms, even when the total number of cases is adequate.
- The analysis of the independent variables’ influence showed that, consistently across the best-performing models, Joint Reflection Cracking, Raveling, Weathering, and Patching and Utility Cut Patching were the most critical distresses for PCI prediction within the tested database. These results are consistent with the findings presented in the literature (e.g., [10,31,51]).
- Despite the limitations imposed by a relatively small database size, limited geographical scope, and airport size, the demonstrated benefits and time savings of using ML algorithms for PCI prediction are promising. These findings underscore the need to organize larger and more diverse databases. Once such complete databases are achieved, the utilization of ML approaches will be especially valuable for resource-limited airports or management entities. By allowing the incorporation of AI-based approaches with low computational demands, this strategy significantly enhances efficiency and improves decision-making in airport pavement maintenance management, particularly for crucial assets like runways.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ritchie, H.; Rodés-Guirao, L.; Mathieu, E.; Gerber, M.; Ortiz-Ospina, E.; Hasell, J. Population Growth. Available online: https://ourworldindata.org/population-growth (accessed on 28 July 2024).
- Federal Aviation Administration. Federal Aviation Administration Advisory Circular No. 150/5320-6G, Airport Pavement Design and Evaluation; US Department of Transportation Federal Aviation Administration: Washington, DC, USA, 2021; pp. 1–195. [Google Scholar]
- Irfan, M.; Khurshid, M.; Iqbal, S.; Khan, A. Framework for Airfield Pavements Management—An Approach Based on Cost-Effectiveness Analysis. Eur. Transp. Res. Rev. 2015, 7, 13. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Common Airport Pavement Maintenance Practices; The National Academies Press: Washington, DC, USA, 2011. [Google Scholar] [CrossRef]
- Basu, D.; Misra, A.; Puppala, A. Sustainability and Geotechnical Engineering: Perspectives and Review. Can. Geotech. J. 2015, 52, 96–113. [Google Scholar] [CrossRef]
- Augeri, M.; Greco, S.; Nicolosi, V. Planning Urban Pavement Maintenance by a New Interactive Multi-Objective Optimization Approach. Eur. Transp. Res. Rev. 2019, 11, 17. [Google Scholar] [CrossRef]
- Slabej, M.; Grinč, M.; Kováč, M.; Decký, M.; Šedivý, Š. Non-Invasive Diagnostic Methods for Investigating the Quality of Zilina Airport’s Runway. Contrib. Geophys. Geod. 2015, 45, 237–254. [Google Scholar] [CrossRef]
- ASTM D5340-23; ASTM International Standard Test Method for Airport Pavement Condition Index Surveys. Advancing Standards Transforming Markets: West Conshohocken, PA, USA, 2023.
- U.S. Army Corps of Engineers, Engineer Research and Development Center (ERDC), Construction Engineering Research Laboratory (CERL). Asphalt Surfaced Roads & Parking Lots-Paver™ Distress Identification Manual; U.S. Army Corps of Engineers: Champaign, IL, USA, 2009. [Google Scholar]
- Santos, B.; Almeida, P.; Feitosa, I.; Lima, D. Validation of an Indirect Data Collection Method to Assess Airport Pavement Condition. Case Stud. Constr. Mater. 2020, 13, e00419. [Google Scholar] [CrossRef]
- Santos, B.; Gavinhos, P.; Almeida, P.; Nery, D. Use of Unmanned Aerial Vehicles (UAVs) for Transport Pavement Inspection. In Proceedings of the 5th International Conference on Transportation Geotechnics (ICTG) 2024, Volume 1, Lecture Notes in Civil Engineering, Sydney, Australia, 20–22 November 2024; Volume 402, pp. 1–9. [Google Scholar] [CrossRef]
- Walker, D. PASER Asphalt Roads Pavement Surface Evaluation and Rating PASER Manual Asphalt Roads; Madison: Lakewood, OH, USA, 2002. [Google Scholar]
- Shahin, M. Pavement Management for Airports, Roads, and Parking Lots, 2nd ed.; Springer: New York, NY, USA, 2005; ISBN 0387234640. [Google Scholar]
- Lima, D. Airport Pavement Management System for Cape Verde. Master Thesis, University of Beira Interior, Covilhã, Portugal, 2016. (In Portuguese). [Google Scholar]
- Osman, S.; Almoshaogeh, M.; Jamal, A.; Alharbi, F.; Al Mojil, A.; Dalhat, M. Intelligent Assessment of Pavement Condition Indices Using Artificial Neural Networks. Sustainability 2022, 15, 561. [Google Scholar] [CrossRef]
- Carvalho, T.; Soares, F.; Vita, R.; Francisco, R.; Basto, J.; Alcalá, S. A Systematic Literature Review of Machine Learning Methods Applied to Predictive Maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Singh, A.; Thakur, N.; Sharma, A. A Review of Supervised Machine Learning Algorithms. In Proceedings of the 10th INDIACom, 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; pp. 1310–1315. [Google Scholar]
- Maroco, J. Análise Estatística Com o SPSS Statistics; ReportNumber: Pêro Pinheiro, Portugal, 2014; ISBN 978-989-96763-4-3. [Google Scholar]
- Sarker, I. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-J.; Bae, S.-J.; Jang, M.-W. Linear Regression Machine Learning Algorithms for Estimating Reference Evapotranspiration Using Limited Climate Data. Sustainability 2022, 14, 11674. [Google Scholar] [CrossRef]
- Schonlau, M.; Zou, R. The Random Forest Algorithm for Statistical Learning. Stata J. 2020, 20, 3–29. [Google Scholar] [CrossRef]
- Kotsiantis, S. Supervised Machine Learning: A Review of Classification Techniques. Informatica 2007, 31, 249–268. [Google Scholar]
- Rudin, C.; Radin, J. Why Are We Using Black Box Models in AI When We Don’t Need To? A Lesson from an Explainable AI Competition. Harv. Data Sci. Rev. 2019, 1, 1–10. [Google Scholar] [CrossRef]
- Tu, J. Advantages and Disadvantages of Using Artificial Neural Networks versus Logistic Regression for Predicting Medical Outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Johnson, J.; Khoshgoftaar, T. Survey on Deep Learning with Class Imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Paracha, A.; Arshad, J.; Farah, M.; Ismail, K. Machine Learning Security and Privacy: A Review of Threats and Countermeasures. EURASIP J. Inf. Secur. 2024, 2024, 10. [Google Scholar] [CrossRef]
- Xu, Z.; Saleh, J. Machine Learning for Reliability Engineering and Safety Applications: Review of Current Status and Future Opportunities. Reliab. Eng. Syst. Saf. 2021, 211, 107530. [Google Scholar] [CrossRef]
- Rebolledo, J.; León, R.; Camapum de Carvalho, J. Performance Evaluation of Rigid Inclusion Foundations in the Reduction of Settlements. Soils Rocks 2019, 42, 265–279. [Google Scholar] [CrossRef]
- Barua, L.; Zou, B. Planning Maintenance and Rehabilitation Activities for Airport Pavements: A Combined Supervised Machine Learning and Reinforcement Learning Approach. Int. J. Transp. Sci. Technol. 2022, 11, 423–435. [Google Scholar] [CrossRef]
- Pietersen, R.; Beauregard, M.; Einstein, H. Automated Method for Airfield Pavement Condition Index Evaluations. Autom. Constr. 2022, 141, 104408. [Google Scholar] [CrossRef]
- Ali, A.; Esekbi, M.; Sreh, M. Predicting Pavement Condition Index Using Machine Learning Algorithms and Conventional Techniques. J. Pure Appl. Sci. 2022, 21, 304–309. [Google Scholar] [CrossRef]
- Kheirati, A.; Golroo, A. Machine Learning for Developing a Pavement Condition Index. Autom. Constr. 2022, 139, 104296. [Google Scholar] [CrossRef]
- Issa, A.; Samaneh, H.; Ghanim, M. Predicting Pavement Condition Index Using Artificial Neural Networks Approach. Ain Shams Eng. J. 2022, 13, 101490. [Google Scholar] [CrossRef]
- Lin, L.; Li, S.; Wang, K.; Guo, B.; Yang, H.; Zhong, W.; Liao, P.; Wang, P. A New FCM-XGBoost System for Predicting Pavement Condition Index. Expert. Syst. Appl. 2024, 249, 123696. [Google Scholar] [CrossRef]
- Shaheen, M.; Elsayed, R.A.; Ghazoly, H.; Bekheet, W.A. Explainable and Economical AI-Based Approach for PCI Assessment. Int. J. Pavement Eng. 2025, 26, 2531195. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.; Witten, I. The WEKA Workbench. In Data Mining; Elsevier: Amsterdam, The Netherlands, 2017; pp. 553–571. [Google Scholar]
- Yang, C.; Fridgeirsson, E.; Kors, J.; Reps, J.; Rijnbeek, P. Impact of Random Oversampling and Random Undersampling on the Performance of Prediction Models Developed Using Observational Health Data. J. Big Data 2024, 11, 7. [Google Scholar] [CrossRef]
- Hayaty, M.; Muthmainah, S.; Ghufran, S. Random and Synthetic Over-Sampling Approach to Resolve Data Imbalance in Classification. Int. J. Artif. Intell. Res. 2021, 4, 86. [Google Scholar] [CrossRef]
- Studart, A. Application of Artificial Intelligence Techniques. Machine Learning for Airport Pavement Condition Index (PCI) Assessment. Master Thesis, University of Beira Interior, Covilhã, Portugal, 2024. [Google Scholar]
- Schober, P.; Schwarte, L. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Mchugh, M. Interrater Reliability: The Kappa Statistic. Biochem. Med. 2012, 22, 272–282. [Google Scholar] [CrossRef]
- Hosmer, D.; Lemeshow, S.; Sturdivant, R. Applied Logistic Regression; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2013; ISBN 9780470582473. [Google Scholar]
- Domingos, A. Determination and Interpretation of the PCI for Airport Pavements. Master Thesis, University of Beira Interior, Covilhã, Portugal, 2017. (In Portuguese). [Google Scholar]
- ASTM D5340-12; ASTM International Standard Test Method for Airport Pavement Condition Index Surveys. Advancing Standards Transforming Markets: West Conshohocken, PA, USA, 2012.
- Quinlan, J. Learning with Continuous Classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Salzberg, S. C4.5: Programs for Machine Learning by J. Ross Quinlan. Morgan Kaufmann Publishers, Inc., 1993. Mach. Learn. 1994, 16, 235–240. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Shevade, S.; Keerthi, S.; Bhattacharyya, C.; Murthy, K. Improvements to the SMO Algorithm for SVM Regression. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef]
- Smola, A.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Feitosa, I.; Santos, B.; Gama, J.; Almeida, P.G. Statistical Analysis of an In-Vehicle Image-Based Data Collection Method for Assessing Airport Pavement Condition. Case Stud. Constr. Mater. 2025, 22, e04792. [Google Scholar] [CrossRef]
- Federal Highway Administration. Long-Term Pavement Performance Information Management System User Guide (Publication No. FHWA-HRT-21-038); U.S. Department of Transportation: Washington, DC, USA, 2021. [Google Scholar]
| PCI Classes | PCI Values | Type of Intervention | Cost-Impact | Performance Improvement |
|---|---|---|---|---|
| Good | 71–100 | Preventive maintenance | Low | Considerable |
| Fair | 56–70 | Short-term preventive maintenance or reconstruction (Rehabilitation trigger) | High | High |
| Poor | 0–55 | Minimum level of serviceability | Very high | Pavements overdo |
| Good | 86–100 | Routine maintenance | Very low | Small |
| Satisfactory | 71–85 | Preventive maintenance | Low | Considerable |
| Fair | 56–70 | Short-term preventive maintenance or reconstruction (Rehabilitation trigger) | High | High |
| Poor | 41–55 | Reconstructive maintenance | Very high | Pavements overdo |
| Very Poor | 26–40 | Short-term reconstruction | Very high | Pavements overdo |
| Serious | 11–25 | Urgent reconstruction | Extremely high | Pavements overdo |
| Failed | 0–10 | Immediate and complete reconstruction | Extremely high | Pavements overdo |
| Distress and Severity Level | No. of Entries | Rank |
|---|---|---|
| Alligator Cracking (Low) | 7 | 20 |
| Alligator Cracking (Medium) | 17 | 13 |
| Alligator Cracking (High) | 1 | 25 |
| Depression (Low) | 3 | 22 |
| Depression (Medium) | 8 | 17 |
| Depression (High) | 13 | 14 |
| Jet-Blast Erosion (Low) | 2 | 23 |
| Join Reflection Cracking (Low) | 117 | 2 |
| Join Reflection Cracking (Medium) | 104 | 3 |
| Join Reflection Cracking (High) | 1 | 25 |
| Longitudinal and Transverse Cracking (Low) | 138 | 1 |
| Longitudinal and Transverse Cracking (Medium) | 92 | 4 |
| Longitudinal and Transverse Cracking (High) | 8 | 17 |
| Oil Spillage (Low) | 1 | 25 |
| Patching and Utility Cut Patching (Low) | 12 | 15 |
| Patching and Utility Cut Patching (Medium) | 31 | 10 |
| Patching and Utility Cut Patching (High) | 81 | 5 |
| Polished Aggregate (Low) | 1 | 25 |
| Raveling (Low) | 19 | 12 |
| Raveling (Medium) | 46 | 9 |
| Raveling (High) | 59 | 7 |
| Rutting (Low) | 2 | 23 |
| Rutting (Medium) | 7 | 20 |
| Swell (Low) | 1 | 25 |
| Swell (Medium) | 8 | 17 |
| Swell (High) | 9 | 16 |
| Weathering (Low) | 20 | 11 |
| Weathering (Medium) | 54 | 8 |
| Weathering (High) | 71 | 6 |
| ML Algorithm | Training Options | PCI Output | Algorithm (WEKA) |
|---|---|---|---|
| Linear Regression (LR) | Training set CV10 80/20 split | Numerical | Linear regression |
| Decision Tree (DT) | Training set CV10 80/20 split | Numerical Categoric | M5P [46] J48 [47] |
| Random Forest (RF) | Training set CV10 80/20 split | Numerical Categoric | Random Forest [48] |
| Artificial Neural Network (ANN) | Training set CV10 80/20 split | Numerical Categoric | Multilayer Perception (MLP) [37] |
| Support Vector Machine (SVM) | Training set CV10 80/20 split | Numerical Categoric | SMOreg [49,50] SMO [49,50] |
| WEKA Hyperparameters | LR | DT (M5P) | RF | ANN (MLP) | SVM (SMOreg) |
|---|---|---|---|---|---|
| attributeSelectionMethod | M5 | - | - | - | - |
| batchSize | 100 | 100 | - | 100 | 100 |
| debug | False | False | False | False | False |
| doNotCheckCapabilities | False | False | False | False | False |
| eliminateColinearAttributes | True | - | - | - | - |
| minimal | False | - | - | - | - |
| numDecimalPlaces | 4 | 4 | 2 | 2 | 2 |
| outputAdditionalStats | False | - | - | - | - |
| ridge | 1.0 × 10−8 | - | - | - | - |
| useQRDecomposition | False | - | - | - | - |
| buildRegressionTree | - | False | - | - | - |
| minNumInstances | - | 4.0 | - | - | - |
| saveInstances | - | False | - | - | - |
| unpruned | - | False | - | - | - |
| useUnsmoothed | - | False | - | - | - |
| bagSizePercent | - | - | 100 | - | - |
| breakTiesRandomly | - | - | False | - | - |
| calcOutOfBag | - | - | False | - | - |
| computeAttributeImportance | - | - | False | - | - |
| maxDeep | - | - | 0 | - | - |
| numExecutionSlots | - | - | 1 | - | - |
| numFeatures | - | - | 0 | - | - |
| outputOutOfBagComplexity Statistics | - | - | 0 | - | - |
| printClassifiers | - | - | False | - | - |
| seed | - | - | 1 | 0 | - |
| storeOutOfBagPredictions | - | - | False | - | - |
| GUI * | - | - | - | False | - |
| autoBuild | - | - | - | True | - |
| decay | - | - | - | Falce | - |
| hiddenLayers | - | - | - | a ** | - |
| learningRate | - | - | - | 0.3 | - |
| momentun | - | - | - | 0.2 | - |
| nominalToBinaryFilter | - | - | - | True | - |
| normalizeAttributes | - | - | - | True | - |
| normalizeNumericClass | - | - | - | True | - |
| reset | - | - | - | True | - |
| resume | - | - | - | False | - |
| trainingTime | - | - | - | 500 epochs | - |
| validationSetSize | - | - | - | 0 | - |
| validationThreshold | - | - | - | 20 | - |
| c *** | - | - | - | - | 1.0 |
| filterType | - | - | - | - | Normalize training data |
| kernel | - | - | - | - | PolyKernel -E 1.0 -C 250007 |
| regOptimizer | - | - | - | - | RegSMOImproved -T 0.001 -V -P 1.0 × 10−12 -L 0.001 |
| WEKA Hyperparameters | DT (J48) | RF | ANN (MLP) | SVM (SMO) |
|---|---|---|---|---|
| batchSize | 100 | 100 | 100 | 100 |
| binarySplits | False | - | - | - |
| collapseTree | True | - | - | - |
| confidenceFactor | 0.25 | - | - | - |
| debug | False | False | False | - |
| doNotCheckCapabilities | False | False | False | - |
| doNotMakeSplitPointActualValue | False | - | - | - |
| minNumObj | 2 | - | - | - |
| numDecimalPlaces | 2 | 2 | 2 | 2 |
| numFolds | 3 | - | - | - |
| reducedErrorPruning | False | - | - | - |
| saveInstanceData | False | - | - | - |
| seed | 1 | 1 | 0 | - |
| subtreeRaising | True | - | - | - |
| unpruned | False | - | - | - |
| useLaplace | False | - | - | - |
| useMDLCorrection | True | - | - | - |
| bagSizePercent | - | 100 | - | - |
| breakTiesRandomly | - | False | - | - |
| calcOutOfBag | - | False | - | - |
| computeAttributeImportance | - | False | - | - |
| naxDepth | - | 0 | - | - |
| numExecutionSlots | - | 1 | - | - |
| numIterations | - | 100 | - | - |
| outputOutOfBagComplexity Statistics | - | False | - | - |
| printClassifiers | - | False | - | - |
| storeOutOfBagPredictions | - | False | - | - |
| GUI * | - | - | False | - |
| autoBuild | - | - | True | - |
| decay | - | - | False | - |
| hiddenLayers | - | - | a ** | - |
| learningRate | - | - | 0.3 | - |
| momentum | - | - | 0.2 | - |
| nominalToBinaryFilter | - | - | True | - |
| normalizeAttributes | - | - | True | - |
| normalizeNumericClass | - | - | True | - |
| reset | - | - | True | - |
| resume | - | - | False | - |
| trainingTime | - | - | 500 epochs | - |
| validationSetSize | - | - | 0 | - |
| validationThreshold | - | - | 20 | - |
| buildCalibrationModels | - | - | - | False |
| c *** | - | - | - | 1.0 |
| calibrator | - | - | - | Logistic -R 1.0 × 10−8 -M −1 -num-decimal-places 4 |
| checksTurnedOff | - | - | - | False |
| epsilon | - | - | - | 1.0 × 10−12 |
| filterType | - | - | - | Normalize training data |
| kernel | - | - | - | PolyKernel -E 1.0 -C 250007 |
| numFolds | - | - | - | −1 |
| randomSeed | - | - | - | 1 |
| toleranceParameter | - | - | - | 0.001 |
| Validation Metric | Algorithms | ||||
|---|---|---|---|---|---|
| LR | DT | RF | ANN | SVM | |
| Training | 80/20 split | CV10 | CV10 | 80/20 split | 80/20 split |
| CC | 0.88 | 0.91 | 0.93 | 0.88 | 0.88 |
| R2 | 0.77 | 0.82 | 0.86 | 0.77 | 0.77 |
| MAE | 8.41 | 6.22 | 5.81 | 7.43 | 8.26 |
| RMSE | 11.48 | 9.22 | 8.73 | 11.39 | 11.38 |
| RAE (%) | 39.83 | 29.97 | 27.97 | 35.18 | 39.13 |
| RRSE (%) | 49.74 | 40.16 | 38.02 | 49.35 | 49.31 |
| aPCI | 58.79 | 58.58 | 58.58 | 58.77 | 58.77 |
| pPCI | 59.68 | 58.83 | 60.10 | 55.87 | 59.50 |
| Error (aPCI-pPCI) | −1.00 | −0.24 | −1.51 | 2.90 | −0.72 |
| Algorithm Ranking | Ranking Analysis | Comparation Analysis | ||
|---|---|---|---|---|
| > (Wins) | < (Losses) | CC (Mean ± sd) | Comparison vs. RF (Victories/Ties/Losses) | |
| RF | 2 | 0 | 0.93 ± 0.03 | - |
| DT | 0 | 0 | 0.90 ± 0.05 | (0, 1, 0) slightly worse, significant difference |
| LR | 0 | 0 | 0.80 ± 0.19 | (0, 1, 0) worse |
| ANN | 0 | 1 | 0.85 ± 0.08 | (0, 0, 1) worse |
| SVM | 0 | 1 | 0.80 ± 0.18 | (0, 0, 1) worse |
| Rank | Attribute (Independent Variable and Severity Level) | Score |
|---|---|---|
| 1 | Raveling (Medium) | 0.0756 |
| 2 | Depression (High) | 0.0513 |
| 3 | Weathering (Medium) | 0.0464 |
| 4 | Rutting (High) | 0.0409 |
| 5 | Swell (High) | 0.0398 |
| 6 | Swell (Medium) | 0.0333 |
| 7 | Alligator Cracking (Medium) | 0.0270 |
| 8 | Raveling (High) | 0.0262 |
| 9 | Alligator Cracking (Low) | 0.0236 |
| 10 | Longitudinal and Transverse Cracking (High) | 0.0226 |
| 11 | Rutting (Medium) | 0.0225 |
| 12 | Weathering (Low) | 0.0181 |
| 13 | Patching and Utility Cut Patching (High) | 0.0170 |
| 14 | Raveling (Low) | 0.0140 |
| 15 | Depression (Medium) | 0.0139 |
| Validation Metric | Algorithms | ||||
|---|---|---|---|---|---|
| LR | DT | RF | ANN | SVM | |
| Training | - | CV10 | CV10 | CV10 | CV10 |
| Kappa statistic | - | 0.80 | 0.88 | 0.82 | 0.80 |
| MAE | - | 0.09 | 0.10 | 0.07 | 0.26 |
| RMSE | - | 0.24 | 0.21 | 0.23 | 0.33 |
| RAE (%) | - | 24.65 | 25.58 | 19.56 | 67.58 |
| RRSE (%) | - | 57.11 | 48.15 | 54.00 | 75.60 |
| Error (%) (Incorrectly classified) | - | 10.72 | 6.51 | 9.96 | 11.11 |
| Confusion Matrix | Precision | ROC Area | Class | ||
|---|---|---|---|---|---|
| a | b | c | |||
| 99 | 4 | 2 | 0.93 | 0.97 | a |
| 6 | 12 | 4 | 0.75 | 0.81 | b |
| 1 | 0 | 133 | 0.95 | 0.992 | c |
| - | - | - | 0.93 | 0.970 | Avg. |
| Algorithm Ranking | Ranking Analysis | Comparation Analysis | ||
|---|---|---|---|---|
| > (Wins) | < (Losses) | Kappa Statistic (Mean ± sd) | Comparison vs. RF (Victories/Ties/Losses) | |
| RF | 2 | 0 | 0.88 ± 0.09 | - |
| ANN | 0 | 0 | 0.82 ± 0.11 | (0, 1, 0) slightly worse, significant difference |
| DT | 0 | 1 | 0.83 ± 0.09 | (0, 0, 1) worse |
| SVM | 0 | 1 | 0.80 ± 0.11 | (0, 0, 1) worse |
| Rank | Attribute (Independent Variable and Severity Level) | Score |
|---|---|---|
| 1 | Join Reflection Cracking (Low) | 0.6776 |
| 2 | Longitudinal and Transverse Cracking (Low) | 0.6032 |
| 3 | Join Reflection Cracking (Medium) | 0.5469 |
| 4 | Patching and Utility Cut Patching (High) | 0.4993 |
| 5 | Weathering (High) | 0.3800 |
| 6 | Longitudinal and Transverse Cracking (Medium) | 0.3542 |
| 7 | Raveling (High) | 0.3216 |
| 8 | Patching and Utility Cut Patching (Medium) | 0.1561 |
| 9 | Weathering (Medium) | 0.1492 |
| 10 | Raveling (Medium) | 0.1235 |
| 11 | Alligator Cracking (Medium) | 0.0905 |
| 12 | Weathering (Low) | 0.0520 |
| 13 | Depression (High) | 0.0520 |
| 14 | Patching and Utility Cut Patching (Low) | 0.0466 |
| 15 | Swell (High) | 0.0466 |
| Validation Metric | Algorithms | ||||
|---|---|---|---|---|---|
| LR | DT | RF | ANN | SVM | |
| Training | - | CV10 | CV10 | CV10 | CV10 |
| Kappa statistic | - | 0.56 | 0.58 | 0.54 | 0.51 |
| MAE | - | 0.09 | 0.10 | 0.10 | 0.21 |
| RMSE | - | 0.2642 | 0.23 | 0.26 | 0.32 |
| RAE (%) | - | 46.78 | 51.34 | 49.09 | 103.70 |
| RRSE (%) | - | 82.53 | 72.83 | 80.52 | 98.85 |
| Error (%) (Incorrectly classified) | - | 30.65 | 29.11 | 32.56 | 33.33 |
| Confusion Matrix | Prec. | ROC Area | Class | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | g | |||
| 33 | 5 | 3 | 5 | 1 | 0 | 0 | 0.51 | 0.89 | a |
| 16 | 9 | 1 | 2 | 1 | 0 | 0 | 0.45 | 0.86 | b |
| 12 | 4 | 7 | 3 | 0 | 0 | 1 | 0.54 | 0.87 | c |
| 3 | 1 | 1 | 12 | 5 | 0 | 0 | 0.52 | 0.83 | d |
| 0 | 1 | 0 | 1 | 117 | 3 | 0 | 0.91 | 0.99 | e |
| 0 | 0 | 0 | 0 | 5 | 7 | 0 | 0.70 | 0.98 | f |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0.00 | 0.99 | g |
| - | - | - | - | - | - | - | 0.68 | 0.93 | Avg. |
| Algorithm Ranking | Ranking Analysis | Comparation Analysis | ||
|---|---|---|---|---|
| > (Wins) | < (Losses) | Kappa Statistic (Mean ± sd) | Comparison vs. RF (Victories/Ties/Losses) | |
| RF | 1 | 0 | 0.59 ± 0.10 | - |
| DT | 0 | 0 | 0.53 ± 0.11 | (0, 1, 0) slightly worse, significant difference |
| ANN | 0 | 0 | 0.54 ± 0.10 | (0, 1, 0) slightly worse, significant difference |
| SVM | 0 | 1 | 0.52 ± 0.08 | (0, 0, 1) worse |
| PCI Classes | No. of Sample Units | ||
|---|---|---|---|
| Original Database | Database After ROS (SMOTE) | Database After RUS | |
| Very Poor | 47 | 94 | 20 |
| Poor | 29 | 116 | 20 |
| Serious | 27 | 108 | 20 |
| Fair | 22 | 88 | 20 |
| Satisfactory | 122 | 122 | 20 |
| Good | 12 | 96 | 12 |
| Failed | 2 | 115 | 2 |
| Total cases | 261 | 739 | 114 |
| Parameters | DT | RF | ||||
|---|---|---|---|---|---|---|
| Original | RUS | ROS (SMOTE) | Original | RUS | ROS (SMOTE) | |
| Training | CV10 | CV10 | CV10 | CV10 | CV10 | CV10 |
| Kappa statistic | 0.56 | 0.46 | 0.80 | 0.58 | 0.55 | 0.91 |
| MAE | 0.09 | 0.13 | 0.05 | 0.10 | 0.15 | 0.05 |
| RMSE | 0.26 | 0.32 | 0.22 | 0.23 | 0.27 | 0.14 |
| RAE (%) | 46.78 | 56.86 | 19.61 | 51.34 | 62.23 | 22.55 |
| RRSE (%) | 82.53 | 94.03 | 62.63 | 72.83 | 78.60 | 39.64 |
| Error (%) (Incorrectly Classified) | 30.65 | 44.73 | 16.78 | 29.11 | 36.84 | 7.17 |
| Parameters | ANN | SVM | ||||
|---|---|---|---|---|---|---|
| Original | RUS | ROS (SMOTE) | Original | RUS | ROS (SMOTE) | |
| Training | CV10 | CV10 | CV10 | CV10 | CV10 | CV10 |
| Kappa statistic | 0.54 | 0.48 | 0.83 | 0.51 | 0.39 | 0.71 |
| MAE | 0.10 | 0.14 | 0.05 | 0.21 | 0.22 | 0.21 |
| RMSE | 0.26 | 0.32 | 0.17 | 0.32 | 0.32 | 0.31 |
| RAE (%) | 49.09 | 57.16 | 20.72 | 103.70 | 90.79 | 85.61 |
| RRSE (%) | 80.52 | 92.68 | 50.29 | 98.85 | 93.13 | 88.52 |
| Error (%) (Incorrectly Classified) | 32.56 | 42.98 | 14.88 | 33.33 | 50.00 | 24.35 |
| Confusion Matrix | Prec. | ROC Area | Class | ||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | e | f | g | |||
| 78 | 8 | 3 | 4 | 1 | 0 | 0 | 0.84 | 0.98 | a |
| 9 | 103 | 0 | 3 | 1 | 0 | 0 | 0.88 | 0.99 | b |
| 4 | 3 | 100 | 1 | 0 | 0 | 0 | 0.95 | 0.99 | c |
| 2 | 2 | 1 | 80 | 3 | 0 | 0 | 0.90 | 0.99 | d |
| 0 | 1 | 0 | 1 | 115 | 5 | 0 | 0.96 | 0.99 | e |
| 0 | 0 | 0 | 0 | 0 | 96 | 0 | 0.95 | 1.00 | f |
| 0 | 0 | 1 | 0 | 0 | 0 | 104 | 1.00 | 1.00 | g |
| - | - | - | - | - | - | - | 0.93 | 0.99 | Avg. |
| Algorithm Ranking | Ranking Analysis | Comparation Analysis | ||
|---|---|---|---|---|
| > (Wins) | < (Losses) | Kappa Statistic (Mean ± sd) | Comparison vs. RF (Victories/Ties/Losses) | |
| RF | 3 | 0 | 0.92 ± 0.03 | - |
| DT | 1 | 1 | 0.84 ± 0.05 | (0, 0, 1) worse |
| ANN | 1 | 1 | 0.83 ± 0.05 | (0, 0, 1) worse |
| SVM | 0 | 3 | 0.70 ± 0.05 | (0, 0, 1) worse |
| Rank | Attribute (Independent Variable and Severity Level) | Score |
|---|---|---|
| 1 | Raveling (High) | 0.9552 |
| 2 | Patching and Utility Cut Patching (High) | 0.7793 |
| 3 | Alligator Cracking (Medium) | 0.7650 |
| 4 | Rutting (High) | 0.6651 |
| 5 | Join Reflection Cracking (Low) | 0.6624 |
| 6 | Raveling (Medium) | 0.6523 |
| 7 | Swell (High) | 0.6038 |
| 8 | Jet-Blast Erosion (Low) | 0.5986 |
| 9 | Swell (Medium) | 0.5969 |
| 10 | Join Reflection Cracking (Medium) | 0.5708 |
| 11 | Weathering (High) | 0.5112 |
| 12 | Longitudinal and Transverse Cracking (Medium) | 0.4897 |
| 13 | Longitudinal and Transverse Cracking (Low) | 0.4814 |
| 14 | Weathering (Medium) | 0.3445 |
| 15 | Patching and Utility Cut Patching (Medium) | 0.3333 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, B.; Studart, A.; Almeida, P. Assessment of Airport Pavement Condition Index (PCI) Using Machine Learning. Appl. Syst. Innov. 2025, 8, 162. https://doi.org/10.3390/asi8060162
Santos B, Studart A, Almeida P. Assessment of Airport Pavement Condition Index (PCI) Using Machine Learning. Applied System Innovation. 2025; 8(6):162. https://doi.org/10.3390/asi8060162
Chicago/Turabian StyleSantos, Bertha, André Studart, and Pedro Almeida. 2025. "Assessment of Airport Pavement Condition Index (PCI) Using Machine Learning" Applied System Innovation 8, no. 6: 162. https://doi.org/10.3390/asi8060162
APA StyleSantos, B., Studart, A., & Almeida, P. (2025). Assessment of Airport Pavement Condition Index (PCI) Using Machine Learning. Applied System Innovation, 8(6), 162. https://doi.org/10.3390/asi8060162






