Leveraging Explainable Artificial Intelligence for Genotype-to-Phenotype Prediction: A Case Study in Arabidopsis thaliana

Abstract

Predicting phenotypes from genomic data can significantly advance agriculture. Genomic selection, which uses genome-wide DNA markers to identify individuals with high genetic value, enhances the accuracy of breeding programs. While linear models are routinely used for genomic selection (GS), machine learning (ML) models offer complementary potential. In this study, robust ML-based models were developed to predict five phenotypic traits—three related to flowering time and two to leaf number—in Arabidopsis thaliana, a model plant with a fully sequenced genome. Using explainable artificial intelligence (XAI), specifically SHapley Additive exPlanations (SHAP) values, we identified SNPs that contributed most to trait prediction. Many of these SNPs were located in or near genes known to regulate flowering and stem elongation, such as DOG1 and VIN3, supporting the biological plausibility of the model. SHAP also enabled local interpretability at the single-plant level, revealing the genotypic basis of individual predictions. Our results indicate that integrating ML with XAI improves model interpretability and provides predictive performance comparable to traditional methods. This approach confirms known genotype–phenotype relationships and highlights new candidate loci, paving the way for functional validation. The proposed methodology offers promising applications in precision breeding and translation of insights from Arabidopsis to crop species.

1. Introduction

Predicting phenotypes from genomic information is a pivotal challenge in modern breeding, which needs to enhance cultivars for complex traits, including adaptation to climate changes, while enhancing resource use efficiency. Genomic selection (GS) has emerged as a promising approach, enabling breeders to select plants with desired traits directly from genotypic data. GS uses genome-wide markers to forecast phenotypes or breeding values, as initially proposed by Meuwissen et al. [1]. State-of-the-art methods such as the Best Linear Unbiased Predictor (BLUP) and its variants, including genomic BLUP (GBLUP) and Ridge Regression BLUP (RR-BLUP), have become central to predicting additive genetic effects in plant breeding across diverse species and traits [2,3]. However, as breeding challenges become more complex, particularly with non-additive genetic effects, machine learning (ML) techniques have emerged to complement these traditional methods [4,5,6,7]. Recently, transformer-based architectures and multi-task learning have also shown promise for crop genomic prediction. In particular, models such as Cropformer and MtCro have reported improved ability to capture complex genomic patterns and to enhance prediction across multiple traits [8,9,10].

Ensemble-based methods like Random Forests (RFs) and gradient boosting techniques such as XGBoost (XGB) and CatBoost have gained traction for their ability to capture complex genetic architectures and improve prediction accuracy [11,12,13]. Studies indicate that ML algorithms can enhance accuracy in genomic selection [14,15,16], making it possible to utilize intricate and complex data.

Moreover, to make these sophisticated ML models more interpretable and biologically meaningful, combining ML with explainable artificial intelligence (XAI) has gained traction, offering the potential to illuminate the genetic mechanisms underlying trait prediction [17,18]. XAI techniques aim to augment the interpretability of ML models, providing transparency and insights into the biological bases underlying genotype-to-phenotype predictions [19].

XAI comprises methods that make complex models transparent by attributing predictions to input features at both the global (model-level) and local (sample-level) scales. Among these, SHAP (SHapley Additive exPlanations) provides theoretically grounded, additive attributions for individual predictions and has become a widely adopted tool for interpreting black-box models [20]. XAI has been increasingly applied across the life sciences to bridge predictive accuracy with biological insight: from clinical decision support and healthcare model design [21,22] to omics-driven discovery where interpretable attributions help prioritize variants, genes, and pathways for hypothesis generation [23]. Building on this literature, our study leverages SHAP to connect predictive performance with mechanistic clues in genomic prediction, enabling trait- and plant-specific interpretations.

In the context of crop improvement, GS has revolutionized the association of Single-Nucleotide Polymorphisms (SNPs) with breeding values, expediting breeding cycles and enhancing genetic gains in crops [3,24]. Despite ongoing research, the biological mechanisms driving genotype-to-phenotype predictions remain elusive. While integrating associated SNPs through supervised feature selection techniques into prediction models has proven promising, outcomes have been varied. Consequently, there is a growing need to explore non-linear models and leverage data from feature selection algorithms to refine predictions [25,26]. Identifying critical loci is crucial not only for model construction but also for data reduction through feature selection in subsequent iterations.

In this study, feature selection was applied not only to optimize model accuracy but also to reduce data dimensionality. This is particularly important given the high number of SNPs relative to the number of samples, as it reduces computational time and mitigates the risk of overfitting, all while maintaining model interpretability within the context of XAI.

Exploring a variety of ML algorithms is advisable when predicting genotype-to-phenotype relationships, as each algorithm operates based on unique assumptions and biases. No single algorithm universally delivers optimal performance across all traits [27]. In this study, robust prediction models were developed for five phenotypic traits in Arabidopsis thaliana, a model plant for genomic studies for which high-quality genomes and phenotypes of more than 1000 genotypes are publicly available.

By employing explainable artificial intelligence, specifically SHapley Additive exPlanations (SHAP) values, we enhance interpretability in genomic prediction models. SHAP values provide insights into the contribution of each feature to the model’s predictions, elucidating the underlying mechanisms driving genotype-to-phenotype predictions. By offering local explanations, SHAP enables precise, plant-specific insights, identifying the most relevant SNPs for each plant. This capability is particularly valuable for precision breeding, where decisions must be tailored to individual plants.

While previous studies have explored the application of machine learning models for genotype-to-phenotype prediction, our work contributes to the field by systematically integrating SHAP-based explainability with ensemble methods across multiple traits in Arabidopsis thaliana. This integrated approach, applied to a large-scale dataset from the 1001 Genomes Project, enables trait-specific interpretation at the individual plant level, which is essential for precision breeding.

This comprehensive background sets the stage for exploring genomic prediction methodologies in Arabidopsis thaliana, highlighting the intersection of machine learning and traditional breeding practices in crop improvement endeavors.

2. Materials and Methods

In Figure 1, the workflow of the analysis is depicted. We utilized publicly available SNP genotype data, integrating it with various phenotypic variables to predict these variables based on genetic factors. The initial step involved preprocessing the SNP data. The processed data were then fed into regression algorithms to obtain phenotype predictions. The results obtained from mixed linear models were compared with those derived from an XAI-based approach. Specifically, for the XAI approach, additional steps were taken to interpret the results obtained.

Figure 1. Workflow of the analysis. The process involves data preprocessing, regression using mixed linear models and XAI models, genotype-to-phenotype prediction, and explanation of the predictions.

2.1. Materials

The SNP genotypic data used in our study pertains to the model plant species Arabidopsis thaliana, for which extensive genomic and phenotypic information is publicly available [28]. Specifically, we used the SNP matrix file of the 1001 Genomes Consortium [29,30], which contains about 10 million variants and is filtered for heterozygous loci that might introduce bias due to duplicated regions [31]. This dataset encompasses genetic information from 1135 A. thaliana accessions selected from a globally representative hierarchical collection [32]. The genetic data consisted of approximately 10 million biallelic SNPs that had undergone quality control filtering.

Regarding the phenotypic variables targeted for prediction, five traits were considered (Table 1), namely Days Until Emergence of Visible Flowering Buds in the Center of the Rosette from Time of Sowing (DTF1), Days Until the Inflorescence Stem Elongated to 1 cm (DTF2), Days Until First Open Flower (DTF3), Rosette Leaf Number (RL), and Cauline Leaf Number (CL). Table 1 also provides the number of accessions available for each trait. Plants were grown under controlled conditions, as specified in Table 1. For the phenotypic traits analyzed, not all 1135 accessions were available. As shown in Table 1, each phenotype was measured on a specific subset: 936 for DTF1, 931 for DTF2, 923 for DTF3, 850 for RL, and 904 for CL. The machine learning models were trained and validated on these subsets, using only accessions with complete phenotype data.

Table 1. Overview of the phenotypic traits selected for this study. Growth conditions: Seeds from 1135 Arabidopsis thaliana accessions (1001 Genomes Consortium, 2016) were surface-sterilized in 95% ethanol for 5 min and air-dried. After 6 days of stratification at 4 °C in 0.1% agarose, seeds were distributed across 4800 pots as four replicates in a randomized block design. Plants were grown in controlled chambers (16 h light/8 h dark, 16 °C constant temperature, 65% humidity). Trays were rotated every other day to minimize position effects.

ID	Phenotypic Trait	Abbreviation	Number of Accessions	URL
1	Days until emergence of visible flowering buds in the center of the rosette from time of sowing	DTF1	936	https://arapheno.1001genomes.org/phenotype/703/ (accessed on 4 April 2024)
2	Days until the inflorescence stem elongated to 1 cm	DTF2	931	https://arapheno.1001genomes.org/phenotype/701/ (accessed on 4 April 2024)
3	Days until first open flower	DTF3	923	https://arapheno.1001genomes.org/phenotype/702/ (accessed on 4 April 2024)
4	Rosette leaf number	RL	850	https://arapheno.1001genomes.org/phenotype/704/ (accessed on 4 April 2024)
5	Cauline leaf number	CL	904	https://arapheno.1001genomes.org/phenotype/705/ (accessed on 4 April 2024)

2.2. Methods

2.2.1. Preprocessing

SNP data underwent preprocessing to enhance quality and informativeness, ensuring suitability for accurate and robust downstream genotype–phenotype prediction analyses (Figure 2). In more detail, the input Variant Call Format (VCF) file containing 10,709,949 SNPs was initially filtered using the software PLINK 1.9 [33]. Variants with a minor allele frequency (MAF) of less than $0.05$ were removed from the dataset to filter out rare variants and reduce their impact on subsequent analyses [34]. Subsequently, SNPs were subjected to linkage disequilibrium (LD) pruning using PLINK 1.9, a tool for whole-genome association analysis. At each step of LD pruning, pairs of variants within the current window were assessed for LD, with variants having an $R^2$ greater than the threshold of $0.8$ being identified. This threshold was chosen to minimize collinearity between SNPs while retaining informative markers. The greedy pruning approach employed by PLINK 1.9 ensures that we systematically reduce LD within a window size, further optimizing the feature set for model training [35,36].

Figure 2. SNP data preprocessing workflow. The figure illustrates the preprocessing steps applied to the SNP dataset. The input consisted of $10.7$ M SNPs. After applying a minor allele frequency (MAF) filter (<0.05), $1.69$ M SNPs remained (15.8% of the initial dataset). Linkage disequilibrium (LD) pruning with $R^2>0.8$ further reduced the set to 522 K SNPs (4.9% of the initial dataset). The final step involves imputation to handle missing genotype data.

Lastly, for handling missing data, genotype imputation was conducted using Beagle 5.1, a state-of-the-art imputation tool. Beagle uses phased haplotypes to accurately impute missing genotypes by leveraging population-level linkage patterns. This ensures the completeness of the genetic data without biasing model training due to incomplete genotypes [37,38].

After the completion of the genotype data preprocessing steps, the following encoding of genomic data was conducted for subsequent analyses:

• “0/0”, representing genotypes homozygous for the reference allele (REF), were encoded as “0”;
• “1/1”, indicating genotypes homozygous for the alternate allele (ALT), were encoded as “1”.

2.2.2. Regression Analysis

In this study, we compared the results of various regression models to predict each phenotypic trait from genotypic data. We evaluated both state-of-the-art genomic prediction models, represented by mixed linear regressors, and machine learning-based models. The validation procedure, depicted in Figure 3, was designed to measure the performance of the models accurately.

Figure 3. Workflow of the validation procedure. The full dataset was divided into 10 folds for cross-validation. In each iteration, 9 folds were used for training and 1 fold was used for validation. Feature selection was performed within each training fold to prevent data leakage. The SHAP values were then calculated for each model across the validation folds, providing insights into the contribution of each feature to the model’s predictions. This comprehensive validation approach ensured the reliability and generalizability of the predictive models.

To evaluate the performance of the models, a 10-fold cross-validation (K = 10) was adopted. Ten different models were trained, and predictions were calculated for each cycle of the cross-validation on the remaining validation fold. The machine learning-based approach also involved feature selection algorithms due to the necessity of reducing the number of features, as an excessive number of variables compared to the number of accessions could lead to overfitting [39]. The primary goal of feature selection was not solely to enhance predictive performance but also to reduce the dimensionality of the dataset, improving computational efficiency and minimizing the risk of overfitting. Given the large number of SNPs compared to samples, feature selection is critical for ensuring interpretability, particularly when using SHAP for explainable artificial intelligence (XAI). To ensure integrity and independence of the test set, feature selection was nested within the cross-validation to prevent data leakage. Performing feature selection on all of the data and then cross-validating could bias the performance analysis since the test data in each fold of the CV procedure would also be used to choose the features [40,41]. Thus, feature selection was applied to each split of the CV, followed by training an ML regression model.

For the computation of SHAP values aimed at providing an explanation of results, the SHAP value for each strain was calculated by combining the SHAP values across the ten models trained in cross-validation. This comprehensive validation approach ensured the reliability and generalizability of the predictive models developed in this study.

2.2.3. Mixed Linear Models

Ridge Regression BLUP (rrBLUP) assumes a linear mixed additive model where each marker is assigned an effect as a solution of the equation

$$y=\mu +Gu+ϵ$$

(1)

where y is the array of observed phenotypes with mean value $\mu$, where G is the genotype matrix with values in [0, 1, 2] (for diploid SNP markers), $u\sim N(0,I{\sigma }_u^2)$ contains the marker effects to be estimated, and $ϵ$ contains the residuals. The standard ridge regression solution becomes

$$\widehat{u}=G^{\prime }{(G{G}^{\prime }+\lambda I)}^{-1}(y-\mu )$$

(2)

with $\lambda ={\sigma }_e^2/{\sigma }_u^2$ being the ridge parameter, i.e., the ratio between residual and marker variance. We obtained the estimated allele effects by solving the above equations on the training set. We then used $\widehat{u}$ to predict $\widehat{y}$ for the samples in the validation set. Cross-validations, model solutions and predictions, and performance metrics were computed using the R package GROAN [6], which internally leveraged the rrBLUP package [42].

2.2.4. XAI Models

Feature Selection

Feature selection plays a pivotal role in data preprocessing as it determines the essential features for analysis. Not only does it eliminate irrelevant features, but it also identifies the most significant ones, thereby enhancing the model’s performance. In our work, we employed a feature selection technique based on Mutual Information (MI) Gain [43,44,45]. This method, a univariate filtering approach, offers improved accuracy to the model [46]. MI estimates the mutual information for continuous target variables in regression problems (phenotypic traits), leveraging the entropy of the variables (SNPs). It quantifies the dependency between variables, with higher values indicating stronger dependency. Essentially, MI measures the information one variable provides about another. Like other feature selection techniques, its goal is to reduce the size of the input feature set. This reduction in features can simplify the problem, reduce computational time, and potentially enhance model performance.

For each studied phenotypic trait, we analyzed its Manhattan plot. We then selected only SNPs with mutual information above the $0.90$ quantile. To test the robustness of this choice, we further evaluated alternative thresholds (0.80, 0.85, 0.95, 0.975, and 0.99), and the results are reported in Supplementary Table S2.

Machine Learning Regressors

Ensemble learning has emerged as a highly popular option for regression tasks in recent years. Among the various choices available, Random Forest (RF) has garnered widespread adoption [47]. Random Forests are built by bootstrapping the data sample and growing multiple regression trees, each utilizing a different bootstrap sample from the original dataset. Notably, RF introduces an additional layer of randomness compared to bagging strategies, as each tree is grown with a different set of predictors randomly selected at each node split. One of the primary advantages of RF over traditional regression strategies lies in its robustness against overfitting. This characteristic makes it particularly valuable in practical applications where generalization is crucial. Additionally, RF offers the advantage of providing insights into feature importance, thus facilitating the interpretation of model results. This capability is especially valuable in domains such as clinical applications, where understanding the relationship between independent and dependent variables is essential. For this study, RF regression was implemented using the default parameters of the scikit-learn package.

Gradient boosting is a class of ensemble machine learning algorithms widely used for regression predictive modeling tasks. These ensembles are built from decision tree models, with trees added sequentially to the ensemble and trained to correct prediction errors made by prior models. This approach, known as boosting, enhances the predictive power of the ensemble. XGBoost, short for Extreme Gradient Boosting, represents an efficient open-source implementation of the gradient boosting algorithm. It stands out for its computational efficiency and effectiveness, often surpassing other open-source implementations in terms of performance. XGBoost is designed to optimize both execution speed and model accuracy, making it a preferred choice for many regression tasks [48]. In this study, XGBoost regression was employed using the default parameters of the xgboost Python package, ensuring consistency and ease of implementation in the analysis pipeline.

CatBoost, a recently introduced open-source machine learning tool, represents a robust algorithm within the realm of gradient boosted decision trees. It has demonstrated promising outcomes across various standard machine learning tasks [49]. One of the distinguishing features of the CatBoost model is its utilization of ordered boosting and its adept handling of categorical features during the training process, marking a significant advancement compared to conventional gradient boosted decision trees. Notably, CatBoost has showcased superior performance when dealing with non-numeric or categorical features, outperforming other gradient boosting algorithms [50]. For this study, we employed the default parameters of the CatBoost Python package.

Explainability

To conduct the explainable artificial intelligence analysis and ensure interpretation and transparency of the results, we computed SHAP (SHapley Additive exPlanations) values. The calculation of SHAP facilitates the interpretation of complex machine learning models by providing insights into the contribution of individual features to model predictions. SHAP values offer explanations for model predictions by utilizing classic equations derived from cooperative game theory [51]. These values quantify the degree of interaction between features and the predicted values, providing insights into the impact of each feature on the overall predictions. The computation of SHAP values involves evaluating the difference in model output predictions with and without specific features, considering all possible feature subsets. Consequently, the model necessitates retraining on all subsets F of the complete set S of features ($F\subseteq S$). The SHAP value for the $j-th$ feature of the instance x is determined by aggregating it across all possible subsets:

$$SHA{P}_j\left(x\right)=\sum _{F\subseteq S-\left\{j\right\}}{\displaystyle \frac{\left|F\right|!\left(\right|S|-|F|-1)!}{\left|S\right|!}}[f_x(F\cup j)-f_x\left(F\right)]$$

(3)

where $\left|F\right|!$ represents the permutations of features in the subset F, $\left(\right|S|-|F|-1)!$ represents the permutations of features in the subset $S-(F\cup \{j\left\}\right)$, $\left|S\right|!$ is the total number of feature permutations, and $f_x(F\cup j)$ and $f_x\left(F\right)$ denote, respectively, the regression score obtained by including and not including the j-th feature.

To prevent data leakage, feature selection was nested within the cross-validation process. For the SHAP-based interpretability analysis, we computed SHAP values using the subset of features that were consistently selected across all folds. This strategy ensures that the interpretation reflects robust and recurrent patterns rather than fold-specific artifacts, while also improving computational efficiency by reducing the dimensionality of the explanation space.

2.2.5. Evaluation Metrics

We assessed the performance of the regression models by computing the following metrics for each algorithm:

• Pearson correlation:

  $$corr={\displaystyle \frac{{\sum }_{i=1}^n(y_i-m_y)({\widehat{y}}_i-m_{\widehat{y}})}{\sqrt{{\sum }_{i=1}^n{(y_i-m_y)}^2{\sum }_{i=1}^n{({\widehat{y}}_i-m_{\widehat{y}})}^2}}}$$

  (4)
• Coefficient of determination:

  $$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-m_y)}^2}}$$

  (5)
• Root mean squared error:

  $$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2}$$

  (6)

where ${\widehat{y}}_i$ is the predicted values, $m_{\widehat{y}}$ denotes their average, $y_i$ is the observed values of phenotypic traits, and $m_y$ denotes their average. These metrics were computed for each algorithm to allow a fair comparison across models. All metrics were averaged across the 10 folds of cross-validation to ensure robust and unbiased estimates of model performance.

All machine learning models (Random Forest, XGBoost, and CatBoost) were implemented in Python (v.3.12) using the scikit-learn, xgboost, and catboost libraries, respectively. In addition, rrBLUP analyses were run in R using the GROAN/rrBLUP packages (see Section 2.2.3). Model explainability was performed with the shap library (TreeExplainer) to compute SHAP values and generate summary plots.

3. Results

The aim of this study was to implement regression models predicting phenotypic traits exclusively from genotypic data. Our focus lies on the outcomes of the artificial intelligence workflow, as we examined the regression performance of various machine learning algorithms alongside traditional algorithms and evaluated the biological significance of the genomic position of SNP loci exerting the most significant influence on predictions.

Following the procedures outlined in the Methods Section, after preprocessing the SNPs and performing feature selection to reduce the variables from approximately $5\times {10}^5$ to $5\times {10}^4$, we applied different regression models for each of the following phenotypic traits: DTF1, DTF2, DTF3, CL, and RL (Table 1). The results of the predictive models are presented in Table 2, in which the models are compared based on the $R^2$, Pearson coefficient, and RMSE. The values reported in the tables represent the mean and standard deviation obtained through cross-validation.

Table 2. Evaluation metrics for five phenotypic traits: Days to Flowering Time 1 (DTF1), Days to Flowering Time 2 (DTF2), Days to Flowering Time 3 (DTF3), Cauline Leaf Number (CL), and Rosette Leaf Number (RL). The table compares the performance of different regression models—CatBoost, Random Forest (RF), and XGBoost—with and without feature selection (Feat sel) and Ridge Regression BLUP (rrBLUP) without feature selection. Performance metrics include Pearson Correlation, Coefficient of Determination (${\mathrm{R}}^2$), and Root Mean Squared Error (RMSE), with standard deviations calculated through cross-validation. Bold values indicate the best-performing model for each metric within each phenotypic trait.

Trait	Regressor	Pearson Correlation	${\mathit{R}}^2$	RMSE
	CatBoost	$0.830\pm 0.034$	$0.682\pm 0.056$	$14.60\pm 1.05$
	CatBoost + Feat sel	$\mathbf{0}.\mathbf{833}\pm \mathbf{0}.\mathbf{034}$	$\mathbf{0}.\mathbf{688}\pm \mathbf{0}.\mathbf{057}$	$\mathbf{14}.\mathbf{45}\pm \mathbf{1}.\mathbf{11}$
	RF	$0.798\pm 0.037$	$0.618\pm 0.055$	$16.05\pm 0.96$
DTF1	RF + Feat sel	$0.802\pm 0.038$	$0.627\pm 0.057$	$15.84\pm 1.07$
	XGBoost	$0.780\pm 0.036$	$0.605\pm 0.056$	$16.30\pm 0.91$
	XGBoost + Feat sel	$0.778\pm 0.042$	$0.602\pm 0.065$	$16.37\pm 1.08$
	rrBLUP	$0.830\pm 0.038$	$0.678\pm 0.061$	$14.69\pm 1.16$
	CatBoost	$0.824\pm 0.037$	$0.672\pm 0.063$	$14.79\pm 1.38$
	CatBoost + Feat sel	$\mathbf{0}.\mathbf{831}\pm \mathbf{0}.\mathbf{032}$	$\mathbf{0}.\mathbf{683}\pm \mathbf{0}.\mathbf{056}$	$\mathbf{14}.\mathbf{55}\pm \mathbf{1}.\mathbf{32}$
	RF	$0.788\pm 0.036$	$0.603\pm 0.054$	$16.33\pm 1.16$
DTF2	RF + Feat sel	$0.794\pm 0.036$	$0.617\pm 0.056$	$16.04\pm 1.19$
	XGBoost	$0.756\pm 0.047$	$0.562\pm 0.073$	$17.12\pm 1.24$
	XGBoost + Feat sel	$0.772\pm 0.026$	$0.588\pm 0.042$	$16.69\pm 1.15$
	rrBLUP	$0.826\pm 0.036$	$0.675\pm 0.061$	$14.74\pm 1.28$
	CatBoost	$\mathbf{0}.\mathbf{824}\pm \mathbf{0}.\mathbf{020}$	$\mathbf{0}.\mathbf{672}\pm \mathbf{0}.\mathbf{031}$	$14.80\pm 0.75$
	CatBoost + Feat sel	$0.823\pm 0.024$	$0.672\pm 0.038$	$\mathbf{14}.\mathbf{79}\pm \mathbf{0}.\mathbf{77}$
	RF	$0.786\pm 0.025$	$0.598\pm 0.034$	$16.41\pm 0.91$
DTF3	RF + Feat sel	$0.796\pm 0.023$	$0.615\pm 0.032$	$16.05\pm 0.86$
	XGBoost	$0.755\pm 0.017$	$0.568\pm 0.027$	$17.02\pm 0.80$
	XGBoost + Feat sel	$0.745\pm 0.019$	$0.550\pm 0.030$	$17.35\pm 0.60$
	rrBLUP	$0.823\pm 0.028$	$0.671\pm 0.040$	$14.81\pm 0.92$
	CatBoost	$0.658\pm 0.047$	$0.423\pm 0.070$	$3.42\pm 0.38$
	CatBoost + Feat sel	$0.660\pm 0.049$	$0.425\pm 0.075$	$3.41\pm 0.39$
	RF	$0.654\pm 0.051$	$0.406\pm 0.068$	$3.47\pm 0.41$
CL	RF + Feat sel	$0.653\pm 0.050$	$0.409\pm 0.070$	$3.46\pm 0.40$
	XGBoost	$0.613\pm 0.076$	$0.354\pm 0.126$	$3.61\pm 0.44$
	XGBoost + Feat sel	$0.590\pm 0.060$	$0.315\pm 0.101$	$3.71\pm 0.35$
	rrBLUP	$\mathbf{0}.\mathbf{680}\pm \mathbf{0}.\mathbf{049}$	$\mathbf{0}.\mathbf{449}\pm \mathbf{0}.\mathbf{072}$	$\mathbf{3}.\mathbf{34}\pm \mathbf{0}.\mathbf{41}$
	CatBoost	$\mathbf{0}.\mathbf{743}\pm \mathbf{0}.\mathbf{046}$	$\mathbf{0}.\mathbf{541}\pm \mathbf{0}.\mathbf{071}$	$\mathbf{11}.\mathbf{23}\pm \mathbf{0}.\mathbf{79}$
	CatBoost + Feat sel	$0.736\pm 0.046$	$0.532\pm 0.070$	$11.34\pm 0.68$
	RF	$0.714\pm 0.050$	$0.480\pm 0.068$	$11.97\pm 0.74$
RL	RF + Feat sel	$0.715\pm 0.047$	$0.487\pm 0.066$	$11.88\pm 0.75$
	XGBoost	$0.678\pm 0.045$	$0.443\pm 0.080$	$12.40\pm 1.03$
	XGBoost + Feat sel	$0.666\pm 0.076$	$0.425\pm 0.125$	$12.52\pm 0.89$
	rrBLUP	$0.743\pm 0.056$	$0.540\pm 0.085$	$11.25\pm 1.02$

Among the ML models, CatBoost outperformed both Random Forest and XGBoost across all the traits under investigation. The CatBoost model, whether used alone or with preceding feature selection, showed performance that was generally comparable to standard parametric linear models across all traits considered. Therefore, CatBoost presents itself as a viable alternative to rrBLUP. Additionally, the integration of XAI with ML models enhances the interpretability of prediction results.

Feature selection resulted in modest improvements for certain phenotypic traits, such as DTF1, DTF2, and CL. More importantly, despite the reduction in features, the performance of the models remained stable across all traits, demonstrating that feature selection contributed to computational efficiency without compromising accuracy.

We further assessed the robustness of feature selection by varying the mutual information percentile threshold (0.80, 0.85, 0.90, 0.95, 0.975, and 0.99) within a CatBoost pipeline. As reported in Supplementary Table S2, performance remained stable across thresholds for all traits (Pearson, $R^2$, RMSE within overlapping standard deviations), supporting the choice of the 0.90 quantile as a parsimonious operating point that balances predictive performance with computational efficiency by limiting the number of features entering subsequent analyses.

A closer inspection of the results by trait confirms this trend (Table 2). For DTF1, CatBoost with feature selection achieved the best values across all metrics (Pearson $0.833\pm 0.034$, $R^2=0.688\pm 0.057$, and RMSE $14.45\pm 1.11$), with rrBLUP performing very closely. For DTF2, CatBoost with feature selection again led for all metrics (Pearson $0.831\pm 0.032$, $R^2=0.683\pm 0.056$, and RMSE $14.55\pm 1.32$). For DTF3, CatBoost (with and without feature selection) provided the top Pearson and $R^2$ values ($\approx 0.824$ and $\approx 0.672$), with the lowest RMSE obtained by CatBoost with feature selection ($14.79\pm 0.77$). For CL, rrBLUP yielded the best performance on all three metrics (Pearson $0.680\pm 0.049$, $R^2=0.449\pm 0.072$, and RMSE $3.34\pm 0.41$). Finally, for RL, CatBoost reached the top values (Pearson $0.743\pm 0.046$, $R^2=0.541\pm 0.071$, and RMSE $11.23\pm 0.79$).

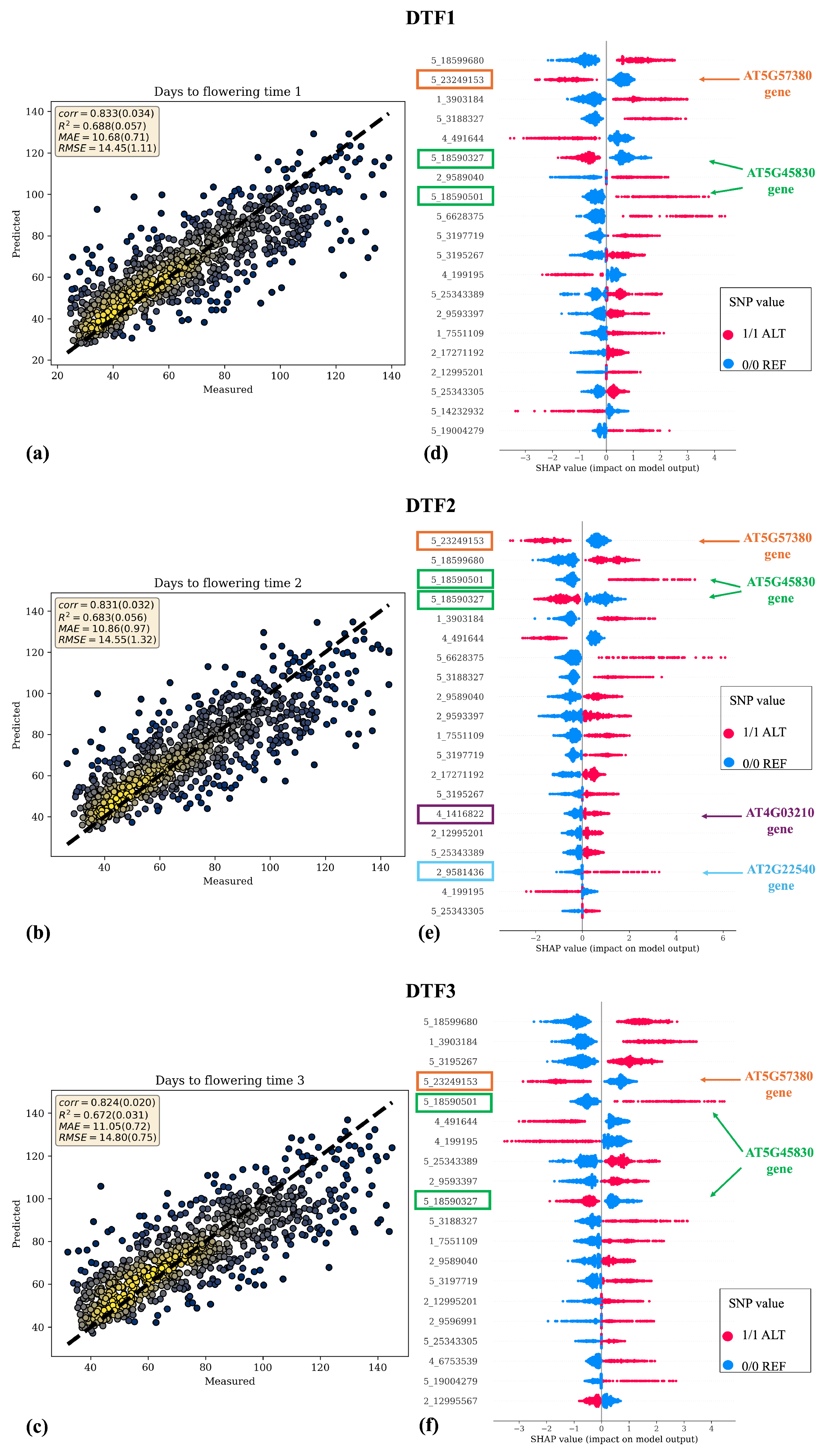
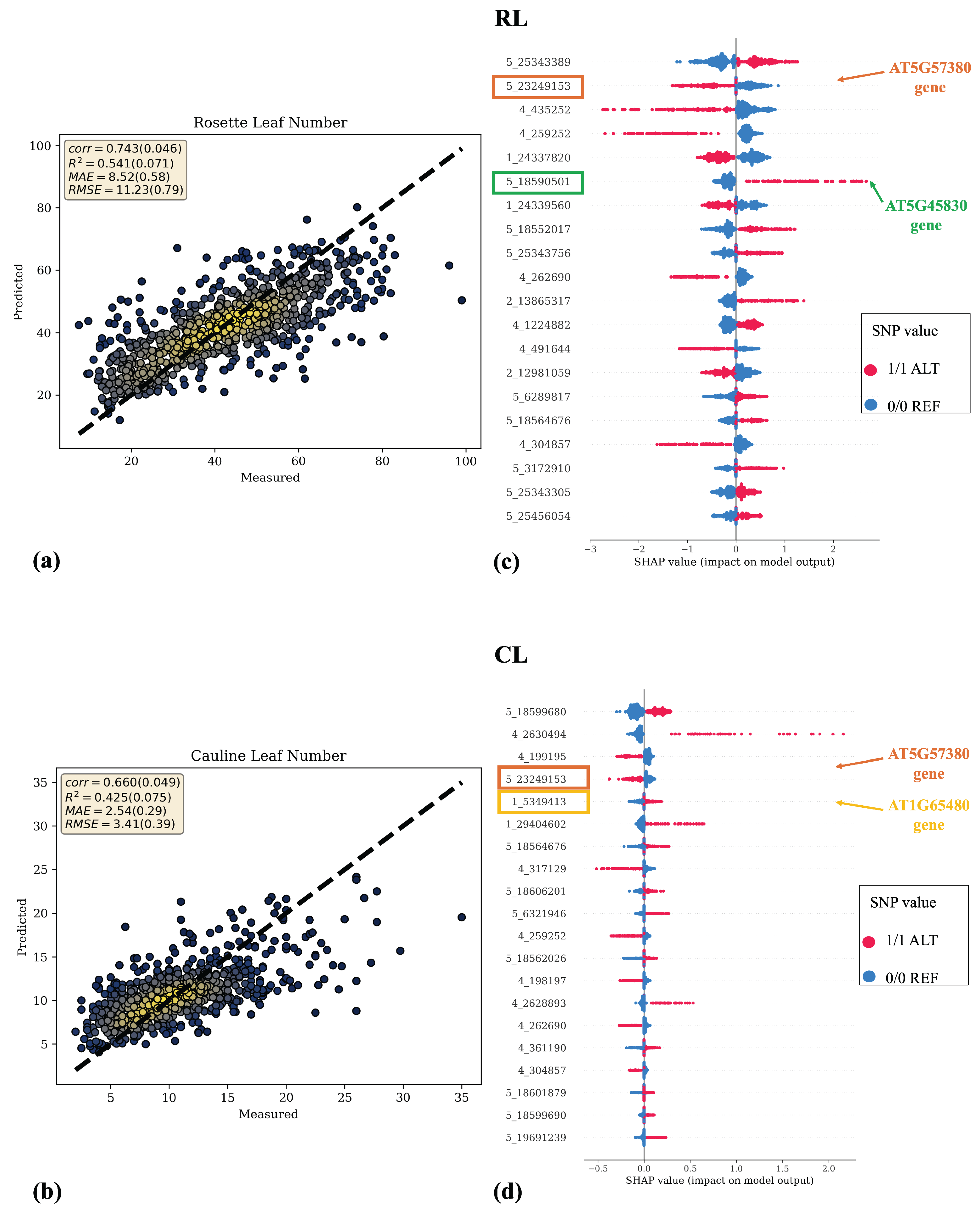
Additionally, to provide further insights into the performance and interpretability of the CatBoost regressor, we present visualizations in Figure 4 and Figure 5. Figure 4a–c and Figure 5a,b depict scatter plots of the analyzed phenotypic traits, with actual values on the x-axis ($y_i$) and predicted values on the y-axis ($\widehat{y_i}$). Notably, a close adherence of predicted values to the actual ones is observed, especially for the days to flowering traits. Except for RL, where Catboost without feature selection performed better, for all other traits, the combination of Catboost preceded by feature selection obtained better results. Therefore, in Figure 4a–c and in Figure 5c, the results related to the Catboost model preceded by feature selection are represented, whereas in Figure 5d, the scatter plot of the Catboost model without feature selection is represented.

Figure 4. Scatter plots (a–c) and SHAP summary plots (d–f) for days to flowering time traits. Scatter plots represent actual phenotypic values on the x-axis and predicted values $\widehat{y_i}$ on the y-axis, along with evaluation metrics of regression models. The yellow color in the scatter plots represents the density of data points, with higher densities shown in more intense yellow regions. SHAP summary plots depict the feature importance of SNPs based on SHAP values. The 20 most important SNPs are ranked from most to least important based on the absolute values of their SHAP scores. Additionally, the color code provides information on the direction of effects, with red indicating the ALT allele and blue indicating the REF allele. Each point in every row represents the SHAP value of a specific SNP for each strain. The SNPs within the rectangles are those for which a biological meaning has been found, as they fall within genes of interest, which are described in more detail in the Discussion Section.

Figure 5. Scatter plots (a,b) and SHAP summary plots (c,d) for leaf number traits. Scatter plots represent actual phenotypic values on the x-axis and predicted values $\widehat{y_i}$ on the y-axis, along with evaluation metrics of regression models. The yellow color in the scatter plots represents the density of data points, with more intense yellow regions indicating higher data point densities. SHAP summary plots depict the feature importance of SNPs based on SHAP values. The 20 most important SNPs are ranked from most to least important based on the absolute values of their SHAP scores. Additionally, the color code provides information on the direction of effects, with red indicating the ALT allele and blue indicating the REF allele. Each point in every row represents the SHAP value of a specific SNP for each strain. The SNPs within the rectangles are those for which a biological meaning has been found, as they fall within genes of interest, which are described in more detail in the Discussion Section.

The scatter plots in Figure 4 and Figure 5 show tight alignment of predicted vs. measured values for the three flowering time traits, consistent with their higher heritability, and a wider spread for leaf number traits.

Furthermore, Figure 4d–f and Figure 5c,d present the results of feature importance based on SHAP values calculated by Equation (3). SHAP values provide insights into how specific features influence predictions, with positive and negative values indicating contributions towards high or low values of the phenotypic variable under regression, respectively. Each data point in each row of the summary plot represents the SHAP value of that particular SNP for a specific strain. Higher absolute SHAP values denote greater feature relevance in the prediction. The top 20 SNPs are represented in descending order of importance.

Moreover, from the analysis of SHAP values, further insight into the direction of effects can be deduced. Certain SNPs with ALT alleles (highlighted in red points) are associated with higher phenotypic values, while those with REF alleles (highlighted in blue points) are linked to lower phenotypic values. Conversely, some SNPs exhibit the opposite pattern, suggesting a correlation between alternative alleles and lower phenotypic values.

4. Discussion

In this study, we aimed to develop and evaluate an artificial intelligence workflow for genotype-to-phenotype prediction in Arabidopsis thaliana, integrating both machine learning and mixed linear models with explainable AI techniques. The workflow was applied to DNA polymorphism data from the Arabidopsis 1001 Genomes Project [29] to predict five phenotypic traits, including days to flowering and leaf number. Combining linear and machine learning models may thus be a valuable strategy, as the latter can capture complex, non-additive genetic effects that traditional linear approaches may not fully capture [52,53,54]. By combining predictive modeling with SHAP-based interpretability, our objective was not only to achieve accurate trait prediction but also to gain biologically meaningful insights into the genetic variants contributing to these traits.

A key innovation of our workflow lies in the use of SHAP values within the XAI framework. This integration not only identifies the variants contributing most to overall predictions, but also provides individual-level explanations, pinpointing specific SNPs that drive each plant’s predicted phenotype. While functional validation will be necessary to confirm the causal role of these variants, such local interpretability offers a promising avenue for future precision breeding applications by helping to prioritize candidate SNPs for further investigation.

Although the application of a data-driven feature selection procedure did not substantially improve model accuracy for all traits, it significantly reduced the number of input variables, which is critical in high-dimensional genomic datasets. This step contributed to minimizing computational costs and enhancing SHAP-based model interpretability by limiting the number of features involved in the explanation space.

In our study, three traits described the number of days from sowing to specific flowering phenological stages (DTF1–3), while two traits (RL and CL) captured leaf number. Flowering time is a major breeding target, as this trait strongly influences adaptation to environmental stress and yield [55,56]. Leaf number also impacts crop productivity [57,58] and, in Arabidopsis, rosette and cauline leaf numbers are established morphological proxies of flowering time [59]. Our results confirm that traits related to days to flowering display higher genetic heritability than those related to leaf number, in agreement with previous reports [60,61].

Notably, several high-SHAP (Figure 4 and Figure 5) SNPs mapped within genes with well-established roles in flowering and developmental timing (Supplementary Table S1). Specifically, SNPs 5_18590327 and 5_18590501, associated with DTF1, DTF2, and DTF3, reside in the DELAY OF GERMINATION 1 (DOG1, AT5G45830) gene, which regulates flowering time [62]. Similarly, SNP 5_23249153 is located in the VERNALIZATION INSENSITIVE 3 (VIN3, AT5G57380) gene, which represses FLOWERING LOCUS C (FLC) during vernalization [63]. Other SNPs of interest for DTF2 include 4_1416822 in XYLOGLUCAN ENDOTRANSGLUCOSYLASE/HYDROLASE 9 (XTH9, AT4G03210), involved in inflorescence stem elongation [64], and 2_9581436 in AGAMOUS-LIKE 22 (AGL22, AT2G22540), a regulator of flowering [65]. For DTF3, SNP 2_9596991 resides in the gene ATKH6 (AT2G22600), a nucleic acid-binding protein with a K-homologous (KH) domain linked to floral development [66]. Interestingly, several of these SNPs also contributed to leaf number traits, highlighting a shared genetic basis. Consistently, the above-mentioned VIN3 SNP 5_23249153 also showed high SHAP values for RL and CL, and the DOG1 SNP 5_18590501 was also strongly associated with RL (Supplementary Table S1). Moreover, SNP 1_24337820, located near FLOWERING LOCUS T (FT, AT1G65480), displayed high SHAP values for RL, consistent with the role of FT as a key flowering integrator [67]. These findings reinforce the physiological and genetic connection between flowering time and leaf number and support the use of leaf number as a morphological indicator of flowering earliness in Arabidopsis.

One of the strengths of our study is the use of a comprehensive public dataset encompassing over a thousand genotypes. Nonetheless, some limitations should be acknowledged. First, the analysis was restricted to five phenotypic traits. Second, the workflow was trained and evaluated exclusively on the Arabidopsis 1001 Genomes dataset. This reliance on a single source may limit the generalizability of the findings. While the internal cross-validation design provides a robust estimate of predictive performance within this dataset, future validation on additional datasets or other species will be essential to fully assess the broader applicability of the workflow.

An important consideration emerging from our results is the trade-off between computational efficiency and interpretability. While rrBLUP offers computational simplicity and fast execution suitable for large-scale breeding programs, CatBoost combined with SHAP provides deeper biological insights at the cost of increased computational complexity. For routine genomic selection where speed is prioritized, rrBLUP remains highly valuable. However, when biological understanding and precision breeding decisions are paramount, the additional computational investment in ensemble methods with XAI techniques like SHAP proves worthwhile, as demonstrated by our identification of functionally relevant SNPs in key flowering genes.

In summary, our results demonstrate the potential of integrating AI with XAI techniques to advance genomic selection methodologies. SHAP, in particular, provides both global and local interpretability, enabling the identification of SNPs that drive trait prediction at the level of individual plants. This dual perspective combines predictive accuracy with biological insight, making the approach a valuable resource for precision breeding.

5. Conclusions

In this study, we implemented and benchmarked machine learning regressors against established genomic regression methods for predicting phenotypic traits from genotype data. Across the five traits considered, machine learning achieved performance comparable to, and at times exceeding, state-of-the-art genomic regressors, indicating its capacity to model complex genetic structures and offering a credible alternative within genomic prediction workflows.

We further integrated explainable AI to ground these predictions biologically. SHAP attributions quantified the contribution of individual SNPs to trait predictions, providing complementary global and plant-level explanations. This framework clarifies why specific variants are prioritized by the models and strengthens the interpretability of genotype–phenotype links.

Our analysis targeted three flowering time traits and two leaf number traits, both of direct relevance to breeding under changing climates. The accuracy obtained suggests practical utility for tasks such as yield estimation and planning for shifts in growing seasons.

The present analysis is limited to five traits and to a single public cohort of A. thaliana accessions. Performance estimates and feature attributions are derived from internal validation and may not extend beyond this population. External evaluation on independent cohorts and additional species will be required to assess generalizability and robustness across distinct genetic backgrounds and environments.

Overall, the results support the use of machine learning for genotype–phenotype prediction and demonstrate the utility of coupling these models with SHAP-based interpretation. The combination of competitive accuracy and traceable, variant-level attributions can inform biologically grounded, model-assisted breeding decisions.