Enhancing Axial Flow in Hydrokinetic Turbines via Multi-Slot Diffuser Design: A Computational Study

Abstract

Straight-walled diffusers can boost the power density of horizontal-axis hydrokinetic turbines (HKTs), but are prone to boundary layer separation when the divergence angle is too large. We perform a systematic factorial study of three diffuser configurations, slotless, mid-length single-slot, and outlet-slot with dual divergence angles, using a two-dimensional, transient SST k–$\omega$ Reynolds-averaged Navier–Stokes model validated against wind tunnel data (maximum error 6.4%). Eight geometries per configuration are generated through a $2^3$ Design of Experiments with variation in the divergence angle, flange or slot position, and inlet section. The optimal outlet-slot design re-energises the boundary layer, shortens the recirculation zone by more than 50%, and raises the mean axial velocity along the diffuser centreline by 12.6% compared with an equally compact slotless diffuser, and by 42.6% relative to an open flow without a diffuser. Parametric analysis shows that the slot position in the radial (Y) direction and the first divergence angle have the strongest influence on velocity augmentation. In contrast, the flange angle and axial slot location (X) are second-order effects. The results provide fabrication-friendly guidelines, restricted to straight walls and a single slot, that are capable of improving HKT performance in shallow or remote waterways where complex curved diffusers are impractical. The study also identifies key geometric and turbulence model sensitivities that should be addressed in future three-dimensional and multi-slot investigations.

1. Introduction

Sustainable development demands reliable access to low-cost energy resources that minimise social and environmental impacts [1]. Without significant policy shifts, global primary energy demand is projected to rise by 55% between 2005 and 2030, with developing regions relying on fossil fuels for 84% of supply and a consequent 57% increase in greenhouse gas emissions [2]. Accordingly, coal, oil, and natural gas fail to meet long-term sustainability criteria, whereas solar, wind, and hydroelectric sources offer enduring alternatives [3]. Access to electricity underpins socioeconomic advancement and enhances living standards; hence, small-scale hydroelectric plants represent an effective way to deploy energy in remote, water-rich areas [4]. Horizontal-axis hydrokinetic turbines (HKTs) exploit river currents without damming or diverting the flow, which imposes lower ecosystem disturbance compared with Pelton, Francis, or Kaplan turbines. However, HKTs currently achieve peak efficiencies near 30%, whereas the efficiency of Pelton designs can reach 90% [5,6,7].

Several key design parameters influence the enhancement of HKTs. Improvements in rotor architecture [8,9,10], blade geometry [11,12], and operational alignment [13] all contribute to performance gains. Comparable CFD analyses performed for Pelton injectors show that modest geometric changes, such as a 75° needle-tip angle, can raise jet efficiency from 94% to 96%, showing how sensitive hydroturbine performance is to small design parameters [14]. Recent CFD work on gravitational-vortex concepts has also shown that rotor choice strongly affects energy capture [15], while an H-Darrieus rotor proved more efficient than the conventional Archimedes screw in the same basin geometry [16]. Nevertheless, modifications to these parameters alone cannot surpass the 59.3% Betz limit for energy extraction from a free stream [17,18]. To overcome this barrier, augmented diffusers create downstream low-pressure regions that boost mass flow and velocity through the turbine [19,20,21], thereby reducing flow misalignment and stagnation-pressure losses and enhancing overall efficiency [22].

Investigations of HKTs equipped with augmented diffusers have demonstrated substantial gains. Mehmood et al. employed a NACA 0018 diffuser for marine currents and, using CFD, obtained up to two-fold velocity increases [23]. Tampier et al. compared bare and diffuser-augmented turbines, recording a 39.4% efficiency gain and underscoring the need for co-design of turbines and diffusers [24]. Song et al. confirmed that a parallel design approach adapts turbine geometry to accelerated-flow conditions [25]. Vaz and Wood refined HKT blade aerodynamics based on diffuser acceleration ratios, achieving a power coefficient of 0.607, thereby surpassing the Betz limit [26]. Park et al. presented an optimised 5 kW ducted hydrokinetic turbine that attains up to 50% efficiency under practical constraints [27]. Vaz et al. carried out a numerical study of a conical-diffuser HKT, reporting a 55% increase in the power coefficient at a tip-speed ratio of 5.4, equivalent to a 1.5-fold rise in generated power [28]. Similarly, Ng et al. determined the geometric effect of augmented diffusers via CFD, showing that curved diffusers outperform flat ones with average gains of 2.2% in $C_p$ and 4% in $C_t$ relative to undiffused cases [29].

State-of-the-art diffuser designs fall into three categories: convergent–divergent profiles (first generation), straight-walled sections with flanges (second generation), and multi-slot diffusers (third generation). Convergent–divergent shapes yield significant performance improvements, but require complex fabrication; straight-walled diffusers simplify production, yet suffer separation at large divergence angles; and multi-slot designs energise the boundary layer through injected flow, mitigating separation, although their use in hydrokinetic applications remains limited [19].

This study investigates the influence of straight-walled, slotless, and single-slot diffuser geometries on internal velocity profiles to increase the available kinetic energy for HKTs. Three configurations are analysed using three experimental designs: a slotless design and two single-slot variants. Computational simulations quantify velocity augmentation and inform design guidelines for diffuser-augmented hydrokinetic systems.

The present study extends current knowledge by (i) providing a systematic parametric comparison of straight-walled, slotless, and single-slot diffusers normalised by rotor diameter; (ii) quantifying how the slot location and divergence angle jointly influence boundary layer re-energisation and pressure recovery; and (iii) identifying a geometric regime that raises the mean axial velocity by 12.6% relative to a slotless diffuser design while markedly suppressing separation. From an industrial standpoint, the findings provide fabrication-friendly design guidelines for low-head, low-maintenance HKTs suitable for isolated communities, thereby reducing the levelised cost of electricity and simplifying field installation.

Section 2 details the diffuser parameterisation, the experimental designs proposed, the numerical model, and the mesh-convergence protocol. Section 3 validates the computational framework against benchmark data and presents velocity and pressure fields for the three diffuser geometries seleted. Section 4 discusses the implications for turbine design, operational reliability, and future optimisation strategies. Finally, Section 5 summarises the principal findings, outlines limitations, and proposes avenues for experimental and three-dimensional extensions.

2. Methodology

The hydrokinetic turbine (HKT) extracts kinetic energy from a water current impinging perpendicular to its rotor axis, converting it into mechanical torque and rotational power [30]. As shown in Figure 1, flow deceleration occurs as energy transfers to the blades, causing the spacing of streamlines to increase downstream under constant mass flow conditions.

Under steady inflow, the instantaneous power output P of an HKT is given by

$$P=\frac{1}{2}\rho U^3{A}_r{C}_p\eta ,$$

(1)

where $\rho$ is the water density, U is the free-stream velocity, $A_r$ is the swept rotor area, $C_p$ is the power coefficient, and $\eta$ is the overall mechanical–electrical efficiency. The coefficient $C_p$ represents the fraction of the available kinetic power that the turbine captures:

$$C_p={\displaystyle \frac{P}{\frac{1}{2}\rho U^3{A}_r\eta }}.$$

(2)

In this study, all the dimensions of the diffuser are normalised concerning the rotor diameter D (1512 mm) to ensure scalability across different HKT sizes. However, the presence of the HKT itself is not considered in this analysis.

2.1. Diffuser Geometry and Experimental Designs

The diffuser-augmented configurations studied here were defined after an extensive survey of the literature on both hydrokinetic and wind turbine diffuser designs [19,21,24]. Twelve geometric parameters were identified as most influential on axial acceleration and boundary layer behaviour (

Table 1. Diffuser geometric parameters (normalised by rotor diameter D).

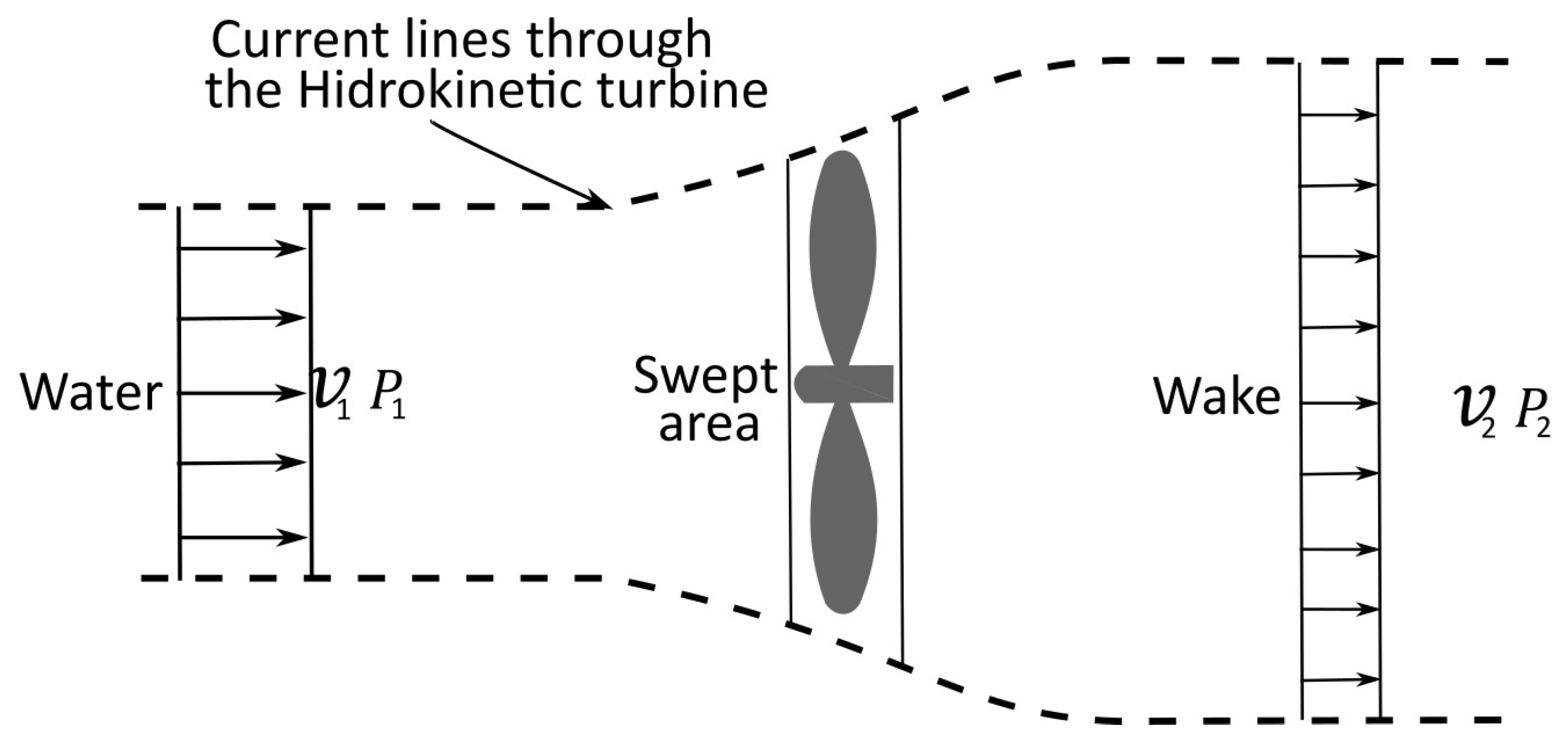
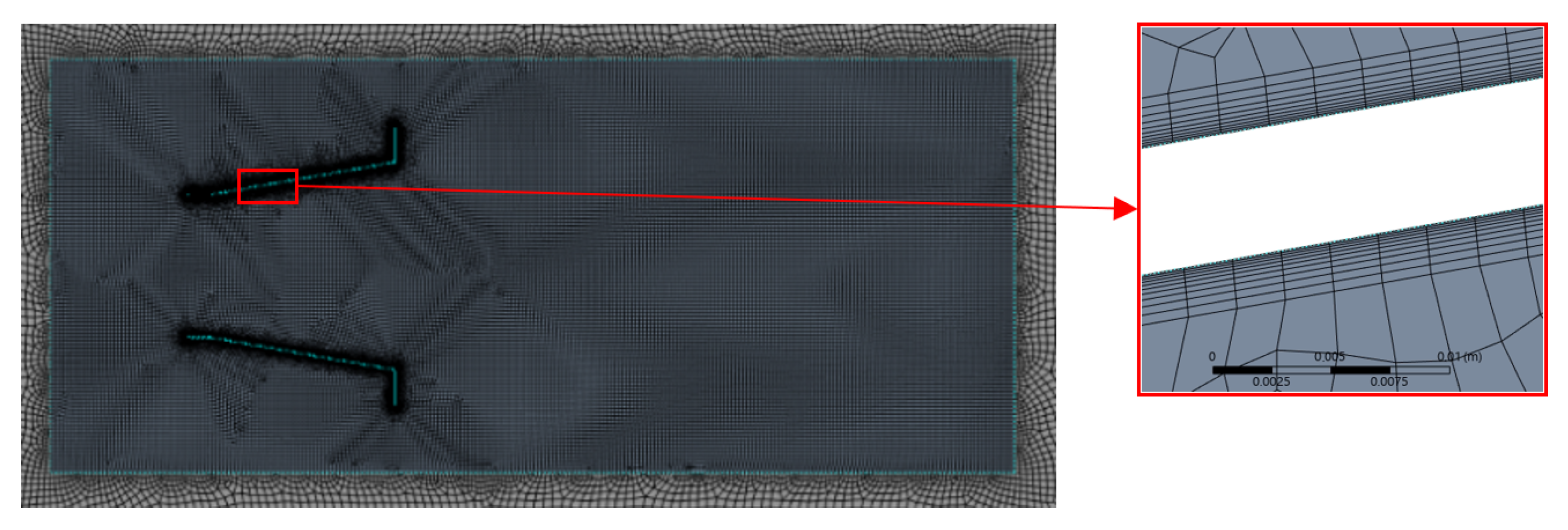
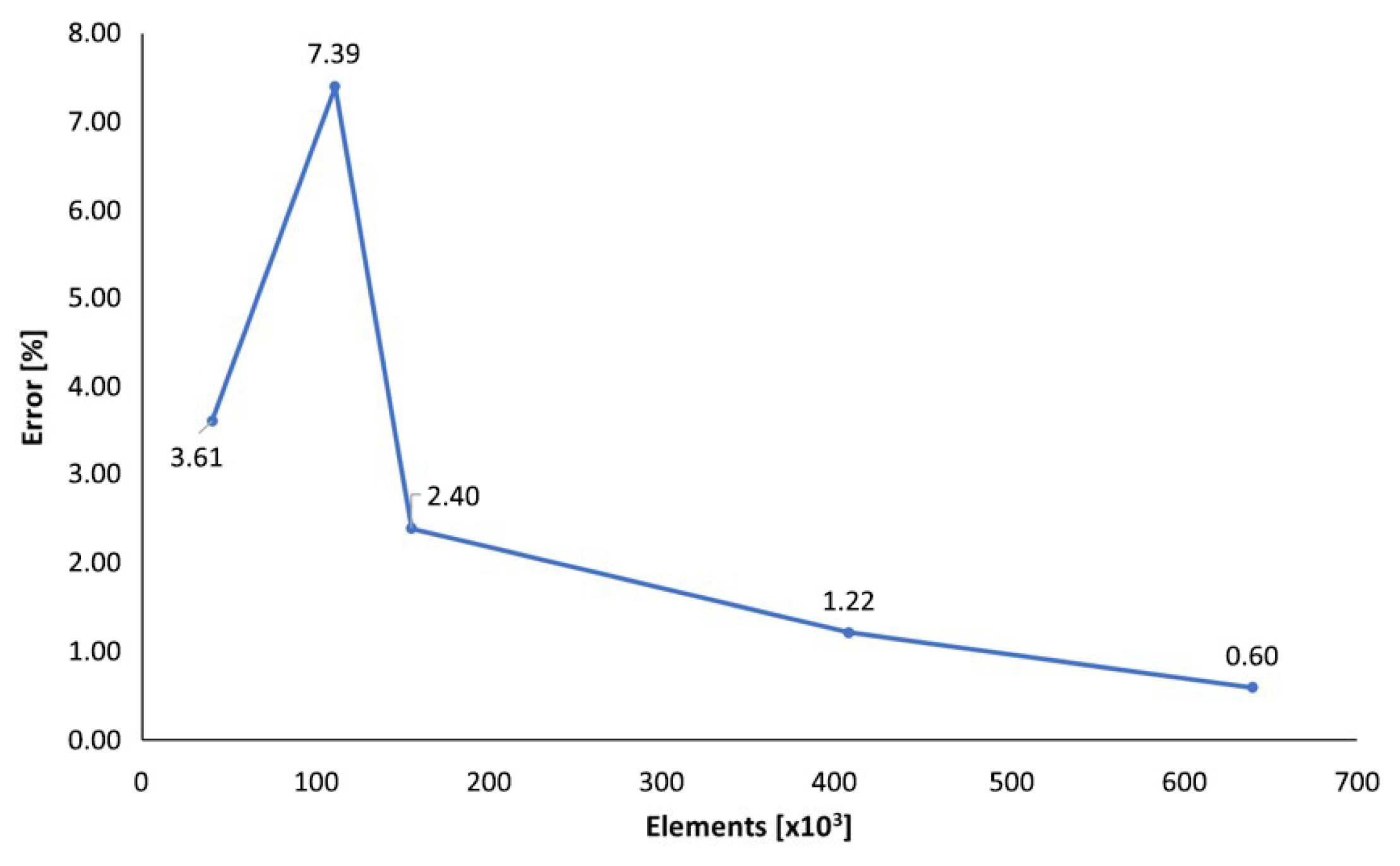
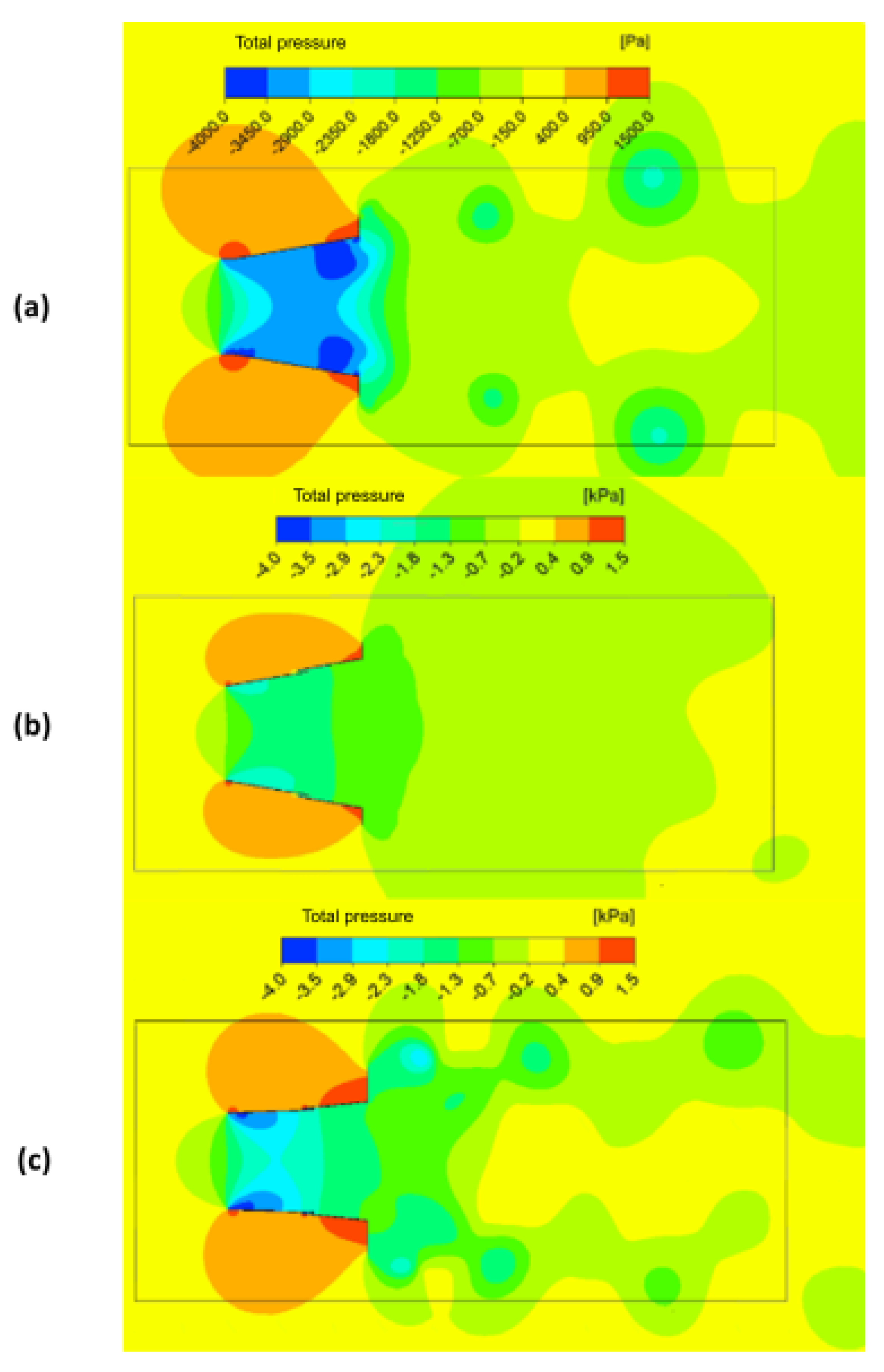
Parameter	Definition
$\alpha$	Flange angle at diffuser outlet
$\theta$	Divergence angle of first section
$\beta$	Divergence angle of second section
$D_{\mathrm{in}}$	Inlet diameter
$D_{\mathrm{flange}}$	Outlet flange diameter
c	Length of straight inlet section
$L_t$	Total diffuser length
$\Delta r$	Radial clearance between rotor and wall
h	Flange height
X	Axial position of slot
Y	Radial position of slot
L	Distance from slot to diffuser outlet

). Convergent–divergent profiles were excluded to focus on straight-walled diffusers that are simpler to manufacture and assemble.

To isolate the effects of slot geometry and divergence angles on the internal flow, only c, $\alpha$, $\theta$, $\beta$, and the slot coordinates (X, Y) were varied. All other dimensions ($D_{\mathrm{in}}$, $D_{\mathrm{flange}}$, $L_t$, $\Delta r$, h) were held constant across configurations. Normalising each length by the rotor diameter D ensures scalability to different HKT sizes.

Three diffuser variants were modelled

• Diffuser 1: Straight-walled slotless design (Silva et al. methodology [21]).
• Diffuser 2: Straight-walled with a single slot.
• Diffuser 3: Straight-walled with a single slot and two divergence angles.

Taking the above into account, a $2^3$ factorial Design of Experiments (DOE) was implemented for each augmented diffuser using Minitab v18 software. Each DOE considered three factors, each evaluated at two levels. As a result, each experimental design comprised eight distinct geometries, enabling a quantitative assessment of the geometric parameters with the greatest influence on the average axial velocity within the augmented diffuser.

DOE 1 investigates the effects of the divergence angle ($\theta$), flange angle ($\alpha$), and inlet section (c). DOE 2 focuses on the position of the slot (X and Y) and also includes the divergence angle ($\theta$), since it was identified in DOE 1 as the parameter with the greatest influence on the response variable. Therefore, the divergence angle was kept at the same level to evaluate and compare the performance of the augmented diffuser with and without a slot, using identical divergence angles. In DOE 3, two divergence angles are proposed, each corresponding to a different section of the diffuser: the inlet section is defined by divergence angle $\theta$, and the outlet section by divergence angle $\beta$. Additionally, only the slot position in the Y direction is considered, as DOE 2 revealed that the slot position in the X direction does not significantly affect the response variable.

The levels for each parameter were selected based on the values reported in the literature. However, none of the referenced studies combine the specific parameters and levels used in this work.

Table 2. Designs of experiments. Source: Own elaboration.

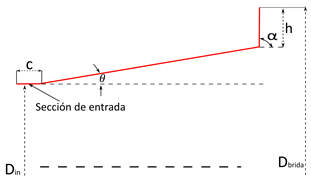	DOE 1—Straight-Walled Diffuser
	Factor	Description	Level 1	Level 2	Refs.
	$P_1=\theta$	Divergence angle (°)	10	16	[31,32]
	$P_2=\alpha$	Flange angle (°)	90	75	[21,31,33]
	$P_3=c$	Inlet section	With inlet	Without inlet	[21,33,34]
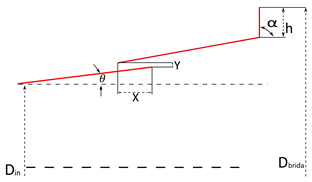	DOE 2—Single-Slot Diffuser
	Factor	Description	Level 1	Level 2	Refs.
	$P_1=\theta$	Divergence angle (°)	10	16	[31,32]
	$P_2=Y$	Slot Y-position	0.0125 D	0.04 D	[35,36]
	$P_3=X$	Slot X-position	0.250 D	0.125 D	[35,36]
	DOE 3—Dual-Angle Diffuser
	Factor	Description	Level 1	Level 2	Refs.
	$P_1=\theta$	Divergence angle 1 (°)	2	4	[21,37]
	$P_2=\beta$	Divergence angle 2 (°)	6	8	[31,38]
	$P_3=Y$	Slot Y-position	0.01 D	0.06 D	[35,36,39]

summarizes the information from the three DOEs, providing a clearer overview of the factors considered in this study.

2.2. Computational Model

The two-dimensional, incompressible flow through each diffuser configuration was simulated by solving the Reynolds-averaged Navier–Stokes (RANS) equations with the Shear-Stress Transport (SST) k–$\omega$ turbulence model [40,41,42,43]. The SST formulation blends the k–$\omega$ model near walls with a k–$\epsilon$ approach in the free stream, improving accuracy for adverse pressure gradients and boundary layer separation.

The computational domain (Figure 2) spans $20D$ in the vertical direction and $31D$ in the streamwise direction. To minimize inlet–outlet interactions, the diffuser was centred between $10D$ downstream of the inlet and $21D$ upstream of the outlet. A structured mesh with localised refinement around the diffuser walls and slot region was generated in ANSYS Fluent 2023R1. Inflation layers (10 layers, growth rate 1.2, first-layer height $\Delta y=0.1$ mm) ensured $y^{+}<5$ along all solid surfaces, as shown in Figure 3. A mesh independence study confirmed that $155\times {10}^3$ elements yielded changes below 3% in peak axial velocity.

Boundary conditions were applied as follows:

• Inlet: Uniform velocity $U=1.5$ m/s.
• Outlet: Gauge pressure set to 0 Pa.
• Walls: No-slip on diffuser and blade surfaces; slip (symmetry) on outer domain boundaries.

Transient simulations employed the PISO algorithm with a time step $\Delta t={10}^{-3}$ s, guaranteeing a maximum Courant number below 1.0. Second-order implicit time discretisation and second-order upwind spatial schemes were used for momentum and turbulence transport equations. Each case was run for 40s of physical time, by which point residuals had converged by at least four orders of magnitude and monitored velocity probes reached steady behaviour.

A mesh convergence study was performed to ensure numerical accuracy and computational efficiency. An initial global element size of 10 mm was successively halved until further refinement produced changes of less than 3% in the normalised axial velocity along the diffuser’s centreline. Mesh quality was verified against ANSYS™ guidelines (skewness < 0.35, orthogonal quality > 0.20) before each simulation [44].

Six meshes were evaluated, containing approximately $13\times {10}^3$, $40\times {10}^3$, $111\times {10}^3$, $155\times {10}^3$, $407\times {10}^3$, and $640\times {10}^3$ elements. The response metric was the average axial velocity along the symmetry axis, sampled from $2D$ upstream to $4D$ downstream of the diffuser [21,45,46]. Relative differences between successive meshes are plotted in Figure 4.

The mesh with $155\times {10}^3$ elements exhibited a relative error of 2.40% compared to the next finer grid, satisfying the convergence criterion. Consequently, all three diffuser geometries were discretised with this mesh density for consistent comparison.

The SST $k–\omega$ turbulence model was selected for its well-established performance in predicting flow separation and adverse pressure gradients, as supported by previous studies [28,29]. This model combines the advantages of the $k–\omega$ formulation near walls with the $k–\epsilon$ model in the free stream, yielding improved accuracy for attached and mildly separated flows. While alternative models such as the realizable $k–\epsilon$ and Reynolds Stress Model (RSM) could provide additional insights, especially in highly anisotropic turbulence, we prioritised model robustness and computational efficiency due to the large number of diffuser geometries evaluated. A comparative turbulence model sensitivity analysis is proposed as future work to complement the present geometric investigation.

3. Results

Accurate prediction of diffuser performance demands thorough validation of the numerical model against reliable benchmarks. Given the limited availability of experimental data for diffuser-augmented turbines, validation relies on reproducing published wind tunnel results. Once the model reproduces the reference case within acceptable error bounds, it is applied to the slotted configurations under study.

3.1. Numerical Validation

The RANS solver and mesh settings were validated against the experimental–theoretical dataset of Barboza et al. [47]. Their wind tunnel geometry and inlet conditions were replicated in both three-dimensional (3D) and two-dimensional (2D) simulations. Figure 5 overlays the normalised axial velocity $U_{\mathrm{x}}/U$ along the diffuser centreline, plotted against the normalised distance $x/D$ from the diffuser inlet.

The 3D simulation aligns closely with the experimental measurements, exhibiting a maximum deviation of 2%. The 2D model reproduces the overall velocity trend, but underestimates the peak by 6.4% relative to the 3D result. This discrepancy falls within the 6% error range reported by Rahmatian et al. for 2D vs. 3D diffuser simulations [33], confirming that the 2D model captures the essential flow features and is suitable for parametric investigation of slotted diffuser geometries.

3.2. Numerical Results

After validating the numerical model, the $2^3$ factorial DOE analysis for Diffuser 1 was carried out. It was found that the geometry providing the best velocity profile performance inside Diffuser 1 corresponds to a divergence angle of 10° and a defined inlet section. Since the flange angle was found to have no statistically significant effect on the response variable in this study, the model with a flange angle of 90° was selected. Therefore, the geometry selected from the DOE for Diffuser 1 corresponds to Geometry 1; see

Table 3. Response variable behaviour from the $2^3$ factorial DOE for Diffuser 1.

Geometry	Divergence Angle (°)	Flange Angle (°)	Inlet Section	Average Normalised Axial Velocity
5	16	90	With inlet	0.975
7	16	75	With inlet	0.906
8	16	75	Without inlet	0.889
3	10	75	With inlet	1.227
2	10	90	Without inlet	1.106
4	10	75	Without inlet	1.084
6	10	90	With inlet	0.897
1	16	90	With inlet	1.269

.

Then, the $2^3$ factorial DOE analysis was conducted for Diffuser 2. It was determined that the geometry providing the best velocity profile performance inside Diffuser 2 corresponds to a divergence angle of 10° and a Y-direction slot position of 0.0125D. Since the slot position in the X-direction was found to have no significant effect on the response variable, a value of 0.125D was selected. Therefore, the geometry selected from the DOE for Diffuser 2 corresponds to Geometry 3; see

Table 4. Response variable behaviour from the $2^3$ factorial DOE for Diffuser 2.

Geometry	Divergence Angle (°)	Slot Y-Position	Slot X-Position	Average Normalised Axial Velocity
8	16	0.0400 D	0.125 D	0.857
6	16	0.0400 D	0.250 D	0.835
3	10	0.0125 D	0.125 D	1.044
7	10	0.0400 D	0.125 D	1.046
2	16	0.0125 D	0.250 D	0.853
1	10	0.0125 D	0.250 D	1.044
5	10	0.0400 D	0.250 D	1.044
4	16	0.0125 D	0.125 D	0.848

.

Finally, from a comprehensive analysis of the $2^3$ factorial DOE for Diffuser 3, it was determined that the geometry providing the best velocity profile performance inside Diffuser 3 corresponds to a divergence angle $\theta$ of 2° and a Y-direction slot position of 0.01D. Since the divergence angle $\beta$ was found to have no significant effect on the response variable, a value of 6° was selected. Therefore, the geometry selected from the DOE for Diffuser 3 corresponds to Geometry 1; see

Table 5. Response variable behaviour from the $2^3$ factorial DOE for Diffuser 3.

Geometry	Divergence Angle 1 (°)	Divergence Angle 2 (°)	Slot Y-Position	Average Normalised Axial Velocity
8	4	10	0.06 D	1.313
2	4	6	0.01 D	1.329
5	2	6	0.06 D	1.387
3	2	10	0.01 D	1.394
4	4	10	0.01 D	1.310
6	4	6	0.06 D	1.304
1	2	6	0.01 D	1.426
7	2	10	0.06 D	1.387

.

After conducting the numerical simulations for the 24 augmented diffuser geometries, one geometry was selected from each DOE based on the average axial velocity across the radial distance of the augmented diffuser. Finally, Figure 6 provides a summary of the selected designs for the three (3) augmented diffusers, listing the geometries identified through the application of each DOE.

After selecting the three augmented diffuser designs with the best performance, a detailed analysis was carried out to evaluate the influence of the selected geometric parameters on the velocity profile. Axial velocity contours and vector fields reveal the impact of slot placement and divergence angles on flow acceleration, separation, and uniformity. Figure 7 presents mid-plane contours of normalised axial velocity $U_{\mathrm{x}}/U$ for all three diffuser configurations.

In the slotless design (Diffuser 1), the flow accelerates smoothly through the expansion section, achieving its maximum at $x=1.2D$. Downstream of this point, adverse pressure gradients induce large recirculation zones along the walls, as evidenced by near-wall backflow and transient fluctuations in the velocity profile. These separation eddies compromise both energy capture and structural loading consistency.

Introducing a single slot (Diffuser 2) injects external fluid into the main stream, which energizes the boundary layer and suppresses the most severe separation events. Although the peak axial velocity falls by 40% relative to the slotless design, the flow becomes markedly more uniform and steady. This stabilisation suggests lower unsteady loading on the turbine and improved overall hydraulic performance under variable inflow conditions.

Optimising the inlet divergence angle and relocating the slot closer to the outlet (Diffuser 3) further enhances flow quality. Separation zones shrink significantly, and near-wall reverse flow is almost eliminated. Compared to Diffuser 2, the peak axial velocity recovers by 19.8%, while the average normalised velocity along the symmetry axis increases from 1.044 to 1.426. These improvements indicate that the combined adjustment of geometric parameters yields the most uniform velocity distribution and the highest potential for consistent power extraction.

The total pressure distribution within the diffuser dictates the strength and location of favourable and adverse pressure gradients, which in turn influence both flow acceleration and separation behaviour. A detailed comparison of mid-plane total pressure contours (normalised by the inlet dynamic pressure, $\frac{1}{2}\rho U_{\infty }^2$) for the three designs is shown in Figure 8.

Velocity vector plots (Figure 9) and radial profiles at the location of peak flow (Figure 10) corroborate these findings: slot injection consistently reduces the size and intensity of recirculation eddies. In contrast, strategic slot positioning and angle reduction maximize axial acceleration and flow uniformity inside the diffuser.

In the slotless design (Figure 8a), the diffuser’s flange produces a pronounced high-pressure ridge at the outlet, evident as warm tones near the outer wall. Upstream of the inlet, a deep pressure trough develops, creating strong suction that draws fluid into the expansion. Between these regions, the gradient of total pressure reverses sharply, generating adverse forces that detach the boundary layer along the wall. The pressure recovery downstream of separation, with contours smoothing back toward freestream values, reflects energy losses in the recirculation zone and the associated turbulence generation.

Introducing a slot (Diffuser 2, Figure 8b) moderates the inlet pressure drop: the low-pressure region upstream of the inlet is shallower, indicating reduced suction intensity. Immediately downstream of the slot, a localised high-pressure patch appears, marking where the injected flow impinges on the mainstream. This local recovery acts to re-energize the boundary layer by replenishing momentum near the wall, thus limiting the spatial extent of separation. However, the slot’s injection also smooths the overall pressure gradient, lowering the flange-induced peak pressure by approximately 8% compared to the baseline, consistent with the 40% reduction in peak axial velocity noted in Section 3.2.

The optimised configuration (Diffuser 3, Figure 8c) combines a reduced inlet divergence angle with a slot relocated closer to the outlet. Here, the inlet pressure trough deepens slightly relative to Diffuser 2 (but remains less extreme than Diffuser 1), steering a stronger accelerating gradient through the expansion. The downstream slot injection again creates a pressure bump, but its location at $x\approx 2.5D$ avoids interference with early-separation zones. Overall, the optimised design exhibits a more gradual pressure recovery: the contours transition smoothly from the low-pressure region to the flange ridge, indicating that boundary layer reattachment occurs more uniformly along the wall.

The velocity vector fields in Figure 9 further illustrate these effects. In the baseline, reversed vectors extend up to $0.2D$ from the wall, signifying a large recirculation bubble. With the slot, this recirculation length shrinks by over 50% and downstream vectors align more closely with the freestream direction, indicating reduced shear layer thickness. The optimised design nearly eliminates upstream backflow: vectors remain within ±5° of the axial direction across most of the diffuser height, evidencing an almost attached boundary layer.

Radial profiles of normalised axial velocity $U_{\mathrm{x}}/U$ at the axial station of maximum flow, shown in Figure 10, quantify the net impact on flow uniformity. The baseline profile features a flattened “top-hat” shape with a 5.6% lower peak and significant asymmetry due to unsteady separation. The slot raises the mean profile but widens the distribution, yielding an average $U_{\mathrm{x}}/U=1.044$. In contrast, the optimised slot concentrates momentum near the centreline, producing a Gaussian-like profile with an average of 1.426, an improvement of 12.6% over the baseline and 37.5% over the slot design. The standard deviation of $U_{\mathrm{x}}/U$ across the channel height drops by 35%, indicating a more uniform flow that would reduce mechanical vibrations and increase adequate torque on the turbine shaft.

Taken together, the pressure and velocity analyses demonstrate that slot injection can be strategically deployed to tailor pressure gradients and boundary layer momentum. The optimised design’s balanced pressure trough and recovery, minimal separation, and peaked velocity profile suggest that it has the potential to yield the highest power coefficient and the most stable hydraulic loading among the configurations tested.

4. Discussion

The numerical results presented in this study reveal the significant role that diffuser geometry, and specifically slot design, plays in governing internal flow dynamics within hydrokinetic systems. Beyond enhancing peak axial velocity, the strategic integration of slot injection fundamentally alters the pressure recovery mechanism and boundary layer behaviour, suggesting new pathways for improving turbine efficiency and operational stability.

First, the reduction of boundary layer separation via slot injection suggests a promising avenue for extending operational reliability in low-Reynolds-number or variable-inflow environments, such as rivers with fluctuating discharge or tidal zones with intermittent reversals. The improved flow attachment observed in Diffuser 3 is not only beneficial for energy capture, but may also mitigate cyclic mechanical loads on the turbine structure. This has implications for reducing fatigue, life concerns, and maintenance intervals, all of which are required in remote deployments.

Second, the improved flow uniformity observed in Diffuser 3 suggests a more efficient aerodynamic alignment between the diffuser and the rotor design. A more homogeneous axial velocity field reduces flow distortion at the rotor interface, leading to greater torque consistency and potentially minimising the need for advanced control mechanisms or variable-pitch blades. This design simplification can lower overall system costs and enhance long-term operational robustness, particularly in micro-hydrokinetic applications where simplicity is a critical design factor. However, it is essential to account for specific site conditions, especially local flow velocities, as these may negatively impact marine fauna.

Interestingly, although Diffuser 2 exhibited a lower peak velocity compared to the slotless design, its enhanced flow stability may offer advantages in real applications such as fish-friendly turbines, where extreme velocities and high shear gradients must be avoided. Therefore, the choice of diffuser configuration should be application-specific, balancing maximum energy extraction with ecological or mechanical constraints.

It is also worth noting that the two-dimensional framework, while sufficient for capturing core flow trends, may overlook important three-dimensional effects such as vortex shedding, crossflow dynamics near the flange, and secondary flow structures at the slot edges. Experimental validation and fully three-dimensional simulations are proposed as interesting directions for future work.

The results suggest a broader methodological implication: diffuser design optimisation should not be confined to maximising axial velocity alone. Instead, future design procedures should incorporate multi-objective formulations that include flow uniformity, recirculation suppression, and mechanical loading stability as concurrent targets. Integrating such criteria into a parametric design space exploration, potentially through surrogate modelling or bio-inspired algorithms, could yield generalised diffuser topologies that are suitable for diverse hydrokinetic environments.

Although the improved flow uniformity and reattachment observed in Diffuser 3 suggest beneficial boundary layer dynamics, a detailed quantitative analysis of the momentum transfer mechanism was not performed in this initial study. Specifically, shear stress distributions and boundary layer thickness evolution were not extracted from the simulations. Future work will address this by evaluating the momentum thickness and wall shear stress profiles, allowing deeper insight into how slot location and divergence angles interact to promote or inhibit flow separation. This analysis would also help to bridge the results with classical boundary layer theory.

5. Conclusions

5.1. Key Conclusions

This study has demonstrated that the integration of a single slot into a straight-walled diffuser significantly alters the internal flow dynamics by re-energising the boundary layer and suppressing extensive recirculation zones. Among the three configurations analysed, Diffuser 3, characterised by a reduced inlet divergence angle (2°), an outlet divergence angle of 6°, and a slot positioned at 0.01D in the Y-direction and 0.125D in the X-direction, achieved the most uniform axial velocity distribution and the highest momentum concentration along the central axis. Quantitatively, the configurations of Diffusers 1, 2, and 3 exhibited increases in axial velocity relative to the flow without a diffuser of 26.9%, 4.6%, and 42.6%, respectively.

Furthermore, the results obtained from the Designs of Experiments (DOEs) indicate that the slot position along the X-axis has little influence on the average axial velocity. In contrast, variations along the Y-axis have a significant impact. These findings underscore the importance of slot placement in the design of augmented diffusers and highlight the need for further investigation into the effects of alternative X and Y positions on internal flow behaviour.

The results also indicate that divergence angles beyond 10° exacerbate adverse pressure gradients, leading to earlier separation and unsteady fluctuations that degrade flow quality. In contrast, carefully tailored slot placement can both moderate inlet suction and generate localised pressure recovery downstream, thereby sustaining attached flow and maximising kinetic energy delivery to the turbine rotor.

5.2. Limitations and Future Work

For future diffuser-augmented HKT designs, the average axial velocity along the symmetry axis is recommended as a primary performance metric, since it directly reflects the net energy available for extraction. Further investigations should explore multi-slot arrangements, detailed slot geometry (width, number, and angular orientation), and three-dimensional effects to refine diffuser performance. Experimental validation in a controlled facility would also strengthen confidence in these numerical findings and support scale-up to prototype turbines. Despite the promising results, several limitations must be acknowledged. The study employed a two-dimensional numerical model under transient-inflow conditions, which, while sufficient for capturing primary flow phenomena, does not account for three-dimensional effects such as azimuthal vorticity, lateral slot wake interactions, or swirl generated by turbine blades. Furthermore, the impact of diffuser geometry on turbine loading and efficiency was inferred from flow metrics alone, without direct coupling to rotor dynamics. Future work should address these limitations by conducting fully three-dimensional simulations that include rotor–diffuser interaction and transient-inflow effects. Experimental validation in a controlled hydraulic test facility is also essential for confirming numerical predictions and evaluating real-world manufacturing. Additional investigations should explore multi-slot designs, vary slot width and orientation, and assess the influence of turbulence intensity on diffuser performance.