Analysis of Spatiotemporal Characteristics of Intercity Travelers Within Urban Agglomeration Based on Trip Chain and K-Prototypes Algorithm
Abstract
1. Introduction
2. Study Area and Trip Chain Data
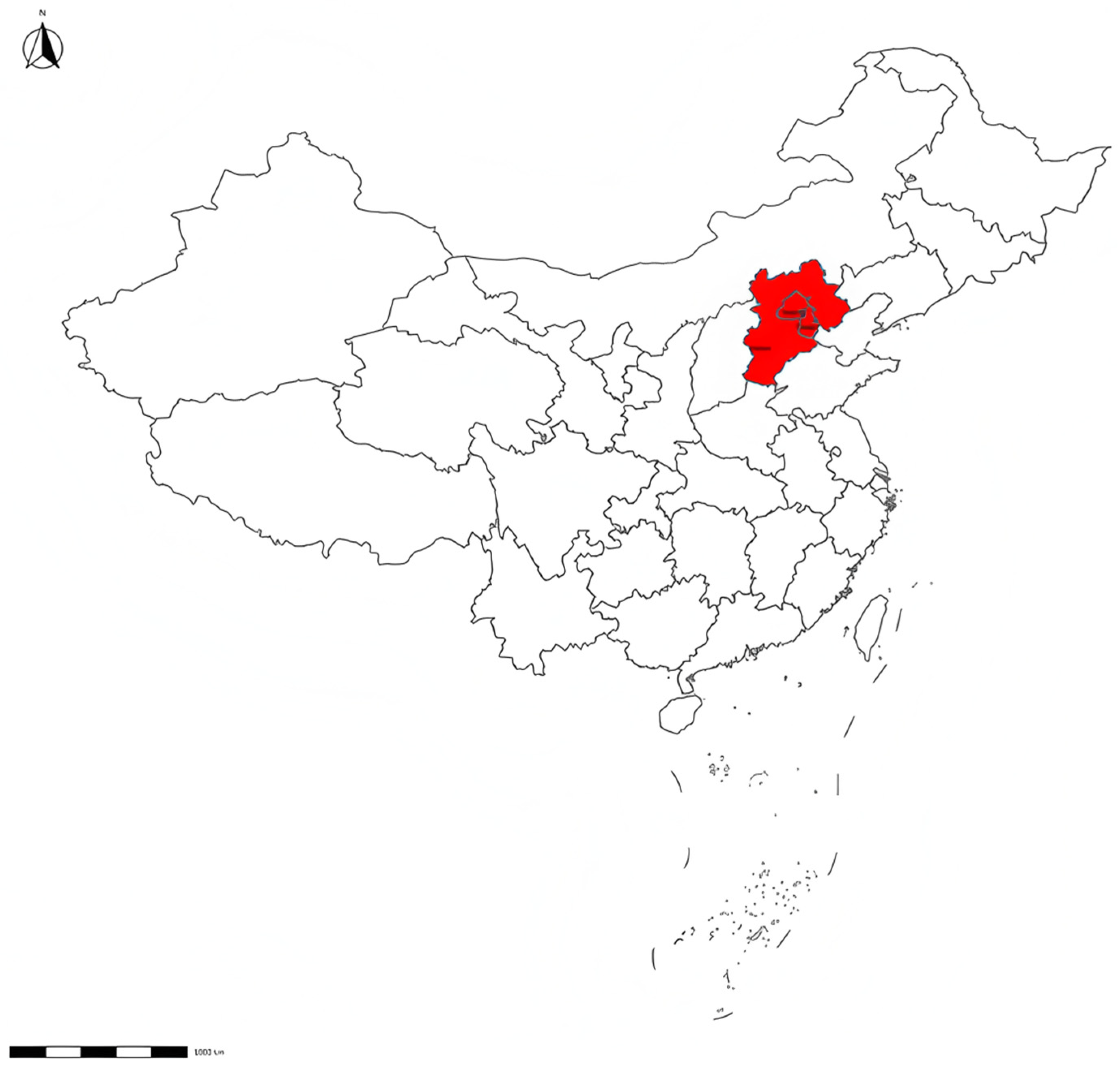
2.1. Study Area
2.2. Trip Chain Data
3. Methods
3.1. Variable Selection for Clustering Based on Cramer’s V—Spearman Correlation Coefficient
- Cramer’s V coefficient method
- 2.
- Spearman correlation coefficient
3.2. Silhouette Coefficient Method
3.3. K-Prototypes Algorithm
4. Results and Discussion
4.1. Variable Selection
4.2. Optimal Number of Clusters
4.3. Clustering Results Analysis
4.3.1. Comparative Analysis of Intercity Trip Chains from a Temporal Perspective
4.3.2. Comparative Analysis of Intercity Trip Chains from a Spatial Perspective
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, C.; Yu, D. Urban agglomeration: An evolving concept of an emerging phenomenon. Landsc. Urban Plan. 2017, 162, 126–136. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, L.; Wang, Y. Revealing the roles of climate, urban form, and vegetation greening in shaping the land surface temperature of urban agglomerations in the Yangtze River Economic Belt of China. J. Environ. Manag. 2025, 377, 124602. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Luo, J. Effects of spatial structure on carbon emissions of urban agglomerations in China. Cities 2025, 163, 106021. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Wu, S. Urban agglomeration policy and coordinated road infrastructure development. Transp. Res. Part A 2025, 195, 104433. [Google Scholar] [CrossRef]
- The Central Committee of the Communist Party of China and the State Council have issued the Transport Power Construction Outline. Available online: https://www.gov.cn/gongbao/content/2019/content_5437132.html (accessed on 4 April 2025).
- Notice of the State Council on issuing the 14th Five-Year Plan for Transportation Development. Available online: https://www.gov.cn/zhengce/zhengceku/2022-01/18/content_5669049.html (accessed on 4 April 2025).
- Guo, L.; Tang, M.; Wu, Y.; Bao, S.; Wu, Q. Government-led regional integration and economic growth: Evidence from a quasi-natural experiment of urban agglomeration development planning policies in China. Cities 2025, 156, 105482. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, D.; Mao, Z. Across the city boundaries: Exploring the impact of neighborhood environment on intercity commuters’ life satisfaction. Transp. Res. Part D Transp. Environ. 2024, 136, 104433. [Google Scholar] [CrossRef]
- Wang, L.; Shao, J. How does regional integration policy affect urban energy efficiency? A quasi-natural experiment based on policy of national urban agglomeration. Energy 2025, 319, 135003. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, J.; Gao, C.; Li, X.; Wang, Z.; Li, X. Assessing temporal-spatial characteristics of urban travel behaviors from multiday smart-card data. Physica A 2021, 576, 126058. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.J. Effects of high-speed rail on intercity travels, utility and social welfare in urban agglomerations: A game-theoretic perspective. Transp. Res. Part E 2024, 192, 103800. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Huang, J.; Yang, W.; Chen, Z. Exploring the dynamic impacts of COVID-19 on intercity travel in China. J. Transp. Geogr. 2021, 95, 103153. [Google Scholar] [CrossRef]
- Wei, S.; Pan, J. Spatiotemporal characteristics of residents’ intercity travel in China under the impact of COVID-19 pandemic. Cities 2024, 152, 105206. [Google Scholar] [CrossRef]
- Patra, S.S.; Chilukuri, B.R.; Vanajakshi, L. Analysis of road traffic pattern changes due to activity restrictions during COVID-19 pandemic in Chennai. Transp. Lett. 2021, 13, 473–481. [Google Scholar] [CrossRef]
- Aloi, A.; Alonso, B.; Benavente, J.; Cordera, R.; Echániz, E.; González, F.; Ladisa, C.; Lezama-Romanelli, R.; López-Parra, Á.; Mazzei, V.; et al. Effects of the COVID-19 Lockdown on Urban Mobility: Empirical Evidence from the City of Santander (Spain). Sustainability 2020, 12, 3870. [Google Scholar] [CrossRef]
- Muley, D.; Ghanim, M.S.; Mohammad, A.; Kharbeche, M. Quantifying the impact of COVID–19 preventive measures on traffic in the State of Qatar. Transp. Policy 2021, 103, 45–59. [Google Scholar] [CrossRef]
- Shamshiripour, A.; Rahimi, E.; Shabanpour, R.; Mohammadian, A. How is COVID-19 reshaping activity-travel behavior? Evidence from a comprehensive survey in Chicago. Transp. Res. Interdiscip. Perspect. 2020, 7, 100216. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.B.; Yu, J.Q.; Yang, Y.; Chen, N.; Jin, S.; Hu, Y.W.; Bai, C.C. Understanding travel behavior adjustment under COVID-19. Commun. Transp. Res. 2022, 2, 100068. [Google Scholar] [CrossRef]
- Welch, T.F.; Widita, A. Big data in public transportation: A review of sources and methods. Transp. Rev. 2019, 39, 795–818. [Google Scholar] [CrossRef]
- Yan, X.; Levine, J.; Zhao, X. Integrating ridesourcing services with public transit: An evaluation of traveler responses combining revealed and stated preference data. Transp. Res. Part C 2019, 105, 683–696. [Google Scholar] [CrossRef]
- Lei, D.; Chen, X.; Cheng, L.; Zhang, L.; Wang, P.; Wang, K. Minimum entropy rate-improved trip-chain method for origin–destination estimation using smart card data. Transp. Res. Part C 2021, 130, 103307. [Google Scholar] [CrossRef]
- Ko, E.; Lee, S.; Jang, K.; Kim, S. Changes in inter-city car travel behavior over the course of a year during the COVID-19 pandemic: A decision tree approach. Cities 2024, 146, 104758. [Google Scholar] [CrossRef]
- Kumar, P.; Khani, A.; He, Q. A robust method for estimating transit passenger trajectories using automated data. Transp. Res. Part C 2018, 95, 731–747. [Google Scholar] [CrossRef]
- Rahman, F.; Mazumder, R.J.R.; Kabir, S.; Hadiuzzaman, M. An exploratory analysis of factors affecting comfort level of work trip chaining and mode choice: A case study for Dhaka City. Transp. Dev. Econ. 2020, 6, 11. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, X.; Ma, X. Does the clusters of high-speed railway network match the urban agglomerations? A case study in China. Socioecon. Plann. Sci. 2024, 95, 101968. [Google Scholar] [CrossRef]
- Feng, Y.; Zhao, J.; Sun, H.; Wu, J.; Gao, Z. Choices of intercity multimodal passenger travel modes. Phys. A 2022, 600, 127500. [Google Scholar] [CrossRef]
- Cui, C.; Wu, X.; Liu, L.; Zhang, W. The spatial-temporal dynamics of daily intercity mobility in the Yangtze River Delta: An analysis using big data. Habitat Int. 2020, 106, 102174. [Google Scholar] [CrossRef]
- Bautista, H.; Dorian, A. Individual, household, and urban form determinants of trip chaining of non-work travel in México City. J. Transp. Geogr. 2022, 98, 103227. [Google Scholar] [CrossRef]
- Li, X.; Shi, L.; Shi, Y.; Tang, J.; Zhao, P.; Wang, Y.; Chen, J. Exploring interactive and nonlinear effects of key factors on intercity travel mode choice using XGBoost. Appl. Geogr. 2024, 166, 103264. [Google Scholar] [CrossRef]
- Cécile, S.; Clément, D.; Camelia, G. Variable selection methods for Log-Gaussian Cox processes: A case-study on accident data. Spat. Stat. 2024, 61, 100831. [Google Scholar]
- Wang, Y.; Tian, C.; Zhang, Z.; Li, K.; Chung, K.L.; Yang, B. Clustering algorithm for experimental datasets using global sensitivity-based affinity propagation (GSAP). Combust. Flame. 2024, 259, 113121. [Google Scholar] [CrossRef]
- Tatah, L.; Foley, L.; Oni, T.; Pearce, M.; Lwanga, C.; Were, V.; Assah, F.; Wasnyo, Y.; Mogo, E.; Okello, G.; et al. Comparing travel behaviour characteristics and correlates between large and small Kenyan cities (Nairobi versus Kisumu). J. Transp. Geogr. 2023, 110, 103625. [Google Scholar] [CrossRef]
- Yang, H.; Lv, S.; Guo, B.; Dai, J.; Wang, P. Uncovering spatiotemporal human mobility patterns in urban agglomerations: A mobility field based approach. Phys. A 2024, 637, 129571. [Google Scholar] [CrossRef]
- Cats, O.; Ferranti, F. Unravelling the spatial properties of individual mobility patterns using longitudinal travel data. J. Urban Mobil. 2022, 2, 100035. [Google Scholar] [CrossRef]
- Ma, W.; Gao, H. Impact of high-speed railway network improvement on consumption synergy in Beijing-Tianjin-Hebei region. Transp. Policy 2024, 158, 29–41. [Google Scholar] [CrossRef]
- Wang, W.; Wu, F.; Zhang, F. Assembling state power through rescaling: Inter-jurisdictional development in the Beijing-Tianjin Zhongguancun Tech Town. J. Polit. Geogr. 2024, 112, 103131. [Google Scholar] [CrossRef]
- Zhao, M.; Ji, Y.; Xie, J.; Yin, P.; Liu, J. Understanding patterns of adaptive comfort behavior in university graduate research offices–––A case study of a university in Beijing. Energy Build. 2024, 307, 113945. [Google Scholar] [CrossRef]
- Peng, H.; Li, Y.; Niu, X.; Tang, H.; Meng, X.; Li, Z.; Wan, K.; Li, W.; Song, W. Characteristics analysis of leakage diseases of Beijing underground subway stations based on the field investigation and data statistics. Transp. Geotech. 2024, 48, 101317. [Google Scholar] [CrossRef]
- Zhao, N.; Zhang, Y.; Chen, X.; Xiao, J.; Lu, Y.; Zhai, W.; Zhai, G. Resilience measurement and enhancement of population mobility network in Beijing-Tianjin-Hebei urban agglomeration under extreme rainfall impact. J. Transp. Geogr. 2025, 126, 104253. [Google Scholar] [CrossRef]
- Zou, L.; Wang, Z.; Guo, R.; Zhao, L.; Ma, L. Urban dynamics unveiled: A comprehensive analysis of Beijing’s subway evolution over the past decade. Tunn. Undergr. Space Technol. 2025, 157, 106284. [Google Scholar] [CrossRef]
- Kang, L.; Xiao, Y.; Sun, H.; Wu, J.; Luo, S.; Buhigiro, N. Nsabimana Buhigiro, Decisions on train rescheduling and locomotive assignment during the COVID-19 outbreak: A case of the Beijing-Tianjin intercity railway. Decis. Support Syst. 2022, 161, 113600. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Chen, Y.; Liu, J. Identification and integration of ventilation corridors in Shijiazhuang City, China. Sustain. Cities Soc. 2024, 112, 105543. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, L.; Sun, Z.; Wang, X. Spatiotemporal differentiation and the factors influencing urbanization and ecological environment synergistic effects within the Beijing-Tianjin-Hebei urban agglomeration. J. Environ. Manag. 2019, 243, 227–239. [Google Scholar] [CrossRef]
- Li, X.; Zhang, S.; Wu, Y.; Wang, Y.; Wang, W.; Chen, X. Exploring influencing factors of intercity mode choice from view of entire travel chain. J. Adv. Transp. 2021, 2021, 9454873. [Google Scholar] [CrossRef]
- Rao, J.; Lin, H.; Ma, J.; Chai, Y. Exploring the relationships among life satisfaction, neighborhood satisfaction and travel satisfaction in Beijing. Travel Behav. Soc. 2025, 39, 100979. [Google Scholar] [CrossRef]
- Yu, S.; Li, B.; Liu, D. Exploring the Public Health of Travel Behaviors in High-Speed Railway Environment during the COVID-19 Pandemic from the Perspective of Trip Chain: A Case Study of Beijing-Tianjin-Hebei Urban Agglomeration, China. Int. J. Environ. Res. Public Health 2023, 20, 1416. [Google Scholar] [CrossRef] [PubMed]
- Stopher, P.R.; Daigler, V.; Griffith, S. Smartphone app versus GPS Logger: A comparative study. Transp. Res. Procedia 2018, 32, 135–145. [Google Scholar] [CrossRef]
- Yu, D.D.; Matthews, L.; Scott, D.; Li, S.; Guo, Z.Y. Climate suitability for tourism in China in an era of climate change: A multiscale analysis using holiday climate index. Curr. Issues Tour. 2022, 25, 2269–2284. [Google Scholar] [CrossRef]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Dinh, D.T.; Fujinami, T.; Huynh, V.N. Estimating the optimal number of clusters in categorical data clustering by silhouette coefficient. In Knowledge and Systems Sciences; Springer: Singapore, 2019; pp. 1–17. [Google Scholar]
- Soria, J.; Chen, Y.; Stathopoulos, A. K-prototypes segmentation analysis on large-scale ridesourcing trip data. Transp. Res. Rec. 2020, 2674, 383–394. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, L.; Ni, A.; Liu, X. Analysis of travel mode choice and trip chain pattern relationships based on multi-day GPS data: A case study in Shanghai, China. J. Transp. Geogr. 2021, 93, 103070. [Google Scholar] [CrossRef]
- Omar, N.; Aly, H.; Little, T. Optimized feature selection based on a least-redundant and highest-relevant framework for a solar irradiance forecasting model. IEEE Access 2022, 10, 48643–48659. [Google Scholar] [CrossRef]
- Ali Abd Al-Hameed, K. Spearman’s correlation coefficient in statistical analysis. Int. J. Nonlinear Anal. Appl. 2022, 13, 3249–3255. [Google Scholar]
- Meybodi, E.E.; DastBaravarde, A.; Hussain, S.K.; Karimdost, S. Machine-learning method applied to provide the best predictive model for rock mass deformability modulus (Em). Environ. Earth Sci. 2023, 82, 149. [Google Scholar] [CrossRef]
- Sapra, R.L.; Saluja, S. Understanding statistical association and correlation. Curr. Med. Res. Pract. 2021, 11, 31–38. [Google Scholar] [CrossRef]
- Miola, A.C.; Miot, H.A. Comparing categorical variables in clinical and experimental studies. J. Vasc. Bras. 2022, 21, e20210225. [Google Scholar] [CrossRef] [PubMed]
- Ahmadzade, H.; Gao, R. Covariance of uncertain random variables and its application to portfolio optimization. J. Ambient Intell. Humaniz. Comput. 2020, 11, 2613–2624. [Google Scholar] [CrossRef]
- Surya, F.S.; Mutasowifin, A. Selection of agricultural industry stocks by application of K-means algorithm with Elbow method. BIO Web Conf. 2025, 171, 04003. [Google Scholar]
- Du, P.; Li, F.; Shao, J. Multi-agent reinforcement learning clustering algorithm based on silhouette coefficient. Neurocomputing. 2024, 596, 127901. [Google Scholar] [CrossRef]
- Syakur, M.A.; Khotimah, B.K.; Rochman, E.M.S.; Satoto, B.D. Integration of K-Means Clustering Method and Elbow Method for Identification of the Best Customer Profile Cluster. IOP Conf. Series Mater. Sci. Eng. 2018, 336, 012017. [Google Scholar] [CrossRef]
- Bagirov, A.; Aliguliyev, R.; Sultanova, N. Finding compact and well-separated clusters: Clustering using silhouette coefficients. Pattern Recognit. 2022, 135, 109144. [Google Scholar] [CrossRef]
- Jun, L.; Tingjin, L.; Kai, L. A forward k-means algorithm for regression clustering. Inf. Sci. 2025, 711, 122105. [Google Scholar]
- Akay, Z.; Güzin, Y. Clustering the mixed panel dataset using Gower’s distance and K-prototypes algorithms. Commun. Stat. Simul. Comput. 2018, 47, 3031–3041. [Google Scholar] [CrossRef]
- Schneider, J.W. Null hypothesis significance tests: A mix-up of two different theories—The basis for widespread confusion and numerous misinterpretations. Scientometrics 2015, 102, 411–432. [Google Scholar] [CrossRef]
- Tao, D.; Ning, J.; Shoufeng, M.; Shu, X.; Ghim, P.O.; Peng, L.; Hai, H. Impacts of intercity com-muting on travel characteristics and urban performances in a two-city system. Transp. Res. Part E 2022, 164, 102792. [Google Scholar]
- Wu, J.; Liao, H. Weather, travel mode choice, and impacts on subway ridership in Beijing. Transp. Res. Part A 2020, 135, 264–279. [Google Scholar] [CrossRef]
- Qin, T.; Dong, W.; Huang, H. Perceptions of space and time of public transport travel associated with human brain activities: A case study of bus travel in Beijing. Comput. Environ. Urban 2023, 99, 101919. [Google Scholar] [CrossRef]
- Yang, X.; Qu, L.; Li, Y.; Kang, Y. Alighting and boarding time prediction in different types of waiting areas at subway stations. Tunn. Undergr. Space Technol. 2023, 141, 105337. [Google Scholar] [CrossRef]
- Nezir, A.; Ali, O.K.; Muhammet, D. The impacts of COVID-19 on travel behavior and initial perception of public transport measures in Istanbul. Decis. Anal. J. 2022, 2, 100029. [Google Scholar]
- Yannis, G.; Chaziris, A. Transport system and infrastructure. Transp. Res. 2022, 60, 6–11. [Google Scholar] [CrossRef]
- Zheng, W.; Du, N.; Wang, X. Understanding the city-transport system of urban agglomeration through improved space syntax analysis. Int. Reg. Sci. Rev. 2022, 45, 161–187. [Google Scholar] [CrossRef]


| No. | Variable | Description | Information Fields |
|---|---|---|---|
| 1 | Weekday | Type of the day | 1: Holiday |
| 2: Weekend | |||
| 3: Weekday | |||
| 2 | Gender | The sex of the traveler | 1: Male |
| 2: Female | |||
| 3 | Age | The age of the traveler | 1: 0–18 |
| 2: 19–24 | |||
| 3: 25–29 | |||
| 4: 30–34 | |||
| 5: 35–39 | |||
| … | |||
| 4 | Type-O | Origin Type | 1: Residence |
| 5 | Type-D | Destination Type | 2: Work |
| 3: Visit | |||
| 6 | Mode-O | Transportation mode of origin city | 1: Road transport |
| 7 | Mode-D | Transportation mode of destination city | 2: Railway |
| 3: Airplane | |||
| 4: Subway | |||
| 5: Others | |||
| 8 | MOT-O | Departure time from origin city | 1: 0:00–1:00 |
| 9 | MOT-D | Arrival time at destination city | 2: 1:00–2:00 |
| 10 | THub-O | Arrival time at origin city hub | 3: 2:00–3:00 |
| 11 | THub-D | Arrival time at destination city hub | 4:3:00–4:00 |
| 12 | De-O | Departure time from origin city hub | … |
| 13 | De-D | Departure time from destination city hub | 23: 23:00–24:00 |
| 14 | Ds-O | Travel distance within origin city | 1: 0–5 km |
| 15 | Ds-D | Travel distance within destination city | 2: 5–10 km |
| 3: 10–25 km | |||
| … | |||
| 16 | Tr-T-O | Travel time within origin city | 1: 0–5 min |
| 17 | Tr-T-D | Travel time within destination city | 2: 5–10 min |
| 18 | Wt-O | Waiting time at origin city hub | 3: 10–15 min |
| 19 | Wt-D | Waiting time at the destination city hub | 4:15–20 min |
| … |
| May 2019 | May 2021 | |||
|---|---|---|---|---|
| Direction | Number of Trip Chains | Percentage | Number of Trip Chains | Percentage |
| Beijing–Tianjin | 36,920 | 42.11% | 27,518 | 37.13% |
| Tianjin–Beijing | 34,100 | 38.89% | 20,199 | 27.25% |
| Beijing–Shijiazhuang | 6965 | 7.94% | 10,956 | 14.78% |
| Shijiazhuang–Beijing | 3964 | 4.52% | 7829 | 10.56% |
| Tianjin–Shijiazhuang | 3058 | 3.49% | 4126 | 5.57% |
| Shijiazhuang–Tianjin | 2675 | 3.05% | 3487 | 4.70% |
| Total | 87,682 | 100% | 74,115 | 100% |
| Weekday | Gender | Age | Cost | MOT-O | Type-O | Mode-O | Ds-O | Tr-T-O | THub-O | Wt-O | De-O | Thub-D | Wt-D | De-D | Mode-D | Ds-D | Tr-T-D | MOT-D | Type-D | Weekday | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weekday | r | 1.000 | 0.060 | 0.120 | 0.062 | 0.130 | 0.139 | 0.018 | −0.051 | −0.031 | 0.127 | −0.124 | 0.113 | 0.093 | −0.089 | 0.085 | 0.019 | 0.067 | 0.035 | 0.086 | 0.124 | 1.000 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Gender | r | 0.060 | 1.000 | −0.013 | −0.049 | −0.008 | 0.024 | 0.013 | −0.017 | −0.020 | −0.011 | 0.017 | −0.009 | −0.010 | 0.010 | −0.009 | 0.018 | −0.052 | −0.028 | −0.011 | 0.023 | 0.060 |
| Sig. | 0.000 | 0.000 | 0.010 | 0.000 | 0.108 | 0.000 | 0.012 | 0.001 | 0.000 | 0.043 | 0.001 | 0.087 | 0.065 | 0.059 | 0.090 | 0.001 | 0.000 | 0.000 | 0.035 | 0.000 | 0.000 | |
| Age | r | 0.120 | −0.013 | 1.000 | −0.126 | −0.009 | 0.039 | −0.113 | −0.115 | −0.109 | −0.019 | 0.028 | −0.016 | −0.014 | −0.044 | −0.019 | −0.076 | −0.023 | −0.024 | −0.020 | 0.048 | 0.120 |
| Sig. | 0.000 | 0.010 | 0.000 | 0.000 | 0.091 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.009 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Cost | r | 0.062 | −0.049 | −0.126 | 1.000 | −0.020 | 0.007 | −0.042 | 0.010 | 0.013 | −0.020 | −0.010 | −0.021 | −0.030 | −0.030 | −0.032 | 0.006 | 0.004 | 0.003 | −0.033 | 0.005 | 0.062 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.158 | 0.000 | 0.047 | 0.016 | 0.000 | 0.065 | 0.000 | 0.000 | 0.000 | 0.000 | 0.230 | 0.440 | 0.624 | 0.000 | 0.300 | 0.000 | |
| MOT-O | r | 0.130 | −0.008 | −0.009 | −0.020 | 1.000 | 0.012 | −0.006 | −0.177 | −0.113 | 0.990 | −0.010 | 0.984 | 0.957 | −0.127 | 0.952 | −0.032 | 0.077 | 0.028 | 0.950 | −0.038 | 0.130 |
| Sig. | 0.000 | 0.108 | 0.091 | 0.000 | 0.000 | 0.021 | 0.290 | 0.000 | 0.000 | 0.000 | 0.055 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Type-O | r | 0.139 | 0.024 | 0.039 | 0.007 | 0.012 | 1.000 | 0.015 | −0.024 | 0.014 | 0.010 | −0.040 | 0.006 | 0.002 | −0.014 | 0.001 | 0.010 | −0.018 | −0.019 | 0.000 | 0.056 | 0.139 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.158 | 0.021 | 0.000 | 0.016 | 0.000 | 0.007 | 0.054 | 0.000 | 0.247 | 0.691 | 0.007 | 0.807 | 0.132 | 0.001 | 0.000 | 0.944 | 0.000 | 0.000 | |
| Mode-O | r | 0.018 | 0.013 | −0.113 | −0.042 | −0.006 | 0.015 | 1.000 | 0.293 | 0.474 | 0.036 | −0.091 | 0.024 | 0.019 | 0.000 | 0.018 | 0.079 | −0.020 | 0.013 | 0.019 | 0.011 | 0.018 |
| Sig. | 0.003 | 0.012 | 0.000 | 0.000 | 0.290 | 0.016 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.948 | 0.000 | 0.000 | 0.000 | 0.014 | 0.000 | 0.130 | 0.003 | |
| Ds-O | r | −0.051 | −0.017 | −0.115 | 0.010 | −0.177 | −0.024 | 0.293 | 1.000 | 0.745 | −0.105 | 0.009 | −0.104 | −0.098 | 0.035 | −0.096 | 0.032 | 0.005 | 0.003 | −0.095 | −0.006 | −0.051 |
| Sig. | 0.000 | 0.001 | 0.000 | 0.047 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.079 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.340 | 0.578 | 0.000 | 0.218 | 0.000 | |
| Tr-T-O | r | −0.031 | −0.020 | −0.109 | 0.013 | −0.113 | 0.014 | 0.474 | 0.745 | 1.000 | −0.020 | −0.012 | −0.022 | −0.029 | 0.017 | −0.028 | 0.055 | 0.011 | 0.024 | −0.026 | −0.008 | −0.031 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.016 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.020 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.038 | 0.000 | 0.000 | 0.141 | 0.000 | |
| THub-O | r | 0.127 | −0.011 | −0.019 | −0.020 | 0.990 | 0.010 | 0.036 | −0.105 | −0.020 | 1.000 | −0.010 | 0.990 | 0.962 | −0.126 | 0.956 | −0.027 | 0.079 | 0.031 | 0.954 | −0.041 | 0.127 |
| Sig. | 0.000 | 0.043 | 0.000 | 0.000 | 0.000 | 0.054 | 0.000 | 0.000 | 0.000 | 0.000 | 0.063 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Wt-O | r | −0.124 | 0.017 | 0.028 | −0.010 | −0.010 | −0.040 | −0.091 | 0.009 | −0.012 | −0.010 | 1.000 | 0.093 | 0.040 | 0.026 | 0.043 | −0.023 | −0.008 | −0.004 | 0.042 | −0.001 | −0.124 |
| Sig. | 0.000 | 0.001 | 0.000 | 0.065 | 0.055 | 0.000 | 0.000 | 0.079 | 0.020 | 0.063 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.110 | 0.441 | 0.000 | 0.893 | 0.000 | |
| De-O | r | 0.113 | −0.009 | −0.016 | −0.021 | 0.984 | 0.006 | 0.024 | −0.104 | −0.022 | 0.990 | 0.093 | 1.000 | 0.960 | −0.124 | 0.956 | −0.030 | 0.077 | 0.030 | 0.954 | −0.040 | 0.113 |
| Sig. | 0.000 | 0.087 | 0.002 | 0.000 | 0.000 | 0.247 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Thub-D | r | 0.093 | −0.010 | −0.014 | −0.030 | 0.957 | 0.002 | 0.019 | −0.098 | −0.029 | 0.962 | 0.040 | 0.960 | 1.000 | −0.115 | 0.991 | −0.040 | 0.078 | 0.020 | 0.989 | −0.053 | 0.093 |
| Sig. | 0.000 | 0.065 | 0.009 | 0.000 | 0.000 | 0.691 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Wt-D | r | −0.089 | 0.010 | −0.044 | −0.030 | −0.127 | −0.014 | 0.000 | 0.035 | 0.017 | −0.126 | 0.026 | −0.124 | −0.115 | 1.000 | −0.028 | −0.054 | −0.069 | −0.084 | −0.031 | −0.055 | −0.089 |
| Sig. | 0.000 | 0.059 | 0.000 | 0.000 | 0.000 | 0.007 | 0.948 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| De-D | r | 0.085 | −0.009 | −0.019 | −0.032 | 0.952 | 0.001 | 0.018 | −0.096 | −0.028 | 0.956 | 0.043 | 0.956 | 0.991 | −0.028 | 1.000 | −0.045 | 0.072 | 0.012 | 0.994 | −0.061 | 0.085 |
| Sig. | 0.000 | 0.090 | 0.000 | 0.000 | 0.000 | 0.807 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000 | |
| Mode-D | r | 0.019 | 0.018 | −0.076 | 0.006 | −0.032 | 0.010 | 0.079 | 0.032 | 0.055 | −0.027 | −0.023 | −0.030 | −0.040 | −0.054 | −0.045 | 1.000 | 0.345 | 0.410 | −0.018 | 0.013 | 0.019 |
| Sig. | 0.002 | 0.001 | 0.000 | 0.230 | 0.000 | 0.132 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.037 | 0.002 | |
| Ds-D | r | 0.067 | −0.052 | −0.023 | 0.004 | 0.077 | −0.018 | −0.020 | 0.005 | 0.011 | 0.079 | −0.008 | 0.077 | 0.078 | −0.069 | 0.072 | 0.345 | 1.000 | 0.658 | 0.115 | −0.017 | 0.067 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.440 | 0.000 | 0.001 | 0.000 | 0.340 | 0.038 | 0.000 | 0.110 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | |
| Tr-T-D | r | 0.035 | −0.028 | −0.024 | 0.003 | 0.028 | −0.019 | 0.013 | 0.003 | 0.024 | 0.031 | −0.004 | 0.030 | 0.020 | −0.084 | 0.012 | 0.410 | 0.658 | 1.000 | 0.075 | −0.022 | 0.035 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.624 | 0.000 | 0.000 | 0.014 | 0.578 | 0.000 | 0.000 | 0.441 | 0.000 | 0.000 | 0.000 | 0.018 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| MOT-D | r | 0.086 | −0.011 | −0.020 | −0.033 | 0.950 | 0.000 | 0.019 | −0.095 | −0.026 | 0.954 | 0.042 | 0.954 | 0.989 | −0.031 | 0.994 | −0.018 | 0.115 | 0.075 | 1.000 | −0.062 | 0.086 |
| Sig. | 0.000 | 0.035 | 0.000 | 0.000 | 0.000 | 0.944 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Type-D | r | 0.124 | 0.023 | 0.048 | 0.005 | −0.038 | 0.056 | 0.011 | −0.006 | −0.008 | −0.041 | −0.001 | −0.040 | −0.053 | −0.055 | −0.061 | 0.013 | −0.017 | −0.022 | −0.062 | 1.000 | 0.124 |
| Sig. | 0.000 | 0.000 | 0.000 | 0.300 | 0.000 | 0.000 | 0.130 | 0.218 | 0.141 | 0.000 | 0.893 | 0.000 | 0.000 | 0.000 | 0.000 | 0.037 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Time | Direction | Optimal Value of K | Maximum Silhouette Coefficient |
|---|---|---|---|
| May 2019 | Beijing–Tianjin | 5 | 0.204 |
| Tianjin–Beijing | 5 | 0.201 | |
| Beijing–Shijiazhuang | 4 | 0.197 | |
| Shijiazhuang–Beijing | 4 | 0.218 | |
| Tianjin–Shijiazhuang | 4 | 0.234 | |
| Shijiazhuang–Tianjin | 3 | 0.233 | |
| May 2021 | Beijing–Tianjin | 4 | 0.192 |
| Tianjin–Beijing | 5 | 0.216 | |
| Beijing–Shijiazhuang | 6 | 0.188 | |
| Shijiazhuang–Beijing | 4 | 0.213 | |
| Tianjin–Shijiazhuang | 3 | 0.251 | |
| Shijiazhuang–Tianjin | 4 | 0.251 |
| Beijing–Tianjin | Tianjin–Beijing | |||
|---|---|---|---|---|
| May 2019 | May 2021 | May 2019 | May 2021 | |
| Weekday | 3 | 3 | 3 | 3 |
| Gender | 1 | 1 | 1 | 1 |
| Type-O | 1 | 1 | 1 | 1 |
| Mode-O | 4 | 4 | 1 | 1 |
| Mode-D | 1 | 1 | 1 | 1 |
| Type-D | 1 | 1 | 1 | 1 |
| Age | 6 | 5 | 6 | 7 |
| MOT-O | 8 | 7 | 10 | 12 |
| Ds-O | 2 | 2 | 1 | 1 |
| Wt-O | 5 | 7 | 6 | 6 |
| Wt-D | 7 | 6 | 5 | 6 |
| Ds-D | 1 | 1 | 2 | 2 |
| Percentage | 55.7% | 54.99% | 47.7% | 49.50% |
| Beijing–Shijiazhuang | Shijiazhuang–Beijing | |||
|---|---|---|---|---|
| May 2019 | May 2021 | May 2019 | May 2021 | |
| Weekday | 3 | 3 | 3 | 3 |
| Gender | 1 | 1 | 1 | 1 |
| Type-O | 1 | 1 | 1 | 1 |
| Mode-O | 4 | 4 | 1 | 1 |
| Mode-D | 1 | 1 | 1 | 1 |
| Type-D | 0 | 1 | 0 | 1 |
| Age | 7 | 5 | 7 | 5 |
| MOT-O | 13 | 8 | 7 | 7 |
| Ds-O | 2 | 2 | 1 | 1 |
| Wt-O | 10 | 9 | 7 | 6 |
| Wt-D | 7 | 5 | 7 | 7 |
| Ds-D | 1 | 1 | 2 | 2 |
| Percentage | 52.6% | 41.39% | 45.4% | 58.76% |
| Tianjin–Shijiazhuang | Shijiazhuang–Tianjin | |||
|---|---|---|---|---|
| May 2019 | May 2021 | May 2019 | May 2021 | |
| Weekday | 3 | 3 | 3 | 3 |
| Gender | 2 | 1 | 1 | 1 |
| Type-O | 1 | 1 | 1 | 1 |
| Mode-O | 1 | 1 | 1 | 1 |
| Mode-D | 1 | 1 | 1 | 1 |
| Type-D | 0 | 1 | 1 | 1 |
| Age | 5 | 5 | 5 | 5 |
| MOT-O | 8 | 7 | 10 | 11 |
| Ds-O | 1 | 1 | 1 | 1 |
| Wt-O | 9 | 7 | 11 | 11 |
| Wt-D | 6 | 8 | 7 | 6 |
| Ds-D | 1 | 1 | 1 | 1 |
| Percentage | 47.6% | 60.98% | 67.9% | 57.14% |
| Attributes | Beijing– Tianjin | Tianjin– Beijing | Beijing– Shijiazhuang | Shijiazhuang–Beijing | Tianjin– Shijiazhuang | Shijiazhuang–Tianjin |
|---|---|---|---|---|---|---|
| Weekday | 3 | 3 | 3 | 3 | 3 | 3 |
| Gender | 1 | 1 | 1 | 1 | 2 | 1 |
| Type-O | 1 | 1 | 1 | 1 | 1 | 1 |
| Mode-O | 4 | 1 | 4 | 1 | 1 | 1 |
| Mode-D | 1 | 1 | 1 | 1 | 1 | 1 |
| Type-D | 1 | 1 | 0 | 0 | 0 | 1 |
| Age | 6 | 6 | 7 | 7 | 5 | 5 |
| MOT-O | 8 | 10 | 13 | 7 | 8 | 10 |
| Ds-O | 2 | 1 | 2 | 1 | 1 | 1 |
| Wt-O | 5 | 6 | 10 | 7 | 9 | 11 |
| Wt-D | 7 | 5 | 7 | 7 | 6 | 7 |
| Ds-D | 1 | 2 | 1 | 2 | 1 | 1 |
| Percentage | 55.7% | 47.7% | 52.6% | 45.4% | 47.6% | 67.9% |
| Attributes | Beijing– Tianjin | Tianjin– Beijing | Beijing– Shijiazhuang | Shijiazhuang–Beijing | Tianjin– Shijiazhuang | Shijiazhuang–Tianjin |
|---|---|---|---|---|---|---|
| Weekday | 3 | 3 | 3 | 3 | 3 | 3 |
| Gender | 1 | 1 | 1 | 1 | 1 | 1 |
| Type-O | 1 | 1 | 1 | 1 | 1 | 1 |
| Mode-O | 4 | 1 | 4 | 1 | 1 | 1 |
| Mode-D | 1 | 1 | 1 | 1 | 1 | 1 |
| Type-D | 1 | 1 | 1 | 1 | 1 | 1 |
| Age | 5 | 7 | 5 | 5 | 5 | 5 |
| MOT-O | 7 | 12 | 8 | 7 | 7 | 11 |
| Ds-O | 2 | 1 | 2 | 1 | 1 | 1 |
| Wt-O | 7 | 6 | 9 | 6 | 7 | 11 |
| Wt-D | 6 | 6 | 5 | 7 | 8 | 6 |
| Ds-D | 1 | 2 | 1 | 2 | 1 | 1 |
| Percentage | 54.99% | 49.50% | 41.39% | 58.76% | 60.98% | 57.14% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Liu, Y.; Hu, S. Analysis of Spatiotemporal Characteristics of Intercity Travelers Within Urban Agglomeration Based on Trip Chain and K-Prototypes Algorithm. Appl. Syst. Innov. 2025, 8, 88. https://doi.org/10.3390/asi8040088
Yu S, Liu Y, Hu S. Analysis of Spatiotemporal Characteristics of Intercity Travelers Within Urban Agglomeration Based on Trip Chain and K-Prototypes Algorithm. Applied System Innovation. 2025; 8(4):88. https://doi.org/10.3390/asi8040088
Chicago/Turabian StyleYu, Shuai, Yuqing Liu, and Song Hu. 2025. "Analysis of Spatiotemporal Characteristics of Intercity Travelers Within Urban Agglomeration Based on Trip Chain and K-Prototypes Algorithm" Applied System Innovation 8, no. 4: 88. https://doi.org/10.3390/asi8040088
APA StyleYu, S., Liu, Y., & Hu, S. (2025). Analysis of Spatiotemporal Characteristics of Intercity Travelers Within Urban Agglomeration Based on Trip Chain and K-Prototypes Algorithm. Applied System Innovation, 8(4), 88. https://doi.org/10.3390/asi8040088




