Microgrid Frequency Regulation Based on Precise Matching Between Power Commands and Load Consumption Using Shallow Neural Networks
Abstract
1. Introduction
- Unlike previous research, which typically defaults power reference values to zero, this paper conducts a comprehensive analysis of optimal power reference value configurations in droop control. A direct relationship is established between the power variations of time-varying public loads and the power reference values in droop control within the controller, leading to enhanced system frequency stability and offset correction.
- Unlike paper [11], which uses quantitative numerical relationship corrections to eliminate operational state deviations, this study’s SNNs are designed to match power commands with load consumption to deliver efficient and accurate results. Moreover, an input enhancement method is proposed to mitigate gradient vanishing and enhance SNN stability when addressing power inputs with zero values.
- To further correct the time delay and data misalignment issues between curves caused by SNN fitting, a dynamic timing regularization is proposed to achieve precise peak-to-peak correspondence between curves. As a result, frequency regulation becomes more stable at the rated value.
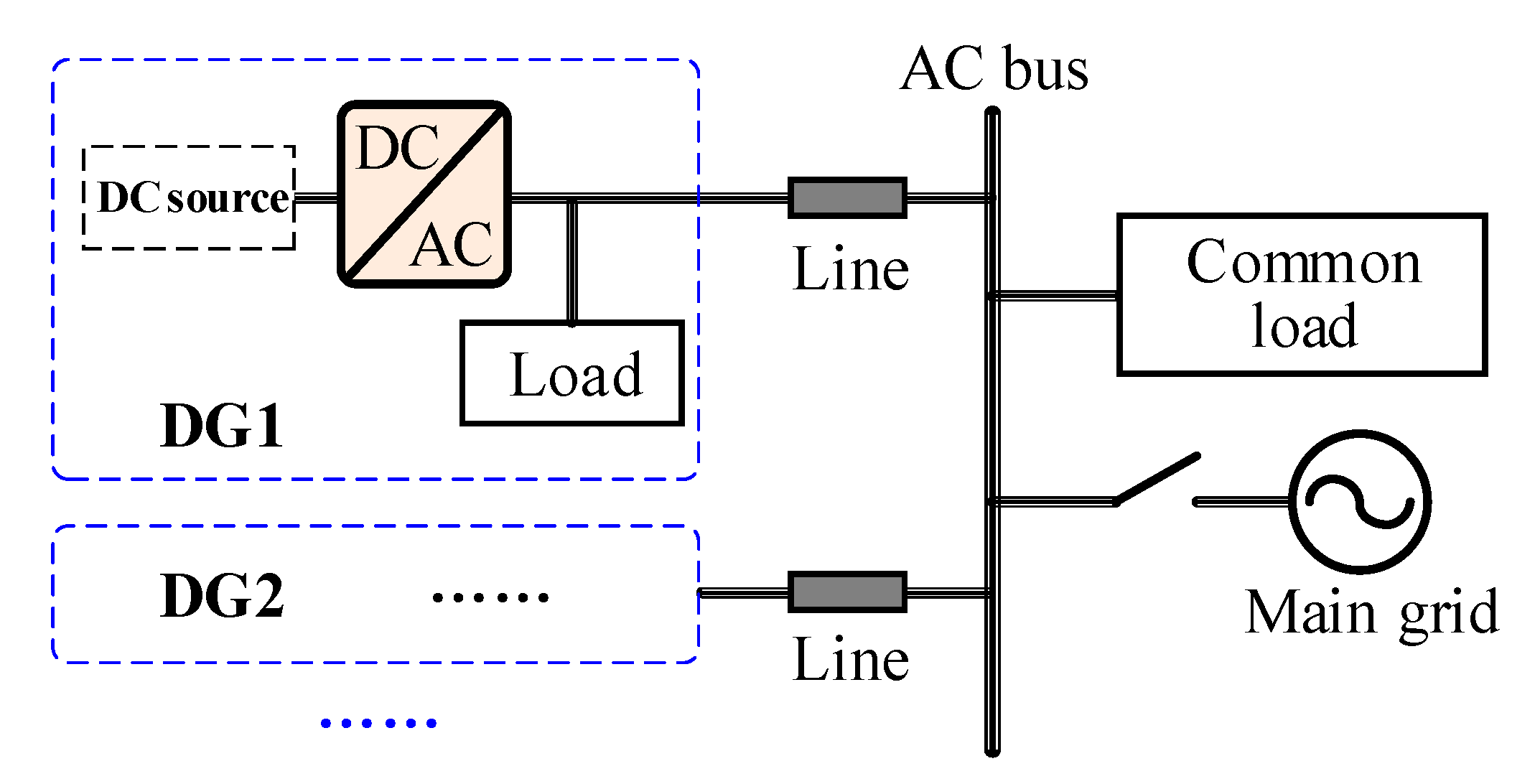
2. Hierarchical Control for Frequency Regulation
2.1. Primary Level
2.2. Secondary Level
2.3. Frequency Regulation
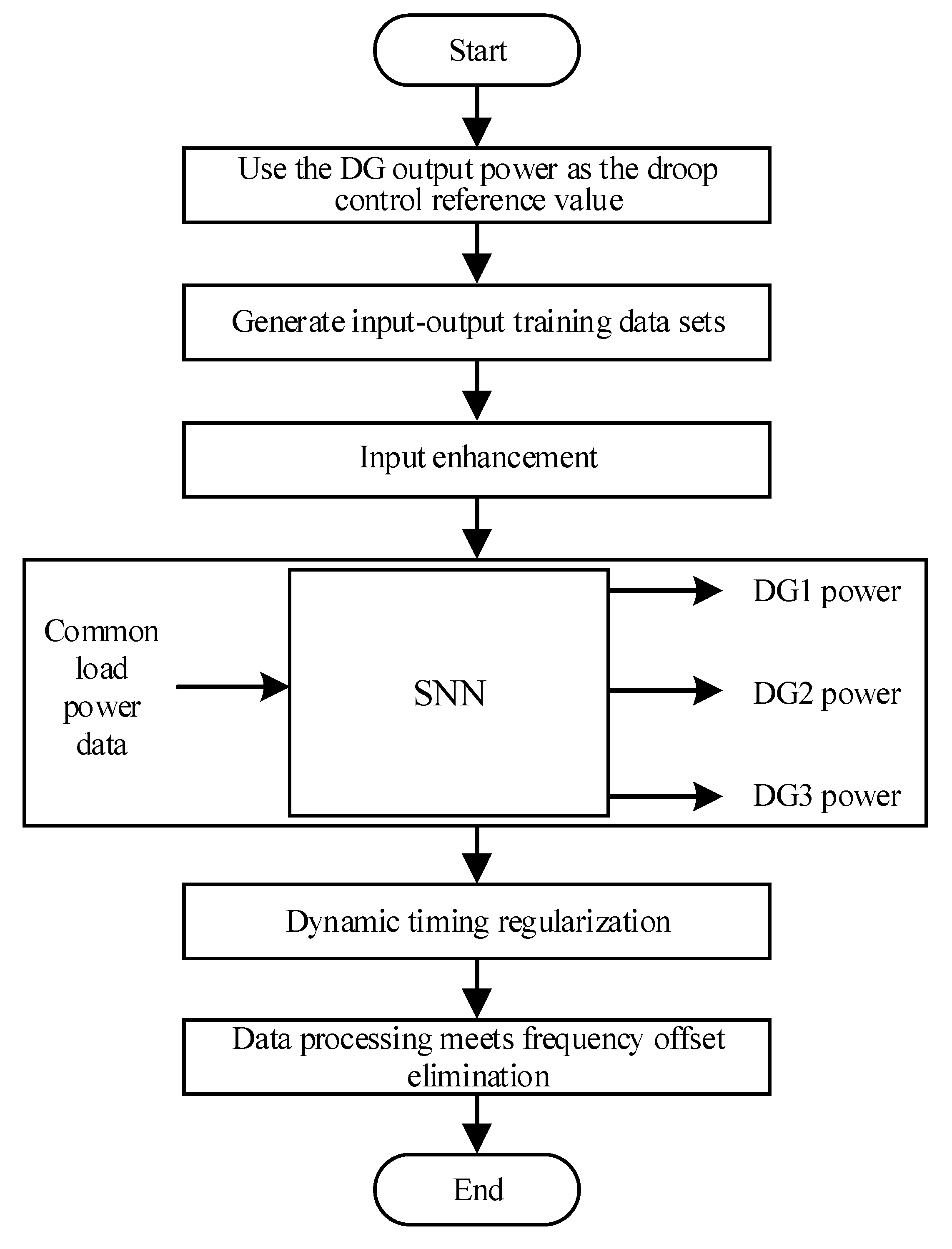
3. Proposed Control Methods
3.1. Data Preparation and Processing
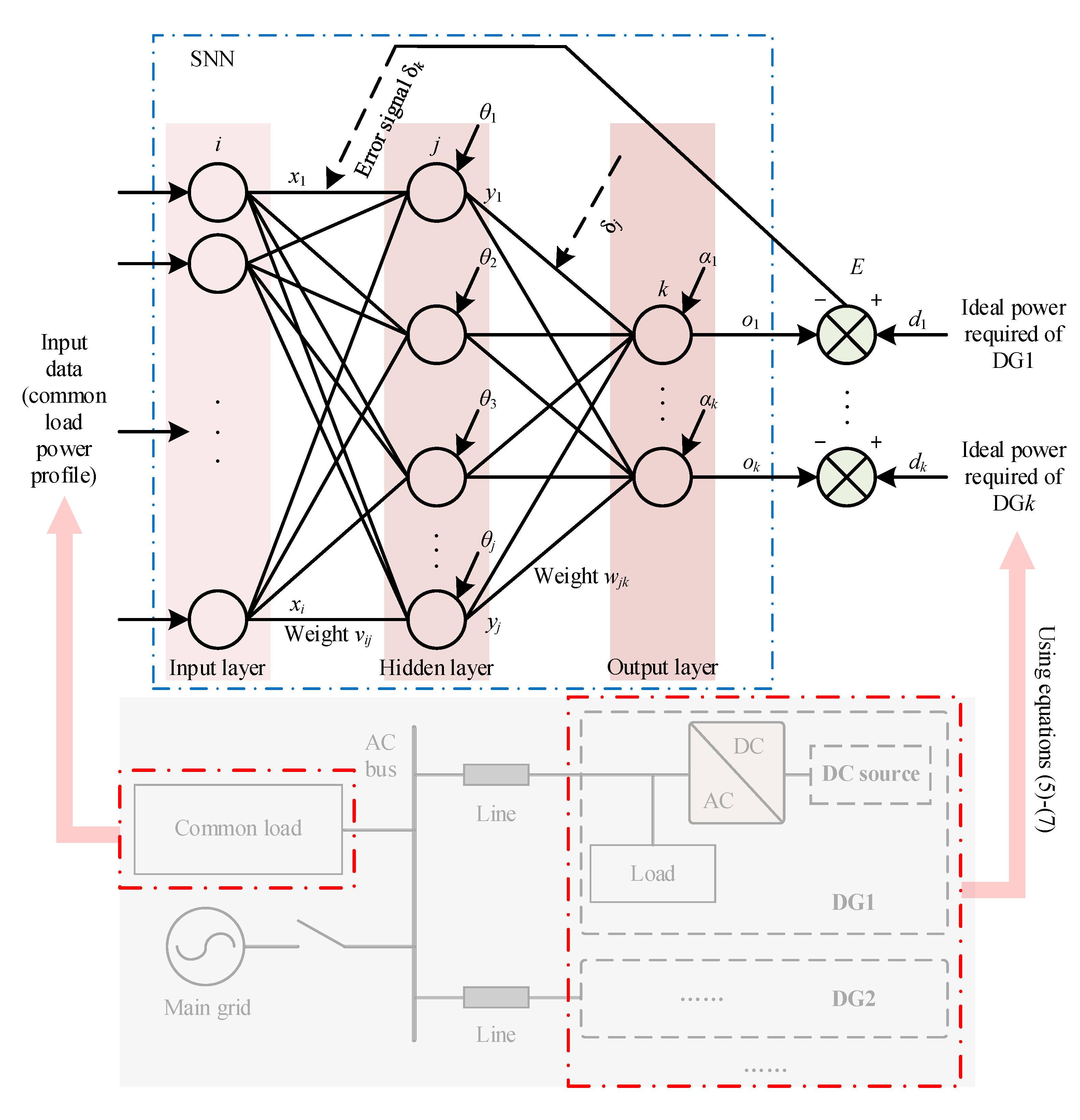
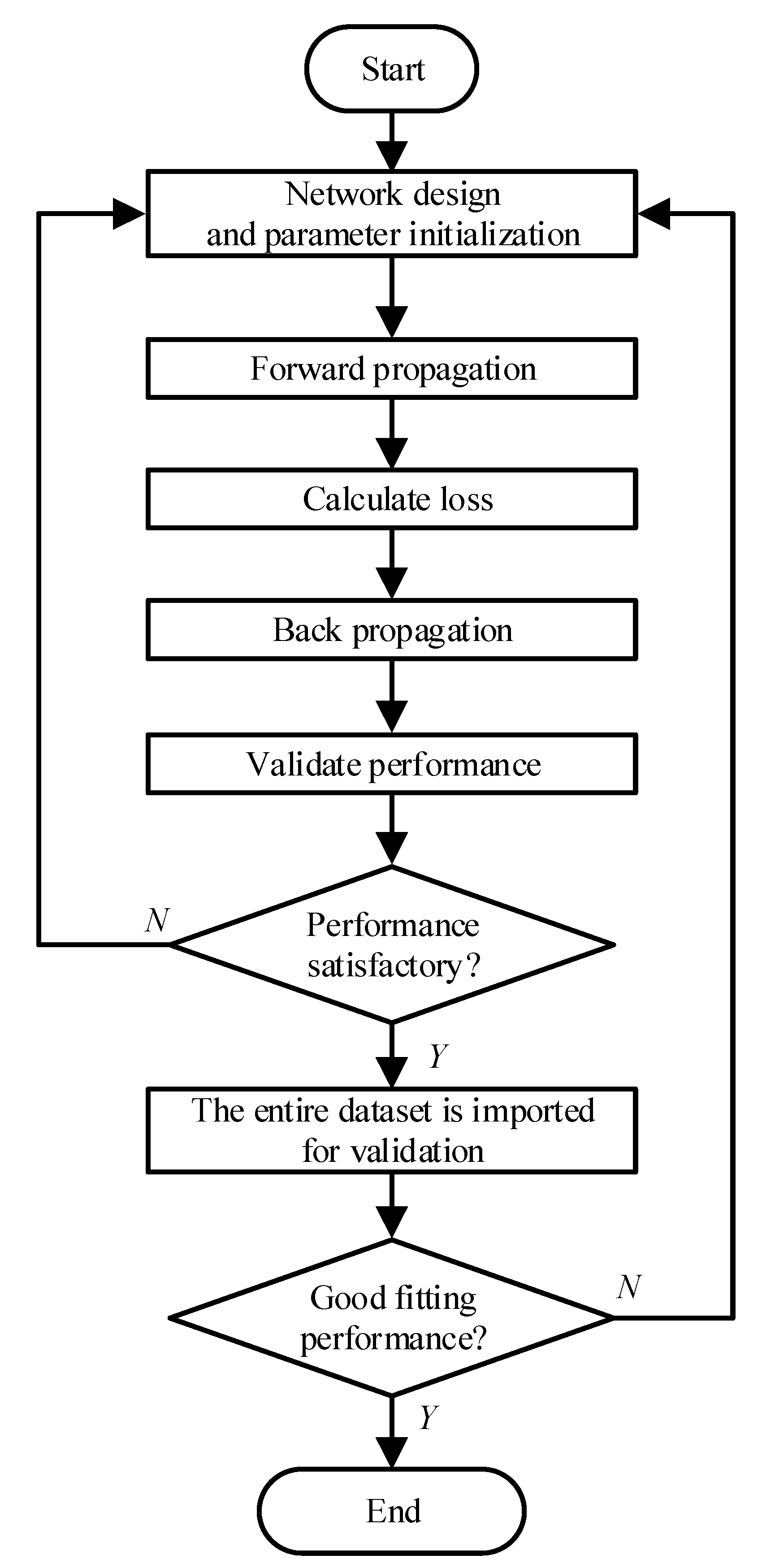
3.2. SNN
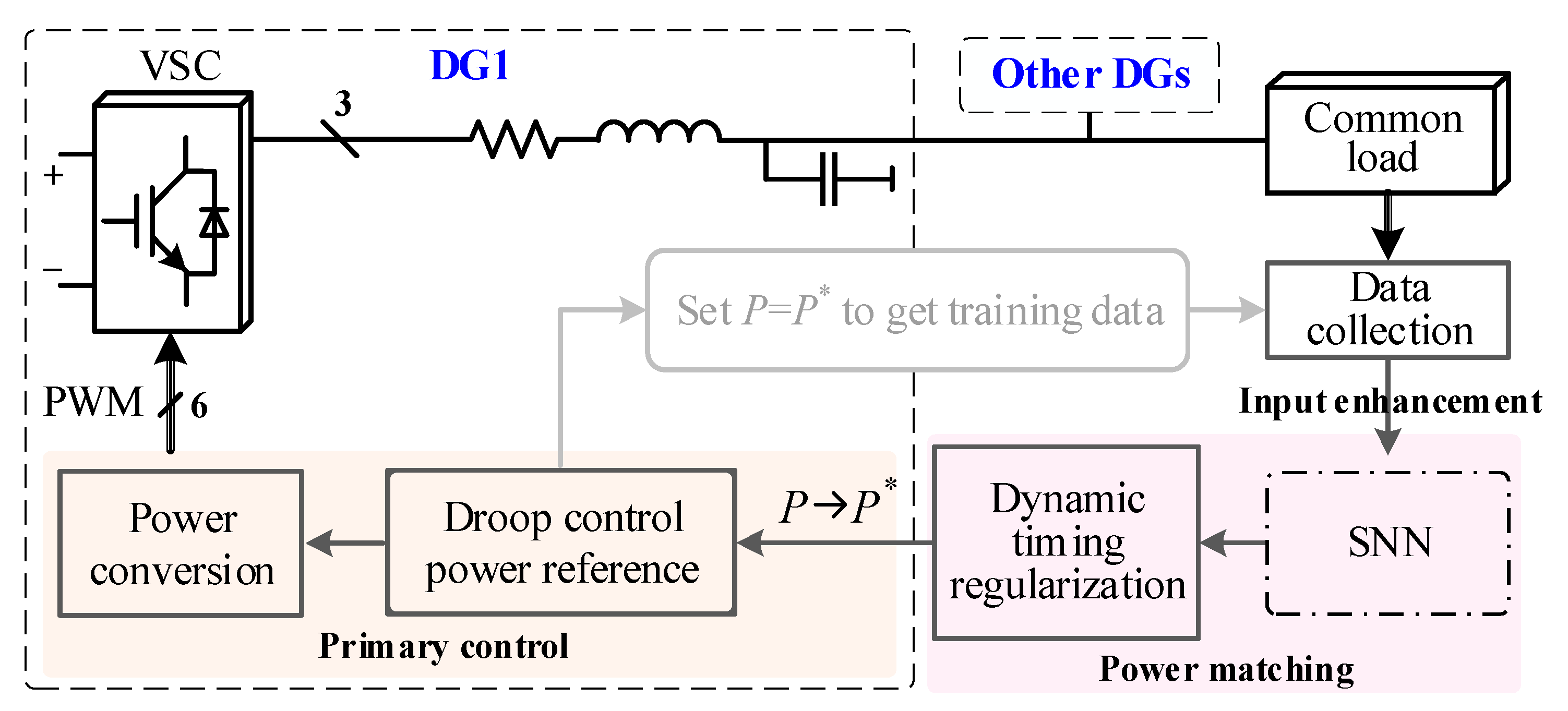
3.3. Power Matching
3.4. Overall Control Diagram
4. Simulation Studies and Performance Assessment
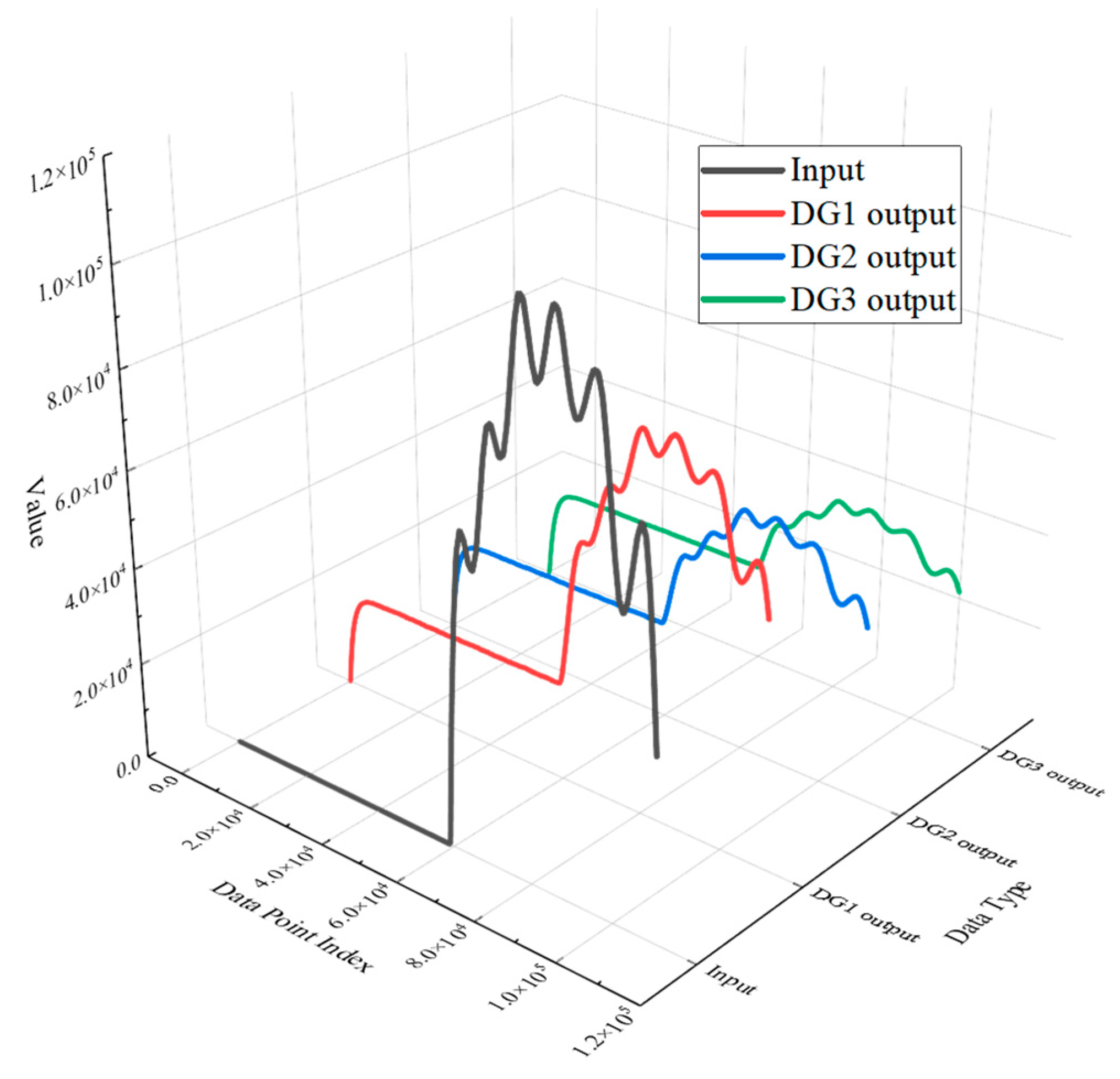
4.1. SNN
4.2. Input Enhancement
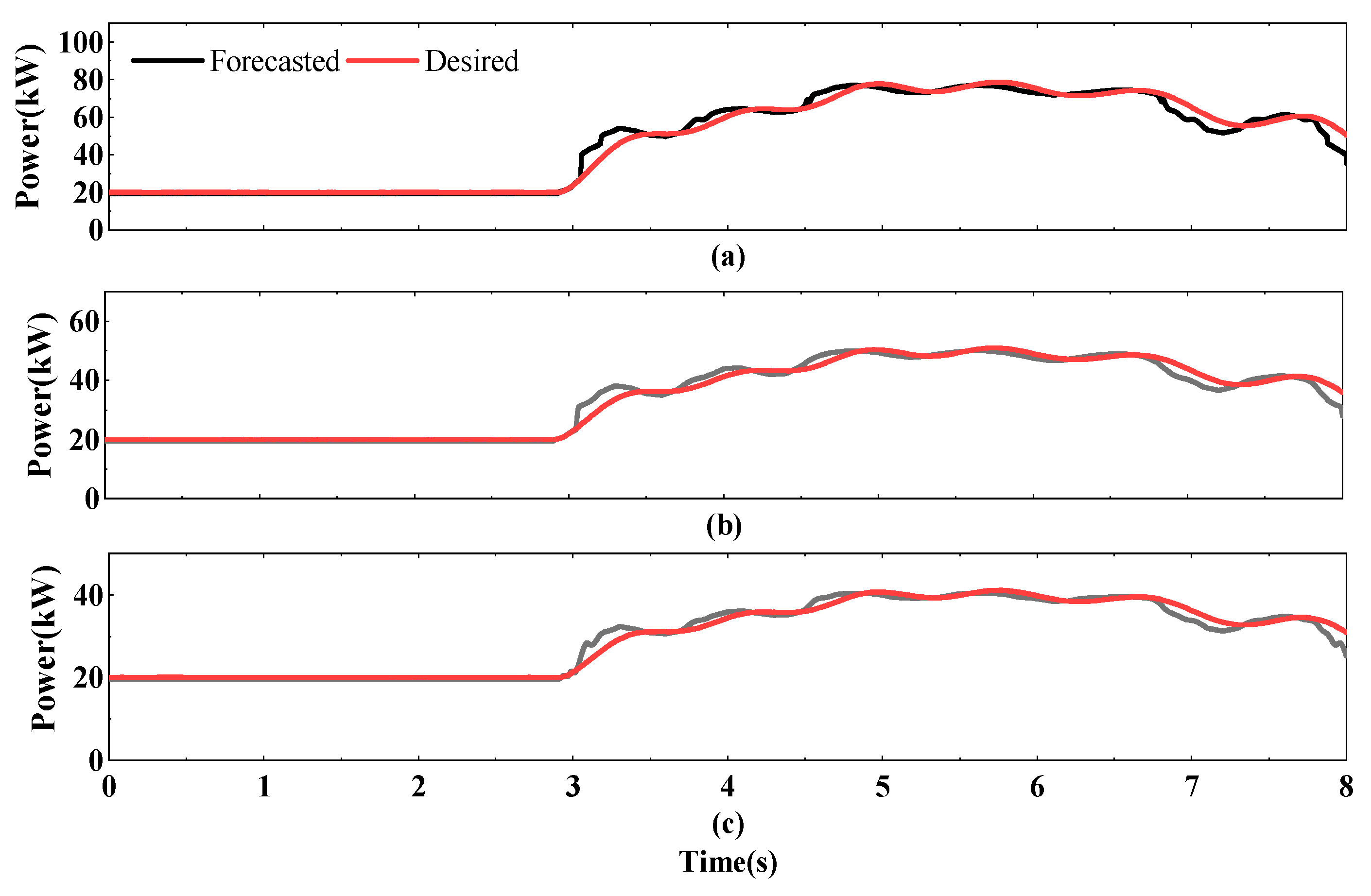
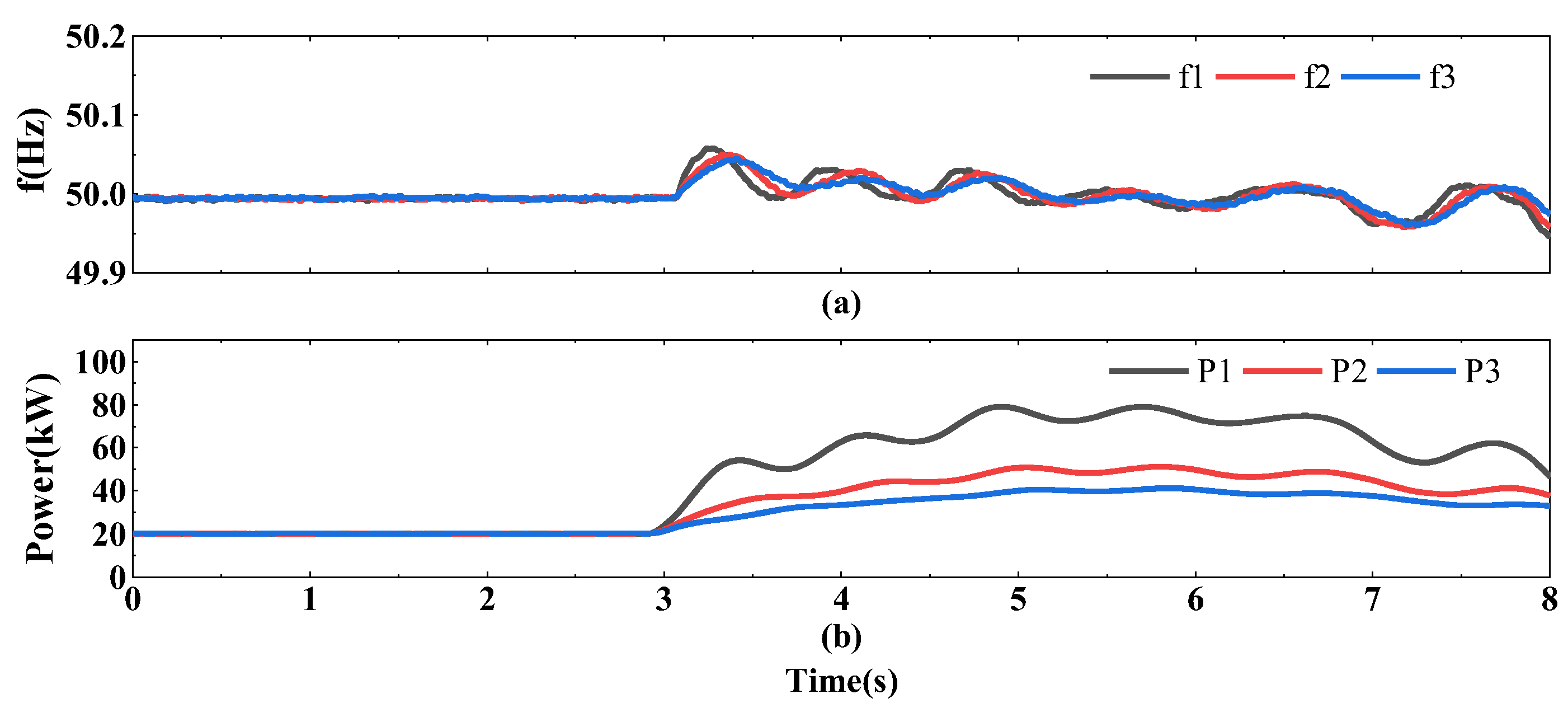
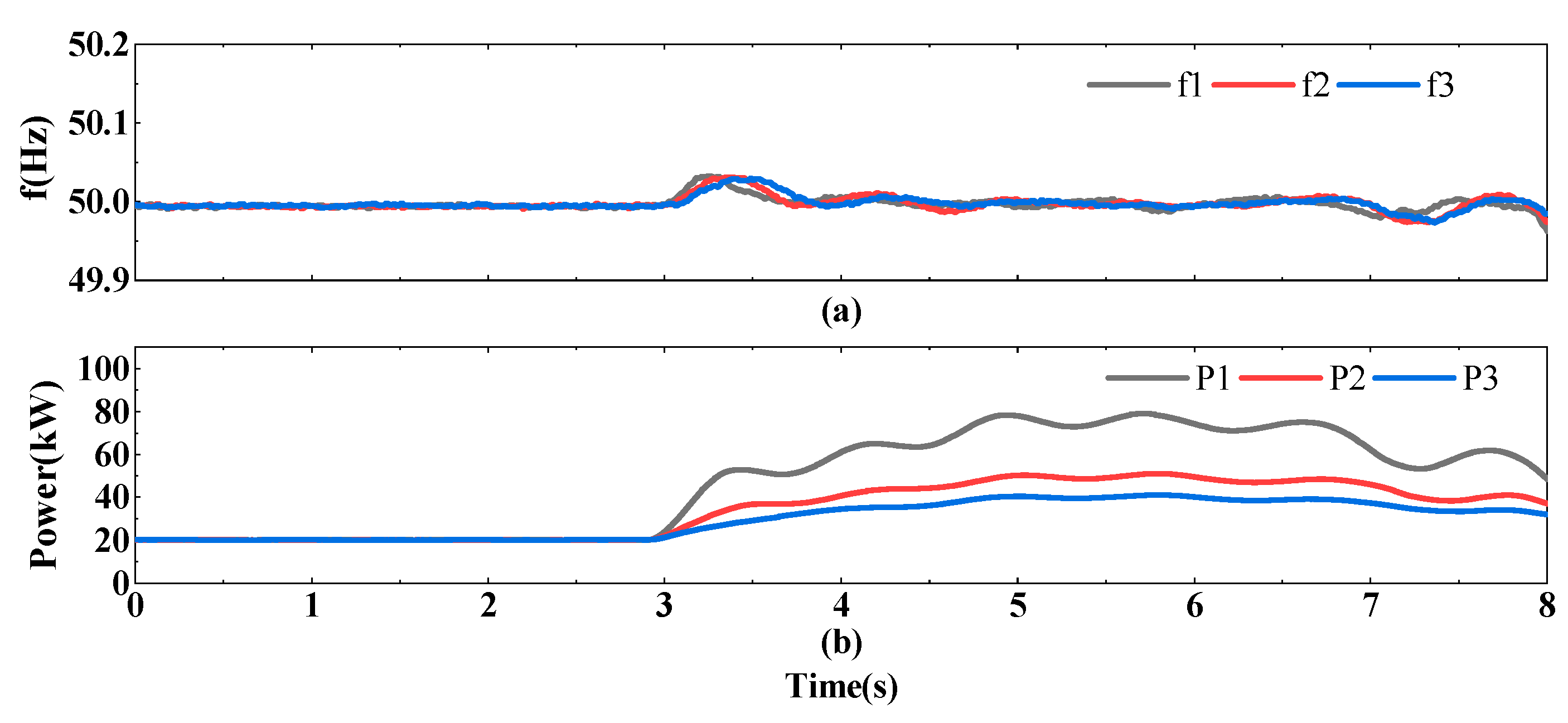
4.3. Control Effects Under SNN Fitting
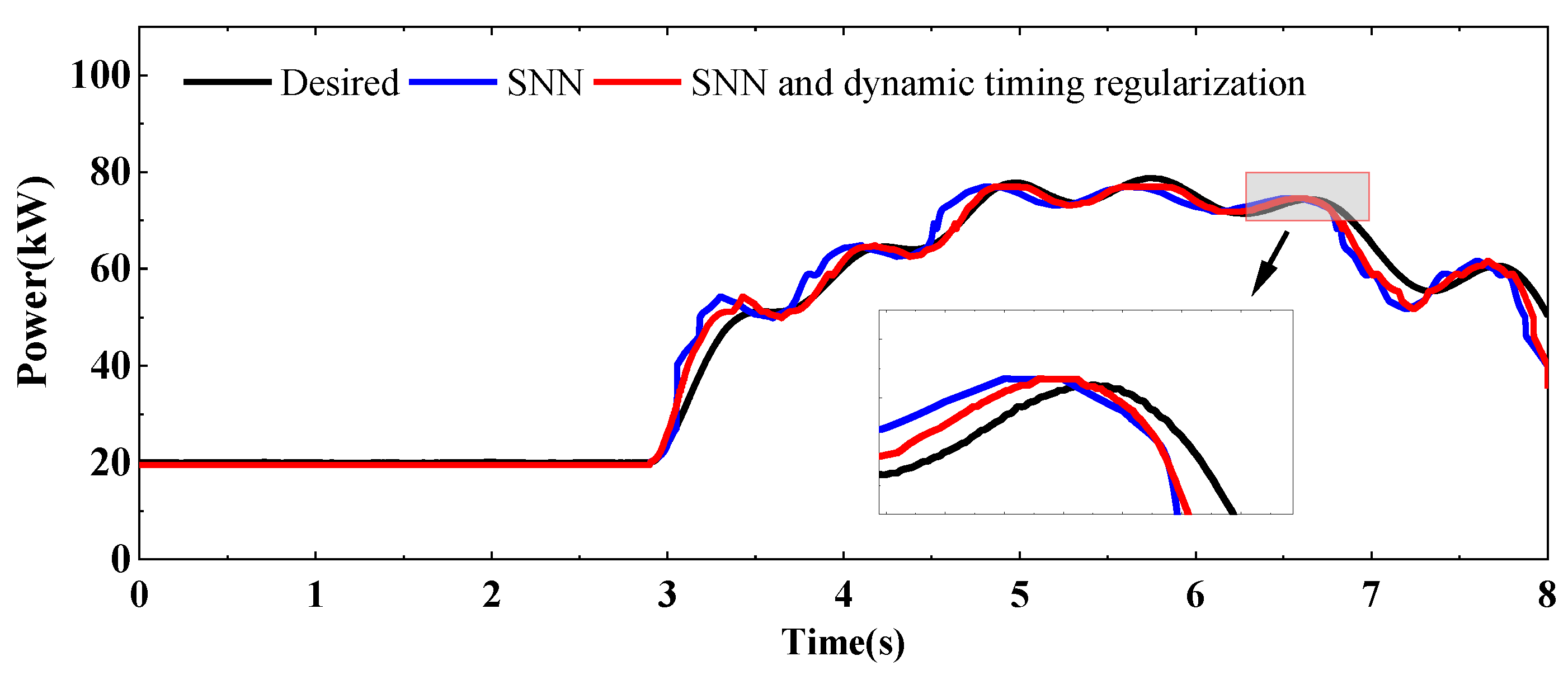
4.4. Dynamic Timing Regularization
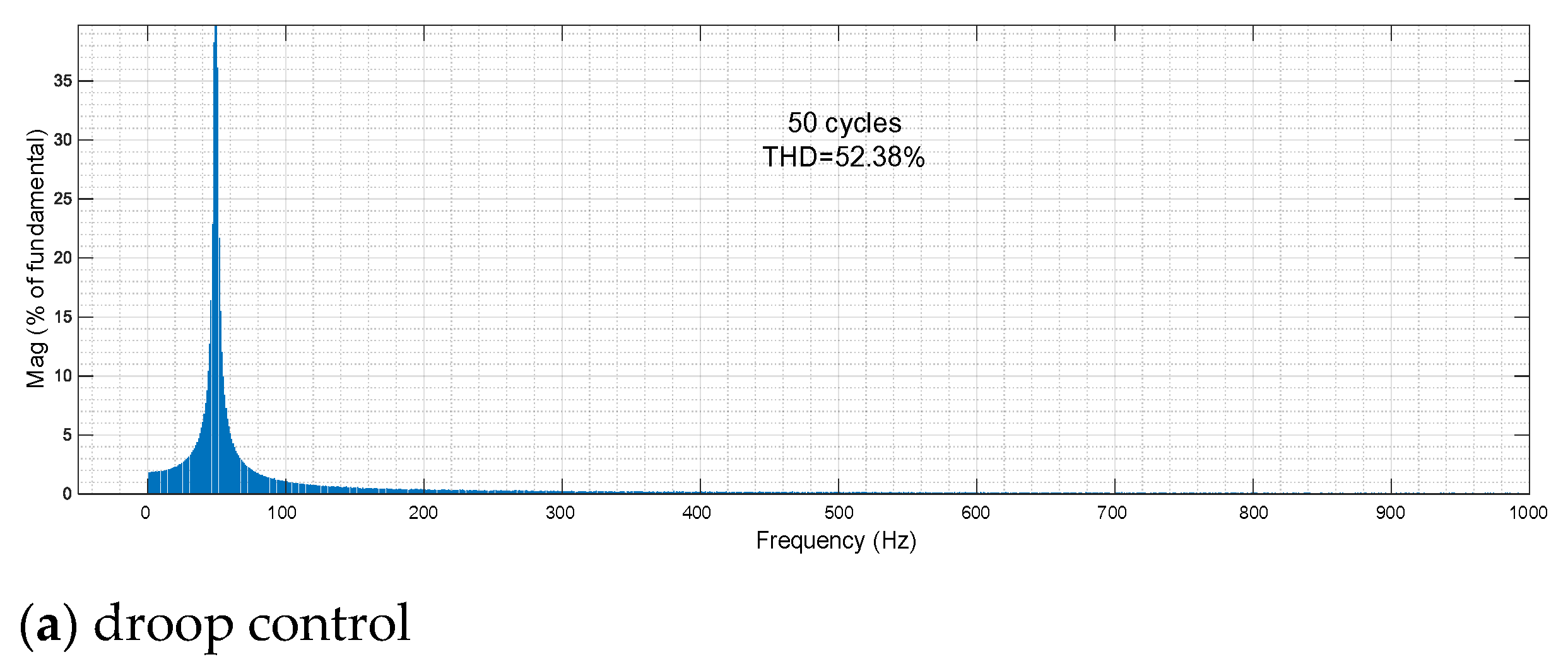
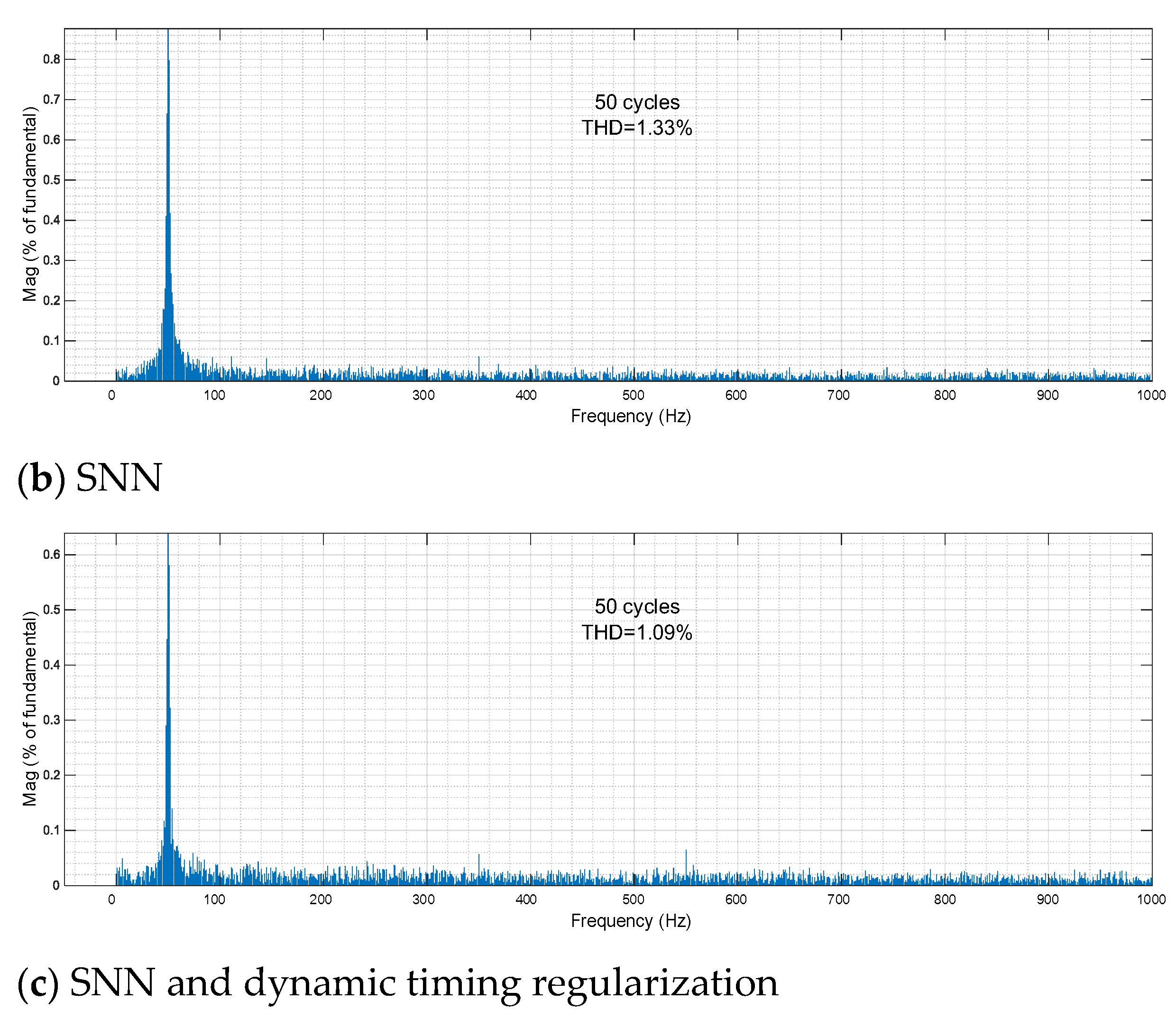
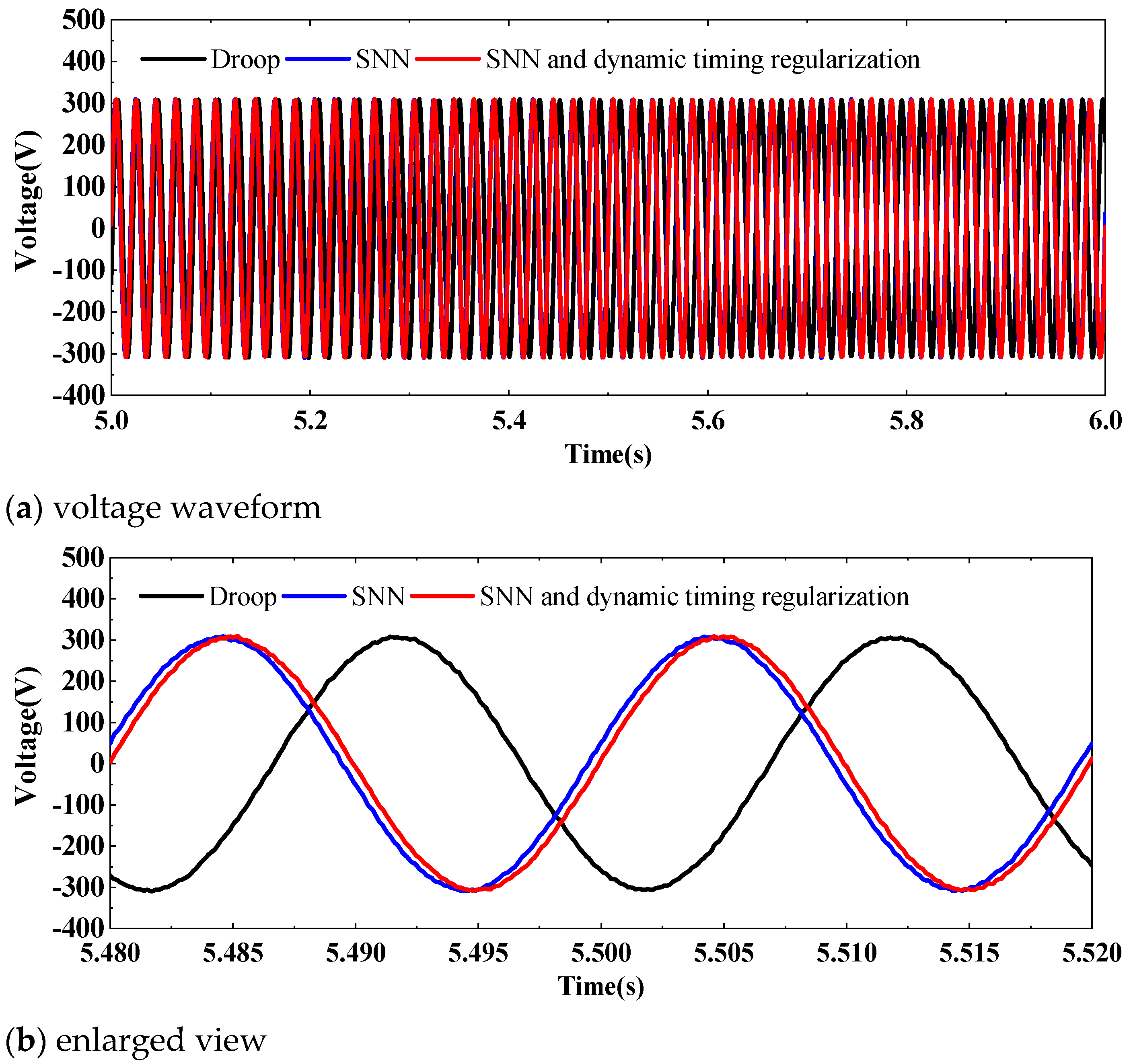
4.5. Voltage Waveform
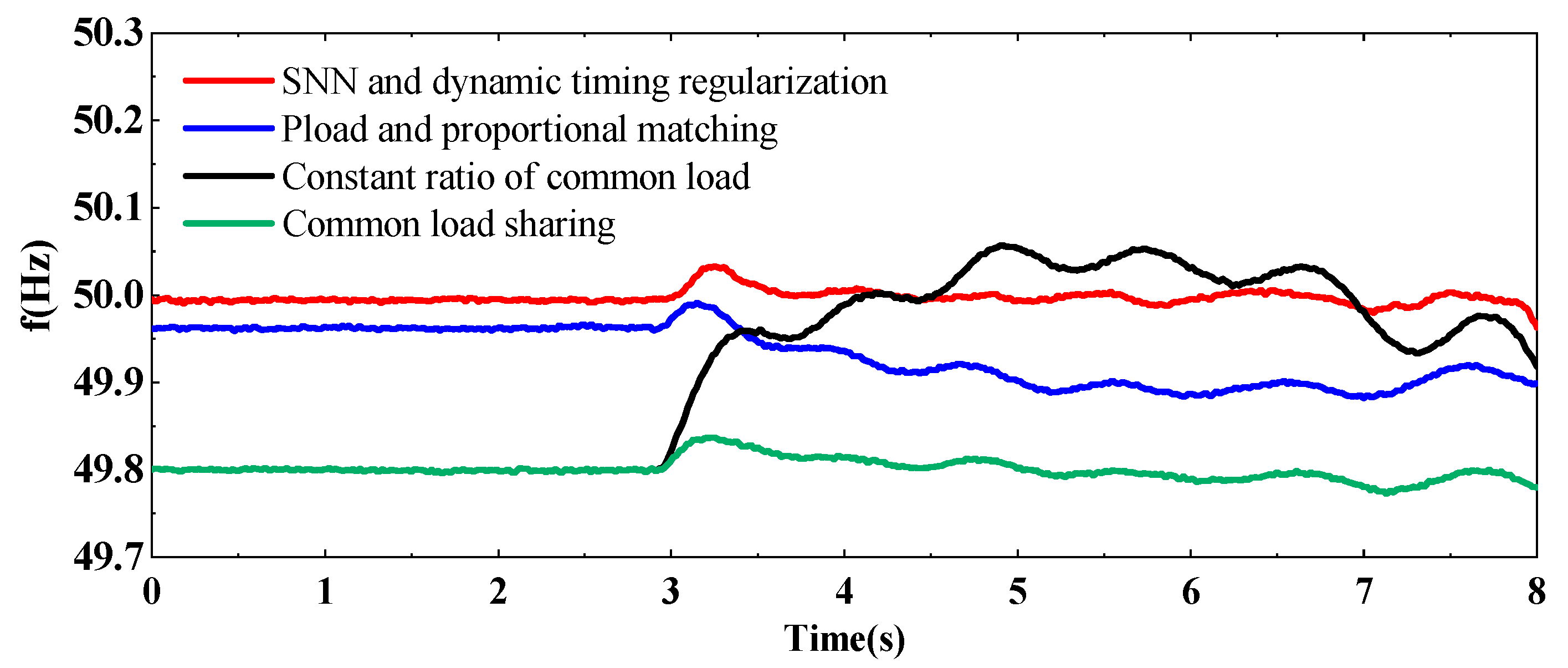
4.6. Comparison with Traditional Mathematical Matching Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Theocharides, S.; Theristis, M.; Makrides, G.; Kynigos, M.; Spanias, C.; Georghiou, G.E. Comparative Analysis of Machine Learning Models for Day-Ahead Photovoltaic Power Production Forecasting. Energies 2021, 14, 1081. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model Predictive Control of Microgrids—An Overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Wang, F.; Han, Z. Research on Hierarchical Control Strategy of AC/DC Hybrid Microgrid Based on Power Coordination Control. Appl. Sci. 2020, 10, 7603. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S. Frequency and State-of-Charge Restoration Method in a Secondary Control of an Islanded Microgrid without Communication. Appl. Sci. 2020, 10, 1558. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z.; Ding, L. Accelerated Secondary Frequency Regulation and Active Power Sharing for Islanded Microgrids with External Disturbances: A Fully Distributed Approach. Automatica 2025, 174, 112146. [Google Scholar] [CrossRef]
- Dangeti, L.s.n.; R., M. Distributed Model Predictive Control Strategy for Microgrid Frequency Regulation. Energy Rep. 2025, 13, 1158–1170. [Google Scholar] [CrossRef]
- Chen, Y.; Qi, D.; Hui, H.; Yang, S.; Gu, Y.; Yan, Y.; Zheng, Y.; Zhang, J. Self-Triggered Coordination of Distributed Renewable Generators for Frequency Restoration in Islanded Microgrids: A Low Communication and Computation Strategy. Adv. Appl. Energy 2023, 10, 100128. [Google Scholar] [CrossRef]
- Agundis Tinajero, G.D.; Guerrero, J.M. Power Flow Modeling for Battery Energy Storage Systems with Hierarchical Control for Islanded Microgrids. Electronics 2024, 13, 4927. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, J.; Ma, N.; Liu, G.; Xin, L.; Liu, Z.; Liu, D.; Xu, Z.; Chen, C. An Improved Secondary Control Strategy for Dynamic Boundary Microgrids toward Resilient Distribution Systems. Energies 2024, 17, 1731. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Liu, Q.; Yue, D.; Liu, G.P. A New Privacy-Preserving Average Consensus Algorithm with Two-Phase Structure: Applications to Load Sharing of Microgrids. Automatica 2024, 167, 111715. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Shen, B. Distributed Secondary Frequency Control for AC Microgrids Using Load Power Forecasting Based on Artificial Neural Network. IEEE Trans. Ind. Inf. 2024, 20, 1651–1662. [Google Scholar] [CrossRef]
- Belgana, S.; Fortin-Blanchette, H. A Novel Neural Network-Based Droop Control Strategy for Single-Phase Power Converters. Energies 2024, 17, 5825. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. A Comparative Analysis of the Arima and Lstm Predictive Models and Their Effectiveness for Predicting Wind Speed. Energies 2021, 14, 6782. [Google Scholar] [CrossRef]
- Mahim, T.M.; Rahim, A.H.M.A.; Rahman, M.M. Adaptive Fuzzy Attention Inference to Control a Microgrid Under Extreme Fault on Grid Bus. IEEE Trans. Fuzzy Syst. 2025. [Google Scholar] [CrossRef]
- Manno, A.; Martelli, E.; Amaldi, E. A Shallow Neural Network Approach for the Short-Term Forecast of Hourly Energy Consumption. Energies 2022, 15, 958. [Google Scholar] [CrossRef]
- Trivedi, R.; Khadem, S. Implementation of Artificial Intelligence Techniques in Microgrid Control Environment: Current Progress and Future Scopes. Energy AI 2022, 8, 100147. [Google Scholar] [CrossRef]
- Huang, Y.; Li, G.; Chen, C.; Bian, Y.; Qian, T.; Bie, Z. Resilient Distribution Networks by Microgrid Formation Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 4918–4930. [Google Scholar] [CrossRef]
- Fang, X.; Khazaei, J. A Two-Stage Deep Learning Approach for Solving Microgrid Economic Dispatch. IEEE Syst. J. 2023, 17, 6237–6247. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Xing, Y.; Chen, J. A Mixture of Shallow Neural Networks for Virtual Sensing: Could Perform Better than Deep Neural Networks. Expert Syst. Appl. 2024, 256, 124870. [Google Scholar] [CrossRef]
- Gong, J.; Qu, Z.; Zhu, Z.; Xu, H.; Yang, Q. Ensemble Models of TCN-LSTM-LightGBM Based on Ensemble Learning Methods for Short-Term Electrical Load Forecasting. Energy 2025, 318, 134757. [Google Scholar] [CrossRef]
- Suto, J.; Oniga, S. Efficiency Investigation from Shallow to Deep Neural Network Techniques in Human Activity Recognition. Cogn. Syst. Res. 2019, 54, 37–49. [Google Scholar] [CrossRef]
- Bejani, M.M.; Ghatee, M. A Systematic Review on Overfitting Control in Shallow and Deep Neural Networks. Artif. Intell. Rev. 2021, 54, 6391–6438. [Google Scholar] [CrossRef]
- Onifade, M.; Lawal, A.I.; Bada, S.O.; Khandelwal, M. Predictive Modelling for Coal Abrasive Index: Unveiling Influential Factors through Shallow and Deep Neural Networks. Fuel 2024, 374, 132319. [Google Scholar] [CrossRef]
- Mishra, B.; Pattnaik, M. A Modified Droop-Based Decentralized Control Strategy for Accurate Power Sharing in a PV-Based Islanded AC Microgrid. ISA Trans. 2024, 153, 467–481. [Google Scholar] [CrossRef]
- Wu, L.; Yang, H.; Wei, J.; Jiang, W. Research on Distributed Coordination Control Method for Microgrid System Based on Finite-Time Event-Triggered Consensus Algorithm. Chin. J. Electr. Eng. 2024, 10, 103–115. [Google Scholar] [CrossRef]
- Yogithanjali Saimadhuri, K.N.; Janaki, M. Advanced Control Strategies for Microgrids: A Review of Droop Control and Virtual Impedance Techniques. Results Eng. 2025, 25, 103799. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, T.; Huang, C.; Shuai, C. Hardware and Software Design and Implementation of Surface-EMG-Based Gesture Recognition and Control System. Electronics 2024, 13, 454. [Google Scholar] [CrossRef]
- Huang, J.; Qin, H.; Shen, K.; Yang, Y.; Jia, B. Study on Hierarchical Model of Hydroelectric Unit Commitment Based on Similarity Schedule and Quadratic Optimization Approach. Energy 2024, 305, 132229. [Google Scholar] [CrossRef]
- Shan, Y.; Ma, L.; Yu, X. Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand. Energies 2023, 16, 5503. [Google Scholar] [CrossRef]
- Wu, X.; Shan, Y.; Fan, K. A Modified Particle Swarm Algorithm for the Multi-Objective Optimization of Wind/Photovoltaic/Diesel/Storage Microgrids. Sustainability 2024, 16, 1065. [Google Scholar] [CrossRef]


| Reference | Offset Elimination Level | Artificial Intelligence Methods Employed | |||
|---|---|---|---|---|---|
| Primary | Secondary | SNN | DNN | ANN (No Clarity Whether It Is Shallow or Deep) | |
| [6] | ✗ | ✓ | ✗ | ✗ | - |
| [7] | ✗ | ✓ | ✗ | ✗ | - |
| [8] | ✗ | ✓ | ✗ | ✗ | - |
| [9] | ✗ | ✓ | ✗ | ✗ | - |
| [11] | ✓ | ✗ | - | - | ✓ but for load power forecasting |
| [12] | - | - | - | - | ✓ |
| [13] | - | - | ✓ | ✓ | - |
| [14] | - | - | ✓ | ✗ | - |
| [15] | - | - | ✓ | ✗ | - |
| [17] | - | - | ✗ | ✓ | - |
| [18] | - | - | ✗ | ✓ | - |
| Description | Value |
|---|---|
| Microgrid | |
| Rated frequency | 50 Hz |
| Controller sampling time | 4 × 10−5 s |
| DG1-DG3 | |
| Droop slope | m = 1 × 10−5 |
| Local load | 20 kW |
| Filter | 0.02 Ω; 3.6 mH; 200 μF |
| DC source voltage | 1 kV |
| Transmission Line | |
| DG1 | 0.05 Ω; 1.2 mH |
| DG2 | 0.10 Ω; 2.4 mH |
| DG3 | 0.15 Ω; 3.6 mH |
| SNN | |
| Hidden layer neurons | 10 |
| Input layer to hidden layer | tansig function |
| Hidden layer to output layer | purelin function |
| Input enhancement | |
| Scaling value | α = 200 |
| Training Times | SNN | SNN with Input Enhancement | ||||
|---|---|---|---|---|---|---|
| Training Epochs | Gradient Values | RMSE | Training Epochs | Gradient Values | RMSE | |
| 1 | 287 | 6.60 × 10−8 | 3244.4896 | 267 | 2.06 × 10−8 | 3244.4976 |
| 2 | 291 | 2.02 × 10−8 | 3244.4948 | 224 | 6.87 × 10−8 | 3244.6135 |
| 3 | 229 | 9.26 × 10−8 | 3244.5632 | 230 | 7.56 × 10−8 | 3244.5714 |
| 4 | 241 | 8.16 × 10−8 | 3244.4918 | 209 | 8.70 × 10−8 | 3244.6388 |
| 5 | 209 | 8.26 × 10−8 | 3244.5627 | 226 | 2.84 × 10−8 | 3244.5948 |
| Average | 251.4 | 6.86 × 10−8 | 3244.5204 | 231.2 | 5.61 × 10−8 | 3244.5832 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Shan, Y. Microgrid Frequency Regulation Based on Precise Matching Between Power Commands and Load Consumption Using Shallow Neural Networks. Appl. Syst. Innov. 2025, 8, 67. https://doi.org/10.3390/asi8030067
Liu Z, Shan Y. Microgrid Frequency Regulation Based on Precise Matching Between Power Commands and Load Consumption Using Shallow Neural Networks. Applied System Innovation. 2025; 8(3):67. https://doi.org/10.3390/asi8030067
Chicago/Turabian StyleLiu, Zhen, and Yinghao Shan. 2025. "Microgrid Frequency Regulation Based on Precise Matching Between Power Commands and Load Consumption Using Shallow Neural Networks" Applied System Innovation 8, no. 3: 67. https://doi.org/10.3390/asi8030067
APA StyleLiu, Z., & Shan, Y. (2025). Microgrid Frequency Regulation Based on Precise Matching Between Power Commands and Load Consumption Using Shallow Neural Networks. Applied System Innovation, 8(3), 67. https://doi.org/10.3390/asi8030067






