IoT-Based Small Scale Anomaly Detection Using Dixon’s Q Test for e-Health Data
Abstract
:1. Introduction
- To propose IoTDixon scheme to detect point anomalies from small-size dataset;
- To integrate Dixon’s Q test as a key statistic for detection of outlier points from small-size data packets;
- To integrate Kolmogorov–Smirnov test statistic as the normality checker.
2. Dixon’s Q Test
2.1. Probability Density of r
2.2. Jacobian Probability Density of r
2.2.1. Derivation of
2.2.2. Derivation of
2.2.3. Derivation of
2.2.4. Derivation of
2.2.5. Derivation of
2.2.6. Derivation of
2.3. Cumulative Distribution of R
2.4. Probability Density of r
2.5. Range Test
3. System Design
3.1. IoTDixon Algorithm
| Algorithm 1: IoTDixon Algorithm |
 |
3.2. Kolmogorov–Smirnov Algorithm
3.3. Dixon’s Q Algorithm
| Algorithm 2: Kolmogorov–Smirnov Algorithm |
 |
| Algorithm 3: Dixon’s Q two-sided Algorithm |
 |
3.4. IoTDixon Dataset
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hansen, E.B.; Bøgh, S. Artificial intelligence and internet of things in small and medium-sized enterprises: A survey. J. Manuf. Syst. 2021, 58, 362–372. [Google Scholar] [CrossRef]
- Han, G.; Tu, J.; Liu, L.; Martinez-Garcia, M.; Choi, C. An Intelligent Signal Processing Data Denoising Method for Control Systems Protection in the Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021. [Google Scholar] [CrossRef]
- Haji, S.H.; Ameen, S.Y. Attack and anomaly detection in iot networks using machine learning techniques: A review. Asian J. Res. Comput. Sci. 2021, 30–46. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhang, X.; Yuan, Z.; Cheng, X. Learning Graph Structures with Transformer for Multivariate Time Series Anomaly Detection in IoT. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Bhatia, M.P.S.; Sangwan, S.R. Soft computing for anomaly detection and prediction to mitigate IoT-based real-time abuse. Pers. Ubiquitous Comput. 2021, 1–11. [Google Scholar] [CrossRef]
- Fan, Z.; Feng, H.; Jiang, J.; Zhao, C.; Jiang, N.; Wang, W.; Zeng, F. Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data. Appl. Sci. 2020, 10, 1876. [Google Scholar] [CrossRef] [Green Version]
- Cauteruccio, F.; Cinelli, L.; Corradini, E.; Terracina, G.; Ursino, D.; Virgili, L.; Savaglio, C.; Liotta Al, F.G. A framework for anomaly detection and classification in Multiple IoT scenarios. Future Gener. Comput. Syst. 2021, 114, 322–335. [Google Scholar] [CrossRef]
- Kayan, H.; Majib, Y.; Alsafery, W.; Barhamgi, M.; Perera, C. AnoML-IoT: An end to end re-configurable multi-protocol anomaly detection pipeline for Internet of Things. Internet Things 2021, 16, 100437. [Google Scholar] [CrossRef]
- Yahyaoui, A.; Abdellatif, T.; Yangui, S.; Attia, R. READ-IoT: Reliable Event and Anomaly Detection Framework for the Internet of Things. IEEE Access 2021, 9, 24168–24186. [Google Scholar] [CrossRef]
- Vangipuram, R.; Gunupudi, R.K.; Puligadda, V.K.; Vinjamuri, J. A machine learning approach for imputation and anomaly detection in IoT environment. Expert Syst. 2020, 37, e12556. [Google Scholar] [CrossRef]
- Huang, K.; Chen, Z.; Yu, M.; Yan, X.; Yin, A. An efficient document skew detection method using probability model and q test. Electronics 2020, 9, 55. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S.; Yu, Y.; Ayoub, M.; Khan, A.; Rehman, R.; Wahid, J.A.; Hou, W. IoT and Deep Learning Based Approach for Rapid Screening and Face Mask Detection for Infection Spread Control of COVID-19. Appl. Sci. 2021, 11, 3495. [Google Scholar] [CrossRef]
- Dean, R.B.; Dixon, W.J. Simplified Statistics for Small Numbers of Observations. Anal. Chem. 1951, 23, 636–638. [Google Scholar] [CrossRef]
- Denkena, B.; Bergmann, B.; Stiehl, T.H. Wear curve based online feature assessment for tool condition monitoring. Procedia CIRP 2020, 88, 312–317. [Google Scholar] [CrossRef]
- McBane, G.C. Programs to Compute Distribution Functions and Critical Values for Extreme Value Ratios for Outlier Detection. J. Stat. Softw. 2006, 16, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, T.; Sahni, S.; Franta, W.R. An Efficient Algorithm for the Kolmogorov-Smirnov and Lilliefors Tests. ACM Trans. Math. Softw. 1977, 3, 60–64. [Google Scholar] [CrossRef]
- Lall, A. Data streaming algorithms for the Kolmogorov-Smirnov test. In Proceedings of the International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 95–104. [Google Scholar]

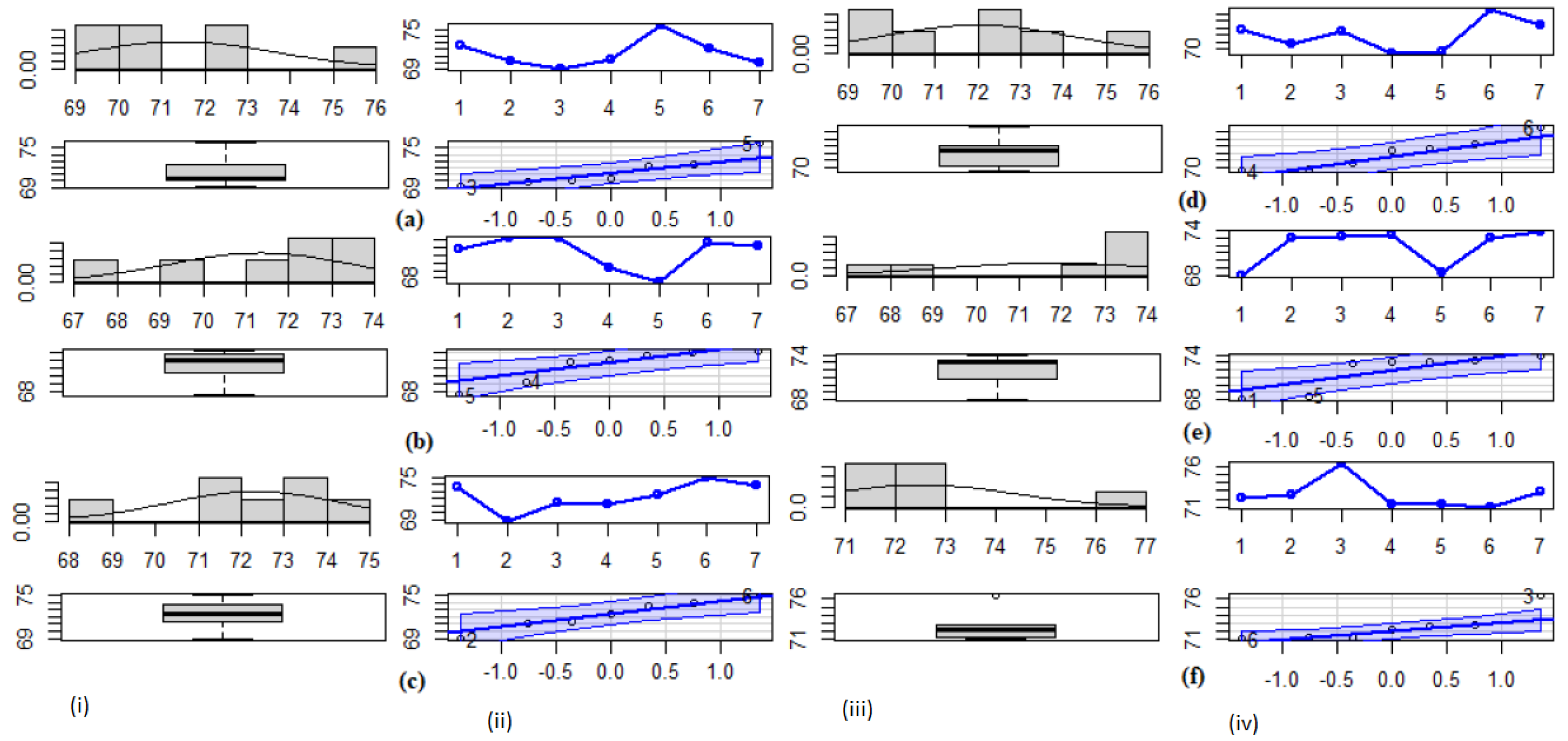

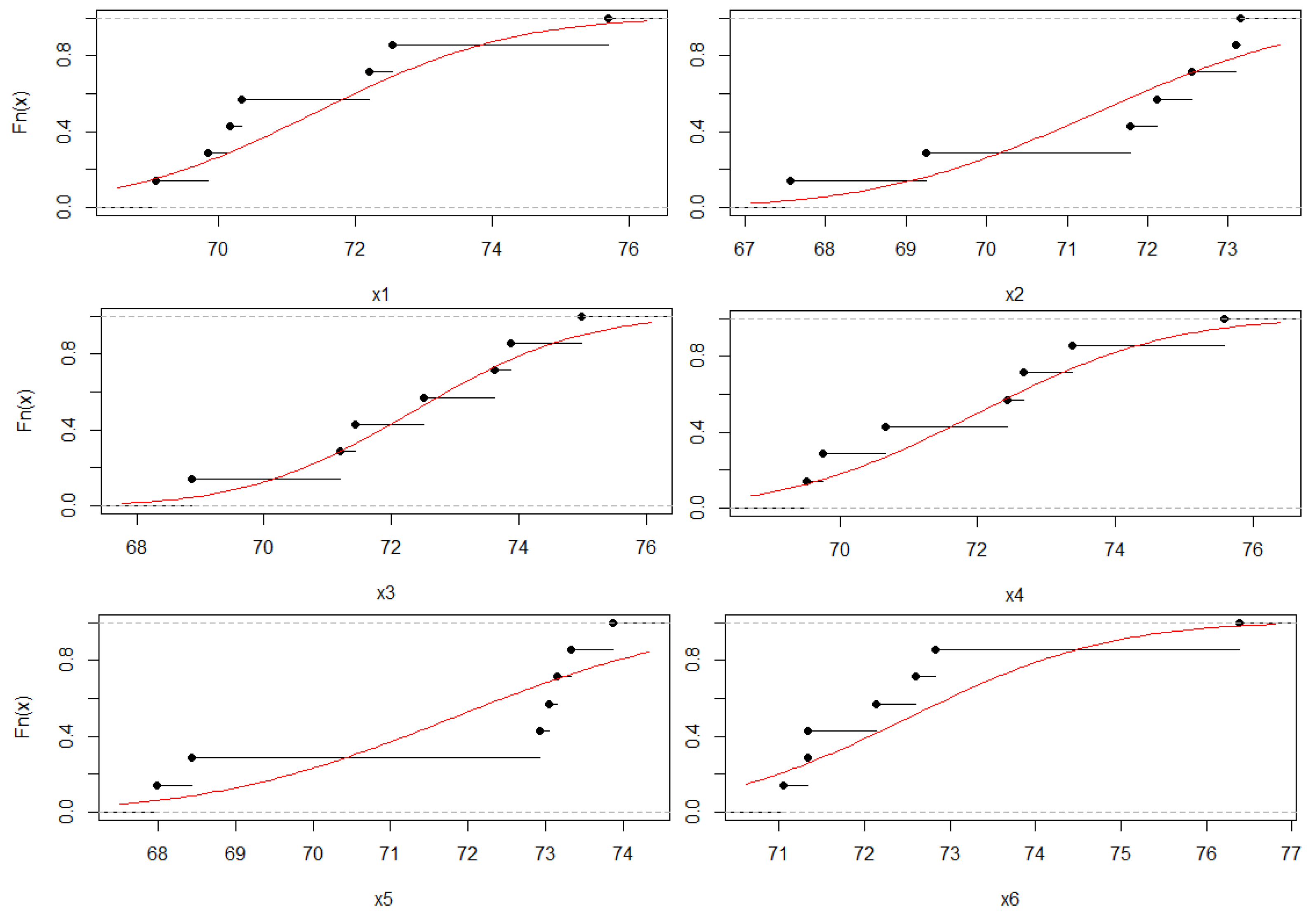
| Q | P | POS | Anomaly | |
|---|---|---|---|---|
| x1 | 0.477 | 0.1343 | 5 | 75.69 |
| x2 | 0.300 | 0.533 | 5 | 67.56 |
| x3 | 0.378 | 0.311 | 2 | 68.86 |
| x4 | 0.365 | 0.344 | 6 | 75.58 |
| x5 | 0.090 | 1 | 7 | 73.85 |
| x6 | 0.665 | 0.012 *** | 3 | 76.37 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ray, P.P.; Dash, D. IoT-Based Small Scale Anomaly Detection Using Dixon’s Q Test for e-Health Data. Appl. Syst. Innov. 2021, 4, 100. https://doi.org/10.3390/asi4040100
Ray PP, Dash D. IoT-Based Small Scale Anomaly Detection Using Dixon’s Q Test for e-Health Data. Applied System Innovation. 2021; 4(4):100. https://doi.org/10.3390/asi4040100
Chicago/Turabian StyleRay, Partha Pratim, and Dinesh Dash. 2021. "IoT-Based Small Scale Anomaly Detection Using Dixon’s Q Test for e-Health Data" Applied System Innovation 4, no. 4: 100. https://doi.org/10.3390/asi4040100
APA StyleRay, P. P., & Dash, D. (2021). IoT-Based Small Scale Anomaly Detection Using Dixon’s Q Test for e-Health Data. Applied System Innovation, 4(4), 100. https://doi.org/10.3390/asi4040100






