Interfacial Flows and Interfacial Shape Modulation Controlled by the Thermal Action of Light Energy
Abstract
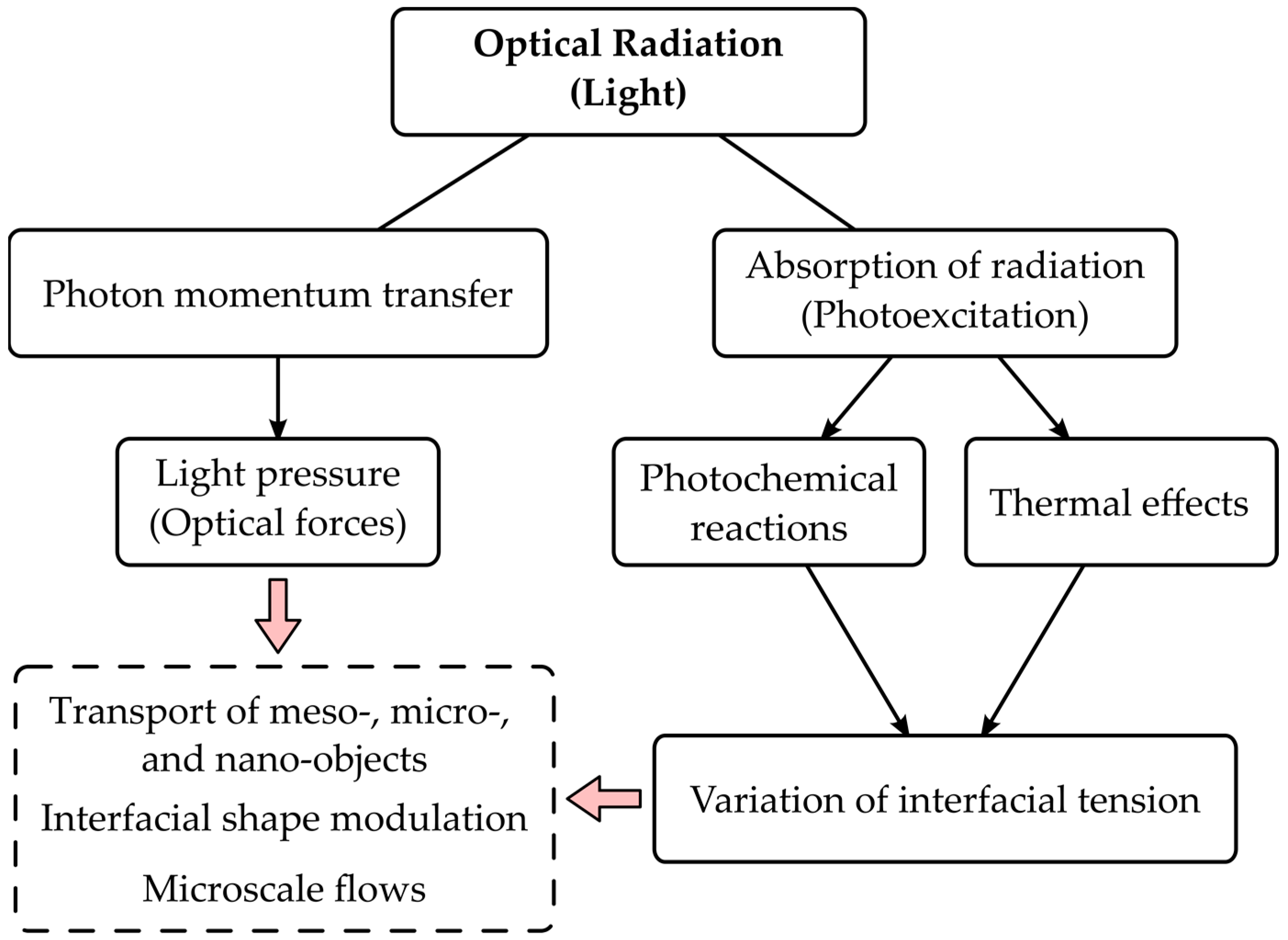
:1. Introduction
2. Laser-Controlled the Liquid–Air Interfaces and Microscale Flows
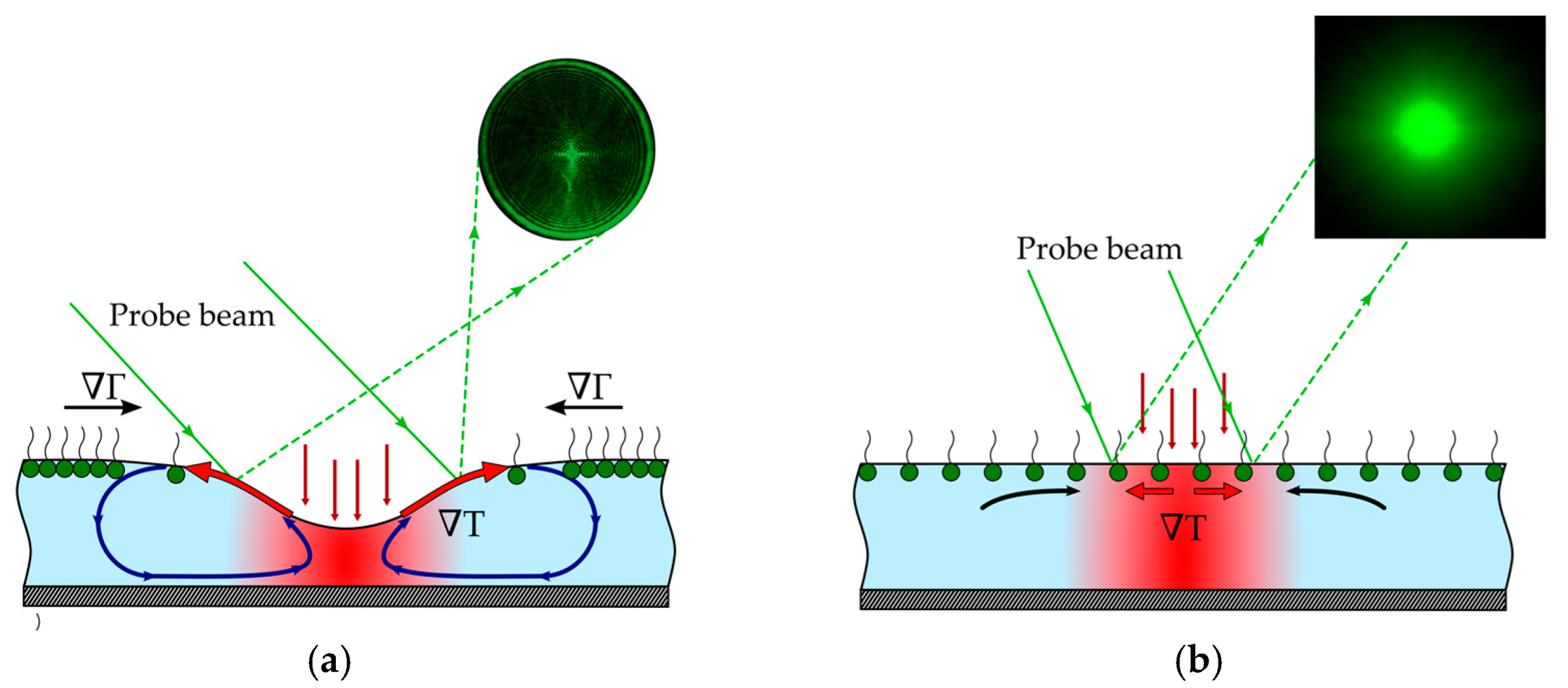
2.1. Photothermocapillary Spectroscopy and Non-Destructive Testing
2.2. Interfacial Shape Exposed to the Light-Induced Thermocapillary Stresses
2.3. Light-Induced Rupture of Thin Films and the Control of the Contact Line Instability
2.4. Laser-Induced Marangoni Flows on the Liquid-Surfactant Interfaces
3. Laser-Controlled the Liquid–Liquid Interfaces in Multilayer Systems
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, B.-W.; Zhong, M.-C.; Ji, F. Laser Induced Aggregation of light absorbing particles by Marangoni convection. Appl. Sci. 2020, 10, 7795. [Google Scholar] [CrossRef]
- Paven, M.; Mayama, H.; Sekido, T.; Butt, H.-J.; Nakamura, Y.; Fujii, S. Light-driven delivery and release of materials using liquid marbles. Adv. Funct. Mater. 2016, 26, 3199–3206. [Google Scholar] [CrossRef]
- Gao, D.; Ding, W.; Nieto-Vesperinas, M.; Ding, X.; Rahman, M.; Zhang, T.; Lim, C.T.; Qiu, C.-W. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light Sci. Appl. 2017, 6, e17039. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, K.; Yamamoto, Y.; Tamura, M.; Tokonami, S.; Iida, T. Damage-free light-induced assembly of intestinal bacteria with a bubble-mimetic substrate. Commun. Biol. 2021, 4, 385. [Google Scholar] [CrossRef]
- Da Costa, G.; Calatroni, J. Transient deformation of liquid surfaces by laser-induced thermocapillarity. Appl. Opt. 1979, 18, 233–235. [Google Scholar] [CrossRef]
- Da Costa, G.; Calatroni, J. Self-holograms of laser-induced surface depressions in heavy hydrocarbons. Appl. Opt. 1978, 17, 2381–2385. [Google Scholar] [CrossRef]
- Da Costa, G.; Calatroni, J. Interferometric determination of the surface profile of a liquid heated by a laser beam. Opt. Commun. 1982, 42, 5–9. [Google Scholar]
- Da Costa, G.; Escalona, R. Focal properties of liquid films deformed by heating with a Gaussian laser beam. Opt. Commun. 1989, 73, 1–6. [Google Scholar] [CrossRef]
- Da Costa, G.; Escalona, R. Time evolution of the caustics of a laser heated liquid film. Appl. Opt. 1990, 29, 1023–1033. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Tarasov, O.A. Sensitivity of the thermocapillary method of thickness determination for transparent liquid films on horizontal absorbing substrates. Tech. Phys. Lett. 2004, 30, 138–140. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Tarasov, O.A.; Chemodanov, S.I. Method of Contactless Measuring of Liquid Viscosity. Patent RF 2305271, BI 24 27 August 2007. [Google Scholar]
- Bezuglyi, B.A.; Tarasov, O.A.; Fedorets, A.A. Modified tilting-plate method for measuring contact angles. Colloid J. 2001, 63, 668–674. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Chemodanov, S.I. Effect of delay of the thermocapillary response of a transparent liquid layer during laser heating of the absorbing substrate. Tech. Phys. 2005, 50, 1243–1245. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Chemodanov, S.I.; Tarasov, O.A. New approach to diagnostics of organic impurities in water. Colloid Surf. A 2004, 239, 11–17. [Google Scholar] [CrossRef]
- Tarasov, O.A. Evaluation of the possibility of using the laser-induced thermocapillary effect for photothermal spectroscopy. Opt. Spectrosc. 2005, 99, 968–974. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Zykov, A.Y.; Semenov, S.V. Photothermocapillary diagnostics of near-surface flaws in a solid under a varnish-and paint coating. Russ. J. Nondestruct. Test. 2008, 44, 391–394. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Zykov, A.Y.; Semenov, S.V. Photothermocapillary method for detecting foreign inclusions in solids under paint and varnish coatings. Tech. Phys. Lett. 2008, 34, 743–746. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Zykov, A.Y. Photothermocapillary method for detecting delamination of paint and varnish coatings. Tech. Phys. Lett. 2009, 35, 650–652. [Google Scholar] [CrossRef]
- Zykov, A.Y.; Ivanova, N.A. Photothermocapillary detection of conductive track ruptures on a printed circuit board coated with a protective film. J. Phys. Conf. Ser. 2019, 1421, 12039. [Google Scholar] [CrossRef]
- Zykov, A.Y.; Ivanova, N.A. Laser-induced thermocapillary convection in thin liquid layers: Effect of thermal conductivity of substrates. Appl. Phys. B 2017, 123, 235. [Google Scholar] [CrossRef]
- Khattari, Z.; Hatta, E.; Heinig, P.; Steffen, P.; Fischer, T.M.; Bruinsma, R. Cavitation of Langmuir monolayers. Phys. Rev. E 2002, 65, 41603. [Google Scholar] [CrossRef]
- Gugliotti, M.; Baptista, M.S.; Politi, M.J. Laser-induced Marangoni Convection in the presence of surfactants monolayers. Langmuir 2002, 18, 9792–9798. [Google Scholar] [CrossRef]
- Muruganathan, R.; Zhang, Y.; Fischer, T.M. Interfacial thermocapillary vortical flow for microfluidic mixing. J. Am. Chem. Soc. 2006, 128, 3474–3475. [Google Scholar] [CrossRef] [PubMed]
- Dixit, S.S.; Kim, H.; Vasilyev, A.; Eid, A.; Faris, G.W. Light-driven formation and rupture of droplet bilayers. Langmuir 2010, 26, 6193–6200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wedershoven, H.M.J.M.; Berendsen, C.W.J.; Zeegers, J.C.H.; Darhuber, A.A. Infrared laser induced rupture of thin liquid films on stationary substrates. Appl. Phys. Lett. 2014, 104, 52101. [Google Scholar] [CrossRef] [Green Version]
- Wedershoven, H.M.J.M.; Berendsen, C.W.J.; Zeegers, J.C.H.; Darhuber, A.A. Infrared-laser-induced thermocapillary deformation and destabilization of thin liquid films on moving substrates. Phys. Rev. Appl. 2015, 3, 24005. [Google Scholar] [CrossRef]
- van den Temple, M.A.; Wedershoven, H.M.J.M.; Zeegers, J.C.H.; Riepen, M.; Darhuber, A.A. Enhancement of contact line mobility by means of infrared laser illumination. I. Experiments. Appl. Phys. Lett. 2016, 119, 84904. [Google Scholar] [CrossRef] [Green Version]
- Ivanova, N.; Starov, V.M.; Trybala, A.; Flyagin, V.M. Removal of micrometer size particles from surfaces using laser-induced thermocapillary flow: Experimental results. J. Colloids Interface Sci. 2016, 473, 120–125. [Google Scholar] [CrossRef] [Green Version]
- Kubochkin, N.S.; Tatosov, A.V.; Al-Muzaiqer, M.; Ivanova, N.A. Detachment of particles from surfaces by thermocapillary flows induced by a moving laser beam. J. Adhes. Sci. Technol. 2019, 33, 1676–1691. [Google Scholar] [CrossRef]
- Du, F.; Felts, J.R.; Xie, X.; Song, J.; Li, Y.; Rosenberger, M.R.; Islam, A.E.; Jin, S.H.; Dunham, S.N.; Zhang, C.; et al. Laser-induced nanoscale thermocapillary flows for purification of aligned arrays of single-walled carbon nanotubes. ACS Nano 2014, 8, 12641–12649. [Google Scholar] [CrossRef]
- Singer, J.P.; Lin, P.-T.; Kooi, S.T.; Kimerling, L.C.; Michel, J.; Thomas, E.L. Direct-write thermocapillary dewetting of polymer thin films by a laser-induced thermal gradient. Adv. Mater. 2013, 25, 6100–6105. [Google Scholar] [CrossRef]
- Bezuglyi, B.A.; Tarasov, O.A. Optical properties of a thermocapillary depression. Opt. Spectrosc. 2002, 92, 609–613. [Google Scholar] [CrossRef]
- Malyuk, A.Y.; Ivanova, N.A. Varifocal liquid lens actuated by laser-induced thermal Marangoni forces. Appl. Phys. Lett. 2018, 112, 103701. [Google Scholar] [CrossRef]
- Klyuev, D.S.; Fliagin, V.M.; Al-Muzaiqer, M.; Ivanova, N.A. Laser-actuated optofluidic diaphragm capable of optical signal tracking. Appl. Phys. Lett. 2019, 114, 11602. [Google Scholar] [CrossRef]
- Loulergue, J.C. Deformation of surfaces of a thin liquid film by thermal perturbation. Thin Solid Film 1981, 82, 61–67. [Google Scholar] [CrossRef]
- Loulergue, J.C.; Manneville, P.; Pomeaut, Y. Interface deflections induced by the Marangoni effect: An application to infrared-visible image conversion. J. Phys. D Appl. Phys. 1981, 14, 1967–1977. [Google Scholar] [CrossRef]
- Loulergue, J.C.; Levy, Y.; Imbert, C. Thermal imaging system with a two-phase ternary mixture of liquids. Opt. Commun. 1983, 45, 149–154. [Google Scholar] [CrossRef]
- Loulergue, J.C.; Xu, S.-L. Infrared photography in liquid films by thermocapillary convection. Int. J. Infrared Millim. Waves 1986, 7, 171–182. [Google Scholar] [CrossRef]
- Viznyuk, S.A.; Pashinin, P.P.; Sukhodolskii, A.T. Recording dynamic diffraction gratings and optical-phase conjugation by light-capillary profiling of thin liquid-films. Opt. Commun. 1991, 85, 254–260. [Google Scholar] [CrossRef]
- Viznyuk, S.A.; Pashinin, P.P.; Sukhodolskii, A.T. Formation of dynamic diffraction gratings and phase conjugation under conditions of optocapillary profiling of thin liquid layers. Sov. J. Quantum Electron. 1991, 21, 560. [Google Scholar] [CrossRef]
- Levich, V.G.; Krylov, V.S. Surface-tension-driven phenomena. Annu. Rev. Fluid Mech. 1969, 1, 293–316. [Google Scholar] [CrossRef]
- Scriven, L.E.; Sternling, C.V. The Marangoni effects. Nature 1960, 187, 186–188. [Google Scholar] [CrossRef]
- Legros, J.C.; Limbourg-Fontaine, M.C.; Petre, G. Influence of a surface tension minimum as a function of temperature on the Marangoni convection. Acta Astronaut. 1984, 11, 143–147. [Google Scholar] [CrossRef]
- Villers, D.; Platten, J.K. Temperature dependence of the interfacial tension between water and long-chain alcohols. J. Phys. Chem. 1988, 92, 4023–4024. [Google Scholar] [CrossRef]
- Myers, D. Surfactant Science and Technology, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tatosova, K.A.; Malyuk, A.Y.; Ivanova, N.A. Droplet formation caused by laser-induced surface-tension-driven flows in binary liquid mixtures. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 22–29. [Google Scholar] [CrossRef]
- Ivanova, N.A.; Tatosov, A.V.; Bezuglyi, B.A. Laser-induced capillary effect in thin layers of water-alcohol mixtures. Eur. Phys. J. E. Soft Matter. 2015, 38, 60. [Google Scholar] [CrossRef]
- Vieyra Salas, J.A.; van der Veen, J.M.; Michels, J.J.; Darhuber, A.A. Active Control of evaporative solution deposition by modulated infrared illumination. J. Phys. Chem. C 2012, 116, 12038–12047. [Google Scholar] [CrossRef]
- Chevallier, E.; Mamane, A.; Stone, H.A.; Tribet, C.; Lequeuxa, F.; Monteux, C. Pumping-out photo-surfactants from an air–water interface using light. Soft Matter 2011, 7, 7866. [Google Scholar] [CrossRef]
- Mamane, A.; Chevallier, E.; Olanier, L.; Lequeux, F.; Monteux, C. Optical control of surface forces and instabilities in foam films using photosurfactants. Soft Matter 2017, 13, 1299–1305. [Google Scholar] [CrossRef]
- Arya, P.; Umlandt, M.; Jelken, J.; Feldmann, D.; Lomadze, N.; Asmolov, E.S.; Vinogradova, O.I.; Santer, S. Light-induced manipulation of passive and active microparticles. Eur. Phys. J. E 2021, 44, 50. [Google Scholar] [CrossRef]
- Wunenburger, R.; Issenmann, B.; Brasselet, E.; Loussert, C.; Hourtane, V.; Delville, J.-P. Fluid flows driven by light scattering. J. Fluid Mech. 2011, 666, 273–307. [Google Scholar] [CrossRef]
- Bayazitoglu, Y.; Lam, T.T. Marangoni convection in irradiating fluids. J. Heat Transf. 1987, 109, 717–721. [Google Scholar] [CrossRef]
- Indeikina, A.E.; Ryazantsev, Y.S.; Shevtsova, V.M. Unsteady thermocapillary convection in a nonuniformly heated fluid layer. Fluid Dyn. 1991, 26, 331–337. [Google Scholar] [CrossRef]
- Longtin, J.P.; Hijikata, K.; Ogawa, K. Laser-induced surface-tension-driven flows in liquids. Int. J. Heat Mass Transf. 1999, 42, 85–93. [Google Scholar] [CrossRef]
- Oron, A. Nonlinear dynamics of irradiated thin volatile liquid films. Phys. Fluids 2000, 12, 29–41. [Google Scholar] [CrossRef]
- Hitt, D.L.; Smith, M.K. Radiation-driven thermocapillary flows in optically thick liquid films. Phys. Fluids A Fluid Dynam. 1993, 5, 2624–2632. [Google Scholar] [CrossRef]
- Karlov, S.P.; Kazenin, D.A.; Myznikova, B.I.; Wertgeim, I.I. Experimental and numerical study of the Marangoni convection due to localized laser heating. J. Non-Equilib. Thermodyn. 2005, 30, 283–304. [Google Scholar]
- Marchuk, I.V. Thermocapillary deformation of a horizontal liquid layer under flash local surface heating. J. Eng. Thermophys. 2015, 24, 381–385. [Google Scholar] [CrossRef]
- Marchuk, I.V. Thermocapillary deformation of a thin locally heated horizontal liquid layer. J. Eng. Thermophys. 2009, 18, 227–237. [Google Scholar] [CrossRef]
- Klyuev, D.S.; Fliagin, V.M.; Semenov, S.V.; Ivanova, N.A. Thermocapillary deformation induced by laser heating of thin liquid layers: Physical and numerical experiments. Int. J. Heat Mass Transf. 2021, 172, 121020. [Google Scholar] [CrossRef]
- Barakhovskaia, E.V.; Marchuk, I.V.; Fedorets, A.A. Thermocapillary deformation in a locally heated layer of silicone oil. J. Phys. Conf. Ser. 2016, 754, 32002. [Google Scholar] [CrossRef]
- Mizev, A.I. Experimental investigation of thermocapillary convection induced by a local temperature inhomogeneity near the liquid surface. 2. Radiation-induced source of heat. J Appl. Mech. Tech. 2004, 45, 699–704. [Google Scholar] [CrossRef]
- Bar-Cohen, A.; Wang, P. Thermal management of on-chip hot spot. ASME J. Heat Transf. 2012, 134, 51017. [Google Scholar] [CrossRef]
- Zaitsev, D.V.; Kabov, O.A. An experimental modeling of gravity effect on rupture of a locally heated liquid film. Microgravity Sci. Technol. 2007, XIX, 174–177. [Google Scholar] [CrossRef]
- Lyulin, Y.V.; Spesivtsev, S.E.; Marchuk, I.V.; Kabov, O.A. Investigation of disruption dynamics of the horizontal liquid layer with spot heating from the substrate side. Tech. Phys. Lett. 2015, 41, 1034–1037. [Google Scholar] [CrossRef]
- Kabova, Y.O.; Alexeev, A.; Gambaryan-Roisman, T.; Stephan, P. Marangoni-induced deformation and rupture of a liquid film on a heated microstructured wall. Phys. Fluids 2006, 18, 12104. [Google Scholar] [CrossRef]
- Zaitsev, D.; Kochkin, D.O.; Kabov, O. Dynamics of liquid film rupture under local heating. Int. J. Heat Mass Transf. 2022, 184, 122376. [Google Scholar] [CrossRef]
- French, R.H.; Tran, H.V. Immersion lithography: Photomask and wafer-level materials. Annu. Rev. Mater. Res. 2009, 39, 93. [Google Scholar] [CrossRef]
- Winkels, K.G.; Peters, I.R.; Evangelista, F.; Riepen, M.; Daerr, A.; Limat, L.; Snoeijer, J.H. Receding contact lines: From sliding drops to immersion lithography. Eur. Phys. J. Spec. Top. 2011, 192, 195–205. [Google Scholar] [CrossRef] [Green Version]
- Garnier, N.; Grigoriev, R.O.; Schatz, M.F. Optical manipulation of microscale fluid flow. Phys. Rev. Lett. 2003, 91, 54501. [Google Scholar] [CrossRef] [Green Version]
- Gao, A.; Butt, H.-J.; Steffen, W.; Schönecker, C. Optical manipulation of liquids by thermal Marangoni flow along the air-water interfaces of a superhydrophobic surface. Langmuir 2021, 37, 8677–8686. [Google Scholar] [CrossRef]
- Mizev, A.; Shmyrov, A.; Shmyrova, A. On the shear-driven surfactant layer instability. J. Fluid Mech. 2022, 939, A24. [Google Scholar] [CrossRef]
- Roke, S.; Schins, J.; Müller, M.; Bonn, M. Vibrational spectroscopic investigation of the phase diagram of a biomimetic lipid monolayer. Phys. Rev. Lett. 2003, 90, 128101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Backus, E.H.G.; Bonn, D.; Cantin, S.; Roke, S.; Bonn, M. Laser-induced displacement of surfactants on the water surface. J. Phys. Chem. B 2012, 116, 2703–2712. [Google Scholar] [CrossRef] [PubMed]
- Pinan Basualdo, F.N.; Terrazas Mallea, R.; Scheid, B.; Bolopion, A.; Gauthier, M.; Lambert, P. Effect of insoluble surfactants on a thermocapillary flow. Phys. Fluids 2021, 33, 72106. [Google Scholar] [CrossRef]
- Bickel, T. Effect of surface-active contaminants on radial thermocapillary flows. Eur. Phys. J. E 2019, 42, 131. [Google Scholar] [CrossRef]
- Koleski, G.; Vilquin, A.; Loudet, J.-C.; Bickel, T.; Pouligny, B. Azimuthal instability of the radial thermocapillary flow around a hot bead trapped at the water–air interface. Phys. Fluids 2020, 32, 92108. [Google Scholar] [CrossRef]
- Nepomnyashchy, A.; Simanovskii, I.; Legros, J.C. Interfacial Convection in Multilayer Systems, 2nd ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Bekezhanova, V.B.; Goncharova, O.N.; Ivanova, N.A.; Klyuev, D.S. Instability of a two-layer system with deformable interfaces under laser beam heating. J. Sib. Fed. Univ. Math. Phys. 2019, 12, 543–550. [Google Scholar] [CrossRef]
- Bekezhanova, V.B.; Fliagin, V.M.; Goncharova, O.N.; Ivanova, N.A.; Klyuev, D.S. Thermocapillary deformations of a two-layer system of liquids under laser beam heating. Int. J. Multiph. Flow. 2020, 132, 103429. [Google Scholar] [CrossRef]
- Chraibi, H.; Delville, J.P. Thermocapillary flows and interface deformations produced by localized laser heating on confident environment. Phys. Fluids 2012, 24, 32102. [Google Scholar] [CrossRef] [Green Version]
- de Saint Vincent, M.R.; Chraibi, H.; Delville, J.-P. Optical flow focusing: Light-induced destabilization of stable liquid threads. Phys. Rev. Appl. 2015, 4, 44005. [Google Scholar] [CrossRef] [Green Version]
- Ovcharova, A.S. Multilayer system of films heated from above. Int. J. Heat Mass Transf. 2017, 114, 992–1000. [Google Scholar] [CrossRef]
- Miyakawa, K.; Adachi, H. Laser-controlled microscale flows near the air-liquid interface of suspension droplets. Phys. Rev. E 2008, 78, 41407. [Google Scholar] [CrossRef] [PubMed]
- Gupta, K.; Kolwankar, K.M.; Gore, B.; Dharmadhikari, J.D.; Dharmadhikari, A.K. Laser-driven Marangoni flow and vortex formation in a liquid droplet. Phys. Fluids 2020, 32, 121701. [Google Scholar] [CrossRef]
- Namura, K.; Nakajima, K.; Kimura, K.; Suzuki, M. Photothermally controlled Marangoni flow around a micro bubble. Appl. Phys. Lett. 2015, 106, 43101. [Google Scholar] [CrossRef] [Green Version]
- Setoura, K.; Ito, S.; Miyasaka, H. Stationary bubble formation and Marangoni convection induced by CW laser heating of a single gold nanoparticle. Nanoscale 2017, 9, 719–730. [Google Scholar] [CrossRef]
- Liu, Z.; Lei, J.; Zhang, Y.; Liu, K.; Liu, W.; Zhang, R.; Zhang, Y.; Yang, X.; Zhang, J.; Yang, J.; et al. All-fiber impurity collector based on laser-induced microbubble. Opt. Commun. 2019, 439, 308–311. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanova, N. Interfacial Flows and Interfacial Shape Modulation Controlled by the Thermal Action of Light Energy. Colloids Interfaces 2022, 6, 31. https://doi.org/10.3390/colloids6020031
Ivanova N. Interfacial Flows and Interfacial Shape Modulation Controlled by the Thermal Action of Light Energy. Colloids and Interfaces. 2022; 6(2):31. https://doi.org/10.3390/colloids6020031
Chicago/Turabian StyleIvanova, Natalia. 2022. "Interfacial Flows and Interfacial Shape Modulation Controlled by the Thermal Action of Light Energy" Colloids and Interfaces 6, no. 2: 31. https://doi.org/10.3390/colloids6020031
APA StyleIvanova, N. (2022). Interfacial Flows and Interfacial Shape Modulation Controlled by the Thermal Action of Light Energy. Colloids and Interfaces, 6(2), 31. https://doi.org/10.3390/colloids6020031





