Abstract
In real life, sessile droplets usually have a three-dimensional shape, making it difficult to understand their forced wetting behavior, both from an experimental and a theoretical perspective. Even in the case of spreading under quasi-static conditions, where the droplet shape is described by the Young–Laplace equation, there is no fundamental approach to describe the contact line evolution. In the present work, a few existing approaches on this issue are analyzed and assessed. It is shown that an experimentally inspired fixed shape for the contact line of droplets that are spreading under the action of tangential forces can be considered equivalent to a theory for contact line motion. There is a lack of experimental data for contact line evolution under arbitrary scenarios of forces. Such data will be very helpful for the further development of the suggested approach to contact line motion. Of particular interest is the case of small contact angle droplets, for which a top view can clearly indicate the contact line location. On the contrary, in such droplets, the direct experimental measurement of contact angle profile is very difficult. This must be estimated theoretically; thus, a special approach has been developed here for this purpose.
1. Introduction
The process of wetting of a solid substrate by a liquid is of paramount importance in several industrial processes [1]. When this is driven by external forces, it is customarily called forced wetting. Forced wetting by a confined liquid—for example, by a droplet—is also termed spreading, when only one edge of the droplet moves, or sliding, when the droplet altogether (both edges) moves. In case of dynamic (non quasi-static) spreading and sliding, hydrodynamics have an essential role and literature on the subject is especially vast. This is because there is no fundamentally exact mesoscopic mathematical description of the problem, and thus several approximate techniques have been developed [2,3,4]. The situation is relatively simpler in the case of quasi-static spreading. The criterion for quasi-static spreading to occur is the characteristic time of force variation being much smaller than the characteristic time of droplet motion. In this case, the shape of the droplet is completely determined by force (or energy) balances. This shape can be easily determined by the well-known Young–Laplace equation. Even in complex cases considering disjoining pressure [5], substrate elasticity [6], and surface roughness [7], the Young–Laplace equation is valid far from the contact line, and the additional complexity can be dealt with by using an effective contact angle instead of the real angle. However, the motion of the contact line, even during quasi-static spreading, is an unresolved issue. In the two-dimensional case, the corresponding problem is somewhat trivial, as the contact line moves when the contact angle exceeds the advancing contact angle value φA [8]. In three dimensions, however, a whole distribution of contact angles may exist. The contact line moves when the maximum angle exceeds φA. This occurs not only at a single point, but with a whole portion of the contact line moving. Thus, a model for the motion of the contact line is needed.
A very elaborated (albeit phenomenological in nature) model based on energy minimization of the droplet was proposed a few years prior to this study [9] and has been employed by several authors [10,11]. The surface evolver open code was used to initially find the contact angle distribution and then the contact line was moved in a way that the moving distance at each point was proportional to a function that included the local contact angle and advancing (or receding φR) contact angle. The whole procedure was iterated until the contact angle profile exceeded φA in no location. This approach led to rather questionable results, as large areas of the contact line with contact angles equal to φA or φR appeared according to results presented in [9]. A different approach, again using surface evolver, was proposed in [12]. The contact line in this model evolved in a way that the contact angle distribution followed a specific functional form proposed in [13].
From the above discussion, it becomes clear that the contact angle distribution knowledge is essential for the development of contact line motion. Several attempts to suggest contact angle profile shapes based on numerical analysis led to controversial results [14,15]. What is considered the best contact angle profile is the generalized third order polynomial function (with respect to the azimuthal angle) proposed in [13]. This was derived on the basis of numerous experiments using a rotating camera. However (although some shape corrections have been made in the techniques) it has not been possible to observe contact angle from an arbitrary point of view. As a virtual experiment to prove this, imagine a square contact line. The camera will observe the same fictitious contact angle from several angles of observation. Further from the contact angle profile, a complete model of the contact line evolution during application of a tangential force to a droplet was proposed in [13], based exclusively on experimental data. According to this model, the contact line is elliptical, with an ellipsis aspect ratio being a specific function of the tangential Bond number, BoT. Another function of BoT was proposed for the ratio of minimum to maximum contact angle during spreading. These functions are independent from droplet volume.
As it is discussed above, the direct experimental identification of contact angle distribution is a very difficult task. On the other hand, identification of the experimental contact line is a very easy process for omniphilic surfaces (only a top image of the droplet is needed). Thus, a large number of experimental data on contact line motion during spreading under several applied force sequences is necessary in order to develop a model for contact line motion. This idea is supported in several ways in the present work. It is stressed that the focus of the present work is not to develop techniques for the solution of the Young–Laplace equation. The proposed techniques are instead used as a vehicle to demonstrate how the experimental results on contact line shape evolution can be handled to produce data for the development of contact line motion theories.
The structure of the present work is the following: First several results for the contact angle distribution as predicted by the non-linear Young–Laplace equation for circular and elliptical contact lines are presented. On the basis of these results, it is shown that ellipsis is not an acceptable shape for the contact line under tangential force. A contradiction with the model of [13] thus appears. Then, a simple semianalytical technique for the linearized Young–Laplace equation is developed and applied for the contact line evolution under a tangential force assuming a specific contact line shape that has been observed experimentally. The results are extensively discussed, and the direction of the required experimental studies on the subject is shown.
2. Problem Formulation, Results, and Discussion
It is noted that any shape of the droplet contact line is admissible as far as the contact line profile includes values between φA and φR. This is why a contact line motion model is needed—to choose the real one from the admissible shapes as the contact line evolves. A contact line shape can be achieved by way of droplet deposition on the substrate and/or by applied force sequences. An alternative situation is one of pinning, in which the contact line shape is determined by the structure of the substrate (e.g., an adverse step). In this case, the advancing contact angle can be (effectively) exceeded with no contact line motion.
The governing equation that determines the shape of the droplet is the so called Young–Laplace equation. This equation is a statement of total droplet energy minimization. In particular, the energy contributions that depend on droplet shape are the surface energy and the potential energy associated with body forces. The relative contribution of the two types of energy (potential/surface) are expressed through the dimensionless parameter called the Bond number. In the case of omniphilic surfaces, the Monge representation of the droplet surface in Cartesian coordinates can be employed [16]. This leads to a much simpler mathematical problem than the spherical coordinate representation, which has the advantage of applicability even for contact angles larger than 90° [17]. If the Cartesian coordinates are denoted by x, y, and z and the droplet shape is denoted by z = f(x,y) the governing equation (in its dimensionless form) for the droplet shape takes the form
where the variables x, y, z, and f are normalized by a characteristic length L. The two Bond numbers (normal BoN and tangential BoT) are computed as ραL2/σ, where ρ and σ are the density and the surface tension of the liquid and α is the corresponding (normal or tangential) acceleration field value. The case of a prescribed droplet basis contour will be treated first. In this case the boundary condition for the solution of the above equation is
f = 0 on F(x,y) = 0.
Equation (1) is defined in the domain C that is included in the curve F(x,y) = 0, which is the functional representation of the contact line.
The parameter G must be derived from the requirement of the prescribed dimensionless liquid volume V (the nondimensionalization is made using L3):
The above mathematical problem is solved numerically as follows: At first, Equation (1) is discretized using quadratic triangular unstructured elements. The resulting system of non-linear algebraic equations is solved through the Newton–Raphson procedure (internal loop). An external Newton–Raphson loop is also employed in order to find the value of G that leads to the required droplet volume. The choice of L is typically based on a characteristic dimension of the droplet basis contour. Indicative results for three basis contours will be presented here.
(1) Circular basis. In this case, the circle radius is taken as characteristic length (i.e., L = R) and F(x,y) = x2 + y2−1. The Young–Laplace equation is solved numerically and the distribution of the contact angle along the contact line is computed by numerical differentiation. This problem has been extensively studied in the past, yet not in this particular context. The usual approach is to present the contact angle distribution with respect to the so-called azimuthal angle but, instead, we found it more fruitful to use the contact line length starting from the rear edge of the droplet for this purpose. The contact angle profiles for a droplet with a circular basis, dimensionless volume 0.6, and several combinations of applied tangential and normal forces are shown in Figure 1. In the case of zero tangential force, the contact angle has a constant value (axisymmetric droplet shape). This constant value increases as the normal force increases and the droplet is squeezed to the surface. In the presence of tangential force the angle profile takes a unimodal shape with minimum at the rear edge and maximum at the front edge of the droplet. The difference between maximum and minimum angles increases as tangential force increases and decreases as normal force increases. In the limit of small contact angles (implying small slopes of the gas-liquid interface) the governing Young–Laplace equation can be linearized and solved analytically. The solution procedure is shown in Appendix A for clarity of presentation. The final result for the interface slope distribution along the contact line is
where is the length along the contact line, as defined previously, and Io, I1 are the modified Bessel functions of first kind with order zero and one, respectively. In terms of contact angle φ and azimuthal angle θ, the above equation can be written in a generalized way as
where A and B are functions of the normal Bond number. The above form qualitatively describes the effect of the parameters BoN, BoT, and V on the contact angle profile. This description is quantitatively accurate for contact angles less than 20°. An attempt is made to fit the contact angle distribution in Figure 1 by Equation (5). The fitted distribution is similar to the actual one but with a somewhat larger spread. This means that the actual distribution can be represented well with a three-term Fourier series expansion (instead of a single term expansion of Equation (5)). The two additional terms accommodate the effect of non-linearity of the governing equations. As the contact angle increases, the number of required Fourier terms for contact profile representation also increases.
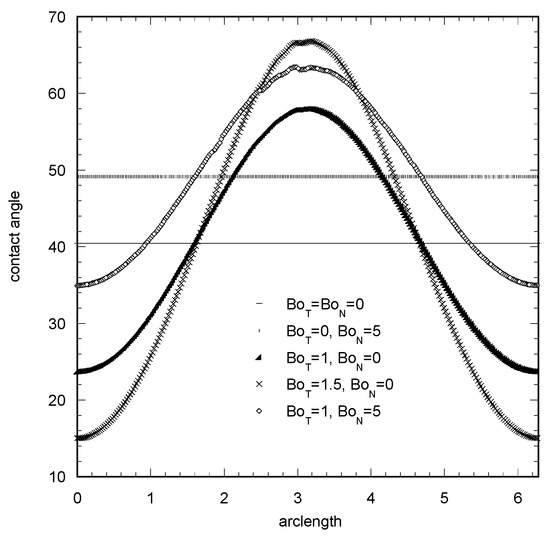
Figure 1.
Contact angle (degrees) distribution along a pinned circular contact line for several values of normal and tangential Bond numbers. Dimensionless volume V = 0.6.
(2) Generalized elliptical basis. This implies an elliptical shape with a high aspect ratio resulting, for example, by pinning the droplet to the surface during deposition (the deformation is too large to be achieved by applied forces). In this case, the average half length of the two axes of the droplet basis is taken as characteristic length. The function F is given now as F(x,y) = (x/b)2 + (y/a)2 −1, where b, a, are the large and the small axis of the ellipsis, respectively. The contact angle profiles for a droplet with V = 0.6, a = 0.8, b = 1.2, and for several combinations of applied forces is shown in Figure 2. In the absence of tangential force, the angle profile is bimodal with the two maximum positions at the side edges of the droplet, and the two minimum positions at the rear and front edges. The increase of the normal force leads simply to a shift of the profile to larger angle values. On the other hand, by increasing the tangential force, the locations of the maximum angle are transferred towards the front section of the droplet. In parallel, the difference between the maximum and the global minimum angle increases whereas the difference between maximum and local minimum decreases. The contact angle profile for tangential force applied to a direction of 45 °C with respect to ellipsis axis is also presented for comparison purposes. The profile is still bimodal, but it loses its symmetry with respect to droplet midplane along the large axis.
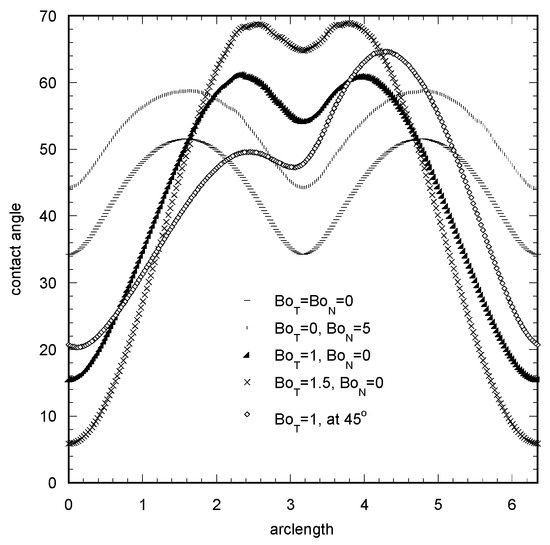
Figure 2.
Contact angle (degrees) distribution along a pinned elliptical contact line (aspect ratio = 1.5) for several values of normal and tangential Bond numbers. Dimensionless volume V = 0.6.
(3) Elliptical basis arising from tangential force to the drop. In this case, we assume an elliptical basis which is not due to deposition pinning but due to applied tangential force. An elliptical shape typical for this case (e.g., see [13,18]) with a = 0.96 and b = 1.2 is considered. An attempt to directly compare with the results of [13] failed, since it is not possible to identify what is used as an equivalent drop diameter in the definition of Bond number in [13]. Thus, an arbitrary characteristic length is considered for the purpose of analyzing the resulting contact angle profiles. These profiles in a case of zero normal force and for increasing tangential force are shown in Figure 3.
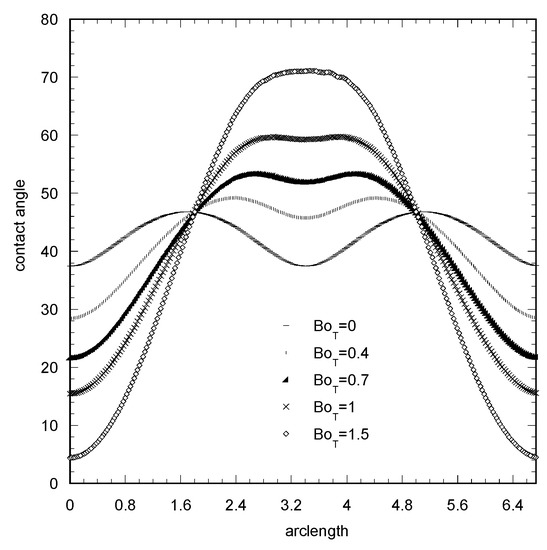
Figure 3.
Contact angle (degrees) distribution along a pinned elliptical contact line (aspect ratio = 1.25) for increasing Bond number. Dimensionless volume V = 0.6.
In the case of small BoT, the angle profile is again bimodal, but as BoT increases it flattens at the front edge and at some force value the contact angle profile becomes unimodal. Hence, under the proper combination of contact line deformation and magnitude of BoT, the elliptical shape could be a possibility for the contact line, as it leads to a unimodal contact angle profile. Let us further examine this possibility by invoking the analysis in [13]. According to that analysis, the BoT (as defined in [13]) corresponding to the present aspect ratio (b/a = 1.25) is BoT = 2.6 (see Figure 12 of [13]). The ratio between the minimum and maximum angles of the contact angle profile should be 0.62 (see Equation (16) and Figure 9 of [13]). This value clearly corresponds to the bimodal profiles of Figure 3. The acceptable unimodal profile has a much smaller value of this ratio. The correlations of [13] are supposed to hold for any droplet volume; thus, the counter example presented here is enough to put it under question. The conclusion is that the contact angle profile shape and the contact line shape, both proposed in [13], and the Young–Laplace equation are not consistent with each other.
Therefore, it appears that the elliptical shape is not the answer to the question of how the droplet contact line shape evolves during spreading induced by a tangential force. According to [13], which refers to older literature, a combination of two ellipses with different large axes and common small axes leads to a much better description of experimental contact lines. More recent extensive experimental results reveal that the above description can be further simplified to a circle for the front (towards the applied force direction) and an ellipsis for the rear (opposite to the applied force direction) parts of the contact line [19,20,21]. This means that if the circle radius is utilized as characteristic length, the shape of the contact line can be fully parameterized using a single parameter, b, which is the fractional elongation of the front part of the droplet (i.e., ellipsis large semiaxis/circle radius—1). In the present work, an approximate mathematical technique is developed for a closed form representation of the droplet shape. The method is restricted to the linearized Young–Laplace equation (small contact angles) and to the absence of normal force. This is a practically significant case, given that for small contact angles there may be considerable spreading, and the normal force has no large effect for slender drops so it can be safely ignored. In addition, a simple technique for the transformation of contact line shape to contact angle distribution is especially welcome in case of small angles, as in this case the direct angle measurement is very difficult and the sensitivity of the shape to the angle is very high. It must be reminded that for small angles the most reliable experimental contact angle measurements are based on the identification of contact line location [22,23].
The proposed method is based on the general approach of boundary weighted residual methods [24]. These methods are based on enforcing a function, which is a solution to the governing equation, to confront the boundary condition. They have been used for the solution of the Stokes (biharmonic) equation for creeping flow [25], Laplace equation for heat conduction [26], and Poisson–Boltzmann equation for electrical double layer calculation [27]. In all cases, some kind of an undulated surface preventing the completely analytical solution to the problem is involved. The method has no solid theoretical support and the domain of convergence is where the shape of the involved surface does not deviate much from the generating surfaces of the coordinate system used for the analytical solution of the governing equation [28]. Thus, the method has been of rather small value and significance in the literature. However, in the present case, the shape of the contact line is never too different from that of a circle (corresponding to a polar coordinate solution) before sliding occurs, and this offers a good opportunity to the particular method as an effective practical tool.
The solution method is described in detail in Appendix B. For an arbitrary shape of the contact line, a system of linear equations is solved for some coefficients and then the droplet’s shape can be written in terms of elementary functions. Let us study the convergence of the method compared with the largest index of expansion terms N for the particular contact angle shape of interest here. This can be written in polar coordinates and in terms of parameter b as
R(θ) = 1,
The application of the method shown in Appendix B for the above profile with b = 0.5 (very distorted contact line) and for BoT = −1 and V = 0.6 for increasing values of N leads to the distribution of the contact angle along the contact line, as shown in Figure 4. The negative tangential bond number means that the tangential force is applied to the opposite direction than the one having created the distortion of the contact line. The convergence study is presented for a negative Bond number because it corresponds to more stringent conditions. It is evident that complete convergence has been achieved at N = 6. Furthermore, to the convergence analysis, the resulting angle distribution is compared to the one resulting from the finite element solution with a fine grid, and coincidence is found. Figure 4 suggests that even for N = 4, an accepted angle distribution can be derived. It is noted that the above situation holds for a relatively distorted contact line with b = 0.5. The required number N for convergence decreases as b decreases. Another issue is that the convergence test is performed against the contact angle, which is a measure based on the derivative of the droplet shape. Such a convergence test is stringent. A convergence test against the droplet shape itself leads to the very interesting result, in that in any case the expansion with N = 3 terms describes accurately the shape of the droplet. For comparison purposes, the number of unknown variables in the finite element technique is several hundreds and in surface evolver is several thousands. The important advantage of the proposed technique is that it offers a simple closed form representation of the droplet shape. This information can be utilized (i) for the reconstruction of the droplet shape from experimental limited image information and (ii) for the derivation of low-order weighted residual methods for the solution of the non-linear Young–Laplace equation. It is noted that the above discussion holds for homogeneous surfaces (at the scale of the contact line, i.e., a scale higher than the microscale). Localized heterogeneities in this scale can create high frequency perturbations to the contact line profile and dramatically increase the number of terms in the eigenfunction expansion needed for the contact line description. In this way, the stability of the solution technique is adversely affected.
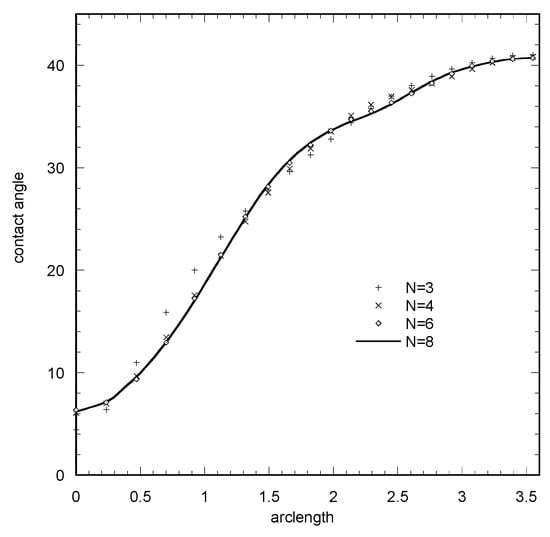
Figure 4.
Convergence of the contact angle (degrees) distribution along the contact line (composite circular–elliptical shape) for increasing number N (accounting for number of terms in boundary collocation expansion).
The proposed approach will be used here to derive the contact angle distribution evolution as the tangential force increases. A droplet with V = 0.6 in the absence of forces is considered at the beginning. The droplet shape is spherical cap and the contact angle is uniform with φ = 36°. Then, the tangential force starts to increase. The contact angle is a function of the position along the contact line with the maximum towards the force direction and the minimum at the opposite direction. This profile has a simple cosine shape and continues to evolve up to the point that the maximum angle reaches the advancing contact angle φA (φA = 44° is assumed here). Then, spreading begins and the contact line shape becomes a function of the tangential force BoT. This shape is completely parameterized through Equation (6), and the evolution problem is transformed to seeking of the b value that leads, through the procedure described in Appendix B, to a maximum contact angle equal to φA. For each value of BoT, the Newton–Raphson method is used to find b. In this way, the evolution of contact angle distribution is computed up to the case of the minimum angle being equal to the receding angle φR where sliding begins. The computed angle distributions along the contact line are presented in Figure 5. It is noted that a non-physical (but slight) overshoot of the contact angle appears close to the front edge of the droplet. However, this overshoot appears only for rear angles closer than 5°, so, in principle, the acquired profiles can be considered as acceptable. In that case, the consideration of a specific contact line shape is equivalent to the development of a contact line evolution model. The corresponding contact line shapes are shown in Figure 6.
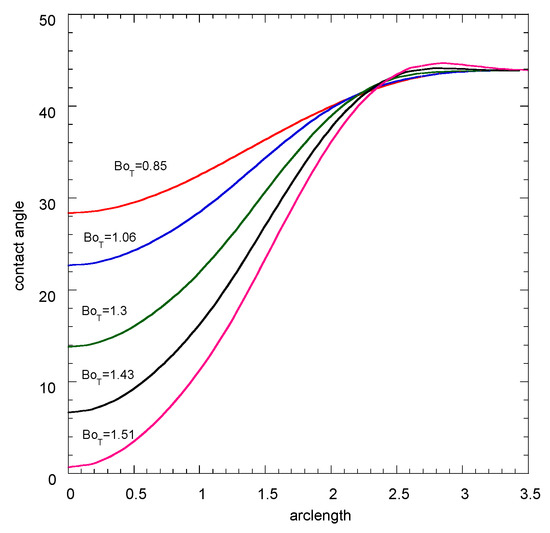
Figure 5.
Evolution of contact angle distribution along the evolved contact line for an increasing tangential Bond number (linear Young–Laplace equation, V = 0.6).
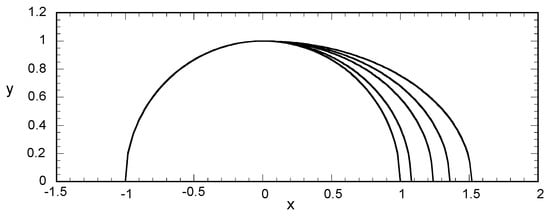
Figure 6.
Evolution of contact line shape corresponding to the contact angle distribution of Figure 5.
Inspired by the fact that the contact angle distribution proposed in [13] under proper normalization can acquire a universal form, let us now try to apply a similar normalization here. The normalized contact angle is defined as Φ = (φ − φmin)/(φmax − φmin), and the arclength along the contact line is replaced by the normalized azimuthal angle Θ = θ/π.
The contact angle distribution evolution in terms of normalized variables is shown in Figure 7. It is obvious that the normalized contact angle distribution tends to a self-similar shape as the tangential Bond number increases. In the case of the initial contact angle being equal to the advancing one, the convergence to self-similarity confirms the universality proposal in [13] converging at a faster rate. However, the resulting distribution is far from the universal one suggested in [13], which takes the form Φ = 2(1 − Θ)3 − 3(1 − Θ)2 + 1 and also appears in Figure 7. The universal shape adequately represents the actual distribution close to the two edges of the droplet, but there is a deviation in intermediate regions (especially in the elliptic part of the contact line). The universal shape is antisymmetric with respect to Θ = ½, which is a rather improbable behavior in light of the present results.
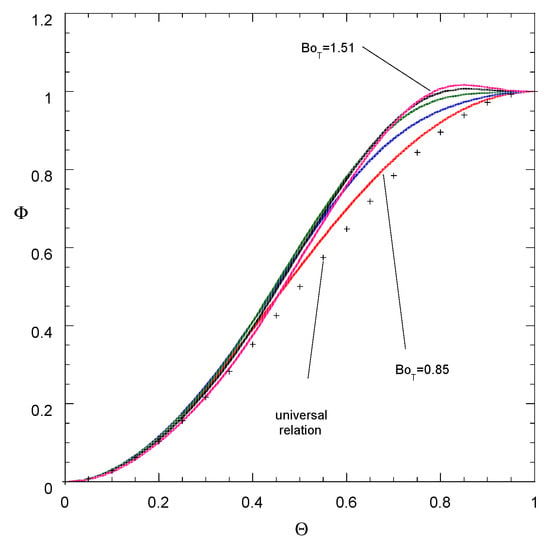
Figure 7.
Normalized contact angle versus normalized azimuthal angle for the cases presented in Figure 5. The variable BoT for the three intermediate curves is 1.03, 1.3, 1.43, respectively (from lower to higher). The universal relation proposed in [13] is also shown.
In order to demonstrate the versatility of the solution method and to shed more physical insight on the problem, the contact angle profiles at the contact line shown in Figure 6 at the inception of spreading but with a force applying to the opposite direction are shown in Figure 8. The corresponding normalized results are presented in Figure 9. The spreading now starts for smaller (in absolute value) Bond numbers, as it is affected by the deformed contact line. It is noted than an elbow appears in the contact angle curve as the contact line deformation increases. The location of this elbow is at the position of transition of the contact line shape from circle to ellipsis. For larger BoT numbers, the evolution is mainly due to the increase of this elbow. In any case, universality does not appear in these curves. The presented example refers to conditions with no strict actual linearity but similar results for the normalized variables are taken for lower values of θA.
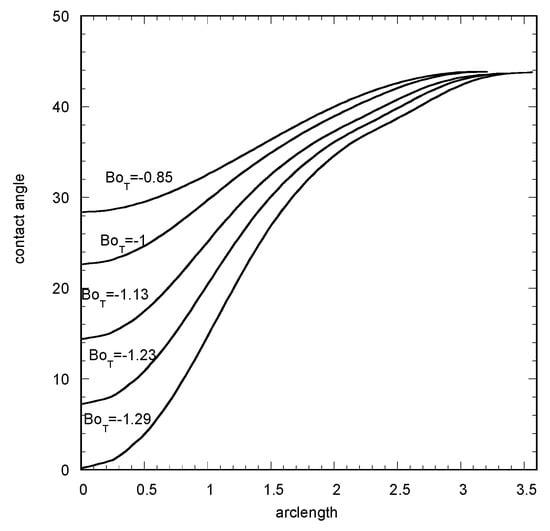
Figure 8.
Evolution of contact angle distribution along the contact lines by inversing the direction of the tangential Bond number at the inception of spreading (linear Young–Laplace equation, V = 0.6).
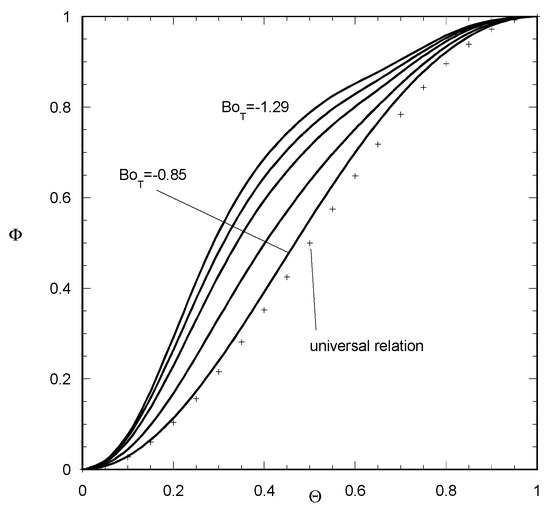
Figure 9.
Normalized contact angle versus normalized azimuthal angle for the cases presented in Figure 8. The variable BoT for the three intermediate curves is −1, −1.13, −1.23, respectively (from lower to higher). The universal relation proposed in [13] is also shown.
The fact is that for experimentally observed contact line shapes (an easy experimentally accessible feature) the resulting contact angle distribution (a very difficult experimentally accessible feature) does not obey the universal shape as suggested in the past. Apparently, the analysis here is in the linear limit, yet it is enough to invalidate the universality principle that should hold under all possible cases. The implication for the measurement techniques is that it is preferable for quasi-static state spreading on omniphilic surfaces to extract the contact angle distribution from the contact line shape than from direct contact angle measurements.
In summary, there are several methods to find the distribution of the contact angle for a sessile droplet spreading under the influence of bulk body forces. These methods start from the molecular scale (molecular dynamics), allowing consideration only of nanodroplets (for computational reasons) [29] and continue with approaches based on precursor films and disjoining pressure profiles (still computationally intensive for three dimensional droplets) [6]. The next level approaches are all based on the solution of the Young–Laplace equation, either combined to an evolution principle for the contact line, assuming a prescribed shape for the contact line, or for the contact angle profile. All approaches contain unknown parameters that have to be estimated by experimental data of contact line shapes. The suggestion in the present work is to use experimental information as much as possible, keeping the mathematical model for the contact line evolution simple. It is noted that the simultaneous variation of tangential and normal Bond numbers discussed in the present work is not experimentally straightforward. This is due to the fact that the relevant experimental studies are done on the basis of the rotation of horizontal drops or for drops on inclined plates. Recently, the device Kerveros [28,30] has been developed, which allows simultaneous control of the two Bond numbers by adjusting both the rotation frequency and inclination angle.
3. Conclusions
It is shown that the existing models for the contact line motion, even for the simple process of quasi-static spreading, suffers from several inconsistencies or artificial features. There is a need for additional experimental data on the process under complex force application scenarios (e.g., using a Kerberos device [28,30]) in order to derive reliable models. The case of small contact angle systems is of particular interest for this purpose, as they exhibit considerable spreading. In such systems, the contact angle distribution is extremely difficult to directly measure; thus, the measured quantity should be the contact line profile. Choosing a particular shape for the contact line is equivalent to choosing a contact line motion model. The composite circle–ellipsis contact line shape has strong experimental support. A special mathematical procedure allowing closed form representation of the droplet surface for this particular contact line shape is developed. The results of application of the above procedure to a droplet undergoing tangential forces are presented and discussed.
Author Contributions
Conceptualization, M.K. and T.K.; methodology, M.K. and T.K.; software, M.K.; formal analysis, M.K.; investigation, M.K. and T.K.; writing—original draft preparation, M.K.; writing—review and editing, T.K.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Analytical Solution of Linear Young–Laplace Equation for Circular Droplet Basis
Linearization of equation by zeroing the first order derivatives leads to
A partial solution can be easily derived as . A new function g is defined as g = f − fo. The polar coordinate system r,θ is defined on the basis plane of the droplet. Substituting g in Equation (A1) and switching to polar coordinates, the problem is transformed to
with boundary condition (derived using x = rcos(θ))
Equation (A2) is solved using the separation of variables technique, leading to an infinite series of products of modified Bessel functions and trigonometric functions. The inspection of the boundary condition (A3) suggests retaining only two terms of the infinite series, so
The unknown coefficients c1, c2 can be found by matching the boundary condition (A3). Summation of g and fo leads to the following droplet shape function:
The next step is to determine the constant G using Equation (3) for the total droplet volume. The integration is performed in polar coordinates and employing the relation , leading finally to
Differentiating f with respect to r along the contact line using the relation leads to Equation (4), with θ instead of π- . The relation between the contact line length and the angle θ is simply = π − θ.
Appendix B
Boundary Collocation Technique for the Linearized Young–Laplace Equation
Let us assume that the contact line is described in polar coordinates by the relation r = R(θ), where R(θ) is a smooth even function. The tangential force is assumed in this case towards the negative x hemiplane for convenience. In the absence of normal force, the governing equation for the droplet shape f in cylindrical coordinates is
with boundary condition f = 0 on r = R(θ).
At first, a partial solution of the problem is sought for. The right-hand side has a θ dependence similar to the θ dependence of the solutions of the Laplace equation. On the basis this, a partial solution of the form fo(r) = f1(r) + f2(r)cos(θ) is considered leading after some algebra to
A new auxiliary function g is defined as g = f − fo. A substitution in the governing Equation (A7) can show that the function g is a solution of the Laplace equation:
with boundary condition
on r = R(θ).
The general even solution of the Laplace equation in an enclosed domain is
where ci are coefficients that have to be determined by the boundary condition (A10). Up to here, only analytical manipulation has been made to the mathematical problem. The next steps are of approximate nature. The boundary weighted residual technique is applied. The series solution (A11) is truncated to the N-th term and then is substituted to the boundary condition. This leads to the following equation:
This equation must be enforced to hold for every value of θ (0 < θ < π) by appropriate choice of the coefficients ci. This problem is overdetermined; thus, it cannot be solved exactly but only in a weak (approximate) manner. There are several ways to do this: (i) A Galerkin approximation consists of multiplying the Equation (A12) with cos(jθ) (j = 0,1,2…N) and integrating over θ. In this way, a linear system of N + 1 equations with N + 1 unknowns is formed. (ii) The least square approximation consisting of creating as objective function the square of the residual of Equation (A12) integrated over θ. Then, the coefficients are determined by requiring minimization of the objective function using the standard differentiation procedure. The final result is again a linear (N + 1) × (N + 1) system. In both the above techniques, a large number of integrals requiring numerical computation appears. Another way, method (iii), is the collocation, which has the advantage of avoiding the appearance of integrals. The coordinate θ is discretized at N + 1 equidistant values θj = jπ/N. Requiring simply that the boundary condition must be fulfilled at these θ values results in the following linear system (j = 0,1,2,…N):
The parameter G is still unknown. It must be computed from the liquid volume balance, which after some algebra takes the form
The above integrals are computed numerically. In order to avoid repeated integrations when BoT or V changes, the following integrals must be computed for each contact line shape (i = 0,1,2...N):
Then, Equation (A14) can be written as
A nice feature of the resulting system is that G appears linearly in both Equations (A13) and (A16). In addition, coefficients ci appear linearly in Equation (A16). This means that the parameter G can be handled as the (N + 2)th unknown in a linear system of N + 2 equations (Equations (A13) and (A16)).
After finding the coefficients ci and G, the distribution of contact angle along the contact line is computed. The slope of the drop shape in the direction normal to the contact line is given in polar coordinates as
where
The length along the contact line is computed as
Summarizing for a given shape of the contact line r = R(θ), the following steps are followed to find the droplet shape: (i) the number of approximation terms N is chosen; (ii) the integrals J, K are numerically evaluated; (iii) for each pair of tangential force (BoT) and volume V, the linear system (N + 2) × (N + 2) of Equations (A13) and (A16) with unknowns, the coefficients ci and G is solved.
In the particular case of an undeformed contact line (circular), the following completely analytical solution can be derived:
This solution for the droplet profile can also be considered as the limit of Equations (A5) and (A6) when BoN approaches zero.
References
- Eral, H.B.; Mannetje, D.J.C.M.; Oh, J.M. Contact angle hysteresis: A review of fundamentals and applications. Colloid Polym. Sci. 2013, 291, 247–260. [Google Scholar] [CrossRef]
- Wang, X.D.; Lee, D.J.; Peng, X.F.; Lai, J.Y. Spreading dynamics and dynamic contact angle of non-Newtonian fluids. Langmuir 2007, 23, 8042–8047. [Google Scholar] [CrossRef] [PubMed]
- Savva, N.; Kalliadasis, S. Influence of gravity on the spreading of two-dimensional droplets over topographical substrates. J. Eng. Math. 2012, 73, 3–16. [Google Scholar] [CrossRef]
- Malgarinos, I.; Nikolopoulos, N.; Marengo, M.; Antonini, C.; Gavaises, M. VOF simulations of the contact angle dynamics during the drop spreading: Standard models and a new wetting force model. Adv. Colloid Interface Sci. 2014, 212, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Yeh, E.K.; Newman, J.; Radke, C.J. Equilibrium configurations of liquid droplets on solid surfaces under the influence of thin-film forces Part I. Thermodynamics. Colloids Surf. A Physicochem. Eng. Asp. 1999, 156, 137–144. [Google Scholar] [CrossRef]
- Koursari, N.; Ahmed, G.; Starov, V.M. Equilibrium droplets on deformable substrates: Equilibrium conditions. Langmuir 2018, 34, 5672–5677. [Google Scholar] [CrossRef] [PubMed]
- Pashos, G.; Kokkoris, G.; Papathanasiou, A.G.; Boudouvis, A.G. Wetting transitions on patterned surfaces with diffuse interaction potentials embedded in a Young-Laplace formulation. J. Chem. Phys. 2014, 144, 034105. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, R.; Rice, D.; Middleman, S. A model for the onset of motion of a sessile liquid drop on a rotating disk. J. Colloid Interface Sci. 1988, 125, 162–169. [Google Scholar] [CrossRef]
- Santos, M.J.; Velasco, S.; White, J.A. Simulation analysis of contact angles and retention forces of liquid drops on inclined surfaces. Langmuir 2012, 28, 11819–11826. [Google Scholar] [CrossRef]
- Prabhala, B.R.; Panchagnula, M.V.; Vedantam, S. Three-dimensional equilibrium shapes of drops on hysteretic surfaces. Colloid Polym. Sci. 2013, 291, 279–289. [Google Scholar] [CrossRef]
- Janardan, N.; Panchagnula, M.V. Effect of the initial conditions on the onset of motion in sessile drops on tilted plates. Colloids Surf. A Physicochem. Eng. Asp. 2014, 456, 238–245. [Google Scholar] [CrossRef]
- Sikarwar, B.S.; Muralidhar, K.; Khandekar, S. Effect of drop shape on heat transfer during dropwise condensation underneath inclined surfaces. Interfacial Phenom. Heat Transf. 2013, 1, 339–356. [Google Scholar] [CrossRef]
- ElSherbini, A.I.; Jacobi, A.M. Liquid droplets on vertical and inclined surfaces: I. An experimental study of droplet geometry. J. Colloid Interface Sci. 2004, 273, 556–565. [Google Scholar] [CrossRef] [PubMed]
- Milinazzo, F.; Shinbrot, M. A numerical study of a drop on a vertical wall. J. Colloid Interface Sci. 1988, 121, 254–264. [Google Scholar] [CrossRef]
- Dimitrakopoulos, P.; Higdon, J.J.L. On the gravitational displacement of three-dimensional fluid dropletlets from inclined solid surfaces. J. Fluid Mech. 1999, 395, 181–209. [Google Scholar] [CrossRef]
- Orr, F.M.; Scriven, L.E.; Rivas, A.P. Menisci in arrays of cylinders: Numerical simulation by finite elements. J. Colloid Interface Sci. 1975, 52, 602–610. [Google Scholar] [CrossRef]
- Brown, R.A.; Orr, F.M.; Scriven, L.E. Static drop on an inclined plate: Analysis by the finite element method. J. Colloid Interface Sci. 1980, 73, 76–87. [Google Scholar] [CrossRef]
- ElSherbini, A.I.; Jacobi, A.M. Liquid droplets on vertical and inclined surfaces: II. A method for approximating drop shapes. J. Colloid Interface Sci. 2004, 273, 566–575. [Google Scholar] [CrossRef]
- Higashine, M.; Katoh, K.; Wakimoto, T.; Azuma, T. Profiles of liquid droplets on solid plates in gravitational and centrifugal fields. J. Jpn. Soc. Exp. Mech. 2008, 8, s49–s54. [Google Scholar]
- Ríos-López, I.; Evgenidis, S.; Kostoglou, M.; Zabulis, X.; Karapantsios, T.D. Effect of initial droplet shape on the tangential force required for spreading and sliding along a solid surface. Colloids Surf. A Physicochem. Eng. Asp. 2018, 549, 164–173. [Google Scholar] [CrossRef]
- Ríos-López, I.; Karamaoynas, P.; Zabulis, X.; Kostoglou, M.; Karapantsios, T.D. Image analysis of axisymmetric droplets in wetting experiments: A new tool for the study of 3D droplet geometry and droplet shape reconstruction. Colloids Surf. A Physicochem. Eng. Asp. 2018, 553, 660–671. [Google Scholar] [CrossRef]
- Graham-Eagle, J.; Pennel, S. Contact angle calculations from the contact/maximum diameter of sessile drops. Int. J. Numer. Methods Fluids 2000, 32, 851–861. [Google Scholar] [CrossRef]
- Dimitrov, A.S.; Kralchevsky, P.A.; Nikolov, A.D.; Noshi, H.; Matsumoto, M. Contact angle measurements with sessile drops and bubbles. J. Colloid Interface Sci. 1991, 145, 279–282. [Google Scholar] [CrossRef]
- Finlayson, B.A. The Method of Weighted Residuals and Variational Principles; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- O’Brien, V. Form factors for deformed spheroids in Stokes flow. Am. Inst. Chem. Eng. J. 1968, 14, 870–875. [Google Scholar] [CrossRef]
- Ruth, D. Extended Fourier series solutions for diffusion problems with irregularly shaped boundaries and mixed boundary conditions. Can. J. Chem. Eng. 1990, 68, 230–236. [Google Scholar] [CrossRef]
- Kostoglou, M.; Karabelas, A.J. Effect of roughness on energy of repulsion between colloidal surfaces. J. Colloid Interface Sci. 1995, 171, 187–199. [Google Scholar] [CrossRef]
- Evgenidis, S.P.; Kalić, K.; Kostoglou, M.; Karapantsios, T.D. Kerberos: A three camera headed centrifugal/tilting device for studying wetting/dewetting under the influence of controlled body forces. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 38–48. [Google Scholar] [CrossRef]
- Fernander-Toledanoa, J.C.; Blake, T.D.; Limat, L.; De Coninck, J.J. A molecular-dynamics study of sliding liquid nanodrops: Dynamic contact angles and the pearling transition. J. Colloid Interface Sci. 2019, 548, 66–76. [Google Scholar] [CrossRef]
- Ríos-López, I.; Petala, M.; Kostoglou, M.; Karapantsios, T.D. Sessile droplets shape response to complex body forces. Colloids Surf. A Physicochem. Eng. Asp. 2019, 572, 97–106. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).