Abstract
The diffusiophoretic migration of a circular cylindrical particle in a nonelectrolyte solution with a solute concentration gradient normal to its axis is analytically studied for a small but finite Péclet number . The interfacial layer of interaction between the solute molecules and the particle is taken to be thin, but the polarization of its mobile molecules is allowed. Using a method of matched asymptotic expansions, we solve the governing equations of conservation of the system and obtain an explicit formula for the diffusiophoretic velocity of the cylinder correct to the order . It is found that the perturbed solute concentration and fluid velocity distributions have the order , but the leading correction to the particle velocity has the higher order . The correction to the particle velocity to the order can be either positive or negative depending on the polarization parameter of the thin interfacial layer, establishing that the solute convection effect is complicated and can enhance or retard the diffusiophoretic motion. The particle velocity at can be about 17% smaller or 0.2% greater than that at . Under practical conditions, the solute convection effect on the diffusiophoretic velocity is much greater for a cylindrical particle than for a spherical particle, whose leading correction has the order .
1. Introduction
A colloidal particle, when suspended in a fluid solution non-uniform in a solute concentration, will spontaneously move as a result of physical interaction between the solute molecules and the particle. This motion is known as diffusiophoresis and was widely applied to particle motility and manipulations [1,2,3,4,5]. In the solution of a nonelectrolyte solute with a uniform concentration gradient , the diffusiophoretic velocity of a colloidal sphere of radius with a thin but polarized interfacial diffuse layer is [6]
where is a characteristic length for the particle-solute interaction, is the Gibbs adsorption length characterizing the strength of adsorption of the molecular solute, is the polarization coefficient of the thin diffuse layer, is the fluid viscosity, is the Boltzmann constant, and is the absolute temperature. On the other hand, the corresponding diffusiophoresis of spheroidal and cylindrical particles has been analyzed [7,8,9], and the migration velocity of a long circular cylindrical particle in transverse solute gradients is also given by Equation (1).
The derivations of Equation (1) for both spherical and circular cylindrical particles assume that the Péclet and Reynolds numbers are zero. For the diffusiophoresis of a large colloidal particle in a high solute concentration gradient, the value of the Péclet number may have the order unity, and the solute convection may become notable in comparison with the solute diffusion in the fluid [10]. The diffusiophoresis of a spherical particle at a nonzero was first studied by Keh and Weng [11] using a perturbation method of matched asymptotic expansions [12,13], and the solute concentration and fluid flow fields around the particle as well as the diffusiophoretic velocity of the particle were determined to . Moreover, numerical calculations of the diffusiophoretic velocity of a colloidal sphere up to and an asymptotic analysis of the diffusiophoresis of a slightly non-spherical particle at a small finite have been presented for the limiting case [14].
The objective of the present work is to analyze the diffusiophoresis of a long circular cylinder in transverse directions when the Péclet number is small but nonzero. We employ the perturbation method to solve the problem, and an analytical formula to correct Equation (1) for the diffusiophoretic velocity up to for an arbitrary value of the polarization parameter will be given by Equation (18) together with Equations (22), (33), and (39).
2. Analysis
2.1. Equations of Conservation and Boundary Conditions
Consider the two-dimensional problem of the diffusiophoresis of a long circular cylindrical particle of radius in a solution of a nonionic solute normal to its axis, as shown in Figure 1. The uniform gradient of the solute concentration prescribed far from the particle is (), and its migration velocity is (with no rotation owing to the symmetry), where is the unit vector in the direction. For convenience, the polar coordinates are set to translate with the particle.
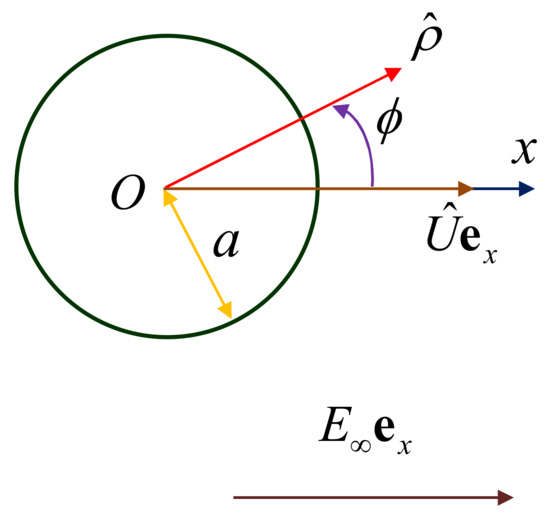
Figure 1.
Geometrical sketch for the diffusiophoresis of a circular cylindrical particle in a transverse direction.
We define some dimensionless operator, variables, and constants as follows:
where , , and are the solute concentration, fluid velocity, and pressure distributions, respectively, is the time, is the prescribed solute concentration at the particle center in the absence of the particle, is the diffusion coefficient of the solute, and is a characteristic particle velocity relating to Equation (1). With these definitions, the equations of conservation and boundary conditions of the molecular solute and fluid momentum at nonzero can be expressed as [11]
where and are the unit vectors in the and directions, respectively. The fluid velocity field and solute concentration distribution will be solved from the previous coupled equations.
2.2. Solution for the Velocity Field
The drag force exerted on the particle vanishes since it is freely suspended in the fluid. The solution to Equation (6) satisfying this requirement and the boundary conditions (8) and (10) can be obtained via
where the coefficients are integrals related to the solute concentration field (with the symmetry ) over the particle surface,
and the diffusiophoretic velocity of the particle is
2.3. Solution for the Solute Concentration Field
We adopt the method of matched asymptotic expansions to solve for the solute concentration distribution. Namely, the “inner” and “outer” solute concentration distributions first satisfy the boundary conditions at the particle surface () and at infinity (), respectively, and then they are matched at some distances from the surface [15,16,17,18]. We hold for the inner concentration distribution and let denote the outer concentration distribution, in which and . Then, will be solved by using Equations (5) and (7), whereas Equations (5) and (9) satisfied by should be expressed as
where and represent the inner and outer fluid velocity fields, respectively.
The inner and outer solute concentration and fluid velocity solutions and the diffusiophoretic velocity of the particle can be expressed in the expansions [19,20]
where , which is the particle velocity at in Equation (1), the coefficients , , , , and with , 1, 2, … are independent of . Subsequently, the inner and outer concentration fields and are determined by matching Equations (16) and (17) at the same orders of through the requirement
Certainly, the fluid velocity expansion coefficients can be written by using Equations (11) and (18) as
where the coefficients should be calculated from Equation (12) with being replaced by and . The leading outer fluid velocity coefficients can be obtained by Equation (22) with the substitution of for ,
The zeroth-order contributions (valid for ) are evident, with the expressions
The solute concentration and fluid velocity fields surrounding the particle are fore-aft symmetric or antisymmetric to this order.
The equations governing the solute concentration coefficients , , , , , , , and are derived from Equations (5), (7), (14)–(20), and (22)–(33) as
where the operator
Solving for the previous equations and matching according to Equation (21) to lead to
where , is the modified Bessel function of the second kind of order and . Note that is independent of position.
The substitution of Equations (41) and (42) into Equations (12) and (13) for results in the following coefficients up to :
Equations (45) and (46) indicate that the correction up to for the solute convection effect on the particle velocity is identically zero. This is a consequence of the fact that only terms of with even exist in Equations (41) and (42) for and , but only the odd term of the solute concentration profile over the particle surface can contribute to the particle velocity in Equation (13). Even so, the solute concentration and fluid velocity distributions surrounding the particle to this order are fore-aft asymmetric.
The equation governing the outer concentration coefficient can be obtained by Equations (14), (17), (19), (20), and (23)–(29) using the lower-order results in Equations (32), (43), and (44),
The solution of Equations (36), (39), and (50) after matching it with is
where the coefficients and will be obtained after the successive matching process.
The governing equation for the inner concentration coefficient obtained from Equations (5), (16), (18), (20), and (22) using the results of , , and in Equations (31), (41), and (42) is
The solutions to Equations (34), (38), and (53) after matching in Equation (52) according to Equation (21) to are
while is also resulted.
Substituting Equations (54) and (55) into Equations (12) and (13) for , we obtain
Equation (60) leads to and .
3. Results and Discussion
The problem of diffusiophoresis of a long circular cylindrical particle normal to its axis at small but finite Péclet numbers is analyzed in the previous section. Through the use of a procedure of matched asymptotic expansions, the diffusiophoretic velocity of the particle correct to is expressed by Equation (20) with the coefficients , , and and given by Equations (56) and (57). The solute concentration and fluid velocity distributions surrounding a circular cylinder undergoing diffusiophoresis are fore-aft symmetric or antisymmetric at . However, these distributions turn asymmetric for finite values of even to , although the first correction to the particle velocity is of .
Some values of the particle velocity correction coefficients and as functions of the polarization parameter () are listed in Table 1. The coefficient first decreases with an increase in from 3/4 at (through the value zero at ) to a minimal value which is slightly negative (at ) and then increases with a further increase in to zero as , while the coefficient first increases with an increase in from a negative value () at (through the value zero at ) to a maximal value which is slightly positive (at ) and then decreases with a further increase in to zero as , showing that the role of solute convection in diffusiophoresis of a cylindrical particle is complex.

Table 1.
The particle velocity correction coefficients and in Equation (20) calculated from Equations (56) and (57) as functions of the polarization parameter .
The leading particle velocity correction terms and in Equation (20), as calculated from Equations (56) and (57), are plotted versus the Péclet number in the range in Figure 2a with as a parameter and are plotted versus in a wide range in Figure 2b with as a parameter. For a given Péclet number, each correction term first increases with an increase in from a negative value at to a maximal value which is slightly positive and then decreases with a further increase in to zero as . The negative/positive nature of these indicate that the solute convection retards/enhances the particle’s movement. Note that the value of decreases with an increase in from zero at to a minimum at and then increases with a further increase in back to zero at . Moreover, results for the case of approaching unity (say, ) in Equation (20) correct to may not be sufficiently accurate [14] and are considered here only for the sake of comparison.
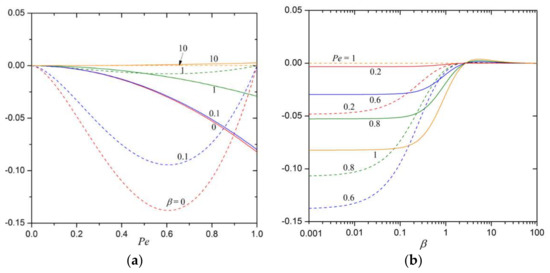
Figure 2.
The quantities (in dashed curves) and (in solid curves) in Equation (20) (a) versus the Péclet number for various values of the polarization parameter ; (b) versus for various values of .
The normalized diffusiophoretic velocity of the cylindrical particle is plotted versus the Péclet number in Figure 3a with as a parameter and is plotted versus in Figure 3b with as a parameter. As expected, an increase in can retard or enhance the particle’s movement. The particle velocity at can be about 17% smaller (for the case , i.e., without the polarization effect) or 0.2% greater (for the case ) than that at .
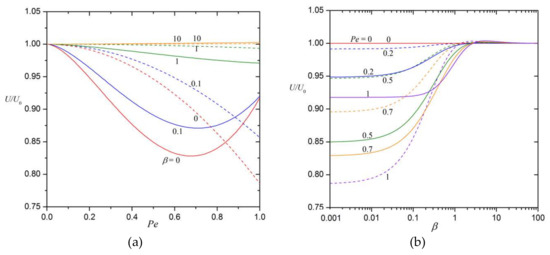
Figure 3.
The normalized diffusiophoretic velocity of colloidal particles (a) versus the Péclet number for various values of the polarization parameter ; (b) versus for various values of . The solid and dashed curves are plotted for a circular cylinder and a sphere, respectively.
For the corresponding diffusiophoresis of a spherical particle of radius , the particle velocity can also be expressed as Equation (20) but with the coefficients [21]
Note that the leading correction to the diffusiophoretic velocity has the order for a spherical particle, in contrast to the order for a cylindrical particle. For a numerical comparison, results of the normalized particle velocity of the spherical particle calculated using Equations (20) and (61) as a function of the parameters and are also plotted in dashed curves in Figure 3a,b. The dependences of on and are qualitatively similar for the spherical and cylindrical particles. Under applicable and practical conditions (say, and ), the value of is substantially smaller (or the solute convection effect on diffusiophoresis is much greater) for a cylindrical particle than for a spherical particle.
4. Conclusions
The diffusiophoresis of a long circular cylindrical particle surrounded by a thin polarized diffuse layer in a nonelectrolyte solution normal to its axis is analyzed for small but nonzero values of the Péclet number . We use the method of matched asymptotic expansions to solve the conservation equations and obtain an explicit formula for the diffusiophoretic velocity of the cylinder to the order . The values of the leading particle velocity correction terms and of this formula vary over a wide range and can be negative or positive, showing that the effect of solute convection in the fluid can reduce or increase the particle velocity. The diffusiophoretic velocity at can be about 17% smaller or 0.2% greater than that at , depending on the polarization parameter of the thin diffuse layer. Under practical conditions, the solute convection effect on diffusiophoresis is much greater for a cylindrical particle than for a spherical particle. Since the role of solute convection is complex, the analytical nature of this work provides physical insight to its effect on diffusiophoresis, which might be absent in numerical studies.
Author Contributions
Conceptualization, H.J.K. and Y.C.C.; methodology, H.J.K. and Y.C.C.; investigation, Y.C.C. and H.J.K.; writing—original draft preparation, H.J.K.; writing—review and editing, Y.C.C. and H.J.K.; supervision, H.J.K.; funding acquisition, H.J.K.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan (Republic of China), grant number MOST 106-2221-E-002-167-MY3.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Smith, R.E.; Prieve, D.C. Accelerated deposition of latex particles onto a rapidly dissolving steel surface. Chem. Eng. Sci. 1982, 37, 1213–1223. [Google Scholar] [CrossRef]
- Palacci, J.; Abecassis, B.; Cottin-Bizonne, C.; Ybert, C.; Bocquet, L. Colloidal motility and pattern formation under rectified diffusiophoresis. Phys. Rev. Lett. 2010, 104, 138302. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; He, R.; Zhu, H.; Hu, H.; Li, M.; Zhao, X. Ultrafast nanotube based diffusiophoresis nanomotors. Appl. Phys. Lett. 2010, 96, 053114. [Google Scholar] [CrossRef]
- Velegol, D.; Garg, A.; Guha, R.; Kar, A.; Kumar, M. Origins of concentration gradients for diffusiophoresis. Soft Matter 2016, 12, 4686–4703. [Google Scholar] [CrossRef] [PubMed]
- Oshanin, G.; Popescu, M.N.; Dietrich, S. Active colloids in the context of chemical kinetics. J. Phys. A: Math. Theor. 2017, 50, 134001. [Google Scholar] [CrossRef]
- Anderson, J.L.; Prieve, D.C. Diffusiophoresis caused by gradients of strongly adsorbing solutes. Langmuir 1991, 7, 403–406. [Google Scholar] [CrossRef]
- Keh, H.J.; Chen, S.B. Diffusiophoresis and electrophoresis of colloidal cylinders. Langmuir 1993, 9, 1142–1149. [Google Scholar] [CrossRef]
- Keh, H.J.; Huang, T.Y. Diffusiophoresis and electrophoresis of colloidal spheroids. J. Colloid Interf. Sci. 1993, 160, 354–371. [Google Scholar] [CrossRef]
- Keh, H.J.; Huang, T.Y. Diffusiophoresis and electrophoresis of elliptic cylindrical particles. Colloid Polym. Sci. 1994, 272, 855–871. [Google Scholar] [CrossRef]
- Michelin, S.; Lauga, E. Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 2014, 747, 572–604. [Google Scholar] [CrossRef]
- Keh, H.J.; Weng, J.C. Diffusiophoresis of colloidal spheres in nonelectrolyte gradients at small but finite Péclet numbers. Colloid Polym. Sci. 2001, 279, 305–311. [Google Scholar] [CrossRef]
- Van Dyke, M. Perturbation Methods in Fluid Mechanics; Parabolic: Stanford, CA, USA, 1975. [Google Scholar]
- Leal, L.G. Laminar Flow and Convective Transport Processes: Scaling Principles and Asymptotic Analysis; Butterworth-Heinemann: Stoneham, MA, USA, 1992. [Google Scholar]
- Khair, A.S. Diffusiophoresis of colloidal particles in neutral solute gradients at finite Péclet number. J. Fluid Mech. 2013, 731, 64–94. [Google Scholar] [CrossRef]
- Subramanian, R.S. Slow migration of a gas bubble in a thermal gradient. AIChE J. 1981, 27, 646–654. [Google Scholar] [CrossRef]
- Subramanian, R.S. Thermocapillary migration of bubbles and droplets. In Advances in Space Research; Malnejac, Y., Ed.; Pergamon Press: Oxford, UK, 1983; Volume 3, pp. 145–153. [Google Scholar]
- Anderson, J.L. Movement of a semipermeable vesicle through an osmotic gradient. Phys. Fluids 1983, 26, 2871–2879. [Google Scholar] [CrossRef]
- Chang, Y.C.; Keh, H.J. Thermophoresis at small but finite numbers. Aerosol Sci. Technol. 2018, 52, 1028–1036. [Google Scholar] [CrossRef]
- Proudman, I.; Pearson, J.R.A. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 1957, 2, 237–262. [Google Scholar] [CrossRef]
- Acrivos, A.; Taylor, T.D. Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 1962, 5, 387–394. [Google Scholar] [CrossRef]
- Chang, Y.C.; Keh, H.J. Diffusiophoresis of colloidal spheres at small Péclet numbers. Trends Chem. Eng. 2019, in press. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).