Calibration Routine for Quantitative Three-Dimensional Flow Field Measurements in Drying Polymer Solutions Subject to Marangoni Convection
Abstract
1. Introduction
1.1. Marangoni Convection in Thin Films
1.2. Mitigating the Coffee Ring Effect in Sessile Droplets by Means of Marangoni Convection
1.3. Measurement Techniques for Surface-Tension Induced Flows
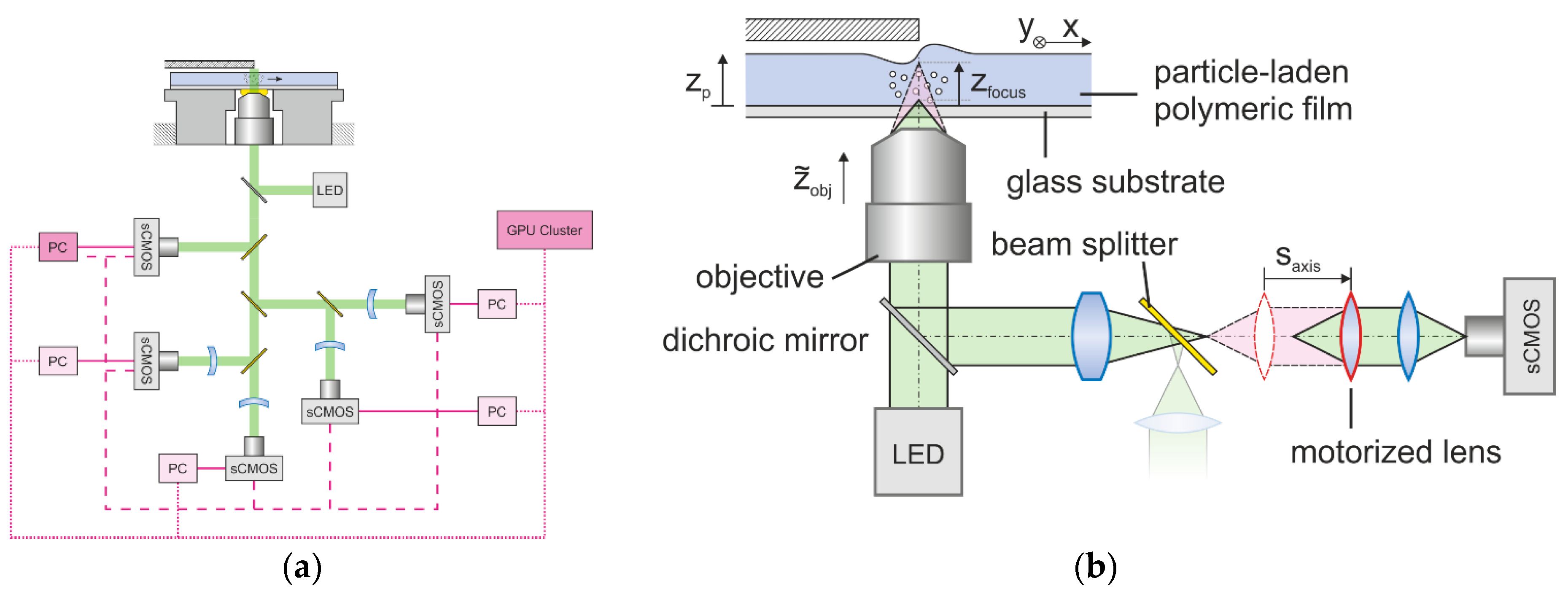
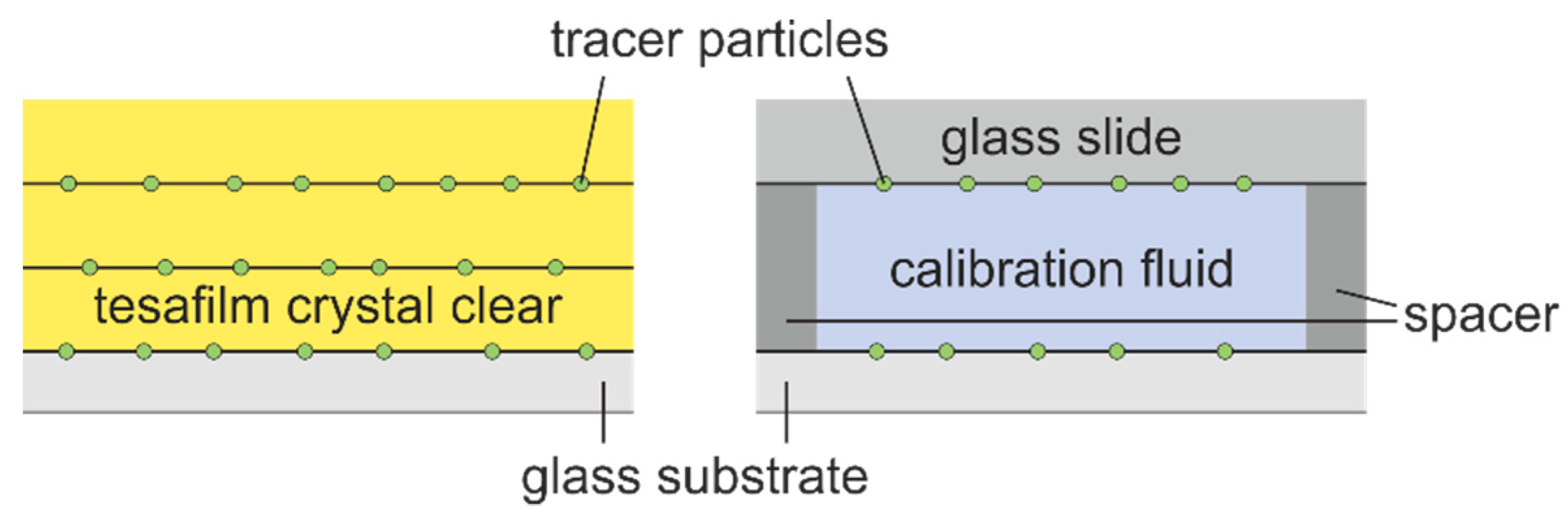
2. Materials and Methods
3. Results
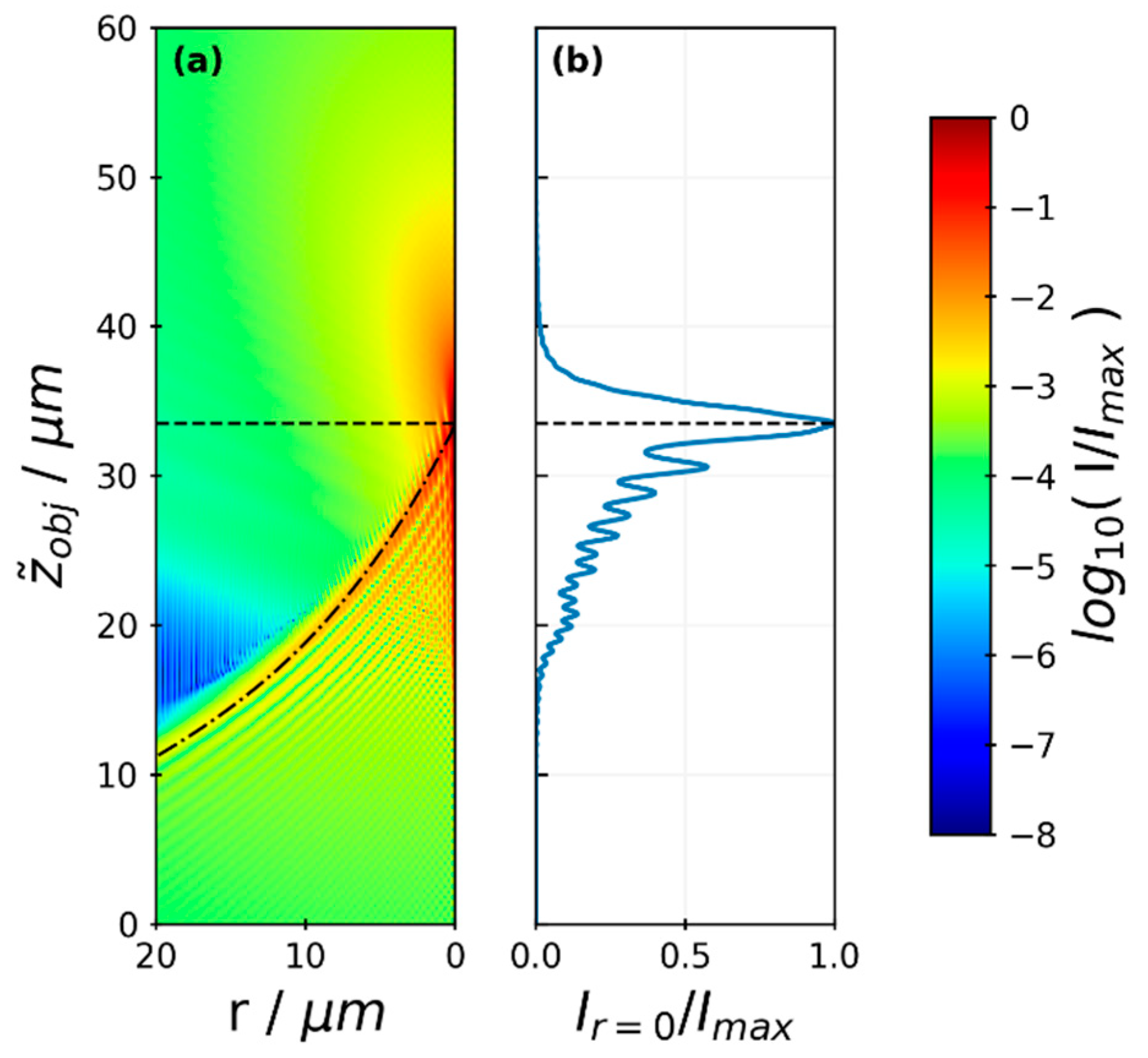
3.1. Focal Displacement Calibration
3.2. Experimental Calibration of Motorized Lens System
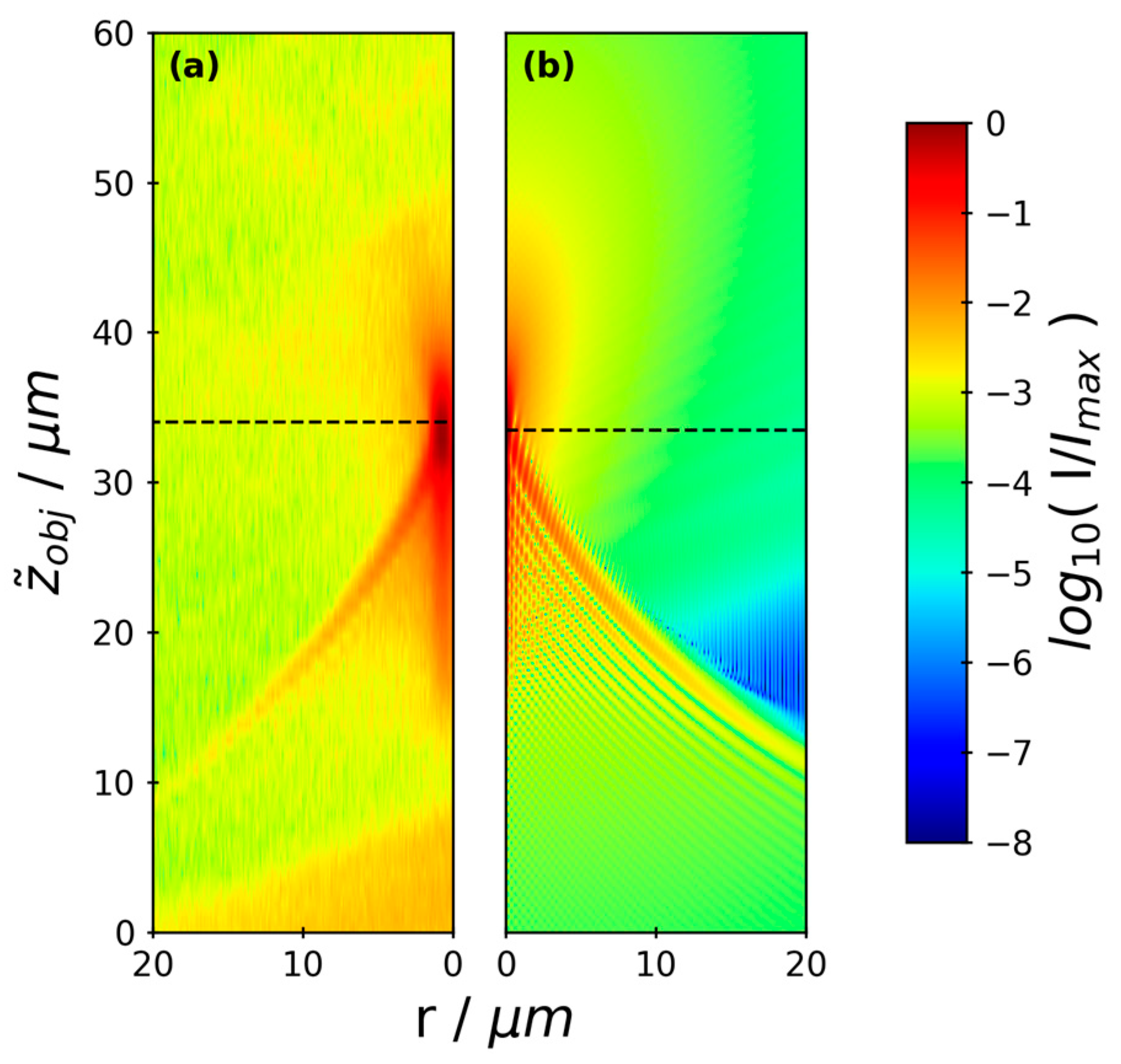
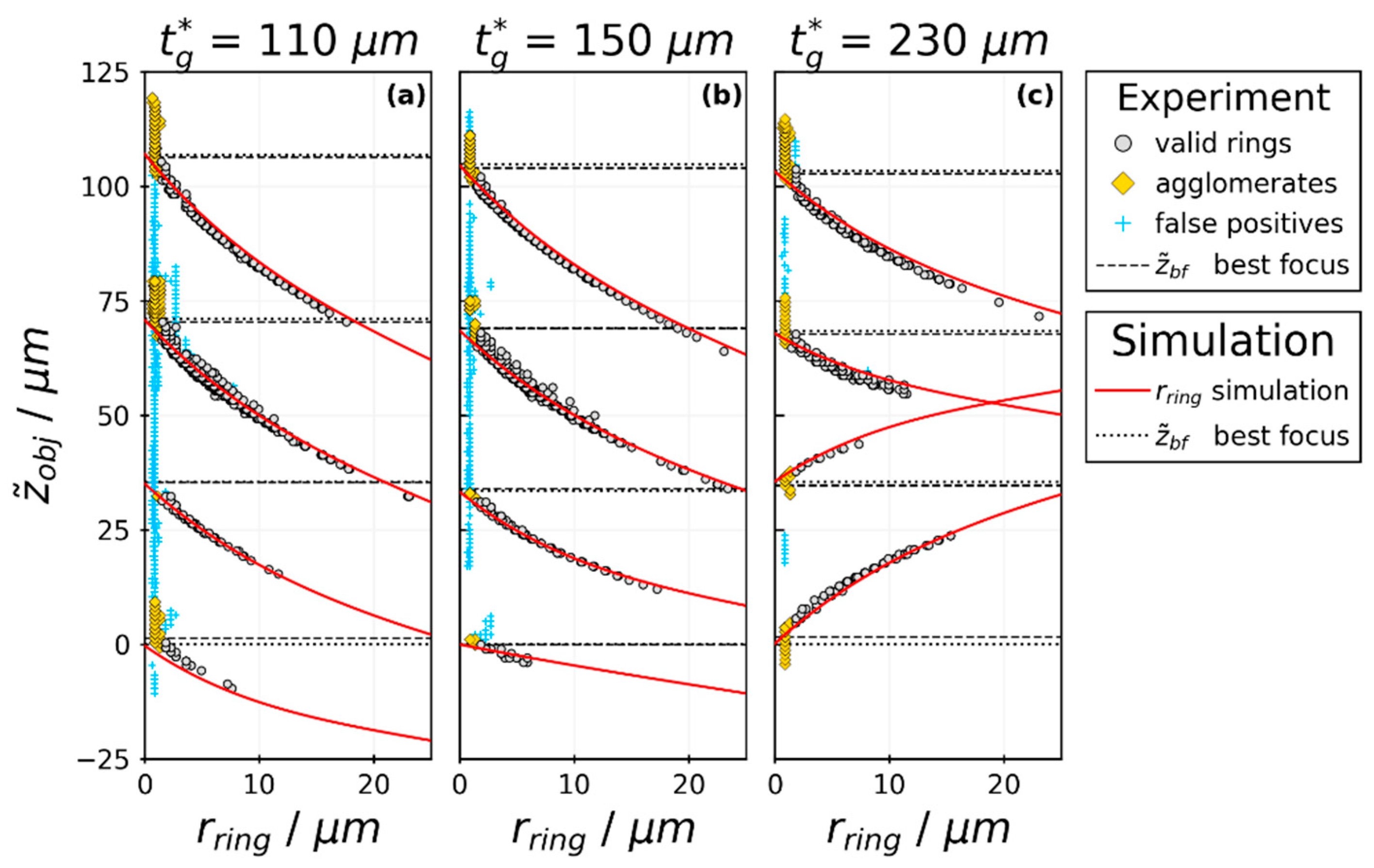
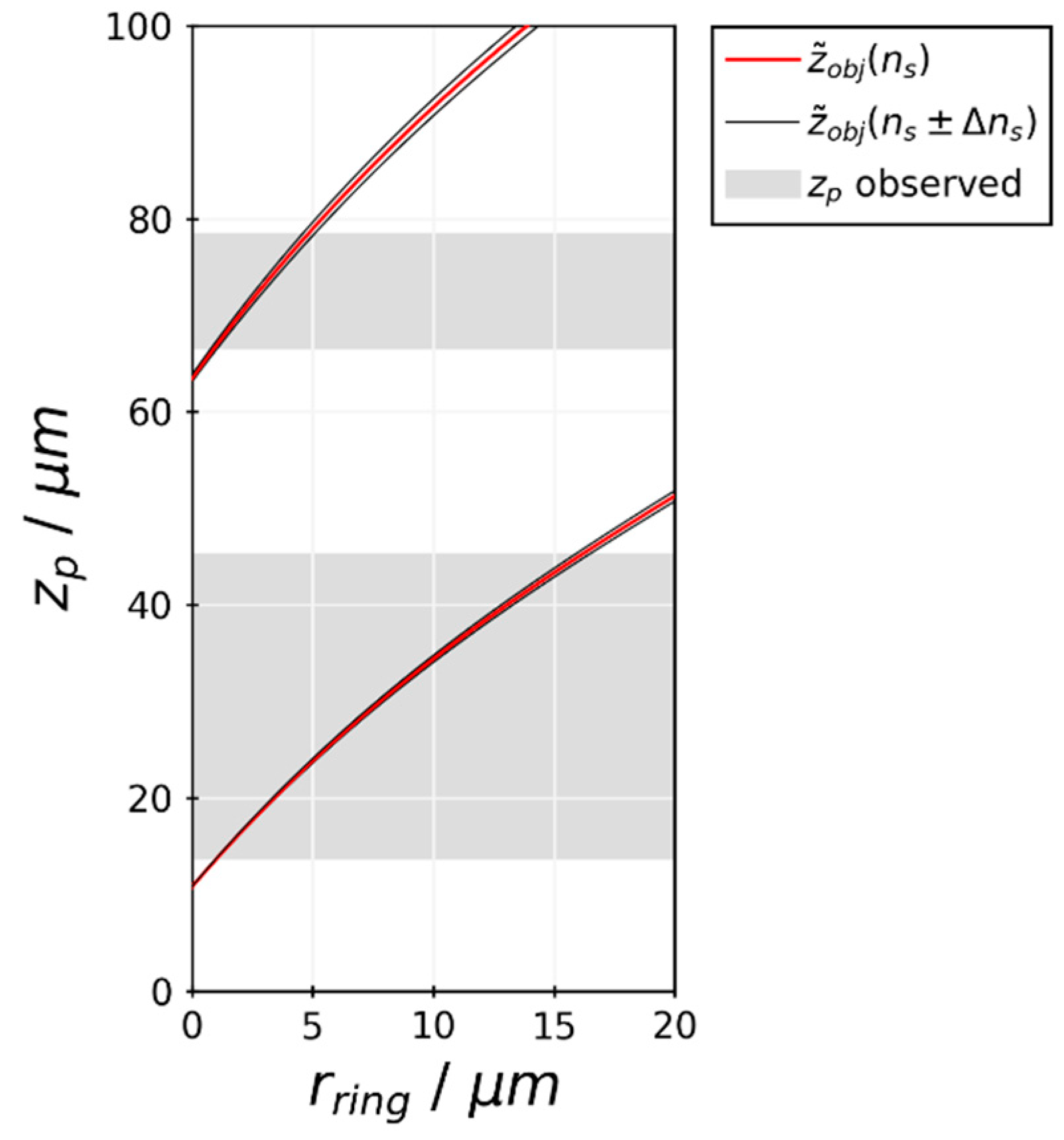
3.3. Diffraction-Ring Size Calibration for Off-Focus Particle Positions
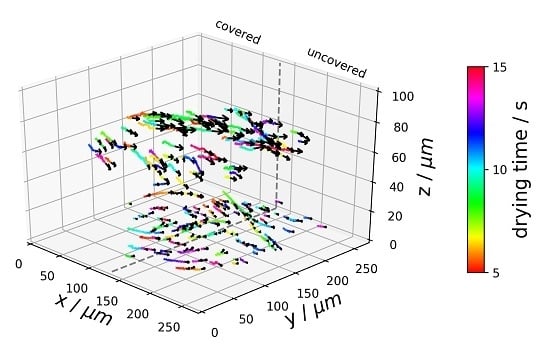
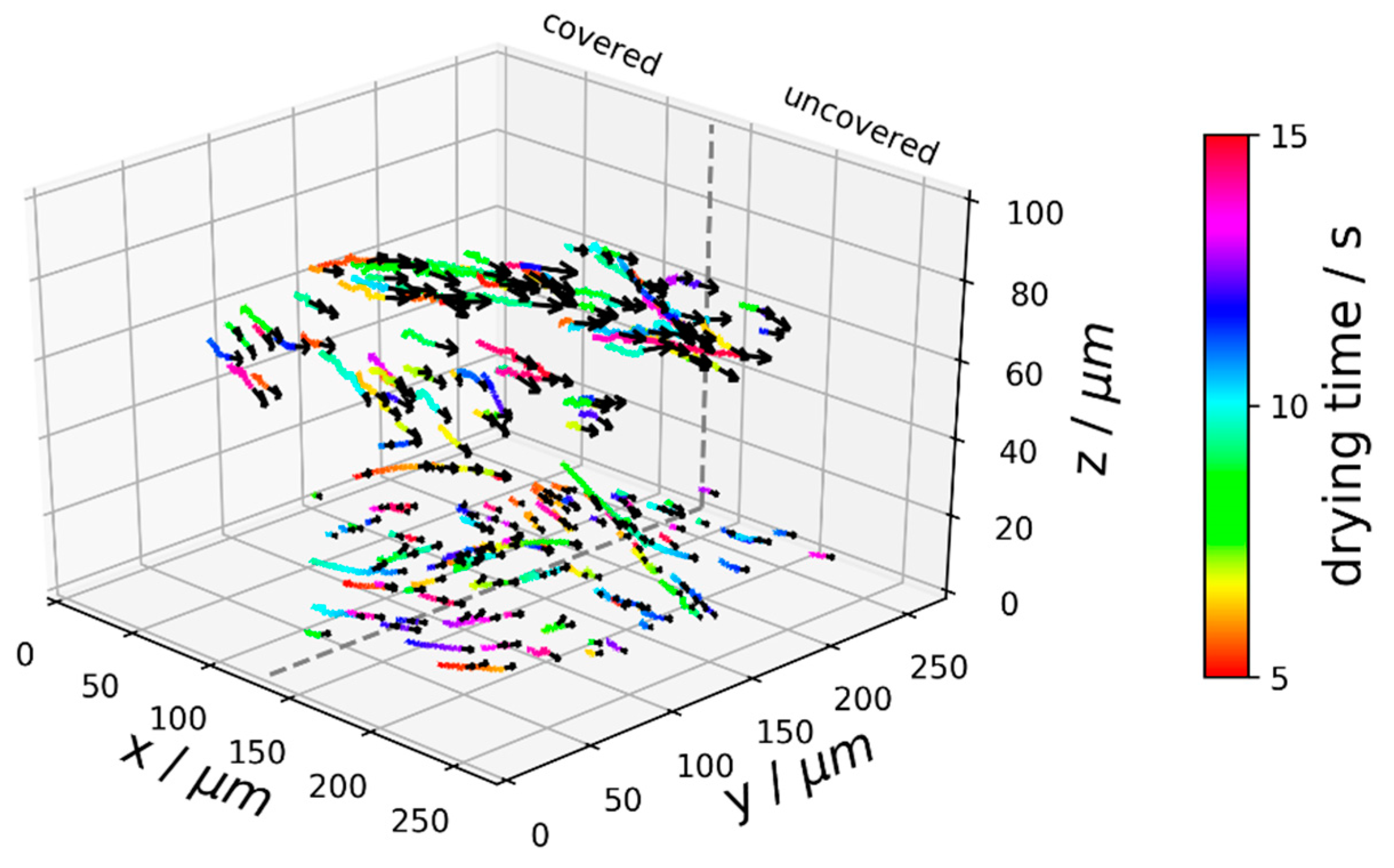
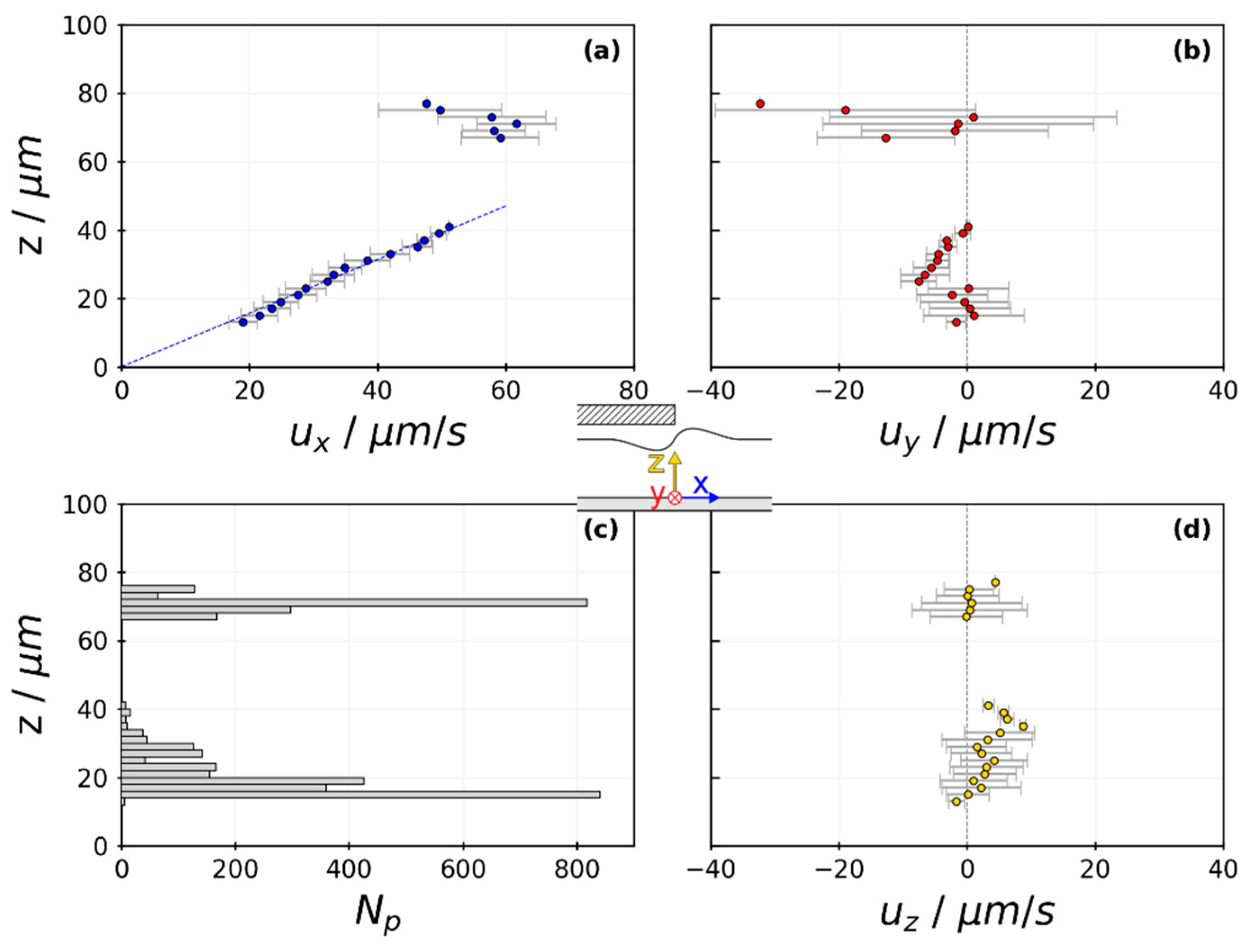
3.4. Flow Field of Partially Covered Drying Experiment
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Quantity | Value | Description |
|---|---|---|
| Tracer particle density | ||
| Coating solution density | ||
| Coating solution dynamic viscosity 1 |
A.1. Sedimentation
A.2. Inertia
A.3. Brownian Motion
References
- Smith, P.J.; Stringer, J. Applications in Inkjet Printing. In Fundamentals of Inkjet Printing: The Science of Inkjet and Droplets; Hoath, S.D., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 397–418. ISBN 978-3-527-33785-9. [Google Scholar]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Capillary flow as the cause of ring stains from dried liquid drops. Nature 1997, 389, 827–829. [Google Scholar] [CrossRef]
- Cavadini, P.; Krenn, J.; Scharfer, P.; Schabel, W. Investigation of surface deformation during drying of thin polymer films due to Marangoni convection. Chem. Eng. Process. 2013, 64, 24–30. [Google Scholar] [CrossRef]
- Cavadini, P.; Erz, J.; Sachsenheimer, D.; Kowalczyk, A.; Willenbacher, N.; Scharfer, P.; Schabel, W. Investigation of the flow field in thin polymer films due to inhomogeneous drying. J. Coat. Technol. Res. 2015, 12, 921–926. [Google Scholar] [CrossRef]
- Block, M.J. Surface Tension as the Cause of Bénard Cells and Surface Deformation in a Liquid Film. Nature 1956, 178, 650–651. [Google Scholar] [CrossRef]
- Pearson, J.R.A. On convection cells induced by surface tension. J. Fluid Mech. 1958, 4, 489. [Google Scholar] [CrossRef]
- Vanhook, S.J.; Schatz, M.F.; Swift, J.B.; McCormick, W.D.; Swinney, H.L. Long-wavelength surface-tension-driven Bénard convection: Experiment and theory. J. Fluid Mech. 1997, 345, 45–78. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Craster, R.V.; Matar, O.K. Marangoni instability of a thin liquid film resting on a locally heated horizontal wall. Phys. Rev. E 2003, 67, 56315. [Google Scholar] [CrossRef] [PubMed]
- Bestehorn, M.; Pototsky, A.; Thiele, U. 3D Large scale Marangoni convection in liquid films. Eur. Phys. J. E Soft Matter 2003, 33, 457–467. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T. Marangoni convection, evaporation and interface deformation in liquid films on heated substrates with non-uniform thermal conductivity. Int. J. Heat Mass Transf. 2010, 53, 390–402. [Google Scholar] [CrossRef]
- Gambaryan-Roisman, T. Modulation of Marangoni convection in liquid films: Reinhard Miller, Honorary Issue. Adv. Colloid Interface Sci. 2015, 222, 319–331. [Google Scholar] [CrossRef] [PubMed]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- Craster, R.V.; Matar, O.K. Dynamics and stability of thin liquid films. Rev. Mod. Phys. 2009, 81, 1131–1198. [Google Scholar] [CrossRef]
- Chai, A.-T.; Zhang, N. Experimental study of Marangoni-Benard convection in a liquid layer induced by evaporation. Exp. Heat Transf. 1998, 11, 187–205. [Google Scholar] [CrossRef]
- Merkt, D.; Bestehorn, M. Bénard–Marangoni convection in a strongly evaporating fluid. Physica D 2003, 185, 196–208. [Google Scholar] [CrossRef]
- Sultan, E.; Boudaoud, A.; Amar, M.B. Evaporation of a thin film: Diffusion of the vapour and Marangoni instabilities. J. Fluid Mech. 2005, 543, 183. [Google Scholar] [CrossRef]
- Doumenc, F.; Boeck, T.; Guerrier, B.; Rossi, M. Transient Rayleigh–Bénard–Marangoni convection due to evaporation: A linear non-normal stability analysis. J. Fluid Mech. 2010, 648, 521. [Google Scholar] [CrossRef]
- Chauvet, F.; Dehaeck, S.; Colinet, P. Threshold of Bénard-Marangoni instability in drying liquid films. Europhys. Lett. 2012, 99, 34001. [Google Scholar] [CrossRef]
- Kanatani, K. Effects of convection and diffusion of the vapour in evaporating liquid films. J. Fluid Mech. 2013, 732, 128–149. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Tamir, S.; Cohen, R.; Nunberg, M.; Gaisin, V.-Z.; Gorelik, M.; Gendelman, O.V. Mesoscopic and submicroscopic patterning in thin polymer films: Impact of the solvent. Mater. Lett. 2005, 59, 2461–2464. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Gendelman, O. Formation of honeycomb patterns in evaporated polymer solutions: Influence of the molecular weight. Mater. Lett. 2005, 59, 3553–3557. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Musin, A.; Stanevsky, O.; Bormashenko, Y.; Whyman, G.; Gendelman, O.; Barkay, Z. Self-assembly in evaporated polymer solutions: Influence of the solution concentration. J. Colloid Interface Sci. 2006, 297, 534–540. [Google Scholar] [CrossRef] [PubMed]
- Toussaint, G.; Bodiguel, H.; Doumenc, F.; Guerrier, B.; Allain, C. Experimental characterization of buoyancy- and surface tension-driven convection during the drying of a polymer solution. Int. J. Heat Mass Transf. 2008, 51, 4228–4237. [Google Scholar] [CrossRef]
- Bormashenko, E.; Pogreb, R.; Stanevsky, O.; Bormashenko, Y.; Stein, T.; Gendelman, O.; Gengelman, O. Mesoscopic patterning in evaporated polymer solutions: New experimental data and physical mechanisms. Langmuir 2005, 21, 9604–9609. [Google Scholar] [CrossRef] [PubMed]
- Kumacheva, E.; Li, L.; Winnik, M.A.; Shinozaki, D.M.; Cheng, P.C. Direct Imaging of Surface and Bulk Structures in Solvent Cast Polymer Blend Films. Langmuir 1997, 13, 2483–2489. [Google Scholar] [CrossRef]
- Bormashenko, E.; Balter, S.; Pogreb, R.; Bormashenko, Y.; Gendelman, O.; Aurbach, D. On the mechanism of patterning in rapidly evaporated polymer solutions: Is temperature-gradient-driven Marangoni instability responsible for the large-scale patterning? J. Colloid Interface Sci. 2010, 343, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-M.; Liu, G.-H.; Fang, Y.-L.; Li, W.-K. Marangoni effect in nonequilibrium multiphase system of material processing. Rev. Chem. Eng. 2016, 32, 2. [Google Scholar] [CrossRef]
- Larson, R.G. Transport and deposition patterns in drying sessile droplets. AIChE J. 2014, 60, 1538–1571. [Google Scholar] [CrossRef]
- Anyfantakis, M.; Baigl, D. Manipulating the Coffee-Ring Effect: Interactions at Work. ChemPhysChem 2015, 16, 2726–2734. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Bao, B.; He, M.; Zhou, H.; Song, Y. Recent Advances in Controlling the Depositing Morphologies of Inkjet Droplets. ACS Appl. Mater. Interfaces 2015. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Larson, R.G. Marangoni effect reverses coffee-ring depositions. J. Phys. Chem. B 2006, 110, 7090–7094. [Google Scholar] [CrossRef] [PubMed]
- De Gans, B.-J.; Duineveld, P.C.; Schubert, U.S. Inkjet Printing of Polymers: State of the Art and Future Developments. Adv. Mater. 2004, 16, 203–213. [Google Scholar] [CrossRef]
- Poulard, C.; Damman, P. Control of spreading and drying of a polymer solution from Marangoni flows. Europhys. Lett. 2007, 80, 64001. [Google Scholar] [CrossRef]
- Kajiya, T.; Doi, M. Dynamics of Drying Process of Polymer Solution Droplets: Analysis of Polymer Transport and Control of Film Profiles. Nihon Reoroji Gakk. 2011, 39, 17–28. [Google Scholar] [CrossRef]
- Trantum, J.R.; Baglia, M.L.; Eagleton, Z.E.; Mernaugh, R.L.; Haselton, F.R. Biosensor design based on Marangoni flow in an evaporating drop. Lab Chip 2014, 14, 315–324. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, S.; Chen, L.; Evans, J.R.G. Shape changes during the drying of droplets of suspensions. Langmuir 2008, 24, 3752–3758. [Google Scholar] [CrossRef] [PubMed]
- Majumder, M.; Rendall, C.S.; Eukel, J.A.; Wang, J.Y.L.; Behabtu, N.; Pint, C.L.; Liu, T.-Y.; Orbaek, A.W.; Mirri, F.; Nam, J.; et al. Overcoming the “coffee-stain” effect by compositional Marangoni-flow-assisted drop-drying. J. Phys. Chem. B 2012, 116, 6536–6542. [Google Scholar] [CrossRef] [PubMed]
- Babatunde, P.O.; Hong, W.J.; Nakaso, K.; Fukai, J. Effect of Solute- and Solvent-Derived Marangoni Flows on the Shape of Polymer Films Formed from Drying Droplets. AIChE J. 2013, 59, 699–702. [Google Scholar] [CrossRef]
- Jafari Kang, S.; Vandadi, V.; Felske, J.D.; Masoud, H. Alternative mechanism for coffee-ring deposition based on active role of free surface. Phys. Rev. E 2016, 94, 63104. [Google Scholar] [CrossRef] [PubMed]
- Kang, Q.; Zhang, J.F.; Hu, L.; Duan, L. Experimental study on Benard-Marangoni convection by PIV and TCL. Proc. SPIE 2003, 5058, 155. [Google Scholar] [CrossRef]
- Kang, K.H.; Lee, S.J.; Lee, C.M.; Kang, I.S. Quantitative visualization of flow inside an evaporating droplet using the ray tracing method. Meas. Sci. Technol. 2004, 15, 1104–1112. [Google Scholar] [CrossRef]
- Kaneda, M.; Hyakuta, K.; Takao, Y.; Ishizuka, H.; Fukai, J. Internal Flow in Polymer Solution Droplets Deposited on a Lyophobic Surface during a Receding Process. Langmuir 2008, 24, 9102–9109. [Google Scholar] [CrossRef] [PubMed]
- Bassou, N.; Rharbi, Y. Role of Bénard-Marangoni instabilities during solvent evaporation in polymer surface corrugations. Langmuir 2009, 25, 624–632. [Google Scholar] [CrossRef] [PubMed]
- Cavadini, P.; Weinhold, H.; Tönsmann, M.; Chilingaryan, S.; Kopmann, A.; Lewkowicz, A.; Miao, C.; Scharfer, P.; Schabel, W. Investigation of the flow structure in thin polymer films using 3D µPTV enhanced by GPU. Exp. Fluids 2018, 59, 370. [Google Scholar] [CrossRef]
- Lindken, R.; Rossi, M.; Grosse, S.; Westerweel, J. Micro-Particle Image Velocimetry (microPIV): Recent developments, applications, and guidelines. Lab Chip 2009, 9, 2551–2567. [Google Scholar] [CrossRef] [PubMed]
- Wereley, S.T.; Meinhart, C.D. Recent Advances in Micro-Particle Image Velocimetry. Annu. Rev. Fluid Mech. 2010, 42, 557–576. [Google Scholar] [CrossRef]
- Cierpka, C.; Kähler, C.J. Particle imaging techniques for volumetric three-component (3D3C) velocity measurements in microfluidics. J. Vis. 2012, 15, 1–31. [Google Scholar] [CrossRef]
- Speidel, M.; Jonáš, A.; Florin, E.-L. Three-dimensional tracking of fluorescent nanoparticles with subnanometer precision by use of off-focus imaging. Opt. Lett. 2003, 28, 69. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Roberts, J.W.; Buckley, M. Three-dimensional fluorescent particle tracking at micron-scale using a single camera. Exp. Fluids 2005, 38, 461–465. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 5th ed.; Pearson: Boston, MA, USA; Columbus, OH, USA; Indianapolis, IN, USA, 2017; ISBN 0-133-97722-6. [Google Scholar]
- Gross, H. Handbook of Optical Systems. In Fundamentals of Technical Optics, 1st ed., 2nd repr.; Wiley-VCH: Weinheim, Germany, 2011; Volume 1, ISBN 3-527-40377-9. [Google Scholar]
- Gibson, S.F.; Lanni, F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. J. Opt. Soc. Am. A 1992, 9, 154. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Xue, F.; Blu, T. Fast and accurate three-dimensional point spread function computation for fluorescence microscopy. J. Opt. Soc. Am. A 2017, 34, 1029–1034. [Google Scholar] [CrossRef] [PubMed]
- Hell, S.; Reiner, G.; Cremer, C.; Stelzer, E.H.K. Aberrations in confocal fluorescence microscopy induced by mismatches in refractive index. J. Microsc. 1993, 169, 391–405. [Google Scholar] [CrossRef]
- Afik, E. Robust and highly performant ring detection algorithm for 3d particle tracking using 2d microscope imaging. Sci. Rep. 2015, 5, 13584. [Google Scholar] [CrossRef] [PubMed]
- Ciddor, P.E. Refractive index of air: New equations for the visible and near infrared. Appl. Opt. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811. [Google Scholar] [CrossRef] [PubMed]
- Schabel, W. Trocknung von Polymerfilmen. Messung von Konzentrationsprofilen mit der Inversen-Mikro-Raman-Spektroskopie. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, Shaker, Aachen, Germany, 2004. [Google Scholar]
- Tasic, A.Z.; Djordjevic, B.D.; Grozdanic, D.K.; Radojkovic, N. Use of mixing rules in predicting refractive indexes and specific refractivities for some binary liquid mixtures. J. Chem. Eng. Data 1992, 37, 310–313. [Google Scholar] [CrossRef]
- Siebel, D.K. Zur Mehrkomponentendiffusion in Polymer-Lösemittel-Systemen. Untersuchungen im Kontext der Polymerfilmtrocknung mittels inverser Mikro-Raman-Spektroskopie. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, Verlag Dr. Hut., München, Germany, 2017. [Google Scholar]
- Erz, J. In-situ Visualisierung von Oberflächendeformationen aufgrund von Marangoni-Konvektion während der Filmtrocknung. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, KIT Scientific Publ., Karlsruhe, Germany, 2014. [Google Scholar]
- VDI e.V. (Ed.) VDI-Wärmeatlas, 11th ed.; Springer Vieweg: Berlin, Germany, 2013; ISBN 978-3-642-19980-6. [Google Scholar]
- García-Mardones, M.; Cea, P.; López, M.C.; Lafuente, C. Refractive properties of binary mixtures containing pyridinium-based ionic liquids and alkanols. Thermochim. Acta 2013, 572, 39–44. [Google Scholar] [CrossRef]
- Afik, E.; Steinberg, V. On the role of initial velocities in pair dispersion in a microfluidic chaotic flow. Nat. Commun. 2017, 8, 468. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Park, J.S.; Kihm, K.D. Three-dimensional micro-PTV using deconvolution microscopy: Experiments in Fluids. Exp. Fluids 2006, 40, 491–499. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin/Heidelberg, Germany, 1998; ISBN 978-3-662-03639-6. [Google Scholar]
- Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Beebe, D.J.; Adrian, R.J. A particle image velocimetry system for microfluidics: Experiments in Fluids. Exp. Fluids 1998, 25, 316–319. [Google Scholar] [CrossRef]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997; ISBN 978-0935702422. [Google Scholar]
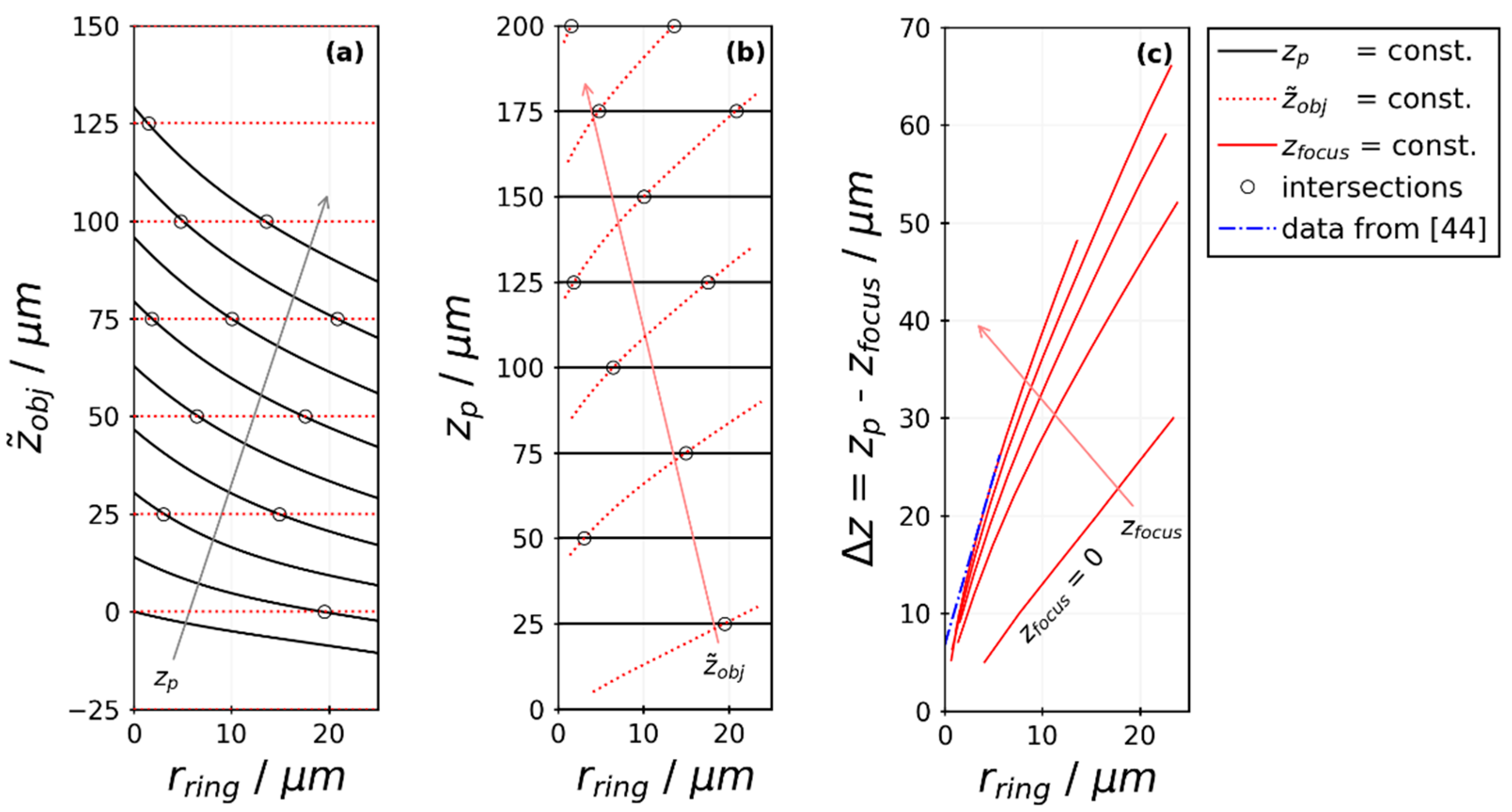
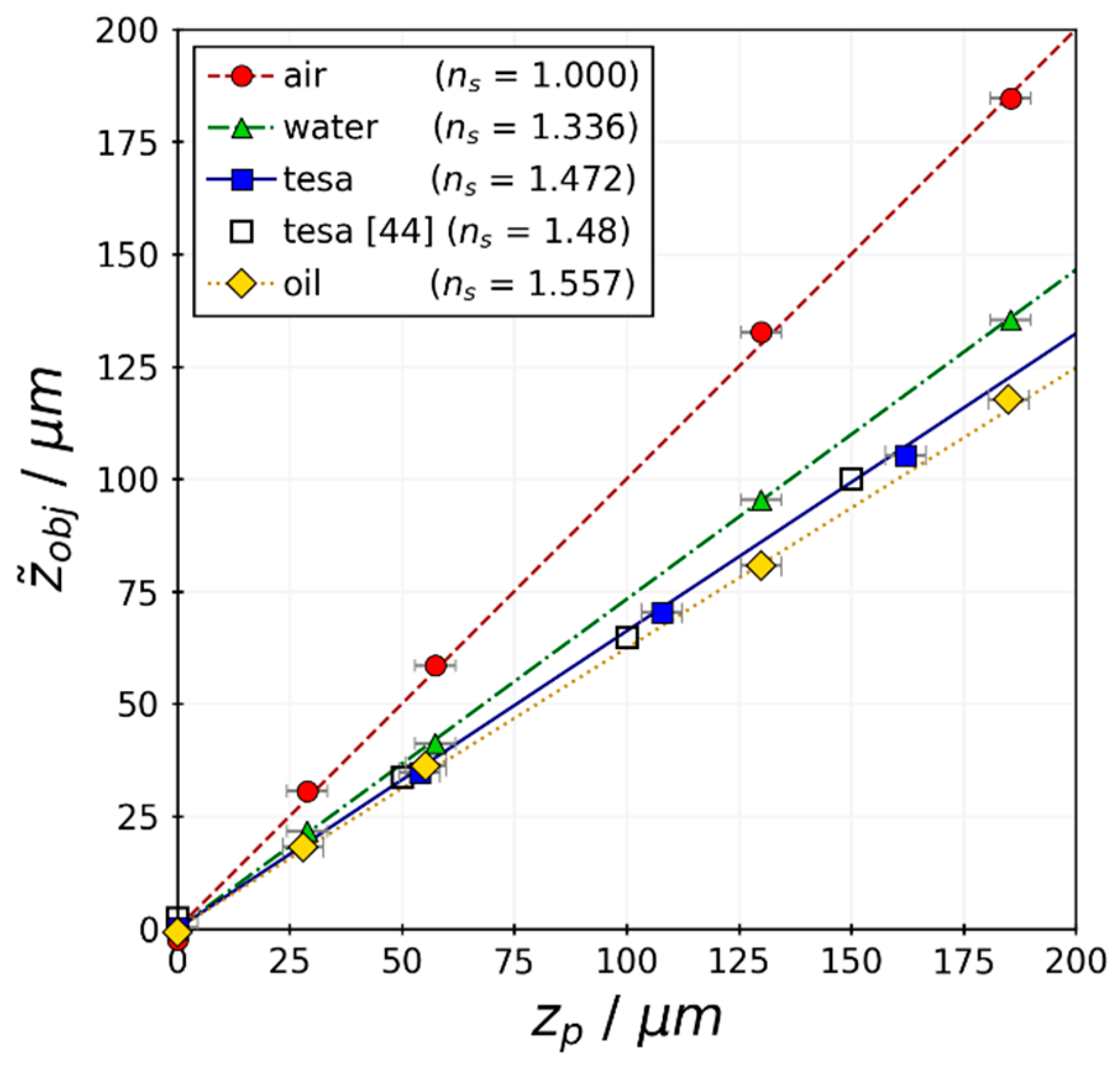
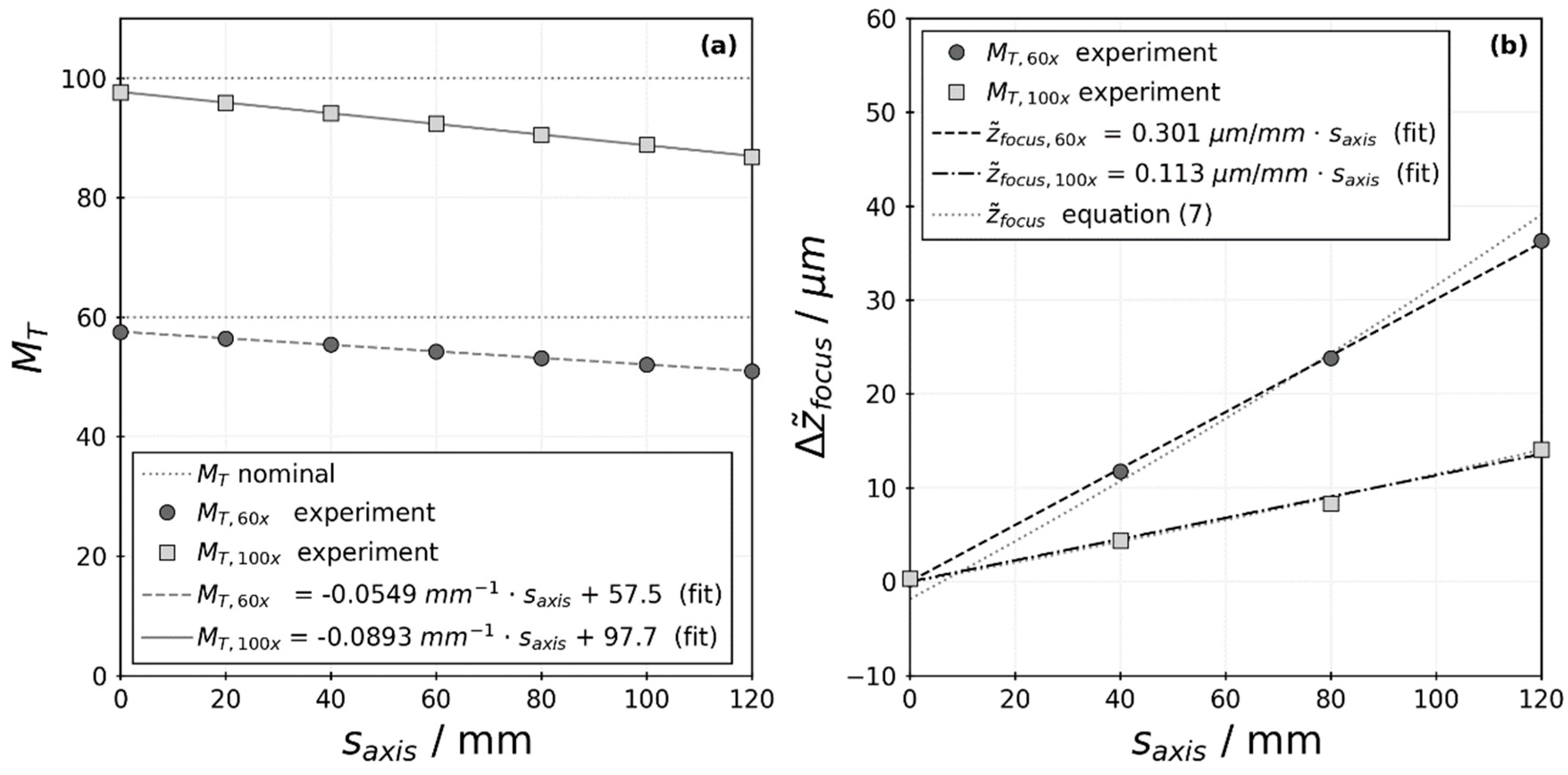
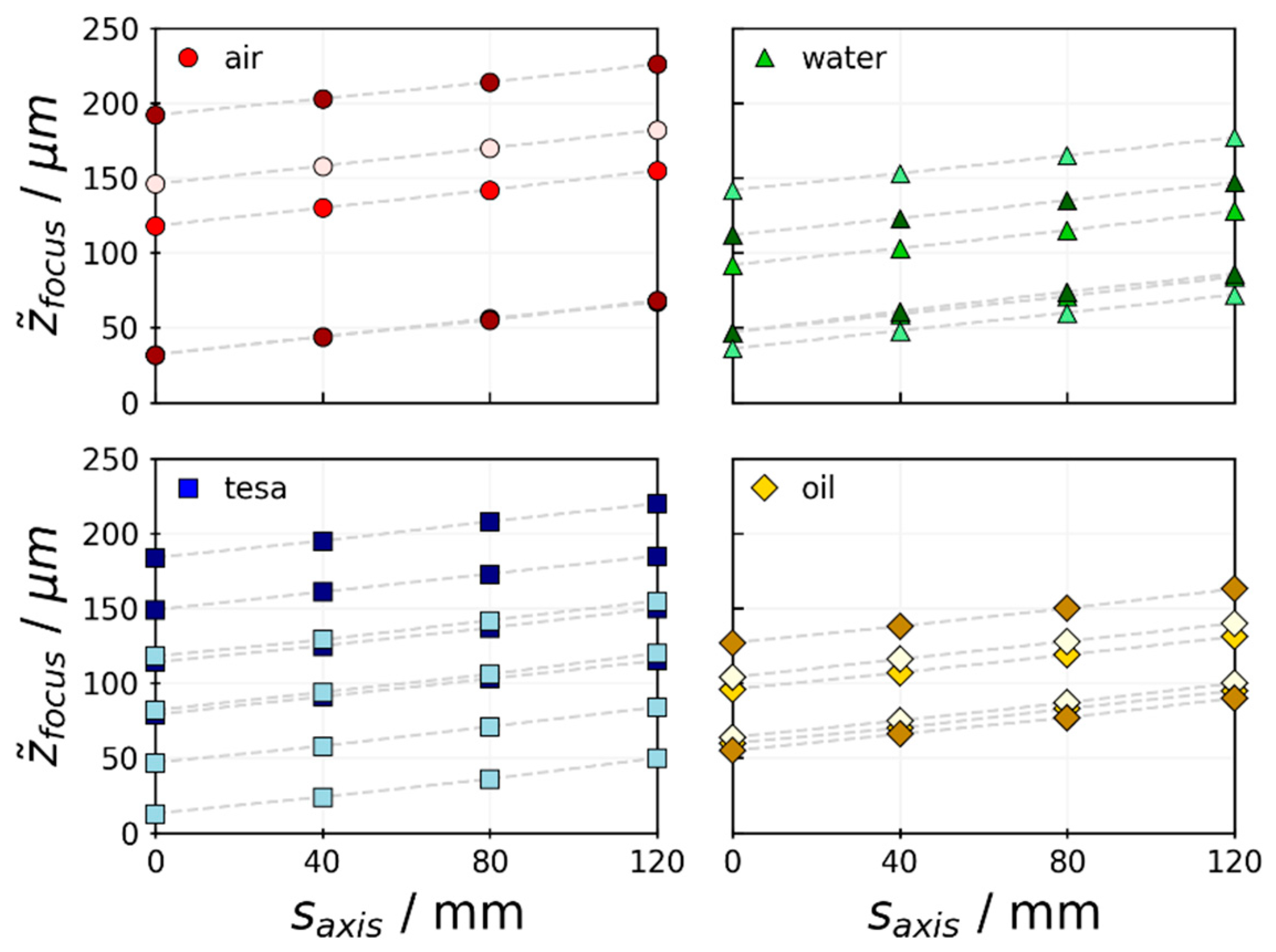
| Quantity | Typical Values | Description |
|---|---|---|
| Vertical position of point-source | ||
| Refractive index of sample | ||
| Numerical aperture of objective lens | ||
| Design cover-glass thickness | ||
| Design refractive index of cover-glass | ||
| Design immersion layer thickness/Working distance | ||
| Design refractive index of immersion medium (air/water/oil) | ||
| Actual cover-glass thickness | ||
| Actual refractive index of cover-glass | ||
| Actual refractive index of immersion medium |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tönsmann, M.; Kröhl, F.; Cavadini, P.; Scharfer, P.; Schabel, W. Calibration Routine for Quantitative Three-Dimensional Flow Field Measurements in Drying Polymer Solutions Subject to Marangoni Convection. Colloids Interfaces 2019, 3, 39. https://doi.org/10.3390/colloids3010039
Tönsmann M, Kröhl F, Cavadini P, Scharfer P, Schabel W. Calibration Routine for Quantitative Three-Dimensional Flow Field Measurements in Drying Polymer Solutions Subject to Marangoni Convection. Colloids and Interfaces. 2019; 3(1):39. https://doi.org/10.3390/colloids3010039
Chicago/Turabian StyleTönsmann, Max, Fabian Kröhl, Philipp Cavadini, Philip Scharfer, and Wilhelm Schabel. 2019. "Calibration Routine for Quantitative Three-Dimensional Flow Field Measurements in Drying Polymer Solutions Subject to Marangoni Convection" Colloids and Interfaces 3, no. 1: 39. https://doi.org/10.3390/colloids3010039
APA StyleTönsmann, M., Kröhl, F., Cavadini, P., Scharfer, P., & Schabel, W. (2019). Calibration Routine for Quantitative Three-Dimensional Flow Field Measurements in Drying Polymer Solutions Subject to Marangoni Convection. Colloids and Interfaces, 3(1), 39. https://doi.org/10.3390/colloids3010039