Kinetics of Spreading over Porous Substrates
Abstract
1. Introduction
2. Spreading over Thin Porous Substrates
2.1. Newtonian Liquids: Complete Wetting
2.2. Non-Newtonian Liquids: Complete and Partial Wetting Case
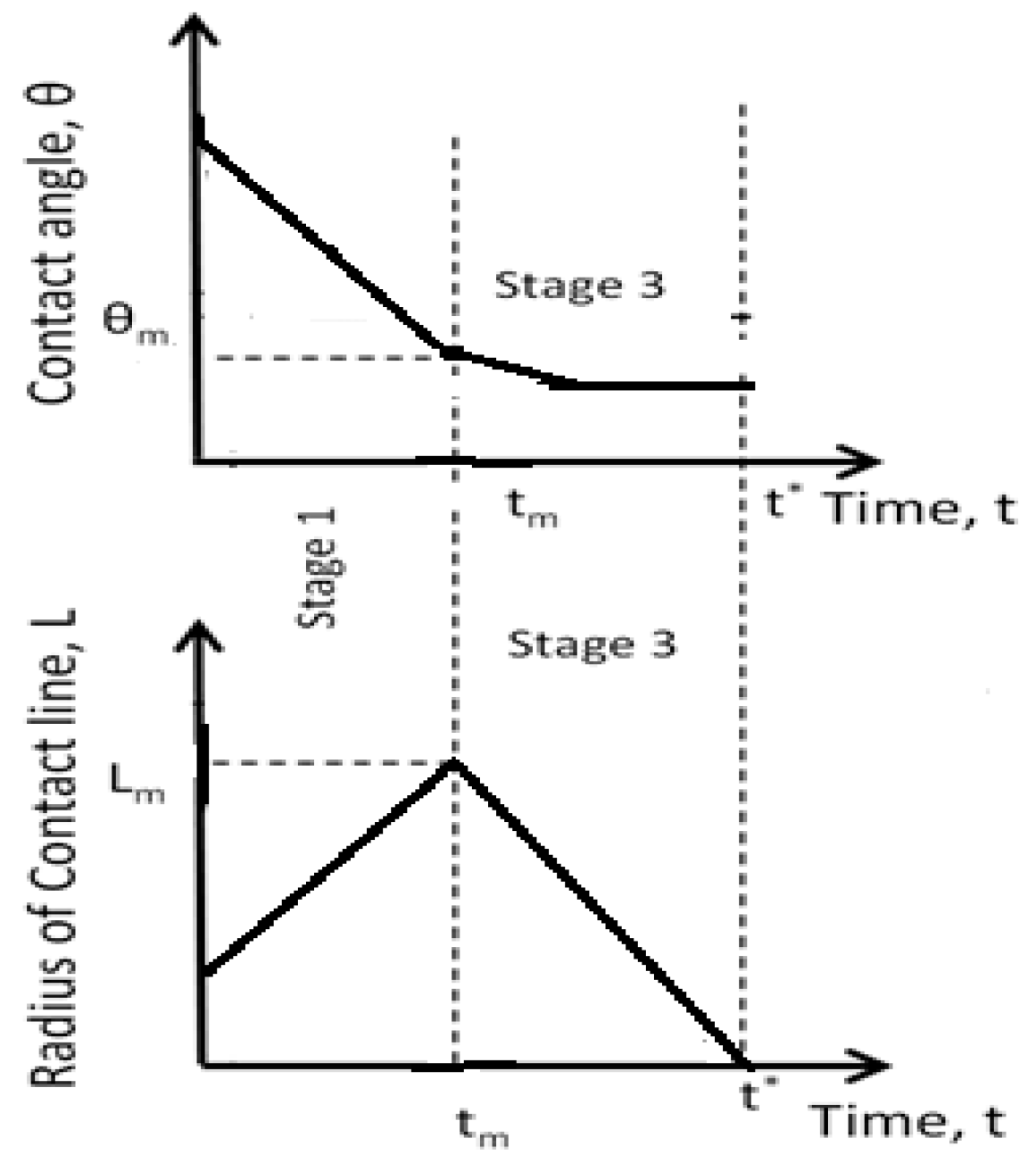
3. Spreading over Thick Porous Substrates
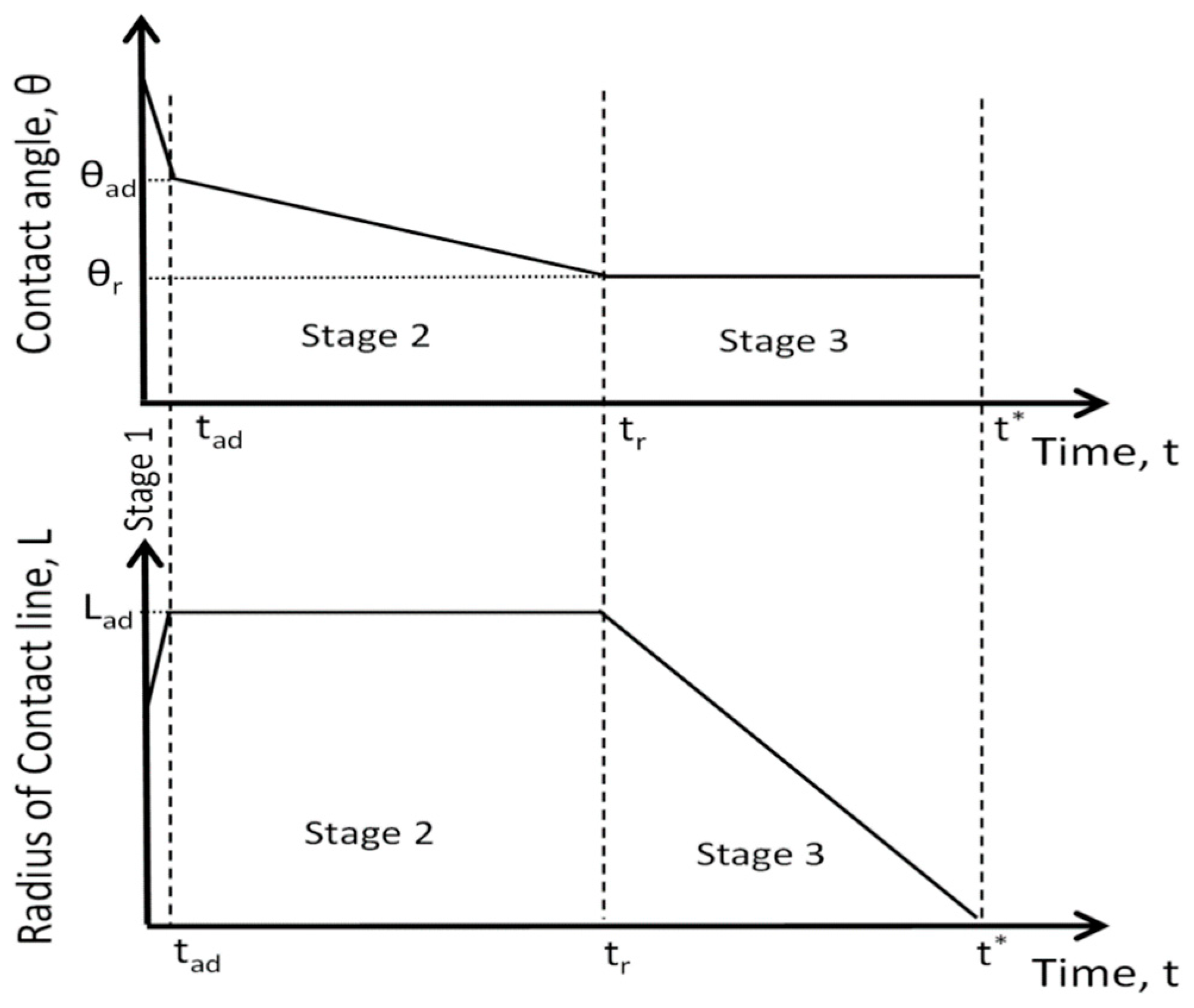
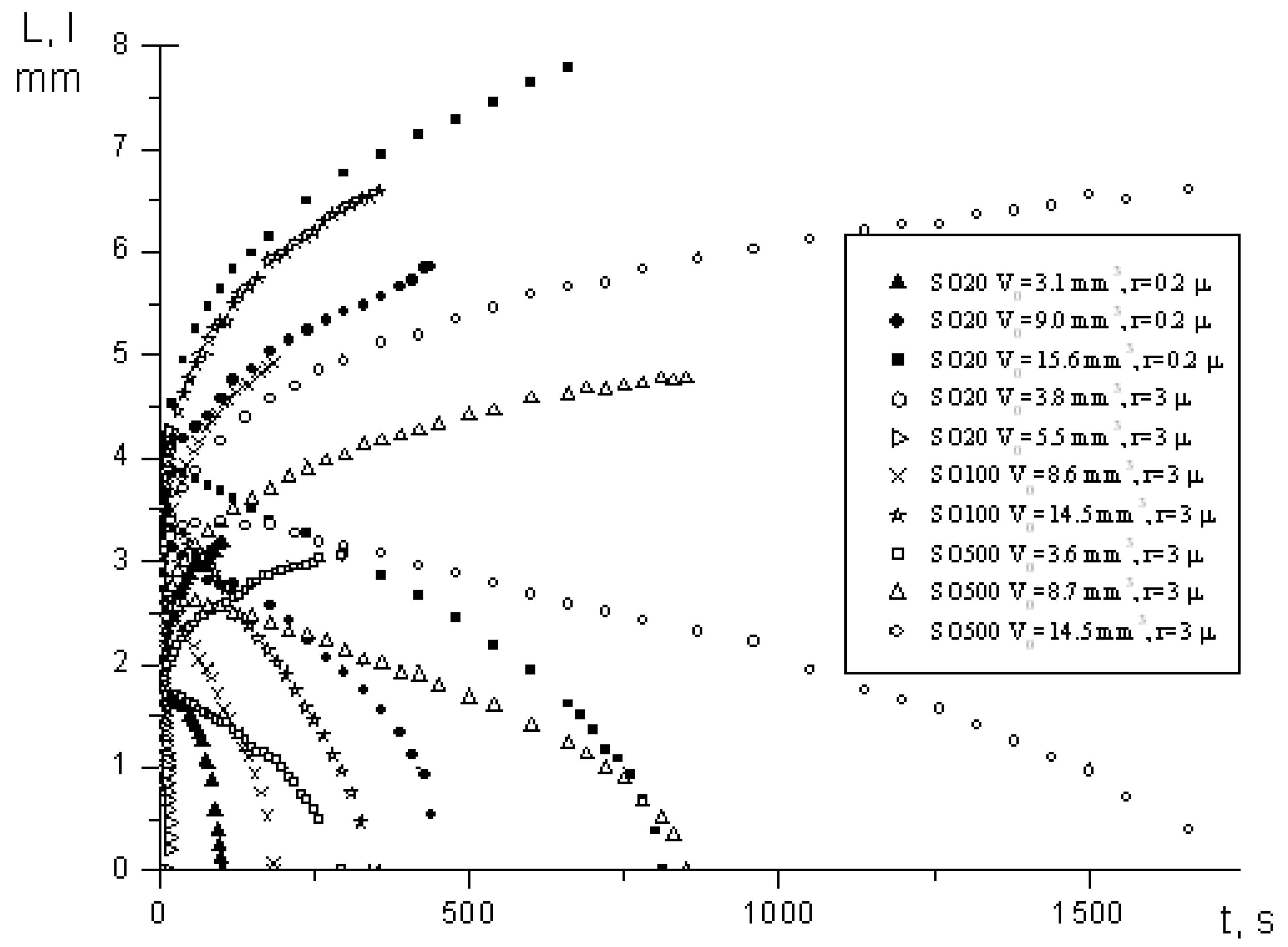
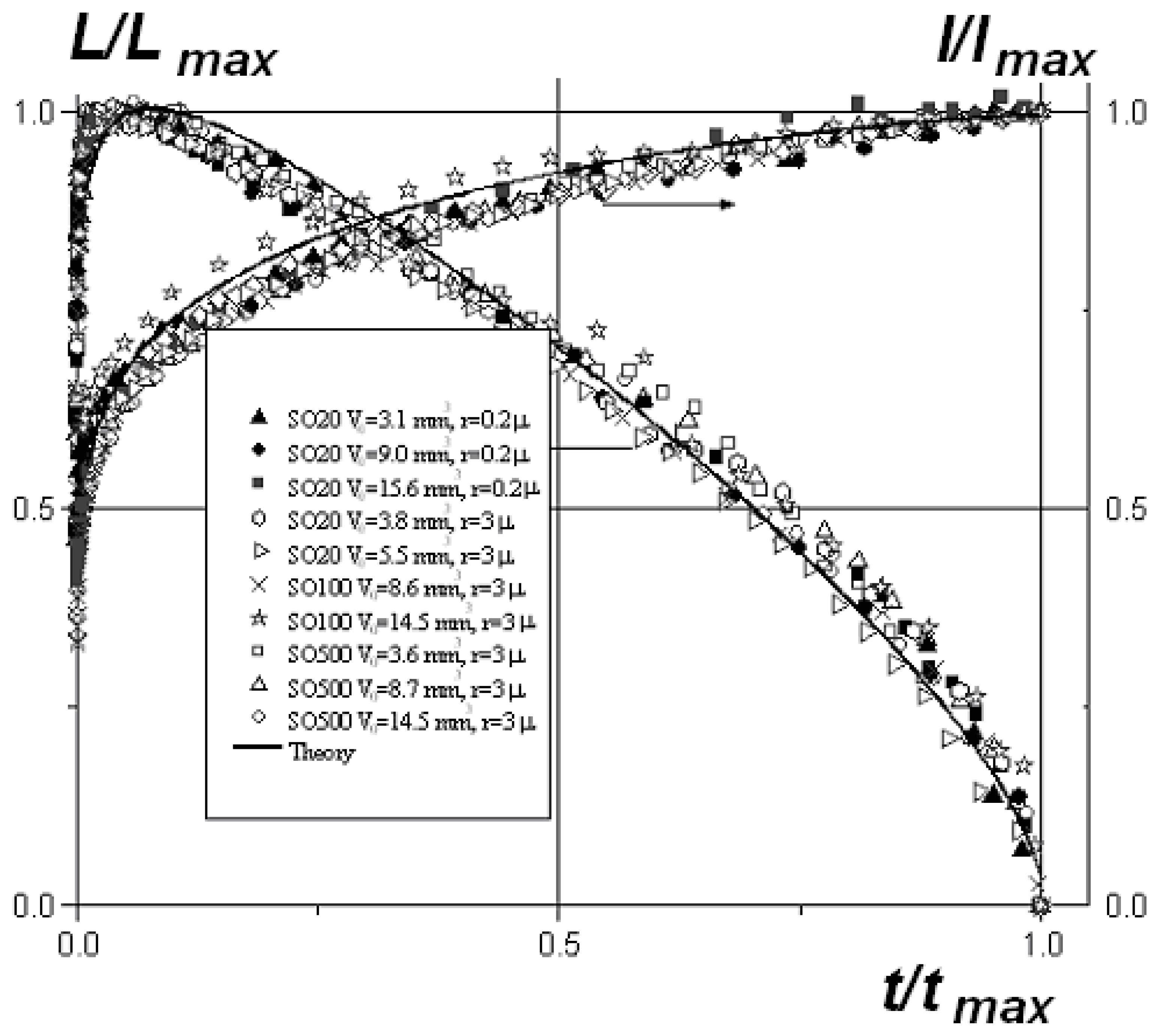
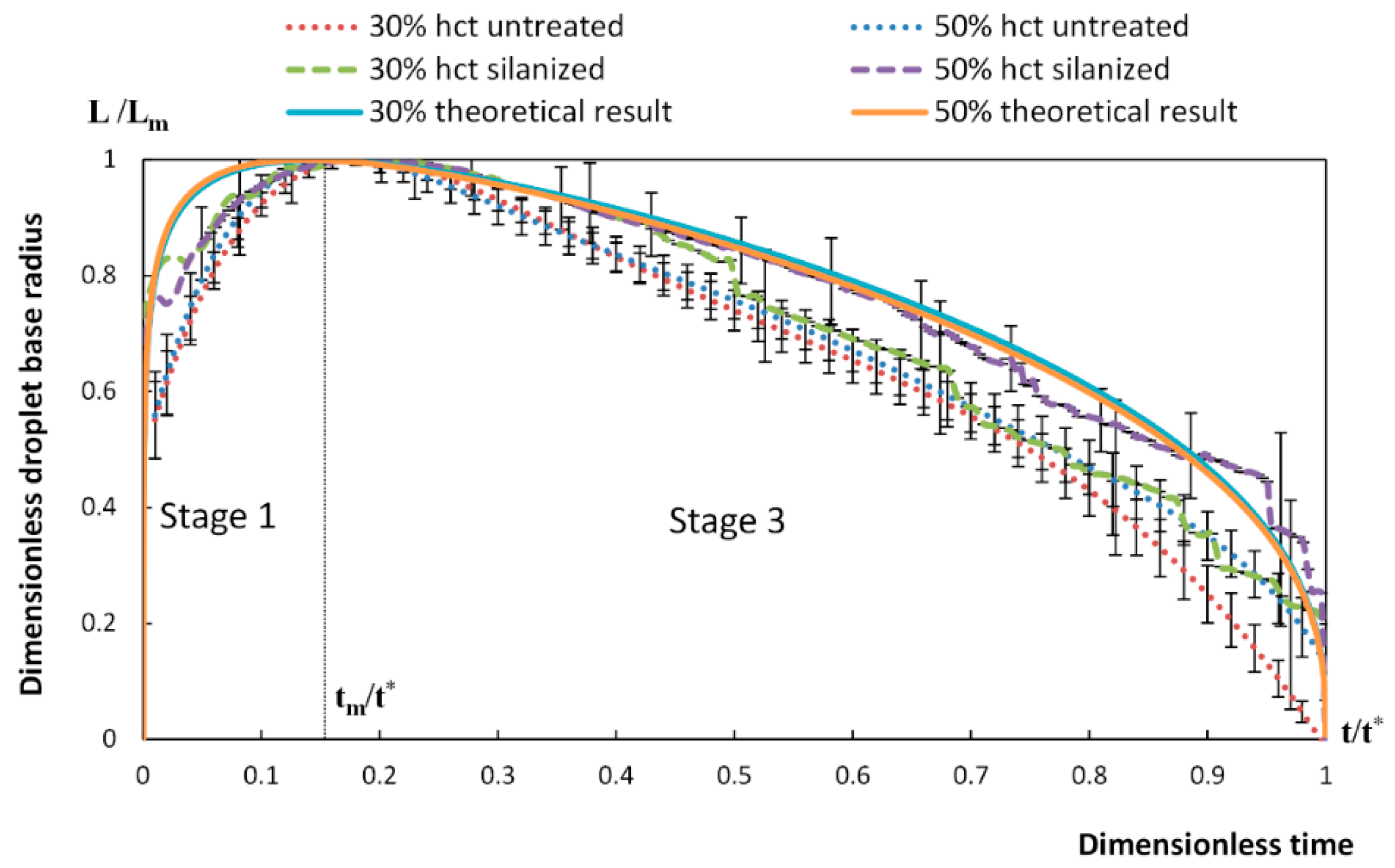
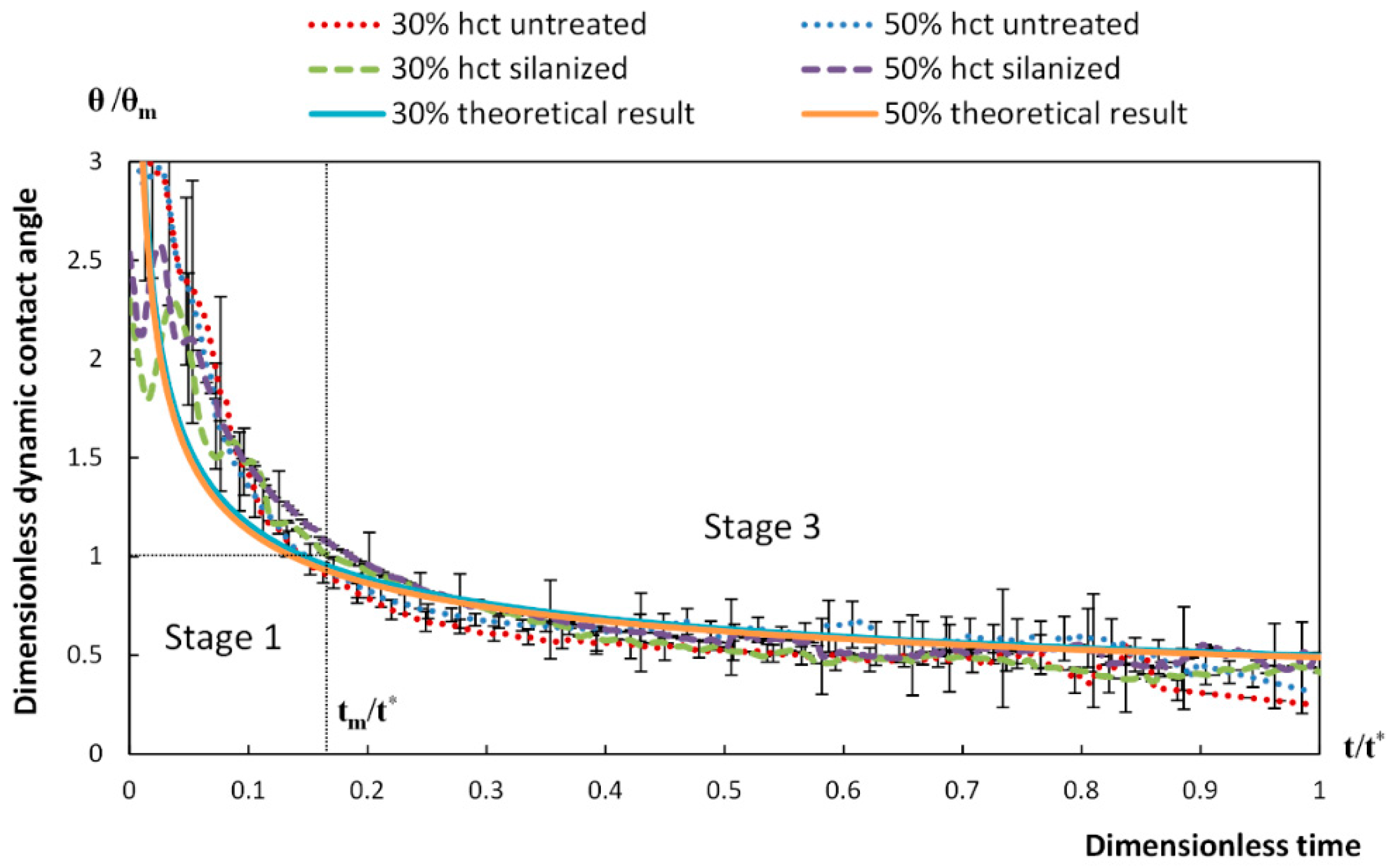
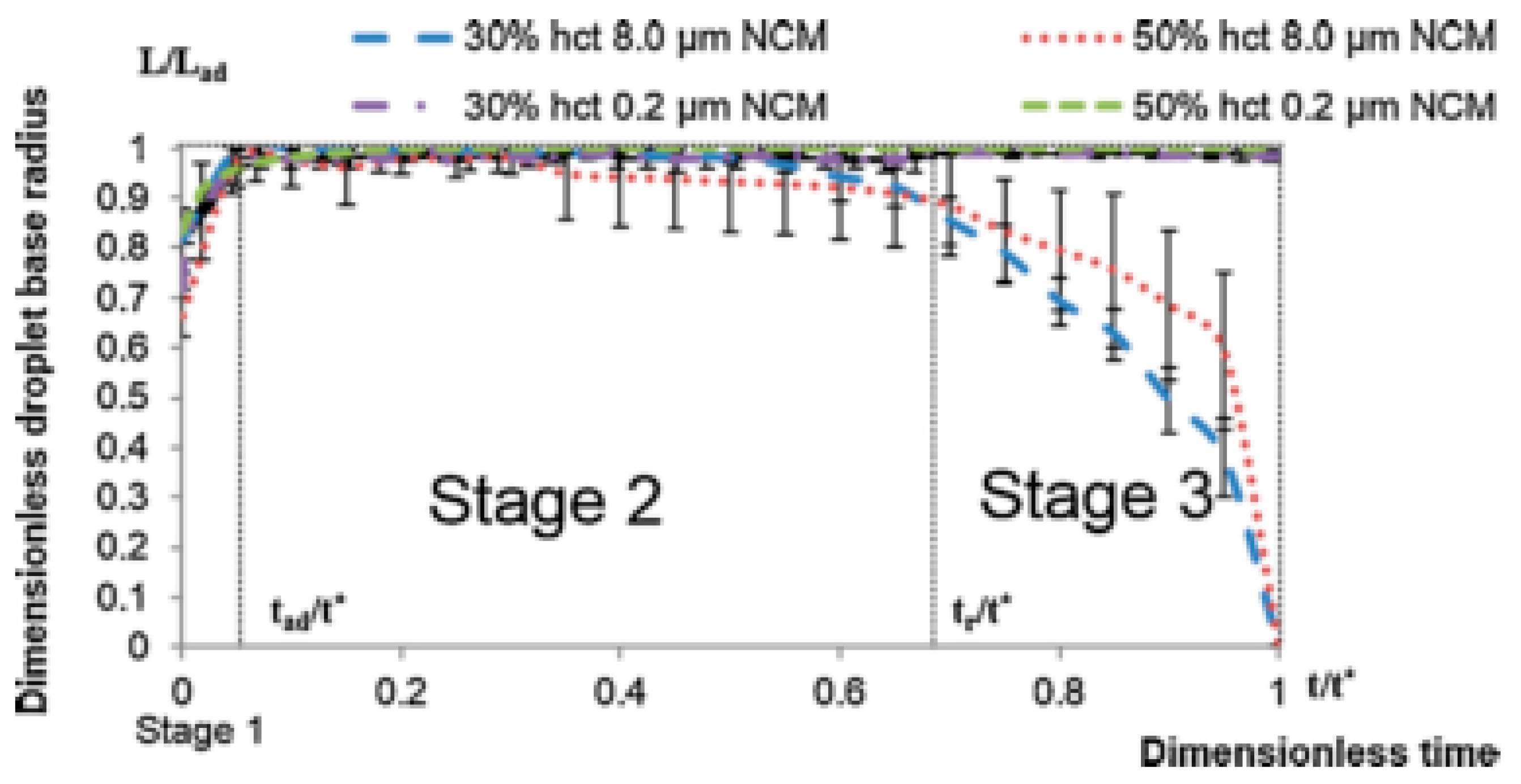
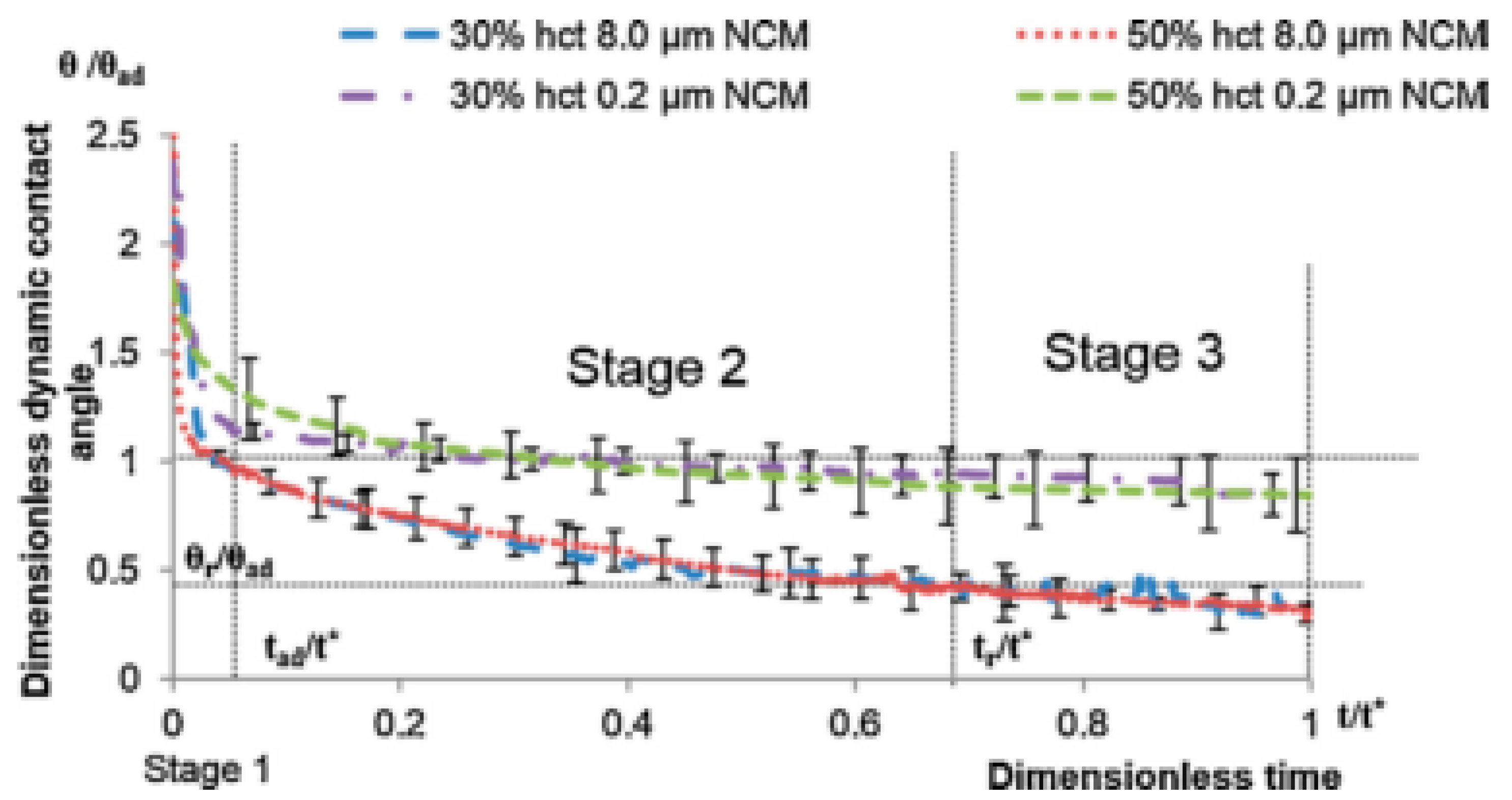
4. Spreading of Surfactant Solutions over Porous Substrates
- Stage one: Drop base expands until a maximum value of drop base is reached and the contact angle rapidly decrease throughout this stage to the value of static advancing contact angle, θad.
- Stage two: Radius of the drop base remains constant and the contact angle decreases linearly with time until hydrodynamic receding contact angle is reached. Note, in the case the static receding contact angle is equal to zero and the observed receding contact angle can be determined by hydrodynamic reasons only, like in the case of complete wetting.
- Stage three: The drop base shrinks and the contact angle remain constant until the complete disappearance of the drop.
5. Spreading over Sponges
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berg, J.C. An Introduction to Interfaces and colloids The Bridge to Nanoscience, 1st ed.; World Scientific Publishing Co.: Singapore, 2010. [Google Scholar]
- Blokhuis, E.M.; Widom, B. Wetting. Curr. Opin. Colloid Interface Sci. 1996, 1, 424–429. [Google Scholar] [CrossRef]
- Oron, A.; Davis, S.H.; Bankoff, S.G. Long-scale evolution of thin liquid films. Rev. Mod. Phys. 1997, 69, 931–980. [Google Scholar] [CrossRef]
- De Gennes, P. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Starov, V.M.; Kalinin, V.; Chen, J.-D. Spreading of liquid drops over dry surfaces. Adv. Colloid Interface Sci. 1994, 50, 187–221. [Google Scholar] [CrossRef]
- Blake, T.D.; Haynes, J. Kinetics of liquid/liquid displacement. J. Colloid Interface Sci. 1969, 30, 421–423. [Google Scholar] [CrossRef]
- Teletzke, G.; Davis, H.; Scriven, L. How Liquids Spread on Solids. Chem. Eng. Commun. 1987, 55, 41–82. [Google Scholar] [CrossRef]
- Wijshoff, H. Drop dynamics in the inkjet printing process. Curr. Opin. Colloid Interface Sci. 2018, 36, 20–27. [Google Scholar] [CrossRef]
- Washburn, F. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Aradian, A.; Raphael, E.; de Gennes, P. Dewetting on porous media with aspiration. Eur. Phys. J. E 2000, 2, 367–376. [Google Scholar] [CrossRef]
- Acton, J.; Huppert, H.; Worster, M.G. Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 2001, 440, 359–380. [Google Scholar] [CrossRef]
- Holman, R.K.; Cima, M.J.; Uhland, S.A.; Sachs, E. Spreading and infiltration of inkjet-printed polymer solution droplets on a porous substrate. J. Colloid Interface Sci. 2002, 249, 432–440. [Google Scholar] [CrossRef] [PubMed]
- Starov, V.M.; Kosvintsev, S.R.; Sobolev, V.D.; Velarde, M.G.; Zhdanov, S.A. Spreading of liquid drops over saturated porous layers. J. Colloid Interface Sci. 2002, 246, 372–379. [Google Scholar] [CrossRef] [PubMed]
- Starov, V.M.; Kostvintsev, S.; Sobolev, V.D.; Zhdanov, S.A.; Velarde, M.G. Spreading of Liquid Drops over Dry Porous Layers: Complete Wetting Case. J. Colloid Interface Sci. 2002, 252, 397–408. [Google Scholar] [CrossRef] [PubMed]
- Starov, V.M.; Zhdanov, S.A.; Velarde, M.G. Spreading of Liquid Drops over Thick Porous Layers: Complete Wetting Case. Langmuir 2002, 18, 9744–9750. [Google Scholar] [CrossRef]
- Alleborn, N.; Raszillier, H. Spreading and Sorption of a Droplet on a Porous Substrate. Chem. Eng. Sci. 2004, 59, 2071–2088. [Google Scholar] [CrossRef]
- Johnson, P.; Routledge, T.; Trybala, A.; Vaccaro, M.; Starov, V. Wetting and spreading of commercially available aqueous surfactants on porous materials. Colloids Interfaces 2018, 3, 14. [Google Scholar] [CrossRef]
- Head, M.K.; Wong, H.S.; Buenfeld, N.R. Characterisation of ‘Hadley’ grains by confocal microscopy. Cem. Concr. Res. 2006, 36, 1483–1489. [Google Scholar] [CrossRef]
- Peng, S.; Hu, Q.; Dultz, S.; Zhang, M. Using X-ray computed tomography in pore structure characterization for a Berea sandstone: Resolution effect. J. Hydrol. 2012, 472–473, 254–261. [Google Scholar] [CrossRef]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1995. [Google Scholar]
- Scheidegger, A. The Physics of Flow Through Porous Media, 3rd ed.; University of Toronto Press: Toronto, ON, Canada, 1974. [Google Scholar]
- Lin, C.; Cohen, M.H. Quantitative methods for microgeometric modeling. J. Appl. Phys. 1982, 53, 4152–4165. [Google Scholar] [CrossRef]
- Schwartz, L.M.; Banavar, J. Transport properties of disordered continuum systems. Phys. Rev. B 1989, 39, 16. [Google Scholar] [CrossRef]
- Taniguchi, M.; Pieracci, J.; Belfort, G. Effect of Undulations on Surface Energy: A Quantitative Assessment. Langmuir 2001, 17, 4312–4315. [Google Scholar] [CrossRef]
- Zadražil, A.; Stepanek, F.; Matar, O.K. Droplet spreading, imbibition and solidification on porous media. J. Fluid Mech. 2006, 562, 1–33. [Google Scholar] [CrossRef]
- Bacri, L.; Brochard-Wyart, F. Droplet suction on porous media. Eur. Phys. J. E 2000, 3, 87–97. [Google Scholar] [CrossRef]
- Kumar, S.M.; Deshpande, A.P. Dynamics of drop spreading on fibrous porous media. Colloids Surf. A Physicochem. Eng. Asp. 2006, 277, 157–163. [Google Scholar] [CrossRef]
- Neogi, P.; Miller, C.A. Spreading kinetics of a drop on a rough solid surface. J. Colloid Interface Sci. 1983, 92, 338–349. [Google Scholar] [CrossRef]
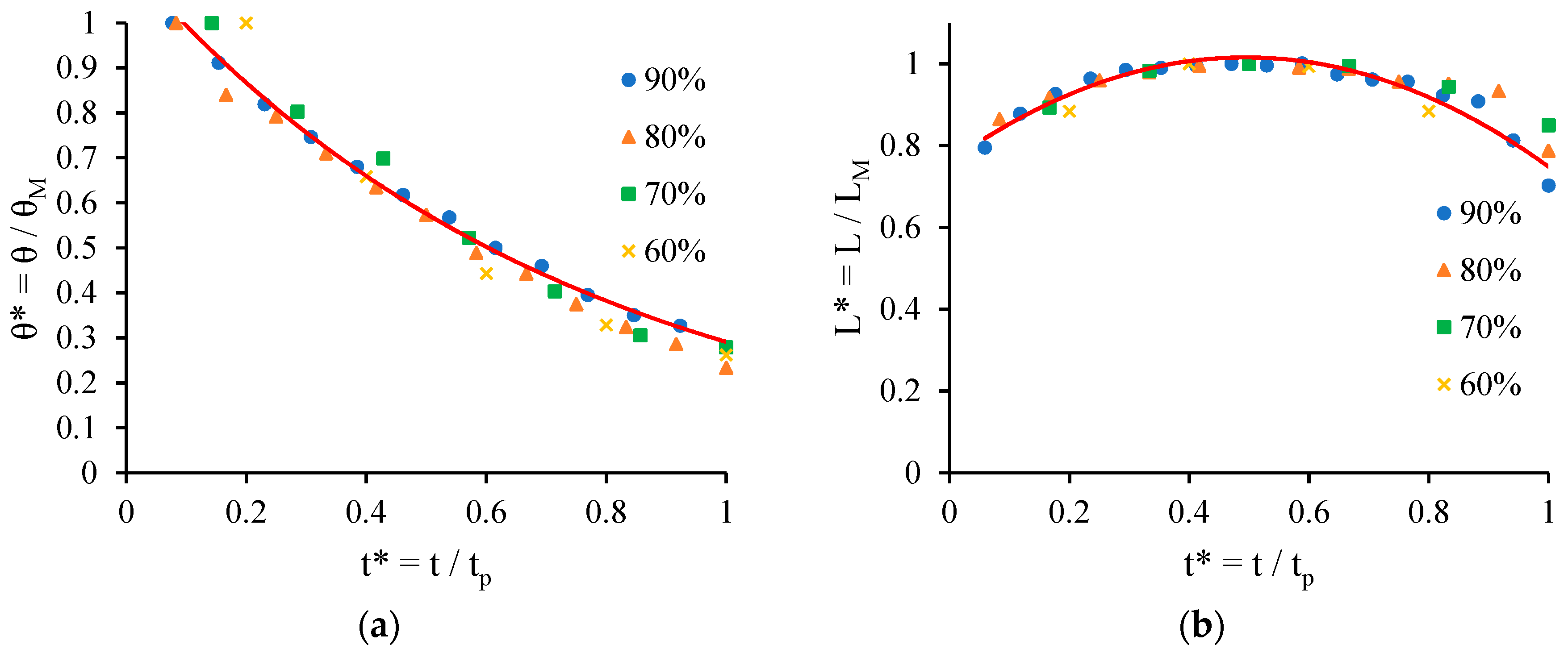
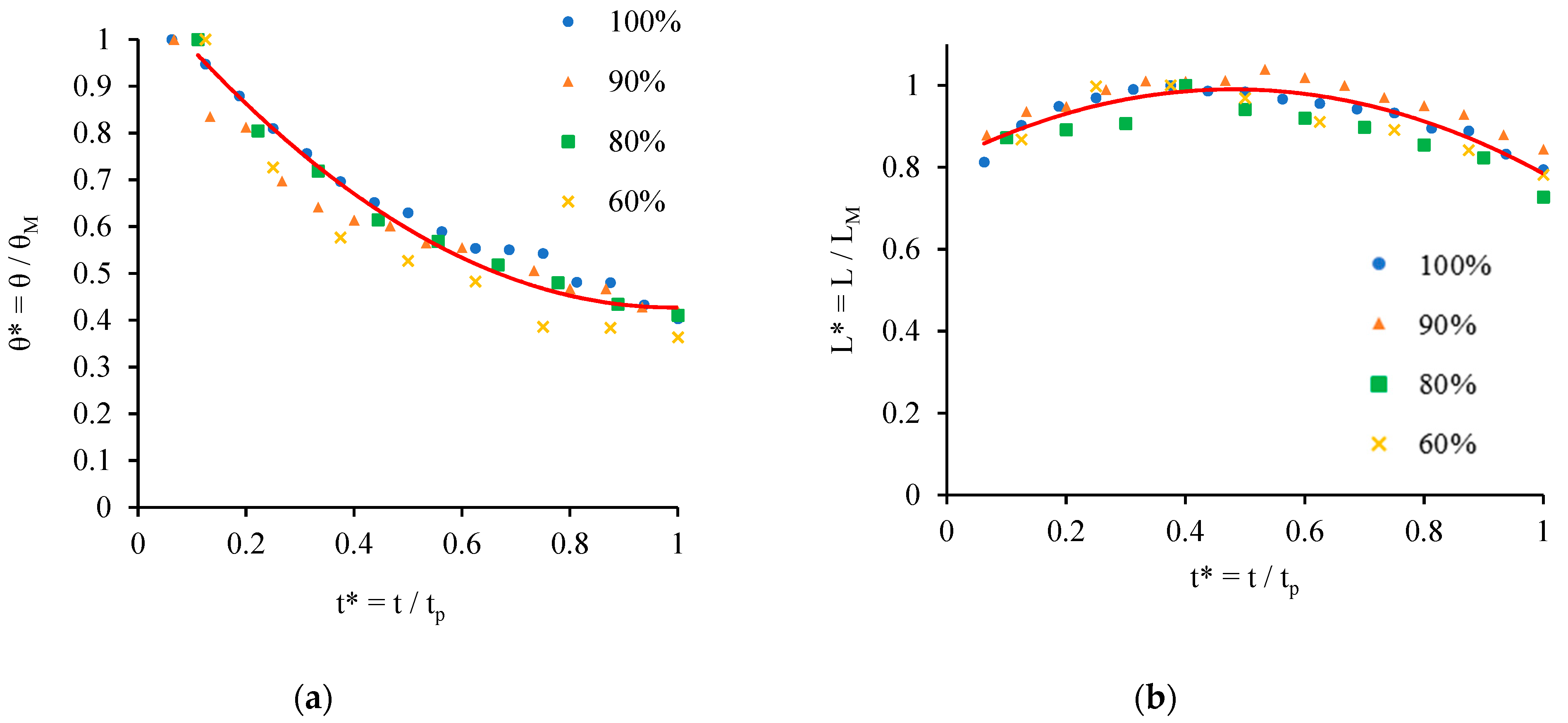
- Chao, T.C.; Arjmandi-Tash, O.; Das, D.B.; Starov, V.M. Spreading of blood drops over dry porous substrate: Complete wetting case. J. Colloid Interface Sci. 2015, 446, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Chao, T.C.; Trybala, A.; Starov, V.; Das, D.B. Influence of haematocrit level on the kinetics of blood spreading on thin porous medium during dried blood spot sampling. Colloids Surf. A Physicochem. Eng. Asp. 2014, 451, 38–47. [Google Scholar] [CrossRef]
- Whitaker, S. The Method of Volume Averaging; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 1999. [Google Scholar]
- Brinkman, H. The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 1952, 20, 4. [Google Scholar] [CrossRef]
- Zhdanov, V.G.; Starov, V.M. Calculation of the effective properties of porous and composite materials. Colloid J. Russ. Acad. Sci. Kolloidn. Zhurnal 2002, 64, 783–792. [Google Scholar]
- Kornev, K.G.; Neimark, A.V. Spontaneous penetration of liquids into capillaries and porous membranes revisited. J. Colloid Interface Sci. 2001, 235, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Starov, V.; Velarde, M.; Radke, C. Dynamics of Wetting and Spreading, 1st ed.; Taylor & Frances: Oxford, UK, 2007. [Google Scholar]
- Koursari, N.; Arjmandi-Tash, O.; Johnson, P.; Trybala, A.; Starov, V.M. Foam Drainage Placed on a Thin Porous Layer. Soft Matter 2015, 11, 3643–3652. [Google Scholar]
- Drelich, J.; Chibowska, D. Spreading kinetics of water drops on self-assembled monolayers of thiols: Significance of inertial effects. Langmuir 2005, 21, 7733–7738. [Google Scholar] [CrossRef] [PubMed]
- Chao, T.C.; Arjmandi-Tash, O.; Das, D.B.; Starov, V.M. Simultaneous spreading and imbibition of blood droplets over porous substrates in the case of partial wetting. Colloids Surf. A Physicochem. Eng. Asp. 2016, 505, 9–17. [Google Scholar] [CrossRef]
- Meesters, R.J.; Hooff, G. State-of-the-art dried blood spot analysis: An overview of recent advances and future trends. Bioanalysis 2003, 5, 17. [Google Scholar] [CrossRef] [PubMed]
- Edelbroek, P.M.; van der Heijden, J.; Stolk, L.M.L. Dried Blood Spot Methods in Therapeutic Drug Monitoring: Methods, Assays, and Pitfalls. Ther. Drug Monit. 2009, 31, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Demirev, P.A. Dried blood spots: Analysis and applications. Anal. Chem. 2013, 85, 779–789. [Google Scholar] [CrossRef] [PubMed]
- Snijdewind, I.J.M.; van Kampen, J.J.A.; Fraaij, P.L.A.; van der Ende, M.E.; Osterhaus, A.D.M.E.; Gruters, R.A. Current and future applications of dried blood spots in viral disease management. Antivir. Res. 2012, 93, 309–321. [Google Scholar] [CrossRef] [PubMed]
- Tanna, S.; Lawson, G. Analytical methods used in conjunction with dried blood spots. Anal. Methods 2011, 3, 1709–1718. [Google Scholar] [CrossRef]
- Lehmann, S.; Delaby, C.; Vialaret, J.; Ducos, J.; Hirtz, C. Current and future use of ‘dried blood spot’ analyses in clinical chemistry. Clin. Chem. Lab. Med. 2013, 51, 1897–1909. [Google Scholar] [CrossRef] [PubMed]
- Zhdanov, S.A.; Starov, V.M.; Sobolev, V.D.; Velarde, M.G. Spreading of aqueous SDS solutions over nitrocellulose membranes. J. Colloid Interface Sci. 2003, 264, 481–489. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, P.; Trybala, A.; Starov, V. Kinetics of Spreading over Porous Substrates. Colloids Interfaces 2019, 3, 38. https://doi.org/10.3390/colloids3010038
Johnson P, Trybala A, Starov V. Kinetics of Spreading over Porous Substrates. Colloids and Interfaces. 2019; 3(1):38. https://doi.org/10.3390/colloids3010038
Chicago/Turabian StyleJohnson, Phillip, Anna Trybala, and Victor Starov. 2019. "Kinetics of Spreading over Porous Substrates" Colloids and Interfaces 3, no. 1: 38. https://doi.org/10.3390/colloids3010038
APA StyleJohnson, P., Trybala, A., & Starov, V. (2019). Kinetics of Spreading over Porous Substrates. Colloids and Interfaces, 3(1), 38. https://doi.org/10.3390/colloids3010038






