Abstract
Wetting of deformable substrates has gained significant interest over the past decade due to a multiplicity of industrial and biological applications. Technological advances in the area of interfacial science have given rise to the ability to capture interfacial behavior between a liquid droplet and an elastic substrate. Researchers have developed several theories to explain the interaction between the two phases and describe the process of wetting of deformable/soft substrates. A summary of the most recent advances on static wetting of deformable substrates is given in this review. It is demonstrated that action of surface forces (disjoining/conjoining pressure) near the apparent three-phase contact line should be considered. Any consideration of equilibrium droplets on deformable (as well as on non-deformable) substrates should be based on consideration of the excess free energy of the system. The equilibrium shapes of both droplet and deformable substrate should correspond to the minimum of the excess free energy of the system. It has never been considered in the literature that the obtained equilibrium profiles must satisfy sufficient Jacobi’s condition. If Jacobi’s condition is not satisfied, it is impossible to claim that the obtained solution really corresponds to equilibrium. In recently published studies, equilibrium of droplets on deformable substrates: (1) provided a solution that corresponds to the minimum of the excess free energy; and (2) the obtained solution satisfies the Jacobi’s condition. Based on consideration of disjoining/conjoining pressure acting in the vicinity of the apparent three-phase contact line, the hysteresis of contact angle of sessile droplets on deformable substrates is considered. It is shown that both advancing and receding contact angles decrease as the elasticity of the substrate is increased and the effect of disjoining/conjoining pressure is discussed. Fluid inside the droplet partially wets the deformable substrate. It is shown that just these forces coupled with the surface elasticity determine the deformation of the deformable substrates.
1. Introduction
Wetting of deformable substrates has gained significant interest over the last decade, particularly due to its wide range of applications. These applications occur in both nature (including biological processes) and a range of industrial processes. Elastic solids, including foams, cosmetics, paper, polymeric materials, gels and melts, have been incorporated in several applications such as inkjet printing [1], forensic science [2], surface coating, pesticide spraying and spray painting [3].
The well-known Young’s equation has been widely used to predict equilibrium contact angle, , on rigid solid substrates [4]. It gives the liquid–solid, liquid–vapor, and vapor–solid surface tension relationships and is based on consideration of the balance of horizontal forces. However, Young’s equation cannot be considered when the substrate is deformable, where the vertical component () of the surface tension remains unbalanced. Substrate deformation should balance this extra force in the case of deformable substrate. However, even after modification, Young’s equation still cannot be applied directly, as it gives rise to deformation singularity (surface deformation goes to infinity) near the three-phase contact line [5,6,7,8,9,10,11,12,13]. To avoid this singularity, several researchers have tried different approaches. It was initially suggested that surface tension should be uniformly distributed near the contact line to mitigate the singularity [6,7,8,9,10].
Lester was the first to model a sessile droplet on a soft substrate where the Neuman’s triangle is considered [5]. The author identified the significance of a vertical component of liquid surface tension applied at the three-phase contact line. Neumann’s triangle [14] is a triangle of forces distributed in a certain way over the contact line so that the resultant force vanishes [5]. Using the same concept, Style and Dufresne generalized a three-dimensional configuration, which allowed applying Neumann’s consideration for small droplets on soft solids [11]. However, it is important to mention that Neumann’s triangle of forces applied near the three-phase contact line could only be regarded as valid in the case of an equilibrium configuration [5] and as long as the necessary equilibrium conditions are satisfied [13].
Unfortunately, Neumann’s approach (despite being widely used) is in a contradiction with thermodynamics because it ignores the full thermodynamic equilibrium of liquid with vapor and solid substrate (see the full discussion in [15]), but most importantly, according to Neuman’s approach, a vapor pressure at which the droplet is at equilibrium is not specified. That is, according to Neumann’s equation, the droplet can be at equilibrium even with undersaturated vapor. The latter is in a drastic contradiction with Kelvin’s equation: according to Kelvin’s equation, droplets can be at equilibrium with over saturated vapor only. It is also important to mention that Neumann’s equation ignores surface forces action in the vicinity of the apparent three phase contact line.
It is worth remembering that surface forces come into play as soon as the thickness of the liquid layer is <0.1 µm. Manifestation of surface forces action appear in thin liquid layers (<0.1 µm, that is in the vicinity of the apparent three-phase contact line) of disjoining/conjoining pressure [15]. Note that the term “apparent three-phase contact line” is used to emphasize that there is no real sharp contact line but instead there is a transition zone, where capillary and surface forces act simultaneously [15]. The disjoining/conjoining pressure acts in the vicinity of the apparent three-phase contact line in both rigid and deformable substrates. That is, surface forces action in the vicinity of the apparent three-phase contact line is compulsory in both rigid and deformable substrates. Consideration of action of disjoining/conjoining pressure in the vicinity of the apparent three-phase contact line in the case of rigid substrates allows calculating via disjoining/conjoining pressure isotherm equilibrium the droplet profiles, equilibrium contact angles [15] and hysteresis of contact angle (static advancing and static receding contact angles) [16]. Recently, surface forces effect near the apparent contact line for droplets on deformable substrates are taken into account [13,15,16,17,18,19,20].
The most recent theoretical and experimental studies are reviewed in this article and a brief description is provided of equilibrium and hysteresis contact angles of sessile droplets where disjoining/conjoining pressure is taken into account [18,19,20].
2. Theoretical and Experimental Analysis
Several experimental studies on droplet wetting of deformable substrate have been undertaken recently primarily due to substantial progress in imaging techniques [21,22,23,24,25,26,27]. High-resolution cameras allow capturing droplet profiles near the three-phase contact line and subsequent substrate deformations. This allows developing understanding of theoretical concepts underlying the experiments [28,29,30,31]. In the most recent experimental studies, Style et al. characterized the indentation of glass particles using confocal microscopy [32] while Camara et al. experimentally investigated the effect of Laplace pressure on deformation caused by drops of 1-butyl-3-methylimidazolium hexafluorophosphate ionic liquid on a silicone elastomeric polymer [26]. The authors also experimentally investigated the effect of the film thickness on the deformation of the substrate and found that for thinner films the solid support located underneath the drop affects both the wetting ridge and the dimple below the liquid [27]. Jerison et al. used confocal microscopy to measure the displacement of water on an elastic substrate and described a symmetric model that fits these profiles [22]. In the past few years, it has been possible to record high resolution images in both temporal and spatial coordinates.
Andreotti et al. presented recent advances of solid capillarity. They discussed the importance of surface stresses on the deformation and several questions related to the mechanics involved at the interface of soft solids were addressed [33]. The authors stated that stretching the interface causes the energy to increase proportionally to the surface energy [33]. However, the Shuttleworth effect arises when the surface energy depends on the strain and in this case the derivative of surface energy also affects the surface stress [33,34]. Other related materials, e.g., polymer melts, and their thermodynamic properties, e.g., glass-transition temperature, in relation to their mechanical properties are also discussed in [33]. It has been reported that the glass-transition temperature of a polymer melt can be reduced depending on the boundary conditions [33,35,36]. The relationship between surface stress and bulk deformation is also discussed in [33]. In the same article, the significance of the critical elastocapillary length on the capillary effects, measured on nano-scale for polymers and micro-scale for gels, is also discussed [33].
The relationship between surface stress and surface energy was analyzed by Style et al. [12] for static wetting problems. In [12] the authors used the term “elastocapillarity” to describe the phenomenon of solid deformation as affected by mechanical properties of the substrates. The surface stresses theory is outlined and the importance of elastocapillary length on surface stress and elasticity is identified. Surface stress causes a stress jump across the interface of the deformable substrate [12].
However, in the above-mentioned theories, the most important phenomena, the action of surface forces near the apparent three-phase contact line and the influence of the surface forces on deformation of soft solids, are ignored.
In the next section, a new modeling technique for the investigation of wetting of soft substrates is reviewed, where surface forces action near the apparent three-phase contact line is considered. Surface forces are introduced using simplified disjoining/conjoining pressure isotherm. Although the selected configuration of the disjoining/conjoining pressure isotherm is simplified, it is still able to capture essential properties of a real disjoining/conjoining isotherm: (i) surface forces are present over short range; (ii) partially wetting droplets are referred to when appropriate values of parameters are selected; and (iii) the regions of influence of surface forces have stable thin fluid films. Elasticity of the soft substrate is introduced using Winkler’s model [37]. Substrate’s deformation and the droplet profile are deduced via the physical characteristics of the disjoining/conjoining pressure isotherm and substrate’s elasticity [18].
For a droplet to be at equilibrium on deformable substrate, four conditions have to be satisfied: (i) the first variation of excess free energy is equal to zero; (ii) second variation is positive; (iii) transversality condition is satisfied; and (iv) Jacobi’s sufficient condition is fulfilled. Until now, the fourth condition has always been neglected by researchers in this area. In [18], a solution is deduced for both droplet and deformable substrate profiles, where disjoining/conjoining pressure action in the vicinity of the apparent three phase contact line was taken into account. For the first time in [19], the essential Jacobi’s condition for the solution of the liquid droplet on a soft substrate obtained in [18] is verified. In Section 4, the verification of the Jacobi’s sufficient condition for already obtained solution of equilibrium droplets on deformable substrates is undertaken.
Contact angle hysteresis (advancing and receding contact angles) is frequently connected to surface roughness and surface heterogeneities. However, these are not the only causes for the existence of contact angles hysteresis. Lately researchers have illustrated that hysteresis exist on smooth homogeneous solid substrates [38,39,40]. It has been observed that contact angle hysteresis on a rigid substrate is dependent on surface forces action in the vicinity of the three-phase contact line [16]. Recently, this theory has been extended and applied to investigation of contact angle hysteresis of droplets on deformable/soft substrates [20]. In Section 5, the findings of these quasi-equilibrium states that exist on deformable substrates are discussed.
3. Equilibrium of Droplets on Soft Substrates
In this section, a new approach for wetting of soft substrates is developed by introducing action of surface forces near the three-phase contact line of the droplet. In this section, a simplified linear disjoining/conjoining pressure isotherm, , is used to introduce surface forces action and elasticity of the substrate is incorporated through the use of Winkler’s model [37,41]. According to Winkler’s model, the deformation in the soft substrate is regional and has a direct relation with the applied pressure, [18]:
where specifies elasticity coefficient of the deformable substrate, and is the local deformation of the substrate in the z-axis due to the pressure applied from the fluid above (see Figure 1).
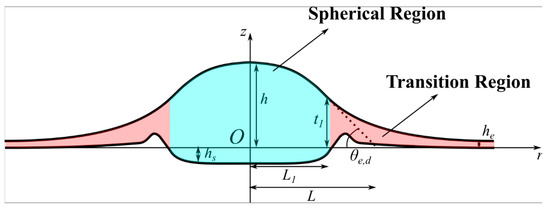
Figure 1.
Schematic diagram of droplet on a deformable substrate: Spherical (Bulk) region, ; Transition region, ; , the liquid profile; , deformation of the substrate; , equilibrium flat film; , apparent equilibrium contact angle; , height of the droplet at which surface forces (disjoining/conjoining pressure) start to act; , radial length corresponding to ; , Effective radius of the droplet; , co-ordinate system.
Assume to be the ambient pressure of air. Local deformation of the deformable substrate due to presence of ambient air pressure is given by:
Equilibrium thin film of fluid covers the deformed soft substrate, which is calculated according to a combination of the Kelvin’s equation and disjoining/conjoining pressure isotherm [15]:
where is the air gas constant, refers to temperature, is fluid’s molar volume, and vapor pressure, , is greater than (saturated pressure). According to Kelvin’s equation, droplet remains at equilibrium only in oversaturated vapor. The excess free energy of the equilibrium thin film on the deformed substrate in front of the liquid droplet per unit area is given by [15,18]:
where , and and are vapor–liquid and liquid–solid surface tensions, respectively. Excess free energy present in a droplet is infinite. Therefore, free energy from the thin film must be subtracted from the free energy that exists in the droplet on a deformable substrate [15,18]. Hence, the droplet excess free energy on a soft substrate is (see Figure 1):
where means “in comparison with a flat equilibrium thin liquid film”.
Equation (5) can be rearranged as:
where
and is the radial length. Under equilibrium conditions, the excess free energy mentioned in Equation (6) should attain a minimum value. To fulfill this condition, the first variation in Equation (6) should equal to zero, which leads to two Euler equations, i.e., for liquid and substrate profiles:
Equations (8) and (9) are two interlinked differential equations for two unknown profiles: for liquid droplet, , and depth of deformed soft substrate, . In case of low slope approximation, , , which is acceptable for small contact angles, is used below. It is important to observe that Equation (8) is unlike the usual capillary equation for the non-deformable substrate, because it now has contribution of in the disjoining/conjoining pressure, which can be determined using Equation (9). Equations (8) and (9) are interconnected and are normally only computed numerically. Therefore, the problem is further simplified with the use of linear disjoining/conjoining pressure isotherm so that analytical solutions are obtained.
where and are defined in Figure 2, is the height of the droplet where influence of surface forces start, and is the slope of the linear disjoining/conjoining pressure isotherm. The subsequent radial length from the origin to the point is (see Figure 1). The selected linear dependency of disjoining/conjoining pressure isotherm on according to Equation (10) still portrays the essential properties mentioned in Section 2 (for details, see [18]).
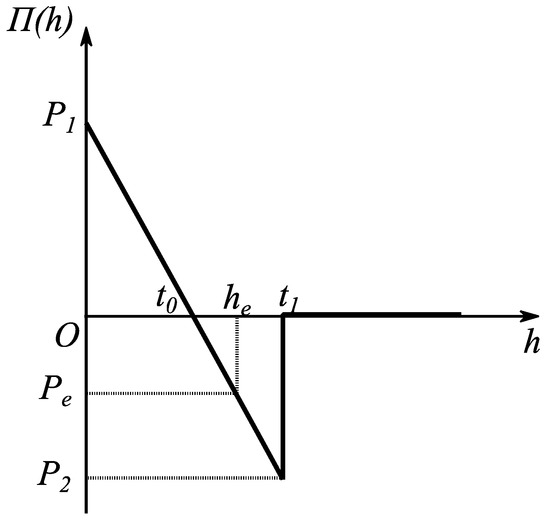
Figure 2.
Selected disjoining/conjoining pressure isotherm. Reproduced with permission from [18]. Copyright © 2017 Elsevier B.V.
Disjoining/conjoining pressure cannot be ignored near the apparent three-phase contact line; therefore, substrate deformation is linked directly with the parameters of the disjoining/conjoining pressure isotherm (see Table 1).

Table 1.
Physical properties used for calculation of droplet profile and deformation in the substrate [18].
Effect of variation of , , and on substrate deformation and its subsequent effect on the droplet profile is presented below.
3.1. Influence of Change of Excess Pressure,
Excess pressure of the droplet is changed according to . Figure 3 illustrate shapes of the droplet and substrate with variation in . An increase in causes equilibrium thin film height, , to reduce. This causes an increase in the span/spread and height of the droplet. Consequently, this also causes an increase to the extent of the deformation of the substrate in the radial direction, but also reduces the depth to which the substrate gets deformed to.
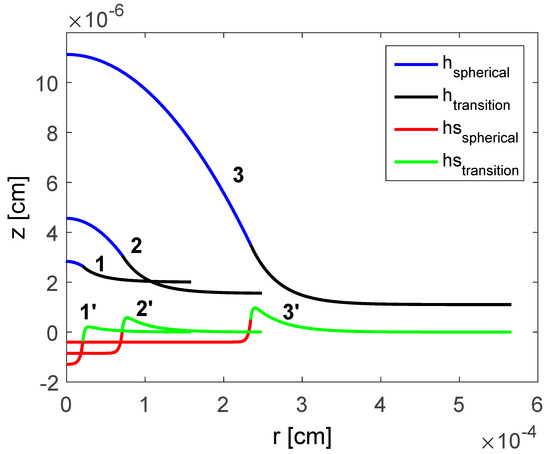
Figure 3.
Computed shapes of the droplet and deformation of the substrate: dyne/cm2; dyne/cm2; and dyne/cm2 [18]. Reproduced with permission from [18]. Copyright © 2017 Elsevier B.V.
3.2. Influence of Change of Slope of the Disjoining/Conjoining Pressure Isotherm,
The value of the slope of the disjoining/conjoining pressure isotherm is varied in the following range dyne/cm3 to see its impact on the depth of deformation in the soft substrate and resulting shape of the droplet. Figure 4 demonstrates that slope also affects the droplet shape: increasing causes the maximum height of the droplet to increase which also increases the span of the droplet in radial direction. The equilibrium contact angle for droplet on a deformable substrate increases as increases. Slope of the adopted disjoining/conjoining pressure isotherm does not affect the vertical depth of deformation of the soft substrate.
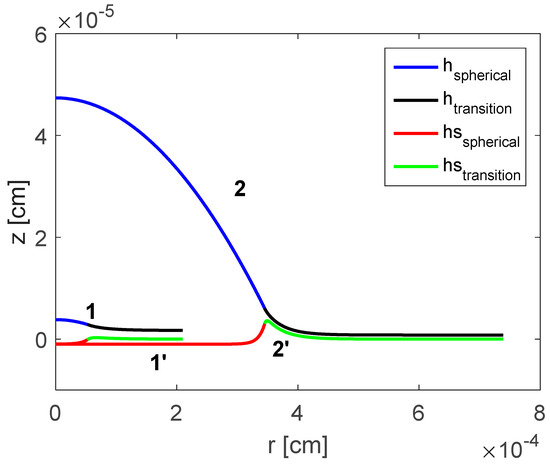
Figure 4.
Computed shapes of the droplet and deformation of the substrate: dyne/cm3 and dyne/cm3 [18]. Reproduced with permission from [18]. Copyright © 2017 Elsevier B.V.
3.3. Influence of Change of Elasticity Coefficient,
Elasticity coefficient controls the depth of deformation of the soft substrate. Here, elasticity coefficient is changed according to cm3/dyne. The effect of decreasing the elasticity coefficient (i.e., ) causes the shape of the droplet on deformable substrate to approach the shape of the droplet on non-deformable substrate (see Figure 5). It is also shown that, as elasticity coefficient is increased (i.e., substrate becomes more elastic), the equilibrium contact angle reduces marginally and the depth of deformation of the soft substrate increases (i.e., more deformation).
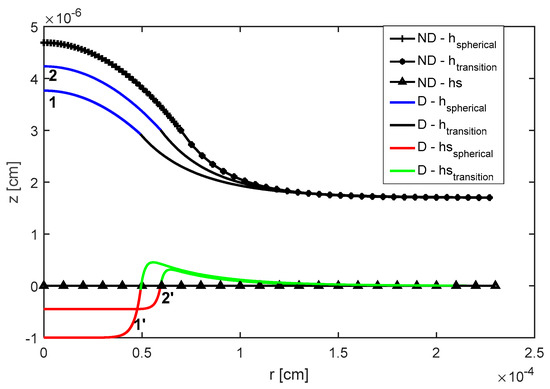
Figure 5.
Computed shapes of the droplet and deformation of the substrate: cm3/dyne and cm3/dyne. ND, Non-Deformable substrate; D, Deformable substrate [18]. Reproduced with permission from [18]. Copyright © 2017 Elsevier B.V.
3.4. Influence of Change of Substrate Surface Tension,
Substrate surface tension is changed in the range dyne/cm. Increasing causes equilibrium contact angle to slightly increase, as displayed in Figure 6. It is also observed that transition from the bulk/spherical part of the droplet to thin liquid film ahead of the droplet is smooth. However, when approaches zero, this transition does not remain smooth and changes to a sharp jump.
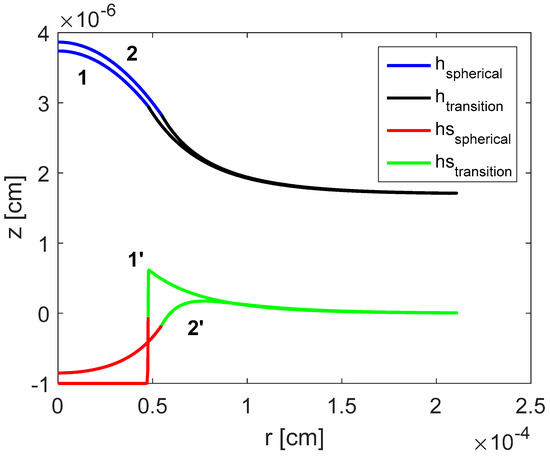
Figure 6.
Computed shapes of the droplet and deformation of the substrate: dyne/cm and dyne/cm [18]. Reproduced with permission from [18]. Copyright © 2017 Elsevier B.V.
4. Equilibrium Conditions of Droplets on Deformable Substrates
As discussed above, excess free energy must remain at minimum in equilibrium conditions. Solely for this situation, the obtained shapes of the liquid droplet and deformed substrate are in actual for equilibrium. For a droplet to be at equilibrium on a deformable substrate, four essential conditions for (i) first variation of the free energy, (ii) second variation of free energy, (iii) transversality condition and (iv) Jacobi’s sufficient condition, must always be satisfied [15,19]. Solution obtained from Jacobi’s condition should not disappear for a droplet on rigid/solid substrate (i.e., one-dimensional problem) [15]. It is important to note that Conditions (i), (ii) and (iii) are necessary conditions of the minimum of the excess free energy, while Condition (iv) is a sufficient condition of the minimum. Altogether, these conditions give necessary and sufficient conditions of the minimum of the excess free energy. Unfortunately, the vital fourth condition is always neglected when deformation of soft solids under liquid droplets is considered. Under equilibrium conditions, simply if the Jacobi’s sufficient condition is fulfilled, the estimated profiles of the fluid droplet and deformable substrate provide the minimum of free energy. To the best of our knowledge, it is for the first time the fourth condition is satisfied and the computed solution actually results in profiles for the droplet and the deformable substrate at equilibrium [19].
For two-dimensional droplet, calculations are considerably easier to investigate if the Jacobi’s condition is satisfied [19]. Therefore, here, two-dimensional droplets are considered. The excess free energy of a liquid droplet resting on a deformable substrate is similar to the three-dimensional case discussed earlier with dimensional modifications in Equations (6) and (7) (see [19])
where subscript 2D is for two-dimensional and
where is the tangential coordinate. The corresponding equations for the two-dimensional droplet profile and deformed substrate are similar to the ones obtained for the three-dimensional case, i.e., Equations (8) and (9). Equations (8) and (9) in two-dimensional case are simplified to:
Solution of Equations (13) and (14) using the parameters of the disjoining/conjoining pressure isotherm mentioned in Table 1 is obtained in low slope approximation as above. Dependency of apparent equilibrium contact angle, , is plotted against elasticity coefficient, , in Figure 7.
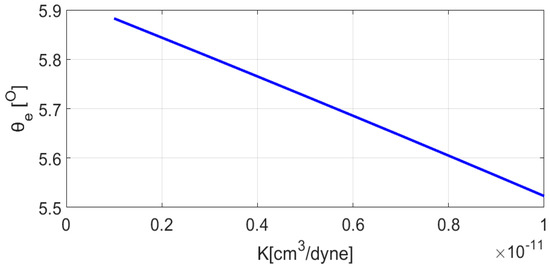
Figure 7.
Equilibrium contact angle, , vs elasticity coefficient, . Reproduced with permission from [19]. Copyright © 2018 American Chemical Society.
As expected, upon increase in the elasticity of the soft substrate the apparent equilibrium contact angle of the droplet decreases. Second essential condition, , is always satisfied [18]. Next is to check if Jacobi’s sufficient condition is fulfilled.
To achieve minimum of Jacobi’s condition, the following should be satisfied: determinant built up by solutions of Jacobi’s equation must not disappear at any location, , within the area of interest (see below) [19,42]. Under low slope approximation, Jacobi equations for the four unknown functions are generated, where for the system of Equations (11) and (12) are as follows:
For the selected disjoining/conjoining pressure isotherm (see Figure 2), Equations (15) and (16) become linear differential equations corresponding to all Jacobi’s functions. Initial conditions for four Jacobi’s functions [19,43]:
Zero initial conditions and linearity of Jacobi’s equations means that and are equal to zero. Therefore, there are only two unknowns, i.e., and . Jacobi’s condition, should be positive for . According to Koursari et al. [19], both and are positive for both spherical and transition regions (see Figure 2). This implies that is positive at all (see Figure 8). Jacobi’s condition is therefore satisfied, which means that solutions for both liquid and deformable substrate provide minimum of the excess free energy of the system [19].
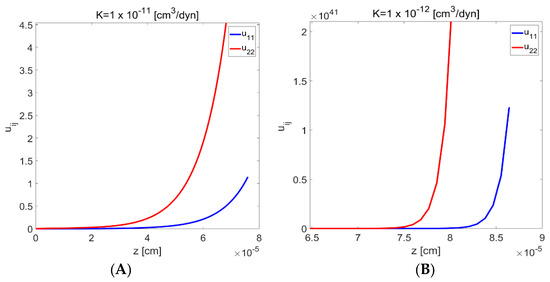
Figure 8.
Jacobi’s functions and plotted against the length of the transition region ), for two different values of the elasticity coefficient,, (A) and (B). Reproduced with permission from [19]. Copyright © 2018 American Chemical Society.
Note that the validity of the Jacobi’s condition for the deduced solutions of both droplet shape and shape of the deformable substrate undertaken in [19], was checked for the first time. The latter means that any solution of the same problem developed earlier or to be developed in the future should be checked for a validity of the Jacobi’s condition for the deduced solution.
5. Hysteresis of Contact Angle for Sessile Droplets on Soft Substrates
There exists only a single equilibrium contact angle, of droplet on a smooth homogeneous substrate. As stated earlier, droplet must be at equilibrium with oversaturated vapor corresponding to Kelvin’s equation [15]. Therefore, experimentally, only quasi-equilibrium contact angles are observed, which are known as hysteresis contact angles: static advancing contact angle , and static receding contact angle [20].
Static advancing and receding contact angles are calculated using quasi-equilibrium states of a droplet on a soft substrate. Let us note, that such consideration is undertaken in [20] for the first time and had not been tried before. Motion of the droplet starts when excess pressure is not equivalent to its value at equilibrium, . This motion can be subdivided into “slow microscopic” before some critical values of applied pressure is reached and “fast macroscopic” processes above the critic value [20]. Fast macroscopic processes occur in the bulk/spherical part of the droplet, whereas slow microscopic motion takes place in the transitional region (see Figure 9).
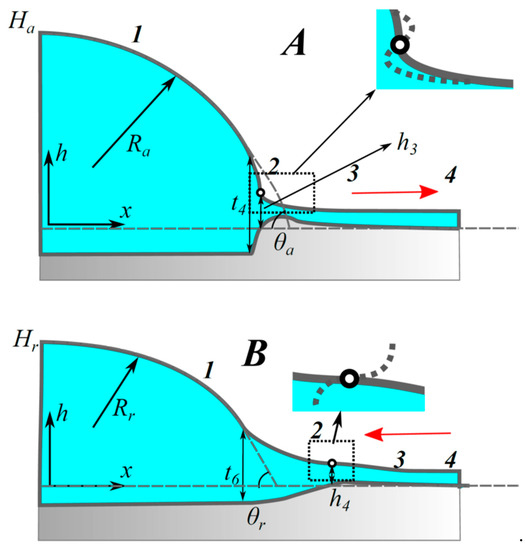
Figure 9.
Droplet on a deformable substrate: just before advancing (A); and just before receding (B) begins (1, quasi-equilibrium part of the droplet; 2, inflection points; 3, flow zone; 4, equilibrium thin liquid film in front). Reproduced with permission from [20]. Copyright © 2018 Elsevier B.V.
In advancing and receding droplets, the value of excess pressure is vital. As it reaches critical values of and , the motion of the droplet changes from microscopic to macroscopic. Subsequently, the macroscopic contact angle reaches and . In advancing droplets, pressure is less than , the gradient of the droplet profile increases and reaches infinity at some critical point (marked in Figure 9A) when excess pressure tends to . Advancing droplet has an apex, , and the radius, , as shown in Figure 9. On the other hand, when pressure is increased from , microscopically the gradient of the droplet profile starts to decrease causing it to become horizontal, i.e., zero slope, as shown in Figure 9B, in which, , is the apex and , is the radius for a receding droplet (see Figure 9B). It is shown in [20] that quasi-equilibrium states of the droplet can be described using Equations (13) and (14) where the equilibrium excess pressure, , is replaced by quasi-equilibrium pressures, or .
Dangerous points (inflection points) exist in advancing and receding droplets. In advancing droplet, inflection point is present at thickness, , and, in receding droplet, inflection point is present at thickness, [20,40] (see Figure 9). Boundary conditions for both cases are:
Numerical solution is only possible for Equations (13) and (14) because of their coupled nature. To simplify calculations, piecewise linear function of disjoining/conjoining pressure isotherm is adopted [20]:
where are different regions of adopted disjoining/conjoining pressure isotherm, and are corresponding slopes of these regions. Selected disjoining/conjoining pressure isotherm has following vital properties: (i) stability condition, when (-films [15] and (-films [15]) is satisfied; (ii) corresponds to partial wetting; and (iii) surface forces action is short ranged, i.e., . These parameters are carefully selected to resemble as closely as possible the actual disjoining/conjoining pressure isotherm used in [40] to verify calculations of advancing/receding contact angles on rigid/solid substrates (see Table 2 and Figure 10) [20]. The additional simplification adopted in [20] is as follows: , the solid/liquid interfacial tension, has been neglected. However, in this case, the low slope approximation has not been used.

Table 2.
Properties of disjoining/conjoining pressure isotherm for advancing/receding contact angles [20].

Figure 10.
Linear (piece-wise) disjoining/conjoining pressure isotherm for quasi-equilibrium cases. Reproduced with permission from [20]. Copyright © 2018 Elsevier B.V.
Effect of variation of advancing droplet volume on advancing contact has been investigated (see Figure 11A). As droplet volume increases, the advancing contact angle reduces. Advancing contact angle on a deformable substrate is always less than on a non-deformable substrate [20,40]. Figure 11B shows the effect of variation of volume on receding contact angle. As the volume of the droplet increases, the receding contact angle reduces. Elasticity of the deformable substrate causes a decrease in receding contact angle in comparison with solid substrate, but the amount of decrease is very small, as depicted from the curves in Figure 11B. Both advancing and receding contact angles decrease for a soft substrate. This behavior has been experimentally observed [44,45].
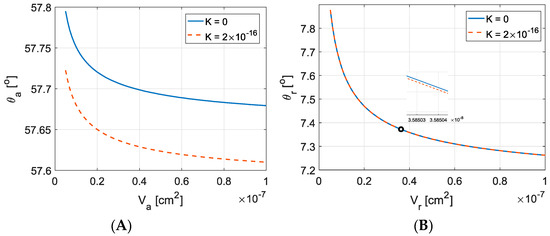
Figure 11.
Effect of variation of volume of the droplet on: (A) advancing; and (B) receding contact angles. Reproduced with permission from [20]. Copyright © 2018 Elsevier B.V.
6. Conclusions and Outlook
The most recent advances are summarized in the area of static wetting of deformable substrates taking into consideration the effect of surface forces action coupled with elasticity of the substrate. Theoretical and experimental studies are reviewed in the area. Significant progress has been achieved in experimental investigations of deformations of soft solids due to recent advances in imaging techniques such as confocal microscopy and several theoretical models have been developed in an attempt to resolve the singularity caused by deformation of the substrates. The main conclusions are as follows: (i) any investigation of equilibrium of droplets on deformable substrates should be based on consideration of surface forces acting in the vicinity of the apparent three-phase contact line; (ii) excess free energy of the system droplet/deformable substrate should be considered and the equilibrium state corresponds to the minimum of the excess free energy; (iii) variation of the excess free energy provide two interconnected equations for both droplet and deformable substrate profiles; and (iv) solution of these two interconnected equations should satisfy the Jacobi’s sufficient condition. Approaches based on Conclusions (i)–(iv) are briefly discussed.
Funding
This research was funded by CoWet project from EU, MAP EVAPORATION project from European Space Agency and Proctor & Gamble, Brussels.
Acknowledgments
This research was supported by CoWet Marie Curie EU project; and MAP EVAPORATION project, European Space Agency and Proctor & Gamble, Brussels.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Slopes of different regions of disjoining/conjoining pressure isotherm | |
| film | |
| film | |
| D | Deformable substrate |
| Jacobi condition | |
| , | Excess free energy in three and two-dimensional cases |
| , | Excess free energy of the equilibrium thin film on the deformed solid in three and two-dimensional cases |
| Surface tension of the fluid | |
| Surface tension of the substrate | |
| Apex of the droplet | |
| Apex of the advancing droplet | |
| Apex of the receding droplet | |
| Film thickness, equilibrium liquid profile, droplet height | |
| Stable equilibrium film thickness | |
| Local deformation of the substrate | |
| Local deformation of the substrate under the action of the ambient pressure | |
| Thickness in the critical point for advancing droplet | |
| Thickness in the critical point for receding droplet | |
| Elasticity coefficient | |
| Characteristic length | |
| Dynamic viscosity | |
| ND | Non-deformable substrate |
| Pressure in the ambient air | |
| Equilibrium excess pressure | |
| Advancing pressure | |
| Receding pressure | |
| Vapor pressure | |
| Saturated vapor pressure | |
| Disjoining/conjoining pressure isotherm | |
| Flow rate | |
| Radius of curvature of the droplet | |
| Radius of curvature of the advancing droplet | |
| Gas constant | |
| Radius of curvature of the receding droplet | |
| Length along radial direction for three-dimensional case | |
| Temperature | |
| Parameters of disjoining/conjoining pressure isotherm | |
| Equilibrium contact angle | |
| Advancing contact angle | |
| Receding contact angle | |
| Solution of Jacobi’s equation | |
| Volume of the fluid | |
| Volume of the advancing droplet | |
| Volume of the receding droplet | |
| Molar volume of the liquid | |
| Length along radial direction for two-dimensional case | |
| Co-ordinate in the tangential direction |
References
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J. Wetting and spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Attinger, D.; Moore, C.; Donaldson, A.; Jafari, A.; Stone, H.A. Fluid dynamics topics in bloodstain pattern analysis: Comparative review and research opportunities. Forensic Sci. Int. 2013, 231, 375–396. [Google Scholar] [CrossRef] [PubMed]
- Eral, H.B.; ’t Mannetje, D.J.C.M.; Oh, J.M. Contact angle hysteresis: A review of fundamentals and applications. Colloid Polym. Sci. 2013, 291, 247–260. [Google Scholar] [CrossRef]
- Young, T. An Essay on the Cohesion of Fluids. Philos. Trans. R. Soc. London 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Lester, G. Contact angles of liquids at deformable solid surfaces. J. Colloid Sci. 1961, 16, 315–326. [Google Scholar] [CrossRef]
- Rusanov, A. Theory of wetting of elastically deformed bodies. 1. Deformation with a finite contact-angle. Colloid J. 1975, 37, 614–622. [Google Scholar]
- Rusanov, A. Theory of wetting of elastically deformed bodies. 2. Equilibrium conditions and work of deformation with a finite contact angle. Colloid J. 1975, 37, 623–628. [Google Scholar]
- Rusanov, A. On the thermodynamics of deformable solid-surfaces. J. Colloid Interface Sci. 1978, 63, 330–345. [Google Scholar] [CrossRef]
- Shanahan, M.E.R. The Spreading Dynamics of a Liquid-Drop on a Viscoelastic Solid. J. Phys. D-Appl. Phys. 1988, 21, 981–985. [Google Scholar] [CrossRef]
- Shanahan, M.; de Gennes, P. The ridge produced by a liquid near the triple line solid liquid fluid. Comptes Rendus De L Academie Des Sciences Serie Ii 1986, 302, 517–521. [Google Scholar]
- Style, R.W.; Dufresne, E.R. Static wetting on deformable substrates, from liquids to soft solids. Soft Matter 2012, 1, 7177–7184. [Google Scholar] [CrossRef]
- 12 Style, R.W.; Jagota, A.; Hui, C.-Y.; Dufresne, E.R. Elastocapillarity: Surface Tension and the Mechanics of Soft Solids. Annu. Rev. Condens. Matter Phys. 2017, 8, 99–118. [Google Scholar] [CrossRef]
- Chen, L.; Bonaccurso, E.; Gambaryan-Roisman, T.; Starov, V.; Koursari, N.; Zhao, Y. Static and dynamic wetting of soft substrates. Curr. Opin. Colloid Interface Sci. 2018, 36, 46–57. [Google Scholar] [CrossRef]
- Neumann, F. Lectures on the Theory of Capillarity. In Teubner; B. G. Teubner: Leipzig, Germany, 1894. [Google Scholar]
- Starov, V.M.; Velarde, M.G.; Radke, C.J. Wetting and Spreading Dynamics; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Arjmandi-Tash, O.; Kovalchuk, N.M.; Trybala, A.; Kuchin, I.V.; Starov, V. Kinetics of Wetting and Spreading of Droplets over Various Substrates. Langmuir 2017, 33, 4367–4385. [Google Scholar] [CrossRef] [PubMed]
- White, L.R. The contact angle on an elastic substrate. 1. The role of disjoining pressure in the surface mechanics. J. Colloid Interface Sci. 2003, 258, 82–96. [Google Scholar] [CrossRef]
- Ahmed, G.; Kalinin, V.V.; Arjmandi-tash, O.; Starov, V.M. Equilibrium of droplets on a deformable substrate: Influence of disjoining pressure. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 3–12. [Google Scholar] [CrossRef]
- Koursari, N.; Ahmed, G.; Starov, V.M. Equilibrium Droplets on Deformable Substrates: Equilibrium Conditions. Langmuir 2018, 34, 5672–5677. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, G.; Koursari, N.; Kuchin, I.V.; Starov, V.M. Hysteresis of Contact Angle of Sessile Droplets on Deformable Substrates: Influence of Disjoining Pressure. Colloids Surf. A 2018, 546, 129–135. [Google Scholar] [CrossRef]
- Carre, A.; Shanahan, M.E.R. Viscoelastic Braking of a Running Drop. Langmuir 2001, 2982–2985. [Google Scholar] [CrossRef]
- Jerison, E.R.; Xu, Y.; Wilen, L.A.; Dufresne, E.R. Deformation of an Elastic Substrate by a Three-Phase Contact Line. Phys. Rev. Lett. 2011, 106, 186103. [Google Scholar] [CrossRef] [PubMed]
- Park, S.J.; Weon, B.M.; Lee, J.S.; Lee, J.; Kim, J.; Je, J.H. Visualization of asymmetric wetting ridges on soft solids with X-ray microscopy. Nat. Commun. 2014, 5, 4369. [Google Scholar] [CrossRef] [PubMed]
- Schulman, R.D.; Dalnoki-Veress, K. Liquid Droplets on a Highly Deformable Membrane. Phys. Rev. Lett. 2015, 115, 206101. [Google Scholar] [CrossRef] [PubMed]
- Style, R.W.; Boltyanskiy, R.; Che, Y.; Wettlaufer, J.S.; Wilen, L.A.; Dufresne, E.R. Universal Deformation of Soft Substrates Near a Contact Line and the Direct Measurement of Solid Surface Stresses. Phys. Rev. Lett. 2013, 110, 066103. [Google Scholar] [CrossRef] [PubMed]
- Pericet-Cámara, R.; Best, A.; Butt, H.-J.; Bonaccurso, E. Effect of Capillary Pressure and Surface Tension on the Deformation of Elastic Surfaces by Sessile Liquid Microdrops: An Experimental Investigation. Langmuir 2008, 24, 10565–10568. [Google Scholar] [CrossRef] [PubMed]
- Pericet-Camara, R.; Auernhammer, G.K.; Koynov, K.; Lorenzoni, S.; Raiteri, R.; Bonaccurso, E. Solid-supported thin elastomer films deformed by microdrops. Soft Matter 2009, 5, 3611. [Google Scholar] [CrossRef]
- Lubbers, L.A.; Weijs, J.H.; Botto, L.; Das, S.; Andreotti, B.; Snoeijer, J.H. Drops on soft solids: Free energy and double transition of contact angles. J. Fluid Mech. 2014, 747. [Google Scholar] [CrossRef]
- Limat, L. Straight contact lines on a soft, incompressible solid. Eur. Phys. J. E 2012, 35, 134. [Google Scholar] [CrossRef] [PubMed]
- Marchand, A.; Das, S.; Snoeijer, J.H.; Andreotti, B. Contact Angles on a Soft Solid: From Young’s Law to Neumann’s Law. Phys. Rev. Lett. 2012, 109, 236101. [Google Scholar] [CrossRef] [PubMed]
- Bico, J.; Reyssat, É.; Roman, B. Elastocapillarity: When Surface Tension Deforms Elastic Solids. Annu. Rev. Fluid Mech. 2018. [Google Scholar] [CrossRef]
- Style, R.W.; Hyland, C.; Boltyanskiy, R.; Wettlaufer, J.S.; Dufresne, E.R. Surface tension and contact with soft elastic solids. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Andreotti, B.; Bäumchen, O.; Boulogne, F.; Daniels, K.E.; Dufresne, E.R.; Perrin, H.; Salez, T.; Snoeijer, J.H.; Style, R.W. Solid capillarity: When and how does surface tension deform soft solids? Soft Matter 2016. [Google Scholar] [CrossRef] [PubMed]
- Shuttleworth, R. The Surface Tension of Solids. Proc. Phys. Soc. Sect. A 1950, 63, 444. [Google Scholar] [CrossRef]
- Keddie, J.L.; Jones, R.A.L.; Cory, R.A. Size-Dependent Depression of the Glass Transition Temperature in Polymer Films. EPL Europhys. Lett. 1994, 27, 59–64. [Google Scholar] [CrossRef]
- Forrest, J.A.; Stevens, J.R.; Dutcher, J.R. Effect of Free Surfaces on the Glass Transition Temperature of Thin Polymer Films. Phys. Rev. Lett. 2002, 77, 8–11. [Google Scholar] [CrossRef]
- Winkler, E. The Theory of Elasticity and Strength with Special Reference to Their Application in the Art for Polytechnics, Building Academies, Engineers, Mechanical Engineers, Architects, Etc; H. Dominicus: Prague, Czech Republic, 1867. [Google Scholar]
- Starov, V. Static contact angle hysteresis on smooth, homogeneous solid substrates. Colloid Polym. Sci. 2013, 291, 261–270. [Google Scholar] [CrossRef]
- Kuchin, I.; Starov, V. Hysteresis of the Contact Angle of a Meniscus Inside a Capillary with Smooth, Homogeneous Solid Walls. Langmuir 2016, 32, 5333–5340. [Google Scholar] [CrossRef] [PubMed]
- Kuchin, I.; Starov, V. Hysteresis of Contact Angle of Sessile Droplets on Smooth Homogeneous Solid Substrates via Disjoining/Conjoining Pressure. Langmuir 2015, 31, 5345–5352. [Google Scholar] [CrossRef] [PubMed]
- Kerr, A.D. Elastic and Viscoelastic Foundation Models. J. Appl. Mech. 1964, 31, 491–498. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Churaev, N.V.; Muller, V.M. Surface Forces; Springer: New York, NY, USA, 1987. [Google Scholar]
- Gelfand, I.M.; Fomin, S.V. Calculus of Variations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Bormashenko, E.; Bormashenko, Y.; Whyman, G.; Pogreb, R.; Musin, A.; Jager, R.; Barkay, Z.; Uni, A.; Applied, W. Contact Angle Hysteresis on Polymer Substrates Established with Various Experimental Techniques, Its Interpretation, and Quantitative Characterization. Langmuir 2008, 8, 4020–4025. [Google Scholar] [CrossRef] [PubMed]
- Rioboo, R.; Voué, M.; Adão, H.; Conti, J.; Vaillant, A.; Seveno, D.; De Coninck, J. Drop impact on soft surfaces: Beyond the static contact angles. Langmuir 2010, 26, 4873–4879. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).