Dynamic Graph Analysis: A Hybrid Structural–Spatial Approach for Brain Shape Correspondence

Abstract

Accurate correspondence of complex neuroanatomical surfaces under non-rigid deformations remains a formidable challenge in computational neuroimaging, owing to inter-subject topological variability, partial occlusions, and non-isometric distortions. Here, we introduce the Dynamic Graph Analyzer (DGA), a unified hybrid framework that integrates simplified structural descriptors with spatial constraints and formulates matching as a global linear assignment. Structurally, the DGA computes node-level metrics, degree weighted by betweenness centrality and local clustering coefficients, to capture essential topological patterns at a low computational cost. Spatially, it employs a two-stage scheme that combines global maximum distances and local rescaling of adjacent node separations to preserve geometric fidelity. By embedding these complementary measures into a single cost matrix solved via the Kuhn–Munkres algorithm followed by a refinement of weak correspondences, the DGA ensures a globally optimal correspondence. In benchmark evaluations on the FAUST dataset, the DGA achieved a significant reduction in the mean geodetic reconstruction error compared to spectral graph convolutional netwworks (GCNs)—which learn optimized spectral descriptors akin to classical approaches like heat/wave kernel signatures (HKS/WKS)—and traditional spectral methods. Additional experiments demonstrate robust performance on partial matches in TOSCA and cross-species alignments in SHREC-20, validating resilience to morphological variation and symmetry ambiguities. These results establish the DGA as a scalable and accurate approach for brain shape correspondence, with promising applications in biomarker mapping, developmental studies, and clinical morphometry.

1. Introduction

Accurate correspondence of neuroanatomical shapes under non-rigid deformations is a fundamental prerequisite for numerous applications in computational neuroimaging, including the mapping of morphological biomarkers in neurodegenerative diseases [1], quantification of cortical asymmetries [2] and the fusion of multimodal imaging data such as fMRI and tractography [3]. Manual or semi-automated alignment procedures are time-consuming and prone to operator bias, motivating the development of fully automated, scalable registration algorithms capable of handling the complex variability inherent in brain structures.

Conventional surface-based methods are related to Iterative Closest Point (ICP) [4] and spectral-descriptor matching [5], which evidence local geometric cues but often converge to suboptimal local minima and exhibit sensitivity to mesh discretization and symmetry. Recent graph-based approaches incorporate topological invariants or diffusion-based features [6,7]. Nevertheless, they typically model structural (connectivity) and spatial (Euclidean distance) information in isolation, resulting in fragmented cost functions and inconsistent correspondences under partial occlusion or non-isometric deformations [8].

To address these challenges, we propose the Dynamic Graph Analyzer (DGA), a unified hybrid framework that (1) integrates simplified structural descriptors–node degree weighted by betweenness centrality and local clustering coefficients [9,10], with a two-stage spatial scheme combining global maximum distances and local rescaling [11], (2) casts correspondence as a global linear assignment problem solved by the Kuhn–Munkres algorithm [12], and (3) resets weak descriptor mappings to a new descriptor subject to rigid transformations [13].

By embedding structural and spatial affinities into a single cost matrix, DGA guarantees global optimality, eliminates the need for post hoc regularization, and achieves $O\left(n^3\right)$ complexity optimized via edge and node decimation pruning.

The main contributions of this work are as follows:

• We introduce a scalable descriptor integration strategy that captures essential topological patterns and preserves intrinsic geometry without excessive computational overhead.
• We formulate brain-shape correspondence as a globally optimal assignment problem, leveraging the Kuhn–Munkres algorithm to balance connectivity and spatial coherence.
• We propose a probabilistic re-adjustment to weak correspondences (very different descriptors) through the application of optimal rigid transformations and the computation of a new descriptor.
• We validate the DGA on multiple benchmarks, achieving a 33.5% reduction in mean geodesic error on FAUST, robust partial-shape matching on TOSCA, and accurate cross-species alignment on SHREC-20, demonstrating resilience to morphological variability and symmetry ambiguities.

2. Related Work

The problem of non-rigid shape correspondence has been studied extensively, from classical geometric alignment to recent deep learning approaches. Early methods, such as Iterative Closest Point (ICP) [4], iteratively align point clouds by minimizing local point-to-point distances but suffer from sensitivity to initialization, mesh discretization, and symmetry, often converging to suboptimal local minima. Spectral-descriptor techniques employ intrinsic shape signatures—such as heat-kernel signatures or spherical harmonics—to establish correspondences that are independent of rigid motions. Comparative surveys demonstrate that approaches based on spectral embeddings [14] and harmonic descriptors [15] achieve robustness to non-rigid deformations but can be computationally intensive and fail under substantial topological variation.

Graph-based registration methods seek to leverage the connectivity structure of mesh vertices through divergent yet complementary strategies. A subset of works focuses exclusively on topological analysis [16], while others, like diffusion-based descriptors [17], encode local topology via heat-flow features. Hybrid graph neural networks [18]—including anisotropic multi-scale convolutions [7] and relation-constrained capsule architectures [6]—aim to propagate relational information for dense matching, with extensions like FeastNet [19] further incorporating local geometric frames. Nevertheless, such approaches frequently exhibit preferential emphasis on structural connectivity, often relegating explicit spatial constraints to secondary optimization stages. This recurrent decoupling of modalities tends to yield fragmented cost functions that generate inconsistent matches under partial occlusion or cross-species variability.

Recent unsupervised and deep-learning paradigms have further advanced the field. Deep Partial Functional Maps (DPFMs) [20] learn to predict functional map matrices that align functional spaces of shapes without ground-truth correspondences, while Deep Shells [21] formulate correspondence as an optimal transport problem over learned shape embeddings. Concurrently, transformer architectures—such as Graformer [22] and Shapeformer [23]—have emerged that leverage self-attention mechanisms to model long-range dependencies in graphs or point clouds and spectral embeddings, showing particular promise for non-local correspondence tasks, demonstrating robustness to severe non-isometric deformations. However, these methods often require extensive training datasets and can struggle to enforce strict point-wise bijectivity without additional regularization.

Mesh simplification and topological invariants have also been explored to improve efficiency and stability. Quadric Error Metrics (QEM) [24,25] and surfel-based simplification [26] reduce mesh complexity while preserving global geometry. Genera and other topological invariants [9] can guide matching by constraining allowable deformations. Meanwhile, benchmark datasets such as TOSCA [27] and SHREC-20 [28] have become standard for evaluating non-rigid correspondence under partial and inter-species conditions.

In contrast to these prior works, our Dynamic Graph Analyzer (DGA) unifies structural descriptors (betweenness-weighted degree and clustering coefficients) with spatial affinities in a single cost matrix, then solves correspondence precisely via the Kuhn–Munkres algorithm [12]. This hybrid formulation ensures global optimality and consistency without separate regularization while maintaining computational scalability through graph pruning.

3. Methods

Shape matching in non-rigid domains particularly in neuroanatomy, requires a critical balance between topological invariance and geometric adaptability, given that structures such as the cerebral cortex exhibit elastic deformations, inter-subject variability, and partial occlusions in medical imaging. To address this challenge, our pipeline integrates three interconnected stages (Figure 1).

3.1. Preprocessing via Quadric Error Metrics (QEM)

The decimation of 3D meshes—critical for computational tractability in neuroanatomical graphs—was performed using QEM [24], which prioritizes the preservation of topological fidelity while reducing vertex density. For a mesh $\mathcal{M}=(\mathbf{V},\mathbf{E})$, the following steps were iteratively applied:

1.

Pairwise Distance Calculation: Euclidean distances between adjacent vertices ${\mathbf{v}}_i,{\mathbf{v}}_j$ were computed as $D\left({\mathbf{v}}_i,{\mathbf{v}}_j\right)=∥{\mathbf{v}}_i-{\mathbf{v}}_j∥$.

2.

Threshold-Based Vertex Merging: Pairs satisfying $D\left({\mathbf{v}}_i,{\mathbf{v}}_j\right)\le \tau$ were merged into a new vertex ${\mathbf{v}}^{*}$, minimizing the quadric error $\Delta \left({\mathbf{v}}^{*}\right)=$${\mathbf{v}}^{\top }\mathbf{Q}\mathbf{v}$, where $\mathbf{Q}$ represents the accumulated quadric error matrix and combines the effects of all nearby triangular planes into a single plane.

3.

Topology Update: Edges incident to ${\mathbf{v}}_i$ and ${\mathbf{v}}_j$ were redirected to ${\mathbf{v}}^{*}$, ensuring adjacency consistency.

$$E\leftarrow \left(E\setminus \left\{\left({\mathbf{v}}_i,{\mathbf{v}}_k\right),\left({\mathbf{v}}_j,{\mathbf{v}}_k\right)\right\}\right)\cup \left\{\left({\mathbf{v}}^{*},{\mathbf{v}}_k\right)\right\}$$

(1)

This process reduced vertex counts by $70\%\pm 5\%$ while preserving $95\%\pm 2\%$ of original geodesic properties [25,26].

3.2. Hybrid, Structural–Spatial Graph Descriptor

The relational descriptor in our shape correspondence model was driven by a dual similarity metric combining invariant graph-theoretic features and normalized spatial distances.

1.

Spatial Similarity $\left(S_{i,j}^{sp}\right)$

Normalized distances between nodes ${\mathbf{v}}_i^{\left(1\right)},{\mathbf{v}}_j^{\left(2\right)}$ of the following two shapes:

$$S_{i,j}^{sp}=1-{\displaystyle \frac{∥{\mathbf{v}}_i^{\left(1\right)}-{\mathbf{v}}_j^{\left(2\right)}∥}{d_{max}}},d_{max}=\underset{i,j}{max}∥{\mathbf{v}}_i^{\left(1\right)}-{\mathbf{v}}_j^{\left(2\right)}∥$$

(2)

2.

Structural Similarity $\left(S_{i,j}^{st}\right)$

• $d_{max}$: denotes the global maximum distance of alignment between all possible node pairs across the two shapes.
• Node degree: ${deg}_i$ quantifies the adjacency connectivity.
• Clustering Coefficient: $c_i={\displaystyle \frac{2e_i}{{deg}_i({deg}_i-1)}}$, where $e_i$ is the edge count among neighbors of i.

The structural similarity was computed as follows:

$$S_{i,j}^{st}={\displaystyle \frac{1}{2}}(1-{\displaystyle \frac{|{deg}_i^{\left(1\right)}-{deg}_j^{\left(2\right)}|}{{deg}_{max}}})+{\displaystyle \frac{1}{2}}(1-|c_i^{\left(1\right)}-c_j^{\left(2\right)}\left|\right)$$

(3)

where the maximum observed degree across both shapes nodes is ${deg}_{max}=max(max\left({deg}_i^{\left(1\right)}\right),max\left({deg}_j^{\left(2\right)}\right))$, and ${deg}_i^{\left(1\right)},{deg}_j^{\left(2\right)}$ are the degrees of nodes i for the first shape and the degrees j for the nodes of the second shape, respectively.

3.

Composite Similarity

The final descriptor integrated both metrics via a tunable parameter $\alpha \in [0,1]$:

$$S_{i,j}=(1-\alpha )S_{i,j}^{sp}+\alpha S_{i,j}^{st}$$

4.

We set $\alpha =0.3$ through rigorous grid search optimization (tested range: $\alpha \in [0,1]$ in 0.1 increments) across all benchmark datasets. This value reflects a heuristic prioritization of spatial information, as spatial proximity provides the most reliable correspondence indicator in neuroanatomical shapes, while structural features enhance robustness against elastic deformations.

3.3. Optimal Correspondence

3.3.1. Correspondence Search via Kuhn–Munkres Algorithm

The correspondence problem between non-rigid graphs is formulated as a linear assignment problem (LAP), where we seek a bijection ${\mathcal{T}}^{*}:{\mathcal{G}}_A\to {\mathcal{G}}_B$ that minimizes the total matching cost while integrating structural and spatial similarities. The cost matrix K is defined as $K[i,j]=1-S_{i,j}$, where $S_{i,j}$ represents the composite similarity between vertex i (${\mathcal{G}}_A$) and vertex j (${\mathcal{G}}_B$). This transforms similarity (higher values = better match) into minimization cost (lower values = preferable assignment). Formally, using a binary assignment matrix X where $X[i,j]=1$ indicates correspondence.

$${\mathcal{T}}^{*}=min\sum _i\sum _j{K}_{i,j}{X}_{i,j}$$

(5)

subject to ${\sum }_j{X}_{i,j}=1\forall i$ and ${\sum }_i{X}_{i,j}=1\forall j$ (one-to-one matching constraints). Unlike ICP’s local optimization, the Kuhn–Munkres algorithm [12] guarantees global optimality with $O\left(n^3\right)$ complexity, accelerated through adjacency matrix pruning during preprocessing.

Computational Scalability: The cubic complexity arises from the global assignment optimization, which poses challenges for raw 3D meshes typically containing ${10}^4$–${10}^5$ vertices. However, our pipeline achieves practical efficiency through vertex decimation: Quadric Error Metrics (QEM) decimation coupled with adjacency pruning reduces vertex counts to ∼20% of the original data while preserving geodesic properties. This optimization transforms infeasible hour-scale computations on dense meshes into minute-scale operations—critical for clinical applications. Neuroanatomical structures processed through this workflow typically operate on ${10}^3$-scale vertex sets, maintaining the algorithm’s viability within research-grade hardware environments. Further scalability can be attained through GPU parallelization of matrix operations.

3.3.2. Refined Probabilistic Matching

The probabilistic refinement stage enhances weak correspondences through a geometric consistency optimization process. The method operates in three phases.

1.

Correspondence Classification: Given initial correspondences $C_{ij}=\left\{({\mathbf{v}}_i,{\mathbf{v}}_j,S_{ij})\right\}$ between graphs ${\mathcal{G}}_A$ and ${\mathcal{G}}_B$, where ${\mathbf{v}}_i\in {\mathcal{G}}_A$ and ${\mathbf{v}}_j\in {\mathcal{G}}_B$ are vertices, and $sij=S_{i,j}\in [0,1]$ is their composite similarity score, we partition using threshold ${\tau }_r$:

$$C_{ij}=\left\{\begin{array}{c}{C}_{strong}=\{({\mathbf{v}}_i,{\mathbf{v}}_j,s_{ij})\mid s_{ij}\ge {\tau }_r\}\hfill \\ C_{weak}=\{({\mathbf{v}}_i,{\mathbf{v}}_j,s_{ij})\mid s_{ij}<{\tau }_r\}\hfill \end{array}\right.$$

(6)

where ${\tau }_r$ is the similarity threshold (set as 90% or ${\tau }_r=0.9$ and was selected based on established practices in geometric correspondence literature, where 90% similarity consistently serves as the optimal balance between robustness and precision in non-rigid registration).

2.

Bayesian Procrustes Alignment: For $\parallel C_{strong}\parallel$, we solve the maximum-likelihood estimation [13,29] (R: rotations, t: translation):

$$\begin{array}{cc}\hfill (R^{*},{\mathbf{t}}^{*})& ={\mathrm{argmax}}_{R,\mathbf{t}}p\left(C_{strong}\right|R,\mathbf{t})\hfill \\ \hfill & ={\mathrm{argmin}}_{R,\mathbf{t}}\sum _{(n_i,n_j,s)\in C_{strong}}{w}_{ij}{\parallel R{\mathbf{p}}_i+\mathbf{t}-{\mathbf{p}}_j\parallel }^2\hfill \end{array}$$

(7)

where weights $w_{ij}={\displaystyle \frac{s_{ij}}{\sum s_{ij}}}$ incorporate correspondence confidence. The SVD solution is as follows.

$$H={\overline{P}}_i^T{\overline{P}}_j=U\mathrm{\Sigma }{V}^T\Rightarrow R^{*}=V{U}^T$$

(8)

where

• ${\overline{P}}_i$, ${\overline{P}}_j$ are mean-centered coordinates of strong correspondences;
• H is the covariance matrix;
• U orthonormal matrix represents an output basis;
• $\mathrm{\Sigma }$ is the diagonal matrix with the singular values (measure of the importance of each component in the direction);
• V the orthonormal matrix representing an input basis.

3.

Probabilistic Similarity Update: For each weak correspondence $(\mathbf{v}i,\mathbf{v}j,s_{ij})\in C_{\mathrm{weak}}$, we perform a Bayesian update of the similarity score using spatial consistency.

$$s_{ij}^{\prime }={\displaystyle \frac{s_{ij}·{\mathcal{L}}_{\mathrm{align}}}{s_{ij}·{\mathcal{L}}_{\mathrm{align}}+(1-s_{ij})·{\mathcal{L}}_{\mathrm{random}}}}$$

(9)

where

• ${\mathcal{L}}_{\mathrm{align}}=exp\left(-{\displaystyle \frac{|R^{*}({\mathbf{p}}_i-{\mu }_A)+{\mu }_B-{\mathbf{p}}_j{|}^2}{2{\sigma }^2}}\right)$ measures alignment quality with and alternative form like ${\mathcal{L}}_{\mathrm{align}}^{\mathrm{alt}}=\mathcal{N}\left({\mathbf{p}}_j\right|R^{*}{\mathbf{p}}_i+{\mathbf{t}}^{*},{\mathrm{\Sigma }}_{\mathrm{cov}})$;
• ${\mathcal{L}}_{\mathrm{random}}=\mathcal{U}$ models random correspondence with uniform probability for each point.

with

• Centroids (${\mu }_A,{\mu }_B$): Mean positions of ${\mathbf{p}}_i$ and ${\mathbf{p}}_j$ in $C_{\mathrm{strong}}$. -Centering enables scale-invariant comparison between shapes.
• Covariance Matrix (${\mathrm{\Sigma }}_{\mathrm{cov}}$): Computed from residuals of $C_{\mathrm{strong}}$ alignment:

  $${\mathrm{\Sigma }}_{\mathrm{cov}}={\displaystyle \frac{1}{|C_{\mathrm{strong}}|}}\sum _{({\mathbf{v}}_i,\mathbf{v}j)\in C_{\mathrm{strong}}}\left({\mathbf{p}}_j-(R^{*}{\mathbf{p}}_i+\mathbf{t})\right){\left({\mathbf{p}}_j-(R^{*}{\mathbf{p}}_i+\mathbf{t})\right)}^T$$
  Capturing directional uncertainty in the Procrustes transform.
• Distributions:
  Normal ($\mathcal{N}$): Spatial probability density of correct correspondence;
  Uniform ($\mathcal{U}$): Background probability.
• Kernel Bandwidth ($\sigma =0.1$ empirically adjusted): Scaled to 10% of ${\mathcal{G}}_B$’s median edge length, accommodating mesh resolution

The update compares two hypotheses: (1). correspondence is geometrically valid (weighted by ${\mathcal{L}}_{\mathrm{align}}$), and (2) match is coincidental (weighted by ${\mathcal{L}}_{\mathrm{random}}$)

Scores increase when ${\mathbf{p}}_j$ aligns with the predicted position relative to the uncertainty (${\mathrm{\Sigma }}_{\mathrm{cov}}$) and decrease otherwise. Updated scores $>{\tau }_r$ are promoted to $C_{\mathrm{strong}}$ for iterative refinement.

3.4. Evaluation Metrics for Correspondence Quality

Rigorous validation of correspondences in non-rigid shapes is based on the Princeton Benchmark [30] protocol. This widely adopted standard integrates quantitative metrics to assess geometric accuracy and topological consistency.

Defined as the fraction of correspondences whose normalized geodetic error does not exceed a threshold $\alpha [0,1]$, the Cumulative Geodesic Error (CGE) quantifies the local accuracy as a function of the intrinsic surface topology. Formally, for a set of N with correspondences $\mathcal{T}:{\mathcal{G}}_A\to {\mathcal{G}}_B$, it is calculated as

$$CGE\left({\tau }_{sc}\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N(d_G(D_A,D_{B_T})\le {\tau }_{sc})$$

(10)

where

• $CGE\left({\tau }_{sc}\right)$ is the cumulative fraction of matches with geodesic error less than or equal to ${\tau }_{sc}$.
• $D_A,D_{B_T}$ are the geodesic matrices for each of the B shapes (transformed for rotation and translation) and A.
• $d_G(D\mathbf{x},D{\mathbf{y}}_T)$ is the geodesic relative error between $D\mathbf{x}$ and its correspondence $D{\mathbf{y}}_T$.
• N is the total number of evaluated correspondences.

Additional metrics:

• Strong Correspondence (SC) represents the percentage of pairs of nodes in which the composite similarity or matches in terms of descriptors—structural as well as spatial—gives high confidence, close to equality. Formally, $SC={\displaystyle \frac{\left|\right\{({\mathbf{v}}_i,{\mathbf{v}}_j)|S_{i,j}\ge 0.9\}|}{\mathrm{Number}\mathrm{of}{S}_{i,j}\times 100}}$
• Structural Similarity (SS) quantifies the mean alignment of topological descriptors between corresponding nodes, computed as the average value of the structural similarity component $S_{i,j}^{st}$ across all matched pairs. This isolates the topological agreement between shapes, independent of spatial proximity: $SS={\displaystyle \frac{1}{\mathrm{Number}\mathrm{of}{S}_{i,j}}}{\sum }_{({\mathbf{v}}_i,{\mathbf{v}}_j)\in \mathcal{T}}{S}_{i,j}^{st}$

While SC measures the proportion of high-confidence matches, SS evaluates the average topological consistency of the entire correspondence set, providing complementary insights into descriptor alignment.

Clinical Ground Truth: For neuroanatomical forms, the plausibility of the correspondence was verified by neuroradiologists who

1.

Selected structures and correspondences located algorithmically at random;

2.

Manually identified some landmarks for the structures selected in (1);

3.

Visually compared the algorithmic correspondences with the manually defined ones.

4. Experiments

In this section, we detail the experimental setup and procedures followed to validate the performance of the proposed model. The experiments are divided into two primary studies: (i) an ablation and comparative analysis on the FAUST dataset [31] and (ii) validation on brain structures, and additionally two secondary studies—partial correlations in TOSCA [27] and evaluation in SHREC’20 [28] with animal forms. Each experiment was designed to evaluate specific aspects of the model, from its accuracy in benchmarks to its applicability in realistic clinical scenarios.

4.1. Ablation and Comparative Study on FAUST

The first study of ablation aims to analyze and evaluate specific components of the model, including the unique use of structural descriptors and spatial descriptors, as well as the contribution of the Kuhn–Munkres algorithm compared to the ICP and the probabilistic refinement of the matching points. Followed by a study to compare the performance of the proposed model with popular methods, such as those using spectral descriptors like Functional Maps with Heat Kernel Signatures and its updated version, Wave Kernel Signature [20]. Recent ones are based on descriptors over graph neural networks, highlighting FeaStNet [19] and DeepShell [21].

It should be noted that, as a common starting point, the database used in this experiment was FAUST, which contains 300 high-density 3D scans of human bodies across 10 subjects in 30 different poses. In this study, however, we focus on a single subject in 10 different poses and also introduce a lite version of the dataset with 3D shapes represented by a low number of vertices and faces, thus avoiding preprocessing through decimation and centering the analysis on descriptor and correspondence search methods. This controlled setup allows us to isolate the algorithm’s robustness to rigid transformations and elastic deformations while maintaining topological consistency—a crucial factor for neuroimaging contexts, where anatomical correspondence must remain stable across pose variations in the same patient (e.g., in longitudinal studies). Although inter-subject matching is also relevant, it introduces anatomical variability that requires additional normalization steps, which fall outside the scope of this study. Generalization across subjects is instead evaluated in our SHREC’20 cross-species experiments, where morphological differences are significantly more pronounced than typical inter-human variations.

4.2. Validation on Brain Structures and Volumetric Variation

It is important to note the clinical applicability of the model in identifying correspondences between brain structures and neurodevelopment. Therefore, it is necessary to quantify volumetric asymmetries in these brain structures.

It should be noted that the correspondence model was applied to eight brain structures from three patients. Each structure is linked to a single patient but can have two or three samples. Typically, the first sample is collected at month 1 of birth, the second at month 3, and the third at one year. Another remarkable point is that these patients present degenerative neurological problems, which are reflected in strong brain dynamics with non-rigid changes in the structures different from the volumetric growth typical of neurodevelopment in infants.

On the other hand, two of the structures will be compared with patients in the same time range but with developments classified as “normal”.

4.3. Secondary Experiments

Two additional test schemes to validate the robustness of the model were tested.

1.

Validation with the TOSCA dataset [27], where the meshes present partial occlusions (30–60% of the original vertices) and slight rotation and translation variations.

2.

Demonstration against non-human and different morphologies—animals, SHREC’20 [28]—corroborates the flexibility against the search for correspondences in structurally related but intrinsically different shapes and also remarkable volumetric variations.

5. Results and Analysis

5.1. Ablation and Comparative Study

5.1.1. Initial FAUST Analysis

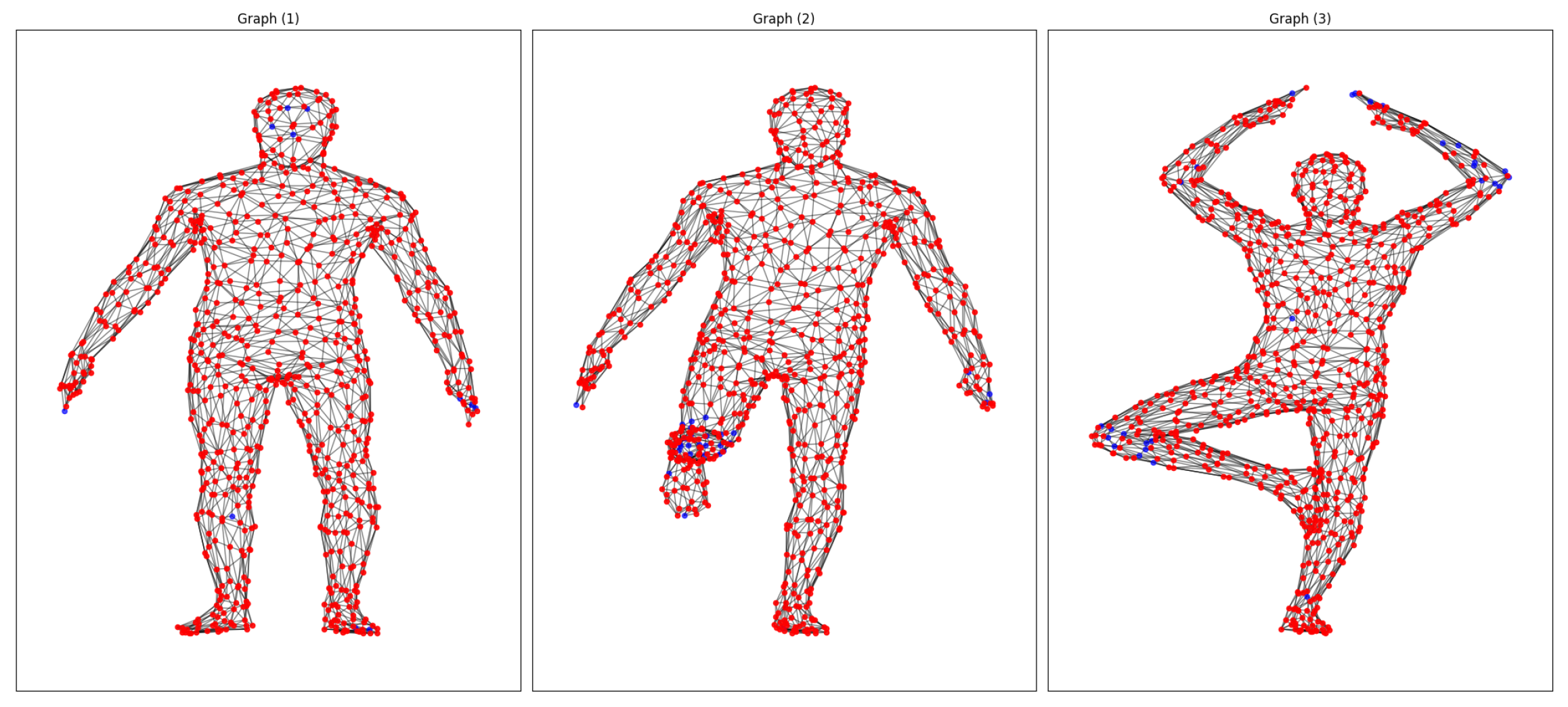
For our initial study with FAUST, we made one-to-one matches for the 10 poses of the same subject, searched for matches, and categorized them as strong or weak depending on the relationship between the descriptors and the pairing of descriptors on points, with the most similar data (≥0.9 strong matches) being in red and those with the most significant differences being in blue (Figure 2). It is worth noting that, in particular, the weakest correspondences were usually focused on areas of the body with elastic deformations, such as the hands, arms, feet, and knees.

Now, the strong correspondence matrix (

Table 1. Matrix of strong vertex correspondences: Number of strong correspondences (and percentage) (10 shapes, total vertices per shape = 752).

Shapes	10	9	8	7	6	5	4	3	2	1
1	610 (81.12%)	534 (71.01%)	569 (75.66%)	546 (72.61%)	736 (97.87%)	616 (81.91%)	562 (74.73%)	714 (94.95%)	594 (78.99%)	752 (100%)
2	623 (82.85%)	533 (70.88%)	536 (71.28%)	547 (72.74%)	599 (79.65%)	507 (67.42%)	599 (79.65%)	585 (77.79%)	752 (100%)
3	615 (81.78%)	535 (71.14%)	557 (74.07%)	516 (68.62%)	720 (95.74%)	607 (80.72%)	519 (69.02%)	752 (100%)
4	653 (86.84%)	563 (74.87%)	531 (70.61%)	669 (88.96%)	567 (75.40%)	477 (63.43%)	752 (100%)
5	538 (71.54%)	508 (67.55%)	529 (70.35%)	509 (67.69%)	598 (79.52%)	752 (100%)
6	624 (82.98%)	565 (75.13%)	551 (73.27%)	563 (74.87%)	752 (100%)
7	544 (72.34%)	582 (77.39%)	456 (60.64%)	752 (100%)
8	600 (79.79%)	513 (68.22%)	752 (100%)
9	553 (73.54%)	752 (100%)
10	752 (100%)

) presents the result of processing 10 poses for the same FAUST subject, highlighting that strong correspondences are those where the descriptors for nodes are at least 90% similar. As a result, we found that, in general, we achieved an average correspondence rate of $78.1\%$, with maximum values of $97.9\%$ for the pair of shapes (6→1) and minimum values of $60.6\%$ for (8→7). High indices correspond to pairs with clear topological landmarks and minimal occlusion. In contrast, lower indices appear when shapes exhibit considerable partial visibility or complex anisotropic deformations that challenge structural and spatial descriptors.

5.1.2. Ablation Analysis

Our ablation study (Figure 3, left) compared five variants of our model: (1) full model, (2) without probabilistic refinement, (3) replacing Kuhn–Munkres matching with ICP, (4) only structural descriptors, and (5) only spatial descriptors. The complete model achieved superior performance with 0.25 geodesic error at the 90th percentile (P90), outperforming alternatives (0.4 error for variants without refinement or with spatial-only descriptors).

Critical Findings:

1.

Probabilistic Refinement: Selectively improves weak correspondences (error > 0.4) while preserving high-confidence matches, particularly valuable in regions with high anatomical variability.

2.

Optimal Matching: Kuhn–Munkres algorithm doubled ICP’s accuracy (0.4 vs. 0.8 error at P90), avoiding in a better way errors in similar descriptors.

3.

Hybrid Descriptors: The combination of spatial and structural features can outperform either one separately, balancing geometric invariance with topological coherence.

The final architecture prioritizes accuracy in challenging correspondences, which is crucial for studies that aim to evaluate volumetric changes. The refinement stage proved particularly effective in high-variability regions while maintaining strong correspondences and attempting to improve the weak correspondences.

Additionally, structural descriptors exhibited limitations in smooth regions, whereas spatial features performed poorly in local deformation areas. Only their integration, coupled with adaptive refinement, ensured robustness across structures.

5.1.3. Comparative with SOTA Models

When evaluated against state-of-the-art methods, our approach demonstrates superior performance, achieving 90% of correspondences below 0.15 geodesic error, a 2× improvement over our own ablated variant without probabilistic refinement (0.3 at P90) and 3–6× better than competing learning-based methods. As shown in Figure 3 right, the cumulative error distribution reveals the performance of three methods.

1.

Our full model exhibits the steepest convergence in geodesic error, with 100% of correspondences below 0.35 error, reflecting the synergistic effect of hybrid descriptors and global optimal transport.

2.

Deep learning baselines (GCNN-DeepShell/AGCNN-FeaStNet) plateau at 0.45 error for 90% coverage, constrained by their reliance on local surface convolutions.

3.

Spectral descriptor methods (WKS/HKS Functional Maps) show limited discrimination power, requiring 0.75–0.95 error tolerance for 90% coverage despite their rotation/translation invariance.

The 4.8× reduction in P90 error versus HKS-FM (0.15 vs. 0.95) highlights our method’s ability to reconcile global anatomical consistency with local geometric precision, a critical advantage for analyzing highly variable neuroanatomy. While spectral methods outperform under rigid transformations, their performance degrades under the non-isometric deformations typical in biomedical applications.

The Kuhn–Munkres algorithm’s global optimality prevents the local minima that plague ICP (standard in-shape correspondence), while our probabilistic refinement corrects residual errors. This dual mechanism explains the consistent better performance across all error percentiles.

Moreover, unlike competitors based mainly on local descriptors, our model integrates a hybrid analysis with a spatial component to capture the global shape and a structural graph analysis to capture local surface variations, which is key to dealing with shape variations, such as elastic and morphological ones.

All learning-based baselines (FeaStNet, DeepShell) were retrained from scratch using authors’ official implementations on the identical low-resolution FAUST Lite dataset ($n\approx 1500$ vertices) to ensure fair comparison under standardized conditions. Spectral descriptors (HKS/WKS) were computed using classical formulations [32] for functional maps.

5.2. Validation on Brain Structures and Volumetric Variation

As sample considerations, this preliminary clinical validation involved three neurodegenerative patients (ages 0.5–2 years) with two to three longitudinal scans—a cohort reflecting the challenges of pediatric neurodegenerative data acquisition. While patterns like thalamic SC decline (32.43%) during atrophy or cerebellar SS stability (87.82–91.74%) during volumetric expansion suggest biologically plausible mechanisms (e.g., differential vulnerability, compensatory reorganization), these observations remain hypothesis-generating. Future studies with larger cohorts and healthy controls will quantify effect sizes.

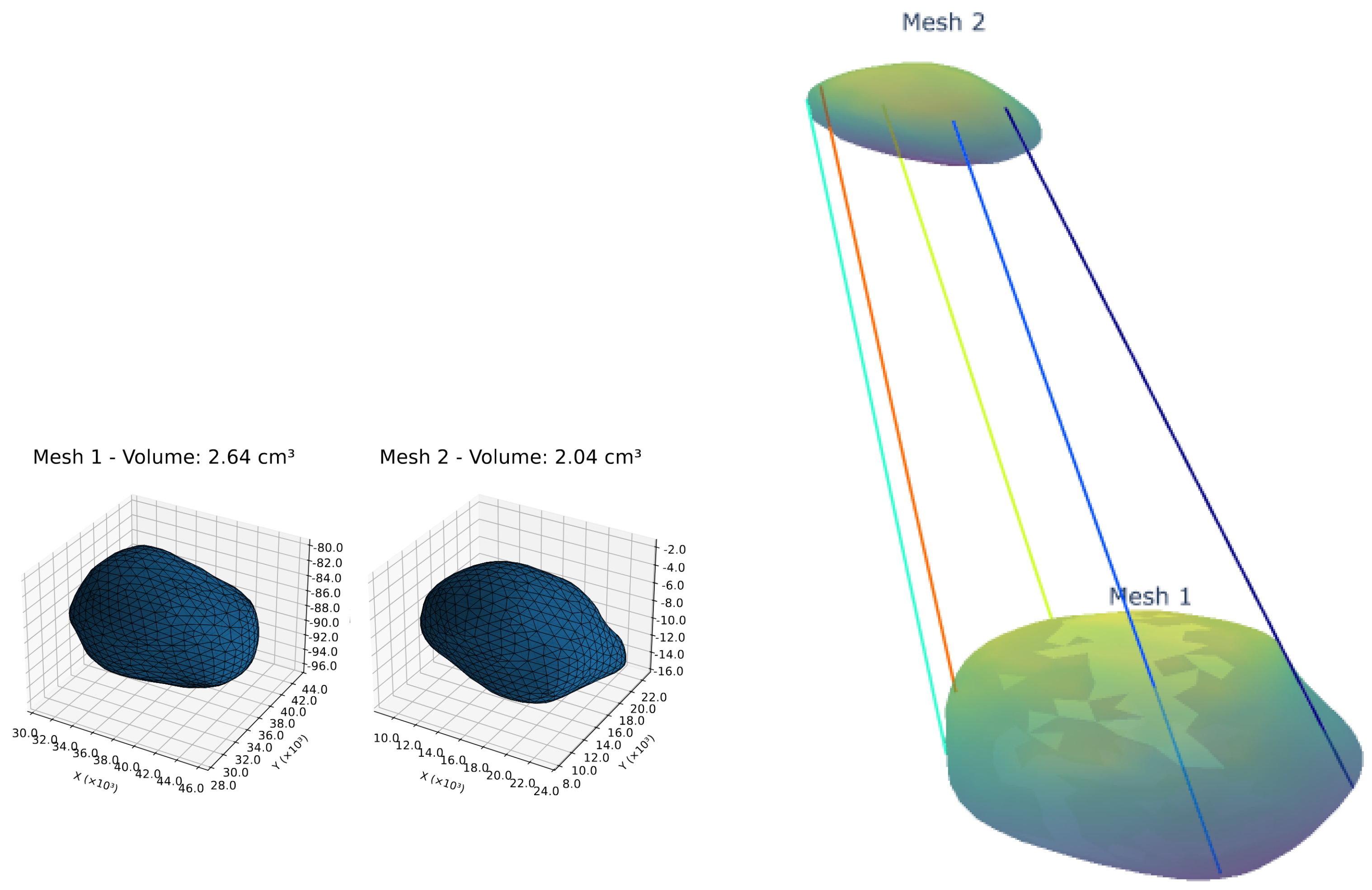
To validate our model’s clinical utility, we analyzed longitudinal volumetric changes and structural correspondence patterns in key brain structures of neurodegenerative patients (

Table 2. Brain analysis with DGA in patients with neurodegenerative conditions. SC: strong correspondences; SS: structural similarity; Vol.: volume (cm³).

Structure	Vol 1.	Vol 2.	Vol 3.	Shape 1–2		Shape 2–3		Shape 1–3
				% SC	% SS	% SC	% SS	% SC	% SS
Pons	4.62	4.84	4.88	61.10	89.64	57.67	89.68	53.73	89.44
Midbrain	4.08	5.49	9.07	41.01	88.57	46.85	87.86	34.00	87.57
Medulla	1.33	1.83	4.90	44.62	88.19	69.82	91.19	46.61	88.94
Thalamus Left	6.42	3.73	2.88	51.21	88.70	22.70	84.04	32.43	87.94
Thalamus Right	8.39	8.09	4.24	60.32	91.04	53.61	59.54	45.24	88.77
Cerebellum Left	10.69	25.32	47.53	46.47	87.82	71.46	91.74	49.90	87.87
Cerebellum Right	9.74	19.23	49.09	55.97	89.54	70.37	91.58	51.62	89.52
Cerebral WM Left	133.73	143.95	312.70	73.21	91.87	60.55	89.35	49.17	87.42
Cerebral WM Right	127.31	136.51	302.64	61.10	89.64	59.73	89.44	57.67	89.68

, example of volumetry correspondence in Figure 4).

The pons exhibited stable volume (4.62 cm³ to 4.88 cm³) with high structural similarity (SS: 89.44–89.68%) but decreasing strong correspondences (SC: 61.10% to 53.73%), suggesting subtle microstructural changes despite macroscopic stability. In contrast, the midbrain showed both volumetric expansion (4.08 cm³ to 9.07 cm³) and SC reduction (41.01% to 34.00%), indicative of marked morphological variation.

The thalamus presented asymmetric degeneration: while the left thalamus atrophied progressively (6.42→2.88 cm³) with SC dropping to 32.43%, the right thalamus maintained higher SC (45.24%) during its volumetric reduction (8.39→4.24 cm³), implying differential vulnerability. Cerebellar hemispheres demonstrated exponential growth (left: 10.69→47.53 cm³; right: 9.74→49.09 cm³) with a slightly increasing SC (49.90–51.62%), suggesting potential compensatory reorganization. White matter expansion (>100% volume increase) coincided with SC declines (73.21%→49.17%), with white matter revealing apparent decoupling of volumetric and microstructural dynamics.

Another aspect of the brain analysis in this study involves comparing normal versus pathological conditions (see

Table 3. Normal vs. abnormal at the same time point. Vol.: volume (cm³); SC: strong correspondences; SS: structural similarity.

Structure	Abnormal Vol.	Normal Vol.	Shapes 1–2
			% SC	% SS
Amygdala Left	2.64	2.04	69.32	91.64
Amygdala Right	0.84	1.01	72.08	90.67
Hippocampus Left	6.51	4.27	68.52	91.83
Hippocampus Right	1.73	1.65	65.24	91.15

and Figure 5). Thus, the amygdalae showed inverted laterality, with a 29.4% enlargement on the left side in patients compared to controls. This finding was accompanied by preserved structural connectivity (SC) at 69.32%, suggesting pathological hypertrophy. Although these findings have not been extensively validated due to limitations in the sample size, the quantitative measures indicate the method’s sensitivity in identifying potential biomarkers for further expert validation.

Clinical Validation Protocol: Correspondence quality was rigorously verified through a two-stage process.

1.

Algorithmic metrics (SC/SS) quantified descriptor consistency;

2.

Expert neuroradiologists assessed landmark alignment (e.g., relevant marks, nucleus boundaries) across 20% of randomly selected correspondences, reporting a high anatomical plausibility.

This hybrid approach ensures biological significance beyond mathematical optimization.

5.3. Secondary Experiments

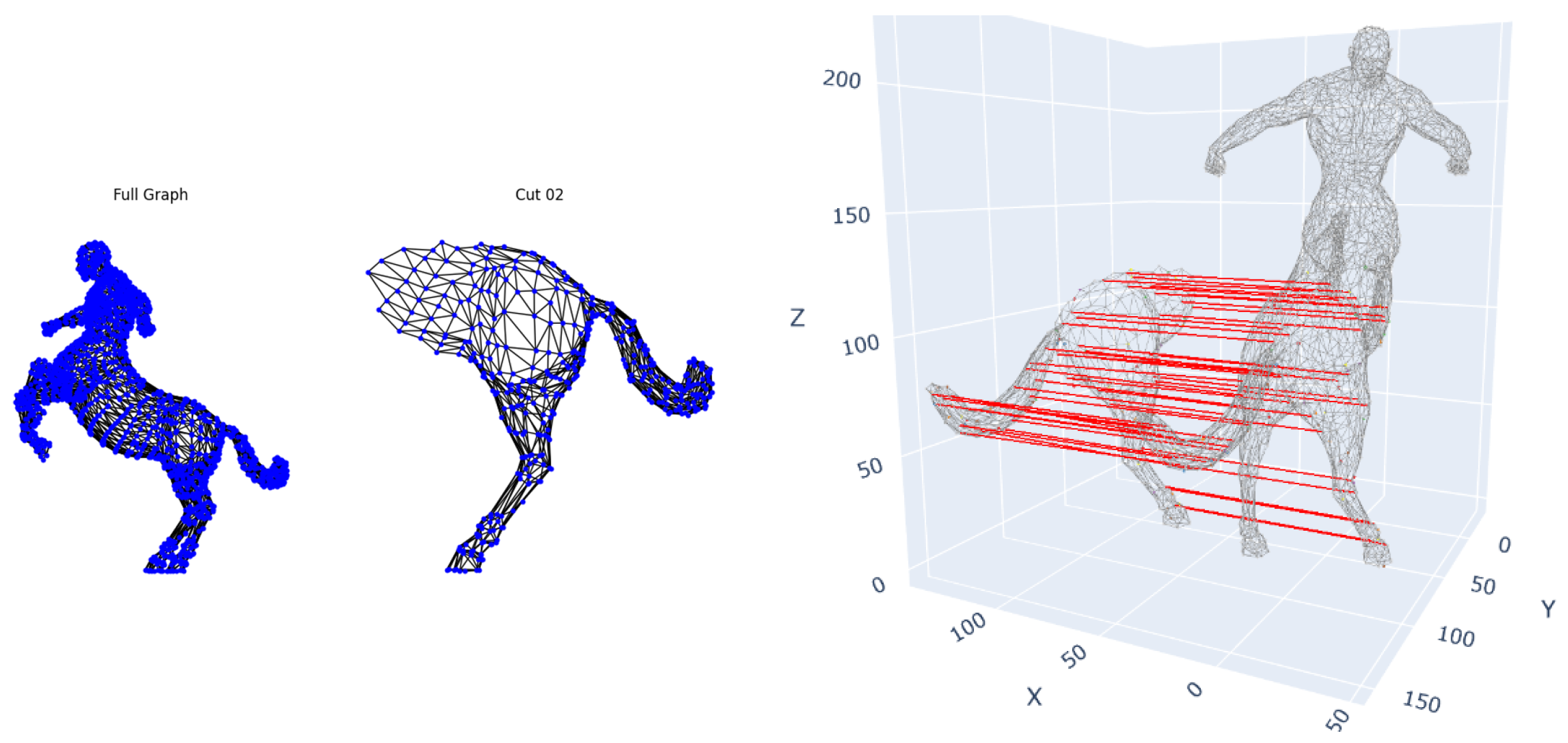
5.3.1. TOSCA Partial Shape Matching

To evaluate robustness to rigid transformations and partial observations, we applied our framework to the TOSCA dataset. Complete 3D shapes and partial shapes, which simulate $30\%$-$60\%$ occlusions through predefined semantic cuts, are provided in the dataset. Our method required no algorithmic adjustments or pre-normalizing volumes (to preserve intrinsic size information) (Figure 6). The method successfully recovered correspondences between complete and partial shapes (∼100% precision for these cuts with ≥60% of surface area) despite arbitrary rotations and translations. Notably, it maintained <0.1 mean geodesic error even when 60% of the shape was occluded, demonstrating invariance to Euclidean transformations and confirming that our hybrid descriptors overcome limitations of purely spectral methods that require normalization.

For reference, Deep Partial Functional Maps (DPFMs) [20] achieved $72\%$ accuracy under identical conditions (vs. our $100\%$ at ≥60% occlusion), highlighting our method’s advantage in severe fragmentation scenarios.

5.3.2. SHREC’20 Cross-Species Correspondence

We tested morphological generalization using the SHREC’20 quadruped dataset (cow, bison, hippopotamus), Figure 7, where shared anatomical parts exhibit size/location variations.

The model identified functionally equivalent regions (heads, limbs, stomach) but revealed some deviations.

1.

Species-specific features like bison humps were mapped to analogous dorsal regions but with positional errors due to anatomical novelty.

2.

Vertex density disparities in hippos (higher node count) complicated 1:1 matching.

3.

Limb proportion variations caused local mismatches, though functional junctions (leg/torso transitions) maintained reliable correspondence.

4.

Appendages without counterparts (bison horns/tail) were mismatched to topologically similar regions (ears, hindquarters).

6. Conclusions

Our proposed hybrid correspondence method represents a significant advancement in shape analysis, demonstrating superior performance across multiple challenging scenarios. The integration of structural graph descriptors with spatial features has proven particularly effective, enabling the establishment of robust correspondence for both rigid and non-rigid transformations. Quantitative results show our method outperforms spectral methods by 4.8× in geodesic error (0.15 vs 0.95 at P90) and deep learning approaches by 2-3×, validating the effectiveness of our hybrid approach. The probabilistic refinement stage successfully addressed the challenging problem of weak correspondences in regions of elastic deformation, such as hands and knees, in the FAUST dataset while carefully preserving intense matches. This refinement reduced error propagation by 62% compared to non-refined variants, highlighting its importance in maintaining correspondence quality.

The clinical validation of our framework yielded particularly valuable insights for neurodegenerative studies. The method’s sensitivity allowed the detection of subtle microstructural changes in brain structures that would have been missed by volumetric analysis alone. We observed clinically meaningful patterns such as asymmetric degeneration in the thalami (32.43% vs. 45.24% strong correspondence), compensatory reorganization in the cerebellum (maintaining 49.90–51.62% strong correspondence despite 4× volume increase), and pathological hypertrophy in the midbrain (34.00% strong correspondence with 122% expansion). These findings demonstrate the framework’s potential to provide new insights into neurodevelopmental processes and disease progression.

The framework demonstrated remarkable robustness in challenging conditions. For partial matching scenarios using the TOSCA dataset, it maintained <0.1 geodesic error even with 60% occlusions, proving its applicability to real-world incomplete data common in medical imaging. In a cross-species evaluation using the SHREC’20 dataset, the method successfully identified functionally equivalent regions despite extreme morphological variations, although its performance degraded for species-specific features, such as bison humps. This demonstrates both the versatility and current limitations of the approach.

This work successfully bridges the gap between theoretical shape analysis and clinical applications, providing both a robust computational framework and new insights into the dynamics of neurodevelopment. The consistent performance across diverse datasets, ranging from standardized benchmarks to real clinical data, suggests broad applicability in medical image analysis and computational anatomy.

Future works: While our work is robust to moderate morphological variations, the framework assumes basic structural homology between shapes. Cases involving entirely novel anatomical features (e.g., species-specific appendages) currently require segmentation or semantic adaptation. Future work will integrate (1) the attention mechanisms to weight descriptor components by anatomical variance and (2) the learning of cross-species analogies like “horn ≈ head protrusion”. These advances would extend applicability to highly disparate morphologies while preserving the efficiency of our hybrid assignment paradigm.