MCTS-Based Policy Improvement for Reinforcement Learning
Abstract
1. Introduction
2. Related Work
3. Contribution
- MCTS is used to optimize the batch sequence during training. This means that several batches are sampled from the memory buffer at the end of every single episode. The batches are used individually to conduct policy updates, and this process is handled as a planning task for MCTS. Consequently, during the training process, MCTS constructs a tree where the MCTS aims to find the path from the root, which is the untrained agent, to a leaf where the agent reaches the best possible performance with the given memory buffer.
- We differentiate our method from established sample prioritization methods by moving focus away from fine-grained assessment of each sample’s contribution to the agent’s policy and towards focusing on the sequence of experiences, choosing a more coarse-grained approach of treating whole randomly drawn batches as chunks of experiences to be ordered as an efficient curriculum.
- We also differentiate the proposed method from any other Curriculum Learning strategies in the literature for RL or SL problems, since our method does not use any heuristic or principle for ordering the batches during training, such as simple samples first, but uses the MCTS algorithm, which can yield the optimal sequence with sufficient iteration.
4. Methodology
4.1. Baseline RL Algorithms
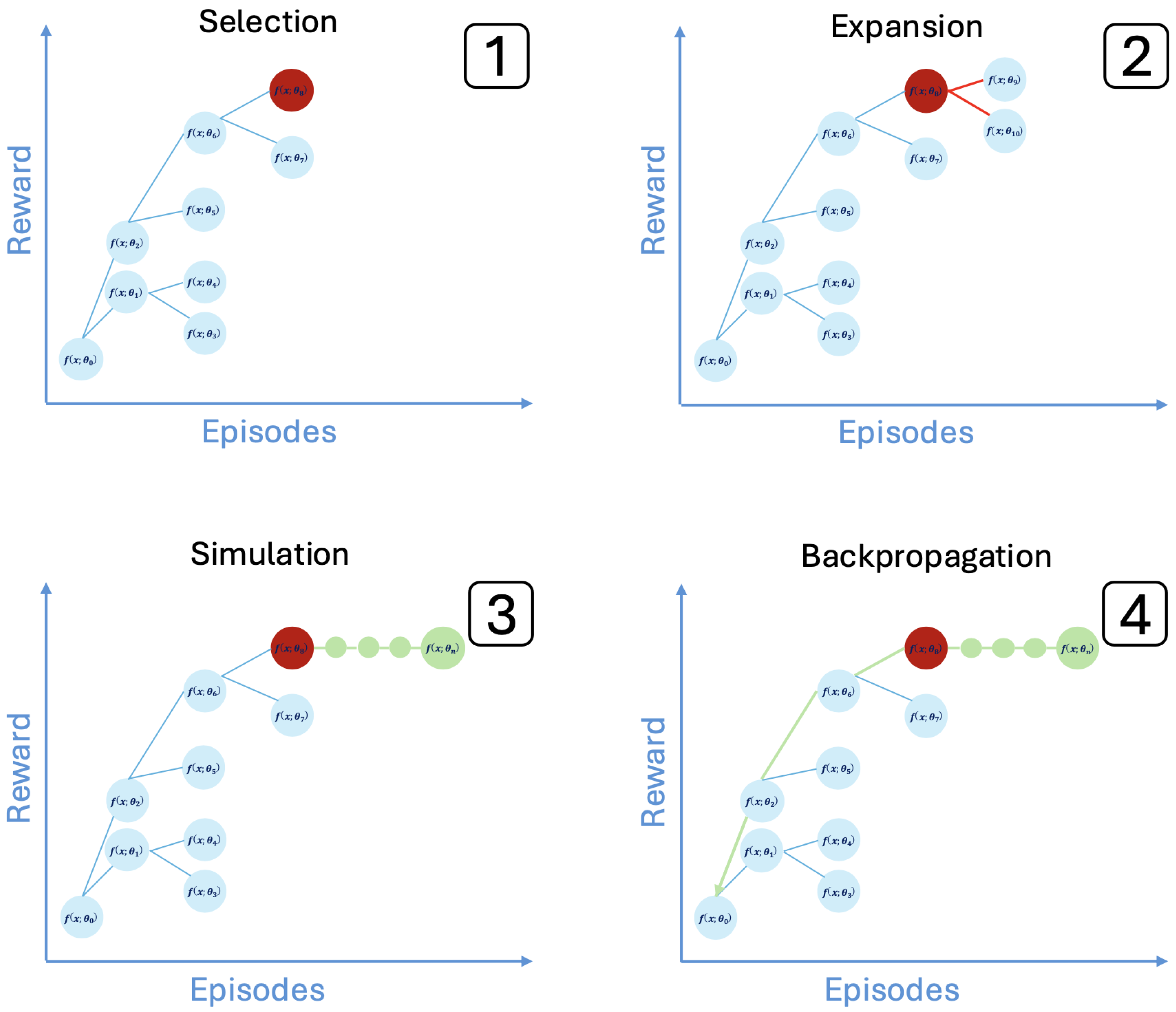
4.2. Integration of MCTS into DQN Training
- The problem of credit assignment, which challenges understanding of the long-term effects of choosing the action in the current state.
- The problem of reward sparsity, which makes it difficult to collect truly valuable learning signals.
| Algorithm 1 MCTS-Guided Batch Sequence Optimization |
External parameters: branching factor B, train episodes T, exploration constant , environment .
|
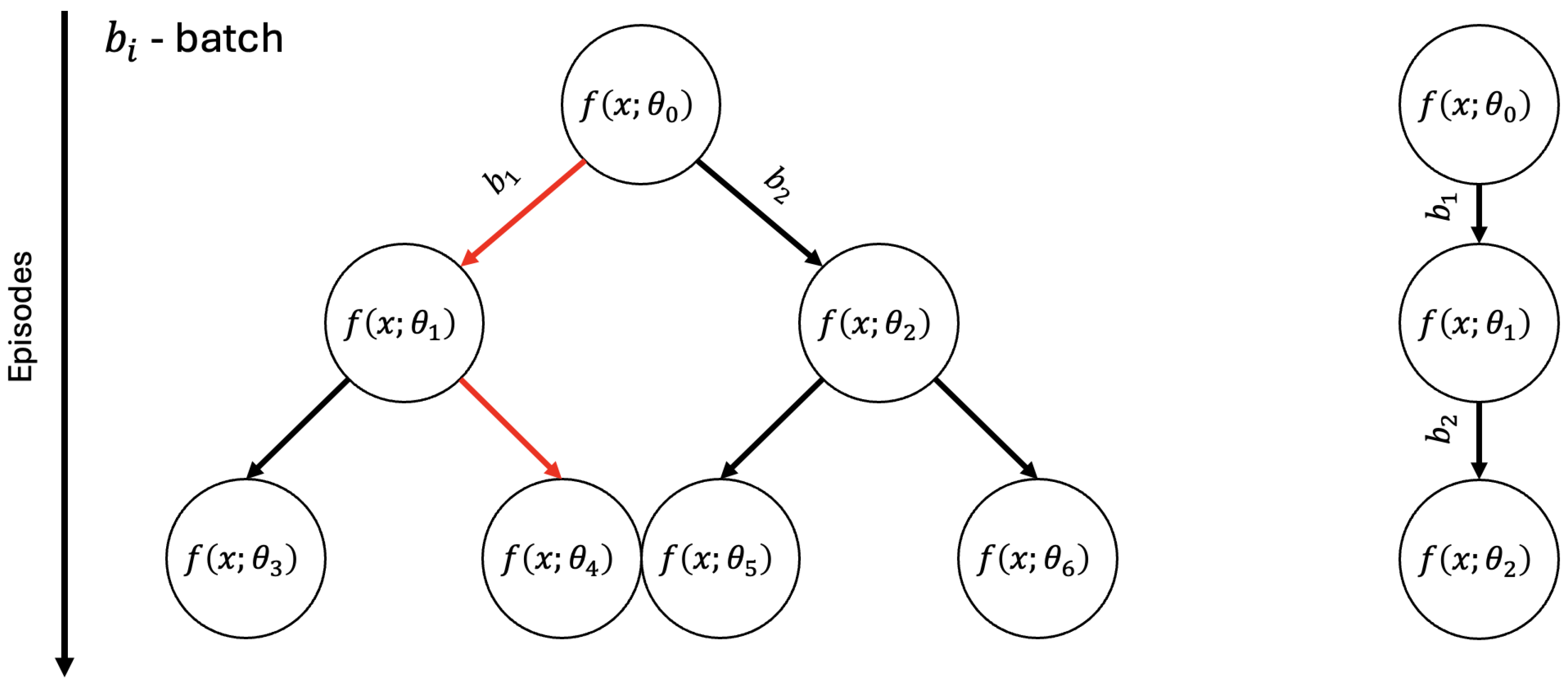
- The nodes in the tree are not the states of the game played by MCTS, but the trained neural network’s weights.
- The edges are not actions that change the state of the game, but batches that are used for updating the policy of the agent.
- In the rollout process, the game is not played with random actions until its conclusion; instead, the steps are individual episodes, with the random actions of the rollout corresponding to fitting the agent with batches in random order.
4.3. Ablation Rationale and Parameter Effects
5. Experiments
5.1. Environments
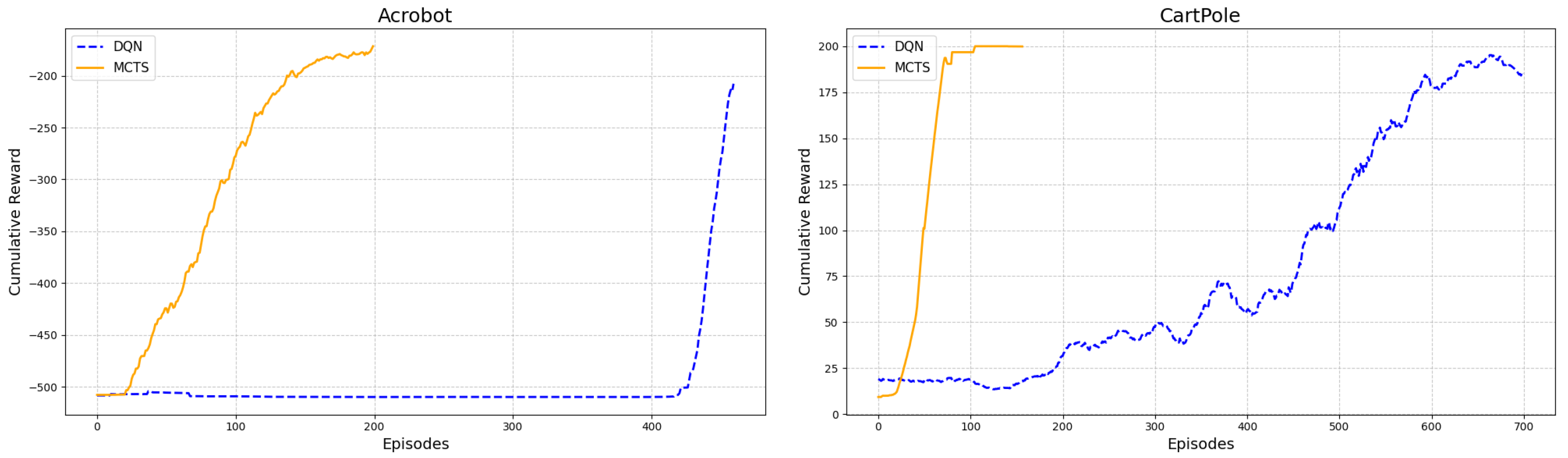
5.2. Results
5.3. General Observations
5.4. Computational Overhead
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kővári, B.; Knáb, I.G.; Esztergár-Kiss, D.; Aradi, S.; Bécsi, T. Distributed highway control: A cooperative reinforcement learning-based approach. IEEE Access 2024, 12, 104463–104472. [Google Scholar] [CrossRef]
- Mihály, A.; Vu, V.T.; Do, T.T.; Thinh, K.D.; Vinh, N.V.; Gáspár, P. Linear Parameter Varying and Reinforcement Learning Approaches for Trajectory Tracking Controller of Autonomous Vehicles. Period. Polytech. Transp. Eng. 2025, 53, 94–102. [Google Scholar] [CrossRef]
- Ichter, B.; Pavone, M. Robot motion planning in learned latent spaces. IEEE Robot. Autom. Lett. 2019, 4, 2407–2414. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S.; Guez, A.; Lockhart, E.; Hassabis, D.; Graepel, T.; et al. Mastering atari, go, chess and shogi by planning with a learned model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef] [PubMed]
- Fawzi, A.; Balog, M.; Huang, A.; Hubert, T.; Romera-Paredes, B.; Barekatain, M.; Novikov, A.; R Ruiz, F.J.; Schrittwieser, J.; Swirszcz, G.; et al. Discovering faster matrix multiplication algorithms with reinforcement learning. Nature 2022, 610, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Mankowitz, D.J.; Michi, A.; Zhernov, A.; Gelmi, M.; Selvi, M.; Paduraru, C.; Leurent, E.; Iqbal, S.; Lespiau, J.B.; Ahern, A.; et al. Faster sorting algorithms discovered using deep reinforcement learning. Nature 2023, 618, 257–263. [Google Scholar] [CrossRef] [PubMed]
- Anoushee, M.; Fartash, M.; Akbari Torkestani, J. An intelligent resource management method in SDN based fog computing using reinforcement learning. Computing 2024, 106, 1051–1080. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C. Bandit Based Monte-Carlo Planning. In Machine Learning: ECML 2006; Fürnkranz, J., Scheffer, T., Spiliopoulou, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4212, pp. 282–293. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Anthony, T.; Tian, Z.; Barber, D. Thinking Fast and Slow with Deep Learning and Tree Search. arXiv 2017, arXiv:1705.08439. [Google Scholar] [CrossRef]
- Guez, A.; Weber, T.; Antonoglou, I.; Simonyan, K.; Vinyals, O.; Wierstra, D.; Munos, R.; Silver, D. Learning to Search with MCTSnets. arXiv 2018, arXiv:1802.04697. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2016, arXiv:1511.05952. [Google Scholar] [CrossRef]
- Zha, D.; Lai, K.H.; Zhou, K.; Hu, X. Experience Replay Optimization. arXiv 2019, arXiv:1906.08387. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; ACM: New York, NY, USA, 2009; pp. 41–48. [Google Scholar] [CrossRef]
- Graves, A.; Bellemare, M.G.; Menick, J.; Munos, R.; Kavukcuoglu, K. Automated Curriculum Learning for Neural Networks. arXiv 2017, arXiv:1704.03003. [Google Scholar] [CrossRef]
- Narvekar, S.; Peng, B.; Leonetti, M.; Sinapov, J.; Taylor, M.E.; Stone, P. Curriculum learning for reinforcement learning domains: A framework and survey. J. Mach. Learn. Res. 2020, 21, 7382–7431. [Google Scholar]
- Wang, L.; Xu, Z.; Stone, P.; Xiao, X. Grounded curriculum learning. arXiv 2024, arXiv:2409.19816. [Google Scholar] [CrossRef]
- Karni, Z.; Simhon, O.; Zarrouk, D.; Berman, S. Automatic curriculum determination for deep reinforcement learning in reconfigurable robots. IEEE Access 2024, 12, 78342–78353. [Google Scholar] [CrossRef]
- Irandoust, S.; Durand, T.; Rakhmangulova, Y.; Zi, W.; Hajimirsadeghi, H. Training a Vision Transformer from scratch in less than 24 hours with 1 GPU. In Proceedings of the Has It Trained Yet? NeurIPS 2022 Workshop, New Orleans, LA, USA, 2 December 2022. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar] [CrossRef]
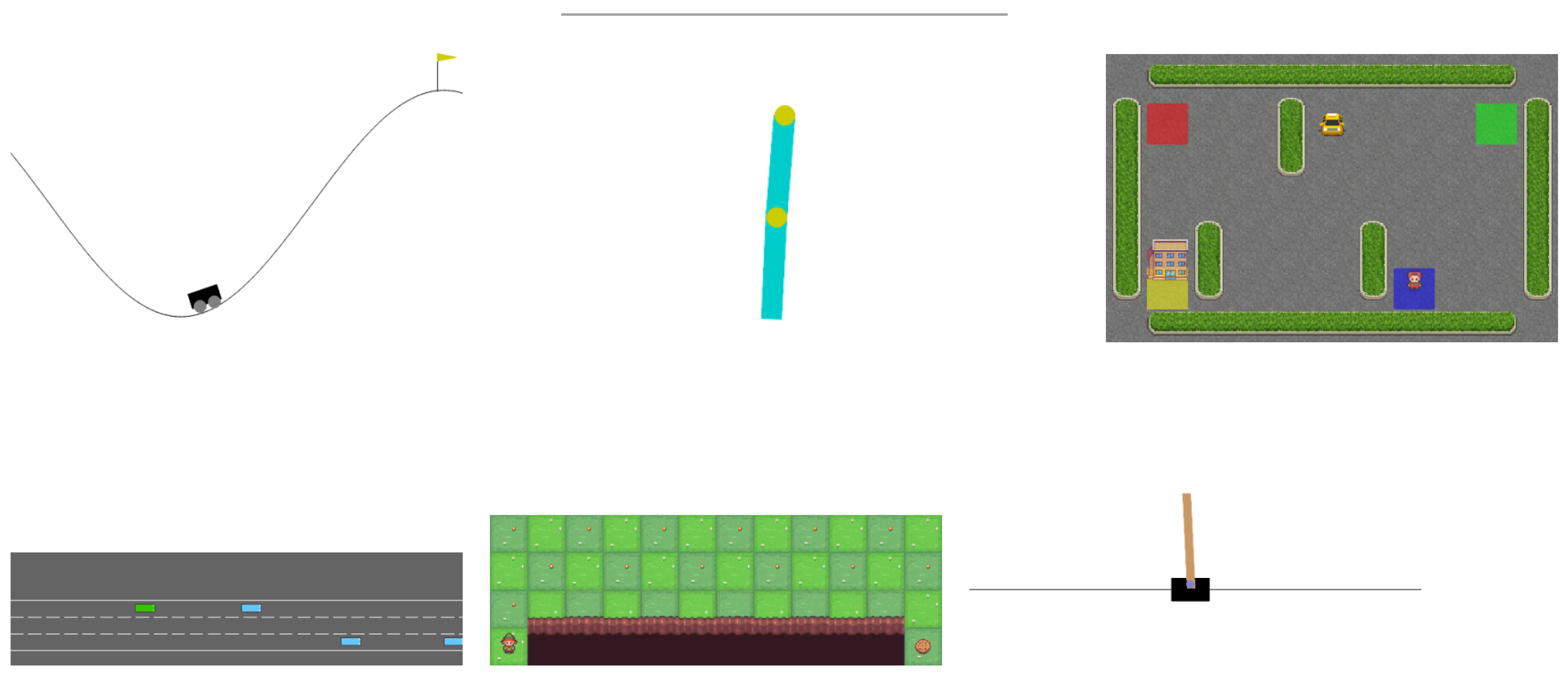
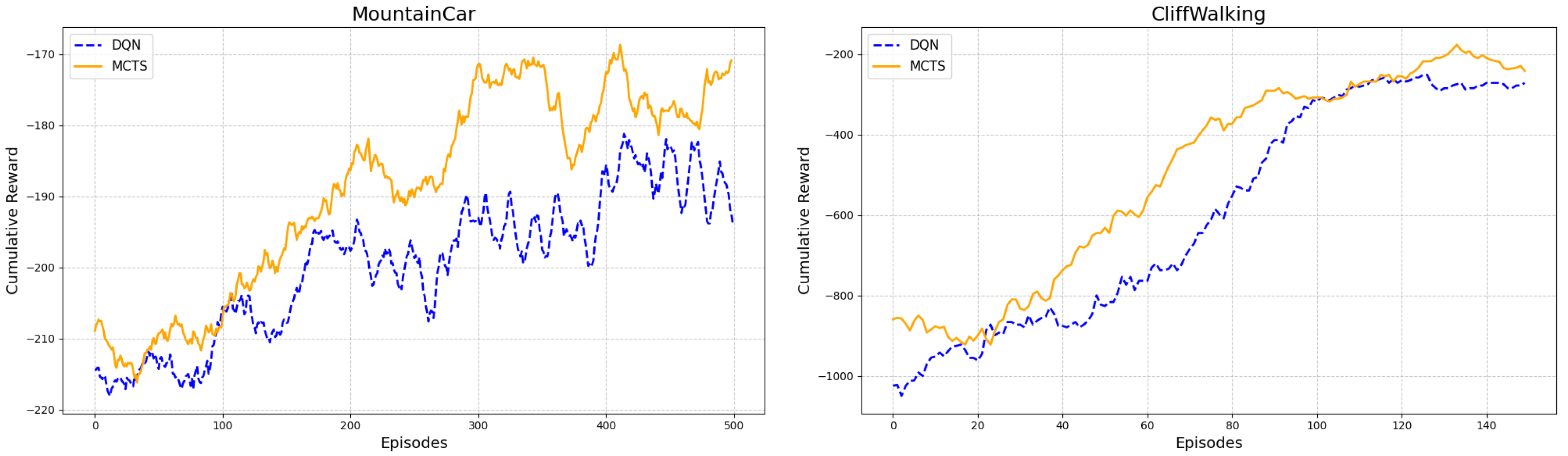
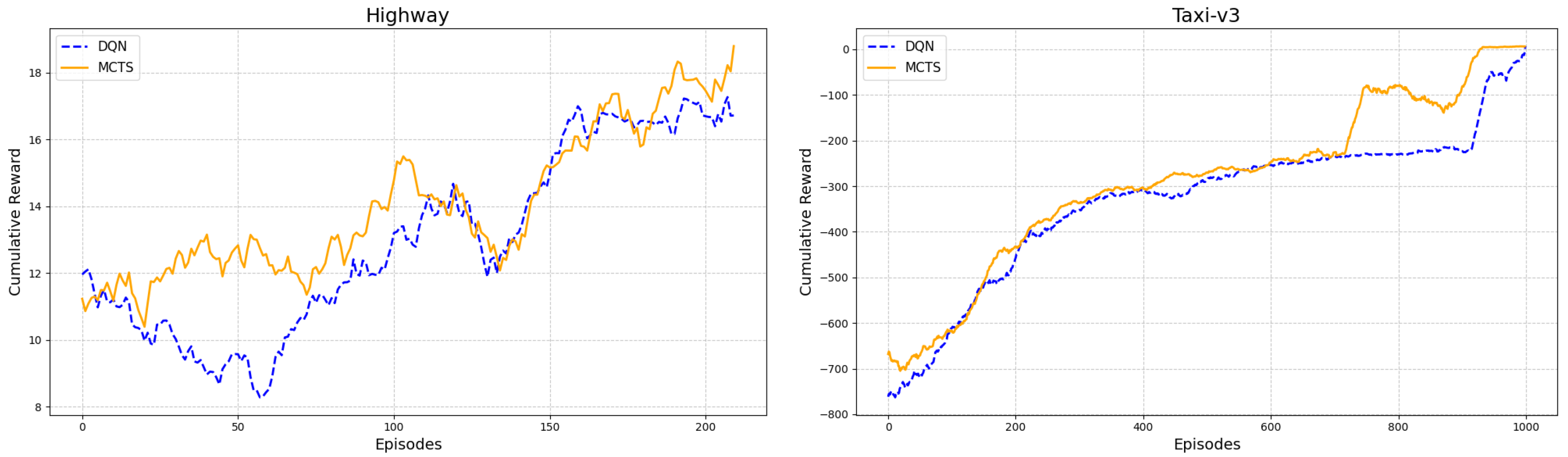
| Environment | Reward Sparsity | Termination | Max Steps |
|---|---|---|---|
| MountainCar | Sparse | Goal or timeout | 200 |
| Acrobot | Sparse | Swing-up or timeout | 500 |
| CartPole | Dense | Failure or timeout | 500 |
| Taxi-v3 | Semi-sparse | Drop-off or timeout | 200 |
| CliffWalking | Sparse | Goal/cliff/timeout | 200 |
| Highway-v0 | Dense | Collision/off-road/timeout | 40 |
| Method | MountainCar | Acrobot | Taxi-v3 | Highway-v0 | CliffWalking | CartPole |
|---|---|---|---|---|---|---|
| Ours | −168.87 | −171.81 | 6.67 | 18.89 | −177.56 | 200.0 |
| RL | −181.45 | −207.23 | 7.56 | 17.23 | −251.65 | 200.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csippán, G.; Péter, I.; Kővári, B.; Bécsi, T. MCTS-Based Policy Improvement for Reinforcement Learning. Mach. Learn. Knowl. Extr. 2025, 7, 98. https://doi.org/10.3390/make7030098
Csippán G, Péter I, Kővári B, Bécsi T. MCTS-Based Policy Improvement for Reinforcement Learning. Machine Learning and Knowledge Extraction. 2025; 7(3):98. https://doi.org/10.3390/make7030098
Chicago/Turabian StyleCsippán, György, István Péter, Bálint Kővári, and Tamás Bécsi. 2025. "MCTS-Based Policy Improvement for Reinforcement Learning" Machine Learning and Knowledge Extraction 7, no. 3: 98. https://doi.org/10.3390/make7030098
APA StyleCsippán, G., Péter, I., Kővári, B., & Bécsi, T. (2025). MCTS-Based Policy Improvement for Reinforcement Learning. Machine Learning and Knowledge Extraction, 7(3), 98. https://doi.org/10.3390/make7030098







