Full Domain Analysis in Fluid Dynamics
Abstract
1. Introduction
- How should designs be encoded to allow for efficiency in both determining solution quality and diversity of solutions?
- How can a large, diverse set of solutions be created efficiently?
- How do we incorporate and/or discover characteristics that produce well-performing designs of shapes?
- How can users understand and navigate large design spaces?
- Encoding of solutions;
- Effective and efficient divergent search;
- Fast CFD solver that supports accurate flow for diverse shapes;
- Statistical learning methods to efficiently sample and predict characteristics of solutions;
- Machine learning methods that learn characteristics and representations of solution sets.
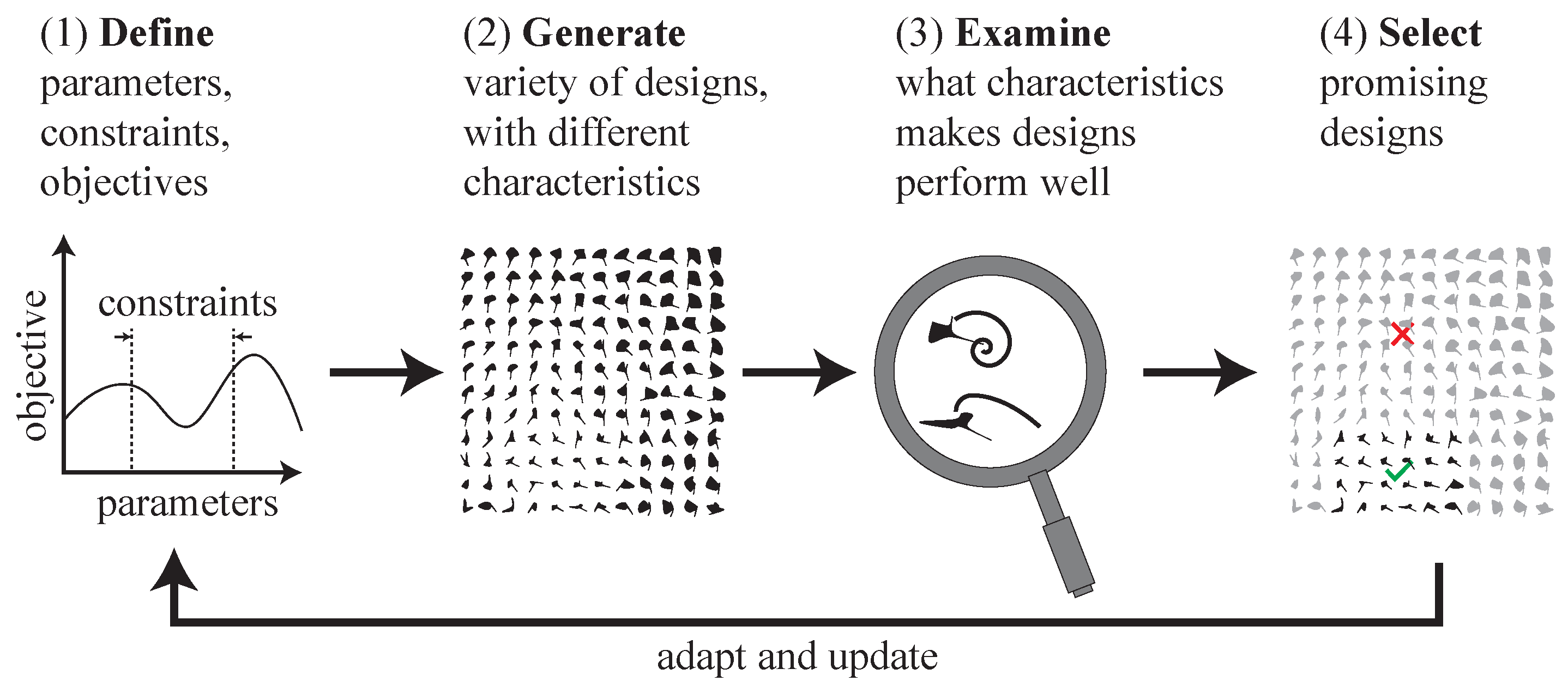
2. Materials and Methods
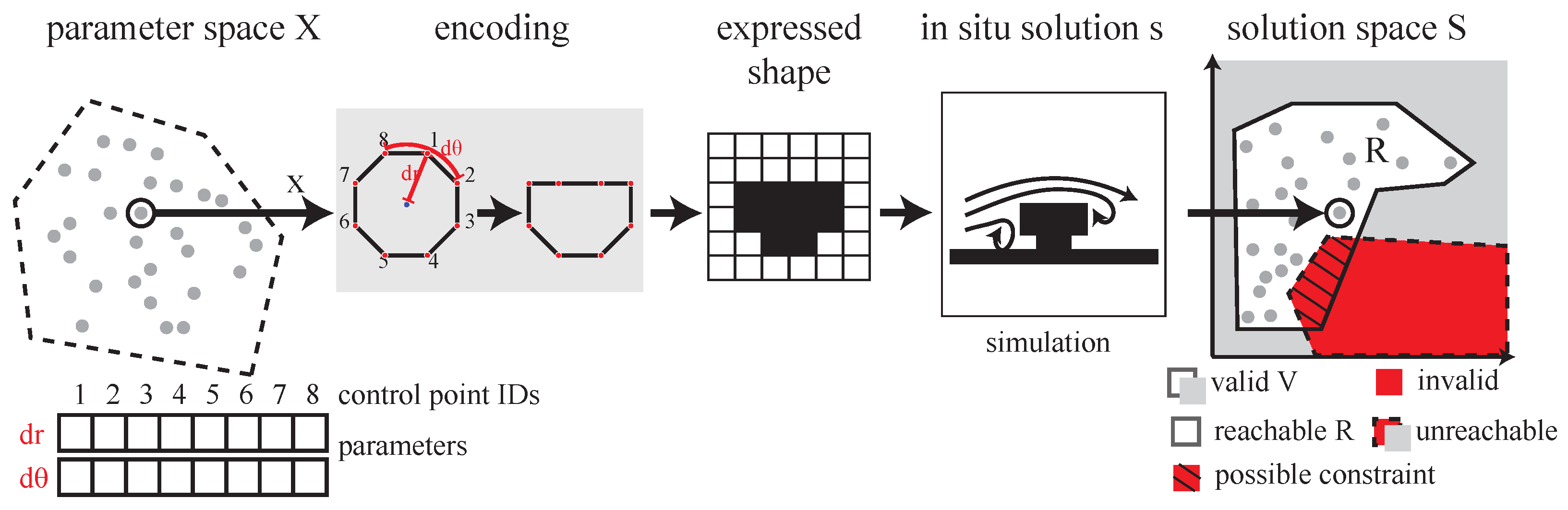
2.1. Encodings
2.1.1. Requirements
Reachability
Validity
Searchability
Predictability
Human Understanding and Effort
Prior Examples
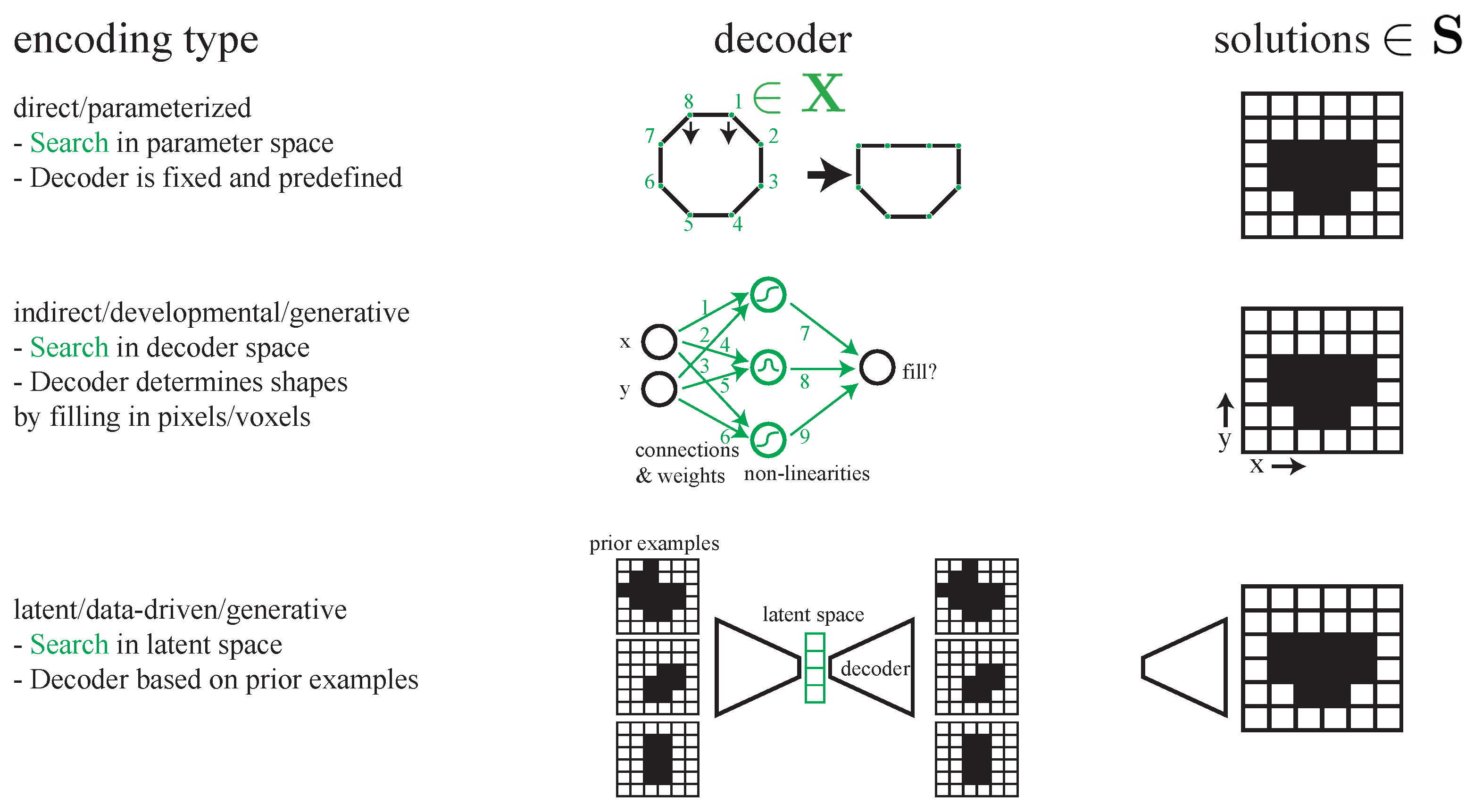
2.1.2. State of the Art
Direct/Parameterized
Indirect, Developmental, and Generative Encodings
Latent-Generative
2.1.3. Discussion
2.2. Search
2.2.1. Requirements
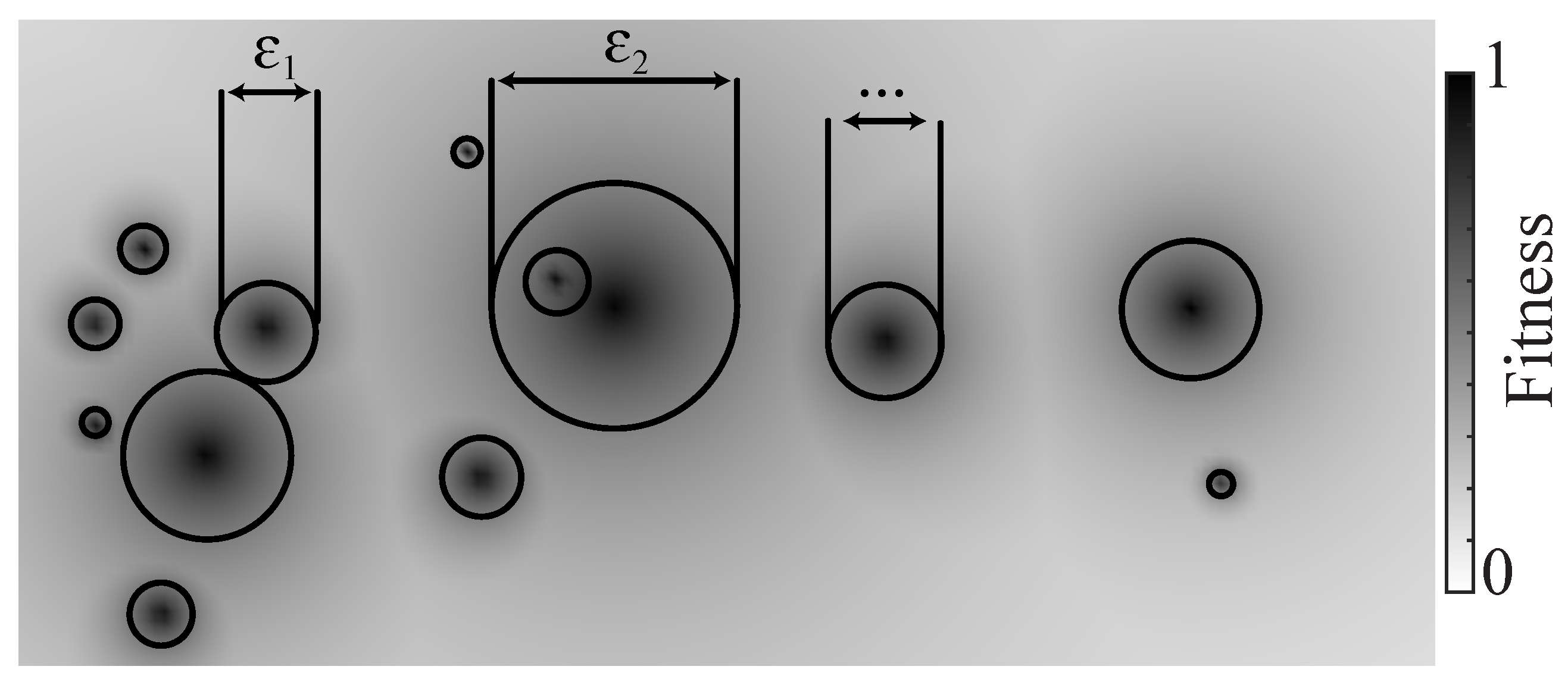
Multiple Solutions
Coverage
Diversity
2.2.2. State of the Art
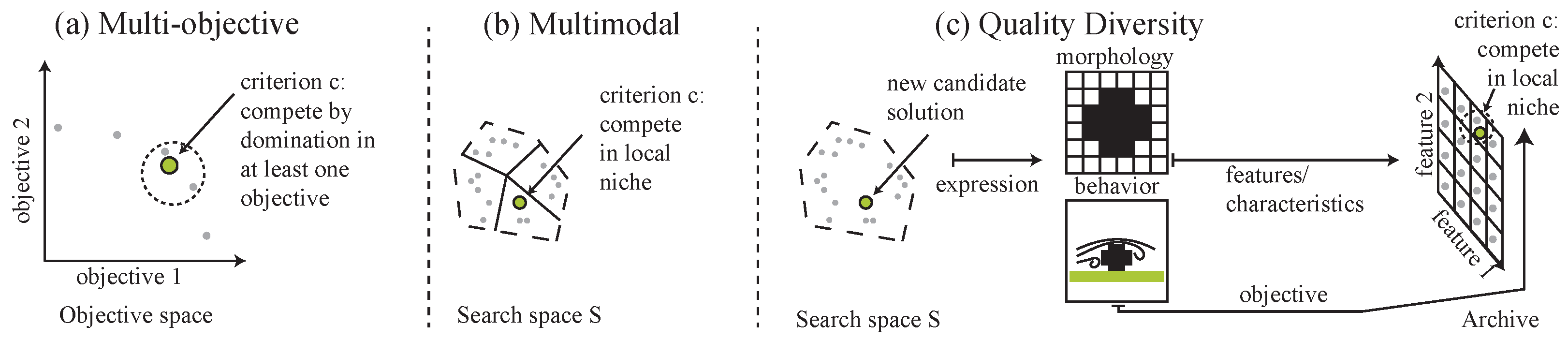
Multiobjective Optimization
Multimodal Optimization
Quality–Diversity
2.2.3. Comparison of Paradigms
2.3. Computational Fluid Dynamics
2.3.1. Level of Detail
2.3.2. Stability vs. Accuracy
2.4. On the Matter of Efficiency
2.4.1. Reduction
2.4.2. Replacement
2.4.3. Generative Surrogates for CFD
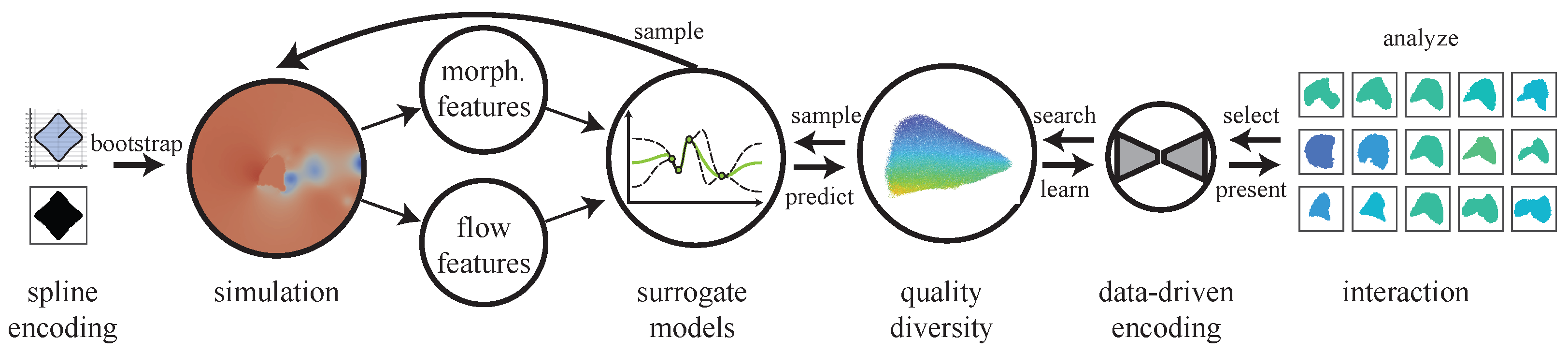
3. Results
- Concise representation of diverse results.
- Compact comparison.
- Constrain by selection.
- Change perspective.
3.1. Example Domain
3.2. Search
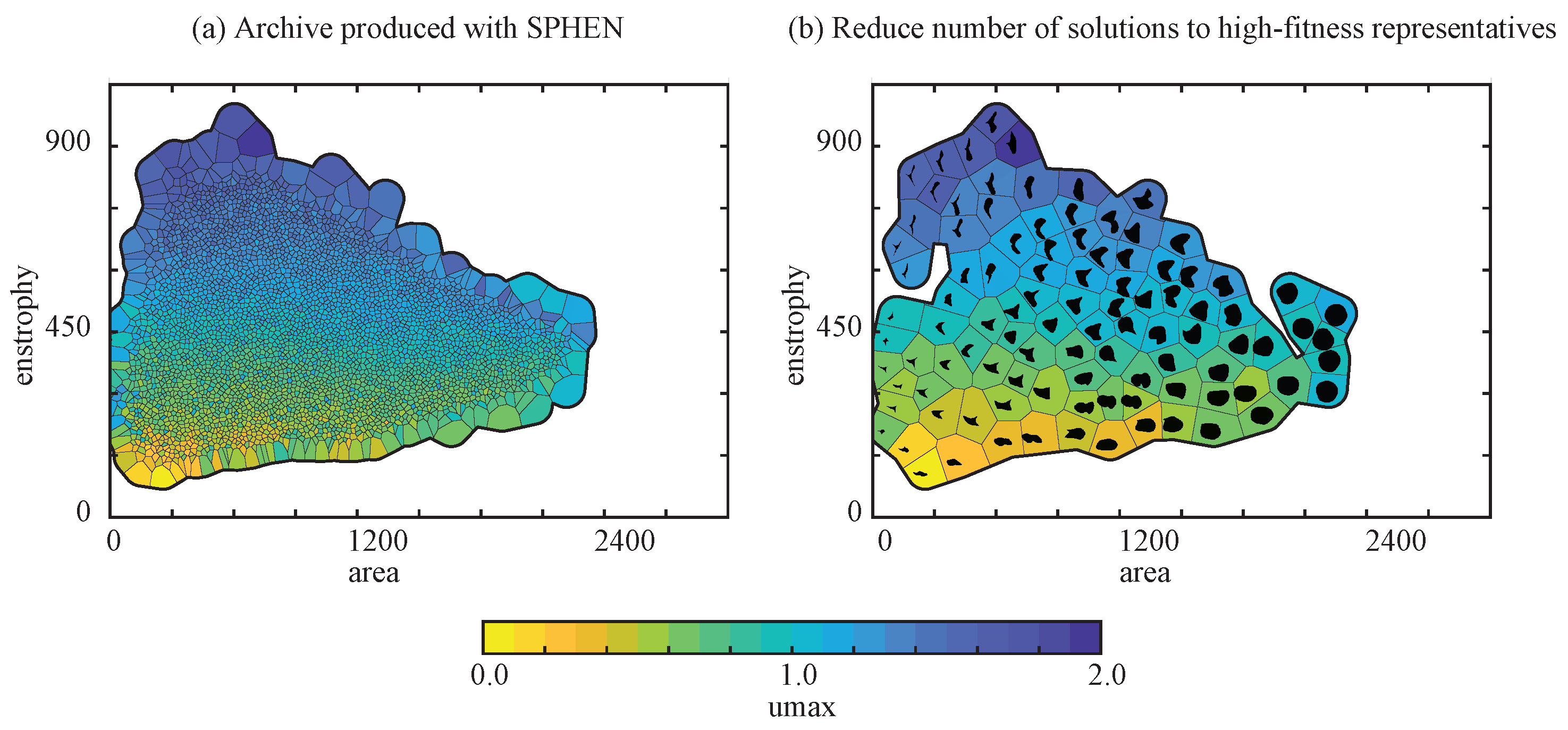
3.3. QD Analysis Step
3.4. Generation Step
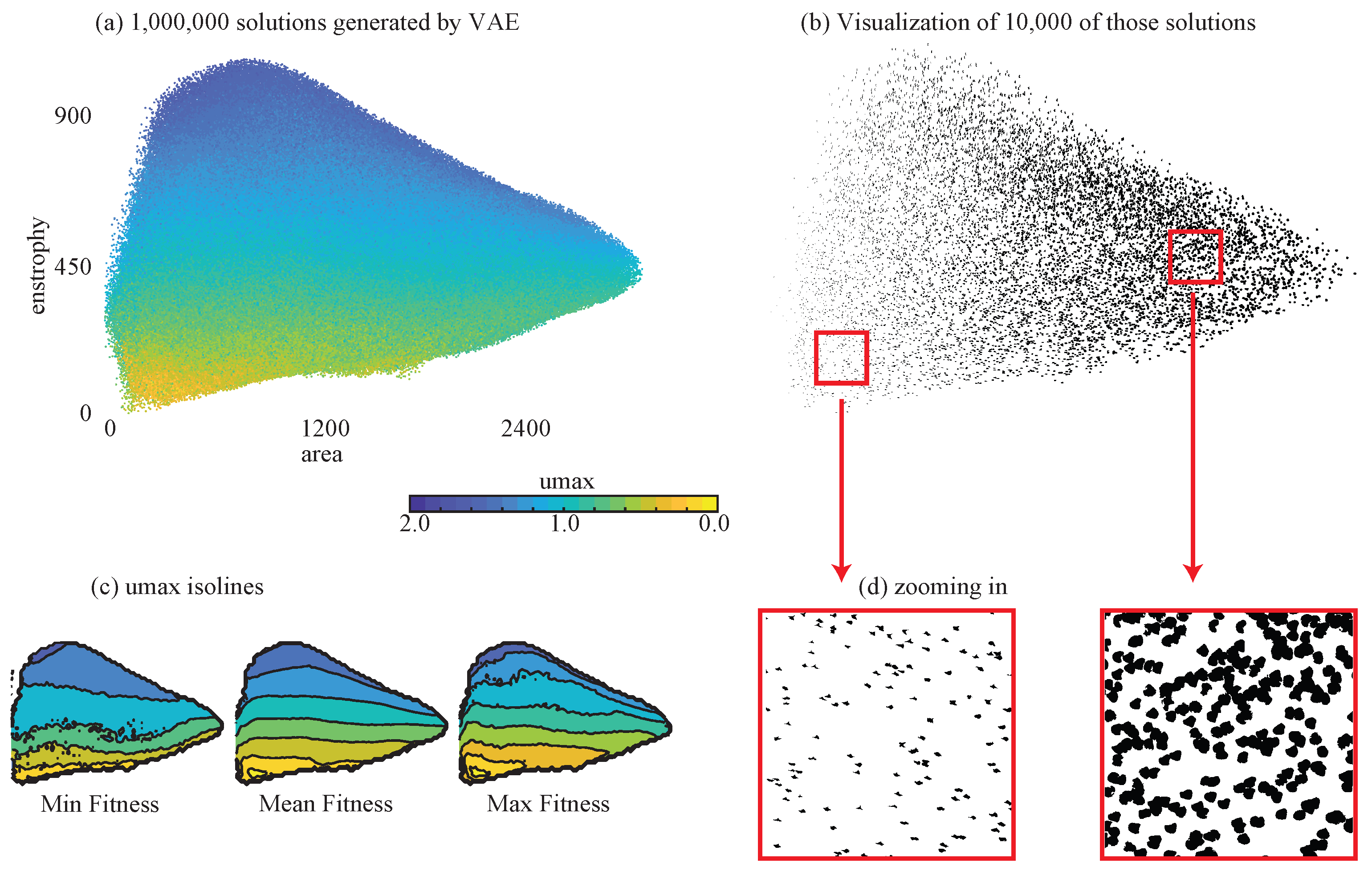
3.5. VAE Analysis Step
3.6. Very Large Solution Sets
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FDA | full domain analysis |
| QD | quality–diversity |
| MMO | multimodal optimization |
| MOO | multiobjective optimization |
| BO | Bayesian optimization |
| GP | Gaussian process model |
| FFD | free form deformation |
| CPPN | compositional pattern producing networks |
| SAO | surrogate-assisted optimization |
| NSGA-II | non-dominated sorting genetic algorithm |
| GM | generative model |
| VAE | variational autoencoder |
| GAN | generative adversarial network |
| GA | genetic algorithm |
| NURBS | non-uniform rational b-splines |
| CFD | computational fluid dynamics |
| SPHEN | surrogate-assisted phenotypic niching |
| LBM | lattice Boltzmann method |
References
- Vinuesa, R.; Brunton, S.L. The potential of machine learning to enhance computational fluid dynamics. arXiv 2021, arXiv:2110.02085. [Google Scholar]
- Wang, Y.; Shimada, K.; Farimani, A.B. Airfoil GAN: Encoding and Synthesizing Airfoils for Aerodynamic-aware Shape Optimization. arXiv 2021, arXiv:2101.04757. [Google Scholar] [CrossRef]
- Gaier, A.; Asteroth, A.; Mouret, J.-B. Data-efficient design exploration through surrogate-assisted illumination. Evol. Comput. 2018, 26, 381–410. [Google Scholar] [CrossRef]
- Hagg, A.; Asteroth, A.; Bäck, T. Modeling user selection in quality diversity. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2019; pp. 116–124. [Google Scholar]
- Jacobs, E.N.; Ward, K.E.; Pinkerton, R.M. The Characteristics of 78 Related Airfoil Section from Tests in the Variable-Density Wind Tunnel, Report No. 460; US Government Printing Office: Washington, DC, USA, 1933. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Olhofer, M.; Sendhoff, B.; Arima, T.; Sonoda, T. Optimisation of a stator blade used in a transonic compressor cascade with evolution strategies. In Evolutionary Design and Manufacture; Springer: London, UK, 2000; pp. 45–54. [Google Scholar]
- Lapok, P. Evolving planar mechanisms for the conceptual stage of mechanical design. Ph.D. Thesis, Edinburgh Napier University, Edinburgh, UK, 2020. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When is “nearest neighbor” meaningful? In Proceedings of the International conference on database theory, Jerusalem, Israel, 10–12 January 1999; Springer: Berlin, Germany, 1999; pp. 217–235. [Google Scholar]
- Hagg, A. Discovering the preference hypervolume: An interactive model for real world computational co-creativity. Ph.D. Thesis, Leiden University, Leiden, The Netherlands, 2021. [Google Scholar]
- Nordmoen, J.; Veenstra, F.; Ellefsen, K.O.; Glette, K. MAP-Elites enables Powerful Stepping Stones and Diversity for Modular Robotics. Front. Robot. AI 2021, 8, 639173. [Google Scholar] [CrossRef]
- Hicks, R.M.; Murman, E.M.; Vanderplaats, G.N. An Assessment of Airfoil Design by Numerical Optimization; NASA Technical Note D-7415; National Aeronautics and Space Administration: Washington, DC, USA, 1974. [Google Scholar]
- Vicini, A.; Quagliarella, D. Airfoil and wing design through hybrid optimization strategies. AIAA J. 1999, 37, 634–641. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. ACM SIGGRAPH Comput. Graph. 1986, 20, 151–160. [Google Scholar] [CrossRef]
- Sarakinos, S.S.; Amoiralis, E.; Nikolos, I.K. Exploring freeform deformation capabilities in aerodynamic shape parameterization. In Proceedings of the EUROCON 2005—The International Conference on “Computer as a Tool”, Belgrade, Serbia and Montenegro, 21–24 November 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 535–538. [Google Scholar]
- Tai, K.; Wang, N.F.; Yang, Y.W. Target geometry matching problem with conflicting objectives for multiobjective topology design optimization using GA. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1873–1878. [Google Scholar]
- Stanley, K.O. Compositional pattern producing networks: A novel abstraction of development. Genet. Program. Evolvable Mach. 2007, 8, 131–162. [Google Scholar] [CrossRef]
- Gaier, A. Evolutionary Design via Indirect Encoding of Non-Uniform Rational Basis Splines. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; pp. 1197–1200. [Google Scholar]
- Hotz, P.E. Comparing direct and developmental encoding schemes in artificial evolution: A case study in evolving lens shapes. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 752–757. [Google Scholar]
- Kicinger, R. Evolutionary Developmental System for Structural Design. In Proceedings of the AAAI Fall Symposium: Developmental Systems, Arlington, VA, USA, 13–15 October 2006; pp. 1–8. [Google Scholar]
- Clune, J.; Stanley, K.O.; Pennock, R.T.; Ofria, C. On the performance of indirect encoding across the continuum of regularity. IEEE Trans. Evol. Comput. 2011, 15, 346–367. [Google Scholar] [CrossRef]
- Yannou, B.; Dihlmann, M.; Cluzel, F. Indirect encoding of the genes of a closed curve for interactively create innovative car silhouettes. In Proceedings of the 10th International Design Conference-DESIGN 2008, Dubrovnik, Croatia, 19–22 May 2008; pp. 1243–1254. [Google Scholar]
- Clune, J.; Chen, A.; Lipson, H. Upload any object and evolve it: Injecting complex geometric patterns into CPPNs for further evolution. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 3395–3402. [Google Scholar]
- Collins, J.; Cottier, B.; Howard, D. Comparing direct and indirect representations for environment-specific robot component design. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2705–2712. [Google Scholar]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Stanley, K.O.; D’Ambrosio, D.B.; Gauci, J. A hypercube-based encoding for evolving large-scale neural networks. Artif. Life 2009, 15, 185–212. [Google Scholar] [CrossRef]
- Hildebrandt, T.; Branke, J. On using surrogates with genetic programming. Evol. Comput. 2015, 23, 343–367. [Google Scholar] [CrossRef]
- Stork, J.; Zaefferer, M.; Bartz-Beielstein, T. Improving neuroevolution efficiency by surrogate model-based optimization with phenotypic distance kernels. In Proceedings of the International Conference on the Applications of Evolutionary Computation (Part of EvoStar), Leipzig, Germany, 24–26 April 2019; Springer: Cham, Switzerland, 2019; pp. 504–519. [Google Scholar]
- Stork, J.; Zaefferer, M.; Fischbach, A.; Rehbach, F.; Bartz-Beielstein, T. Surrogate-Assisted Learning of Neural Networks. arXiv 2017, arXiv:1709.07720. [Google Scholar]
- Hagg, A.; Zaefferer, M.; Stork, J.; Gaier, A. Prediction of neural network performance by phenotypic modeling. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 1576–1582. [Google Scholar]
- Regenwetter, L.; Nobari, A.H.; Ahmed, F.T. Deep generative models in engineering design: A review. Comput. Aided Des. Appl. 2024, 21, 486–510. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rios, T.; van Stein, B.; Wollstadt, P.; Bäck, T.; Sendhoff, B.; Menzel, S. Exploiting Local Geometric Features in Vehicle Design Optimization with 3D Point Cloud Autoencoders. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 514–521. [Google Scholar]
- Hagg, A.; Berns, S.; Asteroth, A.; Colton, S.; Bäck, T. Expressivity of parameterized and data-driven representations in quality diversity search. In Proceedings of the Genetic and Evolutionary Computation Conference, Lille, France, 10–14 July 2021; pp. 678–686. [Google Scholar]
- Bentley, P.J.; Lim, S.L.; Gaier, A.; Tran, L. COIL: Constrained Optimization in Learned Latent Space–Learning Representations for Valid Solutions. arXiv 2022, arXiv:2202.02163. [Google Scholar]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Tripp, A.; Daxberger, E.; Hernández-Lobato, J.M. Sample-efficient optimization in the latent space of deep generative models via weighted retraining. Adv. Neural Inf. Process. Syst. 2020, 33. [Google Scholar]
- Mathieu, E.; Rainforth, T.; Siddharth, N.; Teh, Y.W. Disentangling disentanglement in variational autoencoders. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR, 2019. pp. 4402–4412. [Google Scholar]
- Rios, T.; Van Stein, B.; Bäck, T.; Sendhoff, B.; Menzel, S. Point2FFD: Learning Shape Representations of Simulation-Ready 3D Models for Engineering Design Optimization. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1024–1033. [Google Scholar]
- Wei, Z.; Dufour, E.R.; Pelletier, C.; Fua, P.; Bauerheim, M. DiffAirfoil: An Efficient Novel Airfoil Sampler Based on Latent Space Diffusion Model for Aerodynamic Shape Optimization. In Proceedings of the AIAA AVIATION Forum, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar]
- Graves, R.; Farimani, A.B. Airfoil Diffusion: Denoising Diffusion Model For Conditional Airfoil Generation. arXiv 2024, arXiv:2408.15898. [Google Scholar]
- Morita, H.; Shintani, K.; Yuan, C.; Permenter, F. VehicleSDF: A 3D generative model for constrained engineering design via surrogate modeling. arXiv 2024, arXiv:2410.18986. [Google Scholar]
- Yang, H.; Li, S.; Zhang, Y.; Wang, J. StEik: Stabilizing the Optimization of Neural Signed Distance Representations. In Proceedings of the Advances in Neural Information Processing Systems 36, New Orleans, LA, USA, 10–16 December 2023; pp. 12745–12758. [Google Scholar]
- Wang, Q.; Chen, R.; Zhao, L. NeuVAS: Neural Variational Shape Editing under Sparse Geometric Constraints. ACM Trans. Graph. 2025, 44, 15:1–15:14. [Google Scholar]
- Zhang, Z.; Yao, W.; Li, Y.; Zhou, W.; Chen, X. Topology optimization via implicit neural representations. Comput. Methods Appl. Mech. Eng. 2023, 411, 116052. [Google Scholar] [CrossRef]
- Hahm, K.; Park, S.; Lee, J. Isometric Diffusion: Controllable Generation via Latent-Solution Space Isometry. In Proceedings of the International Conference on Learning Representations, Vienna Austria, 7–11 May 2024. [Google Scholar]
- Vafidis, N.; Thompson, D.; Mitchell, R. NashAE: Disentangled Representation Learning via Nash Equilibrium in Autoencoders. Mach. Learn. 2023, 112, 3021–3045. [Google Scholar]
- Scarton, L.; Hagg, A. On the Suitability of Representations for Quality Diversity Optimization of Shapes. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2023; pp. 963–971. [Google Scholar]
- Gaier, A.; Asteroth, A.; Mouret, J.-B. Are quality diversity algorithms better at generating stepping stones than objective-based search? In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; pp. 115–116. [Google Scholar]
- Hagg, A.; Preuss, M.; Asteroth, A.; Bäck, T. An Analysis of Phenotypic Diversity in multisolution Optimization. In Proceedings of the International Conference on Bioinspired Methods and Their Applications, Brussels, Belgium, 18–19 November 2020; Springer: Cham, Switzerland, 2020; pp. 43–55. [Google Scholar]
- Wang, H.; Jin, Y.; Yao, X. Diversity assessment in many-objective optimization. IEEE Trans. Cybern. 2016, 47, 1510–1522. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. In TIK-Report 103; ETH Zurich: Zurich, Switzerland, 2001. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- DeJong, K.A. Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Wales, D.J.; Doye, J.P.K. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Preuss, M. Improved topological niching for real-valued global optimization. In Proceedings of the European Conference on the Applications of Evolutionary Computation, Málaga, Spain, 11–13 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 386–395. [Google Scholar]
- Pošík, P.; Huyer, W. Restarted local search algorithms for continuous black box optimization. Evol. Comput. 2012, 20, 575–607. [Google Scholar] [CrossRef]
- Cully, A.; Clune, J.; Tarapore, D.; Mouret, J.-B. Robots that can adapt like animals. Nature 2015, 521, 503–507. [Google Scholar] [CrossRef]
- Cully, A. Autonomous Skill Discovery with Quality-Diversity and Unsupervised Descriptors. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019. [Google Scholar]
- Gaier, A.; Asteroth, A.; Mouret, J.-B. Discovering representations for black-box optimization. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 103–111. [Google Scholar]
- Hagg, A.; Asteroth, A.; Bäck, T. Prototype discovery using quality-diversity. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Coimbra, Portugal, 8–12 September 2018; Springer: Cham, Switzerland, 2018; pp. 500–511. [Google Scholar]
- Fontaine, M.C.; Nikolaidis, S. Differentiable Quality Diversity. In Proceedings of the Advances in Neural Information Processing Systems 34, Online, 6–14 December 2021; pp. 10040–10052. [Google Scholar]
- Boyar, A.; Kim, H.; Rodriguez, C. Latent-Consistent Acquisition for Bayesian Optimization in Learned Representations. J. Mach. Learn. Res. 2024, 25, 1–34. [Google Scholar]
- Lee, D.; Patel, N.; Wilson, A. Coordinate Bayesian Optimization for High-Dimensional Structured Domains. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 19234–19251. [Google Scholar]
- Kent, P.; Grover, A.; Abbeel, P. BOP-Elites: Bayesian Optimisation for Quality-Diversity Search. In Proceedings of the Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020; pp. 334–342. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier-Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62. [Google Scholar] [CrossRef]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Löhner, R. Towards overcoming the LES crisis. Int. J. Comput. Fluid Dyn. 2019, 33, 87–97. [Google Scholar] [CrossRef]
- Sanderse, B.; Stinis, P.; Maulik, R.; Ahmed, S.E. Scientific machine learning for closure models in multiscale problems: A review. Comput. Fluids 2025, 291, 106186. [Google Scholar] [CrossRef]
- Möller, T.; Schmidt, K.; Andersson, B. Hybrid RANS-LES Performance Assessment for Industrial Turbomachinery: A Comprehensive Benchmark Study. J. Turbomach. 2024, 146, 071008. [Google Scholar]
- Khaled, S.; Martinez, E.; Brown, J. Deep Learning Enhanced Eddy Viscosity Models for Improved Separated Flow Predictions. Phys. Fluids 2024, 36, 045108. [Google Scholar]
- Ingram, D.M.; Causon, D.M.; Mingham, C.G. Developments in Cartesian cut cell methods. Math. Comput. Simul. 2003, 61, 561–572. [Google Scholar] [CrossRef]
- Mavriplis, D.J. Unstructured grid techniques. Annu. Rev. Fluid Mech. 1997, 29, 473–514. [Google Scholar] [CrossRef]
- Balan, A.; Park, M.A.; Wood, S.L.; Anderson, W.K.; Rangarajan, A.; Sanjaya, D.P.; May, G. A review and comparison of error estimators for anisotropic mesh adaptation for flow simulations. Comput. Fluids 2022, 234, 105259. [Google Scholar] [CrossRef]
- Jin, Y. Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm Evol. Comput. 2011, 1, 61–70. [Google Scholar] [CrossRef]
- Wessing, S. Two-Stage Methods for Multimodal Optimization. Ph.D. Thesis, Technische Universität Dortmund, Dortmund, Germany, 2015. [Google Scholar]
- Hagg, A.; Wilde, D.; Asteroth, A.; Bäck, T. Designing Air Flow with Surrogate-assisted Phenotypic Niching. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2020; Springer: Cham, Switzerland, 2020; pp. 140–153. [Google Scholar]
- Burgess, C.P.; Higgins, I.; Pal, A.; Matthey, L.; Watters, N.; Desjardins, G.; Lerchner, A. Understanding Disentangling in Beta-VAE. In Proceedings of the NIPS Workshop on Learning Disentangled Representations, Long Beach, CA, USA, 8–9 December 2017. [Google Scholar]
- Antonova, R.; Rai, A.; Li, T.; Kragic, D. Bayesian optimization in variational latent spaces with dynamic compression. In Proceedings of the Conference on Robot Learning, Virtual Event, 16–18 November 2020; PMLR, 2020. pp. 456–465. [Google Scholar]
- Wu, H.; Liu, X.; An, W.; Chen, S.; Lyu, H. A deep learning approach for efficiently and accurately evaluating the flow field of supercritical airfoils. Comput. Fluids 2020, 198, 104393. [Google Scholar] [CrossRef]
- Chen, L.-W.; Cakal, B.A.; Hu, X.; Thuerey, N. Numerical investigation of minimum drag profiles in laminar flow using deep learning surrogates. J. Fluid Mech. 2021, 919, A34. [Google Scholar] [CrossRef]
- Lye, K.O.; Mishra, S.; Ray, D. Deep learning observables in computational fluid dynamics. J. Comput. Phys. 2020, 410, 109339. [Google Scholar] [CrossRef]
- Lino, S.; Fotiadis, S.; Bharath, A.A.; Cantwell, C.D. Current and emerging deep-learning methods for the simulation of fluid dynamics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2023, 479, 20230058. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Ibrahim, S.M.; Najmi, M.I. Computational Fluid Dynamics (CFD) Optimization in Smart Factories: AI-Based Predictive Modelling. J. Technol. Inform. Eng. 2025, 4, 56–74. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Koziel, S.; Cheng, Q.S.; Bandler, J.W. Space mapping. IEEE Microw. Mag. 2008, 9, 105–122. [Google Scholar] [CrossRef]
- Li, F.; Wang, S.; Kumar, V. Multi-Fidelity POD-Enhanced Neural Surrogates for Parametric Navier-Stokes Equations. Comput. Methods Appl. Mech. Eng. 2024, 418, 116578. [Google Scholar]
- Zhang, L.; Adams, R.; Taylor, M. Multi-Fidelity Uncertainty Quantification: Methods, Applications, and Future Directions. Annu. Rev. Fluid Mech. 2024, 56, 285–312. [Google Scholar]
- Li, R.; Huang, Z.; Wang, W. PG-Diff: A Physics-Informed Self-Guided Diffusion Model for High-Fidelity Simulations. In Proceedings of the International Conference on Learning Representations, Singapore, 24–28 April 2025. [Google Scholar]
- Du, P.; Parikh, M.H.; Fan, X.; Liu, X.Y.; Wang, J.X. Conditional neural field latent diffusion model for generating spatiotemporal turbulence. Nat. Commun. 2024, 15, 10416. [Google Scholar] [CrossRef]
- NEN 8100; Wind Comfort and Wind Danger in the Built Environment. NEN: Delft, The Netherlands, 2006.
- Bedrunka, M.C.; Wilde, D.; Kliemank, M.; Reith, D.; Foysi, H.; Krämer, A. Lettuce: PyTorch-based Lattice Boltzmann Framework. In Proceedings of the International Conference on High Performance Computing, Frankfurt, Germany, 14–18 June 2021; Springer: Cham, Switzerland, 2021; pp. 40–55. [Google Scholar]
- Sobol’, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. Zh. Vychisl. Mat. Mat. Fiz. 1967, 7, 784–802. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Nickisch, H. Gaussian processes for machine learning (GPML) toolbox. J. Mach. Learn. Res. 2010, 11, 3011–3015. [Google Scholar]
- Fontaine, M.C.; Togelius, J.; Nikolaidis, S.; Hoover, A.K. Covariance matrix adaptation for the rapid illumination of behavior space. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 94–102. [Google Scholar]
- Fontaine, M.; Nikolaidis, S. Differentiable Quality Diversity. Adv. Neural Inf. Process. Syst. 2021, 34, 10040–10052. [Google Scholar]
- Kent, P.; Branke, J. Bop-elites, a bayesian optimisation algorithm for quality-diversity search. arXiv 2020, arXiv:2005.04320. [Google Scholar]
- Grillotti, L.; Faldor, M.; León, B.G.; Cully, A. Quality–Diversity Actor–Critic Learning High–Performing and Diverse Behaviors via Value and Successor Features Critics. arXiv 2024, arXiv:2403.09930. [Google Scholar]
- Timothée, A.; Syrkis, N.; Elhosni, M.; Turati, F.; Legendre, F.; Jaquier, A.; Risi, S. Adversarial Coevolutionary Illumination with Generational Adversarial MAP-Elites. arXiv 2024, arXiv:2402.11951. [Google Scholar]
- Zhang, Y.; Fontaine, M.C.; Hoover, A.K.; Nikolaidis, S. Deep Surrogate Assisted MAP-Elites for Automated Hearthstone Deckbuilding. arXiv 2021, arXiv:2112.12782. [Google Scholar]




| Direct | Indirect | Latent | |
|---|---|---|---|
| Reachability | − Limited, hand-coded | + High | +/− Can be limited by training data |
| Validity | + Controllable | − Hard to constrain | − Hard to constrain |
| Searchability | + Low-dimensional | − No gradients | + Potentially lower dimensionality |
| Predictability | + Well-understood | +/− Context-dependent | +/− Possible, active research |
| Understanding | + Interpretable | − Black-box nature | − Needs disentangling |
| Prior Knowledge | +/− Manual design | +/− Via structure | + Data-driven by design |
| Paradigm | Coverage | Diversity | Applicability |
|---|---|---|---|
| MOO | No, Pareto front | objectives, low | competing features |
| MMO | Yes (par.) | parameters, higher fitness | no features |
| QD | Yes | features, higher diversity | behavioral features |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagg, A.; Gaier, A.; Wilde, D.; Asteroth, A.; Foysi, H.; Reith, D. Full Domain Analysis in Fluid Dynamics. Mach. Learn. Knowl. Extr. 2025, 7, 86. https://doi.org/10.3390/make7030086
Hagg A, Gaier A, Wilde D, Asteroth A, Foysi H, Reith D. Full Domain Analysis in Fluid Dynamics. Machine Learning and Knowledge Extraction. 2025; 7(3):86. https://doi.org/10.3390/make7030086
Chicago/Turabian StyleHagg, Alexander, Adam Gaier, Dominik Wilde, Alexander Asteroth, Holger Foysi, and Dirk Reith. 2025. "Full Domain Analysis in Fluid Dynamics" Machine Learning and Knowledge Extraction 7, no. 3: 86. https://doi.org/10.3390/make7030086
APA StyleHagg, A., Gaier, A., Wilde, D., Asteroth, A., Foysi, H., & Reith, D. (2025). Full Domain Analysis in Fluid Dynamics. Machine Learning and Knowledge Extraction, 7(3), 86. https://doi.org/10.3390/make7030086








