Harnessing Large-Scale University Registrar Data for Predictive Insights: A Data-Driven Approach to Forecasting Undergraduate Student Success with Convolutional Autoencoders

Abstract

Predicting undergraduate student success is critical for informing timely interventions and improving outcomes in higher education. This study leverages over a decade of historical data from Louisiana State University (LSU) to forecast graduation outcomes using advanced machine learning techniques, with a focus on convolutional autoencoders (CAEs). We detail the data processing and transformation steps, including feature selection and imputation, to construct a robust dataset. The CAE effectively extracts meaningful latent features, validated through low-dimensional t-SNE visualizations that reveal clear clusters based on class labels, differentiating students likely to graduate from those at risk. A two-year gap strategy is introduced to ensure rigorous evaluation and simulate real-world conditions by predicting outcomes on unseen future data. Our results demonstrate the promise of CAE-derived embeddings for dimensionality reduction and computational efficiency, with competitive performance in downstream classification tasks. While models trained on embeddings showed slightly reduced performance compared to raw input data, with accuracies of 83% and 85%, respectively, their compactness and computational efficiency highlight their potential for large-scale analyses. The study emphasizes the importance of rigorous preprocessing, feature engineering, and evaluation protocols. By combining these approaches, we provide actionable insights and adaptive modeling strategies to support robust and generalizable predictive systems, enabling educators and administrators to enhance student success initiatives in dynamic educational environments.

1. Introduction

Graduation rates in colleges and universities across the United States serve as critical indicators of student success and institutional performance. According to data from the National Center for Education Statistics (NCES), the average six-year graduation rate for first-time, full-time undergraduate students at four-year degree-granting institutions was approximately 63% for students who began their studies in 2015 [1]. However, significant disparities exist across different types of institutions, demographic groups, and geographic regions. For instance, private nonprofit institutions tend to have higher graduation rates (74%) compared to public institutions (62%) and private for-profit institutions (36%). Demographic factors also play a substantial role in graduation outcomes. The NCES reports that Asian students have the highest graduation rates (74%), followed by White students (67%), Hispanic students (54%), and Black students (45%). Socioeconomic status is another critical factor, with students from lower-income families experiencing lower completion rates due to barriers such as financial constraints, limited access to resources, and greater external responsibilities [2].

These statistics underscore the complex interplay of institutional, demographic, and socioeconomic factors that shape college graduation rates. Understanding these disparities is crucial for developing targeted interventions aimed at improving student outcomes, particularly for underrepresented and underserved populations [3]. Persistent gaps in graduation rates highlight the need for innovative strategies to identify and address the underlying challenges that prevent many students from completing their degrees. Predicting college graduation outcomes plays a critical role in this effort. For students, graduation represents a key milestone with profound implications for long-term socioeconomic mobility, career opportunities, and personal growth. However, numerous barriers, such as financial constraints, academic struggles, and limited access to support services, can impede their progress. For institutions, predictive models offer actionable insights to guide interventions that support student success. By identifying at-risk students early, institutions can implement tailored support measures, such as academic advising, financial aid counseling, and mental health resources, to address individual needs and improve retention. For example, predictive tools can help advisors identify students struggling with course loads or lacking engagement and provide specific resources or adjustments to ensure their success. Predicting graduation outcomes also enables institutions to allocate resources more efficiently, focusing on areas that will have the greatest impact on student retention and completion [4].

Universities routinely collect vast amounts of data on their students, encompassing academic records, demographic information, socioeconomic backgrounds, engagement metrics, and campus resource usage. These data are often compiled over years, creating rich historical datasets that provide a comprehensive view of student experiences and outcomes. While traditionally used for administrative purposes, such as enrollment tracking and compliance reporting, this wealth of information holds great potential for advanced predictive analytics. The increasing availability of such data, combined with advances in machine learning (ML), offers an unprecedented opportunity to develop sophisticated predictive models that can forecast student outcomes, including graduation likelihood. By analyzing patterns and relationships in historical data, ML models can identify key factors that influence student success and uncover subtle trends that may not be immediately apparent through traditional analysis. Predictive models trained on these datasets have the potential to transform how universities support their students. For example, they can help identify at-risk students early in their academic journey, enabling targeted interventions to address challenges before they escalate [5]. These models can also provide actionable insights to inform institutional policies, optimize resource allocation, and enhance the overall effectiveness of student support services.

Several studies have demonstrated the effectiveness of ML techniques in predicting student graduation and success. For instance, ML models were used to predict student performance over time by employing a bilayer structure with multiple base predictors and ensemble predictors to analyze evolving performance states [6]. A novel data-driven approach using latent factor models and probabilistic matrix factorization was introduced to uncover course relevance, enhancing the predictive accuracy of the models. Extensive simulations on a three-year undergraduate dataset from the University of California, Los Angeles, revealed that the proposed method outperforms benchmark approaches, showcasing its potential for improving educational outcomes. Another study investigated the use of various ML algorithms, linear regression (LR), decision trees (DT), and naïve Bayes (NB) classification, to predict student success, with a focus on comparing the impact of feature engineering and algorithm selection on prediction performance [7]. By applying these methods to both raw and feature-engineered versions of two student datasets, the study demonstrated that accurate predictions of student performance are achievable, with NB achieving 98% accuracy on one dataset and DT achieving 78% on the other. These findings emphasized that feature engineering plays a more significant role in improving prediction performance than the choice of ML method in this context.

A study predicting final academic grades and dropout cases highlighted the applicability of ML models in real-world educational settings, achieving notable results. The extra trees (ET) algorithm reached an accuracy of 82.8%, while the majority voting (MV) model outperformed all other approaches with an impressive accuracy of 92.7% [8]. Similarly, ML and data mining techniques have been applied to predict six-year graduation rates, leveraging a dataset of over 14,000 students from six fall cohorts. This dataset, comprising 104 features drawn from pre-existing university data, reduced sparsity, minimized data collection time, and improved coverage of the student body and their activities [9]. The models achieved high predictive performance, identifying the grade point average (GPA) and completed credit hours as the most critical predictors of graduation. These findings underscore the potential of predictive models to support timely interventions and enhance academic outcomes. Additionally, a comprehensive review of studies employing ML to forecast university graduation rates highlights the growing interest and advancements in this field, further emphasizing the transformative role of these techniques in higher education [10].

In the present study, we leverage over a decade of historical student data collected at Louisiana State University (LSU) to develop predictive models of undergraduate graduation outcomes. Our approach integrates advanced machine learning techniques with rigorous data preprocessing, including feature selection, transformation, and contextual imputation, to construct a robust and comprehensive dataset. To uncover meaningful latent structures in this high-dimensional data, we employ a convolutional autoencoder (CAE), which compresses the input into compact representations while preserving critical information. The ability of the encoder to differentiate between graduating and non-graduating students is validated through low-dimensional t-SNE visualizations, revealing clear clustering aligned with graduation status. While convolutional neural networks (CNNs) are traditionally used in image processing [11], there is growing interest in adapting one-dimensional CNNs (1D-CNNs) for feature extraction from non-image data. Recent applications of 1D-CNNs span several fields, including medical diagnostics [12], advanced manufacturing [13], intelligent transportation [14], and neural signal processing [15]. These studies underscore the versatility of 1D-CNNs in capturing local and sequential patterns in structured tabular or time-series datasets.

Building on this emerging trend, our work explores the utility of 1D-CNNs in educational data mining, demonstrating their effectiveness in extracting informative features from registrar records for student success prediction. To further enhance the realism and rigor of model evaluation, we introduce a two-year temporal gap strategy that simulates real-world forecasting by ensuring predictions are made on future, unseen cohorts. By combining automated representation learning with careful preprocessing and forward-looking validation, this study contributes to the development of scalable, generalizable predictive tools to inform student support strategies and institutional decision-making in higher education.

2. Materials and Methods

2.1. Dataset Overview

This study utilized a dataset containing 94,931 student records with 276 features, obtained from the Office of the University Registrar at LSU for the years 2011 through 2023. The features included data on demographics, academic performance, enrollment history, socioeconomic background, campus engagement, and geographic information. To prepare the dataset for ML analysis, feature selection and transformation techniques were applied to optimize its structure. Several challenges arose during data preprocessing. Missing data were prevalent across many fields, including academic performance, geographic information, socioeconomic factors, engagement metrics, and demographic variables. To address these gaps, a context-based imputation method was used to fill in missing values. This approach preserved critical relationships among variables while minimizing potential biases introduced during imputation. Graduation status, the target variable in this study, was defined as a binary outcome. Students who had completed their undergraduate degree by the time of data extraction were labeled as graduates (positive class), while those who had not completed a degree were labeled as non-graduates (negative class), regardless of their enrollment duration or whether they had dropped out or transferred. This binary classification approach was chosen to reflect the overall graduation outcomes, rather than timing or pathway details. The dataset exhibited class imbalance, with 66.4% of records corresponding to graduates and 33.6% to non-graduates. To ensure robust and fair model performance across both classes, strategies such as class weighting in ML algorithms were employed. Evaluation metrics like the F1-score [16] and the area under the receiver operating characteristic curve [17] (AUC-ROC) were also used to accurately assess model effectiveness while addressing the class imbalance issue.

2.2. Numerical and Geographic Data Representation

In preparing the dataset for analysis, our approach prioritized meaningful data representation, ensuring that each feature contributed effectively to model development. The core of our preprocessing strategy was to retain actual numerical values where they held intrinsic significance and to avoid using numerical codes that lacked meaningful order or magnitude. For instance, the GPA was treated as a real number, where higher values indicate better academic performance. Similarly, family income was represented as a numerical value, where higher amounts reflect greater wealth. In cases where numerical codes did not represent true quantities, we avoided using them in their raw form. For example, zone improvement plan (ZIP) codes, though numerical, do not imply any ranking or value comparison; for instance, 77701 in Beaumont, TX, is not “higher” or “better” than 70803 in Baton Rouge, LA. Since these codes serve as identifiers rather than meaningful quantities, we converted them into geographic coordinates. For example, ZIP code 77701 was mapped to 30.07° N, 94.1° W, and ZIP code 70803 to 30.41° N, 91.18° W. This transformation allowed the model to identify broad geographic patterns without misinterpreting ZIP codes as ordinal features Although ZIP codes are frequently used as geographic proxies for socioeconomic characteristics in the U.S. [18], they were originally designed for mail delivery and may cover areas with substantial demographic and economic diversity. As a result, while converting ZIP codes to geographic coordinates can help capture location-based patterns, this approach may not fully account for the socioeconomic heterogeneity that exists within individual ZIP code areas.

2.3. Categorical Feature Encoding

To prepare categorical features for analysis, we encoded various fields numerically to ensure the data was machine-readable and effectively structured for model training. This process involved binary encoding, one-hot encoding, and a scoring system for specific high school (HS) rank categories. Binary encoding was applied to categorical variables such as on-campus status, first-time or transfer student status, full-time or part-time status, gender, domestic or international student status, and Greek life participation. The first-generation status field was encoded with values of 2 for “Yes,” 0 for “No,” and 1 for “Unknown,” to capture its unique distinctions. This approach simplified these fields for analysis. For features with multiple categories, such as primary enrolled college, primary enrolled program, and the college administering the student major, one-hot encoding was used. For example, in the primary enrolled college field, there are 13 categories, so a separate column was created for each college. If a student was enrolled in the College of Engineering, the Engineering column received a value of one, while all other columns for that field were assigned zero. This approach added 146 new features to the dataset. Similarly, one-hot encoding was applied to the HS type field, which included five categories and an additional category for missing data, ensuring each type was distinctly represented in the dataset.

2.4. High School Rank Encoding and Contextual Imputation

HS rank categories, including top 10, top 25, top 50, bottom 25, and bottom 50, were represented using a scoring system to capture their hierarchical nature. These categories reflect students’ relative standing within their HS classes, for example, HS top 10 indicated that a student was in the top 10 percent of their class, while HS top 25 and HS top 50 corresponded to the top 25 percent and top 50 percent, respectively. Conversely, HS bottom 25 and HS bottom 50 represented the lower 25 percent and lower 50 percent. Each category was assigned a score to reflect these distinctions: HS top 10 received 5, HS top 25 received 12.5, HS top 50 received 25, HS bottom 25 received 75, and HS bottom 50 received 87.5. For students with missing HS rank data, an average score of 41 was assigned. This scoring system introduced a consistent hierarchy, enabling the models to distinguish varying levels of high school performance. The scores were included as a new column in the dataset. HS performance metrics, including “best math”, “best English”, “best composition”, “HS academic average”, and “HS overall average”, were imputed using the median based on the student’s high school rank category. For instance, if a “best math” score was missing for a student ranked in the top 10, it was replaced with the median “best math” score from other students in the top 10 category. This method ensured that missing values were contextually relevant and consistent with HS performance categories.

2.5. On-Campus Housing and Academic Records

To measure on-campus presence, a cumulative score was created for each student based on whether they lived on campus during their enrollment period. The dataset included separate columns for each academic term, indicating whether a student lived on campus during that specific semester. Each term was recorded as “yes” (if the student lived on campus) or left blank (if no record was available). A value of 1 was assigned for “yes” and 0 for blanks or missing data. These values were then summed across all terms to generate a total score representing the number of semesters a student lived on campus. This cumulative score was added as a new column to quantify the level of campus engagement over time. Missing values in academic metrics, such as semester GPA, LSU GPA, cumulative GPA, cumulative hours carried, cumulative hours earned, and academic status during the first and second years, were handled using median imputation. For instance, if a student GPA for a particular semester in their first or second year was missing, it was replaced with the median GPA calculated from their other available data during those years. This approach was also applied to other fields, ensuring a complete academic record for each student. Academic status, being categorical, was encoded numerically before missing data were imputed.

2.6. Imputation of Geographic and Socioeconomic Data

Geographic data, such as student ZIP codes, were converted into geographical coordinates (latitude and longitude). For domestic students, their ZIP code was used to determine specific coordinates, while for international students, the coordinates of their home country were used. Missing geographic data, primarily from international students, were assigned coordinates of (0.00, 0.00), representing “null island” as a placeholder. This transformation allowed the model to identify and analyze geographic patterns, such as regions associated with strong high school performance. For expected family contribution and income, we assumed that students from the same area shared similar financial backgrounds. Therefore, for domestic students, missing values were imputed using the median family income for their ZIP code, while a global median was applied for international students. This geographic-based imputation ensured that missing financial data reflected regional socioeconomic patterns.

2.7. Cohort Selection, Data Filtering, and Dataset Partitioning

The original dataset included 94,931 student records with 276 features. However, not all records or features were appropriate for ML analysis focused on graduation outcomes. To ensure reliable labeling, we removed 33,962 records for students who still had time to graduate, allowing a minimum window of four years (eight semesters) for degree completion. This included students who entered the university after Spring 2020, as they had not yet reached the typical graduation timeline at the time of analysis. We also excluded 3138 students who enrolled at LSU to complete prerequisite coursework for programs at other institutions, such as medical or nursing schools, without intending to earn a degree from LSU. To minimize bias and ensure generalizability, we removed additional 747 student-athletes and 803 veteran students, as these groups often receive specialized support and follow academic trajectories distinct from the broader student population. After replacing missing values in key academic metrics, such as semester GPAs, cumulative credit hours, and academic status, 428 records with unresolved inconsistencies were removed. Another 638 observations were excluded due to missing data in critical financial fields, including expected family contribution and income.

To reduce the risk of information leakage, we also excluded any features representing post-graduation outcomes (e.g., employment status), focusing strictly on pre-graduation data. After feature selection and transformation, 36 numerical and continuous variables and 9 categorical variables were retained. One-hot encoding of categorical features resulted in 152 additional columns, yielding a final feature set with 197 variables. Following all filtering steps, the final cleaned dataset consisted of 55,215 student records, fully structured and prepared for predictive analysis. For model training, the features were separated into a feature set X and the target variable Y (graduation status). The data were then split into training and testing sets using an 80/20 ratio, resulting in 80% of the data for training and 20% for testing. From the training set, 20% of the data was further allocated as a validation set, yielding 33,129 records for training, 11,043 for validation, and 11,043 for testing.

2.8. Standardization of Continuous Features and Handling of Categorical Variables

To ensure consistency across features, Z-score standardization [19] was applied to the 36 continuous columns. This process scaled each value based on the number of standard deviations from the mean, calculated as $Z\text{-}\mathrm{score}={\displaystyle \frac{x-\mu }{\sigma }}$, where x represents the observed value, μ is the mean, and σ is the standard deviation. Standardization enhanced model interpretability and stability by ensuring uniformity across continuous features. For features with wide-ranging values, such as income and expected family contributions, their distributions were first assessed using a log transformation to evaluate spread and skewness. Following this assessment, Z-score standardization was applied to these features for consistency across all numerical data.

Binary, one-hot encoded, and categorical variables were not normalized during preprocessing. Normalizing binary or one-hot encoded features would have disrupted their inherent 0 and 1 representation, which directly encodes category membership or binary status. Similarly, normalizing categorical variables with assigned scores would have distorted the intended ordinal relationships, reducing interpretability. Keeping these features unnormalized preserved their categorical distinctions, ensuring proper interpretation by the model without unintended scaling effects. Following the standardization process, feature distributions were reviewed to confirm their alignment with normal distribution assumptions and consistency with their original patterns. This step validated the effectiveness of standardization for features with varying scales, ensuring readiness for model training. 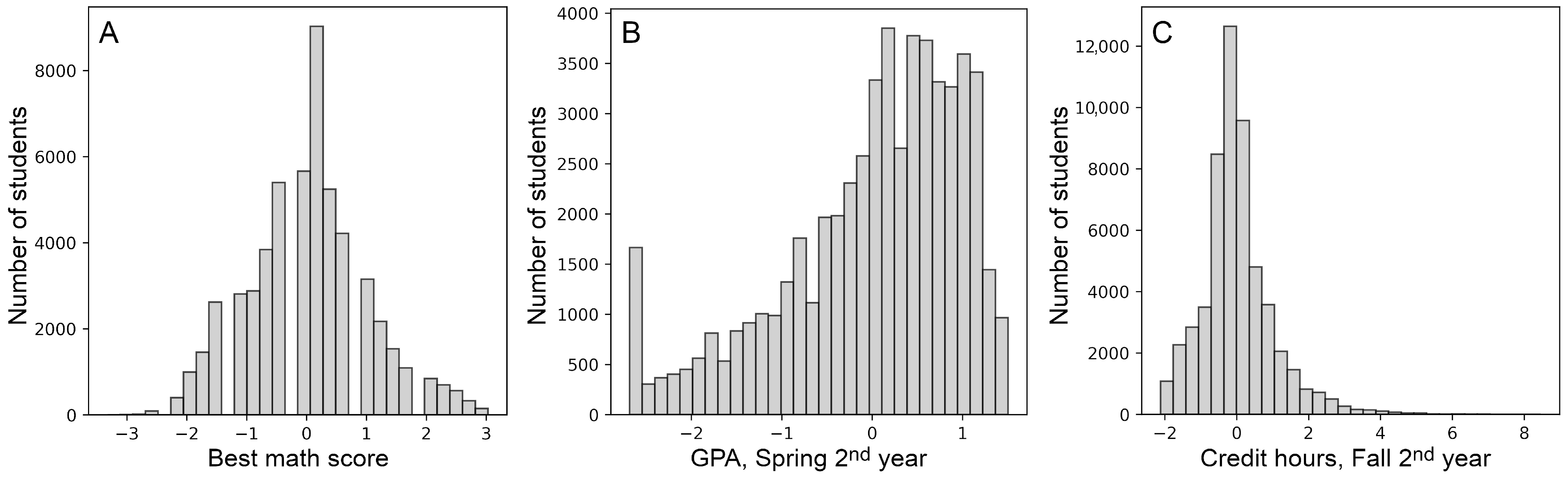Figure 1 shows histograms after Z-score standardization for selected features, such as the best math score, GPA, and cumulative credit hours, demonstrating that their distributions remained consistent after standardization.

2.9. Convolutional Autoencoder for Feature Extraction

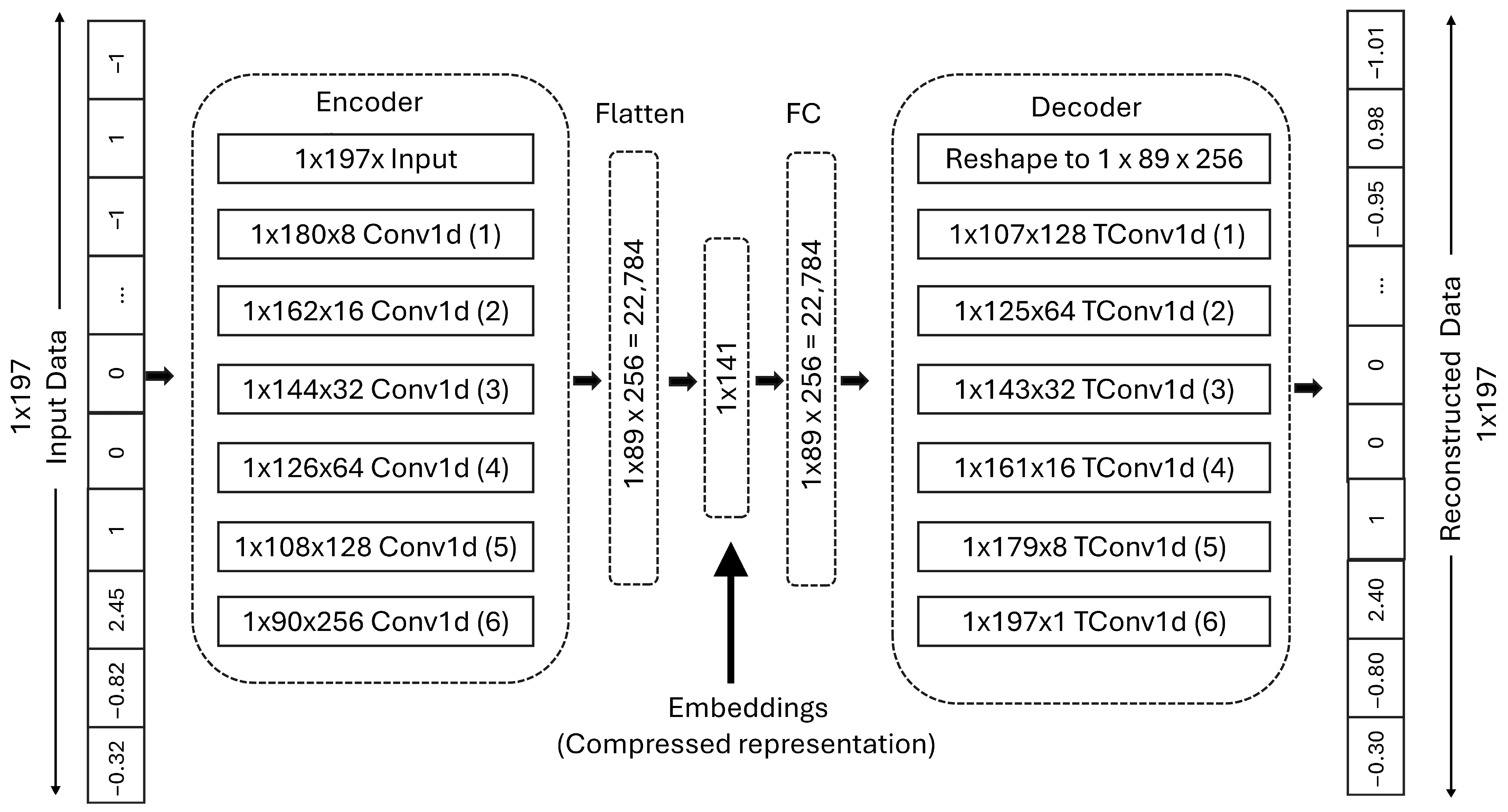
The CAE [20] was employed to extract latent features from the input data and reconstruct it with high accuracy. The CAE was specifically designed to process one-dimensional student data, where the input comprised concatenated features. These features included continuous variables (e.g., GPA, geographical information, age), one-hot encoded categories (e.g., programs, colleges), and binary encodings (e.g., on-campus status, Greek life). Unlike conventional CAEs used for image processing, which typically handle two- or three-dimensional data, this architecture was adapted to handle 1D data, aligning with the structure of student records. The CAE architecture consisted of an encoder with six convolutional layers and a symmetrical decoder for reconstruction. The encoder progressively compressed the input dimensions, extracting meaningful latent features and reducing the data to a 141-dimensional embedding, approximately 71.5% of the original input size. This dimensionality was selected after systematically testing various configurations, starting from shallow architectures and gradually increasing the depth of the layers. The 141-dimensional embedding provided an optimal balance between information retention and dimensionality reduction, ensuring that critical patterns were preserved without excessive complexity. The decoder reconstructed the input data from these embeddings with minimal information loss. Figure 2 illustrates the CAE architecture, depicting the flow of data from the concatenated input through the encoder, embedding layer, and decoder.

To improve generalization and stability, regularization techniques such as dropout (0.1 rate) and batch normalization were applied. LeakyReLU was used as the activation function to introduce non-linearity, enhancing the model ability to capture complex relationships in the data [21]. The model was optimized for GPU acceleration and trained on the LSU high-performance computing (HPC) cluster to ensure efficient large-scale processing. The CAE was trained for up to 300 epochs using a combined loss function. This function included mean squared error (MSE) to minimize the difference between the input and reconstructed data, and L1 regularization to promote sparsity in the embeddings. By encouraging sparsity, L1 regularization reduced redundancy in the latent features, aiding downstream predictive tasks. Early stopping was employed to prevent overfitting, halting training if no improvement in validation loss was observed for 10 consecutive epochs. Training and validation losses were continuously monitored to evaluate the model performance and convergence.

2.10. Random Forest Classification Using Input Features and CAE-Derived Embeddings

A random forest (RF) [22] was employed as a primary classifier to predict graduation status (graduate vs. non-graduate). Due to the class imbalance in the dataset, 36,656 graduate instances and 18,559 non-graduate instances, class balancing techniques were implemented by assigning appropriate weights to each class during training [23]. Entropy was chosen as the criterion for splitting, providing a measure of split quality within the decision trees. To evaluate how the compressed features extracted by the CAE affect classification performance, we used these features (called embeddings) as input for another RF model. We applied the same optimization and balancing methods to this model as we did for the one trained on the original data. Then, we used cross-validation (CV) to measure the model accuracy and consistency across different data splits. This approach allowed us to compare how well the original input data and the CAE-compressed features performed in predicting graduation outcomes.

2.11. k-Nearest Neighbor Algorithm

The k-nearest neighbor (kNN) algorithm is a simple yet effective ML method to classify data points based on their proximity [24]. Its simplicity makes it an ideal baseline for evaluating model performance and analyzing the impact of varying data splits. By leveraging kNN, this study assessed the effects of grouping strategies and temporal separation without introducing the complexity of more advanced algorithms. Initially, the dataset was randomly split, and the kNN model was trained using cosine similarity as the distance metric. A grid search was conducted to optimize the number of neighbors, resulting in a configuration that established a baseline for performance evaluation.

2.12. Two-Year Gap Strategy for Temporal Generalization Evaluation

To test the model under more realistic and challenging conditions, custom grouping strategies were implemented instead of random splits. Students were grouped by their entry year to ensure that no group was represented in both training and testing sets. The final dataset spanned nine academic years (18 semesters), sequentially mapped from Fall 2011 (1) to Spring 2020 (18). Training and testing sets were formed using consecutive semesters, separated by a two-year gap. For example, one fold (configuration) may train on semesters 1 through 4, test on semesters 9 through 12 after a two-year gap, and resume training on semesters 17 through 18 following another two-year gap.

Since most students enrolled in fall semesters, with fewer joining in spring, grouping strategies were carefully designed to maintain balance across all configurations. In the first possible configuration, Fall 2019 (17) and Spring 2020 (18) were excluded from the training set to prevent imbalance in the number of observations across different configurations. Similarly, Fall 2011 (1) and Spring 2012 (2) were excluded in two other configurations to maintain the same balance. These exclusions ensured that no single configuration had significantly more observations than others, preserving consistency across different training and testing configurations. Although these semesters could have been included, their removal was necessary to maintain a uniform number of observations across configurations, minimizing biases and ensuring fair comparisons in model evaluation. Figure 3 illustrates the chronological data split, showing the arrangement of training and testing sets under the two-year gap strategy. This approach simulated real-world scenarios where predictions must generalize to future, unseen data, highlighting the importance of temporal separation in evaluating model performance.

3. Results

3.1. Optimization and Reconstruction Performance of the Convolutional Autoencoder

To evaluate the reconstruction capability and identify an optimal latent dimensionality for the CAE, we trained models with embedding sizes ranging from 180 down to 64 and assessed the reconstruction performance using MSE on the validation set. As shown in

Table 1. Validation reconstruction error (MSE) for various embedding sizes tested with the convolutional autoencoder.

Embedding Size	Validation MSE
180	0.1057
160	0.1037
141	0.1079
128	0.1095
96	0.1102
64	0.1100

, all tested configurations achieved low reconstruction errors, with the best MSE observed at an embedding size of 160 (0.1037). However, the differences across embedding sizes were minimal indicating that the reconstruction accuracy was not highly sensitive to the exact size of the latent space. Notably, the lowest MSE values were observed within the top half of the tested embedding sizes (180–141), suggesting that this range offers a favorable trade-off between dimensionality reduction and reconstruction fidelity. We selected an embedding size of 141 as a representative example for downstream analysis, due to its strong reconstruction performance and suitability for visualization and classification tasks. 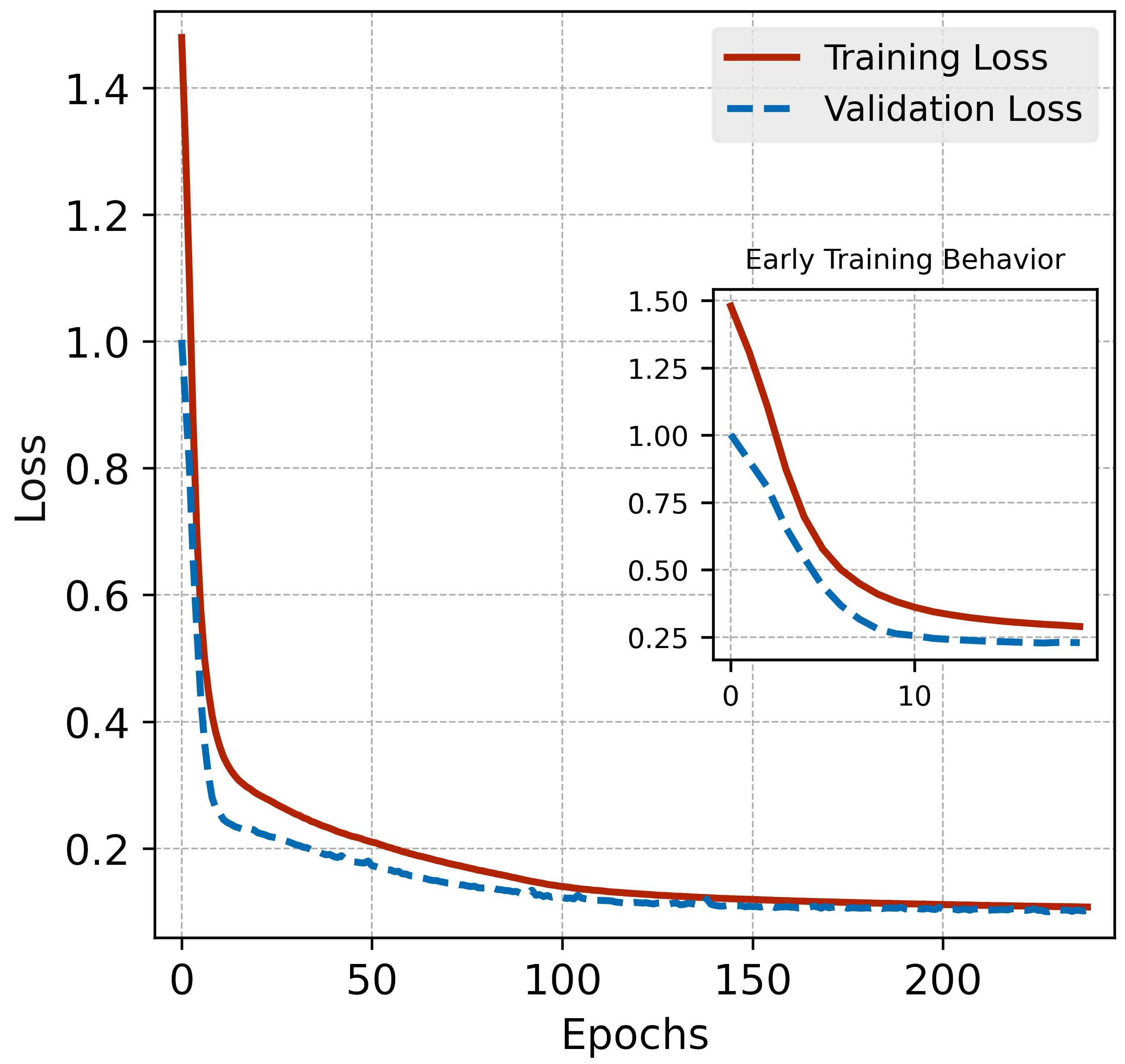As illustrated in Figure 4, the CAE trained with 141 latent dimensions showed consistent improvements in training and validation losses over time, with early stopping triggered at epoch 239. The close alignment between validation and test losses further indicates that the CAE generalized well and avoided overfitting. These results validate the ability of CAE to extract meaningful latent features from high-dimensional, heterogeneous student data. The stable performance across multiple embedding sizes, combined with high reconstruction fidelity, supports the use of CAE-derived embeddings as a compact and interpretable representation for further predictive modeling.

3.2. Cross-Validation and Hyperparameter Tuning

To evaluate the model generalizability and optimize its performance, we employed 5-fold CV and grid search techniques. CV ensures that the model is trained and tested on different subsets of the data, providing a robust assessment of its ability to generalize to unseen data. The training data was split into five subsets, with four folds used for training and one fold for validation in each iteration. For hyperparameter optimization, we conducted a grid search to systematically explore various parameter combinations for each model. For the RF model, the grid search identified the optimal parameters as 300 estimators, a maximum depth of 20, no restriction on the number of features, and minimum sample requirements of 2 and 5 for leaf nodes and splits, respectively. These settings balanced model complexity and generalization, enabling effective splits and reducing overfitting while maintaining robust performance, with a mean CV accuracy of 85.9% and a best test set accuracy of 86% on the input data. For the kNN model, the grid search identified 24 neighbors with cosine similarity as the optimal configuration, achieving a CV accuracy of 84%, which matched its test set accuracy under the random split strategy. The results from CV and hyperparameter tuning underscore the importance of systematic parameter exploration in enhancing predictive performance. The RF model demonstrated robust performance across both input data and embeddings, while the kNN model provided a useful baseline for evaluating grouping strategies and temporal separation.

3.3. Visualizing Latent Representations with t-SNE

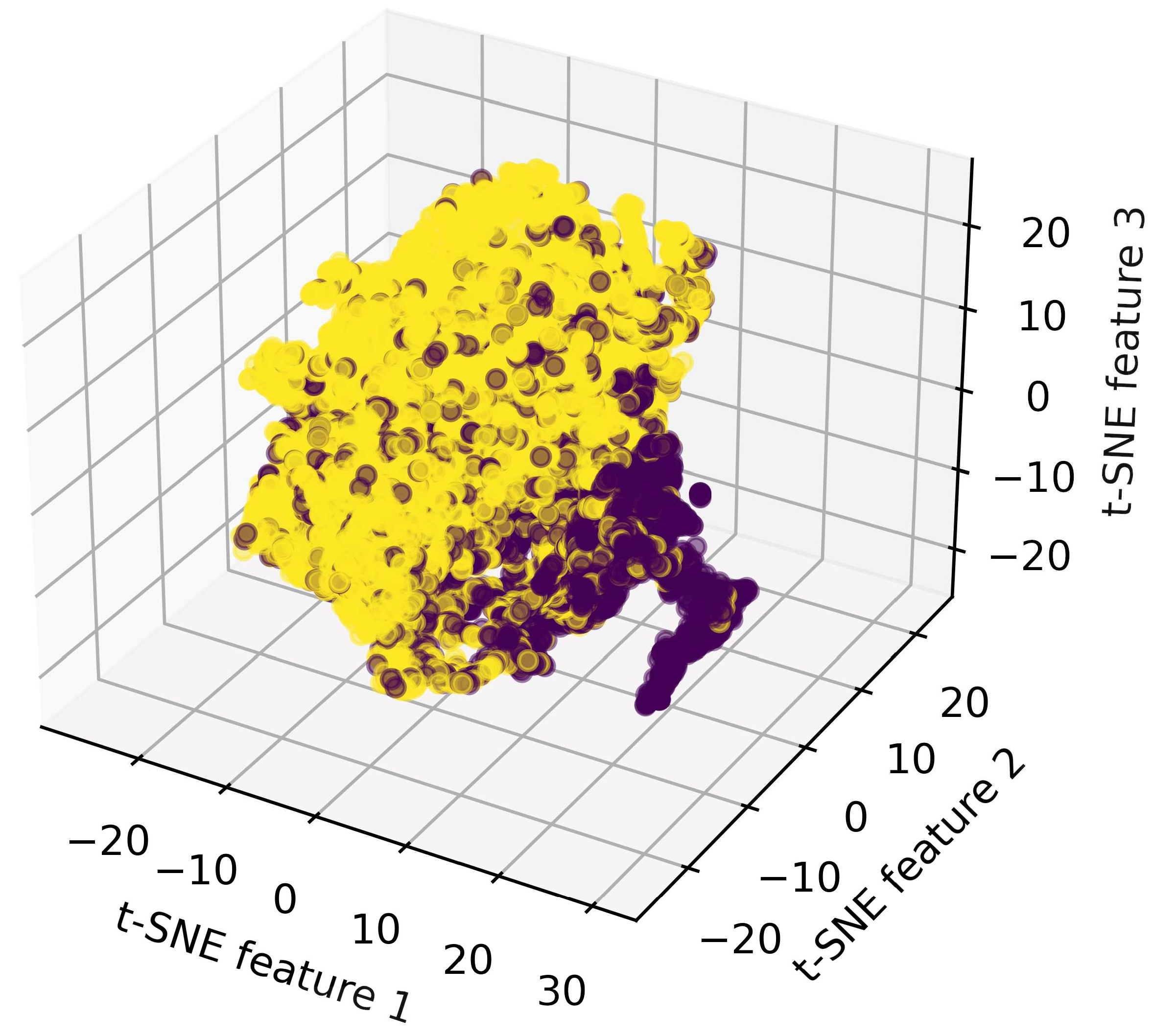
To evaluate the quality of the embeddings generated by the CAE, we applied t-distributed stochastic neighbor embedding (t-SNE), a dimensionality reduction technique [25]. t-SNE projects high-dimensional data into three-dimensional space, preserving local relationships between data points and enabling visualization of the structure and separation of classes. This approach is particularly useful for assessing the effectiveness of feature embeddings in capturing meaningful patterns. The 3D t-SNE visualization, shown in Figure 5, was generated using the 141-dimensional embeddings from the test set and revealed distinct clusters corresponding to different labels (graduates and non-graduates). The clusters demonstrated the ability of the CAE to generate distinguishable feature embeddings, with distinct separation observed between graduates and non-graduates. While the embeddings retained sufficient information to effectively distinguish between the two classes, some overlap occurred likely due to shared characteristics or similar patterns between the groups. These borderline cases may include students with traits such as moderate academic performance, intermittent engagement, or financial uncertainty, that place them near the decision boundary in the latent hyperspace. Such instances reflect the complexity of real-world educational trajectories and are expected to be difficult to classify with complete certainty. Nevertheless, the embeddings retained sufficient structure to distinguish the majority of students effectively. These findings highlight the potential of CAE to capture broad distinctions in the data while leaving room for further refinement to improve class separation. This underscores the utility of autoencoders for dimensionality reduction and their practical value in downstream predictive modeling tasks.

3.4. Benchmarking Random Forest Against Traditional Baseline Models

To assess the predictive performance of RF relative to traditional baseline models, we compared it with logistic regression (LR) and linear discriminant analysis (LDA) using the original input features for student graduation prediction. Model performance was measured using several metrics, including F1-score and AUC-ROC, which are especially appropriate for imbalanced datasets. The F1-score, the harmonic mean of precision and recall [16], offers a balanced measure of the ability to minimize both false positives and false negatives. Similarly, AUC-ROC captures the ability to discriminate between classes across all classification thresholds, providing a threshold-independent assessment of overall classification quality [17].

Table 2. Comparison of the performance of several classification models to predict student graduation.

	Model
	LR	LDA	RF
Accuracy	0.85	0.85	0.85
F1-score	0.88	0.90	0.89
Precision	0.88	0.85	0.85
Recall	0.88	0.95	0.94
AUC-ROC	0.91	0.90	0.90
Mean CV accuracy	0.85	0.86	0.86

LR—logistic regression, LDA—linear discriminant analysis, RF—random forest, AUC-ROC—the area under the receiver operating characteristic curve, CV—cross-validation.

shows that all three models demonstrated strong overall performance, with similar accuracy values, suggesting their ability to distinguish between graduating and non-graduating students using the available features. LDA achieved the highest recall (0.95) and F1-score (0.90), slightly outperforming the other models in identifying true positive cases. However, these gains came at the expense of a modest drop in precision, indicating a higher rate of false positives. This trade-off may be less desirable in settings where over-identifying at-risk students could lead to unnecessary allocation of limited institutional resources.

In contrast, RF offered a more balanced profile across metrics, achieving high recall (0.94) while maintaining precision comparable to LDA. The F1-score of 0.89 further highlights its strength in managing the trade-off between precision and recall. Importantly, RF matched or exceeded the mean CV accuracy of the other models, indicating stable generalization performance across different training and testing splits. The corresponding confusion matrix for RF, which summarizes the classification results, included 6779 true positives (students correctly predicted to graduate), 2393 true negatives (correctly predicted not to graduate), 1333 false positives (incorrectly predicted to graduate), and 538 false negatives (incorrectly predicted not to graduate).Beyond raw performance metrics, the choice of RF is additionally supported by its interpretability and flexibility. These classifiers offer feature importance rankings, which facilitate insights into the relative influence of academic, socioeconomic, and behavioral variables. Moreover, RF is inherently robust to outliers, non-linearity, and multicollinearity, challenges commonly encountered in large-scale registrar datasets. These properties make RF particularly suitable for integration with dimensionality reduction pipelines and real-world deployment where data variability and complexity are expected.

3.5. Comparison of Model Performance Using Input Data vs. Embeddings

To evaluate the effectiveness of the CAE in reducing dimensionality while preserving predictive power, we compared the performance of RF models trained on the original input features against models trained on CAE-derived embeddings with progressively reduced sizes, ranging from 180 down to 64 dimensions, as shown in

Table 3. Performance comparison of random forest models trained on raw input features and embeddings of various sizes.

	Raw Features	Embedding Size
		180	160	141	128	96	64
Accuracy	0.85	0.82	0.82	0.83	0.82	0.81	0.82
F1-score	0.89	0.82	0.81	0.82	0.81	0.81	0.82
Precision	0.85	0.82	0.82	0.83	0.82	0.81	0.82
Recall	0.94	0.82	0.82	0.83	0.82	0.81	0.82
AUC-ROC	0.90	0.87	0.86	0.87	0.86	0.86	0.86
Mean CV accuracy	0.86	0.82	0.81	0.82	0.81	0.81	0.81

AUC-ROC—the area under the receiver operating characteristic curve, CV—cross-validation.

. This comparison allowed us to assess how much performance is retained or lost as feature dimensionality is reduced and to identify the optimal embedding size for downstream classification tasks. As expected, the model trained on the full input feature set achieved the highest performance across most metrics, including accuracy (0.85), F1-score (0.89), and AUC-ROC (0.90). However, embeddings of reduced size demonstrated only modest drops in performance, indicating that essential patterns in the data were retained even after compression. For instance, embeddings with 180 and 141 dimensions maintained AUC-ROC values of 0.87, and an embedding size of 160 achieved an AUC-ROC of 0.86 with stable accuracy and recall, confirming that the compressed representations remained highly informative. While a slight reduction in predictive performance was observed with decreasing embedding size, these differences were relatively small and acceptable given the benefits of dimensionality reduction.

Embeddings offer computational efficiency, reduced memory requirements, and improved scalability for large-scale deployment. More importantly, they facilitate a modular pipeline where compressed representations can be reused across multiple tasks or combined with interpretable models like random forests. Among the different embedding sizes tested, 141-dimensional embeddings emerged as the optimal choice, striking a balance between compression and performance. Despite the reduction from 197 to 141 features, the model retained an AUC-ROC of 0.87, and both precision and recall remained above 0.83. These results suggest that while some fine-grained information may have been lost in the compression process, likely due to the model prioritizing global patterns over specific feature-level nuances, the 141-dimensional embedding preserved sufficient detail to support accurate classification. The ROC curve for this configuration, presented in Figure 6, underscores the ability to discriminate effectively between graduates and non-graduates even with fewer input dimensions. Overall, these findings demonstrate that CAE-derived embeddings are a viable alternative to raw features, especially in scenarios where computational constraints or system efficiency are critical.

3.6. Performance of kNN with Various Data Splits

When the data was split randomly, the kNN model achieved a CV accuracy and test set accuracy of 0.84 using the optimal number of 24 neighbors. These results indicate strong performance but do not account for temporal separation, which is critical for evaluating generalizability. Therefore, to evaluate the kNN model under temporal constraints, we implemented the two-year gap separation strategy with custom grouping across eight configurations of training and testing groups.

Table 4. kNN model accuracy under two-year gap strategy. Accuracy scores are shown for different training and testing configurations based on student entry year, each separated by a two-year gap to simulate future prediction scenarios.

	Testing Groups	Accuracy
(1, 2, 3, 4)	(9, 10, 11, 12)	0.80
(3, 4, 5, 6)	(11, 12, 13, 14)	0.82
(5, 6, 7, 8)	(13, 14, 15, 16)	0.79
(7, 8, 9, 10)	(15, 16, 17, 18)	0.69
(9, 10, 11, 12)	(1, 2, 3, 4)	0.81
(11, 12, 13, 14)	(3, 4, 5, 6)	0.83
(13, 14, 15, 16)	(5, 6, 7, 8)	0.83
(15, 16, 17, 18)	(7, 8, 9, 10)	0.78

summarizes the results, with accuracies ranging from 0.69 to 0.83 across configurations. The average accuracy for this approach was 0.79, reflecting the increased difficulty of generalizing to temporally distinct data. Configurations with earlier training groups (e.g., semesters 1 through 4 training and semesters 9 through 12 testing) generally achieved higher accuracies, with some reaching 0.82–0.83 accuracy. In contrast, later configurations (e.g., semesters 7 through 10 training and semesters 15 through 18 testing) exhibited reduced performance, with the lowest accuracy recorded at 0.69. This trend may indicate that the model struggled to generalize across shifts in student characteristics over time. These shifts likely reflect changes in demographics, academic preparedness, or engagement patterns among students, which can impact the model ability to adapt to and accurately predict outcomes for temporally distinct groups.

The comparison between random split and the two-year gap strategy shows a trade-off between simplicity and realism in model evaluation. Random split resulted in higher accuracy, but the two-year gap approach offered a more realistic way to test how well the model could predict future data. The drop in accuracy from 0.84 to an average of 0.79 highlights the importance of using temporal separation to create training and testing sets, ensuring that models perform well in real-world situations. These findings show the value of evaluating models in realistic scenarios. By simulating future conditions, the two-year gap approach demonstrates how models can adapt to unseen data. This strategy is especially useful in dynamic environments like education, where changes in student populations and behaviors over time can affect outcomes. It provides a practical way to build and test models that are reliable and effective in real-world applications.

4. Discussion

The results of this study offer important insights into effective modeling strategies, data preprocessing techniques, and evaluation protocols for predicting undergraduate graduation outcomes from large-scale registrar data. One of the important strengths of this study is its careful handling of missing data. Instead of applying conventional global mean or median imputation strategies [26], we employed contextual imputation methods tailored to preserve structural patterns. For example, missing high school performance metrics were imputed using medians within each high school rank category, ensuring consistency within performance tiers. Similarly, financial variables such as family income and expected family contribution were imputed using ZIP code-level medians to reflect local socioeconomic contexts. These context-aware strategies enhanced data integrity and helped produce more accurate and generalizable models.

Traditional student success models, such as logistic regression and decision trees, rely heavily on manual feature engineering and often struggle to capture the complexity and heterogeneity of large-scale student data. These models treat features independently, limiting their ability to recognize interactions or local dependencies. In contrast, CAEs are well-suited for this setting due to their ability to perform automated representation learning. By applying 1D convolutions along the feature axis, the CAE effectively detects localized patterns and co-occurring features, such as GPA trends or course enrollment sequences, that may signal academic risk or progress. This local structure modeling, combined with the ability to handle high-dimensional, sparse inputs, allows the CAE to scale efficiently across large datasets without extensive preprocessing. Additionally, the ability to compress input data into compact embeddings enables efficient downstream classification while preserving essential information, making CAEs a powerful alternative to traditional approaches in educational predictive modeling.

The quality of the learned representations was further validated through t-SNE visualizations, which revealed distinct clustering of graduates and non-graduates. While most students were clearly separated in the latent space, some overlap was observed, likely reflecting ambiguous or borderline cases whose outcomes are inherently harder to predict. These students likely fall near class boundaries in the learned feature space, and their characteristics may partially align with both classes. Enhancing the model with additional features or architectural components such as attention mechanisms [27] could help to highlight more salient input signals and improve separation in the latent space. Despite slightly reduced predictive performance compared to models trained on the full input feature set, the CAE-derived embeddings offered notable gains in compactness and computational efficiency, making them well suited for large-scale or resource-constrained applications.

At the same time, the use of CAEs involves a trade-off in interpretability. Unlike traditional models where individual feature contributions can be directly examined, the latent representations learned by the CAE consist of abstract, non-linear combinations of input features optimized for reconstruction and classification. These embeddings are not inherently interpretable at the feature level, limiting their usefulness in contexts that demand transparency in decision-making. Nevertheless, the ability to perform representation learning on complex, high-dimensional educational data without manual feature engineering represents a significant methodological advancement and supports a broader shift toward more flexible, adaptive modeling frameworks.

In evaluating generalizability over time, we found that the kNN model performed well under random data splits but struggled under temporally separated evaluation. The introduction of a two-year gap between training and testing revealed performance degradation, suggesting that even moderate shifts in student population characteristics, such as changes in demographics, academic preparedness, or institutional policies, can hinder model reliability. This underscores the importance of including temporal validation in modeling workflows and highlights the need for adaptive strategies such as incremental retraining, online learning, or concept drift-aware models [28] to maintain predictive accuracy over time in dynamic educational environments.

It is important to note that our study did not include disaggregated analysis by race, ethnicity, or other protected characteristics in order to comply with data privacy and ethical research standards. Nevertheless, we employed several strategies to mitigate potential sources of bias. These included thoughtful preprocessing to avoid introducing artificial ordinal relationships, model-based imputation to preserve subgroup structures, and class weighting to address imbalance. We also excluded student populations with atypical trajectories, such as athletes and veterans, to reduce confounding effects. Interpretable models like random forests were used for indirect monitoring of potential bias signals. While fairness remains a critical concern in educational predictive modeling, its direct assessment was beyond the scope of this study. Future work enabled to perform subgroup analysis based on student background or academic characteristics could extend these efforts and systematically evaluate group fairness and mitigation strategies.

The predictive modeling framework developed here offers practical value for both academic advising and institutional planning. At the student level, early identification of individuals at risk of not graduating can enable timely interventions, such as academic support, financial counseling, or mental health services. At the institutional level, aggregated predictions can inform decisions on resource allocation, curriculum planning, and long-term forecasting. When implemented responsibly, with transparency and ethical safeguards, predictive analytics can complement human judgment and help advance equity, retention, and completion goals in higher education.

5. Conclusions

This study presents a CAE-based framework for predicting undergraduate graduation outcomes using large-scale registrar data. By employing contextual imputation, robust preprocessing, and dimensionality reduction through 1D convolutions, the model effectively captures complex patterns without relying on extensive manual feature engineering. The resulting latent representations support accurate classification while improving computational efficiency making them practical for real-world educational settings. While the CAE-derived embeddings offered strong performance, they come with trade-offs in interpretability. Further, the temporal validation revealed challenges in maintaining predictive accuracy across changing student populations. These findings underscore the importance of adaptive modeling strategies and continual updates to remain aligned with evolving educational contexts. Future work should explore fairness-aware modeling techniques, group-level performance evaluations, and hybrid architectures that combine deep learning with interpretable components. The proposed framework also holds promise for integration into academic advising and institutional decision-making systems, where early identification of at-risk students can inform targeted support and enhance student success outcomes.