Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks
Abstract
:1. Introduction
2. Theoretical Framework
2.1. ARFIMA Model for Long Memory Processes
2.2. Long Memory Parameter Estimation Methods
2.2.1. Periodogram Regression Method
2.2.2. Whittle Estimator Method
2.2.3. Detrended Fluctuation Analysis
2.2.4. Rescaled Range Method
2.2.5. Wavelet-Based Method
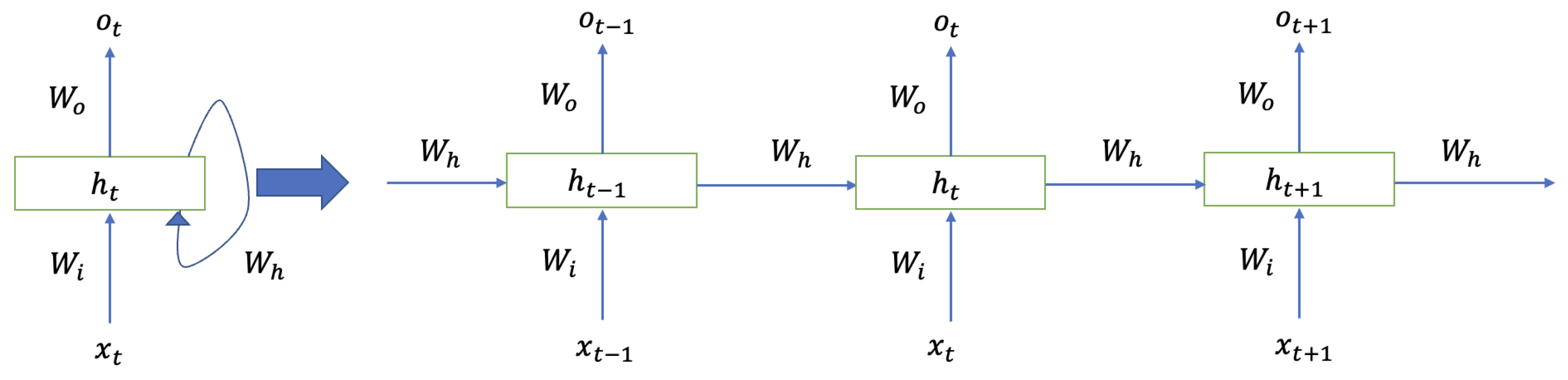
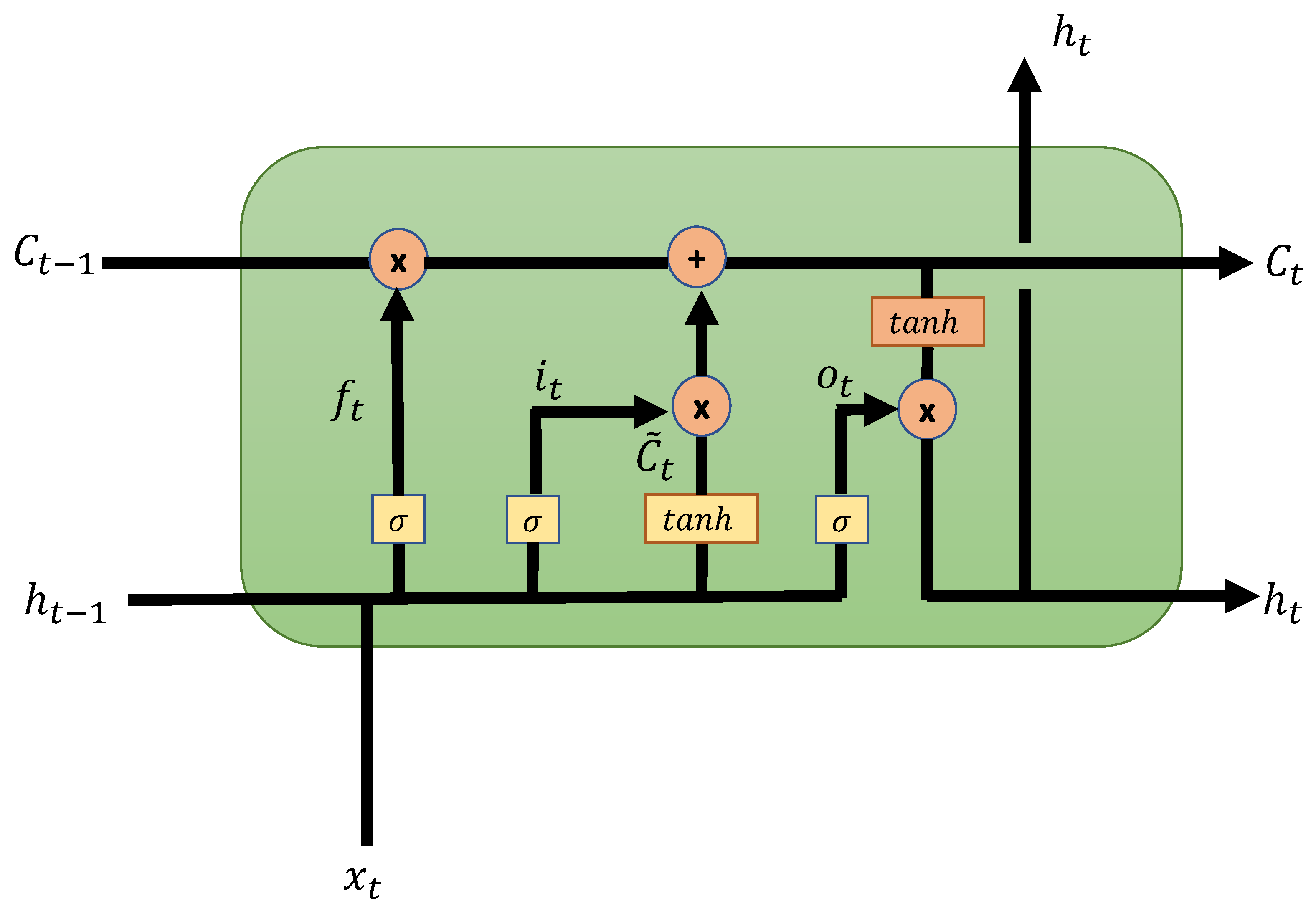
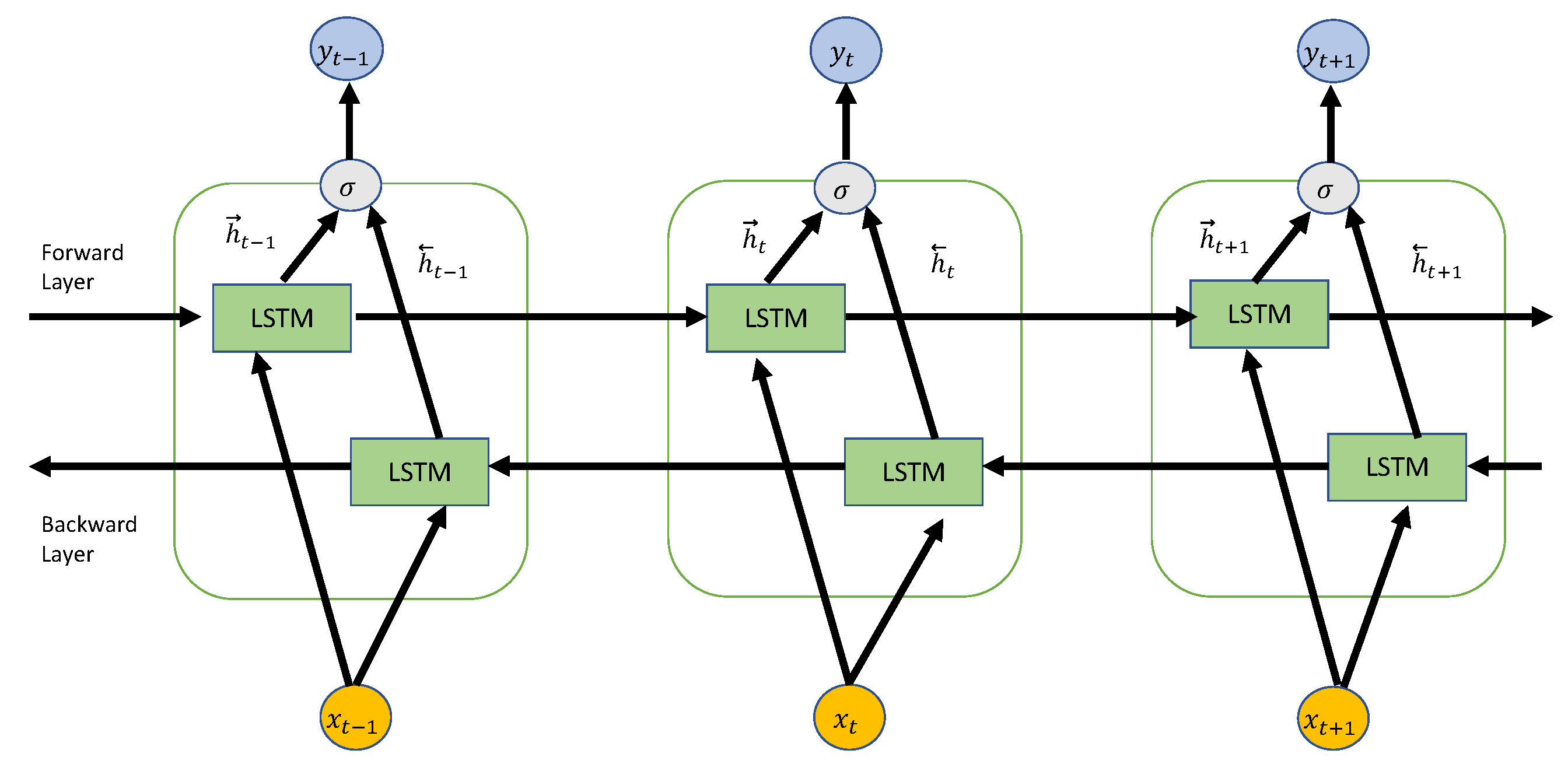
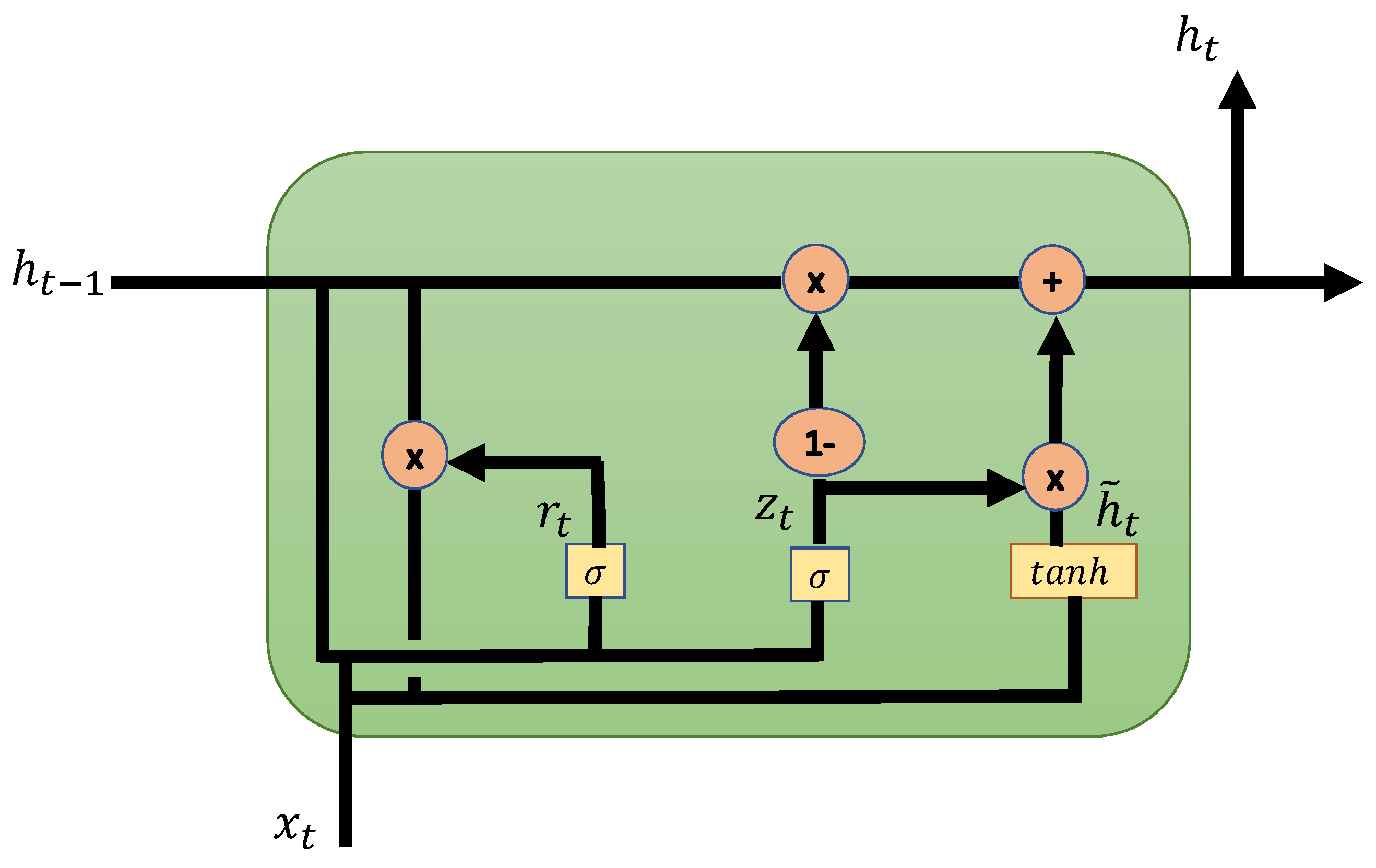
2.3. Recurrent Artificial Neural Networks
3. Materials and Methods
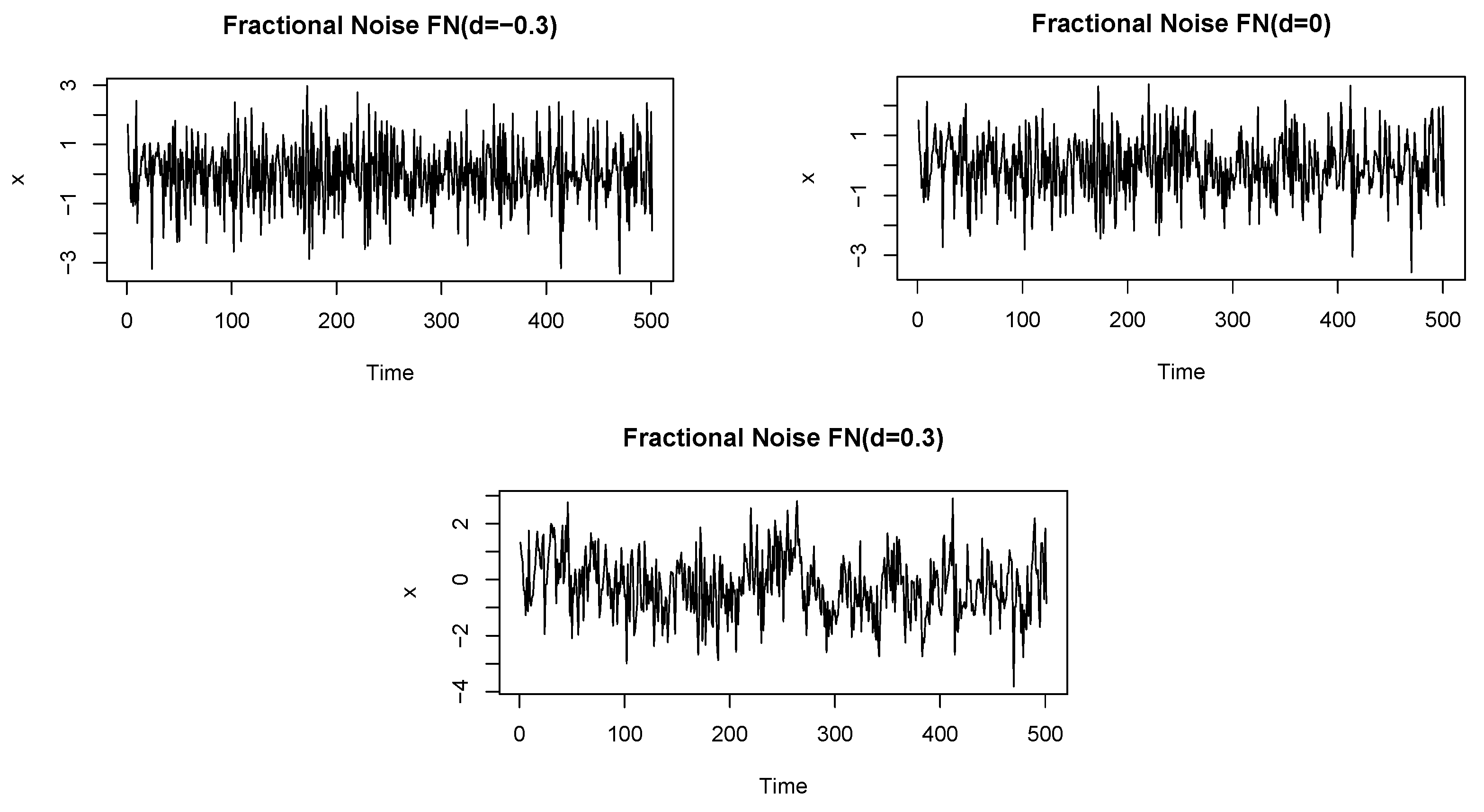
3.1. Dataset Description
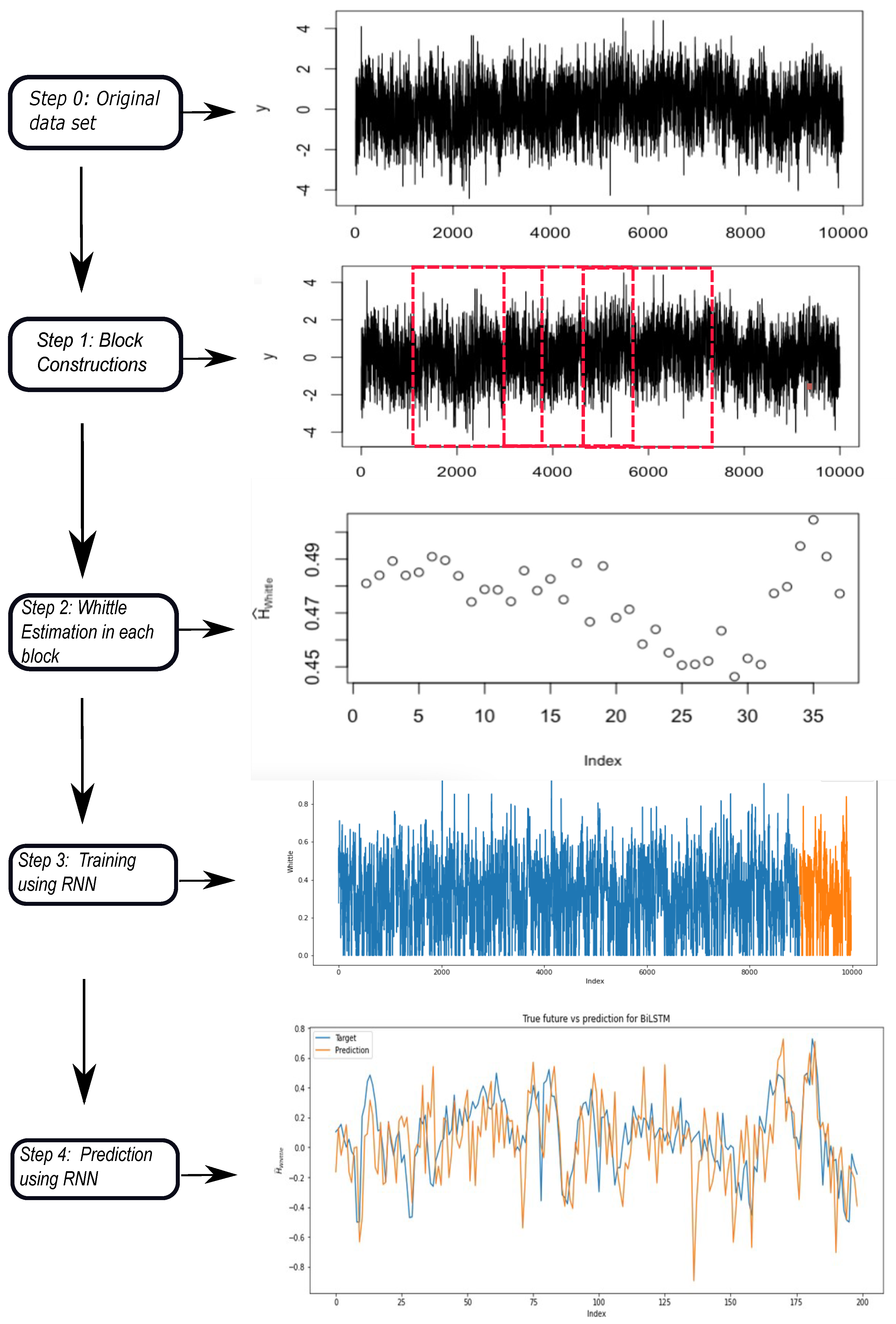
3.2. Methodology
| Algorithm 1 Predicting the Hurst parameter |
|
4. Results
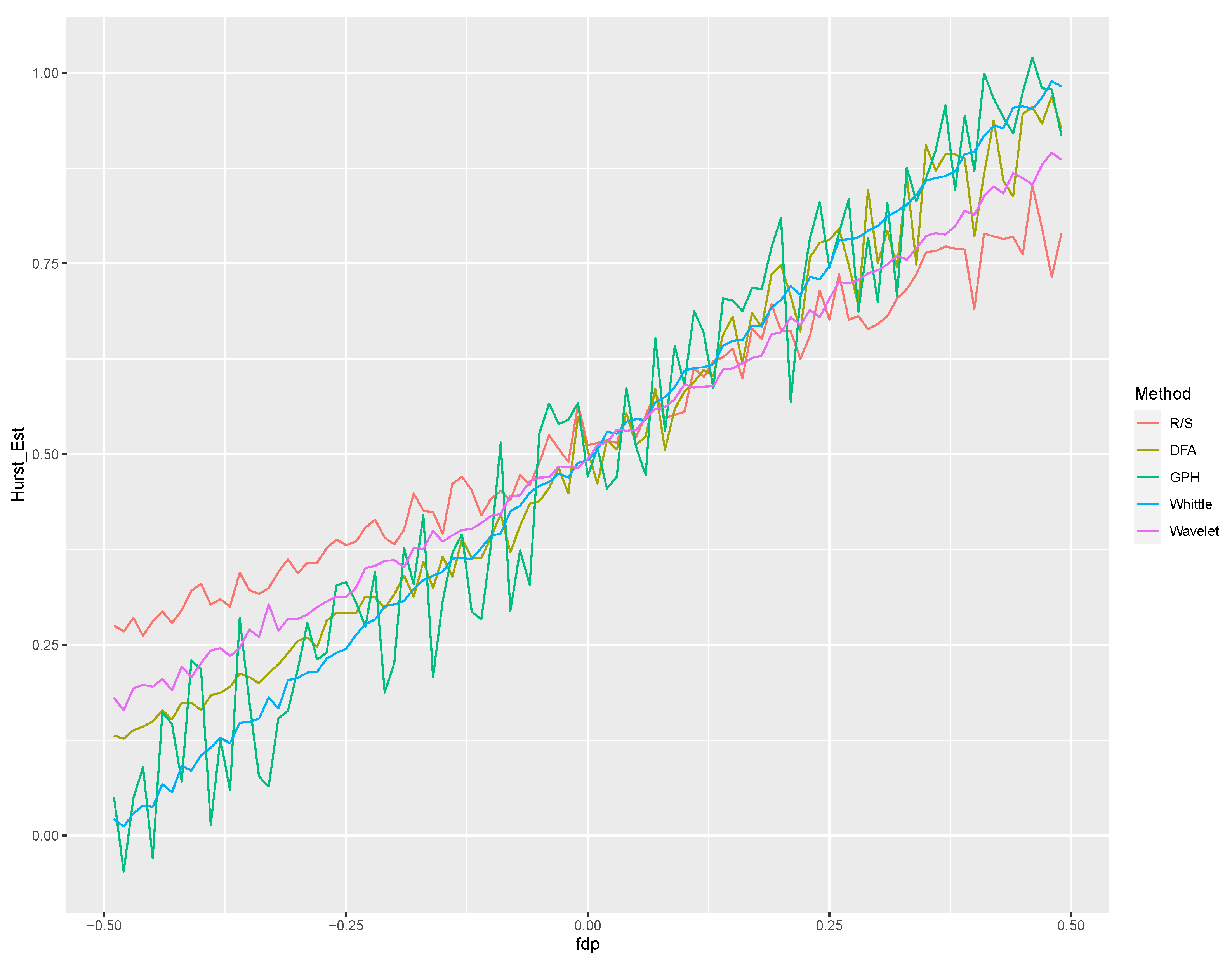
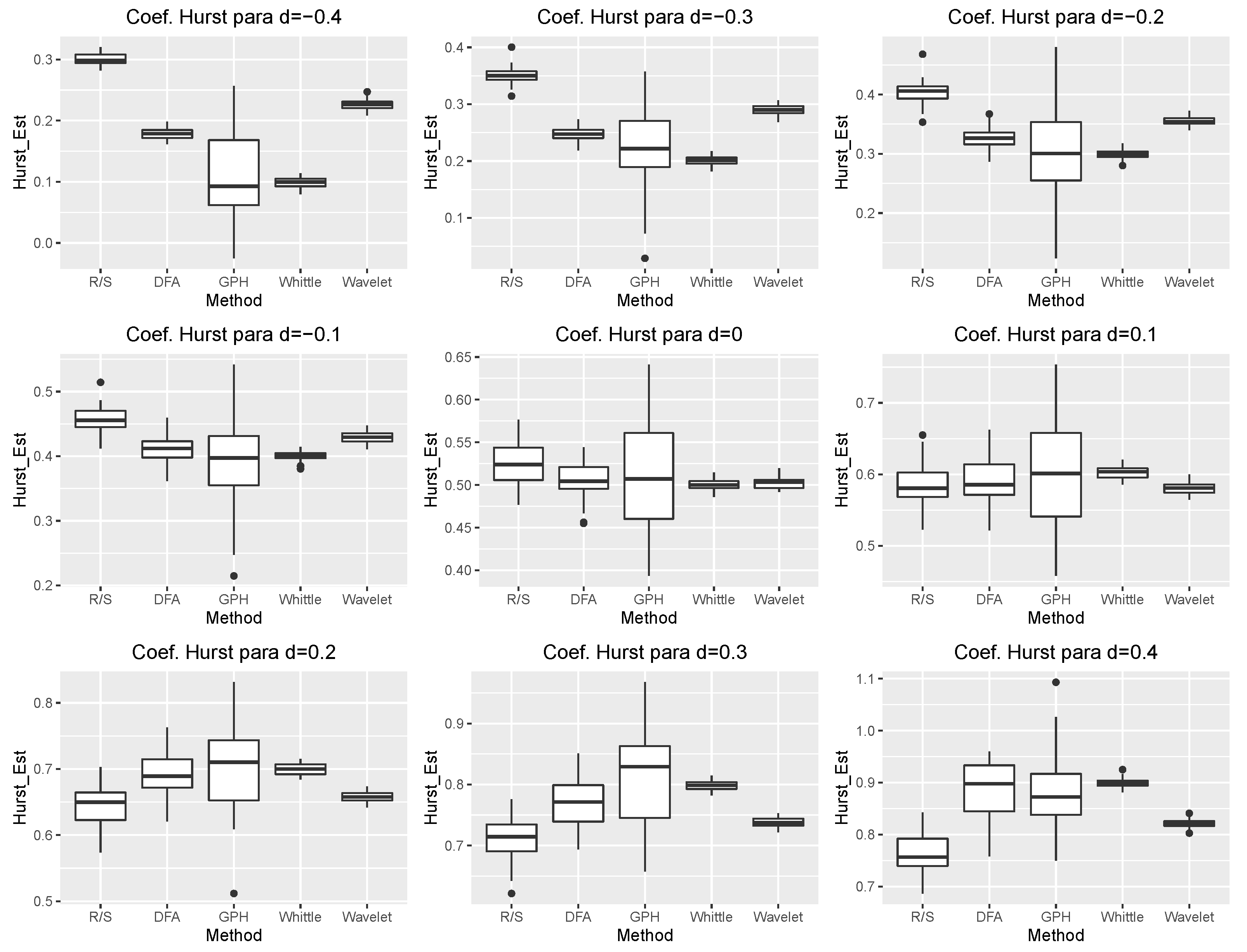
4.1. Comparative Study of Estimation Methods
4.2. Hurst Parameter Prediction Using Recurrent Neural Networks
4.2.1. Synthetic Data
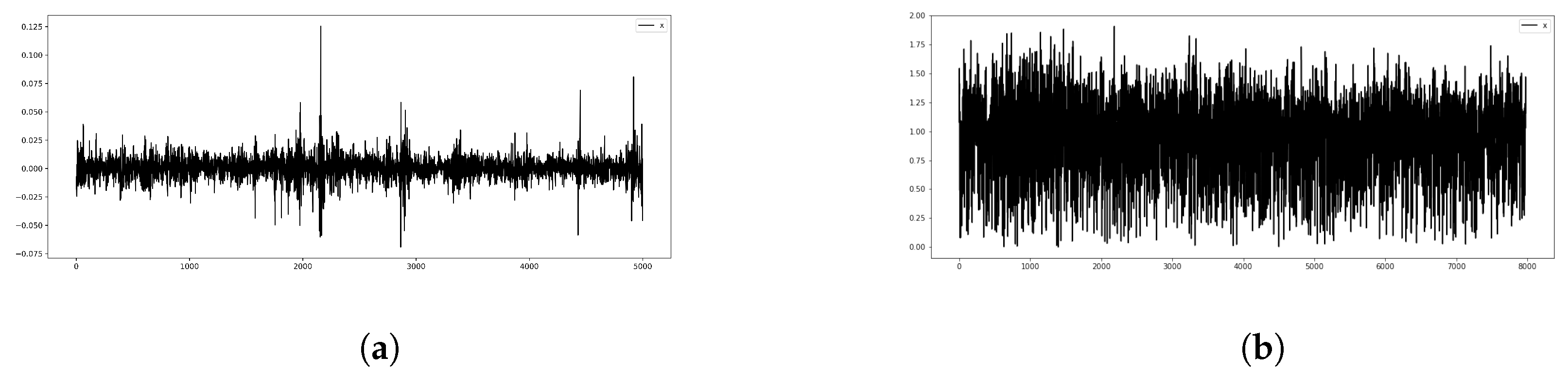
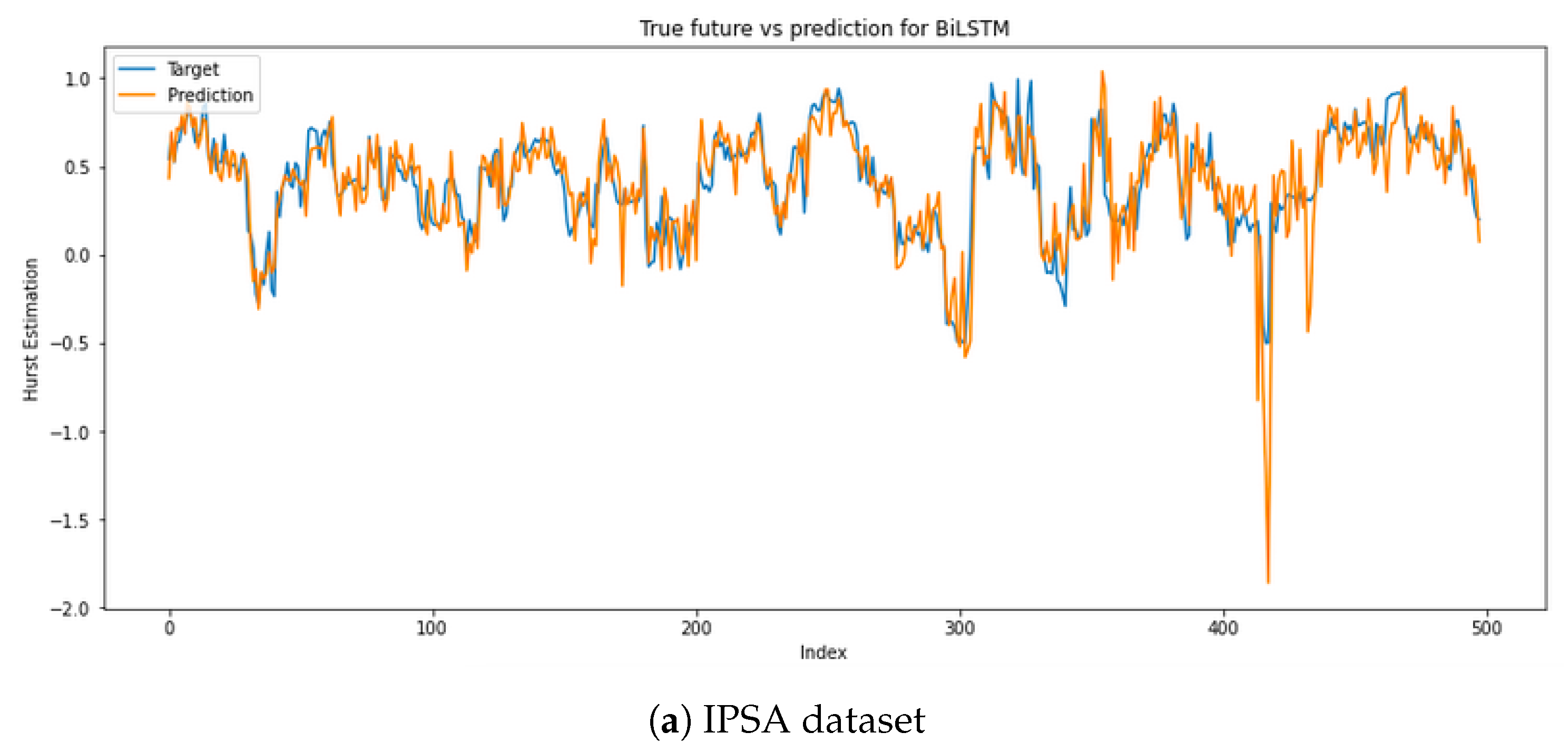
4.2.2. Real Datasets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Di Giorgi, G.; Salas, R.; Avaria, R.; Ubal, C.; Rosas, H.; Torres, R. Volatility Forecasting using Deep Recurrent Neural Networks as GARCH models. Comput. Stat. 2023, 1–27. [Google Scholar] [CrossRef]
- Cordova, C.H.; Portocarrero, M.N.L.; Salas, R.; Torres, R.; Rodrigues, P.C.; López-Gonzales, J.L. Air quality assessment and pollution forecasting using artificial neural networks in Metropolitan Lima-Peru. Sci. Rep. 2021, 11, 24232. [Google Scholar] [CrossRef]
- Leite Coelho da Silva, F.; da Costa, K.; Canas Rodrigues, P.; Salas, R.; López-Gonzales, J.L. Statistical and artificial neural networks models for electricity consumption forecasting in the Brazilian industrial sector. Energies 2022, 15, 588. [Google Scholar] [CrossRef]
- Vivas, E.; de Guenni, L.B.; Allende-Cid, H.; Salas, R. Deep Lagged-Wavelet for monthly rainfall forecasting in a tropical region. Stoch. Environ. Res. Risk Assess. 2023, 37, 831–848. [Google Scholar] [CrossRef]
- Querales, M.; Salas, R.; Morales, Y.; Allende-Cid, H.; Rosas, H. A stacking neuro-fuzzy framework to forecast runoff from distributed meteorological stations. Appl. Soft Comput. 2022, 118, 108535. [Google Scholar] [CrossRef]
- Kovantsev, A.; Gladilin, P. Analysis of multivariate time series predictability based on their features. In Proceedings of the 2020 International Conference on Data Mining Workshops (ICDMW), Sorrento, Italy, 17–20 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 348–355. [Google Scholar]
- Qian, B.; Rasheed, K. Hurst exponent and financial market predictability. In Proceedings of the IASTED Conference on Financial Engineering and Applications, IASTED International Conference, Cambridge, MA, USA, 9–11 November 2004; pp. 203–209. [Google Scholar]
- Siriopoulos, C.; Markellos, R. Neural Network Model Development and Optimization. J. Comput. Intell. Financ. (Former. Neurovest J.) 1996, 7–13. [Google Scholar]
- Siriopoulos, C.; Markellos, R.; Sirlantzis, K. Applications of Artificial Neural Networks in Emerging Financial Markets; World Scientific: Singapore, 1996; pp. 284–302. [Google Scholar]
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar]
- Ledesma-Orozco, S.; Ruiz-Pinales, J.; García-Hernández, G.; Cerda-Villafaña, G.; Hernández-Fusilier, D. Hurst parameter estimation using artificial neural networks. J. Appl. Res. Technol. 2011, 9, 227–241. [Google Scholar] [CrossRef]
- Menezes Jr, J.M.P.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, Z.; Li, R.; Chen, X.; Liu, Z.; Zhang, H. Deep learning with long short-term memory for time series prediction. IEEE Commun. Mag. 2019, 57, 114–119. [Google Scholar] [CrossRef]
- Li, X.; Yu, J.; Xu, L.; Zhang, G. Time Series Classification with Deep Neural Networks Based on Hurst Exponent Analysis. In Proceedings of the ICONIP 2017: Neural Information Processing, Guangzhou, China, 14–18 November 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 194–204. [Google Scholar]
- Hassani, H.; Silva, E.S. A Kolmogorov-Smirnov Based Test for Comparing the Predictive Accuracy of Two Sets of Forecasts. Econometrics 2015, 3, 590–609. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Geweke, J.; Porter-Hudak, S. The estimation and application of long memory time series models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar] [CrossRef]
- Whittle, P. Hypothesis Testing in Time Series Analysis; Almqvist & Wiksells: Upsala, Sweeden, 1951; Volume 4. [Google Scholar]
- Veitch, D.; Abry, P. A wavelet-based joint estimator of the parameters of long-range dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–798. [Google Scholar] [CrossRef]
- Palma, W.; Chan, N.H. Estimation and forecasting of long-memory processes with missing values. J. Forecast. 1997, 16, 395–410. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Fox, R.; Taqqu, M.S. Large-sample properties of parameter estimates for strongly dependent stationary Gaussian time series. Ann. Stat. 1986, 14, 517–532. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent advances in recurrent neural networks. arXiv 2017, arXiv:1801.01078. [Google Scholar]
- Schäfer, A.M.; Zimmermann, H.G. Recurrent neural networks are universal approximators. Int. J. Neural Syst. 2007, 17, 253–263. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies; IEEE Press: Hoboken, NJ, USA, 2001. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Chen, L. Deep Learning and Practice with MindSpore; Springer Nature: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Contreras-Reyes, J.E.; Palma, W. Statistical analysis of autoregressive fractionally integrated moving average models in R. Comput. Stat. 2013, 28, 2309–2331. [Google Scholar] [CrossRef]
- Palma, W.; Olea, R. An efficient estimator for locally stationary Gaussian long-memory processes. Ann. Stat. 2010, 38, 2958–2997. [Google Scholar] [CrossRef]
- Singleton, R. Mixed Radix Fast Fourier Transform; Technical Report; Stanford Research Inst.: Menlo Park, CA, USA, 1972. [Google Scholar]
- Whittle, P. Estimation and information in stationary time series. Ark. Mat. 1953, 2, 423–434. [Google Scholar] [CrossRef]
- Bisaglia, L.; Guegan, D. A comparison of techniques of estimation in long-memory processes. Comput. Stat. Data Anal. 1998, 27, 61–81. [Google Scholar] [CrossRef]
- Dahlhaus, R. Efficient parameter estimation for self-similar processes. Ann. Stat. 1989, 1749–1766. [Google Scholar] [CrossRef]
- Ferreira, G.; Olea Ortega, R.A.; Palma, W. Statistical analysis of locally stationary processes. Chil. J. Stat. 2013, 4, 133–149. [Google Scholar]
- Beran, J.; Feng, Y.; Ghosh, S.; Kulik, R. Long-Memory Processes; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Armstrong, J.S. Evaluating Forecasting Methods. Principles of Forecasting; Springer: Berlin/Heidelberg, Germany, 2001; pp. 443–472. [Google Scholar]

| d | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Training Time (s) | ||||||||||||
| sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | ||
| S = 1 | 18 | 0.721 | 0.742 | 0.706 | 0.729 | 0.171 | 0.164 | 0.175 | 0.168 | 130.9 | 262.3 | 220.9 | 258.7 |
| 20 | 0.709 | 0.746 | 0.716 | 0.736 | 0.161 | 0.151 | 0.160 | 0.154 | 104.5 | 233.4 | 207.0 | 255.1 | |
| 23 | 0.673 | 0.724 | 0.686 | 0.706 | 0.150 | 0.138 | 0.148 | 0.143 | 127.2 | 261.7 | 235.8 | 270.2 | |
| 25 | 0.657 | 0.723 | 0.676 | 0.699 | 0.146 | 0.131 | 0.142 | 0.137 | 128.6 | 266.3 | 265.6 | 265.4 | |
| 28 | 0.652 | 0.731 | 0.666 | 0.699 | 0.141 | 0.125 | 0.138 | 0.132 | 115.1 | 226.8 | 215.7 | 231.1 | |
| 30 | 0.641 | 0.730 | 0.646 | 0.685 | 0.141 | 0.122 | 0.140 | 0.132 | 134.5 | 284.0 | 226.4 | 271.5 | |
| 33 | 0.601 | 0.690 | 0.616 | 0.650 | 0.136 | 0.120 | 0.133 | 0.127 | 124.0 | 240.9 | 209.8 | 246.3 | |
| 35 | 0.534 | 0.670 | 0.605 | 0.644 | 0.138 | 0.116 | 0.127 | 0.121 | 127.1 | 252.0 | 213.6 | 260.2 | |
| S = 5 | 20 | 0.298 | −0.117 | 0.519 | 0.532 | 0.248 | 0.314 | 0.206 | 0.203 | 34.4 | 70.4 | 62.4 | 79.1 |
| 25 | 0.282 | −0.396 | 0.440 | 0.507 | 0.206 | 0.290 | 0.184 | 0.173 | 36.9 | 70.2 | 69.1 | 69.5 | |
| 30 | 0.049 | −0.217 | 0.436 | 0.461 | 0.234 | 0.264 | 0.180 | 0.176 | 32.9 | 76.2 | 60.4 | 69.3 | |
| d = 0 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Training Time (s) | ||||||||||||
| sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | ||
| S = 1 | 18 | 0.771 | 0.833 | 0.776 | 0.782 | 0.167 | 0.142 | 0.166 | 0.163 | 119.0 | 271.3 | 228.0 | 288.6 |
| 20 | 0.767 | 0.813 | 0.761 | 0.779 | 0.158 | 0.141 | 0.159 | 0.154 | 116.2 | 220.5 | 209.8 | 241.7 | |
| 23 | 0.730 | 0.807 | 0.721 | 0.754 | 0.144 | 0.122 | 0.147 | 0.138 | 122.8 | 226.1 | 190.7 | 237.7 | |
| 25 | 0.713 | 0.800 | 0.700 | 0.747 | 0.142 | 0.118 | 0.145 | 0.133 | 168.5 | 329.7 | 303.2 | 344.3 | |
| 28 | 0.721 | 0.815 | 0.697 | 0.737 | 0.132 | 0.108 | 0.138 | 0.128 | 144.3 | 316.6 | 264.3 | 298.5 | |
| 30 | 0.686 | 0.812 | 0.672 | 0.720 | 0.124 | 0.104 | 0.137 | 0.127 | 113.3 | 214.8 | 197.0 | 232.3 | |
| 33 | 0.654 | 0.781 | 0.650 | 0.689 | 0.125 | 0.099 | 0.126 | 0.118 | 119.9 | 212.5 | 188.4 | 221.3 | |
| 35 | 0.670 | 0.782 | 0.611 | 0.673 | 0.114 | 0.093 | 0.124 | 0.114 | 131.6 | 213.0 | 183.4 | 216.8 | |
| S = 5 | 20 | 0.354 | 0.100 | 0.516 | 0.533 | 0.260 | 0.306 | 0.225 | 0.221 | 26.5 | 64.0 | 43.4 | 49.2 |
| 25 | 0.321 | −0.060 | 0.481 | 0.497 | 0.215 | 0.269 | 0.188 | 0.186 | 32.4 | 51.4 | 42.5 | 49.0 | |
| 30 | 0.128 | 0.125 | 0.499 | 0.526 | 0.232 | 0.233 | 0.176 | 0.171 | 31.9 | 52.7 | 44.0 | 61.6 | |
| d = 0.3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Training Time (s) | ||||||||||||
| sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | sRNN | BiLSTM | LSTM | GRU | ||
| S = 1 | 18 | 0.814 | 0.852 | 0.801 | 0.801 | 0.155 | 0.138 | 0.160 | 0.160 | 128.3 | 293.8 | 237.6 | 278.0 |
| 20 | 0.769 | 0.860 | 0.791 | 0.804 | 0.157 | 0.123 | 0.150 | 0.145 | 100.8 | 221.7 | 173.6 | 202.0 | |
| 23 | 0.748 | 0.869 | 0.759 | 0.778 | 0.142 | 0.102 | 0.139 | 0.133 | 124.1 | 239.5 | 208.3 | 261.8 | |
| 25 | 0.756 | 0.877 | 0.753 | 0.773 | 0.135 | 0.096 | 0.135 | 0.130 | 125.2 | 249.9 | 200.1 | 240.1 | |
| 28 | 0.748 | 0.882 | 0.744 | 0.768 | 0.129 | 0.088 | 0.131 | 0.124 | 129.2 | 281.7 | 245.7 | 273.4 | |
| 30 | 0.716 | 0.884 | 0.721 | 0.751 | 0.129 | 0.083 | 0.128 | 0.121 | 120.7 | 260.9 | 197.2 | 247.7 | |
| 33 | 0.685 | 0.859 | 0.676 | 0.714 | 0.121 | 0.081 | 0.122 | 0.115 | 117.6 | 229.1 | 193.3 | 230.4 | |
| 35 | 0.681 | 0.845 | 0.654 | 0.680 | 0.114 | 0.079 | 0.119 | 0.114 | 124.0 | 223.2 | 203.8 | 243.2 | |
| S = 5 | 20 | 0.375 | 0.173 | 0.485 | 0.518 | 0.254 | 0.292 | 0.230 | 0.223 | 37.2 | 83.0 | 81.4 | 82.5 |
| 25 | 0.368 | 0.230 | 0.475 | 0.479 | 0.212 | 0.234 | 0.193 | 0.192 | 39.7 | 86.7 | 75.3 | 104.2 | |
| 30 | 0.307 | 0.111 | 0.461 | 0.504 | 0.208 | 0.235 | 0.183 | 0.176 | 38.9 | 84.1 | 83.5 | 85.9 | |
| IPSA Dataset (BiLSTM) | |||||||
|---|---|---|---|---|---|---|---|
| Train | Test | ||||||
| N | MAE | RMSE | MAE | RMSE | Training Time (s) | ||
| 18 | 0.912 | 0.072 | 0.097 | 0.679 | 0.133 | 0.184 | 147.659 |
| 20 | 0.922 | 0.062 | 0.083 | 0.716 | 0.115 | 0.153 | 136.575 |
| 23 | 0.936 | 0.048 | 0.064 | 0.651 | 0.106 | 0.145 | 111.459 |
| 25 | 0.938 | 0.044 | 0.058 | 0.621 | 0.105 | 0.140 | 131.349 |
| 28 | 0.944 | 0.038 | 0.050 | 0.437 | 0.106 | 0.148 | 122.480 |
| 30 | 0.948 | 0.034 | 0.045 | 0.396 | 0.103 | 0.141 | 112.823 |
| 33 | 0.952 | 0.029 | 0.039 | 0.398 | 0.099 | 0.133 | 133.320 |
| 35 | 0.955 | 0.027 | 0.036 | 0.348 | 0.098 | 0.132 | 109.261 |
| Tree Ring Dataset (BiLSTM) | |||||||
|---|---|---|---|---|---|---|---|
| Train | Test | ||||||
| N | MAE | RMSE | MAE | RMSE | Training (s) | ||
| 18 | 0.912 | 0.076 | 0.102 | 0.799 | 0.109 | 0.150 | 169.029 |
| 20 | 0.925 | 0.066 | 0.087 | 0.818 | 0.097 | 0.133 | 149.533 |
| 23 | 0.937 | 0.052 | 0.068 | 0.822 | 0.084 | 0.115 | 251.819 |
| 25 | 0.943 | 0.046 | 0.061 | 0.830 | 0.080 | 0.106 | 259.888 |
| 28 | 0.949 | 0.042 | 0.054 | 0.828 | 0.074 | 0.098 | 259.807 |
| 30 | 0.949 | 0.039 | 0.051 | 0.819 | 0.073 | 0.095 | 224.713 |
| 33 | 0.953 | 0.035 | 0.045 | 0.790 | 0.071 | 0.094 | 247.332 |
| 35 | 0.956 | 0.032 | 0.042 | 0.786 | 0.069 | 0.090 | 245.959 |
| KS Test | |||
|---|---|---|---|
| Data | N Opt | Statistic Value | p-Value |
| IPSA | 20 | 0.0663 | 0.2244 |
| Treering | 25 | 0.0289 | 0.8937 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ubal, C.; Di-Giorgi, G.; Contreras-Reyes, J.E.; Salas, R. Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks. Mach. Learn. Knowl. Extr. 2023, 5, 1340-1358. https://doi.org/10.3390/make5040068
Ubal C, Di-Giorgi G, Contreras-Reyes JE, Salas R. Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks. Machine Learning and Knowledge Extraction. 2023; 5(4):1340-1358. https://doi.org/10.3390/make5040068
Chicago/Turabian StyleUbal, Cristian, Gustavo Di-Giorgi, Javier E. Contreras-Reyes, and Rodrigo Salas. 2023. "Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks" Machine Learning and Knowledge Extraction 5, no. 4: 1340-1358. https://doi.org/10.3390/make5040068
APA StyleUbal, C., Di-Giorgi, G., Contreras-Reyes, J. E., & Salas, R. (2023). Predicting the Long-Term Dependencies in Time Series Using Recurrent Artificial Neural Networks. Machine Learning and Knowledge Extraction, 5(4), 1340-1358. https://doi.org/10.3390/make5040068







