Input/Output Variables Selection in Data Envelopment Analysis: A Shannon Entropy Approach
Abstract
:1. Introduction
2. Shannon Entropy Technique
3. The Proposed Approach
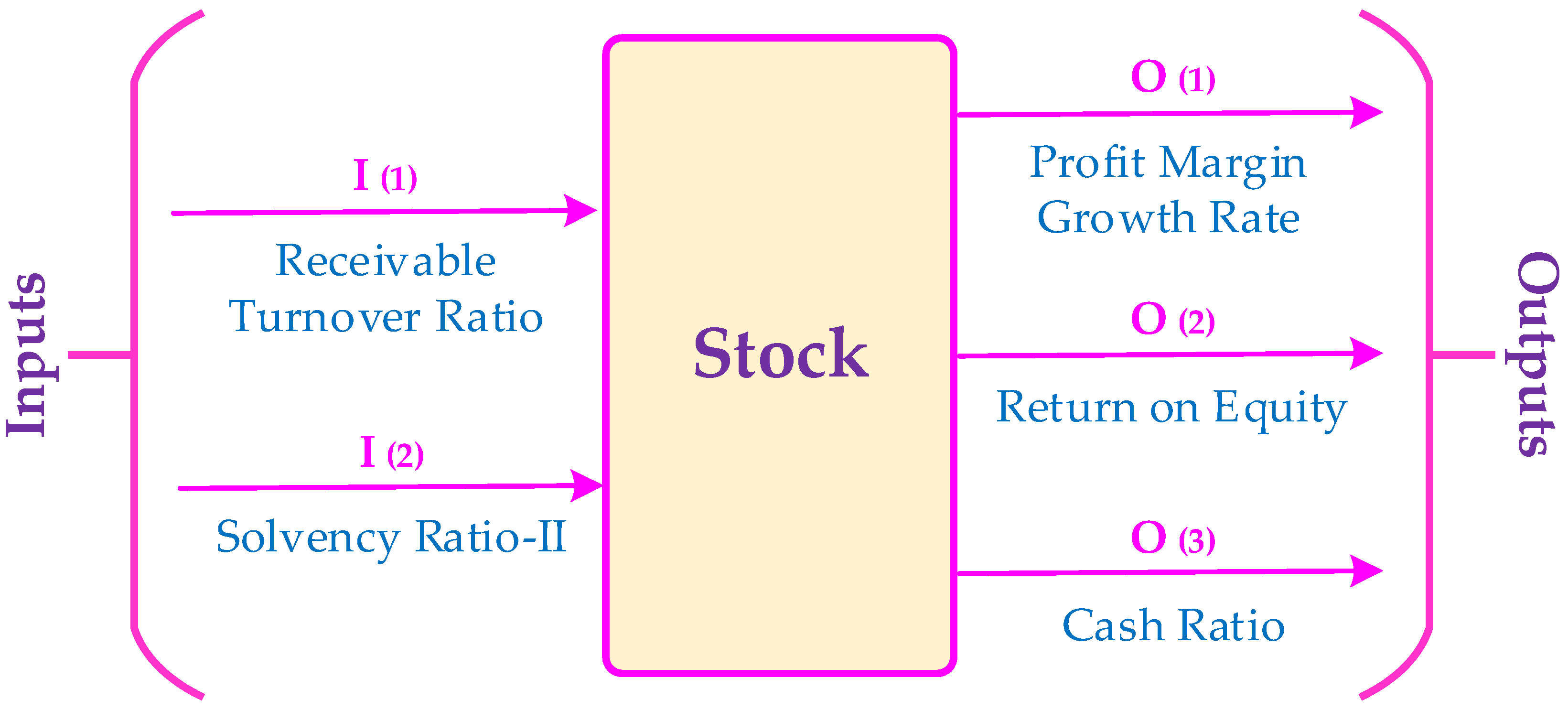
4. Case Study
5. Conclusions and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farrell, M.J. The measurement of productive efficiency. J. R. Stat. Soc. Ser. A (Gen.) 1957, 120, 253–281. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Charnes, A.; Cooper, W.W. Preface to topics in data envelopment analysis. Ann. Oper. Res. 1985, 2, 59–94. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.; Lu, W.M. Research fronts in data envelopment analysis. Omega 2016, 58, 33–45. [Google Scholar] [CrossRef]
- Liu, J.S.; Lu, L.Y.; Lu, W.M.; Lin, B.J. A survey of DEA applications. Omega 2013, 41, 893–902. [Google Scholar] [CrossRef]
- Peykani, P.; Farzipoor Saen, R.; Seyed Esmaeili, F.S.; Gheidar-Kheljani, J. Window data envelopment analysis approach: A review and bibliometric analysis. Expert Syst. 2021, 38, e12721. [Google Scholar] [CrossRef]
- Paradi, J.C.; Zhu, H. A survey on bank branch efficiency and performance research with data envelopment analysis. Omega 2013, 41, 61–79. [Google Scholar] [CrossRef]
- Martínez-Núñez, M.; Pérez-Aguiar, W.S. Efficiency analysis of information technology and online social networks management: An integrated DEA-model assessment. Inf. Manag. 2014, 51, 712–725. [Google Scholar] [CrossRef] [Green Version]
- Vlontzos, G.; Niavis, S.; Manos, B. A DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renew. Sustain. Energy Rev. 2014, 40, 91–96. [Google Scholar] [CrossRef]
- Worthington, A.C. A review of frontier approaches to efficiency and productivity measurement in urban water utilities. Urban Water J. 2014, 11, 55–73. [Google Scholar] [CrossRef]
- García-Alcaraz, J.L.; Díaz-Reza, R.; Maldonado-Macías, A.; Rico-Pérez, L. Recent DEA applications to industry: A literature review from 2010 to 2014. Int. J. Eng. Sci. Invent. 2015, 4, 9–20. [Google Scholar]
- Basso, A.; Funari, S. DEA performance assessment of mutual funds. In Data Envelopment Analysis; Springer: Boston, MA, USA, 2016; pp. 229–287. [Google Scholar]
- Fasone, V.; Zapata-Aguirre, S. Measuring business performance in the airport context: A critical review of literature. Int. J. Product. Perform. Manag. 2016, 65, 1137–1158. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Witte, K.D.; Johnes, J.; Johnes, G.; Karagiannis, G.; Portela, C.S. Applications of data envelopment analysis in education. In Data Envelopment Analysis; Springer: Boston, MA, USA, 2016; pp. 367–438. [Google Scholar]
- Kaffash, S.; Marra, M. Data envelopment analysis in financial services: A citations network analysis of banks, insurance companies and money market funds. Ann. Oper. Res. 2017, 253, 307–344. [Google Scholar] [CrossRef] [Green Version]
- Lima-Junior, F.R.; Carpinetti, L.C.R. Quantitative models for supply chain performance evaluation: A literature review. Comput. Ind. Eng. 2017, 113, 333–346. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Khoshnoudi, M. A comprehensive review of data envelopment analysis (DEA) approach in energy efficiency. Renew. Sustain. Energy Rev. 2017, 70, 1298–1322. [Google Scholar] [CrossRef]
- Soheilirad, S.; Govindan, K.; Mardani, A.; Zavadskas, E.K.; Nilashi, M.; Zakuan, N. Application of data envelopment analysis models in supply chain management: A systematic review and meta-analysis. Ann. Oper. Res. 2018, 271, 915–969. [Google Scholar] [CrossRef]
- Bhat, Z.U.H.; Sultana, D.; Dar, Q.F. A comprehensive review of data envelopment analysis (DEA). Approach in sports. J. Sports Econ. Manag. 2019, 9, 82–109. [Google Scholar]
- Karadayi, M.A.; Ekinci, Y. Evaluating R&D performance of EU countries using categorical DEA. Technol. Anal. Strateg. Manag. 2019, 31, 227–238. [Google Scholar]
- Kohl, S.; Schoenfelder, J.; Fügener, A.; Brunner, J.O. The use of Data Envelopment Analysis (DEA) in healthcare with a focus on hospitals. Health Care Manag. Sci. 2019, 22, 245–286. [Google Scholar] [CrossRef]
- Lee, H.S.; Choi, Y. Environmental performance evaluation of the Korean manufacturing industry based on sequential DEA. Sustainability 2019, 11, 874. [Google Scholar] [CrossRef] [Green Version]
- Cui, Q.; Yu, L.T. A review of data envelopment analysis in airline efficiency: State of the art and prospects. J. Adv. Transp. 2021, 2021, 2931734. [Google Scholar] [CrossRef]
- Kaffash, S.; Azizi, R.; Huang, Y.; Zhu, J. A survey of data envelopment analysis applications in the insurance industry 1993–2018. Eur. J. Oper. Res. 2020, 284, 801–813. [Google Scholar] [CrossRef]
- Mahmoudi, R.; Emrouznejad, A.; Shetab-Boushehri, S.N.; Hejazi, S.R. The origins, development and future directions of data envelopment analysis approach in transportation systems. Socio-Econ. Plan. Sci. 2020, 69, 100672. [Google Scholar] [CrossRef]
- Nurmatov, R.; Lopez, X.L.F.; Millan, P.P.C. Tourism, hospitality, and DEA: Where do we come from and where do we go? Int. J. Hosp. Manag. 2021, 95, 102883. [Google Scholar] [CrossRef]
- Seiford, L.M.; Thrall, R.M. Recent developments in DEA: The mathematical programming approach to frontier analysis. J. Econom. 1990, 46, 7–38. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Lewin, A.Y.; Seiford, L.M. Data envelopment analysis theory, methodology and applications. J. Oper. Res. Soc. 1997, 48, 332–333. [Google Scholar] [CrossRef]
- Nyhan, R.C.; Martin, L.L. Comparative performance measurement: A primer on data envelopment analysis. Public Product. Manag. Rev. 1999, 22, 348–364. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Parker, B.R.; Tavares, G. Evaluation of research in efficiency and productivity: A survey and analysis of the first 30 years of scholarly literature in DEA. Socio-Econ. Plan. Sci. 2008, 42, 151–157. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Zhu, J. Data envelopment analysis: History, models, and interpretations. In Handbook on Data Envelopment Analysis; Springer: Boston, MA, USA, 2011; pp. 1–39. [Google Scholar]
- Emrouznejad, A. Advances in data envelopment analysis. Ann. Oper. Res. 2014, 214, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Joro, T.; Korhonen, P. Extension of Data Envelopment Analysis with Preference Information; Springer: New York, NY, USA, 2015. [Google Scholar]
- Emrouznejad, A.; Yang, G.L. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Friedman, L.; Sinuany-Stern, Z. Combining ranking scales and selecting variables in the DEA context: The case of industrial branches. Comput. Oper. Res. 1998, 25, 781–791. [Google Scholar] [CrossRef]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Sarkis, J. Preparing your data for DEA. In Modeling Data Irregularities and Structural Complexities in Data Envelopment Analysis; Springer: Boston, MA, USA, 2007; pp. 305–320. [Google Scholar]
- Edirisinghe, N.C.P.; Zhang, X. Input/output selection in DEA under expert information, with application to financial markets. Eur. J. Oper. Res. 2010, 207, 1669–1678. [Google Scholar] [CrossRef]
- Luo, Y.; Bi, G.; Liang, L. Input/output indicator selection for DEA efficiency evaluation: An empirical study of Chinese commercial banks. Expert Syst. Appl. 2012, 39, 1118–1123. [Google Scholar] [CrossRef]
- Afsharian, M.; Ahn, H.; Neumann, L. Generalized DEA: An approach for supporting input/output factor determination in DEA. Benchmarking Int. J. 2016, 23, 1892–1909. [Google Scholar] [CrossRef]
- Soleimani-Damaneh, M.; Zarepisheh, M. Shannon’s entropy for combining the efficiency results of different DEA models: Method and application. Expert Syst. Appl. 2009, 36, 5146–5150. [Google Scholar] [CrossRef]
- Bian, Y.; Yang, F. Resource and environment efficiency analysis of provinces in China: A DEA approach based on Shannon’s entropy. Energy Policy 2010, 38, 1909–1917. [Google Scholar] [CrossRef]
- Wu, J.; Sun, J.; Liang, L. DEA cross-efficiency aggregation method based upon Shannon entropy. Int. J. Prod. Res. 2012, 50, 6726–6736. [Google Scholar] [CrossRef]
- Shirouyehzad, H.; Lotfi, F.H.; Dabestani, R. Aggregating the results of ranking models in data envelopment analysis by Shannon’s entropy: A case study in hotel industry. Int. J. Model. Oper. Manag. 2013, 3, 149–163. [Google Scholar] [CrossRef]
- Qi, X.G.; Guo, B. Determining common weights in data envelopment analysis with Shannon’s entropy. Entropy 2014, 16, 6394–6414. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dai, Q.; Li, Y.; Jiang, A. Increasing the discriminatory power of DEA using Shannon’s entropy. Entropy 2014, 16, 1571–1585. [Google Scholar] [CrossRef] [Green Version]
- Lo Storto, C. Ecological efficiency based ranking of cities: A combined DEA cross-efficiency and Shannon’s entropy method. Sustainability 2016, 8, 124. [Google Scholar] [CrossRef] [Green Version]
- Malekian, A.; Azarnivand, A. Application of integrated Shannon’s entropy and VIKOR techniques in prioritization of flood risk in the Shemshak watershed, Iran. Water Resour. Manag. 2016, 30, 409–425. [Google Scholar] [CrossRef]
- Ghosh, S.; Yadav, V.K.; Mukherjee, V.; Yadav, P. Evaluation of relative impact of aerosols on photovoltaic cells through combined Shannon’s entropy and Data Envelopment Analysis (DEA). Renew. Energy 2017, 105, 344–353. [Google Scholar] [CrossRef]
- Song, L.; Liu, F. An improvement in DEA cross-efficiency aggregation based on the Shannon entropy. Int. Trans. Oper. Res. 2018, 25, 705–714. [Google Scholar] [CrossRef]
- Feutrill, A.; Roughan, M. A Review of Shannon and Differential Entropy Rate Estimation. Entropy 2021, 23, 1046. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, W.K.; Zhang, Y.J.; Xu, Y.H. Research on World Food Production Efficiency and Environmental Sustainability Based on Entropy-DEA Model. Complexity 2021, 2021, 8730264. [Google Scholar] [CrossRef]
- Chen, T.Y. An evaluation of the relative performance of university libraries in Taipei. Asian Libr. 1997, 6, 39–50. [Google Scholar] [CrossRef]
- Avkiran, N.K. Productivity Analysis in the Services Sector with Data Envelopment Analysis; SSRN: Camira, Australia, 1999. [Google Scholar]
- Sigala, M. Using data envelopment analysis for measuring and benchmarking productivity in the hotel sector. J. Travel Tour. Mark. 2004, 16, 39–60. [Google Scholar] [CrossRef]
- Panayides, P.M.; Lambertides, N.; Savva, C.S. The relative efficiency of shipping companies. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 681–694. [Google Scholar] [CrossRef]
- Singh, M.R.; Mittal, A.K.; Upadhyay, V. Benchmarking of North Indian urban water utilities. Benchmarking Int. J. 2011, 18, 86–106. [Google Scholar] [CrossRef]
- Udhayakumar, A.; Charles, V.; Kumar, M. Stochastic simulation based genetic algorithm for chance constrained data envelopment analysis problems. Omega 2011, 39, 387–397. [Google Scholar] [CrossRef]
- Wang, E.; Shen, Z.; Alp, N.; Barry, N. Benchmarking energy performance of residential buildings using two-stage multifactor data envelopment analysis with degree-day based simple-normalization approach. Energy Convers. Manag. 2015, 106, 530–542. [Google Scholar] [CrossRef]
- Adusei, M. Modeling the efficiency of universal banks in Ghana. Quant. Financ. Lett. 2016, 4, 60–70. [Google Scholar] [CrossRef]
- Chao, S.L. Integrating multi-stage data envelopment analysis and a fuzzy analytical hierarchical process to evaluate the efficiency of major global liner shipping companies. Marit. Policy Manag. 2017, 44, 496–511. [Google Scholar] [CrossRef]
- Shah, S.A.R.; Brijs, T.; Ahmad, N.; Pirdavani, A.; Shen, Y.; Basheer, M.A. Road safety risk evaluation using GIS-based data envelopment analysis—Artificial neural networks approach. Appl. Sci. 2017, 7, 886. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.G.; Park, S.; Kim, D. Efficiency analysis of official development assistance provided by Korea. Sustainability 2018, 10, 2697. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; He, Y. Applying data envelopment analysis in measuring the efficiency of Chinese listed banks in the context of macroprudential framework. Mathematics 2018, 6, 184. [Google Scholar] [CrossRef] [Green Version]
- Sevinç, A.; Eren, T. Determination of KOSGEB support models for small-and medium-scale enterprises by means of data envelopment analysis and multi-criteria decision making methods. Processes 2019, 7, 130. [Google Scholar] [CrossRef] [Green Version]
- Portela, M.S.; Thanassoulis, E.; Simpson, G. Negative Data in DEA: A Directional Distance Approach Applied to Bank Branches. J. Oper. Res. Soc. 2004, 55, 1111–1121. [Google Scholar] [CrossRef] [Green Version]
- Edirisinghe, N.C.P.; Zhang, X. Generalized DEA model of fundamental analysis and its application to portfolio optimization. J. Bank. Financ. 2007, 31, 3311–3335. [Google Scholar] [CrossRef]
- Edirisinghe, N.C.P.; Zhang, X. Portfolio selection under DEA-based relative financial strength indicators: Case of US industries. J. Oper. Res. Soc. 2008, 59, 842–856. [Google Scholar] [CrossRef]
- Xidonas, P.; Mavrotas, G.; Psarras, J. A multicriteria methodology for equity selection using financial analysis. Comput. Oper. Res. 2009, 36, 3187–3203. [Google Scholar] [CrossRef]
- Lim, S.; Oh, K.W.; Zhu, J. Use of DEA cross-efficiency evaluation in portfolio selection: An application to Korean stock market. Eur. J. Oper. Res. 2014, 236, 361–368. [Google Scholar] [CrossRef]
- Mashayekhi, Z.; Omrani, H. An integrated multi-objective Markowitz–DEA cross-efficiency model with fuzzy returns for portfolio selection problem. Appl. Soft Comput. 2016, 38, 1–9. [Google Scholar] [CrossRef]
- Yi, R.; Chang, Y.W.; Xing, W.; Chen, J. Comparing relative valuation efficiency between two stock markets. Q. Rev. Econ. Financ. 2019, 72, 159–167. [Google Scholar] [CrossRef]
- Cook, W.D.; Tone, K.; Zhu, J. Data envelopment analysis: Prior to choosing a model. Omega 2014, 44, 1–4. [Google Scholar] [CrossRef]
- Wojcik, V.; Dyckhoff, H.; Clermont, M. Is data envelopment analysis a suitable tool for performance measurement and benchmarking in non-production contexts? Bus. Res. 2019, 12, 559–595. [Google Scholar] [CrossRef] [Green Version]
- Hatami-Marbini, A.; Emrouznejad, A.; Tavana, M. A taxonomy and review of the fuzzy data envelopment analysis literature: Two decades in the making. Eur. J. Oper. Res. 2011, 214, 457–472. [Google Scholar] [CrossRef]
- Peykani, P.; Mohammadi, E.; Pishvaee, M.S.; Rostamy-Malkhalifeh, M.; Jabbarzadeh, A. A novel fuzzy data envelopment analysis based on robust possibilistic programming: Possibility, necessity and credibility-based approaches. RAIRO-Oper. Res. 2018, 52, 1445–1463. [Google Scholar] [CrossRef]
- Peykani, P.; Mohammadi, E.; Emrouznejad, A.; Pishvaee, M.S.; Rostamy-Malkhalifeh, M. Fuzzy data envelopment analysis: An adjustable approach. Expert Syst. Appl. 2019, 136, 439–452. [Google Scholar] [CrossRef]
- Arya, A.; Singh, S. Development of two-stage parallel-series system with fuzzy data: A fuzzy DEA approach. Soft Comput. 2021, 25, 3225–3245. [Google Scholar] [CrossRef]
- Peykani, P.; Mohammadi, E.; Emrouznejad, A. An adjustable fuzzy chance-constrained network DEA approach with application to ranking investment firms. Expert Syst. Appl. 2021, 166, 113938. [Google Scholar] [CrossRef]
- Peykani, P.; Namakshenas, M.; Arabjazi, N.; Shirazi, F.; Kavand, N. Optimistic and pessimistic fuzzy data envelopment analysis: Empirical evidence from Tehran stock market. Fuzzy Optim. Modeling J. 2021, 2, 12–21. [Google Scholar]
- Peykani, P.; Nouri, M.; Eshghi, F.; Khamechian, M.; Farrokhi-Asl, M. A novel mathematical approach for fuzzy multi-period multi-objective portfolio optimization problem under uncertain environment and practical constraints. J. Fuzzy Ext. Appl. 2021, 2, 191–203. [Google Scholar]
- Peykani, P.; Seyed Esmaeili, F.S. Malmquist productivity index under fuzzy environment. Fuzzy Optim. Modeling J. 2021, 2, 10–19. [Google Scholar]
- Song, J.; Ma, X.; Chen, R. A Profit Distribution Model of Reverse Logistics Based on Fuzzy DEA Efficiency—Modified Shapley Value. Sustainability 2021, 13, 7354. [Google Scholar] [CrossRef]
- Wu, S.C.; Lu, T.; Liu, S.T. A fuzzy approach to support evaluation of fuzzy cross efficiency. Symmetry 2021, 13, 882. [Google Scholar] [CrossRef]
- Arana-Jiménez, M.; Sánchez-Gil, M.C.; Lozano, S. A fuzzy DEA slacks-based approach. J. Comput. Appl. Math. 2022, 404, 113180. [Google Scholar] [CrossRef]
- Peykani, P.; Hosseinzadeh Lotfi, F.; Sadjadi, S.J.; Ebrahimnejad, A.; Mohammadi, E. Fuzzy chance-constrained data envelopment analysis: A structured literature review, current trends, and future directions. Fuzzy Optim. Decis. Mak. 2022, 21, 197–261. [Google Scholar] [CrossRef]
- Peykani, P.; Memar-Masjed, E.; Arabjazi, N.; Mirmozaffari, M. Dynamic performance assessment of hospitals by applying credibility-based fuzzy window data envelopment analysis. Healthcare 2022, 10, 876. [Google Scholar] [CrossRef] [PubMed]
- Peykani, P.; Namakshenas, M.; Nouri, M.; Kavand, N.; Rostamy-Malkhalifeh, M. A possibilistic programming approach to portfolio optimization problem under fuzzy data. In Advances in Econometrics, Operational Research, Data Science and Actuarial Studies; Springer: Cham, Switzerland, 2022; pp. 377–387. [Google Scholar]
- Peykani, P.; Namazi, M.; Mohammadi, E. Bridging the knowledge gap between technology and business: An innovation strategy perspective. PLoS ONE 2022, 17, e0266843. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, J.K. Transformations in stochastic DEA models. J. Econom. 1990, 46, 109–123. [Google Scholar] [CrossRef]
- Cooper, W.W.; Huang, Z.; Li, S.X. Satisficing DEA models under chance constraints. Ann. Oper. Res. 1996, 66, 279–295. [Google Scholar] [CrossRef]
- Huang, Z.; Li, S.X. Stochastic DEA models with different types of input-output disturbances. J. Product. Anal. 2001, 15, 95–113. [Google Scholar] [CrossRef]
- Cooper, W.W.; Deng, H.; Huang, Z.; Li, S.X. Chance constrained programming approaches to technical efficiencies and inefficiencies in stochastic data envelopment analysis. J. Oper. Res. Soc. 2002, 53, 1347–1356. [Google Scholar] [CrossRef]
- Olesen, O.B.; Petersen, N.C. Stochastic Data Envelopment Analysis—A Review. Eur. J. Oper. Res. 2016, 251, 2–21. [Google Scholar] [CrossRef]
- Arabjazi, N.; Rostamy-Malkhalifeh, M.; Hosseinzadeh Lotfi, F.; Behzadi, M.H. Stochastic Sensitivity Analysis in Data Envelopment Analysis. Fuzzy Optim. Modeling J. 2021, 2, 52–64. [Google Scholar]
- Babaie Asil, H.; Kazemi Matin, R.; Khounsiavash, M.; Moghadas, Z. A modified semi-oriented radial measure to deal with negative and stochastic data: An application in banking industry. Math. Sci. 2021, 1–13. [Google Scholar] [CrossRef]
- Banker, R.D. Stochastic Data Envelopment Analysis. Data Envel. Anal. J. 2021, 5, 281–309. [Google Scholar] [CrossRef]
- Izadikhah, M. Developing a new chance constrained modified ERM model to measure performance of repair and maintenance groups of IRALCO. Int. J. Oper. Res. 2021, 41, 226–243. [Google Scholar] [CrossRef]
- Izadikhah, M.; Farzipoor Saen, R. Developing a linear stochastic two-stage data envelopment analysis model for evaluating sustainability of supply chains: A case study in welding industry. Ann. Oper. Res. 2021, 1–21. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.T. Stochastic efficiencies of network production systems with correlated stochastic data: The case of Taiwanese commercial banks. Ann. Oper. Res. 2021, 1–24. [Google Scholar] [CrossRef]
- Amirteimoori, A.; Sahoo, B.K.; Charles, V.; Mehdizadeh, S. Stochastic Data Envelopment Analysis. In Stochastic Benchmarking; Springer: Cham, Switzerland, 2022; pp. 55–76. [Google Scholar]
- Seyed Esmaeili, F.S. The efficiency of MSBM model with imprecise data (interval). Int. J. Data Envel. Anal. 2014, 2, 343–350. [Google Scholar]
- Peykani, P.; Mohammadi, E. Interval network data envelopment analysis model for classification of investment companies in the presence of uncertain data. J. Ind. Syst. Eng. 2018, 11, 63–72. [Google Scholar]
- Peykani, P.; Mohammadi, E.; Seyed Esmaeili, F.S. Stock evaluation under mixed uncertainties using robust DEA model. J. Qual. Eng. Prod. Optim. 2019, 4, 73–84. [Google Scholar]
- Peykani, P.; Mohammadi, E.; Farzipoor Saen, R.; Sadjadi, S.J.; Rostamy-Malkhalifeh, M. Data envelopment analysis and robust optimization: A review. Expert Syst. 2020, 37, e12534. [Google Scholar] [CrossRef]
- Peykani, P.; Mohammadi, E.; Jabbarzadeh, A.; Rostamy-Malkhalifeh, M.; Pishvaee, M.S. A novel two-phase robust portfolio selection and optimization approach under uncertainty: A case study of Tehran stock exchange. PLoS ONE 2020, 15, e0239810. [Google Scholar] [CrossRef]
- Seyed Esmaeili, F.S.; Rostamy-Malkhalifeh, M.; Hosseinzadeh Lotfi, F. Two-stage network DEA model under interval data. Math. Anal. Convex Optim. 2020, 1, 103–108. [Google Scholar] [CrossRef]
- Seyed Esmaeili, F.S.; Rostamy-Malkhalifeh, M.; Hosseinzadeh Lotfi, F. A hybrid approach using data envelopment analysis, interval programming and robust optimisation for performance assessment of hotels under uncertainty. Int. J. Manag. Decis. Mak. 2021, 20, 308–322. [Google Scholar]
- Dehnokhalaji, A.; Khezri, S.; Emrouznejad, A. A box-uncertainty in DEA: A robust performance measurement framework. Expert Syst. Appl. 2022, 187, 115855. [Google Scholar] [CrossRef]
- Peykani, P.; Emrouznejad, A.; Mohammadi, E.; Gheidar-Kheljani, J. A novel robust network data envelopment analysis approach for performance assessment of mutual funds under uncertainty. Ann. Oper. Res. 2022, 1–27. [Google Scholar] [CrossRef]
- Peykani, P.; Gheidar-Kheljani, J.; Rahmani, D.; Karimi Gavareshki, M.H.; Jabbarzadeh, A. Uncertain super-efficiency data envelopment analysis. In Advances in Econometrics, Operational Research, Data Science and Actuarial Studies; Springer: Cham, Switzerland, 2022; pp. 311–320. [Google Scholar]
- Seyed Esmaeili, F.S.; Rostamy-Malkhalifeh, M.; Hosseinzadeh Lotfi, F. Interval network Malmquist productivity index for examining productivity changes of insurance companies under data uncertainty: A case study. J. Math. Ext. 2022, 16, 9. [Google Scholar]
- Henrique, B.M.; Sobreiro, V.A.; Kimura, H. Literature review: Machine learning techniques applied to financial market prediction. Expert Syst. Appl. 2019, 124, 226–251. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Shadkam, E.; Khalili, S.M.; Yazdani, M. Developing a novel integrated generalised data envelopment analysis (DEA) to evaluate hospitals providing stroke care services. Bioengineering 2021, 8, 207. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Yazdani, M.; Boskabadi, A.; Ahady Dolatsara, H.; Kabirifar, K.; Amiri Golilarz, N. A novel machine learning approach combined with optimization models for eco-efficiency evaluation. Appl. Sci. 2020, 10, 5210. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.; Archontoulis, S.V. Forecasting corn yield with machine learning ensembles. Front. Plant Sci. 2020, 11, 1120. [Google Scholar] [CrossRef]
- Michelucci, U.; Venturini, F. Estimating neural network’s performance with bootstrap: A tutorial. Mach. Learn. Knowl. Extr. 2021, 3, 357–373. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Shadkam, E.; Khalili, S.M.; Kabirifar, K.; Yazdani, R.; Gashteroodkhani, T.A. A novel artificial intelligent approach: Comparison of machine learning tools and algorithms based on optimization DEA Malmquist productivity index for eco-efficiency evaluation. Int. J. Energy Sect. Manag. 2021, 15, 523–550. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Yazdani, R.; Shadkam, E.; Khalili, S.M.; Tavassoli, L.S.; Boskabadi, A. A novel hybrid parametric and non-parametric optimisation model for average technical efficiency assessment in public hospitals during and post-COVID-19 pandemic. Bioengineering 2021, 9, 7. [Google Scholar] [CrossRef] [PubMed]
- Mirmozaffari, M.; Yazdani, R.; Shadkam, E.; Tavassoli, L.S.; Massah, R. VCS and CVS: New combined parametric and non-parametric operation research models. Sustain. Oper. Comput. 2021, 2, 36–56. [Google Scholar] [CrossRef]
- Hassanpour, M.; Riera, M.; González, A. A Survey of Near-Data Processing Architectures for Neural Networks. Mach. Learn. Knowl. Extr. 2022, 4, 66–102. [Google Scholar] [CrossRef]
- Linardos, V.; Drakaki, M.; Tzionas, P.; Karnavas, Y.L. Machine learning in disaster management: Recent developments in methods and applications. Mach. Learn. Knowl. Extr. 2022, 4, 446–473. [Google Scholar] [CrossRef]
- Mirmozaffari, M.; Yazdani, R.; Shadkam, E.; Khalili, S.M.; Mahjoob, M.; Boskabadi, A. An integrated artificial intelligence model for efficiency assessment in pharmaceutical companies during the COVID-19 pandemic. Sustain. Oper. Comput. 2022, 3, 156–167. [Google Scholar] [CrossRef]
- Schmidt, A.; Kabir, M.W.U.; Hoque, M.T. Machine learning based restaurant sales forecasting. Mach. Learn. Knowl. Extr. 2022, 4, 105–130. [Google Scholar] [CrossRef]
| Groups | Perspective | Financial Parameters | |||
|---|---|---|---|---|---|
| Current ratio (CUR) | 0.980 | 0.020 | 0.089 | ||
| 1 | Liquidity | Quick ratio (QUR) | 0.952 | 0.048 | 0.218 |
| Cash ratio (CAR) | 0.846 | 0.154 | 0.694 | ||
| Inventory turnover (INT) | 0.983 | 0.017 | 0.126 | ||
| 2 | Asset utilization | Receivable turnover ratio (RTR) | 0.895 | 0.105 | 0.766 |
| Total assets turnover (TAT) | 0.985 | 0.015 | 0.108 | ||
| Solvency ratio-I (SRI) | 0.981 | 0.019 | 0.058 | ||
| 3 | Leverage | Solvency ratio-II (SRII) | 0.788 | 0.212 | 0.635 |
| Leverage ratio (LER) | 0.897 | 0.103 | 0.307 | ||
| Net profit to sales (NPS) | 0.937 | 0.063 | 0.273 | ||
| 4 | Profitability | Return on assets (ROA) | 0.927 | 0.073 | 0.314 |
| Return on equity (ROE) | 0.904 | 0.096 | 0.413 | ||
| Earnings per share growth rate (EPSGR) | 0.871 | 0.129 | 0.336 | ||
| 5 | Growth | Total revenue growth rate (TRGR) | 0.930 | 0.070 | 0.183 |
| Profit margin growth rate (PMGR) | 0.815 | 0.185 | 0.482 |
| Parameters | Description |
|---|---|
| CUR | Total current assets divided by total current liabilities |
| QUR | Subtract inventory from total current assets divided by total current liabilities |
| CAR | Cash and marketable securities divided by total current liabilities |
| INT | Revenues for the period divided by inventories |
| RTR | Net receivable sales divided by average net receivables |
| TAT | Revenues for the period divided by total assets |
| SRI | Total liability divided by total assets |
| SRII | Total liability divided by shareholders equity |
| LER | Total assets divided by shareholders equity |
| NPS | Net profit after tax divided by sales |
| ROA | Net income divided by the total assets |
| ROE | Net income generated per unit of common shareholders’ equity |
| EPSGR | Current quarter’s EPS divided by the previous quarter’s EPS minus one |
| TRGR | Current quarter’s total revenue divided by the previous quarter’s total revenue minus one |
| PMGR | Current quarter’s profit margin divided by the previous quarter’s profit margin minus one |
| Stocks | Inputs | Outputs | |||
|---|---|---|---|---|---|
| I (1) | I (2) | O (1) | O (2) | O (3) | |
| Stock 01 | 4.98 | 0.83 | 54.47 | −22.37 | 0.86 |
| Stock 02 | 44.74 | 1.31 | 44.82 | −39.67 | 0.15 |
| Stock 03 | 8.87 | 1.04 | 22.93 | 17.01 | 0.13 |
| Stock 04 | 8.35 | 1.09 | 48.34 | −8.84 | 0.06 |
| Stock 05 | 11.89 | 0.29 | 55.86 | −30.66 | 0.83 |
| Stock 06 | 97.36 | 12.25 | 205.27 | 3.47 | 0.07 |
| Stock 07 | 42.98 | 1.51 | 12.23 | 92.04 | 0.04 |
| Stock 08 | 68.52 | 1.75 | 33.72 | −47.46 | 0.07 |
| Stock 09 | 60.87 | 2.33 | 46.72 | −50.78 | 0.15 |
| Stock 10 | 40.46 | 1.77 | 8.64 | 199.24 | 0.06 |
| Stock 11 | 19.77 | 0.48 | 71.89 | −28.33 | 0.68 |
| Stock 12 | 71.00 | 0.70 | 57.86 | −20.91 | 0.19 |
| Stock 13 | 117.57 | 3.08 | 37.01 | 10.31 | 0.31 |
| Stock 14 | 54.46 | 0.82 | 32.55 | −38.06 | 0.22 |
| Stock 15 | 16.87 | 0.58 | 53.31 | 17.08 | 0.36 |
| Min | 4.98 | 0.29 | 8.64 | −50.78 | 0.04 |
| Max | 117.57 | 12.25 | 205.27 | 199.24 | 0.86 |
| Stocks | Inefficiency | Efficiency | |
|---|---|---|---|
| Stock 01 | 0.000 | 1.000 | 1.000 |
| Stock 02 | 0.161 | 0.839 | 0.861 |
| Stock 03 | 0.000 | 1.000 | 1.000 |
| Stock 04 | 0.021 | 0.979 | 0.979 |
| Stock 05 | 0.000 | 1.000 | 1.000 |
| Stock 06 | 0.000 | 1.000 | 1.000 |
| Stock 07 | 0.124 | 0.876 | 0.890 |
| Stock 08 | 0.219 | 0.781 | 0.820 |
| Stock 09 | 0.206 | 0.794 | 0.829 |
| Stock 10 | 0.000 | 1.000 | 1.000 |
| Stock 11 | 0.000 | 1.000 | 1.000 |
| Stock 12 | 0.062 | 0.938 | 0.942 |
| Stock 13 | 0.194 | 0.806 | 0.838 |
| Stock 14 | 0.179 | 0.821 | 0.848 |
| Stock 15 | 0.000 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peykani, P.; Seyed Esmaeili, F.S.; Mirmozaffari, M.; Jabbarzadeh, A.; Khamechian, M. Input/Output Variables Selection in Data Envelopment Analysis: A Shannon Entropy Approach. Mach. Learn. Knowl. Extr. 2022, 4, 688-699. https://doi.org/10.3390/make4030032
Peykani P, Seyed Esmaeili FS, Mirmozaffari M, Jabbarzadeh A, Khamechian M. Input/Output Variables Selection in Data Envelopment Analysis: A Shannon Entropy Approach. Machine Learning and Knowledge Extraction. 2022; 4(3):688-699. https://doi.org/10.3390/make4030032
Chicago/Turabian StylePeykani, Pejman, Fatemeh Sadat Seyed Esmaeili, Mirpouya Mirmozaffari, Armin Jabbarzadeh, and Mohammad Khamechian. 2022. "Input/Output Variables Selection in Data Envelopment Analysis: A Shannon Entropy Approach" Machine Learning and Knowledge Extraction 4, no. 3: 688-699. https://doi.org/10.3390/make4030032
APA StylePeykani, P., Seyed Esmaeili, F. S., Mirmozaffari, M., Jabbarzadeh, A., & Khamechian, M. (2022). Input/Output Variables Selection in Data Envelopment Analysis: A Shannon Entropy Approach. Machine Learning and Knowledge Extraction, 4(3), 688-699. https://doi.org/10.3390/make4030032








