1. Introduction
Nowadays, “data” are at the center of our society, regardless of whether one looks at the science, industry or entertainment [
1,
2]. The availability of such data makes it necessary for them to be analyzed adequately, which explains the recent emergence of a new field called
data science [
3,
4,
5,
6]. For instance, in biology, the biomedical sciences, and pharmacology, the introduction of novel sequencing technologies enabled the generation of high-throughput data from all molecular levels for the study of pathways, gene networks, and drug networks [
7,
8,
9,
10,
11]. Similarly, data from social media can be used for the development of methods to address questions of societal relevance in the computational social sciences [
12,
13,
14].
For the analysis of supervised learning models, such as regression or classification methods [
15,
16,
17,
18,
19,
20], allowing to estimate a prediction error model selection and model assessment are key concepts for finding the best model for a given data set. Interestingly, regarding the definition of a best model, there are two complementary approaches with a different underlying philosophy [
21,
22]. One is defining best model as predictiveness of a model, and the other as descriptiveness. The latter approach aims at identifying the true model, whose interpretation leads to a deeper understanding of the generated data and the underlying processes that generated the data.
Despite the importance of all these concepts, there are few reviews available on the intermediate level that formulate the goals and approaches of model selection and model assessment in a clear way. For instance, advanced reviews are presented by [
21,
23,
24,
25,
26,
27] that are either comprehensive presentations without much detail, or detailed presentations of selected topics. Furthermore, there are elementary introductions to these topics, such as by [
28,
29]. While accessible for beginners, these papers focus only on a small subset of the key concepts, making it hard to recognize the wider picture of model selection and model assessment.
In contrast, the focus of our review is different, with respect to the following points. First, we present the general conceptual ideas behind model selection, model assessment, and their interconnections. For this, we also present theoretical details as far as they are helpful for a deeper understanding. Second, we present practical approaches for their realization and demonstrate these by worked examples for linear polynomial regression models. This allows to close the gap between theoretical understanding and practical application. Third, our explanations aim at an intermediate level of the reader by providing background information frequently omitted in advanced texts. This should ensure that our review is useful for a broad readership with a general interest in data science. Finally, we will give information about the practical application of the methods by providing information about the availability of implementations for the statistical programming language R [
30]. We focus on R because it is a widely used programming language which is freely available and forms the gold standard of the literature on statistics.
This paper is organized as follows. In the next section, we present general preprocessing steps we use before a regression analysis. Thereafter, we discuss the ordinary least squares regression, linear polynomial regression, and ridge regression, because we assume that not all readers are familiar with these models, but an understanding is necessary for the following sections. Then, we discuss the basic problem of model diagnosis, as well as its key concepts model selection and model assessment, including methods for their analysis. Furthermore, we discuss cross-validation as a flexible, generic tool that can be applied to both problems. Finally, we discuss the meaning of learning curves for model diagnosis. The paper finishes with a brief summary and conclusions.
2. Preprocessing of Data and Regression Models
In this section, we briefly review some statistical preliminaries as needed for the models discussed in the following sections. Firstly, we discuss some preprocessing steps used for standardizing the data for all regression models. Secondly, we discuss different basic regression models, with and without regularization. Thirdly, we provide information about the practical realization of such regression models by using the statistical programming language R.
2.1. Preprocessing
Let’s assume we have data of the form with , where n is the number of samples. The vector corresponds to the predictor variables for sample i, whereas and p is the number of predictors; furthermore, is the response variable. We denote by the vector of response variables and by the predictor matrix. The vector corresponds to the regression coefficients.
The predictors and response variable shall be standardized in the following way:
Here, and are the mean and variance of the predictor variables, and is the mean of the response variables.
2.2. Ordinary Least Squares Regression and Linear Polynomial Regression
The general formulation of a multiple regression model [
17,
31] is given by
Here, are p predictor variables that are linearly mapped onto the response variable for sample i. The mapping is defined by the p regression coefficients . Furthermore, the mapping is affected by a noise term assuming values in which are normally distributed. The noise term summarizes all kinds of uncertainties, such as measurement errors.
In order to write Equation (
4) more compactly but also to see the similarity between a multiple linear regression model, having
p predictor variables, and a simple linear regression model, having one predictor variable, one can rewrite Equation (
4) in the form:
Here,
is the inner product (scalar product) between the two p-dimensional vectors
and
. One can further summarize Equation (
5) for all samples
by:
Here, the noise terms assumes the form , whereas is the identity matrix.
In this paper, we will show worked examples for linear polynomial regressions. The general form of this model can be written as:
Equation (
7) is a sum of polynomials with a maximal degree of
d. Interestingly, despite the fact that Equation (
7) is non-linear in
, it is linear in the regression coefficients
and, hence, it can be fitted in the same way as OLS regression models. That means the linear polynomial regression model shown in Equation (
7) is a linear model.
2.3. Regularization: Ridge Regression
For studying the regularization of regression models, one needs to solve optimization problems. These optimization problems are formulated in terms of norms. For a real vector
and
, the Lq-norm is defined by
For the special case
, one obtains the L2-norm (also known as the Euclidean norm) used for ridge regression and for
the L1-norm, which is, for instance, used by the LASSO [
32].
The motivation for improving OLS comes from the observation that OLS models often have a low bias but large variance; put simply, this means the models are too complex for the data. In order to reduce the complexity of models, regularized regressions are used. The regularization leads either to a shrinking of the values of the regression coefficients, or to a vanishing of the coefficients (i.e., a value of zero) [
33].
A base example for regularized regression is Ridge regression, introduced in [
34]. Ridge regression can be formulated as follows:
Here, is the residual sum of squares (RSS) called the loss of the model, is the regularization term or penalty, and is the tuning or regularization parameter. The parameter controls the shrinkage of coefficients. The L2-penalty in Equation (10) is also sometimes called the Tikhonov regularization.
Overall, the advantage of a ridge regression and general regularized regression model is that regularization can reduce the variance by increasing the bias. Interestingly, this can improve the prediction accuracy of a model [
19].
2.4. R Package
OLS regression is included in the base functionality of R. In order to preform regularized regression, the package
glmnet [
35] can be used. This package is very flexible, allowing to perform a variety of different regularized regression models, including ridge regression, LASSO, adaptive LASSO [
36], and elastic net [
37].
3. Overall View on Model Diagnosis
Regardless of what statistical model one is studying, e.g., for classification or regression, there are two basic questions one needs to address: (1) How can one choose between competing models, and (2) how can one evaluate them? Both questions aim at the diagnosis of models.
The above informal questions are formalized by the following two statistical concepts [
18]:
Briefly, model selection refers to the process of optimizing a model family or model candidate. This includes the selection of a model itself from a set of potentially available models, and the estimation of its parameters. The former can relate to deciding which regularization method (e.g., ridge regression, LASSO, or elastic net) should be used, whereas the latter corresponds to estimating the parameters of the selected model. On the other hand, model assessment means the evaluation of the generalization error (also called test error) of the finally selected model for an independent data set. This task aims at estimating the “true prediction error” as could be obtained from an infinitely large test data set. What both concepts have in common is that they are based on the utilization of data to quantify properties of models numerically.
For simplicity, let’s assume that we have been given a very large (or arbitrarily large) data set, D. The best approach for both problems would be to randomly divide the data into three non-overlapping sets:
By “very large data set”, we mean a situation where the sample sizes—that is,
,
, and
for all three data sets are large without necessarily being infinite, but where an increase in their sizes would not lead to changes in the model evaluation. Formally, the relation between the three data sets can be written as:
Based on these data, the training set would be used to estimate or learn the parameters of the models. This is called “model fitting”. The validation data would be used to estimate a selection criterion for model selection, and the test data would be used for estimating the generalization error of the final chosen model.
In practice, the situation is more complicated due to the fact that D is typically not arbitrarily large. In the following sections, we discuss first model assessment and then model selection in detail. The order of our discussion is reversed to the order in which one would perform a practical analysis. However, for reasons of understanding the concepts, this order is beneficial.
4. Model Assessment
Let’s assume we have a general model of the form:
mapping the input
x to the output
y as defined by the function
f. The mapping varies by a noise term
representing, for example, measurement errors. We want to approximate the true (but unknown) mapping function
f by a model
g that depends on parameters
, that is,
Here, the parameters are estimated from a training data set D (strictly denoted by ), making the parameters a function of the training set . The “hat” indicates that the parameters are estimates of the data D. As a short-cut, we are writing instead of .
Based on these entities, we can define the following model evaluation measures:
Here, is the mean value of the predictor variable, and are the residuals; furthermore:
SST is the sum of squares total, also called the total sum of squares (TSS);
SSR is the sum of squares due to regression (variation explained by linear model), also called the explained sum of squares (ESS);
SSE is the sum of squares due to errors (unexplained variation), also called the residual sum of squares (RSS).
There is a remarkable property for the sum of squares given by:
This relation is called
partitioning of the sum of squares [
31].
Furthermore, for summarizing the overall predictions of a model, the
mean squared error (MSE) is useful, given by
The general problem when dealing with predictions is that we would like to know about the generalization abilities of our model. Specifically, for a given training data set
, we can estimate the parameters of our model
leading to estimates
. Ideally, we would like to have that
for any data point
. In order to assess this quantitatively, a loss function, simply called "loss", is defined. Frequent choices are the absolute error
or the squared error
If one would use only the data points from a training set, i.e.,
to assess the loss, these estimates are usually overly optimistic and lead to much smaller estimates than if data points are used from all possible values (i.e.,
) whereas
P is the distribution of all possible values. Formally, we can write this as expectation values of the respective data,
The expectation value in Equation (
24) is called the generalization error of the model given by
. This error is also called
out-of-sample error, or simply test error. The latter name emphasizes the important fact that test data are used for the evaluation of the prediction error (as represented by the distribution
P) of the model, but training data are used to learn its parameters (as indicated by
).
From Equation (
24), one can see that we have an unwanted dependency on the training set
. In order to remove this, we need to assess the generalization error of the model given by
by forming the expectation value with respect to all training sets, i.e.,
This is the expected generalization error of the model, which is no longer dependent on any particular estimates of
. Hence, this error provides the desired assessment of a model. Equation (
25) is also called
expected out-of-sample error [
38]. It is important to emphasize that the training sets
are not infinitely large, but all have the same finite sample size
. Hence, the expected generalization error in Equation (
25) is independent of a particular training set but dependent on the size of these sets. This dependency will be explored in
Section 7 when we discuss learning curves.
On a practical note, we would like to say that in practice, we do not have
all data available—instead, we have one (finite) data set,
D, which we need to utilize in an efficient way to approximate
P for estimating the generalization error of the model in Equation (
25). The gold-standard approach for this is cross-validation (CV), and we discuss practical aspects thereof in
Section 6. However, in the following, we focus first on theoretical aspects of the generalization error of the model.
4.1. Bias-Variance Tradeoff
It is interesting that the above generalization error of the model in Equation (
25) can be decomposed into different components. In the following, we derive this decomposition which is known as the bias–variance tradeoff [
39,
40,
41,
42]. We will see that this decomposition provides valuable insights for understanding the influence of the model complexity on the prediction error.
In the following, we denote the training set briefly by
D to simplify the notation. Furthermore, we write the expectation value with respect to distribution
P as
, and not as
as in Equation (
25), because this makes the derivation more explicit. This argument will become clear when discussing the Equations (31) and (34).
In Equations (28) and (31) we used the independence of the sampling processes for D and to change the order of the expectation values. This allowed us to evaluate the conditional expectation value , because the argument is independent of y.
In Equation (30), we used the short form
to write the expectation value of
with respect to
D, giving a mean model
over all possible training sets
D. Due to the fact that this expectation value integrates over all possible values of
D, the resulting
no longer depends on it.
By utilizing the conditional expectation value
we can further analyze the first term of the above derivation (highlighted in green) by making use of
Here, it is important to note that is a function of x, whereas is not because the expectation value integrates over all possible values of x. For reasons of clarity, we want to note that y actually means , but for notational simplicity we suppress this argument in order to make the derivation more readable.
Specifically, by utilizing this term, we obtain the following decomposition:
Taken together, we obtain the following combined result:
Noise: This term measures the variability within the data, not considering any model. The noise cannot be reduced because it does not depend on the training data D or g, or any other parameter under our control; hence, it is a characteristic of the data. For this reason, this component is also called “irreducible error”.
Variance: This term measures the model variability with respect to changing training sets. This variance can be reduced by using less complex models, g. However, this can increase the bias (underfitting).
Bias: This term measures the inherent error that you obtain from your model, even with infinite training data. This bias can be reduced by using more complex models, g. However, this can increase the variance (overfitting).
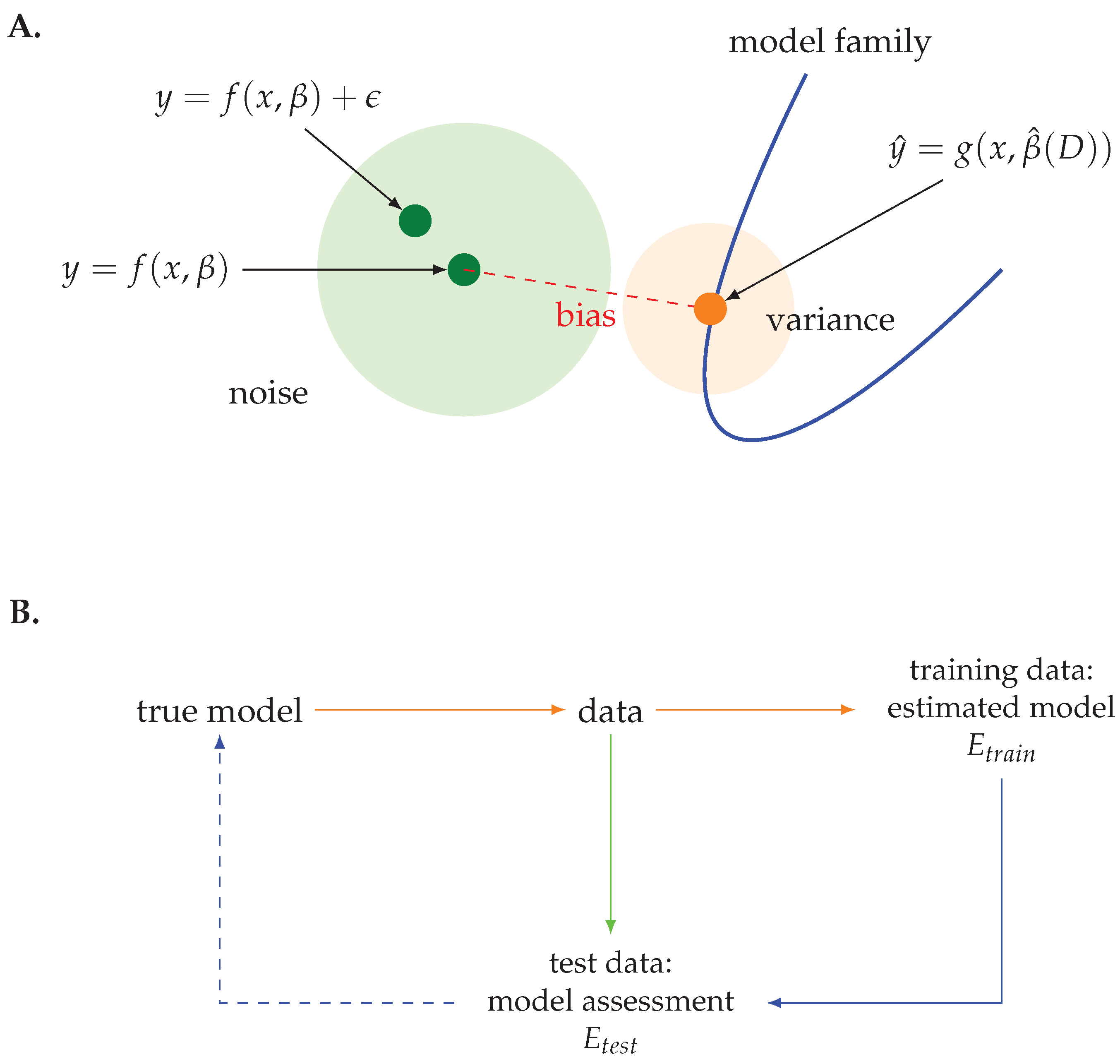
Figure 1 shows a visualization of the model assessment problem and the bias-variance tradeoff. In
Figure 1A, the blue curve corresponds to a model family—that is, a regression model with a fixed number of covariates—and each point along this line corresponds to a particular model obtained from estimating the parameters of the model from a data set. The dark-green point corresponds to the true (but unknown) model and a data set generated by this model. Specifically, this data set has been obtained in the error-free case, i.e.,
for all samples,
i. If another data set is generated from the true model, this data set will vary to some extent because of the noise term
, which is usually not zero. This variation is indicated by the large (light) green circle around the true model.
In case the model family does not include the true model, there will be a bias corresponding to the distance between the true model and the estimated model, indicated by the orange point along the curve of the model family. Specifically, this bias is measured between the error-free data set generated by the true model and the estimated model based on this data set. Also the estimated model will have some variability indicated by the (light) orange circle around the estimated model. This corresponds to the variance of the estimated model.
It is important to realize that there is no possibility of directly comparing the true model and the estimated model with each other because the true model is usually unknown. Instead, this comparison is carried out indirectly via data that have been generated by the true model. Hence, these data are serving two purposes. Firstly, they are used to estimate the parameters of the model, where the training data are used. If one uses the same training data to evaluate the prediction error of this model, the prediction error is called training error
is also called in-sample error. Secondly, they are used to assess the estimated model by quantifying its prediction error, and for this estimation the test data are used. For this reason, the prediction error is called test error
In order to emphasize this, we visualized this process in
Figure 1B.
It is important to note that a prediction error is always evaluated with respect to a given data set. For this reason, we emphasized this explicitly in Equations (
44) and (
45). However, usually this information is omitted whenever it is clear which data set has been used.
We want to emphasize that the training error is only defined as a sample estimate but not as a population estimate, because the training data set is always finite. That means Equation (
44) is estimated by
assuming the sample size of the training data is
. In contrast, the test error in Equation (
45) corresponds to the population estimate given in Equation (
25). In practice, this can be approximated by a sample estimate, similar to Equation (
46), of the form
for a test data set with
samples.
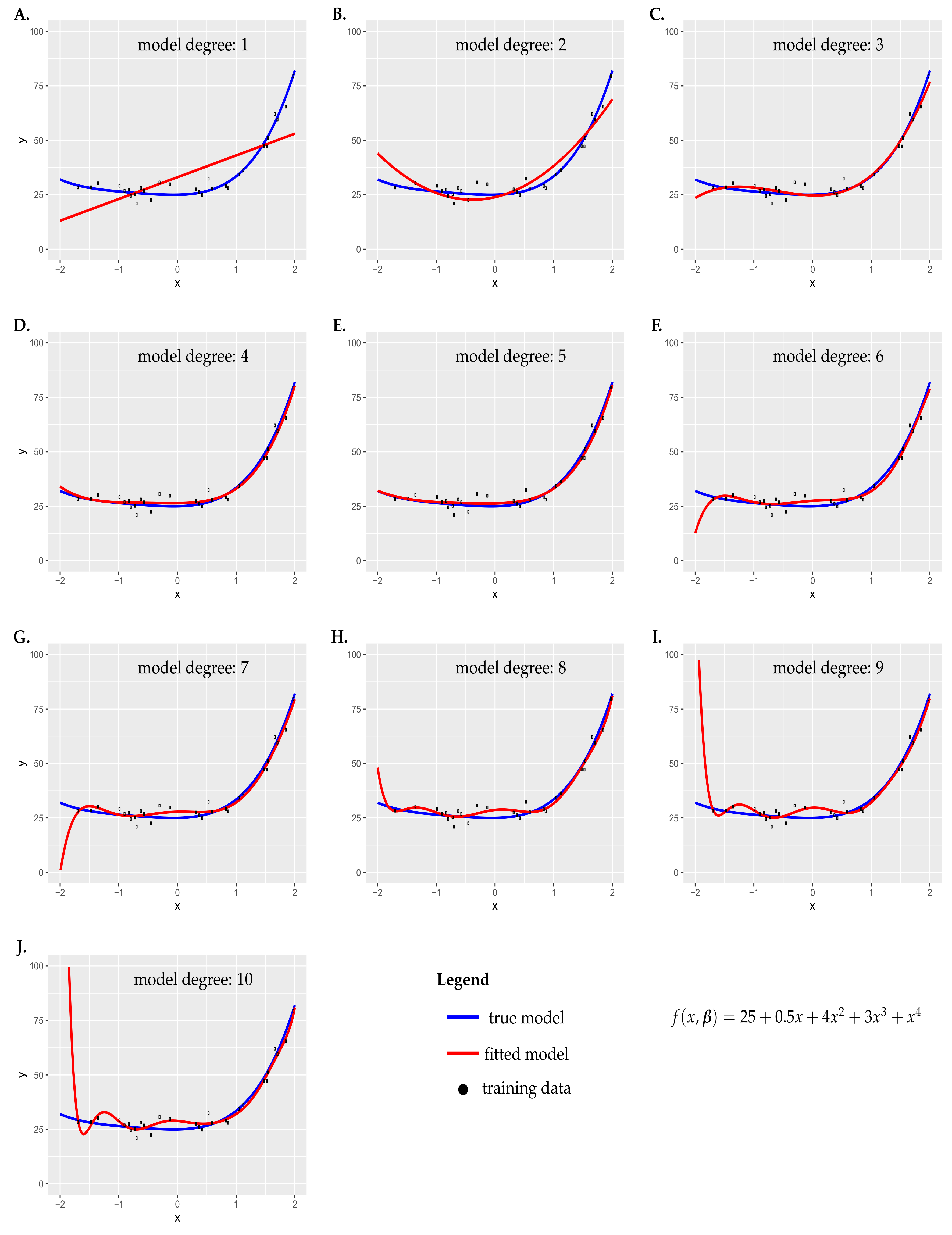
4.2. Example: Linear Polynomial Regression Model
Figure 2 presents an example. Here, the true model is shown in blue, corresponding to
whereas
(see Equation (
15)). The true model is a mixture of polynomials of different degrees, whereas the highest degree is 4, corresponding to a linear polynomial regression model. From this model, we generate training data with a sample size of
(shown by black points) that we use to fit different regression models.
The general model family we use for the regression model is given by
That means we are fitting linear polynomial regression models with a maximal degree of
d. The highest degree corresponds to the model complexity of the polynomial family. For our analysis, we are using polynomials with degree
d from 1 to 10, and we fit these to the training data. The results of these regression analyses are shown as red curves in
Figure 2A–J.
In
Figure 2A–J, the blue curves show the true model, the red curves the fitted models, and the black points correspond to the training data. These results correspond to individual model fits—that is, no averaging has been performed. Furthermore, for all results, the sample size of the training data was kept fixed (varying sample sizes are studied in
Section 7). Because the model degree indicates the complexity of the fitted model, the shown models correspond to different model complexities, from low-complexity (
) to high-complexity (
) models.
One can see that for both low and high degrees of the polynomials, there are clear differences between the true model and the fitted models. However, these differences have a different origin. For low-degree models, the differences come from the low complexity of the models which are not flexible enough to adapt to the variability of the training data. Put simply, the model is too simple. This behavior corresponds to an underfitting of the data (caused by high bias, as explained in detail below). In contrast, for high degrees, the model is too flexible for the few available training samples. In this case, the model is too complex for the training data. This behavior corresponds to an overfitting of the data (caused by high variance, as explained in detail below).
A different angle to the above results can be obtained by showing the expected training and test errors for the different polynomials. This is shown in
Figure 3.
Here, we show two different types of results. The first type, shown in
Figure 3A,C,E,F, corresponds to numerical simulation results fitting a linear polynomial regression to training data, whereas the second type, shown in
Figure 3B,D (emphasized by the dashed red rectangle), corresponds to idealized results that hold for general statistical models beyond our studied examples. The numerical simulation results in
Figure 3A,C,E,F have been obtained by averaging over an ensemble of repeated model fits. For all these fits, the sample size of the training data was kept fixed.
The plots shown in
Figure 3A,B are called
error-complexity curves. They are important for evaluating the learning behavior of models.
Definition 1. Error-complexity curvesshow the training error and test error in dependence on the model complexity. The models underlying these curves are estimated from training data with a fixed sample size.
From
Figure 3A, one can see that the training error decreases with an increasing polynomial degree, while in contrast, the test error is U-shaped. Intuitively, it is clear that more complex models fit the training data better, but there should be an optimal model complexity, and going beyond could worsen the prediction performance. The training error alone clearly does not reflect this, and for this reason, estimates of the test error are needed.
Figure 3B shows idealized results for characteristic behavior of the training and test error for general statistical models.
In
Figure 3C, we show the decomposition of the test error into its noise, bias, and variance components. The noise is constant for all polynomial degrees, whereas the bias is monotonously decreasing and the variance is increasing. Also, this behavior is generic beyond the shown examples. For this reason, we show in
Figure 3D the idealized decomposition (neglecting the noise because of its constant contribution).
In
Figure 3E, we show the percentage breakdown of the noise, bias, and variance for each polynomial degree. In this representation, the behavior of the noise is not constant because of the non-linear decomposition for different complexity values of the model. The numerical values of the percentage breakdown depend on the degree of the polynomial and can vary, as is evident from the Figure.
Figure 3F shows the same as in
Figure 3E, but without the noise part. From these representations, one can see that simple models have a high bias and a low variance, and complex models have a low bias and a high variance. This characterization is also generic and not limited to the particular model we studied.
4.3. Idealized Error-Complexity Curves
From the idealized error-complexity curves in
Figure 3B, one can summarize and clarify a couple of important terms. We say
a model is overfitting if its test error is higher than those of a
less complex model. That means to decide whether a model is overfitting, it is necessary to compare it with a simpler model. Hence, overfitting is detected from a comparison, and it is not an absolute measure.
Figure 3B shows that all models with a model complexity larger than 3.5 are overfitting, with respect to the best model having a model complexity of
= 3.5 leading to the lowest test error. One can formalize this by defining an overfitting model as follows.
Definition 2 (model overfitting)
. A model with complexity c is calledoverfittingif, for the test error of this model, the following holds:with From
Figure 3B we can also see that for all these models, the difference between the test error and the training error increases for increasing complexity values—that is,
Similarly, we say
a model is underfitting if its test error is higher than those of a
more complex model. In other words, to decide whether a model is underfitting, it is necessary to compare it with a more complex model. In
Figure 3B, all models with a model complexity smaller than 3.5 are underfitting, with respect to the best model. The formal definition of this can be given as follows.
Definition 3 (model underfitting)
. A model with complexity c is calledunderfittingif, for the test error of this model, the following holds: Finally, the
generalization capabilities of a model are assessed by its predictive performance of the test error in comparison with the training error. If the distance between the test error and the training error is small (has a small gap), such as
the model has good generalization capabilities [
38]. From
Figure 3B, one can see that models with
have bad generalization capabilities. In contrast, models with
have good generalization capabilities, but not necessarily small error. This makes sense considering the fact that the sample size is kept fixed.
In Definition 4 we formally summarize these characteristics.
Definition 4 (generalization)
. If a model with complexity c holdswe say the model has good generalization capabilities. In practice, one needs to decide what a reasonable value of is, because is usually too strict. This makes the definition of generalization problem specific. Put simply, if one can conclude from the training error to the test error (because they are of similar value), a model generalizes to new data.
Theoretically, for increasing the sample size of the training data, we obtain
for all model complexities
c, because Equations (
46) and (
47) become identical, assuming an infinite large test data set—that is,
.
From the idealized decomposition of the test error shown in
Figure 3D, one can see that a simple model with low variance and high bias generally has good generalization capabilities, whereas for a complex model, its variance is high and the model’s generalization capabilities are poor.
5. Model Selection
The expected generalization error provides the most complete information about the generalization abilities of a model. For this reason, the expected generalization error is used for model assessment [
43,
44,
45]. It would appear natural to also perform model selection based on model assessment of the individual models. If it is possible to estimate the expected generalization error for each individual model, this is the best you can do. Unfortunately, it is not always feasible to estimate the expected generalization error, and for this reason, alternative approaches have been introduced. The underlying idea of these approaches is to estimate an auxiliary function that is different to the expected generalization error, but suffices to order different models in a similar way as could be done with the help of the expected generalization error. This means that the measure used for model selection just needs to result in the same ordering of models as if the generalization errors of the models would have been used for the ordering. Hence, model selection is actually a model ordering problem, and the best model is selected without necessarily estimating the expected generalization error. This explains why model assessment and model selection are generally two different approaches.
There are two schools of thought in model selection, and they differ in the way in which one defines “best model”. The first defines a best model as the “best prediction model”, and the second as the “true model” that generated the data [
21,
22,
46]. For this reason, the latter is referred to as
model identification. The first definition fits seamlessly into our above discussion, whereas the second one is based on the assumption that the true model also has the best generalization error. For very large sample sizes (
), this is uncontroversial; however, for finite sample sizes (as is the case in practice), this may not be the case.
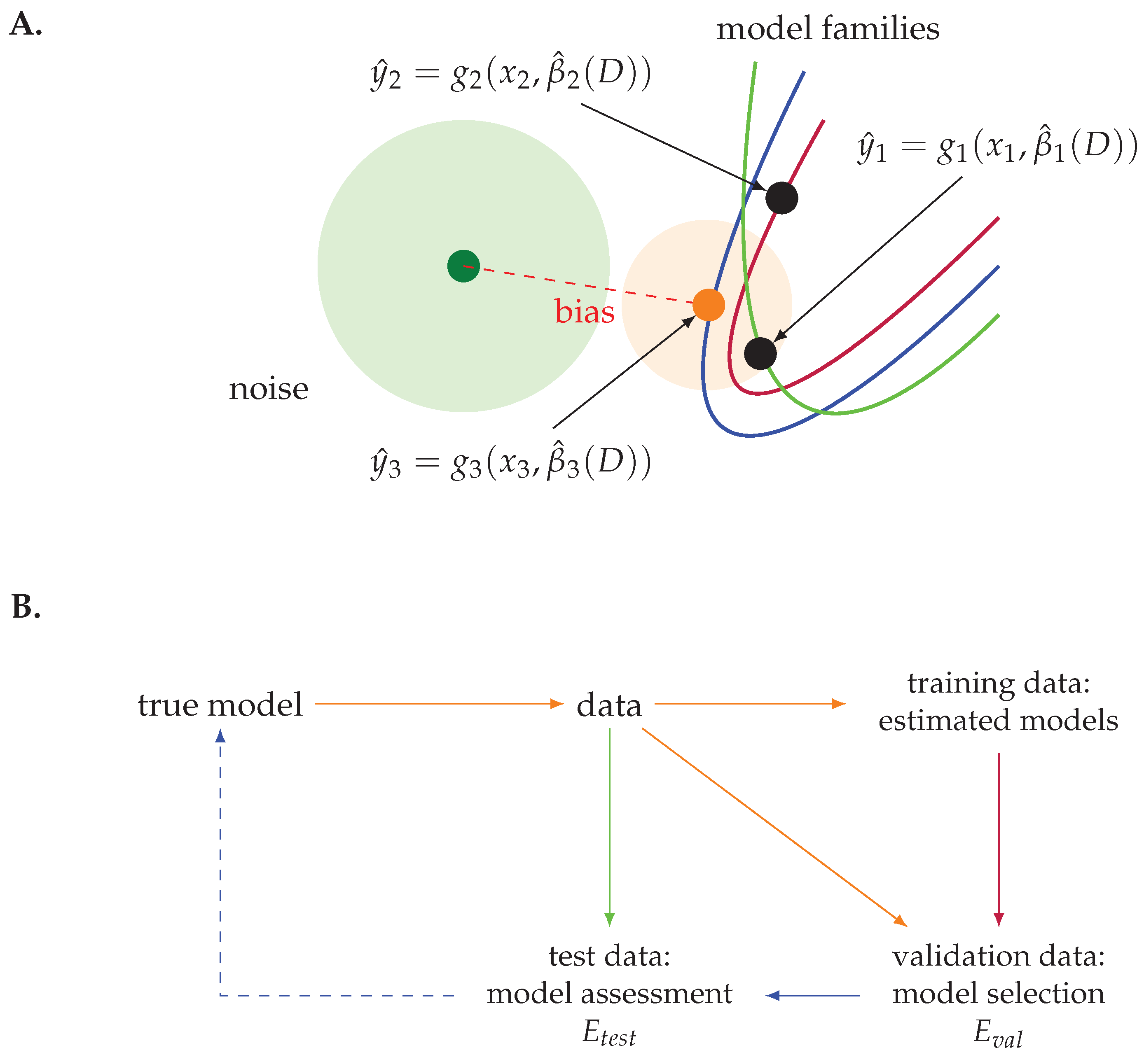
In
Figure 4, we visualize the general problem of model selection. In
Figure 4A we show three model families indicated by the three curves in blue, red, and green. Each of these model families correspond to a statistical model—that is, a linear regression model with covariates of
,
, and
. Similarly to
Figure 1A, each point along these lines correspond to a particular model obtained from estimating the parameters of the models from a data set. These parameter estimates are obtained by using a training data set. Here,
,
, and
are three examples.
After the parameters of the three models have been estimated, one performs a model selection for identifying the best model according to a criterion. For this, a validation data set is used. Finally, one performs a model assessment of the best model by using a test data set.
In
Figure 4B, a summary of the above process is shown. Here, we emphasize that different data (training data, validation data, or test data) are used for the corresponding analysis step. Assuming an ideal (very large) data set
D, there are no problems with the practical realization of this step. However, practically, we have no ideal data set, but one with a finite sample size. This problem will be discussed in detail in
Section 6.
In the following, we discuss various evaluation criteria for model selection that can be used for model ranking.
5.1. and Adjusted
The first measure we discuss is called the
coefficient of determination (COD) [
47,
48]. The COD is defined as
This definition is based on SSR and SST in Equations (17) and (19). The COD is a measure of how well the model explains the variance of the response variables. A disadvantage of is that a submodel of a full model always has a smaller value, regardless of its quality.
For this reason, a modified version of
has been introduced, called the
adjusted coefficient of determination (ACOD). The ACOD is defined as
It can also be written in dependence on
, as
The ACOD adjusts for sample size n of the training data and mode complexity, as measured by the number of covariates, p.
5.2. Mallows’ Cp Statistic
For a general model and in-sample data
used for training and out-sample data
used for testing, one can show that
Furthermore, if the model is linear having
p predictors and an intercept one can show that
The last term in Equation (
62) is called
optimism, because it is the amount by which the in-sample error underestimates the out-sample error. Hence, a large value of the optimism indicates a large discrepancy between both errors. It is interesting to note that:
The optimism increases with ;
The optimism increases with p;
The optimism decreases with n.
Explanations for the above factors are given by:
Adding more noise (indicated by increasing ) and leaving n and p fixed makes it harder for a model to be learned;
Increasing the complexity of the model (indicated by increasing p) and leaving and n fixed makes it easier for a model to fit the test data but is prune to overfitting;
Increasing the test data set (indicated by increasing n) and leaving and p fixed reduces the chances for overfitting.
The problem with Equation (
62) is that
corresponds to the true value of the noise which is unknown. For this reason, one needs to use an estimator to obtain a reasonable approximation. One can show that by estimating
from the largest model, this will be an unbiased estimator of
if the true model is smaller.
Using this estimate for
leads to Mallows’ Cp statistic [
49,
50],
Alternatively, we can write Equation (
63) as:
For model selection, one needs to choose the model that minimizes . Mallows’ is only used for linear regression models that are evaluated with the squared error.
5.3. Akaike’s Information Criterion (AIC), Schwarz’s BIC, and the Bayes Factor
The next two model selection criteria are similar to Equation (
64). Specifically, Akaike’s information criterion (AIC) [
24,
51,
52] for model
is defined by
Here, is the likelihood of model evaluated at the maximum likelihood estimate, and is the dimension of the model corresponding to the number of free parameters. In contrast to Mallows’ , the Akaike’s information criterion selects the model that maximizes .
For a linear model, one can show that the log likelihood is given by
where
is a model independent constant, and the dimension of the model is
Taken together, this gives
with
. For model comparisons, the parameter
C is irrelevant.
The BIC (Bayesian Information Criterion) [
53,
54], also called the Schwarz criterion, has a similar form as the AIC. The BIC is defined by
For a linear model with normal distributed errors, this simplifies to
Also, BIC selects the model that maximizes .
Another model selection criterion is the Bayes’ factor [
55,
56,
57,
58]. Suppose we have a finite set of models
with
, which we can use for fitting the data
D. In order to select the best model from a Bayesian perspective, we need to evaluate the posterior probability of each model,
for the available data. Using Bayes’ theorem, one can write this probability as:
Here, the term is called the evidence for the model , or simply “evidence”.
The ratio of the posterior probabilities for model
and
corresponding to the
posterior odds of the models is given by:
That means the Bayes’ factor of the models is the ratio of the posterior probabilities and the prior probabilities.
If one uses non-informative priors, such as
= 0.5, then the Bayes’ factor simplifies to
Assuming the parameter dependency of a model
on
, then the evidence can be written as
A serious problem with this expression is that it can be very hard to evaluate—especially in high dimensions—if no closed-form solution is available. This makes the Bayes’ factor problematic to apply.
Interestingly, there is a close connection between the BIC and the Bayes’ factor. Specifically, in [
55] it has been proven that for
, the following holds:
Note that the relation is a negative symmetric. Hence, model comparison results for the BIC and the Bayes’ factor can approximate each other.
For a practical application for interpreting the BIC and Bayes factors, [
26] suggested the following evaluation of a comparison of two models—see
Table 1. Here, “min” indicates the model with smaller BIC or posterior probability.
The common idea of AIC and BIC is to penalize larger models. Because , the BIC penalizes more harshly than AIC (usually, data sets have more than 8 samples). Hence, BIC selects smaller models than AIC. BIC has a consistency property which means that when the true unknown model is one of the models under consideration and, for the sample size, holds , BIC selects the correct model. In contrast, AIC does not have this consistency property.
In general, AIC and BIC are considered to have a different view on model selection [
28]. Whereas BIC assumes that the true model is among the studied ones, its goal is to identify the true model. In contrast, AIC does not assume this; instead, the goal of AIC is to find the model that maximizes predictive accuracy. In practice, the true model is rarely among the model families studied, and for this reason the BIC cannot select the true model. For such a case, AIC is the appropriate approach for finding the best approximating model. Several studies suggest to prefer the AIC over BIC for practical applications [
24,
28,
54]. For instance, in [
59] it was found that AIC can select a better model than BIC even for the case when the true model is among the studied models. Specifically for regression models, in [
60] it has been demonstrated that AIC is asymptotically efficient, selecting the model with the least MSE while when the true model is not among the studied models, BIC does not.
In summary, the AIC and BIC have the following characteristics:
BIC selects smaller models (more parsimonious) than AIC and tends to perform underfitting;
AIC selects larger models than BIC and tends to perform overfitting;
AIC represents a frequentist point of view;
BIC represents a Bayesian point of view;
AIC is asymptotically efficient but not consistent;
BIC is consistent but not asymptotically efficient;
AIC should be used when the goal is prediction accuracy of a model;
BIC should be used when the goal is model interpretability.
The AIC and BIC are generic in their applications not limited to linear models, and can be applied whenever we have a likelihood of a model [
61].
5.4. Best Subset Selection
So far, we discussed evaluation criteria which one can use for model selection. However, we did not discuss how these criteria are actually used. In the following, we provide this information, discussing best subset selection (Algorithm 1), forward stepwise selection (Algorithm 2), and backward stepwise selection (Algorithm 3) [
47,
62,
63]. All of these approaches are computational.
| Algorithm 1: Best subset selection. |
![Make 01 00032 i002]() |
| Algorithm 2: Forward stepwise selection. |
![Make 01 00032 i003]() |
| Algorithm 3: Backward stepwise selection. |
![Make 01 00032 i004]() |
The most brute-force model selection strategy is evaluating each possible model. This is the idea of best subset selection (Best).
Best subset selection evaluates each model with k parameters by the MSE or . Due to the fact that each of these models have the same complexity (a model with k parameters), measures considering the model complexity are not needed. However, when comparing the , different models having different parameters (see line 5 in Algorithm 1) a complexity penalizing measure, such as the , AIC, or BIC, needs to be used.
For a linear regression model, one needs to fit all combinations with p predictors. A problem with the best subset selection is that in total, one needs to evaluate different models. For , this already gives over models, leading to computational problems in practice. For this reason, approximations to the best subset selection are needed.
5.5. Stepwise Selection
Two such approximations are discussed in the following. Both of these follow a greedy approach, whereas forward stepwise selection does this in a bottom-up manner, and backward stepwise selection does it in a top-down manner.
5.5.1. Forward Stepwise Selection
The idea of forward stepwise selection (FSS) is to start with a null model without parameters and successively add one parameter at a time, that is best done according to a selection criterion.
For a linear regression model with
p predictors, this gives
models. For
, this gives only 211 different models one needs to evaluate, which is a great improvement compared to best subset selection.
5.5.2. Backward Stepwise Selection
The idea of backward stepwise selection (BSS) is to start with a full model with p parameters and successively remove one parameter at a time that is worst according to a selection criterion.
The number of models that need to be evaluated with backward stepwise selection is the exact same as for forward stepwise selection.
Both stepwise selection strategies are not guaranteed to find the best model containing a subset of the p predictors. However, when p is large, both approaches may be the only ones which are practically feasible. Despite the apparent symmetry of the forward stepwise selection and the backward stepwise selection, there is a difference in situations when , or when we have more parameters than samples in our data. In this case, the forward stepwise selection approach can still be applied because the procedure may be systematically limited to n parameters.
6. Cross-Validation
A cross-validation (CV) approach is the most practical and flexible approach one can use for model selection [
23,
64,
65]. The reasons for this are because (A) it is conceptually simple, (B) it is intuitive, and (C) it can be applied to any statistical model family regardless of its technical details (for instance, to parametric and non-parametric models). Conceptually, cross-validation is a resampling method [
66,
67,
68] and its basic idea is to repeatedly split the data into training and validation data for estimating the parameters of the model and for its evaluation—see
Figure 5 for a visualization of the base functioning of a five-fold cross-validation. Importantly, the test data used for model assessment (MA) are not resampled during this process.
Formally, cross-validation works the following way. For each split
k (
), the parameters of model
m (
) are estimated using the training data, and the prediction error is evaluated using the validation data—that is:
After the last split, the errors are summarized by
This gives estimates of the prediction error for each model
m. The best model can now be selected by
Compared to other approaches for model selection, cross-validation has the following advantages:
Cross-validation is a computational method that is simple in its realization;
Cross-validation makes few assumptions about the true underlying model;
Compared with AIC, BIC, and the adjusted , cross-validation provides a direct estimate of the prediction error;
Every data point is used for both training and testing.
Some drawbacks of cross-validation are:
The computation time can be long because the whole analysis needs to be repeated K times for each model;
The number of folds (K) needs to be determined;
For a small number of folds, the bias of the estimator will be large.
There are many technical variations of cross-validation and other resampling methods (e.g., Boostrap [
69,
70]) to improve the estimates [
23,
71,
72]. We just want to mention that in the case of very limited data,
leave-one-out cross-validation (LOOCV) has some advantages [
72]. In contrast to cross-validation, LOOCV splits the data into
folds, whereas
n corresponds to the total number of samples. The rest of the analysis proceeds like CV.
Using the same idea as for model selection, cross-validation can also be used for model assessment. In this case, the prediction error is estimated by using the test data, instead of the validation data used for model selection—see
Figure 5. That means we estimate the prediction error for each split by
and summarize these errors by the sample average
7. Learning Curves
Finally, we discuss learning curves as another way of model diagnosis. A learning curve shows the performance of a model for different sample sizes of the training data [
73,
74]. The performance of a model is measured by its prediction error. For extracting the most information, one needs to compare the learning curve of the training error and the test error with each other. This leads to complementary information to the error-complexity curves. Hence, learning curves are playing an important role in model diagnosis, but are not strictly considered as part of model assessment methods.
Definition 5. Learning curvesshow the training error and test error in dependence on the sample size of the training data. The models underlying these curves all have the same complexity.
In the following, we first present numerical examples for learning curves for linear polynomial regression models. Then, we discuss the behavior of idealized learning curves that can correspond to any type of statistical model.
7.1. Learning Curves for Linear Polynomial Regression Models
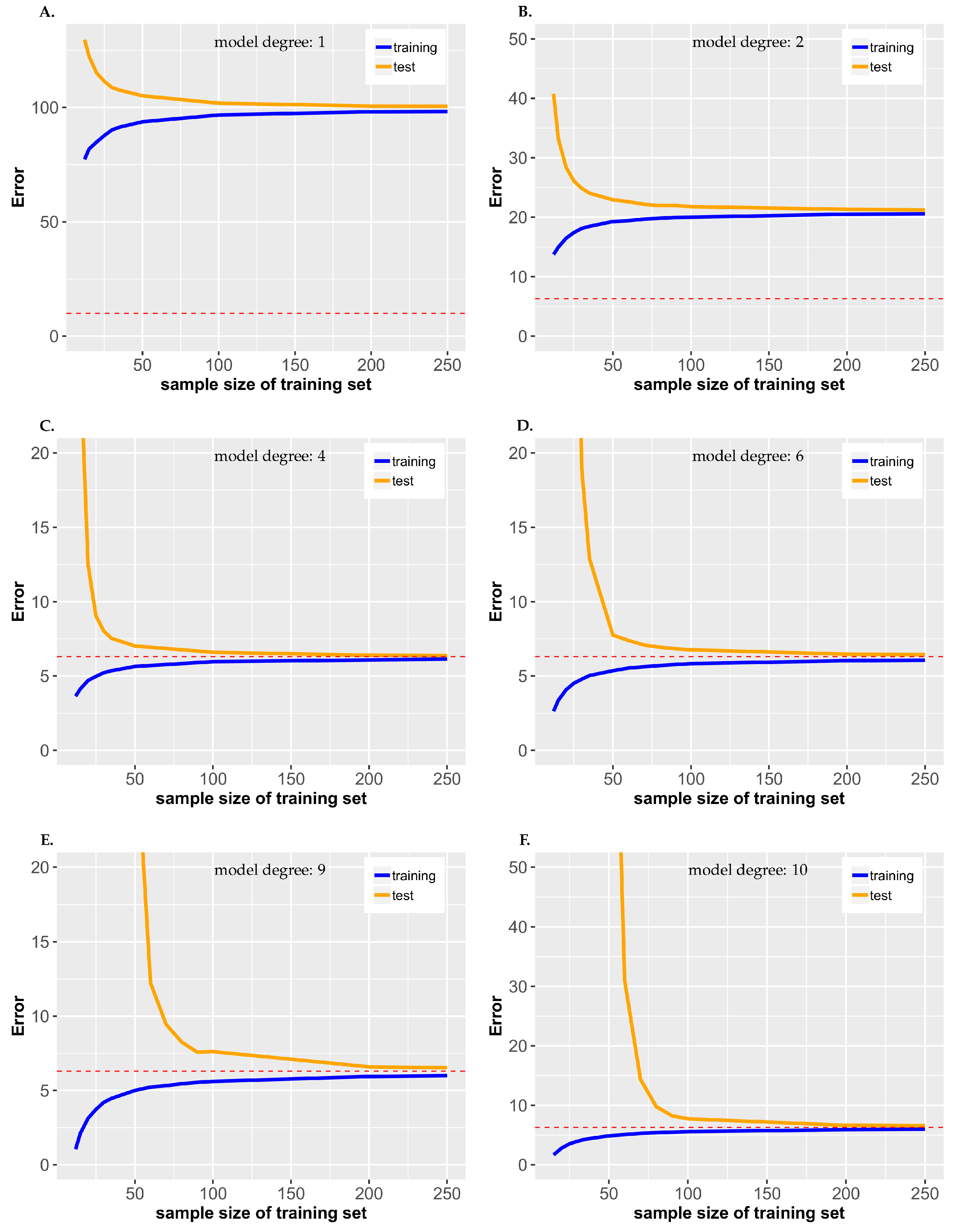
In
Figure 6, we show results for the linear polynomial regression models discussed earlier. It is important to emphasize that each figure shows results for a fixed model complexity, but varying sample sizes of the training data. This is in contrast to the results shown earlier (see
Figure 3) which varied the model complexity but kept the sample size of the training data fixed. We show six examples for six different model degrees. The horizontal red dashed line corresponds to the optimal error
attainable by the model family. The first two examples (
Figure 6A,B) are qualitatively different to all others because neither the training nor the test error converge to
, yet are much higher. This is due to a high bias of the models, because these models are too simple for the data.
Figure 6E exhibits some different extreme behavior. Here, for sample sizes of the training data smaller than
, one can obtain very high test errors and a large difference to the training error. This is due to a high variance of the models, because those models are too complex for the data. In contrast,
Figure 6C shows results for
which are the best results obtainable for this model family and the data.
In general, learning curves can be used to answer the following two questions:
For (1): The learning curves can be used to predict the benefits one can obtain from increasing the number of samples in the training data.
If the curve is still changing (increasing for training error and decreasing for test error) rapidly → need larger sample size;
If the curve is completely flattened out → sample size is sufficient;
If the curve is gradually changing → a much larger sample size is needed.
This assessment is based on evaluating the tangent of a learning curve toward the highest available sample size.
For (2): In order to study this point, one needs to generate several learning curves for models of different complexity. From this, one obtains information about the smallest attainable test error. In the following, we call this the optimal attainable error .
For a specific model, one can evaluate its learning curves as follows.
A model has high bias if the training and test error converge to a value much larger than . In this case, increasing the sample size of the training data will not improve the results. This indicates an underfitting of the data because the model is too simple. In order to improve this, one needs to increase the complexity of the model.
A model has high variance if the training and test error are quite different from each other, with a large gap between both. Here, a gap is defined as for sample size n of the training data. In this case, the training data are fitted much better than the test data, indicating problems with the generalization capabilities of the model. In order to improve the sample size of the training data, needs to be increased.
These assessments are based on evaluating the gap between the test error and the training error toward the highest available sample size of the training data.
7.2. Idealized Learning Curves
In
Figure 7, we show idealized learning curves for the four cases one obtains from combining high/low bias and high/low variance with each other. Specifically, the first/second column shows low/high bias cases, and the first/second row shows low/high variance cases.
Figure 7A shows the ideal case when the model has a low bias and a low variance. In this case, the training and test error both converge to the optimal attainable error
that is shown as a dashed red line.
In
Figure 7B, a model with a high bias and a low variance is shown. In this case, the training and test error both converge to values that are distinct from the optimal attainable error, and an increase in the sample size of the training data will not solve this problem. The small gap between the training and test error is indicative of a low variance. A way to improve the performance is to increase the model complexity, such as by allowing more free parameters or boosting approaches. This case is the ideal example for an
underfitting model.
In
Figure 7C, a model with a low bias and a high variance is shown. In this case, the training and test error both converge to the optimal attainable error. However, the gap between the training and test error is large, indicating a high variance. In order to reduce this variance, the sample size of the training data needs to be increased to possibly much larger values. Also, the model complexity can be reduced, such as by regularization or bagging approaches. This case is the ideal example for an
overfitting model.
In
Figure 7D, a model with a high bias and a high variance is shown. This is the worst-case scenario. In order to improve the performance, one needs to increase the model complexity and possibly the sample size of the training data. This means improving such a model is the most demanding case.
Also, the learning curves allow an evaluation of the generalization capabilities of a model. Only the low variance cases have a small distance between the test error and the training error, indicating the model has good generalization capabilities. Hence, a model with low variance generally has good generalization capabilities, irrespective of the bias. However, models with a high bias perform badly, and may only be considered in exceptional situations.
8. Summary
In this paper, we presented theoretical and practical aspects of model selection, model assessment, and model diagnosis [
75,
76,
77]. The error-complexity curves, the bias–variance tradeoff, and the learning curves provide means for a theoretical understanding of the core concepts. In order to utilize error-complexity curves and learning curves for a practical analysis, cross-validation offers a flexible approach to estimate the involved entities for general statistical models which are not limited to linear models.
In practical terms, model selection is the task of selecting the best statistical model from a model family, given a data set. Possible model selection problems include, but are not limited to:
Selecting predictor variables for linear regression models;
Selecting among different regularization models, such as ridge regression, LASSO, or elastic net;
Selecting the best classification method from a list of candidates, such as random forest, logistic regression, or the support vector machine of neural networks;
Selecting the number of neurons and hidden layers in neural networks.
The general problems one tries to counteract with model selection are overfitting and underfitting of data.
An underfitting model: Such a model is characterized by high bias, low variance, and poor test error. In general, such a model is too simple;
The best model: For such a model, the bias and variance are balanced and the test error makes good predictions;
An overfitting model: Such a model is characterized by low bias, high variance, and poor test error. In general, such a model is too complex.
It is important to realize that these terms are defined for a given data set with a certain sample size. Specifically, the error-complexity curves are estimated from training data with a fixed sample size and, hence, these curves can change if the sample size changes. In contrast, the learning curves investigate the dependency on the sample size of the training data.
We also discussed more elegant methods for model selection, such as AIC or BIC; however, the applicability of these depends on the availability of the analytical results of models, such as about their maximum likelihood. Such results can usually be obtained for linear models, as discussed in our paper, but may not be known for more complex models. Hence, for practical applications, these methods are far less flexible than cross-validation.
The bias-variance tradeoff providing a frequentist view-point of model complexity is for practical problems, for which the true model is unknown, not accessible. Instead, it offers a conceptual framework to think about a problem theoretically. Interestingly, the balancing of bias and variance reflects the underlying philosophy of Ockham’s razor [
78], stating that from two similar models, the simpler one should be chosen. On the other hand, for simulations, the true model is known and the decomposition into noise, bias, and variance is feasible.
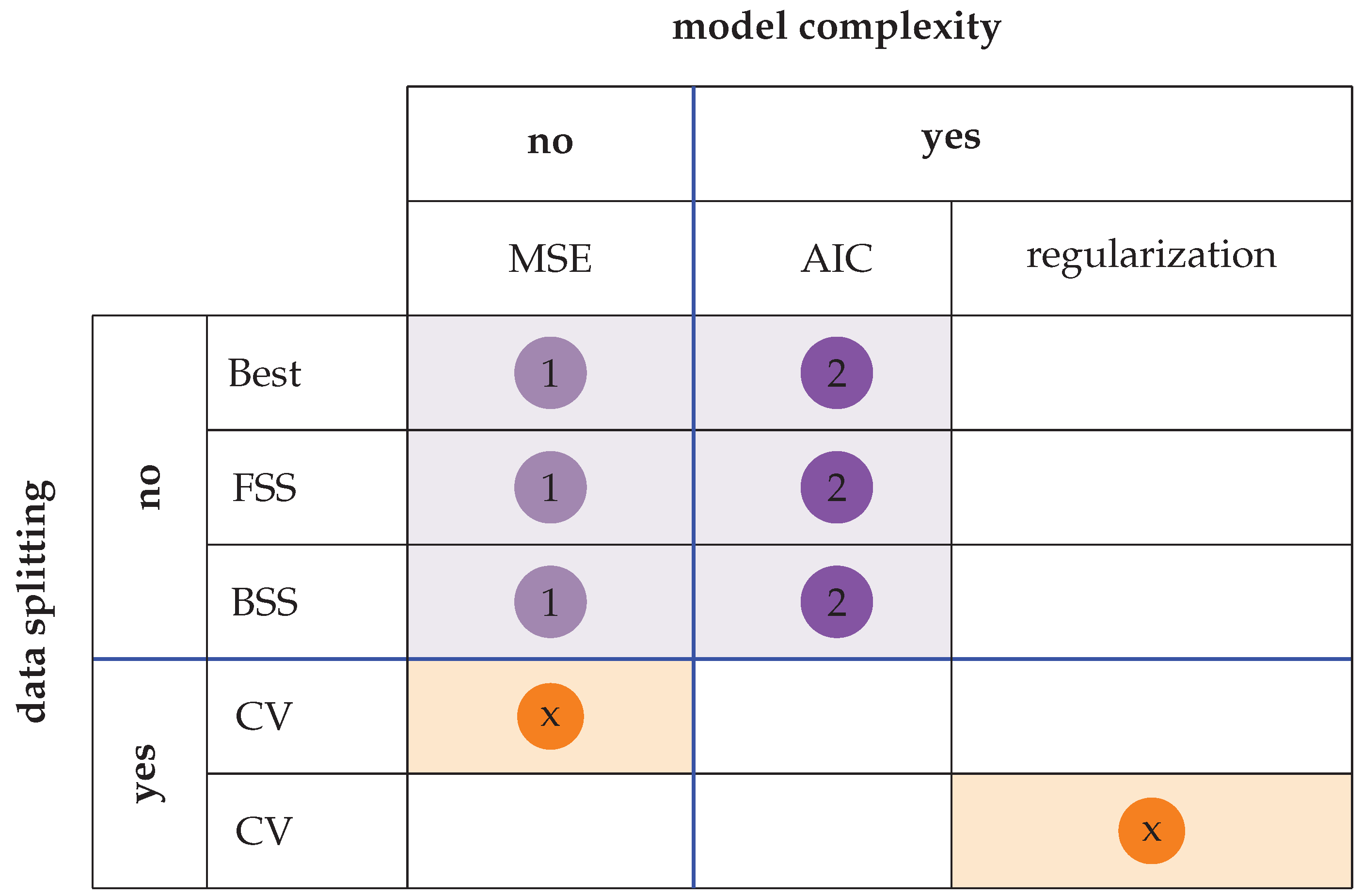
In
Figure 8 we summarize different model selection approaches. In this figure, we highlight two important characteristics of such methods. The first characteristic distinguishes methods regarding data-splitting, and the second regarding model complexity. Neither best subset selection (Best), forward stepwise selection (FSS), nor backward stepwise selection (BSS) apply data-splitting, but they use the entire data for evaluation. Furthermore, each of these approaches is a two-step procedure that employs, in its first step, a measure that does not consider the model complexity. For instance, either the MSE or
is used in this step. In the second step, a measure considering model complexity is used, such as AIC, BIC, or
.
Another class of model selection approaches uses data-splitting. Data-splitting is typically based on resampling of the data, and in this paper we focused on cross-validation. Interestingly, CV can be used without (MSE) or with (regularization) model complexity measures. Regularized regression models, such as ridge regression, LASSO, or elastic net, consider the complexity by varying the value of (regularization parameter).
In practice, the most flexible approach that can be applied to any type of statistical model is cross-validation. Assuming the computations can be completed within an acceptable time frame, it is advised to base the decisions for model selection and model assessment on the estimates of the error-complexity curves and the learning curves. Depending on the data and the model family, there can be technical issues which may require the application of other resampling methods in order to improve the quality of the estimates. However, it is important to emphasize that all of these issues are purely of numerical nature, not conceptual.
In summary, cross-validation, AIC, and all have the same goal—trying to find a model that predicts best. They all tend to choose similar models. On the other hand, BIC is quite different, and tends to choose smaller models. Also, its goal is different because it tries to identify the true model. In general, smaller models are easier to interpret, and obtain an understanding of the underlying process. Overall, cross-validation is the most general approach and can be used for parametric, as well as non-parametric models.
9. Conclusions
Data science is currently receiving much attention across various fields because of the big data-wave which is flooding all areas of science and our society [
79,
80,
81,
82,
83]. Model selection and model assessment are two important concepts when studying statistical inference, and every data scientist needs to be familiar with this in order to select the best model and to assess its prediction capabilities fairly in terms of the generalization error. Despite the importance of these topics, there is a remarkable lack of accessible reviews on the intermediate level in the literature. Given the interdisciplinary character of data science, this level is particularly needed for scientists interested in applications. We aimed to fill this gap with a particular focus on the clarity of the underlying theoretical framework and its practical realizations.