Recent Advances in Supervised Dimension Reduction: A Survey

Abstract

Recently, we have witnessed an explosive growth in both the quantity and dimension of data generated, which aggravates the high dimensionality challenge in tasks such as predictive modeling and decision support. Up to now, a large amount of unsupervised dimension reduction methods have been proposed and studied. However, there is no specific review focusing on the supervised dimension reduction problem. Most studies performed classification or regression after unsupervised dimension reduction methods. However, we recognize the following advantages if learning the low-dimensional representation and the classification/regression model simultaneously: high accuracy and effective representation. Considering classification or regression as being the main goal of dimension reduction, the purpose of this paper is to summarize and organize the current developments in the field into three main classes: PCA-based, Non-negative Matrix Factorization (NMF)-based, and manifold-based supervised dimension reduction methods, as well as provide elaborated discussions on their advantages and disadvantages. Moreover, we outline a dozen open problems that can be further explored to advance the development of this topic.

1. Introduction

Currently, high-dimensional data are very common in the real world. For example, with the advance of the next generation sequencing technique, millions of SNPs (Single Nucleotide Polymorphisms) can be obtained in the Human Genome Project (HGP). Another example is digital images: a 1024 × 1024 image amounts to a 1,048,576-dimensional vector when concatenating rows or columns. In fact, high dimensionality frequently appears in time series data, medical data, and sensor data. Although the data dimension is high, often, only a small amount of key factors are important for a particular modeling task. For instance, often, up to a few hundred SNPs are implicated in a certain disease phenotype, yet the majority of the millions of other SNPs have little association with that disease [1,2,3]. How to identify the important variables or features and help further analysis is a fundamental problem in machine learning and many other application fields. Dimension reduction is the main topic related to this problem, and it refers to the transformation of high-dimensional data to a low-dimensional representation. Feature selection and feature extraction are two popular techniques to implement dimension reduction. Feature selection aims to select an effective subset of the existing variables [4,5], while feature extraction learns a low-dimensional combination of the existing variables [6]. Feature selection is very important in some applications such as identifying a few disease-associated SNPs across the genome. The Least Absolute Shrinkage and Selection Operator (LASSO) is a typical example of a feature selection technique. Compared with feature selection, feature extraction has attracted more attention in the past several decades, and numerous branches have seen extensive development, including Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), Non-negative Matrix Factorization (NMF), the Laplacian Eigenmap (LE), Locally Linear Embedding (LLE), etc.

Most of the general dimension reduction methods belong to the unsupervised learning category because no label information is used. The other two traditional machine learning categories are supervised learning and semi-supervised learning, which use all or a part of the label information. In most real applications, dimension reduction is just an intermediate step toward the final goals, like classification or regression. Separating the dimension reduction and model learning may not be optimal for classification or regression. For example, in the task of document classification, feature selection or feature extraction methods are used first to get a low-dimensional text representation, and then, a classifier is trained to make a prediction [7,8]. Lacking supervision, some important words may be filtered before training the classifier, which affects the final performance [9]. To tackle this problem, supervised dimension reduction methods have emerged and attracted growing attention.

Based on the underlying techniques adopted, we categorize the supervised dimension reduction methods into three classes: PCA-based, NMF-based, and manifold-based dimension reduction methods. Among them, most of PCA-based and NMF-based methods are linear methods, while most of manifold-based methods are non-linear methods. By analyzing the means of exploiting the label information, we find that there are two main ways: LDA and directly integrating the loss function for classification or regression. LDA minimizes the distance within class and maximizes the distance between classes. To integrate the loss function directly for classification or regression, the commonly-used loss functions (e.g., $L_2$ loss, $L_1$ loss, and hinge loss) are mainly adopted in logistic regression, Support Vector Machine (SVM), linear regression, polynomial regression, etc. We will elaborate on them in the subsequent sections.

In the past few decades, dimension reduction had been extensively explored, and several reviews [10,11,12,13,14,15,16,17] on dimension reduction already exist. However, different from those that mainly reviewed existing unsupervised dimension reduction methods, our review focuses on the supervised dimension reduction. To the best of our knowledge, this is the first review to target this direction. We provide a taxonomy to systematically categorize the methods and list important open problems to guide the further development of this topic. Due to the greater popularity of feature extraction compared with feature selection, in our paper, we mainly focus on feature extraction for supervised learning. With regard to feature selection for supervised learning, we refer the reader to [18].

In the rest of this paper, we provide a formal definition and the taxonomy of supervised dimension reduction in Section 2. In Section 3, we describe supervised dimension reduction methods and their three classes in more detail. Section 4 reviews the real-world applications in which supervised dimension reduction methods are used. In Section 5, several promising future directions that need further exploration are unfolded. Finally, we conclude in Section 6.

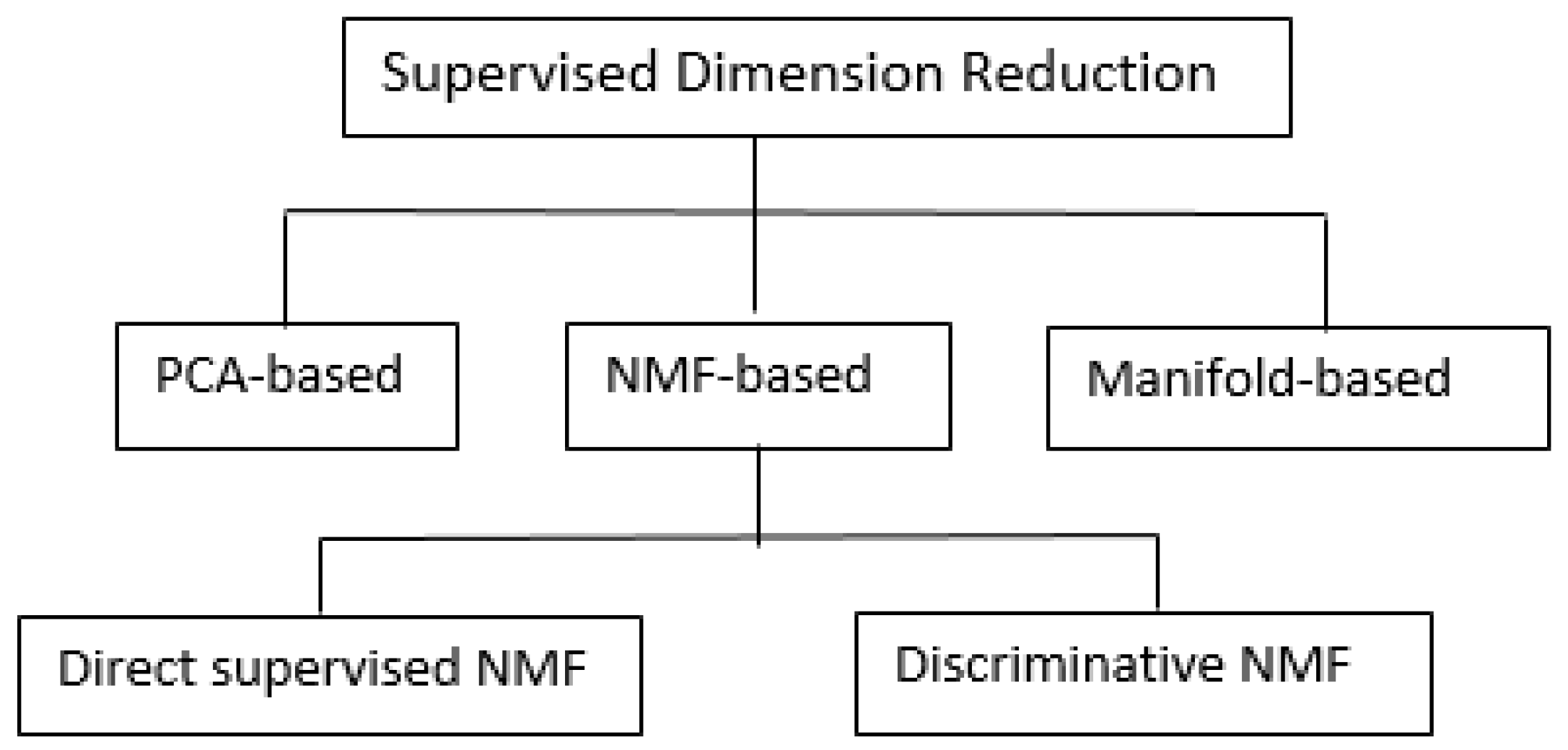
2. Definition and Taxonomy

Given the data matrix ${\mathit{X}}^{N\times D}$ and label vector ${\mathit{Y}}^N$, where N indicates the number of data points and D indicates the dimension of the data, general dimension reduction seeks for a representation ${\mathit{U}}^{N\times d}$ where $d<<D$, to keep as much information as possible. It is worth noting that different general dimension reduction methods retain the information under different assumptions. For example, PCA tries to keep the information by maximizing the variance, while LE aims to keep the manifold information. For supervised dimension reduction, the final result is still the low-dimensional representation ${\mathit{U}}^{N\times d}$, but this representation will be guided to predict the label ${\mathit{Y}}^N$ by using the label information during the dimension reduction process. Using the label information ${\mathit{Y}}^N$ is the main difference between supervised dimension reduction and unsupervised dimension reduction methods.

To obtain a whole picture of the existing supervised dimension reduction methods, we provide Figure 1 to show the taxonomy of supervised and semi-supervised dimension reduction techniques. For simplicity, afterwards, we will just use supervised dimension reduction to include supervised and semi-supervised dimension reduction. We categorize the existing supervised dimension reduction methods into three classes: PCA-based, NMF-based, and manifold-based methods. For NMF-based supervised dimension reduction methods, we further divide them into two subclasses based on the way of using label information.

3. Supervised Dimension Reduction

3.1. PCA-Based Supervised Dimension Reduction

PCA can be considered as the most popular dimension reduction technique. It tries to learn the orthogonal projection of the original data onto a lower dimensional linear space, known as the principal subspace, such that the variance of the projected data is maximized [19].

To help understanding, consider the projection to a one-dimensional space (d = 1). For convenience, the projection vector is defined as ${\mathit{u}}_1$ with the constraint ${\mathit{u}}_1^T{\mathit{u}}_1=1$. The mean of the projected data is ${\mathit{u}}_1^T\overline{\mathit{x}}$, where the sample mean is defined by:

$$\begin{array}{c}\hfill \overline{\mathit{x}}=\frac{1}{N}\sum _{i=1}^N{\mathit{x}}_i.\end{array}$$

(1)

The variance of the projected data is given by $\frac{1}{N}{\sum }_{i=1}^N{({\mathit{u}}_1^T{\mathit{x}}_i-{\mathit{u}}_1^T\overline{x})}^2={\mathit{u}}_1^T\mathit{S}{\mathit{u}}_1$, where $\mathit{S}$ is the data covariance matrix defined by:

$$\begin{array}{c}\hfill \mathit{S}=\frac{1}{N}\sum _{i=1}^N({\mathit{x}}_i-\overline{\mathit{x}}){({\mathit{x}}_i-\overline{\mathit{x}})}^T=\mathrm{Cov}\left(\mathit{X}\right).\end{array}$$

(2)

Now, PCA can be formulated as an optimization problem as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{{\mathit{u}}_1}{\max }{\mathit{u}}_1^T\mathit{S}{\mathit{u}}_1\\ {\mathit{u}}_1^T{\mathit{u}}_1=1.\end{array}\right.\end{array}$$

(3)

By introducing Lagrange multiplier ${\lambda }_1$ and setting the derivative of the Lagrange function with respect to ${\mathit{u}}_1$ equal to zero, we obtain:

$$\begin{array}{c}\hfill \mathit{S}{\mathit{u}}_1={\lambda }_1{\mathit{u}}_1,\end{array}$$

(4)

which shows that ${\mathit{u}}_1$ is the eigenvector of $\mathit{S}$. Left multiply the above equation by ${{\mathit{u}}_1}^T$, and use the constraint ${\mathit{u}}_1^T{u}_1=1$; the variance becomes:

$$\begin{array}{c}\hfill {\mathit{u}}_1^T\mathit{S}{\mathit{u}}_1={\lambda }_1.\end{array}$$

(5)

Therefore, when ${\mathit{u}}_1$ is set to the eigenvector corresponding to the largest eigenvalue, the variance of the data will be maximized, and this eigenvector is known as the first principal component. The subsequent principal components will be obtained by choosing a new direction that maximizes the projected variance among all possible directions orthogonal to those already considered. If d dimensional projection space is considered, the d eigenvectors ${\mathit{u}}_1,\cdots ,{\mathit{u}}_d$ of the data covariance matrix S corresponding to the d largest eigenvalues ${\lambda }_1,\cdots ,{\lambda }_d$ are the projection matrices we seek. Let $\mathit{U}=[{\mathit{u}}_1,\cdots ,{\mathit{u}}_d]$; $\mathit{X}\mathit{U}$ will be the low-dimensional representation. Note that in PCA-related methods, $\mathit{U}$ represents the projection matrix and is not the low-dimensional representation.

One heuristic to perform supervised PCA is to first select a subset of the original features based on their correlation with the label information and then apply the conventional PCA to the subset of the features to conduct dimension reduction [20]. In [21], an independence criterion named the Hilbert–Schmidt independence criterion [22] in Reproducing Kernel Hilbert Space (RKHS) is used to measure the dependence between the two variables $\mathcal{X}$ and $\mathcal{Y}$ by computing the Hilbert–Schmidt norm of the cross-covariance operator associated with their RKHSs.

Define two separable RKHSs $\mathcal{F}$ and $\mathcal{G}$ containing all continuous, bounded, and real-valued functions of x from $\mathcal{X}$ to $\mathbb{R}$ and y from $\mathcal{Y}$ to $\mathbb{R}$, respectively. Then, the cross-covariance between elements of $\mathcal{F}$ and $\mathcal{G}$ is $\mathrm{Cov}(f\left(x\right),g\left(y\right))={\mathbf{E}}_{x,y}\left[f\left(x\right)g\left(y\right)\right]-{\mathbf{E}}_x\left[f\left(x\right)\right]{\mathbf{E}}_y\left[g\left(y\right)\right]$. There is a unique linear operator $C_{x,y}:\mathcal{G}\to \mathcal{F}$ mapping elements of $\mathcal{G}$ to the elements of $\mathcal{F}$ such that $<f,C_{x,y}g>=\mathrm{Cov}(f\left(x\right),g\left(y\right))\forall f\in \mathcal{F},\forall g\in \mathcal{G}$. According to [23], this operator can be defined as $C_{x,y}={\mathbb{E}}_{x,y}[(\varphi \left(x\right)-{\mathbb{E}}_x\left[\varphi \left(x\right)\right])\otimes (\psi \left(y\right)-{\mathbb{E}}_y\left[\psi \left(y\right)\right])]$, where × indicates the tensor product and $\varphi$ and $\psi$ are the associated feature maps of $\mathcal{F}$ and $\mathcal{G}$, respectively.

Now, the Hilbert–Schmidt (HS) norm of this operator $C:\mathcal{G}\to \mathcal{F}$ is defined as ${∥C∥}_{HS}^2={\sum }_{i,j}<C{w}_i,h_j{>}_{\mathcal{F}}^2$ where $w_i$ and $h_j$ are orthogonal bases of $\mathcal{F}$ and $\mathcal{G}$, respectively. Assume $P_{\mathcal{X},\mathcal{Y}}$ is the joint distribution of variables $\mathcal{X}$ and $\mathcal{Y}$. HSIC, the square of the HS norm of the cross-covariance operator, can be expressed in terms of kernel functions as:

$$\begin{array}{c}\hfill \mathrm{HSIC}\left(P_{\mathcal{X},\mathcal{Y}}\right)={\mathit{E}}_{x,x^{\prime },y,y^{\prime }}\left[k(x,x^{\prime })l(y,y^{\prime })\right]+{\mathit{E}}_{x,x^{\prime }}\left[k(x,x^{\prime })\right]{\mathit{E}}_{y,y^{\prime }}\left[l(y,y^{\prime })\right]-2{\mathit{E}}_{x,y}\left[{\mathit{E}}_x^{\prime }\left[k(x,x^{\prime })\right]{\mathit{E}}_y^{\prime }\left[l(y,y^{\prime })\right]\right],\end{array}$$

(6)

where k and l are the associated kernel functions of $\mathcal{F}$ and $\mathcal{G}$, respectively. ${\mathit{E}}_{x,x^{\prime },y,y^{\prime }}$ indicates the expectation over independent pairs of $(x,y)$ and $(x^{\prime },y^{\prime })$ drawn from $P_{\mathcal{X},\mathcal{Y}}$. In real applications, we will use an empirical estimate of HSIC. Suppose data $\mathcal{Z}=(x_1,y_1),\cdots ,(x_N,y_N)\subset \mathcal{X}\times \mathcal{Y}$ are drawn independently from $P_{\mathcal{X},\mathcal{Y}}$. The empirical estimate of HSIC is given by:

$$\begin{array}{c}\hfill \mathrm{HSIC}\left(\mathcal{Z},\mathcal{F},\mathcal{G}\right)={(N-1)}^2\mathit{tr}\left(\mathit{K}\mathit{H}\mathit{L}\mathit{H}\right),\end{array}$$

(7)

where $\mathit{H},\mathit{K},\mathit{L}\in {\mathbf{R}}^{\mathbf{n}\times \mathbf{n}},K_{ij}=k(x_i,x_j),L_{ij}=l(y_i,y_j)$ and $\mathit{H}=\mathit{I}-N^{-1}\mathit{e}{\mathit{e}}^T$ is the centering matrix.

After introducing HSIC, we will introduce the supervised PCA method using HSIC. The problem is to seek for the subspace ${\mathit{U}}^T{\mathit{X}}^T$ such that the dependence between the projected data ${\mathit{U}}^T{\mathit{X}}^T$ and the label matrix $\mathit{Y}$ is maximized. It can be formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U}}{\max }\mathit{tr}\left(\mathit{K}\mathit{H}\mathit{L}\mathit{H}\right)=\mathit{tr}\left(\mathit{X}\mathit{U}{\mathit{U}}^T{\mathit{X}}^T\mathit{H}\mathit{L}\mathit{H}\right)=\mathit{tr}\left({\mathit{U}}^T{\mathit{X}}^T\mathit{H}\mathit{L}\mathit{H}\mathit{X}\mathit{U}\right)\\ s.t.{\mathit{U}}^T\mathit{U}=\mathit{I}.\end{array}\right.\end{array}$$

(8)

Obviously, this optimization problem has a closed-form solution. The eigenvectors $u_1,\cdots ,u_d$ corresponding to the d largest eigenvalues ${\lambda }_1,\cdots ,{\lambda }_d$ of the symmetric matrix ${\mathit{X}}^T\mathit{H}\mathit{L}\mathit{H}\mathit{X}$ form the optimal solution $\mathit{U}=[u_1,\cdots ,u_d]$. It is noted that when $\mathit{L}=\mathit{I}$, supervised PCA [21] degenerates to the traditional PCA.

Bin et al. [24] compared the supervised PCA with four traditional regression methods and illustrated the superiority of supervised PCA. Roberts and Martin [25] applied supervised PCA proposed in [20] to assess multiple pollutant effects. Yu et al. [26] proposed a supervised probabilistic PCA that possesses good interpretability and can handle missing values.

3.2. NMF-Based Supervised Dimension Reduction

NMF [27] aims to factorize the data matrix $\mathit{X}$ into two nonnegative matrices: one is the representation (coefficient) matrix ${\mathit{U}}^{N\times d}$ and the other one is the basis matrix ${\mathit{V}}^{d\times D}$. The general NMF is formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }\mathit{X}=\mathit{U}\mathit{V}\\ \mathit{U}\ge 0\mathit{V}\ge 0.\end{array}\right.\end{array}$$

(9)

NMF can be considered as approximating the true data matrix $\mathit{X}$ with data matrix $\mathit{Z}$, which exactly equals $\mathit{U}\mathit{V}$. Two main loss functions are adopted to measure the divergence between $\mathit{X}$ and $\mathit{Z}$; one is the Frobenius loss function, and the other one is the generalized Kullback–Leibler divergence (I-divergence [28]) function. Corresponding to these two loss functions, two NMF versions are formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }{∥\mathit{X}-\mathit{Z}∥}_F^2\\ \mathit{Z}=\mathit{U}\mathit{V}\\ \mathit{U}\ge 0\mathit{V}\ge 0,\end{array}\right.\end{array}$$

(10)

and:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }D\left(\mathit{X}\right|\left|\mathit{Z}\right)\\ \mathit{Z}=\mathit{U}\mathit{V}\\ \mathit{U}\ge 0\mathit{V}\ge 0,\end{array}\right.\end{array}$$

(11)

where $D\left(\mathit{X}\right|\left|\mathit{Z}\right)={\sum }_{ij}\left(X_{ij}\log \frac{X_{ij}}{Z_{ij}}+X_{ij}-Z_{ij}\right)$.

In [27], the authors approximated the data matrix $\mathit{X}$ that concatenates the pixel vectors from human face images. Each row of basis matrix ${\mathit{V}}^{d\times D}$ can be considered as a basis image, which represents part of the human image, while each row of representation matrix $U^{N\times d}$ is the coefficient we can use to reconstruct the original human face images. Normally, $d<<D$ indicates that representation matrix $U^{N\times d}$ is the desirable low-dimensional representation. To deal with outliers, Kong et al. [29] provided a robust NMF by enforcing the ${\ell }_{2,1}$ norm ${∥\mathit{X}-\mathit{U}\mathit{V}∥}_{2,1}={\sum }_{i=1}^N\sqrt[]{{\sum }_{j=1}^D{(\mathit{X}-\mathit{U}\mathit{V})}_{j,i}^2}$, which is not squared, and thus, the large errors due to outliers do not dominate the objective function. There are many algorithms to solve this problem, like the classical multiplicative updates [30], projected gradient descent [31], coordinate descent [32], and the Alternating Direction Method of Multipliers (ADMM) [33].

Based on the above NMF, two groups of supervised NMF methods are proposed according to the means of using the label information. The first group introduced the loss function involving the label information into the objective function, while the second group borrowed the idea of LDA to improve the prediction ability of the obtained low-dimensional representation. We call them direct supervised NMF and discriminative NMF, respectively.

3.2.1. Direct Supervised NMF

In supervised learning like classification and regression, the label information is exploited in loss functions. Common loss functions for regression include quadratic loss, mean absolute error, and Huber loss, while common loss functions for classification include logistic loss, hinge loss, and KL divergence.

Lee et al. [34] integrated the quadratic loss into general NMF to form a semi-supervised NMF as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }{∥\mathit{W}\odot (\mathit{X}-\mathit{U}\mathit{V})∥}^2+\alpha {∥\mathit{W}\odot (\mathit{Y}-\mathit{U}\mathit{S})∥}^2\\ \mathit{U}\ge 0\mathit{V}\ge 0,\end{array}\right.\end{array}$$

(12)

where $\alpha$ indicates the trade-off parameter. Assuming the number of classes is C, $\mathit{Y}\in {\mathbb{R}}^{N\times C}$ denotes the label matrix. $\mathit{W}$ is the indicator matrix that indicates whether ${\mathit{Y}}_{ij}$ is observed, i.e.,

$${\mathit{W}}_{ij}=\left\{\begin{array}{cc}1\hfill & {\mathit{Y}}_{ij}\mathrm{is}\mathrm{observed}\hfill \\ 0\hfill & {\mathit{Y}}_{ij}\mathrm{is}\mathrm{missing}.\hfill \end{array}\right.$$

(13)

Based on [34], ref. [35] enforced an additional regularization to retain the difference of data points between different classes and formed their supervised NMF as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }{∥\mathit{X}-\mathit{U}\mathit{V}∥}^2+\alpha {∥\mathit{X}-\mathit{U}\mathit{S}∥}^2+\beta \mathrm{tr}({\mathit{U}}^T\Theta \mathit{U})\\ \mathit{U}\ge 0,\mathit{V}\ge 0,\Theta \ge 0,\end{array}\right.\end{array}$$

(14)

where $\Theta$ is an $N\times N$ matrix with each entry ${\Theta }_{ij}$ equaling one if $y_i=y_j$ or zero otherwise, for $i,j=1,\cdots ,N$. $\beta$ is the trade-off parameter. The introduction of the third item is to make the low-dimensional representations of data points in different classes differ greatly.

In order to combine NMF and the Support Vector Machine (SVM) classifier, Gupta and Xiao [36] proposed the general formulation for this problem as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V},\mathit{w}}{\min }{∥\mathit{X}-\mathit{U}\mathit{V}∥}^2+\left(\left.∥\mathit{w}\right|{\parallel }^2+C\sum _{i=1}^{N}L(y_i,{\mathit{w}}^T{\mathit{u}}_i+w_0)\right)\\ s.t.\mathit{U}\in {\mathcal{R}}_{+}^{N\times d},\mathit{V}\in {\mathbb{R}}_{+}^{d\times D},\mathit{w}\in {\mathbb{R}}^{d\times 1},y_i\in \{+1,-1\}\forall i,w_0\in \mathbb{R}\end{array}\right.\end{array}$$

(15)

where $(\mathit{X},\mathit{Y})$ are the original data matrix and label vector. $\mathit{Y}$ is composed of $y_i,i=1,\cdots ,N$. $\mathit{V}$ is the basis matrix. $\mathit{U}$ is the coefficient matrix. ${\mathit{u}}_i$ is each row of $\mathit{U}$. $L(·,·)$ is the loss function for the classifier. $\mathit{w}$ and $w_0$ are the weight parameters and bias of the classifier, respectively. This type of supervised NMF can be considered as transforming the classification task from domain $(\mathit{X},\mathit{Y})$ to $(\mathit{U},\mathit{Y})$. Gupta and Xiao [36] adopted the loss function $L(y,t)=\max {(0,1-yt)}^p$, and p is a hyperparameter. It can be seen that when the margin $yt$ is larger than one, there is no loss; this is a max-margin classifier. An alternative optimization strategy is then adopted to solve this problem.

Shu et al. [37] introduced multinomial loss into the framework (15) to deal with the multi-class classification problem. Chao et al. [38] integrated logistic loss and NMF into the unified framework explicitly and solved it with a projected gradient descent algorithm. They showed improved performance in predicting ICU 30-day mortality, compared with its unsupervised counterpart [39].

Mairal et al. [40,41] proposed a task-driven dictionary learning, which would become supervised NMF when requiring the dictionary and coefficient parameter to be nonnegative. Its main idea is integrating the dictionary learning and training of the classifier into a joint optimization problem, which is similar to that in [36]. Based on [41], Zhang et al. [42] enforced ${\ell }_1$ regularization to make the new method robust to noises. To solve the acoustic separation problem, Bisot et al. [43] and Sprechmann et al. [44] made a modification by classifying the mean of the projections to adapt to the specific task.

3.2.2. Discriminative NMF

LDA aims to find a transformation to maximize the between-class distance and minimize the within-class distance. It is obviously a way to utilize the label information, and this idea was firstly reflected in [45] to conduct supervised NMF.

Let $S_w$ and $S_b$ measure the within-class and between-class scatter, respectively. Suppose there are C classes, and let $n_i$ denote the number of vectors in the $i\mathrm{th}$ class.

$$\begin{array}{c}\hfill S_w=\frac{1}{C}\sum _{i=1}^C\frac{1}{n_i}\sum _{j=1}^{n_i}{({\mathit{u}}_j-{\mathit{m}}_i)}^T({\mathit{u}}_j-{\mathit{m}}_i)\end{array}$$

(16)

$$\begin{array}{c}\hfill S_b=\frac{1}{C(C-1)}\sum _{i,j=1}^C\sum _{j=1}^{n_i}{({\mathit{m}}_i-{\mathit{m}}_j)}^T({\mathit{m}}_i-{\mathit{m}}_j)\end{array}$$

(17)

where ${\mathit{m}}_i=\frac{1}{n_i}{\sum }_{j=1}^{n_i}{\mathit{u}}_j$ indicates the mean vector of class i in $\mathit{U}$.

Based on the above concepts, Fisher (LDA is also called Fisher LDA) NMF [45] is formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U},\mathit{V}}{\min }D\left(\mathit{X}\right|\left|\mathit{Z}\right)+\alpha S_w-\alpha S_b\\ \mathit{Z}=\mathit{U}\mathit{V}\\ \mathit{U}\ge 0\mathit{V}\ge 0,\end{array}\right.\end{array}$$

(18)

where $\alpha$ is the trade-off parameter. It can be noted that when $\alpha =0$, it becomes the unsupervised NMF.

With the same idea, Zafeiriou et al. [46] and Kotsia et al. [47] provided another approach by setting different weights to the between-class and within-class scatter items instead of the same weight like $\alpha$ in Equation (18). Guan et al. [48] and Lu et al. [49] added more desirable properties such as smooth or discriminative in the basis matrix to discriminant NMF. Vilamala et al. [50] and Lee et al. [51] successfully applied discriminative NMF to human brain tumor classification and emotion classification.

3.3. Manifold-Based Supervised Dimension Reduction

Manifold learning assumes that the high-dimensional data points have a low-dimensional manifold, and the task of manifold learning is to uncover this low-dimensional manifold. Manifold-based dimension reduction methods exploit the geometric properties of the manifold on which the data points are supposed to lie. Common manifold-based dimension reduction methods include Isomap [52], Locally Linear Embedding (LLE) [53], and Laplacian Eigenmap (LE) [54]. We will introduce the above unsupervised manifold-based dimension reduction methods and their corresponding supervised versions in the following three subsections.

3.3.1. Isomap-Based Supervised Dimension Reduction

An earlier classical dimension reduction method, Multidimensional Scaling (MDS) [55], just retains the Euclidean distance and does not consider the neighborhood distribution, so it cannot deal with the case where high-dimensional data points lie on or near a curved manifold, like the Swiss roll dataset [52]. To overcome this drawback, Isomap attempts to preserve the pairwise geodesic distance that is measured on the manifold. It can be considered as the extension of MDS. To facilitate the understanding of supervised Isomap, we display algorithms of MDS and Isomap in Algorithms 1 and 2, respectively.

Algorithm 1 MDS algorithm.

Input: Distance matrix $\mathit{D}\in {\mathbb{R}}^{N\times N},d$ 1. Calculate $\mathit{B}=-\frac{1}{2}\mathit{H}\mathit{D}\mathit{H}$, where $\mathit{H}=\mathit{I}-\frac{1}{N}\mathbf{1}{\mathbf{1}}^T$ is the centering matrix. 2. Conduct eigenvalue decomposition of $\mathit{B}:\mathit{B}\mathit{v}=\lambda \mathit{v}$. Output: $\mathit{U}=\mathit{V}{\Lambda }^{\frac{1}{2}}$; $\mathit{V}$ indicates the matrix of d eigenvectors, and $\mathit{\lambda }$ is a diagonal matrix with diagonal entries as the largest deigenvalues.

Algorithm 2 Isomap algorithm.

Input: $x_1,\cdots ,x_N\in {\mathbb{R}}^D$ 1. Construct a graph with edge weight ${\mathit{W}}_{ij}=\left||x_i-x_j\right||$ for points $x_i,x_j$ in the k-nearest neighborhood or $ϵ$-ball. 2. Compute the shortest distances between all pairs of points using Dijkstra’s or Floyd’s algorithm, and obtain the squares of the distances in matrix $\mathit{D}$. Output: MDS($\mathit{D}$).

The work in [56] was the first to explore supervised Isomap by combining the Isomap procedure with the nearest neighbor classifier. Two supervised Isomap methods named WeightedIso and Iso+Ada, which took into consideration the label information by modifying the transformation performed by Isomap, were proposed in [56]. By designing the dissimilarity measures to integrate the label information, Ribeiro et al. [57] proposed an enhanced supervised Isomap. The dissimilarity measure [58] involved is defined as:

$$\begin{array}{c}\hfill D(x_i,x_j)=\left\{\begin{array}{c}{((a-1)/a)}^{1/2}\mathrm{if}{c}_i=c_j\\ a^{1/2}-d_0\mathrm{if}{c}_i\ne c_j\end{array}\right.\end{array}$$

(19)

where $a=1/e^{-d_{ij}^2/\sigma }$ with $d_{ij}$ set to be any distance measure, $\sigma$ is a smoothing parameter, $d_0$ is a constant ($0\le d_0\le 1$), and $c_i,c_j$ are the data class labels. The between-class dissimilarity is larger than the within-class dissimilarity, conferring a high discriminative power to this method.

Based on the above dissimilarity distance, the enhanced supervised Isomap is summarized in Algorithm 3.

Algorithm 3 Enhanced supervised Isomap.

Input: ${\mathit{x}}_1,\cdots ,{\mathit{x}}_N\in {\mathbb{R}}^D,k,c_i,i=1,2$ 1. Compute the dissimilarity matrix using label information from Equation (19). 2. Run Isomap in Algorithm 2 to obtain low embedding map $\mathit{U}$. 3. Learn the embedded mapping $\mathit{D}$ to construct dissimilarity kernels. 4. SVM tests on new points. Output: $\mathit{D}$

Li and Guo [59] not only obtained explicit mapping from high-dimensional space to low-dimensional space during supervised Isomap learning, but also adopted geodesic distance instead of Euclidean distance to make this Isomap robust to noise. To exploit the labeled and unlabeled data points, Zhang et al. [60] provided a semi-supervised Isomap by mining the pairwise within-class distances in the same manifold and maximizing the distances between different manifolds.

3.3.2. LLE-Based Supervised Dimension Reduction

In contrast with Isomap, which retains the global structure property, LLE attempts to preserve the local structure property. It assumes that each data point in the original space can be represented as a linear combination of their nearest neighbors, and it tries to look for the low-dimensional representations of these data points to keep this linear combination property.

Suppose that a data point ${\mathit{x}}_i$ can be written as a linear combination $w_{ij}$ of its k nearest neighbors ${\mathit{x}}_j$. Note that the k nearest neighbors are identified by ranking the dissimilarity matrix $\Delta$. The LLE can be formulated as the following optimization problem.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U}}{\min }\sum _{i=1}^N{∥{\mathit{u}}_i-\sum _{j=1}^k{w}_{ij}{\mathit{u}}_j∥}^2\\ s.t.\frac{1}{N}{\mathit{U}}^T\mathit{U}=\mathit{I}.\end{array}\right.\end{array}$$

(20)

where $u^k$ indicates the k column of the solution matrix $\mathit{U}$. The constraint is enforced to avoid the trivial solution $\mathit{U}=\mathbf{0}$.

By modifying the dissimilarity, De Ridder and Duin [61] and De Ridder et al. [62] proposed the supervised LLE. The modified dissimilarity matrix ${\Delta }^{{}^{\prime }}=\Delta +\alpha \max (\Delta )$ where $0\le \alpha \le 1$, $\max (\Delta )$ is the maximum entry of $\Delta$ and ${\Lambda }_{ij}=1$ if ${\mathit{x}}_i$ and ${\mathit{x}}_j$ belong to the same class, and zero otherwise. Obviously, when $\alpha =0$, it becomes unsupervised LLE. When $\alpha =1$, it is the fully-supervised LLE, and when $0<\alpha <1$, it is the semi-supervised LLE. After modifying the dissimilarity matrix, all the subsequent steps are the same as for LLE.

Zhang [63] and Liu et al. [64] adopted the same idea that the between-class dissimilarity is larger than within-class dissimilarity to conduct supervised LLE. Moreover, Liu et al. [64] extended supervised LLE in tensor space to handle high order data to retain their structure information in each order. We can sum up that all these supervised LLE methods reflect the LDA idea.

3.3.3. LE-Based Supervised Dimension Reduction

LE [54] attempts to preserve the local neighborhood structure by using the Laplacian of the graph. The similarity matrix can be constructed by using Gaussian function $W_{ij}=exp(-\frac{\left||x_i-x_j\right|{|}^2}{\beta })$ where $i,j=1,\cdots ,N,\beta$ is a scale parameter that is usually set to the average of squared distances between all pairs. LE tries to seek the low-dimensional representation $u_i,i=1,\cdots ,N$ by minimizing $-\frac{1}{2}{\sum }_{i,j}\left||x_i-x_j\right|{|}^2{W}_{i,j}=\mathrm{tr}\left({\mathit{U}}^T\mathit{L}\mathit{U}\right)$. Therefore, LE can be formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U}}{\min }\mathrm{tr}\left({\mathit{U}}^T\mathit{L}\mathit{U}\right)\\ s.t.{\mathit{U}}^T\mathit{D}\mathit{U}=\mathit{I},\\ {\mathit{U}}^T\mathit{L}\mathit{e}=\mathbf{0}.\end{array}\right.\end{array}$$

(21)

where $\mathit{I}$ is the identity matrix and $\mathit{e}={(1,\cdots ,1)}^T$, $\mathit{D}$ is the diagonal matrix whose entries are column or row sums of similarity matrix $\mathit{W}$, $\mathit{L}=\mathit{D}-\mathit{W}$ is the Laplacian matrix, and $\mathit{U}$ is the low-dimensional matrix we seek. The two constraints in Equation (21) are used to avoid the trivial solutions $\mathit{U}=\mathbf{0}$ and $\mathit{U}=\mathit{e}$. Applying the Lagrange multiplier method and using the fact $\mathit{L}\mathit{e}=\mathbf{0}$, the solutions of Equation (21) can be obtained by forming a matrix by the eigenvectors corresponding to the smallest deigenvalues (excluding zero) of the generalized eigenvector problem as:

$$\begin{array}{c}\hfill \mathit{L}\mathit{u}=\lambda \mathit{D}\mathit{u}.\end{array}$$

(22)

In order to adapt LE for the classification task, borrowing the idea of LDA, Raducanu and Dornaika [65] proposed a supervised LE. By minimizing the margin between homogeneous data points and maximizing the margin between heterogeneous data points, supervised LE [65] exploited the label information well and learned the supervised low-dimensional representation finally. To define the margin, for each data point ${\mathit{x}}_i$, they defined two sets $N_w\left({\mathit{x}}_i\right)$ and $N_b\left({\mathit{x}}_i\right)$ to indicate the within-class neighbors and between-class neighbors with a similarity higher than the average one, respectively.

$$\begin{array}{c}\hfill N_w\left({\mathit{x}}_i\right)=\{{\mathit{x}}_j|y_j=y_i,\exp (-\frac{\left||x_i-x_j\right|{|}^2}{\beta })>AS\left({\mathit{x}}_i\right)\}\end{array}$$

(23)

$$\begin{array}{c}\hfill N_w\left({\mathit{x}}_i\right)=\{{\mathit{x}}_j|y_j{\ne }_i,\exp (-\frac{\left||x_i-x_j\right|{|}^2}{\beta })>AS\left({\mathit{x}}_i\right)\}\end{array}$$

(24)

where $AS\left({\mathit{x}}_i\right)=\frac{1}{N}{\sum }_{k=1}^N\exp (-\frac{\left||x_i-x_j\right|{|}^2}{\beta })$ indicates the average similarity of the sample ${\mathit{x}}_i$ to all the rest of the data points.

With these two sets defined, two weight matrices corresponding to Equations (23) and (24) are defined as:

$$\begin{array}{c}\hfill W_{w,ij}=\left\{\begin{array}{c}\exp (-\frac{\left||x_i-x_j\right|{|}^2}{\beta })\mathrm{if}{\mathit{x}}_j\in N_w\left({\mathit{x}}_i\right)\mathrm{or}{\mathit{x}}_i\in N_w\left({\mathit{x}}_j\right)\\ 0\mathrm{otherwise}\end{array}\right.\end{array}$$

(25)

$$\begin{array}{c}\hfill W_{w,ij}=\left\{\begin{array}{c}1\mathrm{if}{\mathit{x}}_j\in N_b\left({\mathit{x}}_i\right)\mathrm{or}{\mathit{x}}_i\in N_b\left({\mathit{x}}_j\right)\hfill \\ 0\mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(26)

To get the low-dimensional representation $\mathit{U}$, two objective functions can be optimized as follows:

$$\begin{array}{c}\hfill \min \frac{1}{2}\sum _{i,j}\left||{\mathit{u}}_i-{\mathit{u}}_j\right|{|}^2{W}_{w,ij}=\mathrm{tr}\left({\mathit{U}}^T{\mathit{L}}_w\mathit{U}\right)\end{array}$$

(27)

$$\begin{array}{c}\hfill \max \frac{1}{2}\sum _{i,j}\left||{\mathit{u}}_i-{\mathit{u}}_j\right|{|}^2{W}_{b,ij}=\mathrm{tr}\left({\mathit{U}}^T{\mathit{L}}_b\mathit{U}\right)\end{array}$$

(28)

where ${\mathit{L}}_w={\mathit{D}}_w-{\mathit{W}}_w$ and ${\mathit{L}}_b={\mathit{D}}_b-{\mathit{W}}_b$ indicate the corresponding Laplacians.

By merging the above two objective functions, the final optimization problem is formulated as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U}}{\max }\mathrm{tr}\left({\mathit{U}}^T{\mathit{L}}_b\mathit{U}\right)+(1-\gamma )\mathrm{tr}\left({\mathit{U}}^T{\mathit{L}}_w\mathit{U}\right)\\ s.t.{\mathit{U}}^T{\mathit{D}}_w\mathit{U}=\mathit{I}.\end{array}\right.\end{array}$$

(29)

By defining matrix $\mathit{B}=\gamma {\mathit{L}}_b+(1-\gamma ){\mathit{W}}_w$, the above problem can be transformed as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underset{\mathit{U}}{\max }\mathrm{tr}\left({\mathit{U}}^T\mathit{B}\mathit{U}\right)\\ s.t.{\mathit{U}}^T{\mathit{D}}_w\mathit{U}=\mathit{I}.\end{array}\right.\end{array}$$

(30)

This formulation is easy to solve by the generalized eigenvalue problem.

Besides the above popular supervised LE method, Zheng et al. [66] explored another way to integrate the label information by optimizing the weight matrix using the labels after constructing the similarity matrix from local neighborhood relation. Wu et al. [67] proposed a deep learning-based supervised LE method whose deep architecture consists of multiple stacked layers and computes an intermediate representation that is fed to a nearest-neighbor classifier. Jiang and Jia [68] integrated the label information into the process of constructing the dissimilarity matrix, and the other steps are the same as for the general LE.

3.4. Discussion

In the three introduced classes of supervised or semi-supervised dimension reduction methods, supervised NMF has been successfully applied in computer vision and speech recognition, because NMF has a very good interpretability due to its non-negativity property. PCA-based methods can be used in all the classification or regression problems, but their performance may not be as competitive as NMF-based methods in the computer vision and speech recognition fields. Manifold-based methods assume that the data points are located in a low-dimensional manifold or each data point can be represented as the linear combination of its neighbors; thus, they are not as general as PCA-based method, but more general than NMF-based methods. In addition, manifold-based methods are normally time consuming due to the inverse of the Laplacian matrix. In summary, from the perspective of generality, the three classes of supervised or semi-supervised methods are ranked as PCA-based methods, manifold-based methods, and then, NMF-based methods.

4. Application

Supervised dimension reduction has been successfully applied to a variety of applications including computer vision, biomedical informatics, speech recognition, visualization, etc.

4.1. Computer Vision

From the inception of NMF [27], it had been successfully applied to face recognition due to its ability to produce interpretable bases. Naturally, Face recognition becomes the typically successful application of supervised NMF. Discriminative NMFs [46,47,69] are the earlier successful attempts of supervised NMF methods at face recognition, and then, many direct NMF methods [35,36,37,70] also demonstrated superior performance in this task.

Apart from face recognition, all this object or action recognition also involves the application of supervised dimension reduction. Wu et al. [67] proposed a supervised Laplacian eigenmap to recognize visual objects. Kumar [71] adopted supervised dictionary learning to recognize the actions and locations of the objects in the images. Santiago-Mozos et al. [72] applied supervised PCA to object detection in infrared images and demonstrated good performance. Recently, Xinfang et al. [73] proposed a semi-supervised local discriminant analysis by combing the idea of LDA and LLE for polarimetric SAR image classification.

4.2. Biomedical Informatics

In bioinformatics, especially genetics, due to the large amount of gene markers, it is challenging to identify the true gene marker that results in a certain disease directly. Two tough goals, high dimension and classification, should be simultaneously tackled; thus, supervised dimension reduction becomes the ideal choice. Zhang et al. [74] proposed a semi-supervised projective NMF method for cancer classification. Gaujoux and Seoighe [75] adopted another semi-supervised NMF method for gene expression deconvolution. Supervised PCA [76] was successfully applied to gene set analysis, while supervised categorical PCA [77,78] was successfully applied in genome-wide association analyses. Moreover, supervised probabilistic PCA [26] performed rather well in gene classification.

In medical informatics, with the fast development of medical devices, a variety of features are collected in real applications. Inevitably, some noisy, redundant, or useless features are included, which hinders identifying certain diseases. How to identify the effective features for certain diseases is challenging, and supervised dimension reduction becomes a good option to solve this problem. Vilamala et al. [50] designed a discriminative NMF and successfully applied ti to human brain tumor classification. Chao et al. [38] proposed a supervised NMF by combing NMF and logistic regression and improved the ICU mortality prediction performance. Fuse et al. [79] combined NMF and SVM to diagnose Alzheimer’s disease and obtained an improved performance. Supervised PCA [20] has been successfully used in DNA microarray data analysis and cancer diagnosis. It is noted that the process of knowledge discovery in biomedical informatics is mostly performed by biomedical domain experts. This is mostly due to the high complexity of the research domain, which requires deep domain knowledge. At the same time, these domain experts face major obstacles in handling and analyzing their high-dimensional, heterogeneous, and complex research data. A recent work [80] outlined that ontology-centered data infrastructure for scientific research, which actively supports the medical domain experts in data acquisition, processing, and exploration, can be very beneficial here.

4.3. Speech Recognition

Speech recognition is another successful application of NMF, and thus, supervised NMF is naturally successfully used in this kind of application. Lee et al. [51] used discriminative NMF to classify the emotional difference in speech. Bisot et al. [43] applied supervised NMF to acoustic scene classification and obtained rather good performance. Sprechmann et al. [44] and Weninger et al. [81] solved the audio source separation with supervised NMF, while Nakajima et al. [82] and Kitamura et al. [83] adopted supervised NMF for music signal separation.

Although there exist an amount of successful applications in speech recognition, more attempts can be made in the future. As we can see that almost all of the existing supervised dimension reduction methods are NMF-based, both PCA-based and manifold-based methods can be investigated and compared with the existing methods.

4.4. Visualization

High-dimensional data are hard to explain. Take the ICU mortality prediction problem [38] as an example: there are many vital sign features, and it is difficult to interpret them individually due to the high dimensionality. As far as we know, biomedical experts are increasingly confronted with complex high-dimensional data. As the number of dimensions is often very large, one needs to map them to a smaller number of relevant dimensions to be more amenable to expert analysis. This is because irrelevant, redundant, and conflicting dimensions can negatively affect the effectiveness and efficiency of the analytic process. This is also the so-called curse of dimensionality problem. To deal with this problem, dimension reduction is a possible means, but the possible mappings from high- to low-dimensional spaces are ambiguous. Subspace analysis [84,85] can be used to seek solutions. Since high-dimensional data are difficult to interpret, a rough picture of the data is quite helpful; thus, visualization is very important, and it is also an important application of supervised dimension reduction. Barshan et al. [21] provided a supervised PCA to conduct visualization, while Vlachos et al. [56] gave another supervised dimension reduction method by borrowing the LDA idea for visualization. Geng et al. [58] proposed a supervised Isomap to visualize. Compared with visualization from general unsupervised dimension reduction, visualization from supervised dimension reduction has clear separability due to its supervised learning property.

Apart from all the above applications, text mining is probably another good application of supervised dimension reduction. Although there are already many works [86,87,88] on unsupervised dimension reduction, there are few works on supervised dimension reduction.

5. Potential Future Research Issues

Although supervised dimension reduction has developed greatly and been successfully applied to many applications during the last two decades, there are still some challenging problems that need to be tackled in the future. Below, we unfold some important open problems worth further exploration.

5.1. Scalability

For PCA-based methods, the time complexity of covariance matrix computation is $O\left(D^{2}N\right)$, and that of its eigenvalue decomposition is $O\left(D^3\right)$. Therefore, the complexity of PCA is $O(D^{2}N+D^3)$. For NMF-based methods, some fast solving methods like the projected gradient descent method [31] do not work due to the additional objective function items, then the time complexity of its most time-costly part is $O\left(tNDd\right)$; t is the iteration numbers it needs to converge. For manifold-based methods, the time complexity of constructing the similarity matrix is $O\left(N^{2}D\right)$, and the frequently-used solving strategy is generalized eigenvalue decomposition; the time complexity is $O\left(D^3\right)$. One of the main goals of supervised dimension reduction is to solve high-dimensional problems, but when the feature dimension is high, the time costs of the existing supervised dimension reduction methods are still high, because some specifically-designed unsupervised dimension reduction methods do not work due to the appearance of new objective items or constraints on label information. When dataset is huge in sample size, like in social networks, there are millions of data points, and the time cost for supervised dimension reduction is still unacceptable. Therefore, some specific algorithms directed at supervised dimension reduction are urgently in need, especially due to the data explosion in this era.

5.2. Missing Values

Missing values are a common phenomenon in many applications due to a variety of factors like the failure of sensors in computer vision and missing certain laboratory test results over time for some patients in the clinical setting [89]. The existing strategy is imputation with zero, the mean, or the maximum value, or multiple imputation [90]. In order to tackle missing values, Lee et al. [34] introduced an auxiliary matrix to indicate whether the entry was missed or not. Obviously, no specific designs are involved in the supervised dimension reduction process. Some tricks to handle missing values like the E-M algorithm [91] can be considered to be incorporated into some supervised dimension reduction methods. In addition, multi-view information of the data has consensus, and they are complementary to each other [92,93,94], which can be the other direction to handle the missing value problem.

5.3. Heterogeneous Types

Data may contain heterogeneous types of features such as numerical, categorical, symbolic, ordinal features, etc. How to integrate different types of data together to perform supervised dimension reduction is a challenging problem. A natural way to handle this problem is to convert all of them to the categorical type. However, much information will be lost during this phase. For instance, the difference of the continuous values categorized into the same category is ignored [95]. Therefore, how to exploit the information within mixed data types is worth exploring in the future.

Besides the above three potential research issues, an emerging future research issue that will become very important in the future is the explanation part, and this will require supervised dimension reduction to make results from arbitrarily high-dimensional spaces understandable for a human, who can perceive information only in the lower dimensions. We can refer to the recent work [96] to learn about this direction. Apart from supervised dimension reduction, it is also intriguing to explore other ways to explain high-dimensional data well.

6. Conclusions

The field of supervised dimension reduction has seen extensive growth at an increasing rate. We have outlined the state-of-the-art research in this review by categorizing it into three main classes: PCA-based, NMF-based, and manifold-based supervised dimension reduction methods. To understand their characteristics better, we provide a discussion to elaborate their advantages and disadvantages. To advance the further development of this topic, we also list some open problems waiting for analytical study in the future. This review will be helpful for researchers who want to develop advanced supervised dimension reduction methods or who seek methods to learn low-dimensional representation for certain supervised learning applications. We believe that supervised dimension reduction will continue to remain an active area of study in the years to come, owing to an increase in the high-dimensional data and sustained community efforts. In addition, their tighter integration into specific application systems will continuously shape the emerging landscape and provide opportunities for researcher contribution.