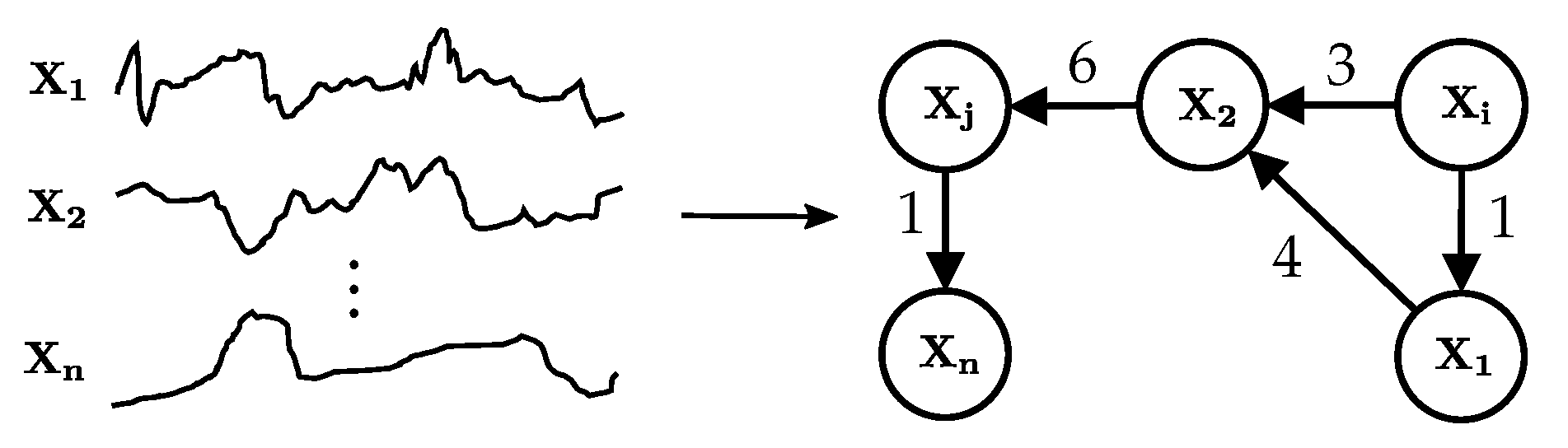
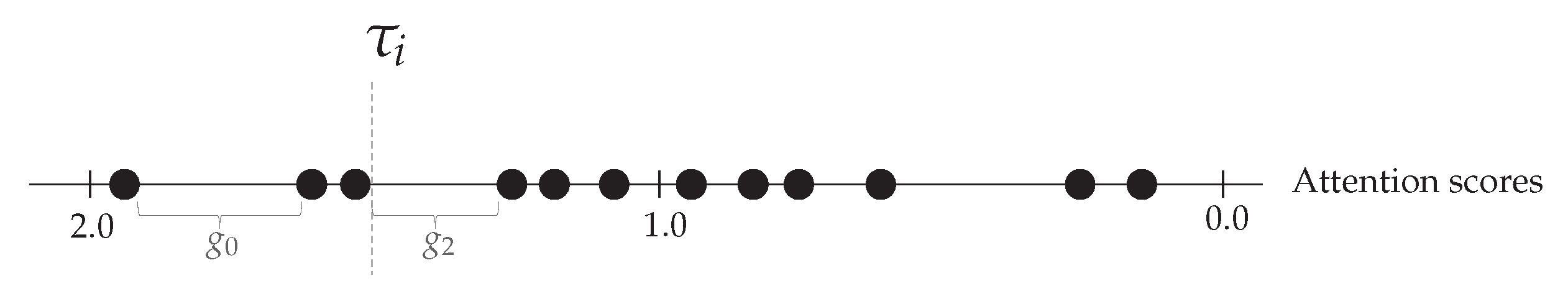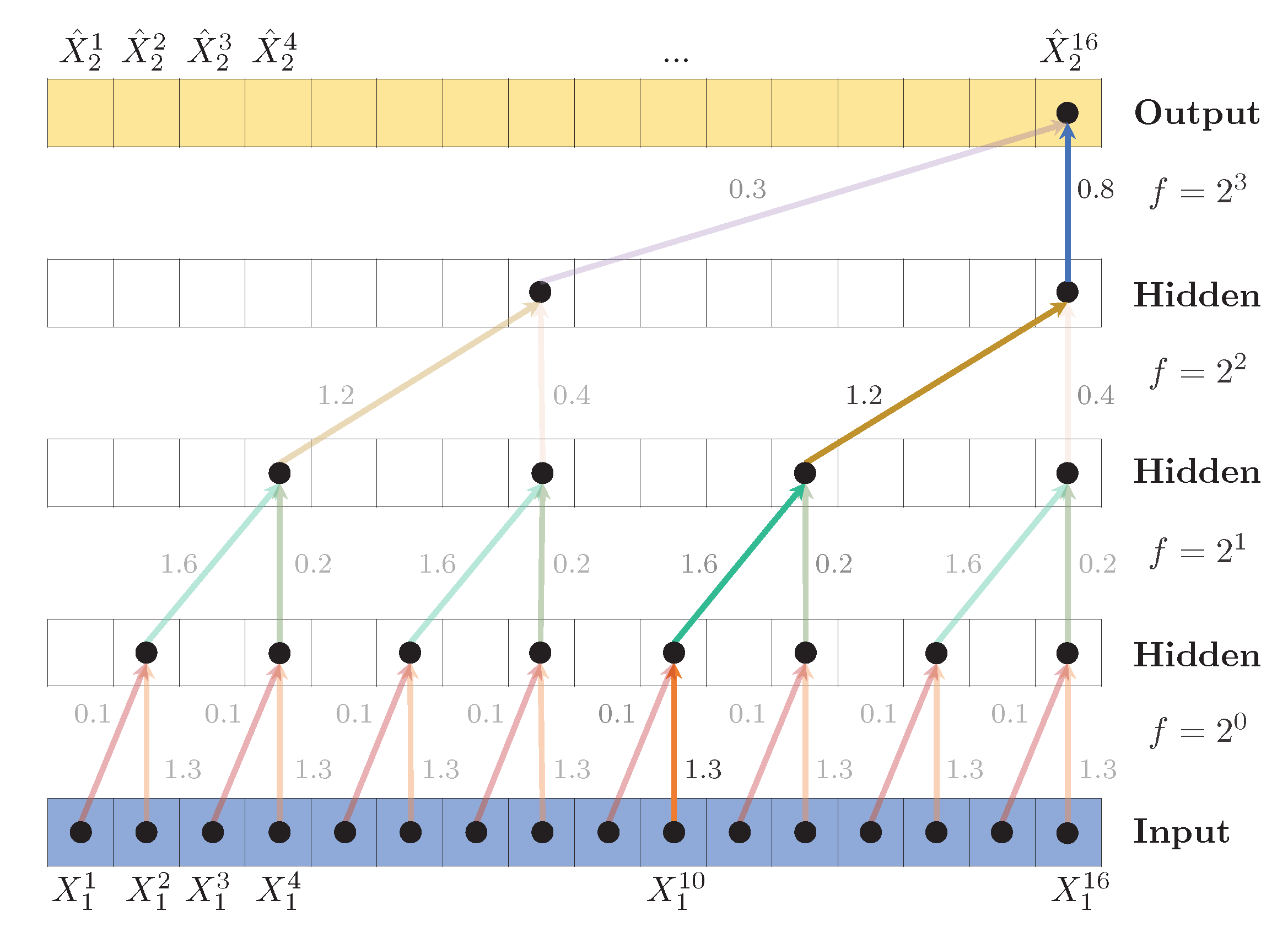Figure 1.
A temporal causal graph learnt from multivariate observational time series data. A graph node models one time series. A directed edge denotes a causal relationship and is annotated with the time delay between cause and effect.
Figure 1.
A temporal causal graph learnt from multivariate observational time series data. A graph node models one time series. A directed edge denotes a causal relationship and is annotated with the time delay between cause and effect.
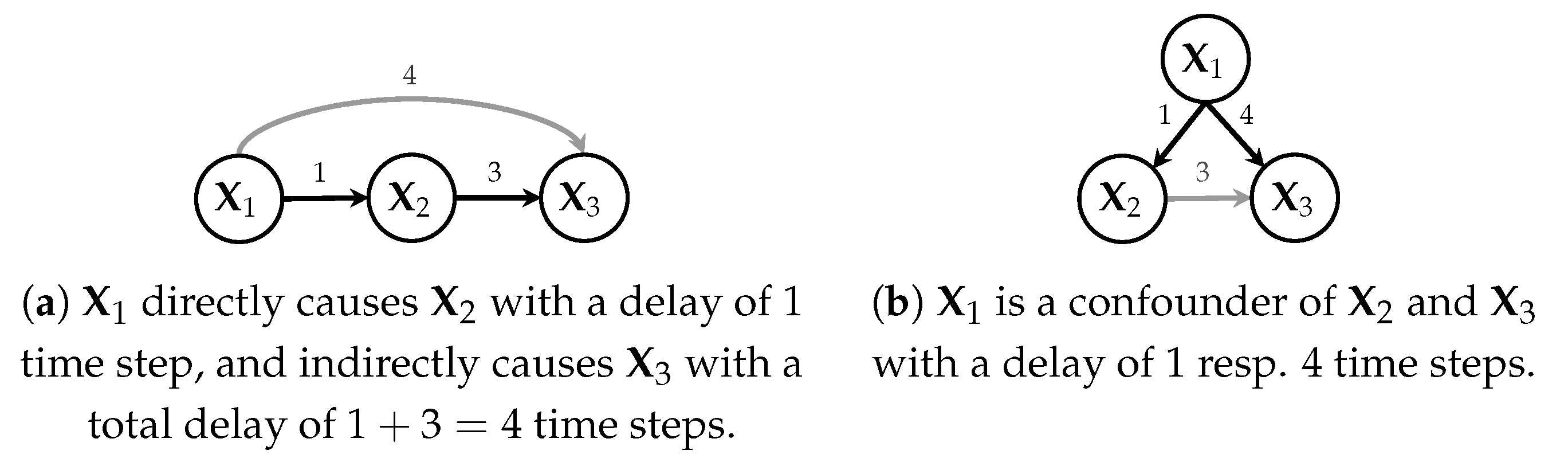
Figure 2.
Temporal causal graphs showing causal relationships and delays between cause and effect.
Figure 2.
Temporal causal graphs showing causal relationships and delays between cause and effect.
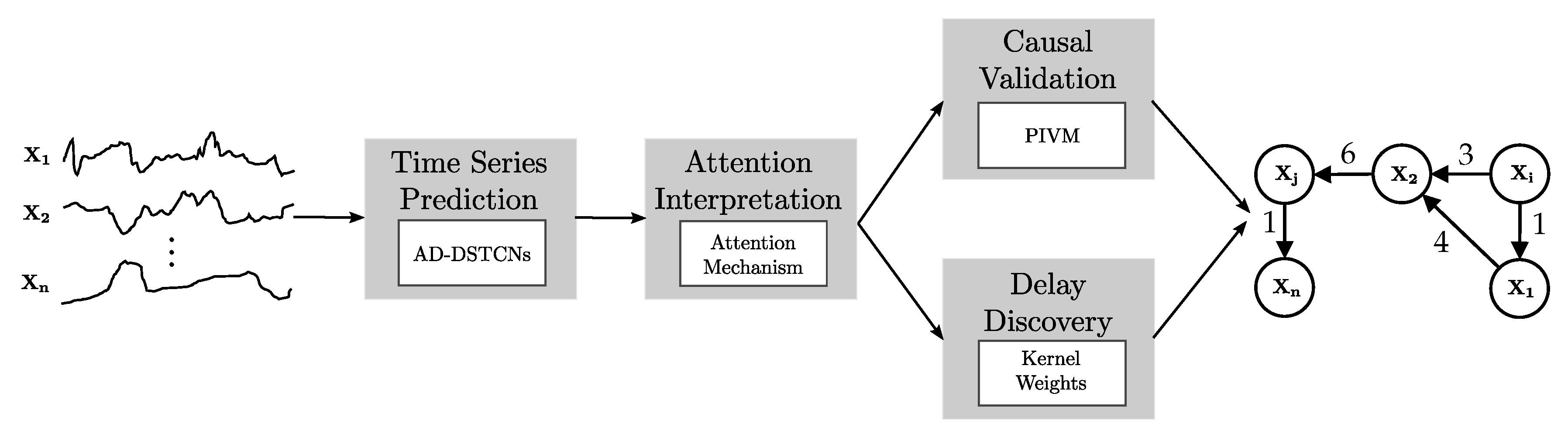
Figure 3.
Overview of Temporal Causal Discovery Framework (TCDF). With time series data as input, TCDF performs four steps (gray boxes) using the technique described in the white box and outputs a temporal causal graph.
Figure 3.
Overview of Temporal Causal Discovery Framework (TCDF). With time series data as input, TCDF performs four steps (gray boxes) using the technique described in the white box and outputs a temporal causal graph.
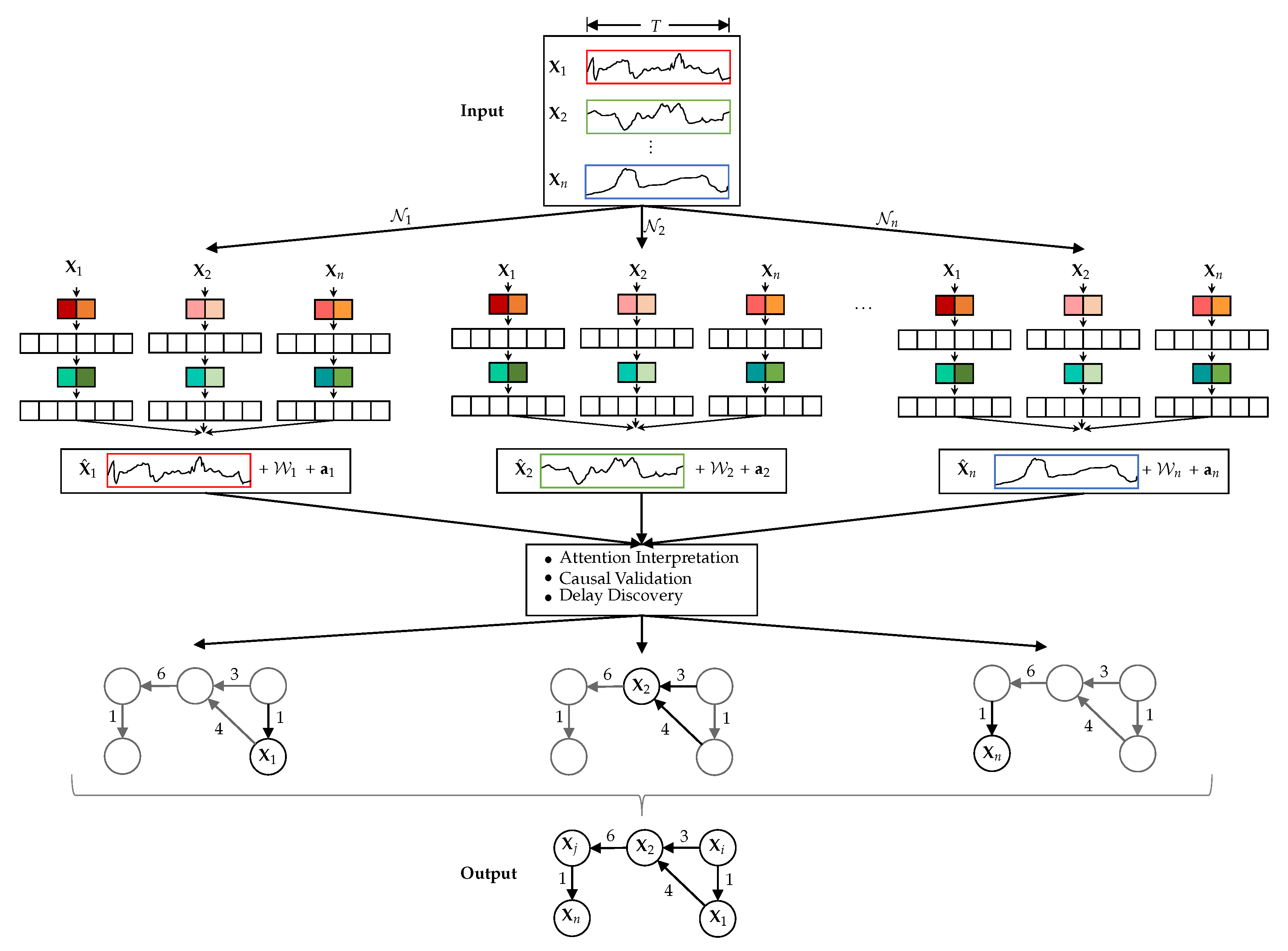
Figure 4.
TCDF with N independent CNNs …, all having time series … of length T as input (N is equal to the number of time series in the input data set). predicts and also outputs, besides , the kernel weights and attention scores . After attention interpretation, causal validation and delay discovery, TCDF constructs a temporal causal graph.
Figure 4.
TCDF with N independent CNNs …, all having time series … of length T as input (N is equal to the number of time series in the input data set). predicts and also outputs, besides , the kernel weights and attention scores . After attention interpretation, causal validation and delay discovery, TCDF constructs a temporal causal graph.
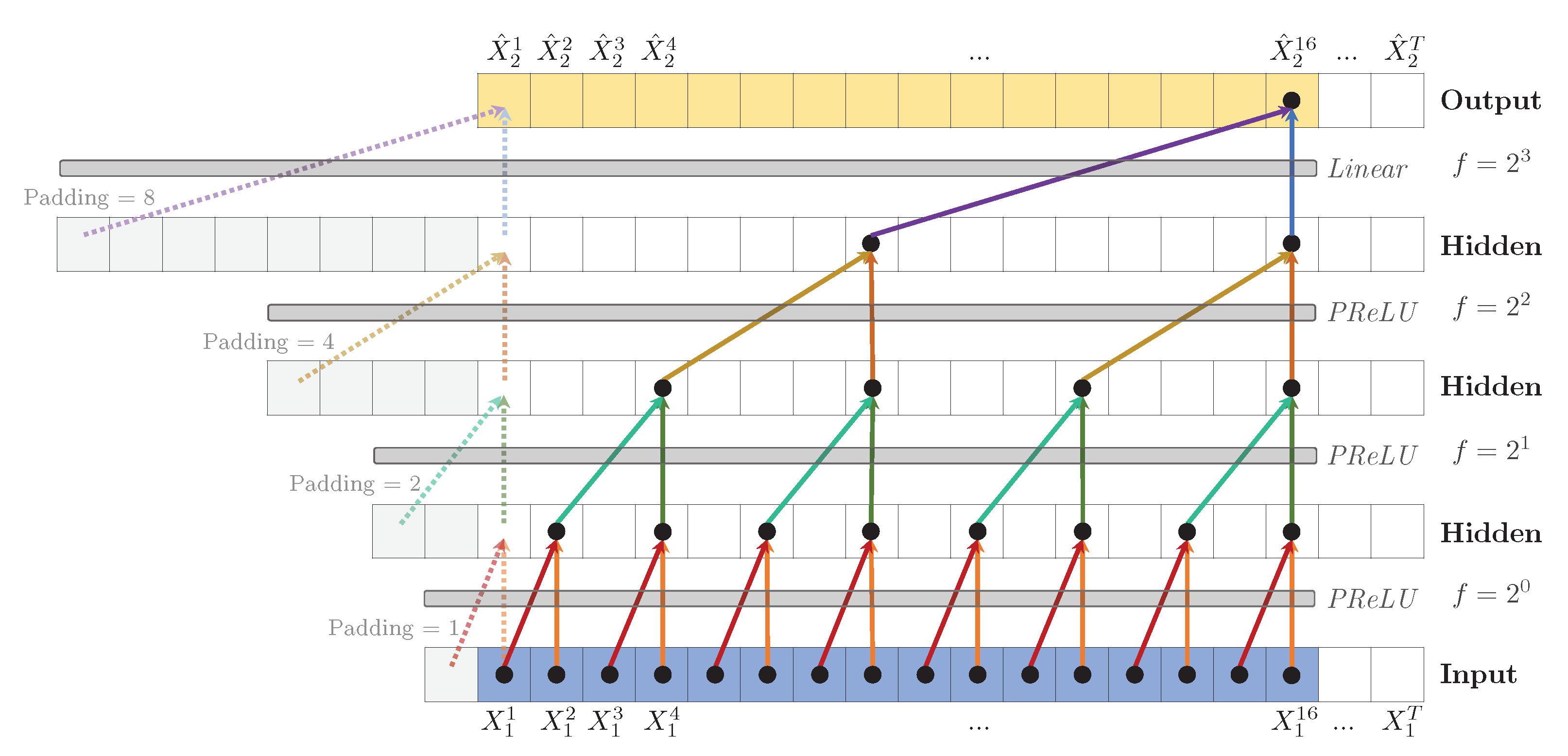
Figure 5.
Dilated TCN to predict , with hidden layers, kernel size (shown as arrows) and dilation coefficient , leading to a receptive field . A PReLU activation function is applied after each convolution. To predict the first values (shown as dashed arrows), zero padding is added to the left of the sequence. Weights are shared across layers, indicated by the identical colors.
Figure 5.
Dilated TCN to predict , with hidden layers, kernel size (shown as arrows) and dilation coefficient , leading to a receptive field . A PReLU activation function is applied after each convolution. To predict the first values (shown as dashed arrows), zero padding is added to the left of the sequence. Weights are shared across layers, indicated by the identical colors.
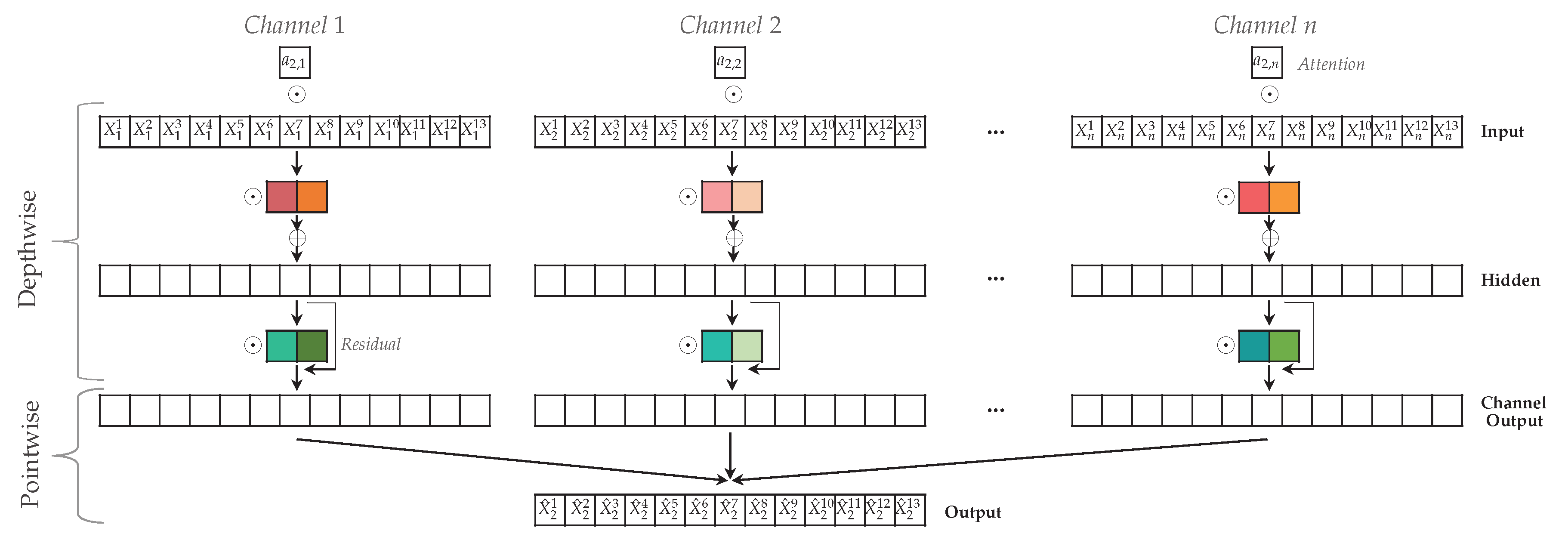
Figure 6.
Attention-based Dilated Depthwise Separable Temporal Convolutional Network to predict target time series . The N channels have time steps, hidden layer in the depthwise convolution and kernels with kernel size (denoted by colored blocks). The attention scores a are multiplied element-wise with the input time series, followed by an element-wise multiplication with the kernel. In the pointwise convolution, all channel outputs are combined to construct the prediction .
Figure 6.
Attention-based Dilated Depthwise Separable Temporal Convolutional Network to predict target time series . The N channels have time steps, hidden layer in the depthwise convolution and kernels with kernel size (denoted by colored blocks). The attention scores a are multiplied element-wise with the input time series, followed by an element-wise multiplication with the kernel. In the pointwise convolution, all channel outputs are combined to construct the prediction .
Figure 7.
Threshold is set equal to the attention score at the left side of the largest gap where and . In this example, is set equal to the third largest attention score.
Figure 7.
Threshold is set equal to the attention score at the left side of the largest gap where and . In this example, is set equal to the third largest attention score.
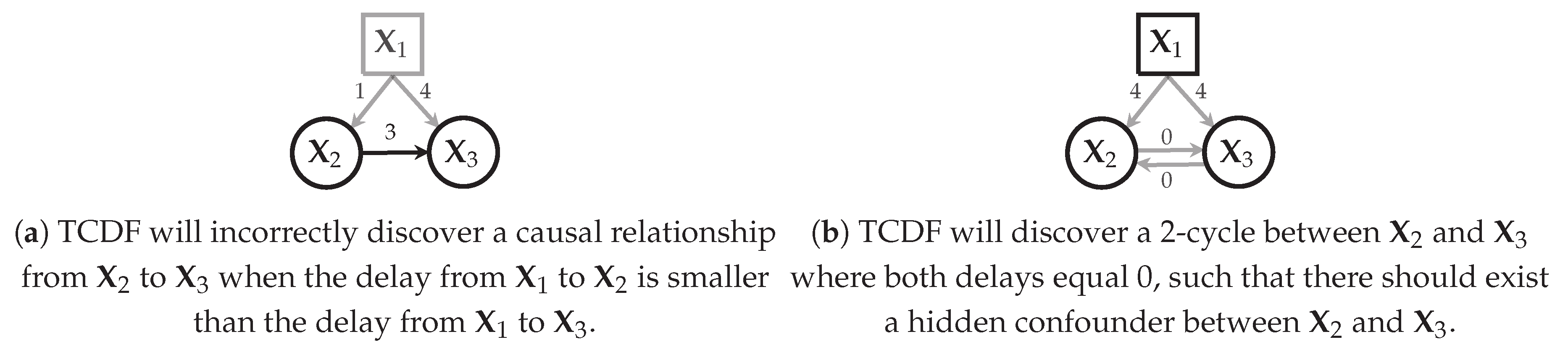
Figure 8.
How TCDF deals, in theory, with hidden confounders (denoted by squares). A black square indicates that the hidden confounder is discovered by TCDF; a grey square indicates that it is not discovered. Black edges indicate causal relationships that will be included in the learnt temporal causal graph ; grey edges will not be included in .
Figure 8.
How TCDF deals, in theory, with hidden confounders (denoted by squares). A black square indicates that the hidden confounder is discovered by TCDF; a grey square indicates that it is not discovered. Black edges indicate causal relationships that will be included in the learnt temporal causal graph ; grey edges will not be included in .
Figure 9.
Discovering the delay between cause and target , both having . Starting from the top convolutional layer, the algorithm traverses through the path with the highest kernel weights. Eventually, the algorithm ends in input value , indicating a delay of time steps.
Figure 9.
Discovering the delay between cause and target , both having . Starting from the top convolutional layer, the algorithm traverses through the path with the highest kernel weights. Eventually, the algorithm ends in input value , indicating a delay of time steps.
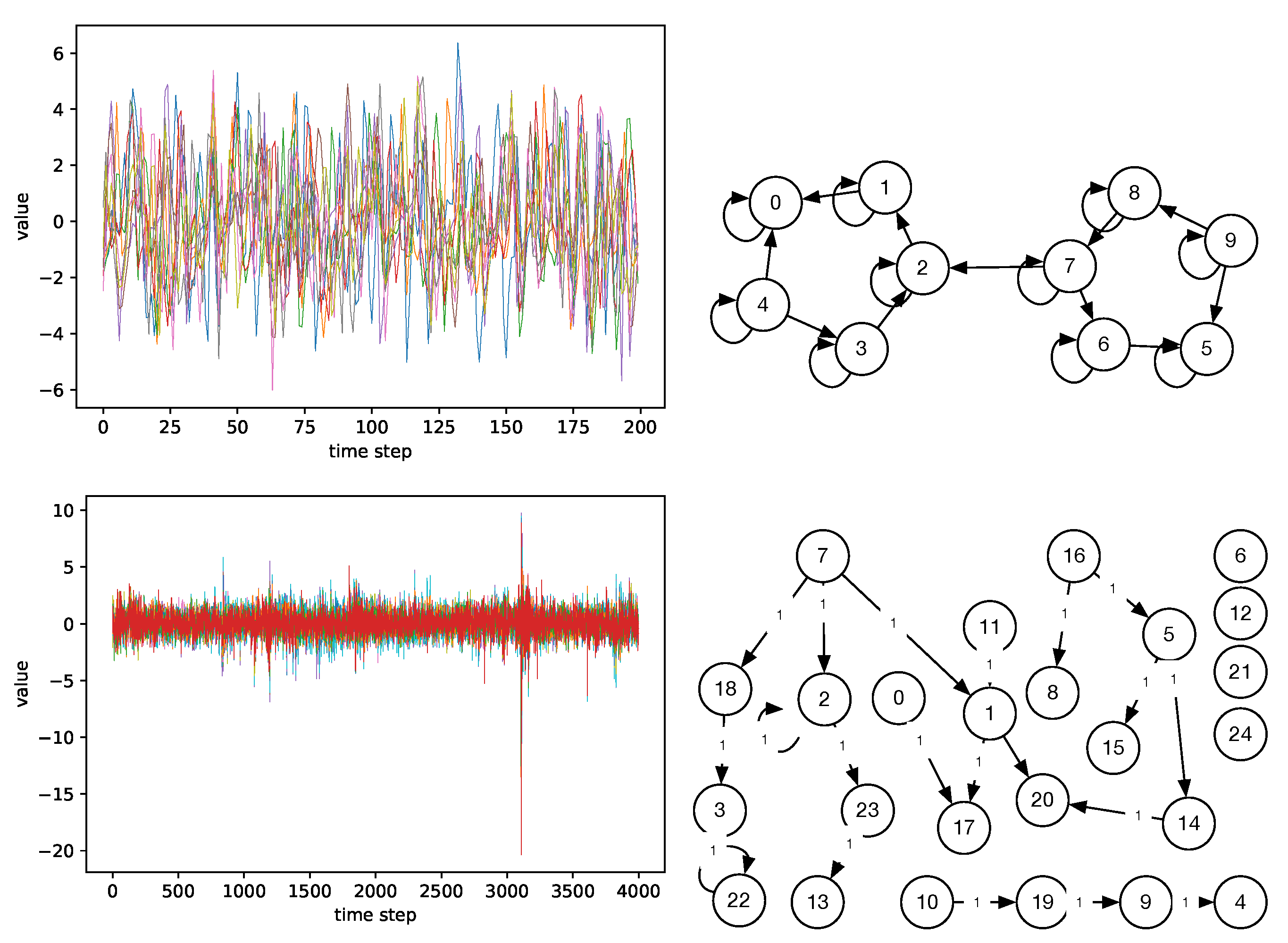
Figure 10.
Example datasets and causal graphs: simulation 17 from FMRI (top), graph 20-1A from FINANCE (bottom). A colored line corresponds to one time series (node) in the causal graph.
Figure 10.
Example datasets and causal graphs: simulation 17 from FMRI (top), graph 20-1A from FINANCE (bottom). A colored line corresponds to one time series (node) in the causal graph.
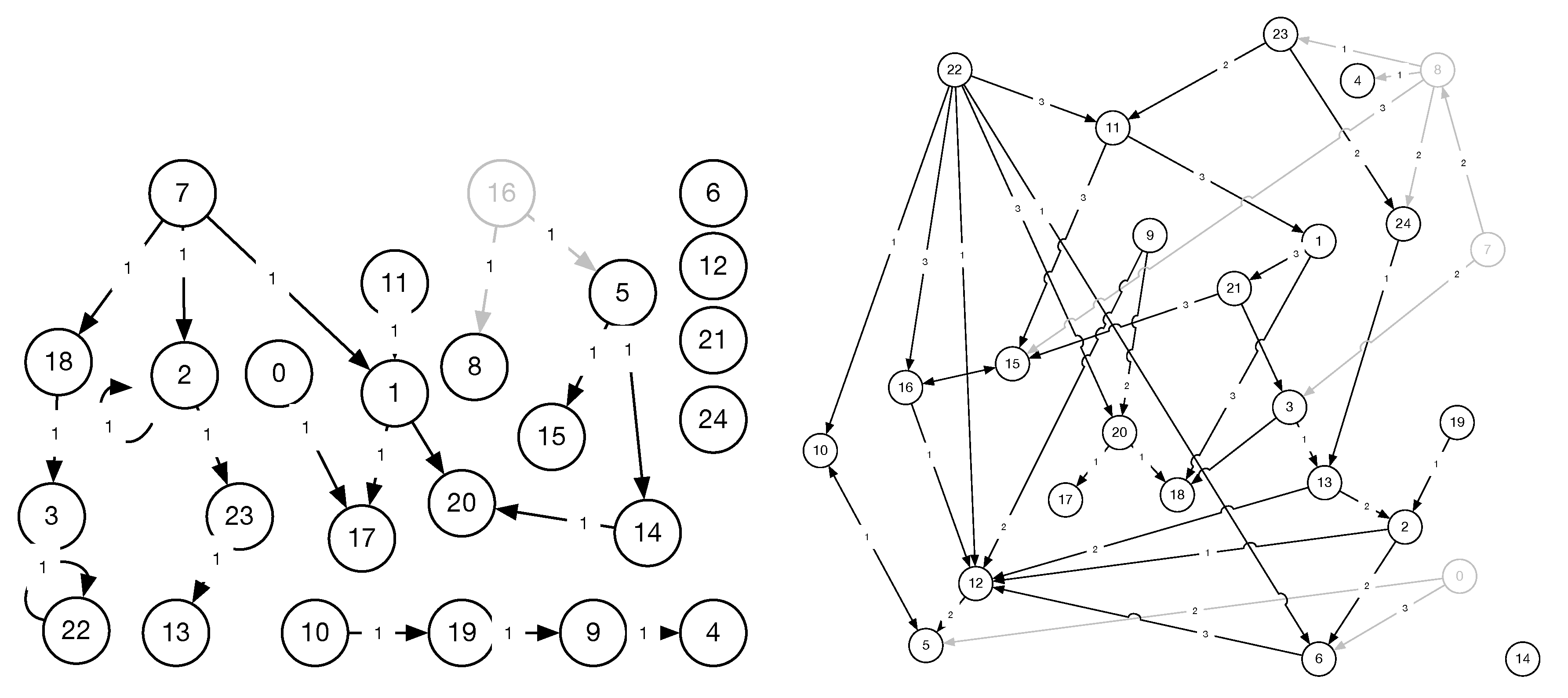
Figure 11.
Adapted ground truth for the hidden confounder experiment, showing graphs 20-1A (left) and 40-1-3 (right) from FINANCE. Only one grey node was removed per experiment.
Figure 11.
Adapted ground truth for the hidden confounder experiment, showing graphs 20-1A (left) and 40-1-3 (right) from FINANCE. Only one grey node was removed per experiment.
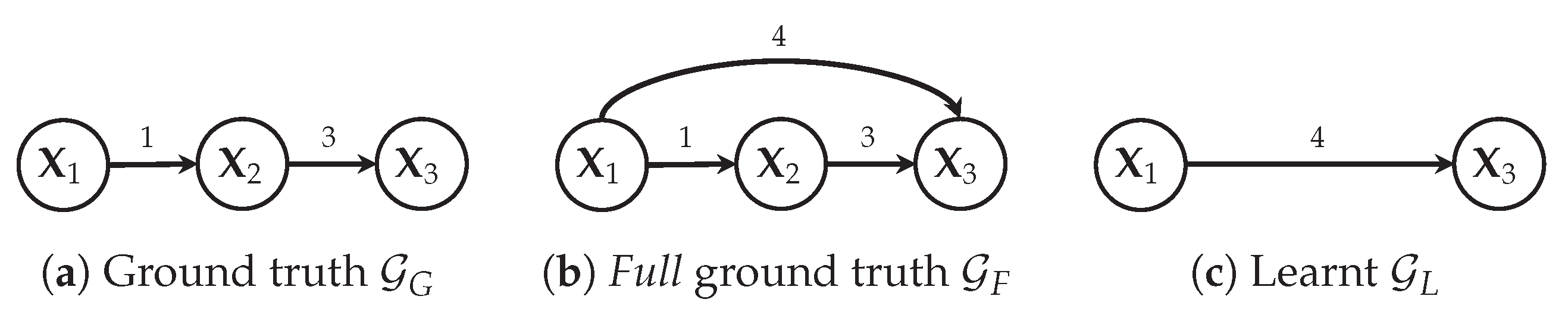
Figure 12.
Example with three variables showing that has TP = 0, FP = 1 (), TP’ = 1 (), FP’ = 0 and FN = 2 ( and ). Therefore, F1 = 0 and F1’= 0.5.
Figure 12.
Example with three variables showing that has TP = 0, FP = 1 (), TP’ = 1 (), FP’ = 0 and FN = 2 ( and ). Therefore, F1 = 0 and F1’= 0.5.
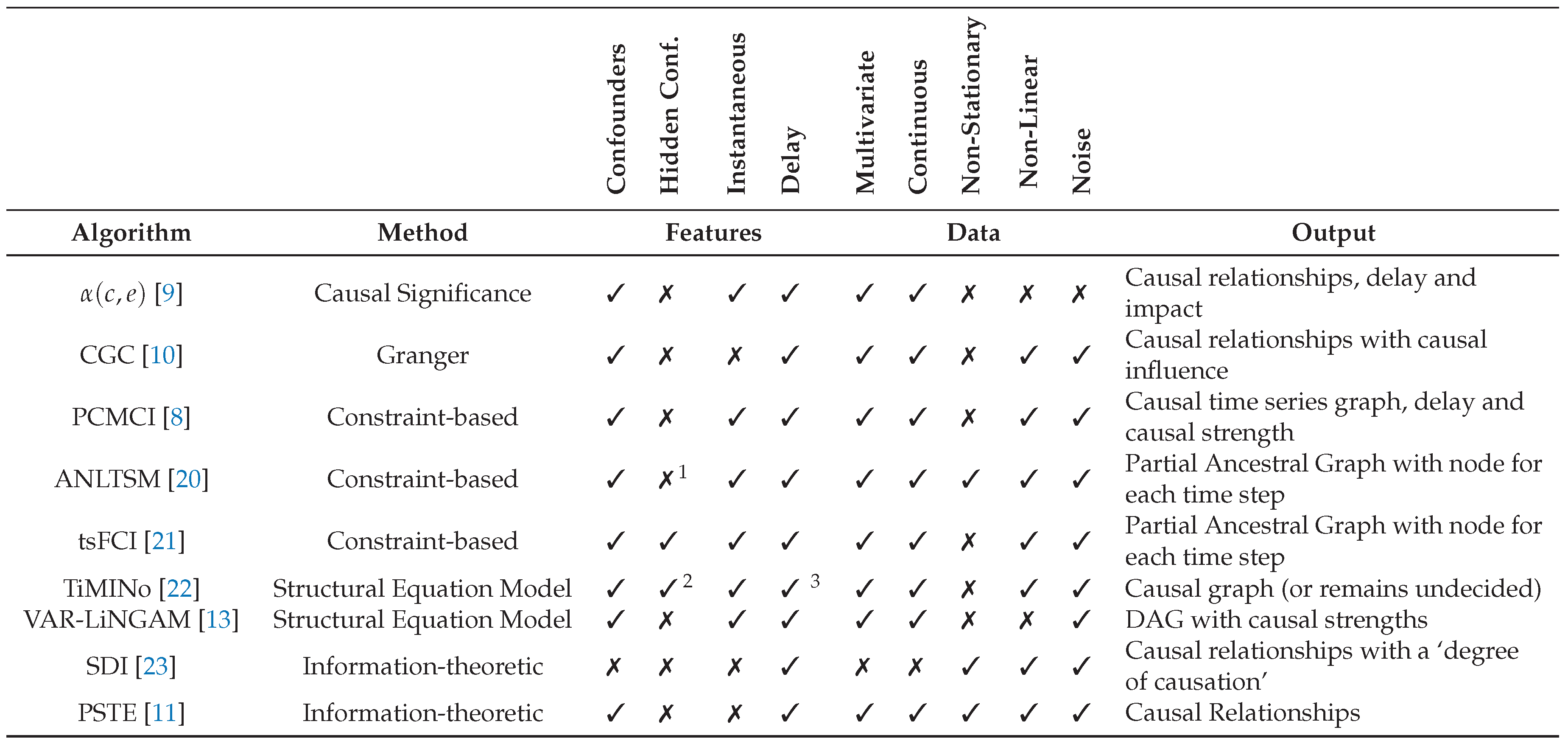
Table 1.
Causal discovery methods for time series data, classified among various dimensions.
Table 1.
Causal discovery methods for time series data, classified among various dimensions.
Table 2.
Summary of evaluation benchmarks. Delays between cause and effect not available in FMRI.
Table 2.
Summary of evaluation benchmarks. Delays between cause and effect not available in FMRI.
| | FINANCE | FMRI | FMRI |
|---|
| #datasets | 9 | 27 | 6 |
| #non-stationary datasets | 0 | 1 | 0 |
| #variables (time series) | 25 | | {5, 10} |
| #causal relationships | | | |
| time series length | 4000 | 50–5000 (mean: 774) | 1000–5000 (mean: 2867) |
| delays [timesteps] | 1–3 | n.a. | n.a. |
| self-causation | ✓ | ✓ | ✓ |
| confounders | ✓ | ✓ | ✓ |
| type of relationship | linear | non-linear | non-linear |
Table 3.
Time series prediction performance of TCDF, in terms of the mean absolute scaled error (MASE) averaged across all datasets, plus its standard deviation. Best results are highlighted in bold.
Table 3.
Time series prediction performance of TCDF, in terms of the mean absolute scaled error (MASE) averaged across all datasets, plus its standard deviation. Best results are highlighted in bold.
| | FINANCE TEST | FMRI TEST | FMRI TEST |
|---|
| TCDF () | 0.38 ± 0.09 | 0.84 ± 0.38 | 0.71 ± 0.05 |
| TCDF () | 0.38 ± 0.10 | 1.06 ± 0.49 | 0.72 ± 0.07 |
| TCDF () | 0.40 ± 0.10 | 1.13 ± 0.45 | 0.74 ± 0.08 |
Table 4.
Causal discovery overview for all data sets and all methods. Showing macro-averaged F1 and F1’ scores and standard deviations. The highest score per benchmark is highlighted in bold.
Table 4.
Causal discovery overview for all data sets and all methods. Showing macro-averaged F1 and F1’ scores and standard deviations. The highest score per benchmark is highlighted in bold.
| | FINANCE (9 Data Sets) | FMRI (27 Data Sets) | FMRI (6 Data Sets) |
|---|
| | F1 | F1′ | F1 | F1′ | F1 | F1′ |
| TCDF () | 0.64 ± 0.06 | 0.77 ± 0.08 | 0.60 ± 0.09 | 0.63 ± 0.09 | 0.68 ± 0.05 | 0.68 ± 0.05 |
| TCDF () | 0.65 ± 0.09 | 0.78 ± 0.10 | 0.58 ± 0.15 | 0.62 ± 0.14 | 0.65 ± 0.13 | 0.68 ± 0.11 |
| TCDF () | 0.64 ± 0.09 | 0.77 ± 0.09 | 0.55 ± 0.13 | 0.63 ± 0.11 | 0.70 ± 0.09 | 0.73 ± 0.08 |
| PCMCI | 0.55 ± 0.22 | 0.56 ± 0.22 | 0.63 ± 0.10 | 0.67 ± 0.11 | 0.67 ± 0.04 | 0.67 ± 0.04 |
| tsFCI | 0.37 ± 0.11 | 0.37 ± 0.12 | 0.49 ± 0.22 | 0.49 ± 0.22 | 0.48 ± 0.28 | 0.48 ± 0.28 |
| TiMINo | 0.13 ± 0.05 | 0.21 ± 0.10 | 0.23 ± 0.12 | 0.37 ± 0.14 | 0.23 ± 0.11 | 0.37 ± 0.15 |
Table 5.
Run time in seconds, averaged over all datasets in the benchmark. TCDF (without parallelism) and TiMINo are run on a Ubuntu 16.04.4 LTS computer with an Intel® Xeon® E5-2683-v4 CPU and NVIDIA TitanX 12GB GPU. PCMCI and tsFCI are run on a Windows 10 1803 computer with an Intel® Core™ i7-5500U CPU.
Table 5.
Run time in seconds, averaged over all datasets in the benchmark. TCDF (without parallelism) and TiMINo are run on a Ubuntu 16.04.4 LTS computer with an Intel® Xeon® E5-2683-v4 CPU and NVIDIA TitanX 12GB GPU. PCMCI and tsFCI are run on a Windows 10 1803 computer with an Intel® Core™ i7-5500U CPU.
| | TCDF () | PCMCI | tsFCI | TiMINo |
|---|
| FINANCE | 318 s | 10 s | 93 s | 499 s |
| FMRI | 74 s | 1 s | 1 s | 14 s |
Table 6.
Delay discovery overview for all data sets of the FINANCE benchmark (nine datasets). Showing macro-averaged percentage of delays that are correctly discovered w.r.t. the full ground truth, and standard deviation. TiMINo does not discover delays.
Table 6.
Delay discovery overview for all data sets of the FINANCE benchmark (nine datasets). Showing macro-averaged percentage of delays that are correctly discovered w.r.t. the full ground truth, and standard deviation. TiMINo does not discover delays.
| | TCDF () | TCDF () | TCDF () | PCMCI | tsFCI | TiMINo |
|---|
| FINANCE | 97.79% ± 2.56 | 96.42% ± 3.68 | 95.49% ± 4.15 | 100.00% ± 0.00 | 98.77% ± 3.49 | n.a. |
Table 7.
Impact of causal validation step. Showing macro-averaged F1 scores and standard deviation for TCDF with PIVM and TCDF without PIVM. shows the change in F1-score or F1’-score in percent.
Table 7.
Impact of causal validation step. Showing macro-averaged F1 scores and standard deviation for TCDF with PIVM and TCDF without PIVM. shows the change in F1-score or F1’-score in percent.
| | FINANCE (9 Data Sets) | FMRI (27 Data Sets) | FMRI (6 Data Sets) |
|---|
| | F1 | F1′ | F1 | F1′ | F1 | F1′ |
| TCDF () | 0.64 ± 0.06 | 0.77 ± 0.08 | 0.60 ± 0.09 | 0.63 ± 0.09 | 0.68 ± 0.05 | 0.68 ± 0.05 |
| TCDF () w/o PIVM | 0.22 ± 0.09 | 0.30 ± 0.13 | 0.60 ± 0.09 | 0.63 ± 0.09 | 0.68 ± 0.05 | 0.68 ± 0.05 |
| (PIVM) | −66% | −61% | 0% | 0% | 0% | 0% |
Table 8.
Results of our TCDF () applied to FINANCE HIDDEN. ‘Equal Delays’ denotes whether the delays from the confounder (conf.) to the confounder’s effects are equal. Grey causal relationships denote that the discovered relationship was not causal according to the ground truth.
Table 8.
Results of our TCDF () applied to FINANCE HIDDEN. ‘Equal Delays’ denotes whether the delays from the confounder (conf.) to the confounder’s effects are equal. Grey causal relationships denote that the discovered relationship was not causal according to the ground truth.
| Dataset | Hidden Conf. | Effects | Equal Delays | Conf. Discovered | Learnt Causal Relationships |
|---|
| 20-1A | | , | ✓ | ✓ | , |
| 40-1-3 | | , | ✓ | ✓ | , |
| 40-1-3 | | , | ✗ | ✗ | |
| 40-1-3 | | , | ✓ | ✓ | , |
| 40-1-3 | | , | ✗ | ✗ | - |
| 40-1-3 | | , | ✗ | ✗ | - |
| 40-1-3 | | , | ✗ | ✗ | - |
| 40-1-3 | | , | ✗ | ✗ | |
| 40-1-3 | | , | ✗ | ✗ | - |
Table 9.
Results of TCDF compared with PCMCI, tsFCI and TiMINo when applied to datasets with hidden confounders. The first row denotes the number of incorrect causal relationships that were discovered between the effects of the hidden confounders. The second row denotes the number of hidden confounders that were located.
Table 9.
Results of TCDF compared with PCMCI, tsFCI and TiMINo when applied to datasets with hidden confounders. The first row denotes the number of incorrect causal relationships that were discovered between the effects of the hidden confounders. The second row denotes the number of hidden confounders that were located.
| FINANCE HIDDEN | TCDF () | PCMCI | tsFCI | TiMINo |
|---|
| # Incorrect Causal Relationships | 2 | 0 | 3 | 8 |
| # Discovered Hidden Confounders | 3 | 0 | 0 | 0 |