Implementation of Composite Materials for Lightweighting of Industrial Vehicle Chassis
Abstract
1. Introduction
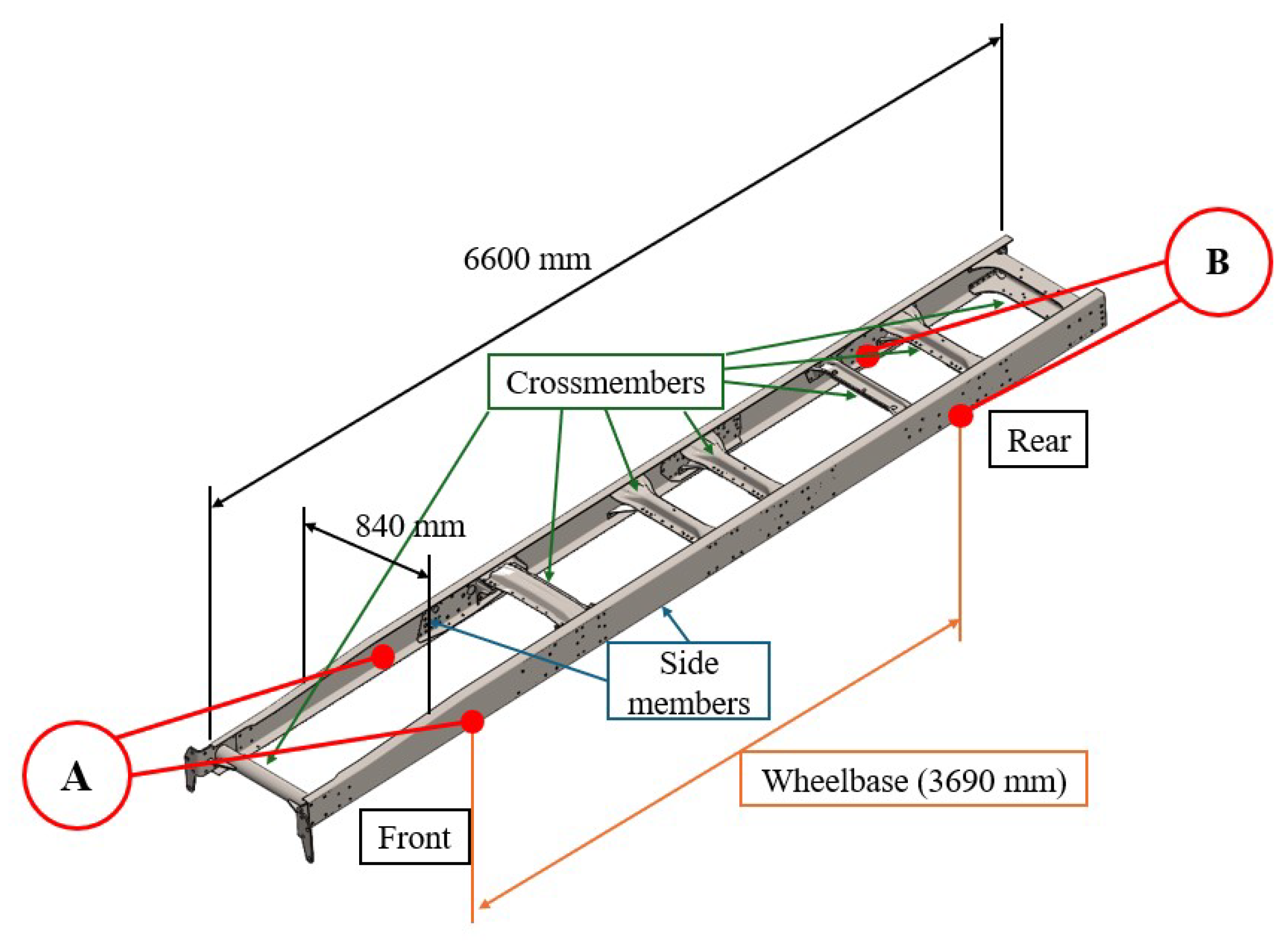
2. Description of the Component
3. Materials and Methods
3.1. Theoretical Background of the Design Approach
- weight of the body, passengers, and cargo loads;
- vertical and twisting load owing to uneven road surfaces;
- lateral forces caused by the road camber, side wind, and steering of the vehicle;
- inertial forces caused by sudden acceleration or braking and sharp turns.
3.2. Methods and Criteria Adopted
3.3. Choice of the Materials
3.4. Experimental Setup and Procedure
- Front Support: the front side of the chassis frame was constrained to the test bench at the front suspension mounting points as shown in Figure 5. This configuration permitted the frame the rotation, enabling load application at this side. The front suspension was replaced by a rigid element that can tilt.Figure 5. Front constraints of the HCV chassis frame.
- Rear Support: the rear side of the chassis frame was constrained to the test bench at the rear suspension mounting points. The rear support was fixed to the longitudinal beams of the chassis frame to prevent excessive stiffness increase while stabilizing the structure under load. The rear suspension was represented by a structure that can be seen in Figure 6, which mimics the air bellows of the first rear axle in the HCV configuration.Figure 6. Rear constraints of the HCV chassis frame.
- Linearity: ±0.25% full-scale output
- Repeatability: ±0.1% full-scale output
- Operating range: 10–10,000 N
- Operating temperature: −54 °C to +121 °C
- Linearity: ±0.25% full-scale output
- Repeatability: ±0.01% full-scale output
- Operating range: ±30°
- Operating temperature: −55 °C to +125 °C
- Torsional Deformation: measured as the rotation of the chassis frame’s side members. Sensors were positioned along the length of the side members (Y-axis) to capture this deformation;
- Torsional Stiffness: determined by the difference in rotation between the front axle section (where the load was applied) and the rear axle section.
3.5. Numerical Simulations
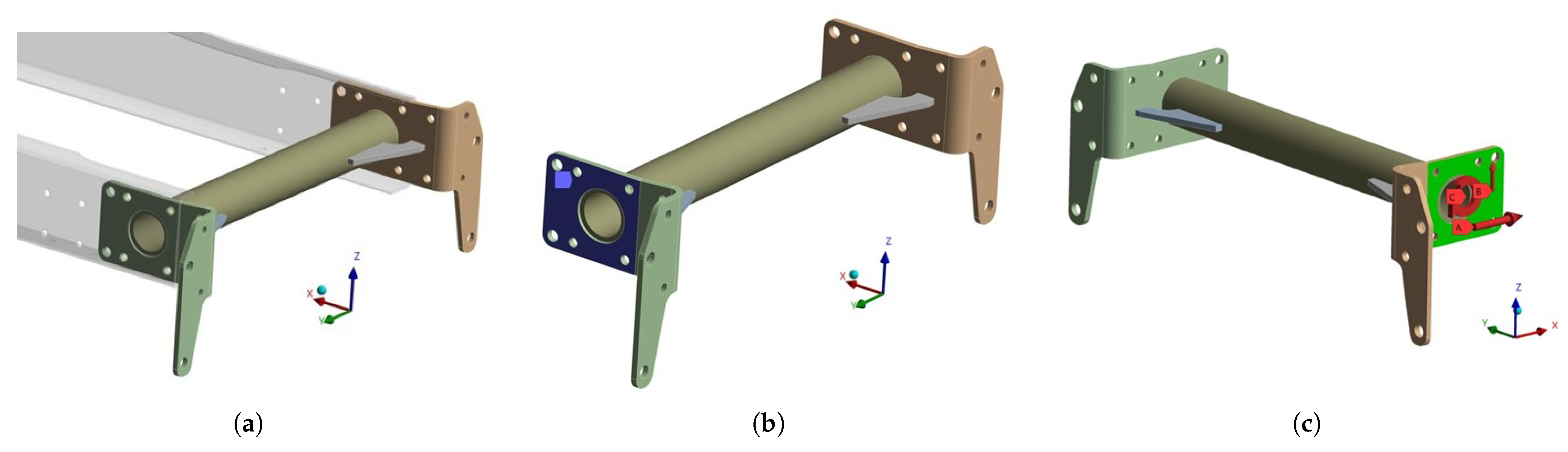
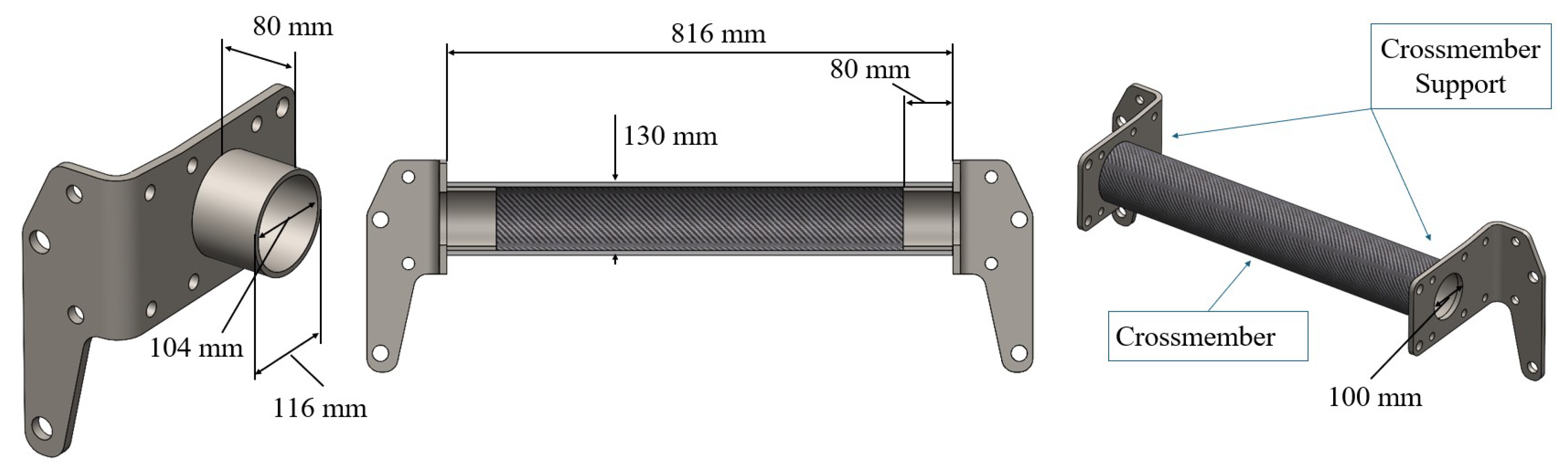
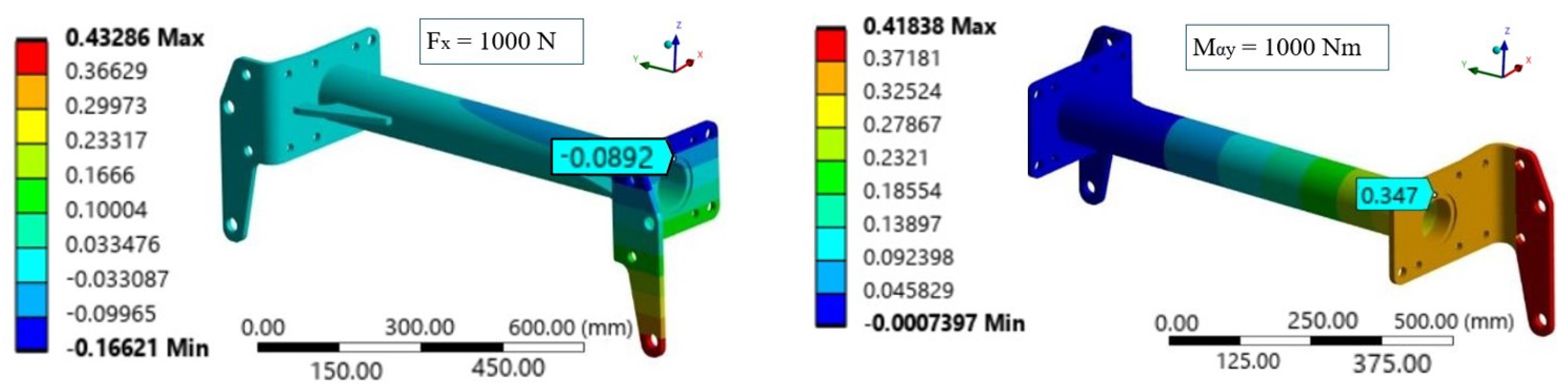
3.5.1. Crossmembers Simulation
- For the bending stiffness: N.
- For the torsion stiffness: Nm.
3.5.2. CFRP Crossmember Solution
- Tubular profile with 7 mm wall thickness.
- 28-layer laminate (each ply defined by 0.25 mm of thickness).
- Layer Stacking Sequence (LSS) including 15% of the plies oriented at 5°, 15% at −5°, 27.5% at 45°, 27.5% at −45° and 15% at 90°.
4. Results
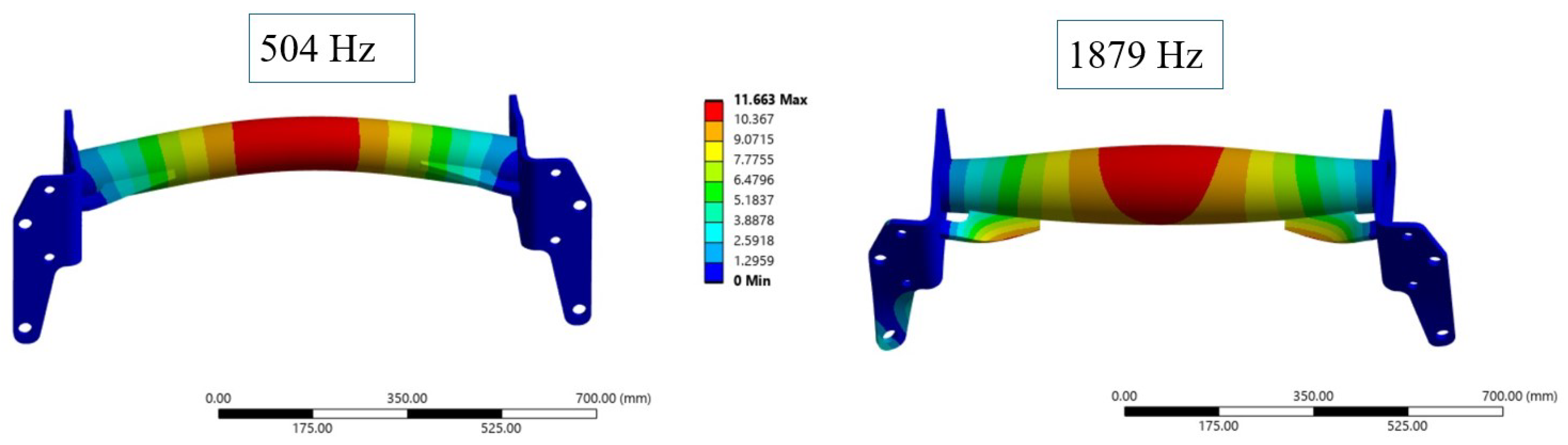
4.1. Simulation of the First Crossmember
- +5% higher for bending stiffness.
- +6.8% higher for torsional stiffness.
4.2. Chassis Frame Results Comparison
5. Discussion
6. Conclusions
- Reduction of computational cost: Focusing on the single crossmember allowed a significant decrease in simulation time and resources compared to a full chassis analysis during the design stage.
- Weight savings: The CFRP crossmember achieved a 68.08% reduction in weight compared to the traditional steel solution.
- Stiffness performance: The CFRP solution demonstrated a +5% increase in bending stiffness and a +6.8% increase in torsional stiffness over steel.
- Economic benefits: Although the initial cost increased by 241.14%, the solution is economically viable with a payback time of approximately 3 years, considering fuel savings during vehicle operation.
- Validation with experimental data: Numerical FEM results showed excellent agreement with experimental tests on the steel chassis and confirmed the robustness of the simulation approach.
- Environmental impact: For both diesel and electric HCVs, the CFRP solution led to important reductions in CO2 emissions and operating expenses.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HCV | Heavy Commercial Vehicle |
| LWD | Lightweight Design |
| FE | Finite-Element |
| FEM | Finite-Element Method |
| CFRP | Carbon Fibre Reinforced Polymer |
| GFRP | Glass Fibre Reinforced Polymer |
References
- Eurostat. Freight Transport Statistics–Modal Split. Statistics Explained. 2024. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?oldid=194460 (accessed on 9 May 2025).
- Road/Total Inland Freight Transport in Italy 2005–2023. Statista. 2023. Available online: www.statista.com/statistics/1069154/italy-road-freight-share-of-inland-transport/ (accessed on 3 July 2025).
- Carboni, M.; Dall-Orsoletta, A.; Hawkes, A.; Giarola, S. The future of road freight transport and alternative technologies: A case study for Italy. Energy Convers. Manag. 2024, 299, 117819. [Google Scholar] [CrossRef]
- Czerwinski, F. Current trends in automotive lightweighting strategies and materials. Materials 2021, 14, 6631. [Google Scholar] [CrossRef]
- Topac, M.M.; Karaca, M.; Aksoy, B.; Deryal, U.; Bilal, L. Lightweight design of a rear axle connection bracket for a heavy commercial vehicle by using topology optimisation: A case study. Mechanics 2020, 26, 64–72. [Google Scholar] [CrossRef]
- Lowrie, J.; Pang, H.; Ngaile, G. Weight reduction of heavy-duty truck components through hollow geometry and intensive quenching. J. Manuf. Processes 2017, 28, 523–530. [Google Scholar] [CrossRef]
- Lim, S.; Misawa, R.; Furuta, K.; Maruyama, S.; Izui, K.; Nishiwaki, S. Weight reduction design of multi-material vehicle components using level set-based topology optimization. Struct. Multidiscip. Optim. 2022, 65, 100. [Google Scholar] [CrossRef]
- Poulikidou, S.; Schneider, C.; Björklund, A.; Kazemahvazi, S.; Wennhage, P.; Zenkert, D. A material selection approach to evaluate material substitution for minimizing the life cycle environmental impact of vehicles. Mater. Des. 2015, 83, 704–712. [Google Scholar] [CrossRef]
- Santos, J.; Gouveia, R.M.; Silva, F.J.G. Designing a new sustainable approach to the change for lightweight materials in structural components used in truck industry. J. Clean. Prod. 2017, 164, 115–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, L.; Su, H.; Qin, J.; Chen, Z.; Deng, K. Multi-Scale Design and Optimization of Composite Material Structure for Heavy-Duty Truck Protection Device. Comput. Model. Eng. Sci. (CMES) 2024, 139, 1961. [Google Scholar] [CrossRef]
- Kezhi, L.H.; Gao, F.Y.; Li, X.L.; Zhang, D.W.; Xiao, B.L. Structure lightweight optimization of truck axle on fatigue failure. Adv. Mater. Res. 2018, 1145, 27–32. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, S.; Sun, W.; Hao, W.; Zhang, X.; Yang, Z. Analysis and Validation of Lightweight Carriage Structures Using Basalt Fiber Composites. Materials 2024, 17, 5723. [Google Scholar] [CrossRef] [PubMed]
- Solazzi, L.; Danzi, N. Jib crane lightweighting through composite material and prestressing technique. Compos. Struct. 2024, 343, 118283. [Google Scholar] [CrossRef]
- Solazzi, L.; Tomasi, I. Design of an Overhead Crane in Steel, Aluminium and Composite Material Using the Prestress Method. J. Compos. Sci. 2024, 8, 380. [Google Scholar] [CrossRef]
- Ufuk, R.; Ereke, M. Composite material optimization for heavy duty chassis by finite element analysis. Adv. Automot. Eng. 2018, 1, 41–59. [Google Scholar]
- Siraj, A.; Babu, N.R.; Reddy, K.S. Static analysis of dump truck chassis frame made of composite materials. Int. J. Eng. Sci. Technol. 2019, 11, 21–32. [Google Scholar] [CrossRef]
- Agarwal, A.; Mthembu, L. Weight optimization of heavy-duty truck chassis by optimal space fill design using light weight Graphite Al GA 7-230 MMC. Mater. Today Proc. 2022, 52, 1278–1287. [Google Scholar] [CrossRef]
- Svensson, L.E.; Karlsson, L.; Söder, R. Welding enabling light weight design of heavy vehicle chassis. Sci. Technol. Weld. Join. 2015, 20, 473–482. [Google Scholar] [CrossRef]
- Tomasi, I.; Grandi, S.; Solazzi, L. Implementation of Composite Materials for an Industrial Vehicle Component: A Design Approach. J. Compos. Sci. 2025, 9, 168. [Google Scholar] [CrossRef]
- Gawande, S.H.; Muley, A.A.; Yerrawar, R.N. Optimization of torsional stiffness for heavy commercial vehicle chassis frame. Automot. Innov. 2018, 1, 352–361. [Google Scholar] [CrossRef]
- Carpinteri, A. Scienza Delle Costruzioni 1; Società Editrice Esculapio: Bologna, Italy, 2023. [Google Scholar]
- Lombaert, G.; Degrande, G. The experimental validation of a numerical model for the prediction of the vibrations in the free field produced by road traffic. J. Sound Vib. 2003, 262, 309–331. [Google Scholar] [CrossRef]
- Ashby, M.F.; Cebon, D. Materials selection in mechanical design. MRS Bull. 2005, 30, 995. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Naik, N.K.; Kumar, R.S. Compressive strength of unidirectional composites: Evaluation and comparison of prediction models. Compos. Struct. 1999, 46, 299–308. [Google Scholar] [CrossRef]
- Xu, Y.L.; Reifsnider, K.L. Micromechanical modeling of composite compressive strength. J. Compos. Mater. 1993, 27, 572–588. [Google Scholar] [CrossRef]
- Fleck, N.A.; Budiansky, B. Compressive failure of fibre composites due to microbuckling. In Proceedings of the Inelastic Deformation of Composite Materials: IUTAM Symposium, Troy, NY, USA, 29 May–1 June 1990; Springer: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Solazzi, L.; Vaccari, M. Reliability design of a pressure vessel made of composite materials. Compos. Struct. 2022, 279, 114726. [Google Scholar] [CrossRef]
- Solazzi, L. Reliability evaluation of critical local buckling load on the thin walled cylindrical shell made of composite material. Compos. Struct. 2022, 284, 115163. [Google Scholar] [CrossRef]
- Stojcevski, F.; Hilditch, T.; Henderson, L.C. Henderson. A modern account of Iosipescu testing. Compos. Part A Appl. Sci. Manuf. 2018, 107, 545–554. [Google Scholar] [CrossRef]
- Komartin, R.S.; Balanuca, B.; Necolau, M.I.; Cojocaru, A.; Stan, R. Composite materials from renewable resources as sustainable corrosion protection coatings. Polymers 2021, 13, 3792. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, Y. Constructing multi-protective functional polyurethane composite coating via internal-external dual modification: Achieving superhydrophobicity, enhanced barrier, corrosion inhibition, and UV aging resistance properties. Prog. Org. Coat. 2024, 194, 108540. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). EN 10149-2:2013—Hot Rolled Flat Products Made of High Yield Strength Steels for Cold Forming—Part 2: Technical Delivery Conditions for Thermomechanically Rolled Steels; CEN: Brussels, Belgium, 2013. [Google Scholar]
- Visconti, I.C.; Caprino, G.; Langella, A. Materiali Compositi: Tecnologie, Progettazione, Applicazioni; U. Hoepli: Milano, Italy, 2009. [Google Scholar]
- Toray Composite Materials America Inc. M50J High Modulus Carbon Fiber. Available online: https://cdn.thomasnet.com/ccp/30164375/140079.pdf (accessed on 3 July 2025).
- Mates s.r.l. SX10–Scheda Tecnica Della Resina Epossidica SX10. n.d. Available online: https://fileserver.mates.it/Prodotti/2_Matrici/TDS/Resine/Mates/SX10_DS.pdf (accessed on 3 July 2025).
- Ke, L.; Li, C.; Luo, N.; He, J.; Jiao, Y.; Liu, Y. Enhanced comprehensive performance of bonding interface between CFRP and steel by a novel film adhesive. Compos. Struct. 2019, 229, 111393. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, L.; Dong, H. Lightweight 3D carbon fibre reinforced composite lattice structures of high thermal-dimensional stability. Compos. Struct. 2023, 304, 116471. [Google Scholar] [CrossRef]
- Meszler, D.; Delgado, O.; Rodríguez, F.; Muncrief, R. European Heavy-Duty Vehicles: Cost-Effectiveness of Fuel-Efficiency Technologies For Long-Haul Tractor-Trailers in the 2025–2030 Timeframe; International Council on Clean Transportation: Washington, DC, USA, 2018. [Google Scholar]
- Zhu, X.; Shen, X.; Chen, K.; Zhang, Z. Research on the prediction and influencing factors of heavy duty truck fuel consumption based on LightGBM. Energy 2024, 296, 131221. [Google Scholar] [CrossRef]
- Sato, S.; Jiang, Y.J.; Russell, R.L.; Miller, J.W.; Karavalakis, G.; Durbin, T.D.; Johnson, K.C. Experimental driving performance evaluation of battery-powered medium and heavy duty all-electric vehicles. Int. J. Electr. Power Energy Syst. 2022, 141, 108100. [Google Scholar] [CrossRef]
- Kim, H.C.; Wallington, T.J. Life cycle assessment of vehicle lightweighting: A physics-based model to estimate use-phase fuel consumption of electrified vehicles. Environ. Sci. Technol. 2016, 50, 11226–11233. [Google Scholar] [CrossRef] [PubMed]
- Del Pero, F.; Berzi, L.; Antonacci, A.; Delogu, M. Automotive lightweight design: Simulation modeling of mass-related consumption for electric vehicles. Machines 2020, 8, 51. [Google Scholar] [CrossRef]
- Agenzia per la Protezione dell’Ambiente e dei Servizi Tecnici. Analisi dei Fattori di Emissione di CO2 dal Settore dei Trasporti. Available online: https://www.isprambiente.gov.it/contentfiles/00003900/3906-rapporti-03-28.pdf (accessed on 2 July 2025).
- Scarlat, N.; Prussi, M.; Padella, M. Quantification of the carbon intensity of electricity produced and used in Europe. Appl. Energy 2022, 305, 117901. [Google Scholar] [CrossRef]
- Cost Components of End Consumer Diesel Prices in the European Union as of February 2024, by Country. Available online: https://www.statista.com/statistics/1488574/eu-diesel-price-breakdown-by-country/ (accessed on 25 June 2025).
- Electricity Prices for Enterprises Worldwide in September 2024, by Select Country. Available online: https://www.statista.com/statistics/1369634/business-electricity-price-worldwide-in-selected-countries/ (accessed on 25 June 2025).









| Ultimate Tensile Strength | Yield Strength | Young’s Module | Density | Poisson’s Coefficient |
|---|---|---|---|---|
| [MPa] | [MPa] | E [MPa] | [kg/m3] | |
| 480 | 420 | 210,000 | 7860 | 0.29 |
| [N/m] | [N/m] | [N/m] | [Nm/rad] | [Nm/rad] | [Nm/rad] |
|---|---|---|---|---|---|
| 48,500,000 | 32,000,000 | 48,500,000 | 30 | 160 | 30 |
| Carbon Fibre | Epoxy Resin | |||
|---|---|---|---|---|
| Property | Symbol | Value | Symbol | Value |
| Density | 1880 kg/m3 | 1200 kg/m3 | ||
| Young modulus | 475 GPa | 3.3 GPa | ||
| Tensile strength | 4120 MPa | 65 MPa | ||
| Compressive strength | - | 120 MPa | ||
| Poisson ratio | 0.28 | 0.34 | ||
| Mechanical Property | Symbol | Value | U.O.M. |
|---|---|---|---|
| Longitudinal tensile elasticity modulus | 286 | GPa | |
| Transversal tensile elasticity modulus | 8.16 | GPa | |
| Shear elasticity modulus | 3 | GPa | |
| Longitudinal tensile strength | 2472 | MPa | |
| Transversal tensile strength | 45 | MPa | |
| Longitudinal compression strength | 880 | GPa | |
| Transversal compression strength | 99.2 | MPa | |
| Shear strength | S | 59 | MPa |
| Density | 1608 | kg/m3 | |
| Poisson ratio | 0.3 | ||
| carbon fiber percentage | 60 | % |
| X-axis lateral force N | ||||
| Solution | Displacement [m] | Load [N] | Stiffness | Variation [%] |
| Traditional | 8.92 × | 1000 | 1.12 × | - |
| CFRP | 8.49 × | 1000 | 1.18 × | +5% |
| Torque Nm | ||||
| Solution | Rotation [rad] | Torque [Nm] | Stiffness | Variation [%] |
| Traditional | 3.47 × | 1000 | 2.88 × | - |
| CFRP | 3.24 × | 1000 | 3.09 × | +6.8% |
| Results Type | Chassis Type | Torque [Nm] | Torsional Stiffness | Relative Error |
|---|---|---|---|---|
| Experimental | Traditional | 2400 | 27,502 | - |
| Numerical | Traditional | 2427 | 27,811 | 1.13% |
| Numerical | CFRP solution | 2613 | 29,943 | 7.66% |
| Steel S420MC | Carbon Fibre Reinforced Polymer | |||
|---|---|---|---|---|
| Weight [kg] | Cost [€] | Weight [kg] | Cost [€] | |
| crossmember | 19.23 | 65 | 3.55 | 212.95 |
| links | - | - | 2.59 | 8.75 |
| Total | 19.23 | 65 | 6.14 | 221.70 |
| Percentage change | - | - | −68.08% | +241.14% |
| Property | Value CFRP (Diesel) | Value CFRP (Electric) | U.O.M. |
|---|---|---|---|
| Standard consumption [40,41] | 0.4367 | 1.54 | L/km–kWh/km |
| Annual mileage [39] | 135,000 | 135,000 | km/year |
| Fuel—Energy consumption | 58,954.5 | 207,900 | L/year–kWh/year |
| Fuel—Energy consumption variation index for Internal Combustion Engine Vehicles (ICEVs) [42]—Electric Vehicles (EVs) [43] | 0.000025 | 0.000082 | L/(km kg)–kWh/(km kg) |
| Mass decrease with respect to the standard solution | 80.75 | 80.75 | kg |
| Optimized consumption | 0.0020 | 0.0066 | L/km–kWh/km |
| Fuel—Energy consumption (optimized chassis) | 58,682 | 207,006.1 | L/year–kWh/year |
| Fuel—Energy consumption decrease (with respect to the standard solution) | 272.5 | 893.9 | L/year–kWh/year |
| CO2 emissions per kilogram of diesel [44] | 3.17 | - | kgCO2/kgdiesel |
| Density of diesel (at 15 °C) | 820 | - | kg/m3 |
| CO2 emissions per liter of diesel/CO2 emissions per kWh [45] | 2.60 | 0.334 | kgCO2/Ldiesel–kgCO2/kWh |
| Reduction of CO2 emissions (with respect to the standard solution) | 708.4 | 298.6 | kgCO2/year |
| Current diesel price/Current electric energy price [46,47] | 1.7 | 0.335 | €/L–€/kWh |
| Economic saving (with respect to the standard solution) | 463.28 | 299.80 | €/year |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomasi, I.; Grandi, S.; Donzella, G.; Solazzi, L. Implementation of Composite Materials for Lightweighting of Industrial Vehicle Chassis. J. Compos. Sci. 2025, 9, 611. https://doi.org/10.3390/jcs9110611
Tomasi I, Grandi S, Donzella G, Solazzi L. Implementation of Composite Materials for Lightweighting of Industrial Vehicle Chassis. Journal of Composites Science. 2025; 9(11):611. https://doi.org/10.3390/jcs9110611
Chicago/Turabian StyleTomasi, Ivan, Stefano Grandi, Giorgio Donzella, and Luigi Solazzi. 2025. "Implementation of Composite Materials for Lightweighting of Industrial Vehicle Chassis" Journal of Composites Science 9, no. 11: 611. https://doi.org/10.3390/jcs9110611
APA StyleTomasi, I., Grandi, S., Donzella, G., & Solazzi, L. (2025). Implementation of Composite Materials for Lightweighting of Industrial Vehicle Chassis. Journal of Composites Science, 9(11), 611. https://doi.org/10.3390/jcs9110611









