Glass-Forming Ionic Liquid Crystal Gold–Carbon Nanocomposites with Ultrafast Optical Nonlinearity Sign Reversal
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
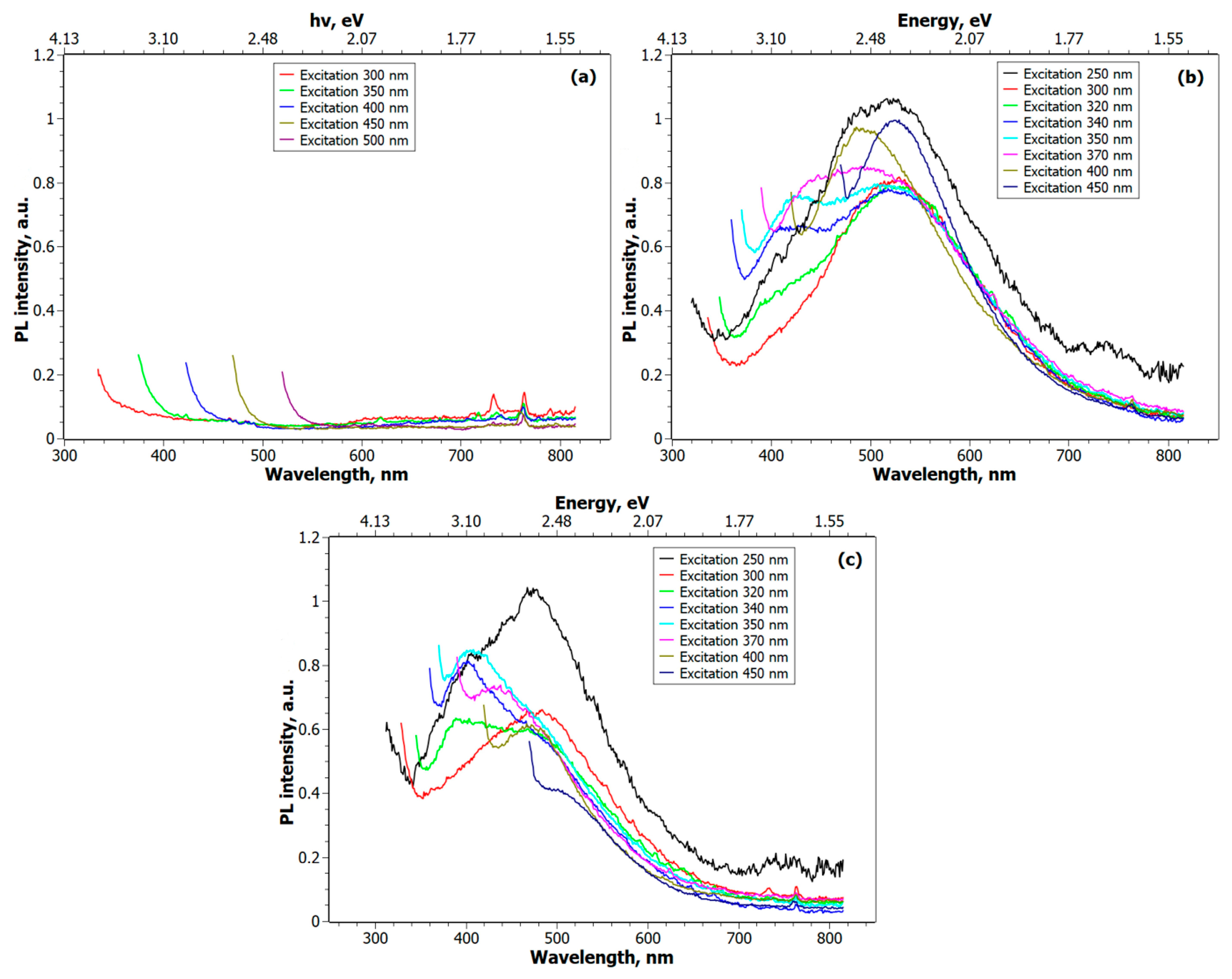
3.1. Linear Optical Properties: Light Absorption and Fluorescence
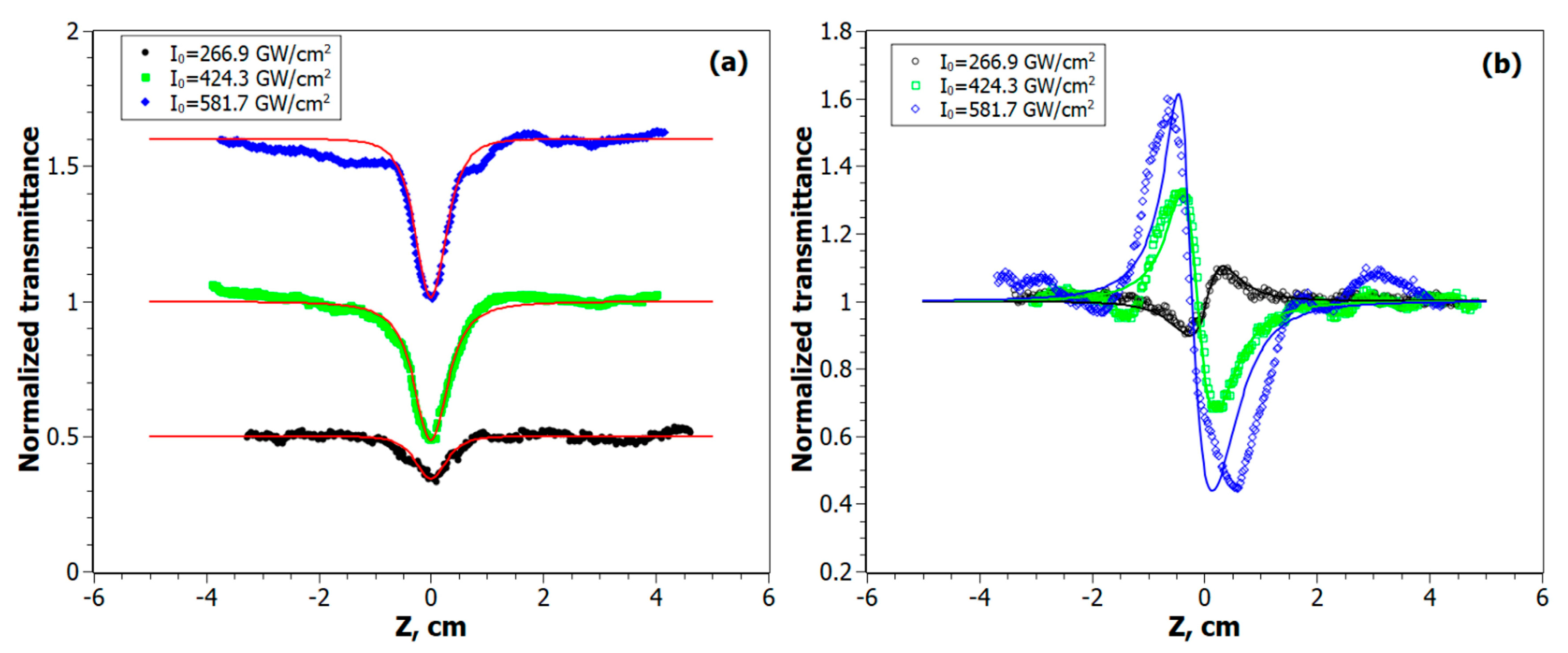
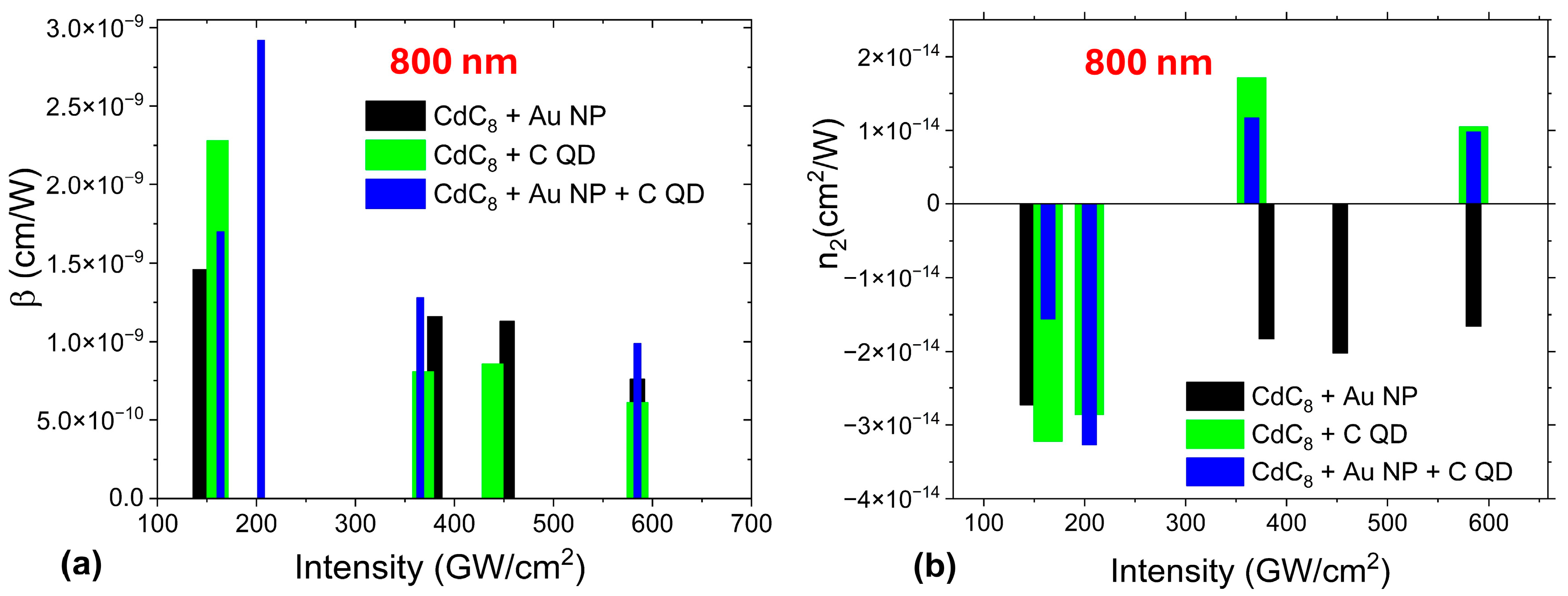
3.2. Nonlinear Optical Properties at λ = 800 nm
3.3. Nonlinear Optical Properties at λ = 600 nm
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vermeulen, N.; Espinosa, D.; Ball, A.; Ballato, J.M.; Boucaud, P.; Boudebs, G.; Campos, C.L.A.V.; Dragic, P.D.; Gomes, A.; Huttunen, M.J.; et al. Post-2000 nonlinear optical materials and measurements: Data tables and best practices. J. Phys. Photonics 2023, 5, 035001. [Google Scholar] [CrossRef]
- Palpant, B. Third order nonlinear optical response of metal nanoparticles. In Nonlinear Optical Properties of Matter; Papadopoulos, M.G., Andrzej, J.S., Jerzy, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zhang, Y.-X.; Wang, Y.-H. Nonlinear optical properties of metal nanoparticles: A review. RSC Adv. 2017, 7, 45129–45144. [Google Scholar] [CrossRef]
- Ganeev, R.A. Nonlinear Optical Refraction and Absorption of Media. In Nonlinear Optical Properties of Materials; Springer: Dordrecht, Germany, 2013. [Google Scholar]
- Nath, S.; Puthukkudi, A.; Mohapatra, J.; Biswal, B.P. Covalent Organic Frameworks as Emerging Nonlinear Optical Materials. Angew. Chem. 2023, 135, e202218974. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H.; Yang, Y.; Yang, D.; Cui, Y.; Qian, G. Aligned chromophores in a host–guest MOF crystal for switchable polarized nonlinear optical response. J. Mater. Chem. C 2022, 10, 14915–14920. [Google Scholar] [CrossRef]
- Mitus, A.C.; Saphiannikova, M.; Radosz, W.; Toshchevikov, V.; Pawlik, G. Modeling of Nonlinear Optical Phenomena in Host-Guest Systems Using Bond Fluctuation Monte Carlo Model: A Review. Materials 2021, 14, 1454. [Google Scholar] [CrossRef]
- Chen, Y.-B.; Zhang, C.; Luo, D.; Chen, R.; Zhang, J.; Chen, S.; Fang, W. Host-Guest Chemistry and Nonlinear Optical Behaviors of Aluminum Molecular Rings. Chin. J. Chem. 2024, 42, 2581. [Google Scholar] [CrossRef]
- Khoo, I.C. Nonlinear optics, active plasmonic and tunable metamaterials with liquid crystals. Prog. Quantum Electron. 2014, 38, 77–117. [Google Scholar] [CrossRef]
- Xu, J.; Yang, R.; Fan, Y.; Fu, Q.; Zhang, F. A Review of Tunable Electromagnetic Metamaterials with Anisotropic Liquid Crystals. Front. Phys. 2021, 9, 633104. [Google Scholar] [CrossRef]
- Si, G.; Zhao, Y.; Leong, E.S.P.; Liu, Y.J. Liquid-Crystal-Enabled Active Plasmonics: A Review. Materials 2014, 7, 1296–1317. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, Y.; Valenzuela, C.; Zhang, X.; Wang, L.; Feng, W.; Li, Q. Liquid crystal-templated chiral nanomaterials: From chiral plasmonics to circularly polarized luminescence. Light. Sci. Appl. 2022, 11, 223. [Google Scholar] [CrossRef] [PubMed]
- Yamane, M.; Asahara, Y. Glasses for Photonics; Cambridge University: New York, NY, USA, 2000. [Google Scholar]
- Petzold, U. Optical Glass: A High-Tech Base Material as Key Enabler for Photonics. In Advances in Glass Science and Technology; Sglavo, V., Ed.; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Vasconcelos, H.C. Optical Nonlinearities in Glasses’. In Nonlinear Optics—Nonlinear Nanophotonics and Novel Materials for Nonlinear Optics; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Chen, H.M.P.; Ou, J.J.; Chen, S.H. Glassy liquid crystals as self-organized films for robust optoelectronic devices. In Nanoscience with Liquid Crystals; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 179–208. [Google Scholar]
- Gujral, A.; Yu, L.; Ediger, M.D. Anisotropic organic glasses. Curr. Opin. Solid State Mater. Sci. 2018, 22, 49–57. [Google Scholar] [CrossRef]
- Bunning, T.J.; Mather, P.T.; Hood, P.J.; Barnes, W. Mid-wavelength IR (MWIR) polarizers from glassy cholesteric liquid crystals. Liq. Cryst. 1999, 26, 557–565. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Wu, C.G.; Jia, Y.G. Preparation and optical properties of linear polysiloxane-based glassy cholesteric liquid crystals with green reflected color. Liq. Cryst. 2021, 48, 215–222. [Google Scholar] [CrossRef]
- Hu, G.; Kelly, S.M.; Kitney, S.P.; Harrison, W.; Lambert, B. Novel nematic and glassy liquid crystalline oligomers as electroluminescent organic semiconductors. Liq. Cryst. 2021, 48, 626–640. [Google Scholar] [CrossRef]
- Casado, F.J.M.; Riesco, M.R.; Yélamos, M.I.R.; Arenas, A.S.; Cheda, J.A.R. The role of calorimetry in the structural study of mesophases and their glass states. J. Therm. Anal. Calorim. 2012, 108, 399–413. [Google Scholar] [CrossRef]
- Klimusheva, G.; Mirnaya, T.; Garbovskiy, Y. Versatile nonlinear-optical materials based on mesomorphic metal alkanoates: Design, properties, and applications. Liq. Cryst. Rev. 2015, 3, 28–57. [Google Scholar] [CrossRef]
- Martínez-Casado, F.J.; Ramos-Riesco, M.; Rodríguez-Cheda, J.A.R.; Cucinotta, F.; Fernández-Martínez, A.; Garrido, L.; Matesanz, E.; Marchese, L. Short lead(II) soaps: From weakly fluorescent crystals to strongly phosphorescent and structurally varied vitreous phases. A thermal, structural and spectroscopic study. J. Mater. Chem. C 2014, 2, 9489–9496. [Google Scholar] [CrossRef]
- Nagaraj, M. Liquid Crystals Templating. Crystals 2020, 10, 648. [Google Scholar] [CrossRef]
- Lyashchova, A.; Fedorenko, D.; Garbovskiy, Y.; Klimusheva, G.; Mirnaya, T.; Asaula, V. Strong thermal optical nonlinearity causes by CdSe nanoparticles synthesized in smectic ionic liquid crystals. Liq. Cryst. 2013, 40, 1377. [Google Scholar] [CrossRef]
- Zhulai, D.; Koval’chuk, A.; Bugaychuk, S.; Klimusheva, G.; Mirnaya, T.; Vitusevich, S. Photoconductivity of ionic thermotropic liquid crystal with semiconductor nanoparticles. J. Mol. Liq. 2018, 267, 405–410. [Google Scholar] [CrossRef]
- Rudenko, V.; Garbosvkiy, Y.; Klimusheva, G.; Mirnaya, T. Intensity dependent nonlinear absorption coefficients and nonlinear refractive indices of glass-forming ionic liquid crystals doped with gold and silver nanoparticles. J. Mol. Liq. 2018, 267, 56–60. [Google Scholar] [CrossRef]
- Rudenko, V.; Garbovskiy, Y.; Klimusheva, G.; Mirnaya, T.; Yaremchuk, G. Enhanced optical nonlinearity of the “nonlinear host–nonlinear guest” glassy nanocomposites made of the mesomorphic cobalt octanoate and noble metal nanoparticles. J. Opt. Soc. Am. B 2016, 33, 648–655. [Google Scholar] [CrossRef]
- Rudenko, V.; Tolochko, A.; Zhulai, D.; Klimusheva, G.; Mirnaya, T.; Yaremchuk, G.; Asaula, V. Nonlinear optical properties of metal alkanoate composites with hybrid core/shell nanoparticles. Appl. Nanosci. 2018, 8, 823–829. [Google Scholar] [CrossRef]
- Rudenko, V.; Tolochko, A.; Bugaychuk, S.; Zhulai, D.; Klimusheva, G.; Yaremchuk, G.; Mirnaya, T.; Garbovskiy, Y. Probing Optical Nonlinearities of Unconventional Glass Nanocomposites Made of Ionic Liquid Crystals and Bimetallic Nanoparticles. Nanomaterials 2022, 12, 924. [Google Scholar] [CrossRef]
- Rudenko, V.; Tolochko, A.; Bugaychuk, S.; Zhulai, D.; Klimusheva, G.; Yaremchuk, G.; Mirnaya, T.; Garbovskiy, Y. Intensity-dependent optical nonlinearities of composite materials made of ionic liquid crystal glass and bimetallic nanoparticles. Liq. Cryst. 2023, 50, 174–180. [Google Scholar] [CrossRef]
- Rudenko, V.; Tolochko, A.; Bugaychuk, S.; Zhulai, D.; Klimusheva, G.; Yaremchuk, G.; Mirnaya, T.; Garbovskiy, Y. Modifying optical nonlinearities of ionic liquid crystal glass by adding gold and carbon nanoparticles. J. Mol. Liq. 2024, 393, 123641. [Google Scholar] [CrossRef]
- Gurushantha, K.; Jagannath, G.; Kolavekar, S.; Pramod, A.; Almuqrin, A.H.; Sayyed, M.; Murthy, N.L.; Rao, S.V.; Keshavamurthy, K. Gold nanoparticles enhanced femtosecond nonlinear optical properties of sodium borate oxide glasses. Infrared Phys. Technol. 2023, 131, 104663. [Google Scholar] [CrossRef]
- Jagannathan, A.; Rajaramakrishna, R.; Gangareddy, J.; Rajashekara, K.; Soma, V.R.; Kaewkhao, J.; Kothan, S.; Surzhikova, D.P. Third order nonlinear optical properties of lithium zinc calcium fluoroborate glasses embedded with Au–Ag nanoparticles. Opt. Mater. 2024, 149, 115013. [Google Scholar] [CrossRef]
- Hernández-Acosta, M.A.; Torres-Torres, C.; Bornacelli, J.; García-Merino, J.A.; Can-Uc, B.; Rangel-Rojo, R.; Oliver, A. A comprehensive study of the nonlinear optical response exhibited by ion-implanted silica plates with Au and Pt nanostructures. Results Opt. 2021, 4, 100098. [Google Scholar] [CrossRef]
- Chen, S.; Niu, R.; Gao, Y.; Li, Z.; Liu, K.; Wang, Y.; Song, Y.; Zhang, X. Tunable nonlinear absorption of gold nanostars and application as a saturable absorber. Opt. Laser Technol. 2024, 168, 109873. [Google Scholar] [CrossRef]
- Tan, Z.; Dong, J.; Liu, Y.; Luo, Q.; Li, Z.; Yun, T.; Jiang, T.; Cheng, X.; Huang, D. Nonlinear optics of graphitic carbon allotropes: From 0D to 3D. Nanoscale 2025, 17, 1171–1212. [Google Scholar] [CrossRef]
- Yadav, R.K.; Aneesh, J.; Sharma, R.; Abhiramnath, P.; Maji, T.K.; Omar, G.J.; Mishra, A.K.; Karmakar, D.; Adarsh, K.V. Designing Hybrids of Graphene Oxide and Gold Nanoparticles for Nonlinear Optical Response. Phys. Rev. Appl. 2018, 9, 044043. [Google Scholar] [CrossRef]
- Biswas, S.; Kole, A.K.; Tiwary, C.S.; Kumbhakar, P. Enhanced Nonlinear Optical Properties of Graphene Oxide–Silver Nanocomposites Measured by Z-Scan Technique. RSC Adv. 2016, 6, 10319–10325. [Google Scholar] [CrossRef]
- Abhijith, T.; Edappadikkunnummal, S.; Suthar, R.; Thomas, S.; Karak, S. Au–WS2 Nanohybrids with Enhanced Optical Nonlinearity for Optical Limiting Applications. ACS Appl. Nano Mater. 2023, 6, 2327. [Google Scholar] [CrossRef]
- Ren, J.; Yang, P.; Wang, A.; Zhu, W.; Shang, D.; Song, Y. Synergistic promoted nonlinear optical effects in polyaniline nanohybrids covalently functionalized with tin porphyrin. Colloids Surf. A Physicochem. Eng. Asp. 2022, 650, 129588. [Google Scholar] [CrossRef]
- Salah, A.; Hassab-Elnaby, S.; Ramadan, M.A. Boosting the nonlinear optical absorption of graphene oxide, and gold nanorods by tailoring graphene oxide-gold nanorods hybrids. SN Appl. Sci. 2023, 5, 288. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, F.; Wu, J.; Zhu, B.; Gu, Y. Synthesis and Third-Order Nonlinear Synergistic Effect of ZrO2/RGO Composites. Nanomaterials 2021, 11, 2741. [Google Scholar] [CrossRef]
- Saravanan, M. Nonlinear and Optical Limiting Properties of Graphene–Ferrite Nanocomposites: A Review. Phys. Status Solidi RRL 2024, 18, 2400105. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, F.; Cao, Y.; Wang, C.; Wang, J.; Gu, Y. Nonlinear optical enhancement induced by synergistic effect of graphene nanosheets and CdS nanocrystals. Appl. Phys. Lett. 2016, 108, 252106. [Google Scholar] [CrossRef]
- Yan, Z.; Fan, J.; Pan, S.; Zhang, M. Recent advances in rational structure design for nonlinear optical crystals: Leveraging advantageous templates. Chem. Soc. Rev. 2024, 53, 6568–6599. [Google Scholar] [CrossRef]
- Zhang, J.-X.; Zhou, S.-H.; Wu, X.-T.; Lin, H.; Zhu, Q.-L. Nonbonding Electron Inversion-Driven Structural Engineering: Synergistic Enhancement of Linear and Nonlinear Optical Properties. Angew. Chem. Int. Ed. 2025, 64, e202506658. [Google Scholar] [CrossRef]
- Feng, X.; Qiu, J.; Zhou, S. Synergistic effect in nonlinear response in glass ceramics. J. Am. Ceram. Soc. 2024, 107, 1936–1948. [Google Scholar] [CrossRef]
- Konkoly-Thege, I.; Ruff, I.; Adeosun, S.O.; Sime, S.J. Properties of molten carboxylates. Part 6. A quantitative differential thermal analysis study of phase transitions in some zinc and cadmium carboxylates. Thermochim. Acta 1978, 24, 89–96. [Google Scholar] [CrossRef]
- Asaula, V.M.; Myrna, T.A.; Yaremchuk, H.H.; Tolochko, A.S. Mesomorphic and glass formed properties of gomologies series of cadmium alcanoates. Ukr. Chem. J. 2011, 77, 24–27. Available online: http://jnas.nbuv.gov.ua/article/UJRN-0000895786 (accessed on 1 August 2025).
- Klimusheva, G.; Dmitruk, I.; Mirnaya, T.; Tolochko, A.; Bugaychuk, S.; Naumenko, A.; Asaula, V. Monodispersity and ordering of semiconductor quantum dots synthesised in ionic liquid crystalline phase of cadmium alkanoates. Liq. Cryst. 2013, 40, 980–988. [Google Scholar] [CrossRef]
- Zhulai, D.; Boichuk, N.; Pustovyi, D.; Kovalchuk, O.; Garbovskiy, Y.; Klimusheva, G.; Mirnaya, T.; Yaremchuk, G.; Vitusevich, S. Synthesis of Carbon and Gold Nanoparticles in Ionic Liquid Crystals: Structural Properties and Electrical Behavior for Electro-Optical Sensors. Nano Sel. 2025, e202400063. [Google Scholar] [CrossRef]
- Nakashima, S.; Tatewaki, Y.; Okada, S.; Nagakura, H.; Shindo, A.; Mikura, C.; Shiga, K.; Terakawa, K.; Yamada, M. Polymerization of a divalent metal salt of an unsaturated carboxylic acid stimulated by ion exchange with a metal salt of fatty acids. Polym. J. 2016, 48, 855–858. [Google Scholar] [CrossRef]
- Jiang, Y.; Ojo, W.-S.; Mahler, B.; Xu, X.; Abécassis, B.; Dubertret, B. Synthesis of CdSe Nanoplatelets without Short-Chain Ligands: Implication for Their Growth Mechanisms. ACS Omega 2018, 3, 6199–6205. [Google Scholar] [CrossRef]
- van der Bok, J.C.; Prins, P.T.; Montanarella, F.; Maaskant, D.N.; Brzesowsky, F.A.; van der Sluijs, M.M.; Salzmann, B.B.V.; Rabouw, F.T.; Petukhov, A.V.; Donega, C.D.M.; et al. In Situ Optical and X-ray Spectroscopy Reveals Evolution toward Mature CdSe Nanoplatelets by Synergetic Action of Myristate and Acetate Ligands. J. Am. Chem. Soc. 2022, 144, 8096–8105. [Google Scholar] [CrossRef] [PubMed]
- Wagnon, B.; Valleix, R.; Abécassis, B. Cadmium Carboxylate Preparation Method Impacts the Synthesis of CdSe Nanoplatelets through Differences in Dissolution Kinetics. Chem. Mater. 2025, 37, 4291–4300. [Google Scholar] [CrossRef]
- Perumbilavil, S.; Sandeep, C.S.; Matham, M.V. Unconventional z-scan signatures in water arising from the interplay of repetition rate dependent electronic and thermal nonlinearities. J. Mol. Liq. 2025, 425, 127181. [Google Scholar] [CrossRef]
- Sheik-Bahai, M.; Said, A.A.; Wei, T.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Sheik-Bahai, M.; Said, A.A.; Van Stryland, E.W. High-sensitivity, single-beam n2 measurements. Opt. Lett. 1989, 14, 955. [Google Scholar] [CrossRef]
- Chapple, P.B.; Staromlynska, J.; Hermann, J.A.; Mckay, T.J.; Mcduff, R.G. Single-Beam Z-Scan: Measurement Techniques and Analysis. J. Nonlinear Opt. Phys. Mater. 1997, 6, 251. [Google Scholar] [CrossRef]
- Kwak, C.H.; Lee, Y.L.; Kim, S.G. Analysis of asymmetric Z-scan measurement for large optical nonlinearities in an amorphous As2S3 thin film. J. Opt. Soc. Am. B 1999, 16, 600–604. [Google Scholar] [CrossRef]
- Rout, A.; Boltaev, G.S.; Ganeev, R.A.; Fu, Y.; Maurya, S.K.; Kim, V.V.; Rao, K.S.; Guo, C. Nonlinear Optical Studies of Gold Nanoparticle Films. Nanomaterials 2019, 9, 291. [Google Scholar] [CrossRef]
- Boyd, R. Nonlinear Optics, 2nd ed.; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Mehta, V.N.; Jha, S.; Singhal, R.K.; Kailasa, S.K. Preparation of multicolor emitting carbon dots for HeLa cell imaging. New J. Chem. 2014, 38, 6152–6160. [Google Scholar] [CrossRef]
- Mooradian, A. Photoluminescence of Metals. Phys. Rev. Lett. 1969, 22, 185. [Google Scholar] [CrossRef]
- Cheng, Y.; Lu, G.; He, Y.; Shen, H.; Zhao, J.; Xia, K.; Gong, Q. Luminescence Quantum Yields of Gold Nanoparticles Varying with Excitation. Nanoscale 2016, 8, 2188–2194. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Zhou, C.; Yu, M.; Liu, J. Different sized luminescent gold nanoparticles. Nanoscale 2012, 4, 4073–4083. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Fang, B.; Peng, J.; Deng, S.; Hu, L.; Lai, W. Luminescent gold nanoclusters from synthesis to sensing: A comprehensive review. Chem. Eng. J. 2025, 503, 158294. [Google Scholar] [CrossRef]
- Surendran, P.; Lakshmanan, A.; Vinitha, G.; Ramalingam, G.; Rameshkumar, P. Facile preparation of high fluorescent carbon quantum dots from orange waste peels for nonlinear optical applications. Luminescence 2019, 35, 196–202. [Google Scholar] [CrossRef]
- Sun, Y.-P.; Zhou, B.; Lin, Y.; Wang, W.; Fernando, K.S.; Pathak, P.; Meziani, M.J.; Harruff, B.A.; Wang, X.; Wang, H. Quantum-Sized Carbon Dots for Bright and Colorful Photoluminescence. J. Am. Chem. Soc. 2006, 128, 7756–7757. [Google Scholar] [CrossRef]
- Mehta, V.N.; Jha, S.; Basu, H.; Singhal, R.K.; Kailasa, S.K. One-step hydrothermal approach to fabricate carbon dots from apple juice for imaging of mycobacterium and fungal cells. Sens. Actuators B Chem. 2015, 213, 434–443. [Google Scholar] [CrossRef]
- Wang, L.; Li, W.; Li, M.; Su, Q.; Li, Z.; Pen, D.; Wu, M. Ultrastable Amine, Sulfo Cofunctionalized Graphene Quantum Dots with High Two-Photon Fluorescence for Cellular Imaging. ACS Sustain. Chem. Eng. 2018, 6, 4711. [Google Scholar]
- Yan, Y.; Gong, J.; Chen, J.; Zeng, Z.; Huan, W.; Pu, K.; Liu, J.; Chen, P. Recent Advances on Graphene Quantum Dots: From Chemistry and Physics to Applications. Adv. Mater. 2019, 31, e1808283. [Google Scholar] [CrossRef]
- Liu, J.; Li, R.; Yang, B. Carbon Dots: New Type of Carbon-Based Nanomaterial with Wide Applications. ACS Cent. Sci. 2020, 6, 2179–2195. [Google Scholar] [CrossRef]
- Link, S.; Burda, C.; Wang, Z.L.; El-Sayed, M.A. Electron dynamics in gold and gold–silver alloy nanoparticles: The influence of a nonequilibrium electron distribution and the size dependence of the electron–phonon relaxation. J. Chem. Phys. 1999, 111, 1255. [Google Scholar] [CrossRef]
- Orooji, Y.; Gol, H.G.; Jaleh, B.; Vaziri, M.R.R.; Eslamipanah, M. Large Optical Nonlinearity of the Activated Carbon Nanoparticles Prepared by Laser Ablation. Nanomaterials 2021, 11, 737. [Google Scholar] [CrossRef]
- Santos, C.I.M.; Mariz, I.F.A.; Pinto, S.N.; Gonçalves, G.; Bdikin, I.; Marques, P.A.A.P.; Neves, M.G.P.M.S.; Martinho, J.M.G.; Maçôas, E.M.S. Selective two-photon absorption in carbon dots: A piece of the photoluminescence emission puzzle. Nanoscale 2018, 10, 12505–12514. [Google Scholar] [CrossRef]
- e Silva, N.J.B.; Brito, F.d.C.d.M.; Baltar, H.T.; Magalhães, J.L.; Viana, V.G.F.; Santos, F.E.P.; Garcia, H.A. Third- and fifth-order optical nonlinearities of norbixin. Results Opt. 2022, 6, 100205. [Google Scholar] [CrossRef]
- Liberman, V.; Sworin, M.; Kingsborough, R.P.; Geurtsen, G.P.; Rothschild, M. Nonlinear bleaching, absorption, and scattering of 532-nm-irradiated plasmonic nanoparticles. J. Appl. Phys. 2013, 113, 053107. [Google Scholar] [CrossRef]
- Wang, K.; Long, H.; Fu, M.; Yang, G.; Lu, P. Intensity-dependent reversal of nonlinearity sign in a gold nanoparticle array. Opt. Lett. 2010, 35, 1560–1562. [Google Scholar] [CrossRef]
- Dong, N.; Li, Y.; Zhang, S.; McEvoy, N.; Gatensby, R.; Duesberg, G.S.; Wang, J. Saturation of Two-Photon Absorption in Layered Transition Metal Dichalcogenides: Experiment and Theory. ACS Photonics 2018, 5, 1558–1565. [Google Scholar] [CrossRef]
- Mandal, D.; Shrivastava, M.; Sharma, S.; Poonia, A.K.; Marik, S.; Singh, R.P.; Adarsh, K.V. Band Edge Carrier-Induced Sign Reversal of an Ultrafast Nonlinear Optical Response in Few-Layer ReS2 Nanoflakes. ACS Appl. Nano Mater. 2022, 5, 5479–5486. [Google Scholar] [CrossRef]
- Sutherland, R.L. Handbook of Nonlinear Optics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar] [CrossRef]








| Sample | Thickness L, µm | α0 (800 nm), cm−1 | α0 (600 nm), cm−1 |
|---|---|---|---|
| CdC8 + Au NPs | 55.0 | 419.56 | 568.34 |
| CdC8 + C QDs | 43.8 | 126.58 | 206.93 |
| CdC8 + Au NPs + C QDs | 29.0 | 204.71 | 290.62 |
| Sample | Emission Wavelength, nm | τ1, ns | τ2, ns | τ3, ns |
|---|---|---|---|---|
| CdC8 + C QDs | 420 | 0.58 ± 0.02 | 3.18 ± 0.02 | 8.74 ± 0.02 |
| 520 | 0.71 ± 0.02 | 3.43 ± 0.02 | 9.54 ± 0.02 | |
| CdC8 + Au NPs + C QDs | 390 | 0.35 ± 0.02 | 3.20 ± 0.02 | 11.77 ± 0.02 |
| 468 | 0.77 ± 0.02 | 3.79 ± 0.02 | 11.68 ± 0.02 |
| I0, GW/cm2 | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|
| 143.29 | 1.46 × 10−9 | 630 | −2.73 × 10−14 | −1.17 × 10−12 | 5.29 × 10−13 | 1.28 × 10−12 |
| 380.16 | 1.16 × 10−9 | 730 | −1.83 × 10−14 | −0.78 × 10−12 | 4.21 × 10−13 | 0.89 × 10−12 |
| 453.27 | 1.13 × 10−9 | 780 | −2.02 × 10−14 | −0.86 × 10−12 | 4.10 × 10−13 | 0.96 × 10−12 |
| 584.86 | 0.76 × 10−9 | 800 | −1.66 × 10−14 | −0.71 × 10−12 | 2.76 × 10−13 | 0.76 × 10−12 |
| I0, GW/cm2 | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|
| 160.84 | 2.28 × 10−9 | 140 | −3.22 × 10−14 | −1.38 × 10−12 | 0.83 × 10−12 | 1.61 × 10−12 |
| 368.46 | 0.81 × 10−9 | 258 | −2.86 × 10−14 | −1.22 × 10−12 | 0.29 × 10−12 | 1.26 × 10−12 |
| 438.65 | 0.86 × 10−9 | 250 | 1.72 × 10−14 | 0.73 × 10−12 | 0.31 × 10−12 | 0.80 × 10−12 |
| 584.86 | 0.61 × 10−9 | 360 | 1.05 × 10−14 | 0.45 × 10−12 | 0.22 × 10−12 | 0.50 × 10−12 |
| I0, GW/cm2 | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|
| 163.76 | 1.70 × 10−9 | 240 | −1.56 × 10−14 | −0.67 × 10−12 | 0.62 × 10−12 | 0.91 × 10−12 |
| 204.70 | 2.92 × 10−9 | 170 | −3.27 × 10−14 | −1.40 × 10−12 | 1.06 × 10−12 | 1.75 × 10−12 |
| 365.54 | 1.28 × 10−9 | 295 | 1.17 × 10−14 | 0.50 × 10−12 | 0.46 × 10−12 | 0.68 × 10−12 |
| 584.86 | 0.99 × 10−9 | 450 | 0.98 × 10−14 | 0.42 × 10−12 | 0.36 × 10−12 | 0.55 × 10−12 |
| I0, GW/cm2 | ΔT | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|---|
| 266.9 | 0.172 | 1.25 × 10−9 | 670 | 1.32 × 10−14 | 0.57 × 10−12 | 0.34 × 10−12 | 0.66 × 10−12 |
| 424.3 | −0.640 | 1.37 × 10−9 | 750 | −3.1 × 10−14 | −1.33 × 10−12 | 0.37 × 10−12 | 1.38 × 10−12 |
| 581.7 | −1.116 | 1.11 × 10−9 | 750 | −3.94 × 10−14 | −1.69 × 10−12 | 0.29 × 10−12 | 1.71 × 10−12 |
| I0, GW/cm2 | ΔT | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|---|
| 342.18 | −0.915 | 0.8 × 10−9 | 300 | −3.21 × 10−14 | −1.37 × 10−12 | 0.22 × 10−12 | 1.39 × 10−12 |
| 479.05 | −0.092 | 0.62 × 10−9 | 400 | −0.23 × 10−14 | −0.10 × 10−12 | 0.17 × 10−12 | 0.20 × 10−12 |
| 615.92 | −0.573 | 0.66 × 10−9 | 800 | −1.12 × 10−14 | −0.48 × 10−12 | 0.18 × 10−12 | 0.51 × 10−12 |
| I0, GW/cm2 | ΔT | β, cm/W | Is, GW/cm2 | n2, cm2/W | Reχ(3), esu | Imχ(3), esu | χ(3), esu |
|---|---|---|---|---|---|---|---|
| 314.80 | −0.374 | 1.46 × 10−9 | 295 | −2.1 × 10−14 | −8.96 × 10−13 | 3.97 × 10−13 | 9.8 × 10−13 |
| 479.05 | 0.472 | 1.24 × 10−9 | 390 | 1.74 × 10−14 | 7.43 × 10−13 | 3.37 × 10−13 | 8.16 × 10−13 |
| 615.92 | 0.726 | 0.98 × 10−9 | 450 | 2.08 × 10−14 | 8.89 × 10−13 | 2.67 × 10−13 | 9.28 × 10−13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudenko, V.; Tolochko, A.; Bugaychuk, S.; Zhulai, D.; Klimusheva, G.; Yaremchuk, G.; Mirnaya, T.; Garbovskiy, Y. Glass-Forming Ionic Liquid Crystal Gold–Carbon Nanocomposites with Ultrafast Optical Nonlinearity Sign Reversal. J. Compos. Sci. 2025, 9, 472. https://doi.org/10.3390/jcs9090472
Rudenko V, Tolochko A, Bugaychuk S, Zhulai D, Klimusheva G, Yaremchuk G, Mirnaya T, Garbovskiy Y. Glass-Forming Ionic Liquid Crystal Gold–Carbon Nanocomposites with Ultrafast Optical Nonlinearity Sign Reversal. Journal of Composites Science. 2025; 9(9):472. https://doi.org/10.3390/jcs9090472
Chicago/Turabian StyleRudenko, Valentyn, Anatolii Tolochko, Svitlana Bugaychuk, Dmytro Zhulai, Gertruda Klimusheva, Galina Yaremchuk, Tatyana Mirnaya, and Yuriy Garbovskiy. 2025. "Glass-Forming Ionic Liquid Crystal Gold–Carbon Nanocomposites with Ultrafast Optical Nonlinearity Sign Reversal" Journal of Composites Science 9, no. 9: 472. https://doi.org/10.3390/jcs9090472
APA StyleRudenko, V., Tolochko, A., Bugaychuk, S., Zhulai, D., Klimusheva, G., Yaremchuk, G., Mirnaya, T., & Garbovskiy, Y. (2025). Glass-Forming Ionic Liquid Crystal Gold–Carbon Nanocomposites with Ultrafast Optical Nonlinearity Sign Reversal. Journal of Composites Science, 9(9), 472. https://doi.org/10.3390/jcs9090472








