Core Monitoring of Thermoset Polymer Composites’ Curing with Embedded Nanocomposite Sensors: A Key Step Towards Process 4.0
Abstract
1. Introduction
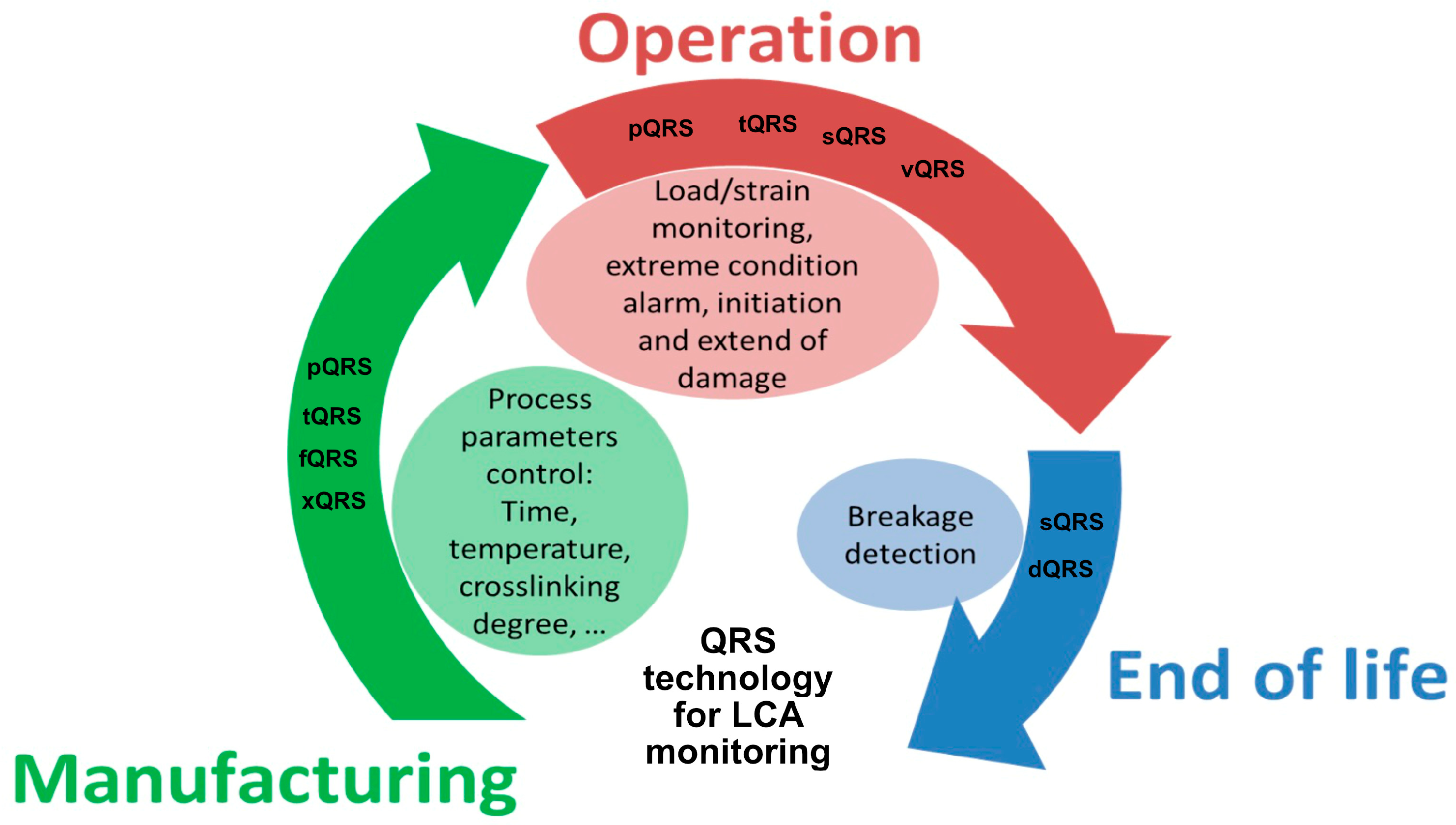
1.1. Brief Overview of Polymer Composites’ Monitoring
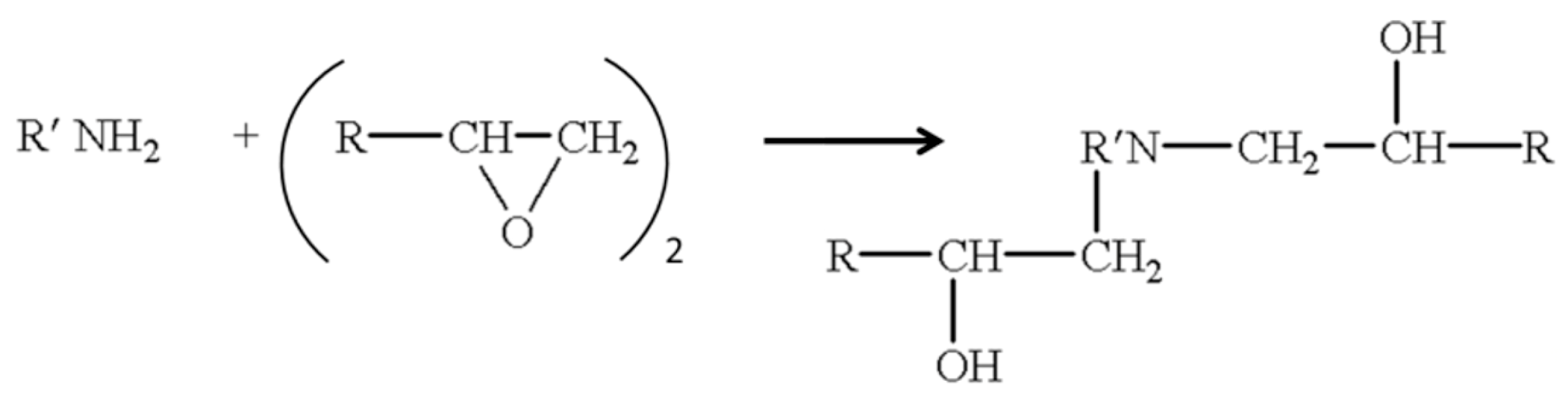
1.2. Strategies for Polymer Crosslinking Monitoring
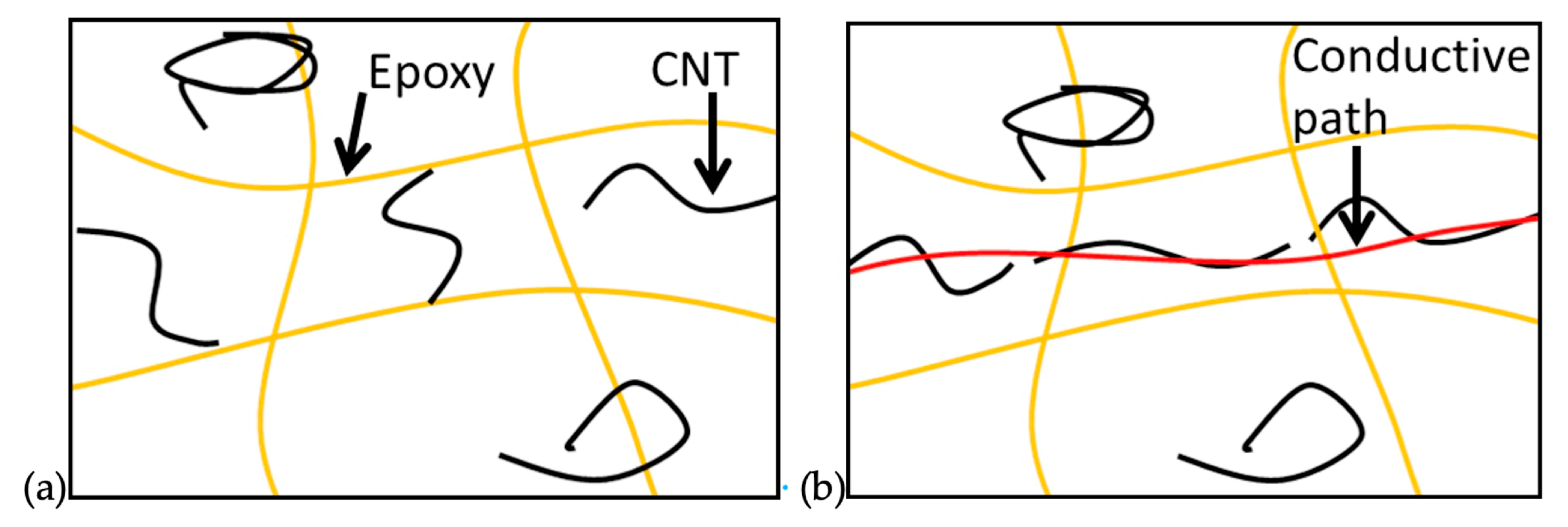
1.3. Using Dynamic Percolation for Living Monitoring of Reticulation
2. Materials and Methods
2.1. Materials
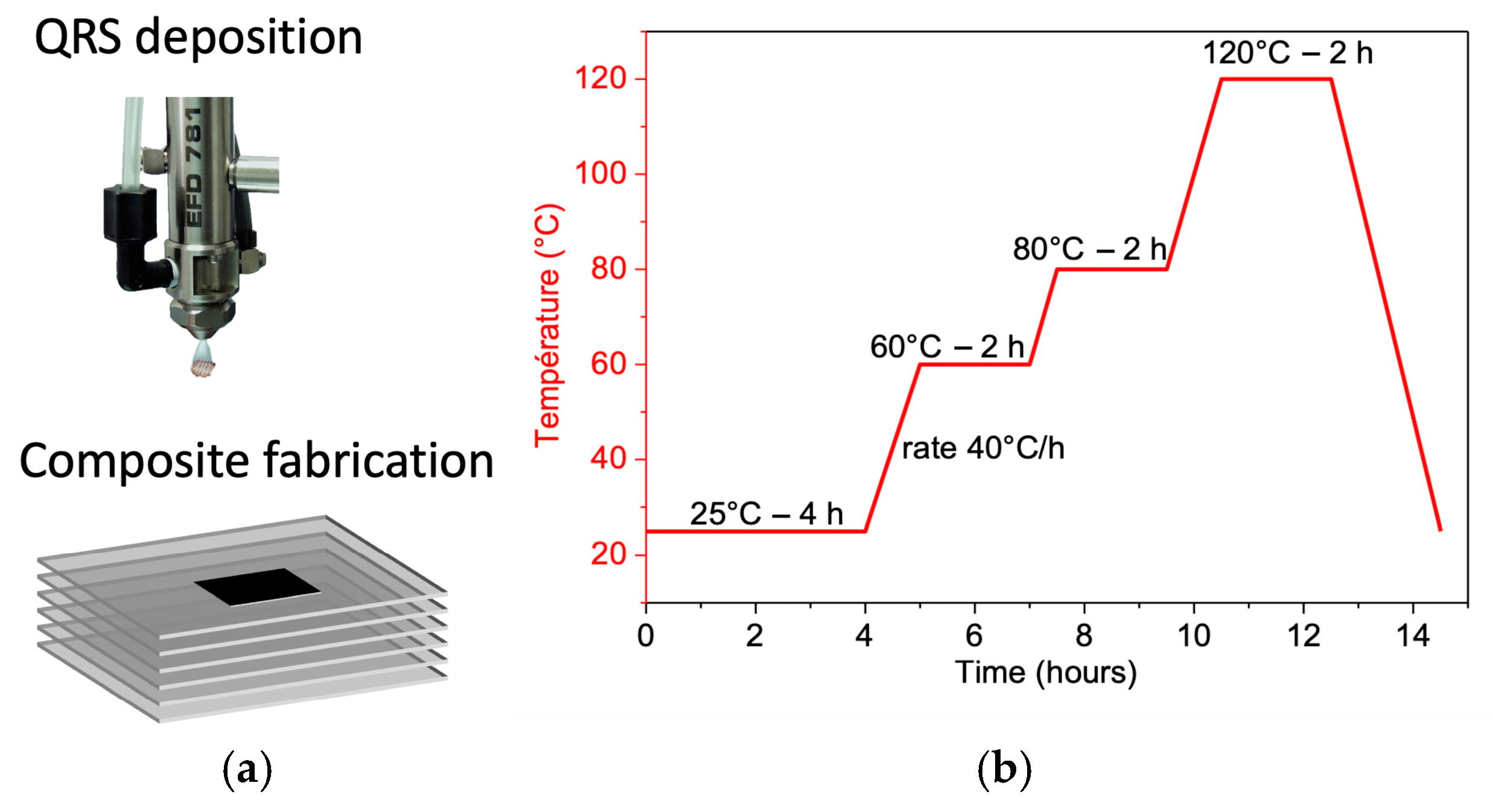
2.2. Fabrication of Samples
2.3. Characterisation Techniques
3. Results and Discussion
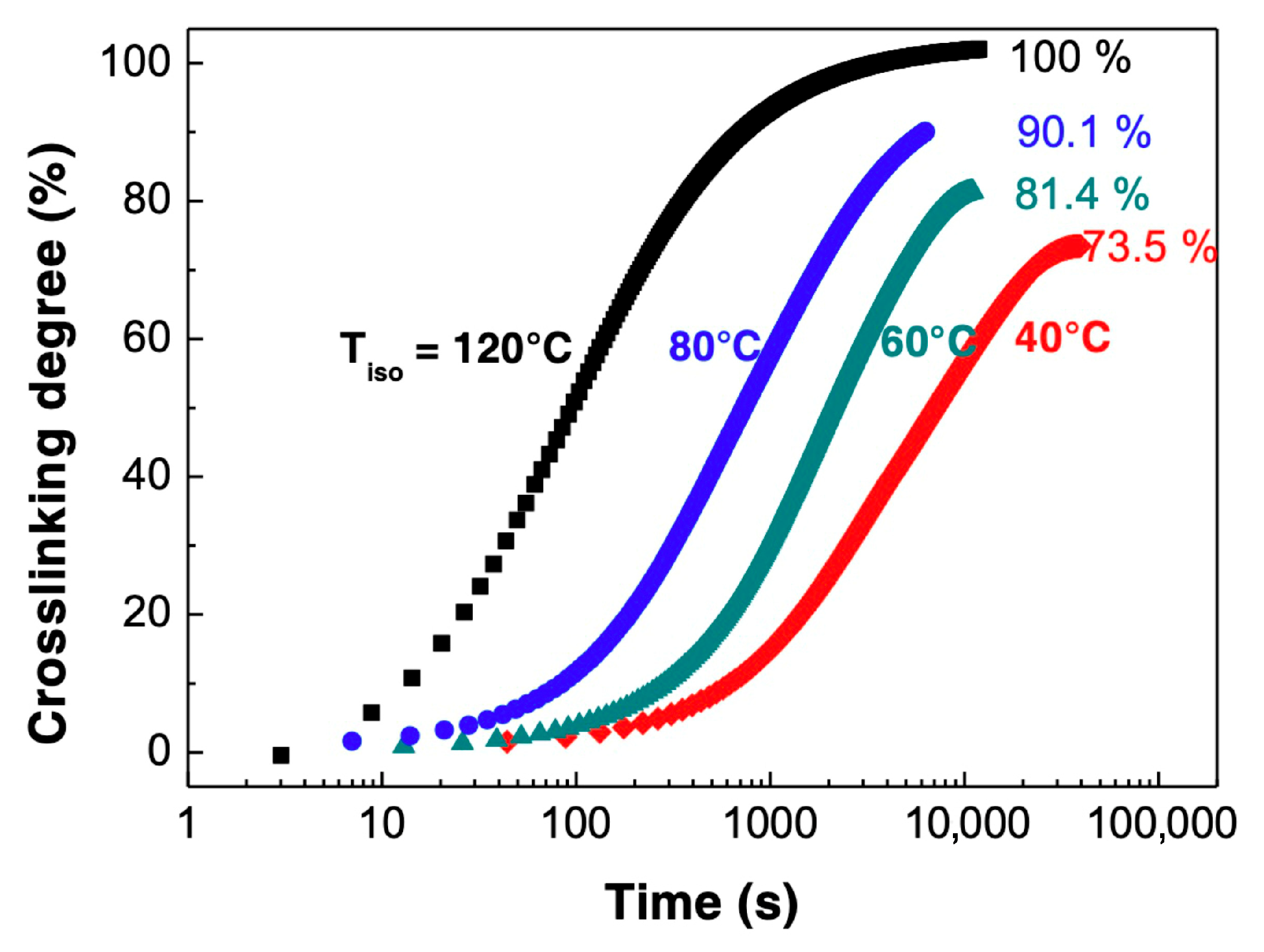
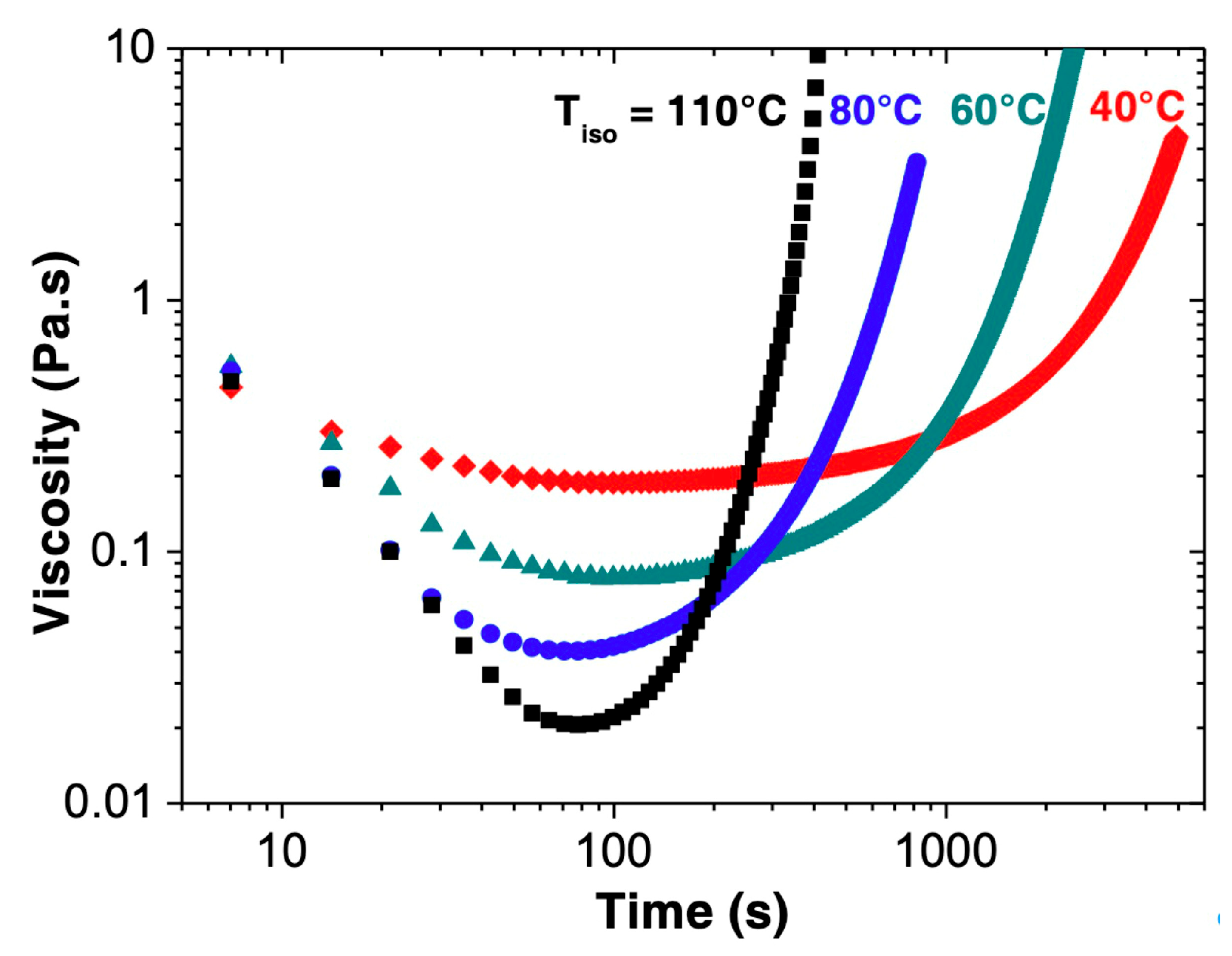
3.1. Isothermal Curing in the Neat Resin
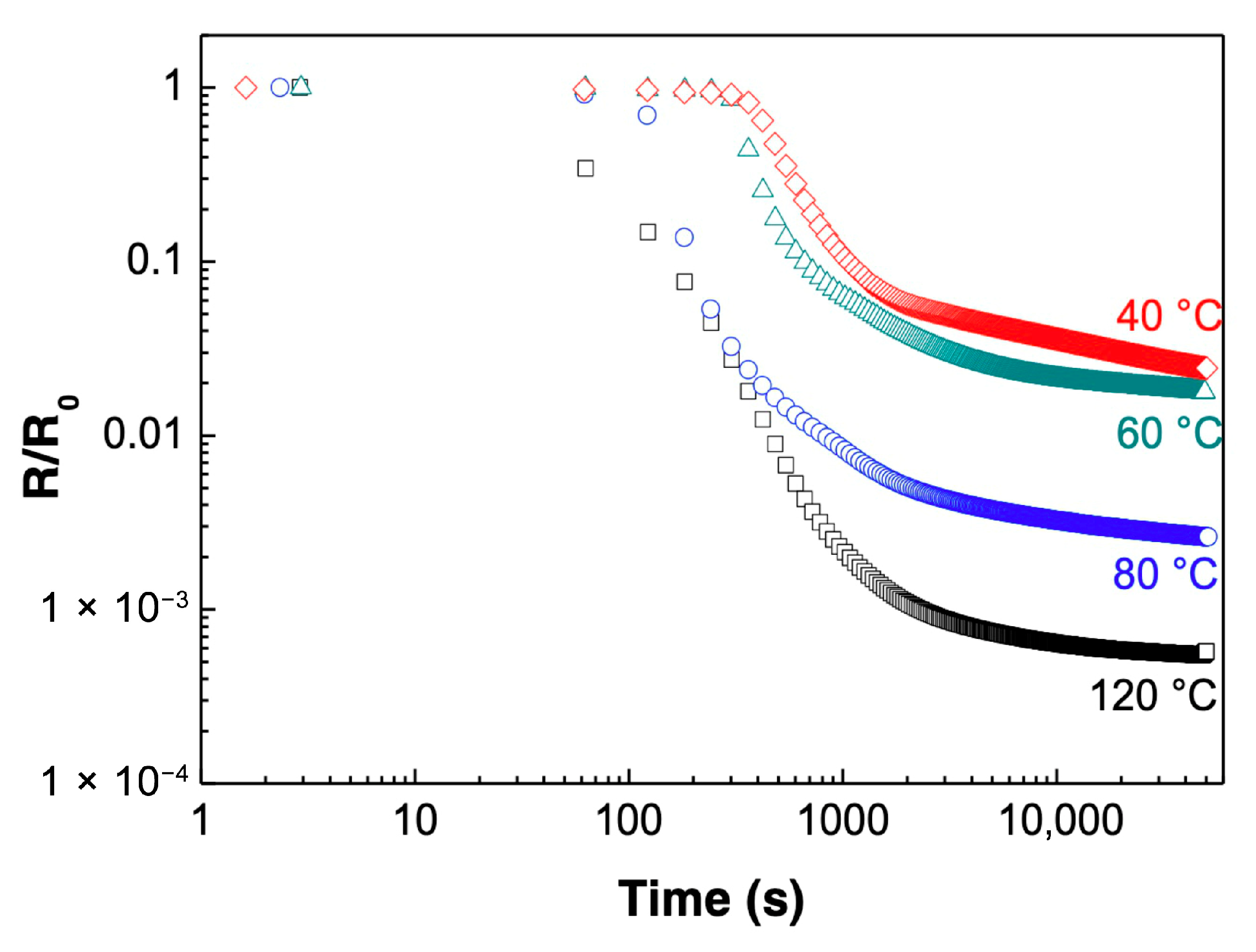
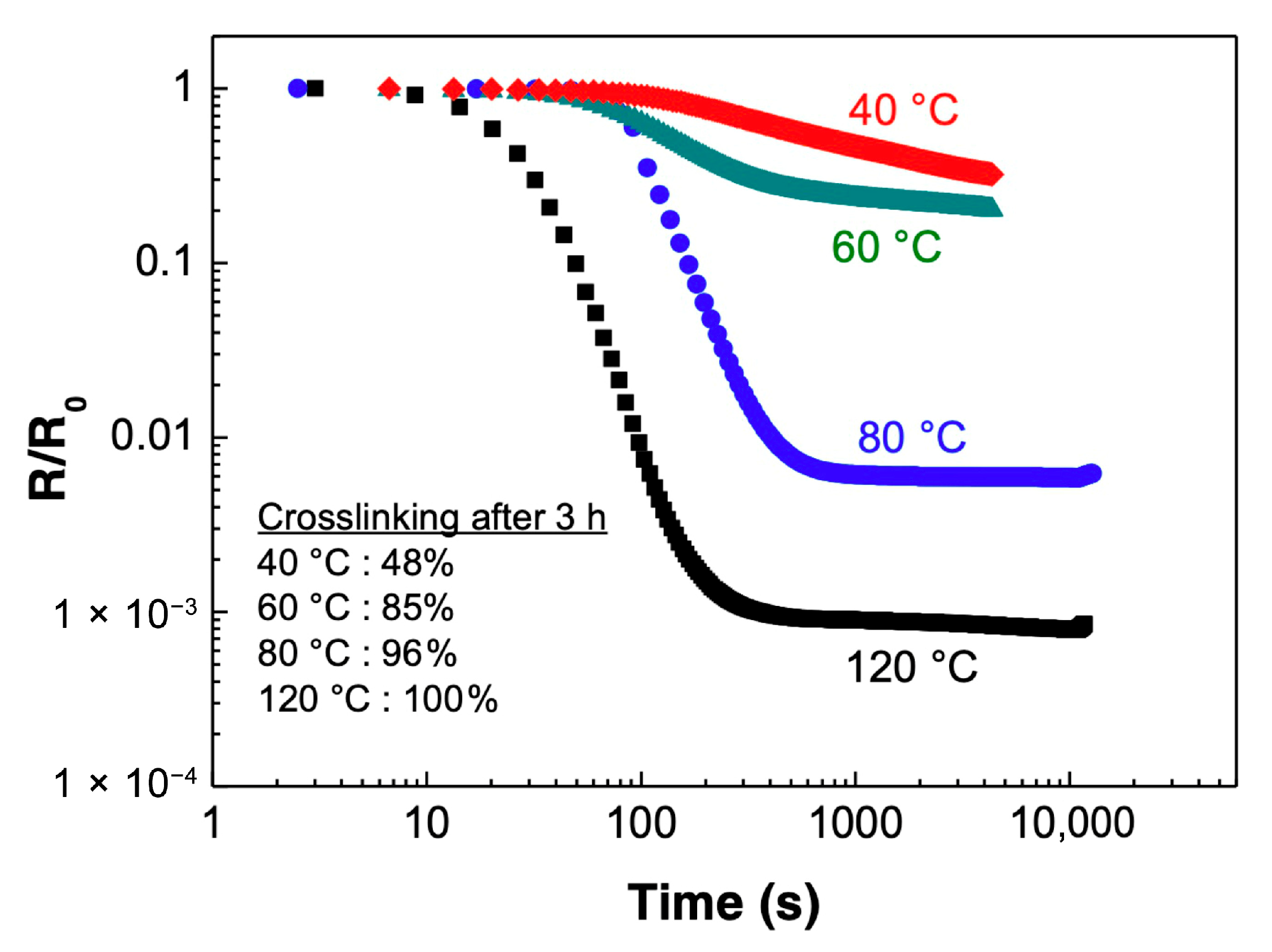
3.2. Resistance Behaviour of an Epoxy–Carbon Nanotubes Nanocomposite Sensor During an Isothermal Treatment
3.3. Case Study: Composite Part Curing Monitoring
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- JEC Group. Overview of the Global Composite Market 2018–2023; JEC Group: Paris, France, 2023. [Google Scholar]
- Das, S.; Warren, J.; West, D.; Schexnayder, S.M. Global Carbon Fiber Composites Supply Chain Competitiveness Analysis; CEMAC: Golden, CO, USA, 2016. [Google Scholar]
- Witten, E.; Mathes, V.; Sauer, M.; Kühnel, M. Composites’ Market: Developments, Trends, Outlooks and Challenges; AVK Federation of Reinforced Plastics: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Balageas, D.; Fritzen, C.-P.; Güemes, A. Structural Health Monitoring; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-1-905209-01-9. [Google Scholar]
- Huston, D. Structural Sensing, Health Monitoring, and Performance Evaluation; Series in Sensors; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781420012354. [Google Scholar]
- Farrar, C.R.; Worden, K. An Introduction to Structural Health Monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Lemartinel, A.; Castro, M.; Fouché, O.; De Luca, J.C.; Feller, J.F. A Review of Nanocarbon-Based Solutions for the Structural Health Monitoring of Composite Parts Used in Renewable Energies. J. Compos. Sci. 2022, 6, 32. [Google Scholar] [CrossRef]
- Lemartinel, A.; Castro, M.; Fouché, O.; De Luca, J.C.; Feller, J.F. Strain Mapping and Damage Tracking in Carbon Fiber Reinforced Epoxy Composites during Dynamic Bending until Fracture with Quantum Resistive Sensors in Array. J. Compos. Sci. 2021, 5, 60. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, Y.; Duongthipthewa, A.; Zhang, J.; Liu, M.; Su, Z.; Zhou, L. An Embedded Non-Intrusive Graphene/Epoxy Broadband Nanocomposite Sensor Co-Cured with GFRP for in Situ Structural Health Monitoring. Compos. Sci. Technol. 2023, 236, 109995. [Google Scholar] [CrossRef]
- Nag-Chowdhury, S.; Bellégou, H.; Pillin, I.; Castro, M.; Longrais, P.; Feller, J.F. Non-Intrusive Health Monitoring of Infused Composites with Embedded Carbon Quantum Piezo-Resistive Sensors. Compos. Sci. Technol. 2016, 123, 286–294. [Google Scholar] [CrossRef]
- MARE-WINT; Ostachowicz, W., McGugan, M., Schröder-Hinrichs, J.U., Luczak, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-39094-9. [Google Scholar]
- de Villoria, R.G.; Miravete, A.; Cuartero, J.; Chiminelli, A.; Tolosana, N. Mechanical Properties of SWNT/Epoxy Composites Using Two Different Curing Cycles. Compos. B Eng. 2006, 37, 273–277. [Google Scholar] [CrossRef]
- Davies, L.; Day, R.; Bond, D.; Nesbitt, A.; Ellis, J.; Gardon, E. Effect of Cure Cycle Heat Transfer Rates on the Physical and Mechanical Properties of an Epoxy Matrix Composite. Compos. Sci. Technol. 2007, 67, 1892–1899. [Google Scholar] [CrossRef]
- Choi, K.; Chung, S.H. Enhanced Time-Slotted Channel Hopping Scheduling with Quick Setup Time for Industrial Internet of Things Networks. Int. J. Distrib. Sens. Netw. 2017, 13, 155014771771362. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Liu, Z. Multi-Task Deep Learning-Empowered Digital Twin for Functional Composite Materials Fabricated by Laser Additive Remanufacturing. CIRP Ann. Manuf. Technol. 2024, 73, 125–128. [Google Scholar] [CrossRef]
- Baalbergen, E.H.; de Marchi, J.A.; Offringa, A.; Hengeveld, S.; Troost, B.; He, K.; Koppert, R.J.; Boikon, B.V.; van den Eijnde, W.A.J. Applying Digital Twin Technology in Thermoplastic Composites Production. In Proceedings of the ITHEC—5th International Conference & Exhibition on Thermoplastic Composites, Bremen, Germany, 13 October 2020. [Google Scholar]
- Polini, W.; Corrado, A. Digital Twin of Composite Assembly Manufacturing Process. Int. J. Prod. Res. 2020, 58, 5238–5252. [Google Scholar] [CrossRef]
- Xu, X.; Wang, G.; Yan, H.; Zhang, L.; Yao, X. Deep-Learning-Enhanced Digital Twinning of Complex Composite Structures and Real-Time Mechanical Interaction. Compos. Sci. Technol. 2023, 241, 110139. [Google Scholar] [CrossRef]
- Marr, B. What Everyone Must Know About Industry 4.0. Forbes, 20 June 2016. Available online: https://www.forbes.com/sites/bernardmarr/2016/06/20/what-everyone-must-know-about-industry-4-0/ (accessed on 11 August 2025).
- Stojkovic, M.; Butt, J. Industry 4.0 Implementation Framework for the Composite Manufacturing Industry. J. Compos. Sci. 2022, 6, 258. [Google Scholar] [CrossRef]
- Merad, L.; Cochez, M.; Margueron, S.; Jauchem, F.; Ferriol, M.; Benyoucef, B.; Bourson, P. In-Situ Monitoring of the Curing of Epoxy Resins by Raman Spectroscopy. Polym. Test. 2009, 28, 42–45. [Google Scholar] [CrossRef]
- Schubel, P.J.; Crossley, R.J.; Boateng, E.K.G.; Hutchinson, J.R. Review of Structural Health and Cure Monitoring Techniques for Large Wind Turbine Blades. Renew. Energy 2013, 51, 113–123. [Google Scholar] [CrossRef]
- Feller, J.F.; Paradis, G.; Lenain, J.C. SENSE in: Enhanse Your Materials. Available online: https://sense-in.fr/en/ (accessed on 11 August 2025).
- Tung, T.T.; Robert, C.; Castro, M.; Feller, J.F.; Kim, T.Y.; Suh, K.S. Enhancing the Sensitivity of Graphene/Polyurethane Nanocomposite Flexible Piezo-Resistive Pressure Sensors with Magnetite Nano-Spacers. Carbon 2016, 108, 450–460. [Google Scholar] [CrossRef]
- Tran, M.T.; Tung, T.T.; Sachan, A.; Losic, D.; Castro, M.; Feller, J.F. 3D Sprayed Polyurethane Functionalized Graphene/Carbon Nanotubes Hybrid Architectures to Enhance the Piezo-Resistive Response of Quantum Resistive Pressure Sensors. Carbon 2020, 168, 564–579. [Google Scholar] [CrossRef]
- Feller, J.F.; Castro, M.; Tran, M.T.; Allègre, W. Pressure Ulcers Monitoring with Combined Piezo- and Chemo-Resistive Nanocomposite Sensors’ Arrays. In Proceedings of the International Conference on Advances in Signal Processing & Artificial Intelligence (ASPAI), Funchal, Portugal, 17–19 April 2024. [Google Scholar]
- Nag-Chowdhury, S.; Bellégou, H.; Pillin, I.; Castro, M.; Longrais, P.; Feller, J.F. Crossed Investigation of Damage in Composites with Embedded Quantum Resistive Strain Sensors (SQRS), Acoustic Emission (AE) and Digital Image Correlation (DIC). Compos. Sci. Technol. 2018, 160, 79–85. [Google Scholar] [CrossRef]
- Lemartinel, A.; Castro, M.; Fouche, O.; De Luca, J.C.; Feller, J.F. Impact and Strain Monitoring in Glass Fiber Reinforced Epoxy Laminates with Embedded Quantum Resistive Sensors (QRS). Compos. Sci. Technol. 2022, 221, 109352. [Google Scholar] [CrossRef]
- Kumar, B.; Castro, M.; Feller, J.F. Controlled Conductive Junction Gap for Chitosan-Carbon Nanotube Quantum Resistive Vapour Sensors. J. Mater. Chem. 2012, 22, 10656–10664. [Google Scholar] [CrossRef]
- Sachan, A.; Castro, M.; Feller, J.F. Volatolomics for Anticipated Diagnosis of Cancers with Chemoresistive Vapour Sensors: A Review. ChemoSensors 2025, 13, 15. [Google Scholar] [CrossRef]
- Beutier, C.; Feller, J.F. Smart Nanocomposites Sensors QRS (Quantum Resistive Sensor) to Develop Process Monitoring. In Proceedings of the JNC 23—Journée Nationale sur les Composites, Besançon, France, 30 June–2 July 2023. [Google Scholar]
- Siddig, N.; Le Bot, P.; Fouché, O.; Denis, Y. Simulation and Monitoring of the Infusion of Thick Composites with Thermoplastic Acrylic Resin. In Proceedings of the 27th ESAFORM International Conference on Material Forming, Toulouse, France, 25 May 2024; pp. 576–585. [Google Scholar]
- Georgelin, L.; Leroy, C.; Paradis, G.; Feller, J.F. Procédé de Suivi de Fabrication d’une Pièce Par Infusion/Injection de Résine Dans Une Préforme Patent. FR2314656, 20 December 2023. [Google Scholar]
- Lapique, F.; Redford, K. Curing Effects on Viscosity and Mechanical Properties of a Commercial Epoxy Resin Adhesive. Int. J. Adhes. Adhes. 2002, 22, 337–346. [Google Scholar] [CrossRef]
- Fernando, G.F. Fibre Optic Sensor Systems for Monitoring Composite Structures. Reinf. Plast. 2005, 49, 41–49. [Google Scholar] [CrossRef]
- Jang, B.Z.; Shih, W.K. Techniques for Cure Monitoring of Thermoset Resins and Composites—A Review. Mater. Manuf. Process. 1990, 5, 301–331. [Google Scholar] [CrossRef]
- Olcese, T.; Spelta, O.; Vargiu, S. Curing Kinetics of Epoxy Resins. J. Polym. Sci. Polym. Symp. 1975, 53, 113–126. [Google Scholar] [CrossRef]
- Kamal, M.R.; Sourour, S. Kinetics and Thermal Characterization of Thermoset Cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Barton, J.M. Monitoring the Cross-Linking of Epoxide Resins by Thermoanalytical Techniques. J. Macromol. Sci. Part A—Chem. 1974, 8, 25–32. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Mechanism and Kinetics of Epoxy−Amine Cure Studied by Differential Scanning Calorimetry. Macromolecules 1996, 29, 1867–1873. [Google Scholar] [CrossRef]
- Bhargava, R.; Wang, S.Q.; Koenig, J.L. Studying Polymer-Dispersed Liquid-Crystal Formation by FTIR Spectroscopy. 1. Monitoring Curing Reactions. Macromolecules 1999, 32, 8982–8988. [Google Scholar] [CrossRef]
- González-González, M.; Cabanelas, J.C.; Baselga, J. Infrared Spectroscopy—Materials Science, Engineering and Technology; Theophile, T., Ed.; InTech: London, UK, 2012; Volume 2, ISBN 978-953-51-0537-4. [Google Scholar]
- Sanchez Soto, M.; Pages, P.; Lacorte, T.; Briceno, K.; Carrasco, F. Curing FTIR Study and Mechanical Characterization of Glass Bead Filled Trifunctional Epoxy Composites. Compos. Sci. Technol. 2007, 67, 1974–1985. [Google Scholar] [CrossRef]
- Roller, M.B. Rheology of Curing Thermosets: A Review. Polym. Eng. Sci. 1986, 26, 432–440. [Google Scholar] [CrossRef]
- Sbirrazzuoli, N.; Vyazovkin, S.; Mititelu, A.; Sladic, C.; Vincent, L. A Study of Epoxy-Amine Cure Kinetics by Combining Isoconversional Analysis with Temperature Modulated DSC and Dynamic Rheometry. Macromol. Chem. Phys. 2003, 204, 1815–1821. [Google Scholar] [CrossRef]
- Winter, H.H. Can the Gel Point of a Cross-linking Polymer Be Detected by the G′–G″ Crossover? Polym. Eng. Sci. 1987, 27, 1698–1702. [Google Scholar] [CrossRef]
- Nass, K.A.; Seferis, J.C. Analysis of the Dielectric Response of Thermosets During Isothermal and Nonisothermal Cure. Polym. Eng. Sci. 1989, 29, 315–324. [Google Scholar] [CrossRef]
- Bidstrup, S.A.; Sheppard, N.F.; Senturia, S.D. Dielectric Analysis of the Cure of Thermosetting Epoxy/Amine Systems. Polym. Eng. Sci. 1989, 29, 325–328. [Google Scholar] [CrossRef]
- Hardis, R.; Jessop, J.L.P.; Peters, F.E.; Kessler, M.R. Cure Kinetics Characterization and Monitoring of an Epoxy Resin Using DSC, Raman Spectroscopy, and DEA. Compos. Part A Appl. Sci. Manuf. 2013, 49, 100–108. [Google Scholar] [CrossRef]
- Boiteux, G.; Dublineau, P.; Feve, M.; Mathieu, C.; Seytre, G.; Ulanski, J. Dielectric and Viscoelastic Studies of Curing Epoxy-Amine Model Systems. Polym. Bull. 1993, 30, 441–447. [Google Scholar] [CrossRef]
- Sampath, U.; Kim, H.; Kim, D.; Kim, Y.; Song, M. In-Situ Cure Monitoring of Wind Turbine Blades by Using Fiber Bragg Grating Sensors and Fresnel Reflection Measurement. Sensors 2015, 15, 18229–18238. [Google Scholar] [CrossRef]
- Moghaddam, M.K.; Breede, A.; Chaloupka, A.; Bödecker, A.; Habben, C.; Meyer, E.-M.; Brauner, C.; Lang, W. Design, Fabrication and Embedding of Microscale Interdigital Sensors for Real-Time Cure Monitoring during Composite Manufacturing. Sens. Actuators A Phys. 2016, 243, 123–133. [Google Scholar] [CrossRef]
- Yang, Y.; Chiesura, G.; Vervust, T.; Bossuyt, F.; Luyckx, G.; Degrieck, J.; Vanfleteren, J. Design and Fabrication of a Flexible Dielectric Sensor System for in Situ and Real-Time Production Monitoring of Glass Fibre Reinforced Composites. Sens. Actuators A Phys. 2016, 243, 103–110. [Google Scholar] [CrossRef]
- Harsch, M.; Karger-Kocsis, J.; Herzog, F. Influence of Cure Regime on the Strain Development in an Epoxy Resin as Monitored by a Fiber Bragg Grating Sensor. Macromol. Mater. Eng. 2007, 292, 474–483. [Google Scholar] [CrossRef]
- Waris, M.; Tortech, B.; Marin, E.; Vautrin, A. Suivi Par Capteur à Fibre Optique Du Procédé Resin Transfer Moulding (RTM). In Proceedings of the 17èmes Journées Nationales sur les Composites (JNC17), Poitiers, France, 15–17 June 2011; pp. 1–10. [Google Scholar]
- Dewynter-Marty, V.; Ferdinand, P.; Bocherens, E.; Carbone, R.; Beranger, H.; Bourasseau, S.; Dupont, M.; Balageas, D. Embedded Fiber Bragg Grating Sensors for Industrial Composite Cure Monitoring. J. Intell. Mater. Syst. Struct. 1998, 9, 785–787. [Google Scholar] [CrossRef]
- Leng, J.; Asundi, A. Structural Health Monitoring of Smart Composite Materials by Using EFPI and FBG Sensors. Sens. Actuators A Phys. 2003, 103, 330–340. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Measurement of (Post-)Curing Strain Development with Fibre Bragg Gratings. Polym. Test. 2010, 29, 291–301. [Google Scholar] [CrossRef]
- Antonucci, V.; Giordano, M.; Cusano, A.; Nasser, J.; Nicolais, L. Real Time Monitoring of Cure and Gelification of a Thermoset Matrix. Compos. Sci. Technol. 2006, 66, 3273–3280. [Google Scholar] [CrossRef]
- Cusano, A.; Breglio, G.; Giordano, M.; Calabrò, A.; Cutolo, A.; Nicolais, L. Optoelectronic Sensor for Cure Monitoring in Thermoset-Based Composites. Sens. Actuators A Phys. 2000, 84, 270–275. [Google Scholar] [CrossRef]
- Drissi-Habti, M.; Raman, V. Fatigue Behavior of Smart Composites with Distributed Fiber Optic Sensors for Offshore Applications. J. Compos. Sci. 2021, 6, 2. [Google Scholar] [CrossRef]
- Wang, L.; Tomlin, A.; Pandita, S.D.; Gupta, B.D.; Malik, S.A.; Hudson, M.; Curtis, P.T.; Fernando, G.F. In-Situ Monitoring of Cross-Linking Reactions Using E-Glass Fibres and Evanescent Wave Spectroscopy. Sens. Actuators B Chem. 2016, 236, 358–366. [Google Scholar] [CrossRef]
- Advise, Cure Performance Monitoring System (CPMS): The Intelligent Way to Optimise and Assure Quality of the Processing of Composites. Available online: https://advise-deta.com/en/pages/products (accessed on 11 August 2025).
- Synthesites, OptiFlow System Is Fully Optimised for Composites Processing Providing Resin Arrival Indication and Temperature Measurements at 4 Channels. Available online: https://www.synthesites.com/application-sector/general/optiflow (accessed on 11 August 2025).
- Thostenson, E.T.; Chou, T.-W. Real-Time in Situ Sensing of Damage Evolution in Advanced Fiber Composites Using Carbon Nanotube Networks. Nanotechnology 2008, 19, 215713. [Google Scholar] [CrossRef]
- Viets, C.; Kaysser, S.; Schulte, K. Damage Mapping of GFRP via Electrical Resistance Measurements Using Nanocomposite Epoxy Matrix Systems. Compos. B Eng. 2014, 65, 80–88. [Google Scholar] [CrossRef]
- Puglia, D.; Valentini, L.; Armentano, I.; Kenny, J.M. Effects of Single-Walled Carbon Nanotube Incorporation on the Cure Reaction of Epoxy Resin and Its Detection by Raman Spectroscopy. Diam. Relat. Mater. 2003, 12, 827–832. [Google Scholar] [CrossRef]
- Valentini, L.; Puglia, D.; Frulloni, E.; Armentano, I.; Kenny, J.M.; Santucci, S. Dielectric Behavior of Epoxy Matrix/Single-Walled Carbon Nanotube Composites. Compos. Sci. Technol. 2004, 64, 23–33. [Google Scholar] [CrossRef]
- Puglia, D.; Valentini, L.; Kenny, J.M. Analysis of the Cure Reaction of Carbon Nanotubes/Epoxy Resin Composites through Thermal Analysis and Raman Spectroscopy. J. Appl. Polym. Sci. 2003, 88, 452–458. [Google Scholar] [CrossRef]
- Choi, W.J.; Powell, R.L.; Kim, D.S. Curing Behavior and Properties of Epoxy Nanocomposites with Amine Functionalized Multiwall Carbon Nanotubes. Polym. Compos. 2009, 30, 415–421. [Google Scholar] [CrossRef]
- Xie, H.; Liu, B.; Yuan, Z.; Shen, J.; Cheng, R. Cure Kinetics of Carbon Nanotube/Tetrafunctional Epoxy Nanocomposites by Isothermal Differential Scanning Calorimetry. J. Polym. Sci. B Polym. Phys. 2004, 42, 3701–3712. [Google Scholar] [CrossRef]
- Fogel, M.; Parlevliet, P.; Geistbeck, M.; Olivier, P.; Dantras, É. Thermal, Rheological and Electrical Analysis of MWCNT/Epoxy Matrices. Compos. Sci. Technol. 2015, 110, 118–125. [Google Scholar] [CrossRef]
- Tao, K.; Yang, S.; Grunlan, J.C.; Kim, Y.-S.; Dang, B.; Deng, Y.; Thomas, R.L.; Wilson, B.L.; Wei, X. Effects of Carbon Nanotube Fillers on the Curing Processes of Epoxy Resin-Based Composites. J. Appl. Polym. Sci. 2006, 102, 5248–5254. [Google Scholar] [CrossRef]
- Sourour, S.; Kamal, M.R. Differential Scanning Calorimetry of Epoxy Cure: Isothermal Cure Kinetics. Thermochim. Acta 1976, 14, 41–59. [Google Scholar] [CrossRef]
- Ryan, M.E.; Dutta, A. Kinetics of Epoxy Cure: A Rapid Technique for Kinetic Parameter Estimation. Polymer 1979, 20, 203–206. [Google Scholar] [CrossRef]
- Rohr, D.F.; Klein, M.T. Modeling Diffusion and Reaction in Crosslinking Epoxy-amine Cure Kinetics: A Dynamic Percolation Approach. Indus. Eng. Chem. Res. 1990, 29, 1210–1218. [Google Scholar] [CrossRef]
- Moroni, A.; Mijovic, J.; Pearce, E.M.; Foun, C.C. Cure Kinetics of Epoxy Resins and Aromatic Diamines. J. Appl. Polym. Sci. 1986, 32, 3761–3773. [Google Scholar] [CrossRef]
- Roller, M.B. Characterization of the Time-Temperature-Viscosity Behavior of Curing B-Staged Epoxy Resin. Polym. Eng. Sci. 1975, 15, 406–414. [Google Scholar] [CrossRef]
- Feller, J.F. Conductive polymer composites: Influence of extrusion conditions on positive temperature coefficient effect of poly(butylene terephthalate)/poly(olefin)-carbon black blends. J. Appl. Polym. Sci. 2004, 91, 2151–2157. [Google Scholar] [CrossRef]
- Rabearison, N.; Jochum, C.; Grandidier, J.C. A Cure Kinetics, Diffusion Controlled and Temperature Dependent, Identification of the Araldite LY556 Epoxy. J. Mater. Sci. 2011, 46, 787–796. [Google Scholar] [CrossRef]
- Wu, G.; Asai, S.; Sumita, M. Carbon Black as a Self-Diagnosing Probe To Trace Polymer Dynamics in Highly Filled Compositions. Macromolecules 2002, 35, 1708–1713. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, P.; Ma, C.; Wu, G.; Sumita, M. Temperature and Time Dependence of Conductive Network Formation: Dynamic Percolation and Percolation Time. Polymer 2006, 47, 466–473. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Wang, J.; Ma, C. Self-Assembly and Conductive Network Formation of Vapor-Grown Carbon Fiber in a Poly(Vinylidene Fluoride) Melt. Carbon 2008, 46, 2053–2058. [Google Scholar] [CrossRef]
- Wu, G.; Miura, T.; Asai, S.; Sumita, M. Carbon Black-Loading Induced Phase Fluctuations in PVDF/PMMA Miscible Blends: Dynamic Percolation Measurements. Polymer 2001, 42, 3271–3279. [Google Scholar] [CrossRef]
- Cipriano, B.H.; Kota, A.K.; Gershon, A.L.; Laskowski, C.J.; Kashiwagi, T.; Bruck, H.A.; Raghavan, S.R. Conductivity Enhancement of Carbon Nanotube and Nanofiber-Based Polymer Nanocomposites by Melt Annealing. Polymer 2008, 49, 4846–4851. [Google Scholar] [CrossRef]
- Bilotti, E.; Zhang, H.; Deng, H.; Zhang, R.; Fu, Q.; Peijs, T. Controlling the Dynamic Percolation of Carbon Nanotube Based Conductive Polymer Composites by Addition of Secondary Nanofillers: The Effect on Electrical Conductivity and Tuneable Sensing Behaviour. Compos. Sci. Technol. 2013, 74, 85–90. [Google Scholar] [CrossRef]
- Bilotti, E.; Zhang, R.; Deng, H.; Baxendale, M.; Peijs, T. Fabrication and Property Prediction of Conductive and Strain Sensing TPU/CNT Nanocomposite Fibres. J. Mater. Chem. 2010, 20, 9449. [Google Scholar] [CrossRef]
- Zhang, H.; Bilotti, E.; Tu, W.; Lew, C.Y.; Peijs, T. Static and Dynamic Percolation of Phenoxy/Carbon Nanotube Nanocomposites. Eur. Polym. J. 2015, 68, 128–138. [Google Scholar] [CrossRef]
- Alig, I.; Skipa, T.; Engel, M.; Lellinger, D.; Pegel, S.; Pötschke, P. Electrical Conductivity Recovery in Carbon Nanotube–Polymer Composites after Transient Shear. Phys. Status Solidi (B) 2007, 244, 4223–4226. [Google Scholar] [CrossRef]
- Davis, C.S.; Orloff, N.D.; Woodcock, J.W.; Long, C.J.; Twedt, K.A.; Natarajan, B.; Seppala, J.E.; McClelland, J.J.; Obrzut, J.; Liddle, J.A.; et al. Cure Temperature Influences Composite Electrical Properties by Carbon Nanotube-Rich Domain Formation. Compos. Sci. Technol. 2016, 133, 23–32. [Google Scholar] [CrossRef]
- Prasse, T.; Flandin, L.; Schulte, K.; Bauhofer, W. In Situ Observation of Electric Field Induced Agglomeration of Carbon Black in Epoxy Resin. Appl. Phys. Lett. 1998, 72, 2903–2905. [Google Scholar] [CrossRef]
- Garschke, C.; Parlevliet, P.P.; Weimer, C.; Fox, B.L. Cure kinetics and viscosity modelling of a high-performance epoxy resin film. Polym. Test. 2013, 32, 150–157. [Google Scholar] [CrossRef]
- Gnidakouong, J.R.N.; Roh, H.D.; Kim, J.; Park, Y.-B. In Situ Process Monitoring of Hierarchical Micro-/Nano-Composites Using Percolated Carbon Nanotube Networks. Compos. Part A Appl. Sci. Manuf. 2016, 84, 281–291. [Google Scholar] [CrossRef]
- Lu, S.; Chen, D.; Wang, X.; Xiong, X.; Ma, K.; Zhang, L.; Meng, Q. Monitoring the Manufacturing Process of Glass Fiber Reinforced Composites with Carbon Nanotube Buckypaper Sensor. Polym. Test. 2016, 52, 79–84. [Google Scholar] [CrossRef]
- Luo, S.; Wang, Y.; Wang, G.; Wang, K.; Wang, Z.; Zhang, C.; Wang, B.; Luo, Y.; Li, L.; Liu, T. CNT Enabled Co-Braided Smart Fabrics: A New Route for Non-Invasive, Highly Sensitive & Large-Area Monitoring of Composites. Sci. Rep. 2017, 7, 44056. [Google Scholar] [CrossRef]
- Battisti, A.; Skordos, A.A.; Partridge, I.K. Dielectric Monitoring of Carbon Nanotube Network Formation in Curing Thermosetting Nanocomposites. J. Phys. D Appl. Phys. 2009, 42, 155402. [Google Scholar] [CrossRef][Green Version]
- de la Vega, A.; Kovacs, J.Z.; Bauhofer, W.; Schulte, K. Combined Raman and Dielectric Spectroscopy on the Curing Behaviour and Stress Build up of Carbon Nanotube–Epoxy Composites. Compos. Sci. Technol. 2009, 69, 1540–1546. [Google Scholar] [CrossRef]
- Shen, J.T.; Buschhorn, S.T.; De Hosson, J.T.M.; Schulte, K.; Fiedler, B. Pressure and Temperature Induced Electrical Resistance Change in Nano-Carbon/Epoxy Composites. Compos. Sci. Technol. 2015, 115, 1–8. [Google Scholar] [CrossRef]
- Gao, L.; Chou, T.-W.; Thostenson, E.T.; Zhang, Z. A Comparative Study of Damage Sensing in Fiber Composites Using Uniformly and Non-Uniformly Dispersed Carbon Nanotubes. Carbon 2010, 48, 3788–3794. [Google Scholar] [CrossRef]
- Gojny, F.H.; Wichmann, M.H.G.; Fiedler, B.; Kinloch, I.A.; Bauhofer, W.; Windle, A.H.; Schulte, K. Evaluation and Identification of Electrical and Thermal Conduction Mechanisms in Carbon Nanotube/Epoxy Composites. Polymer 2006, 47, 2036–2045. [Google Scholar] [CrossRef]
- Pillin, I.; Castro, M.; Nag-Chowdhury, S.; Feller, J.F. Robustness of Carbon Nanotube-Based Sensor to Probe Composites’ Interfacial Damage in Situ. J. Compos. Mater. 2015, 50, 109–113. [Google Scholar] [CrossRef]

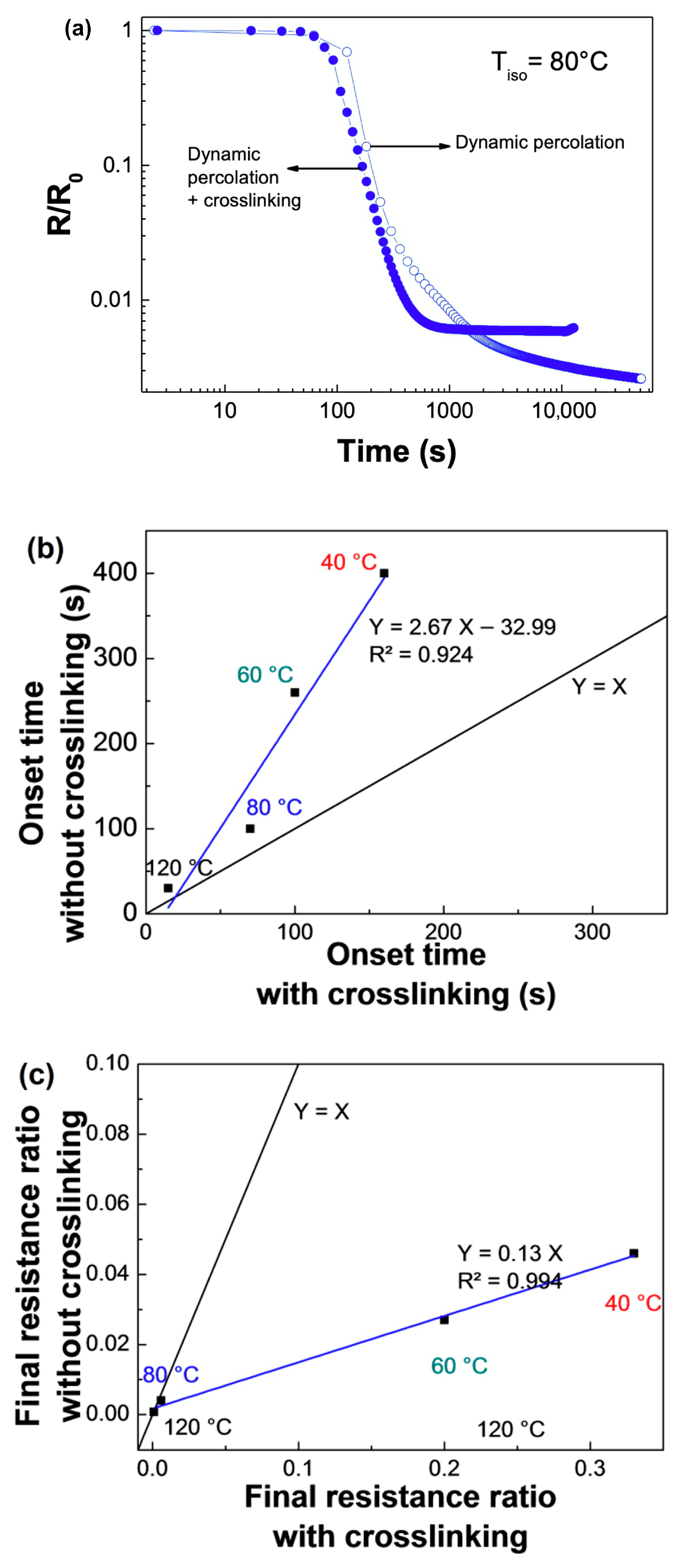
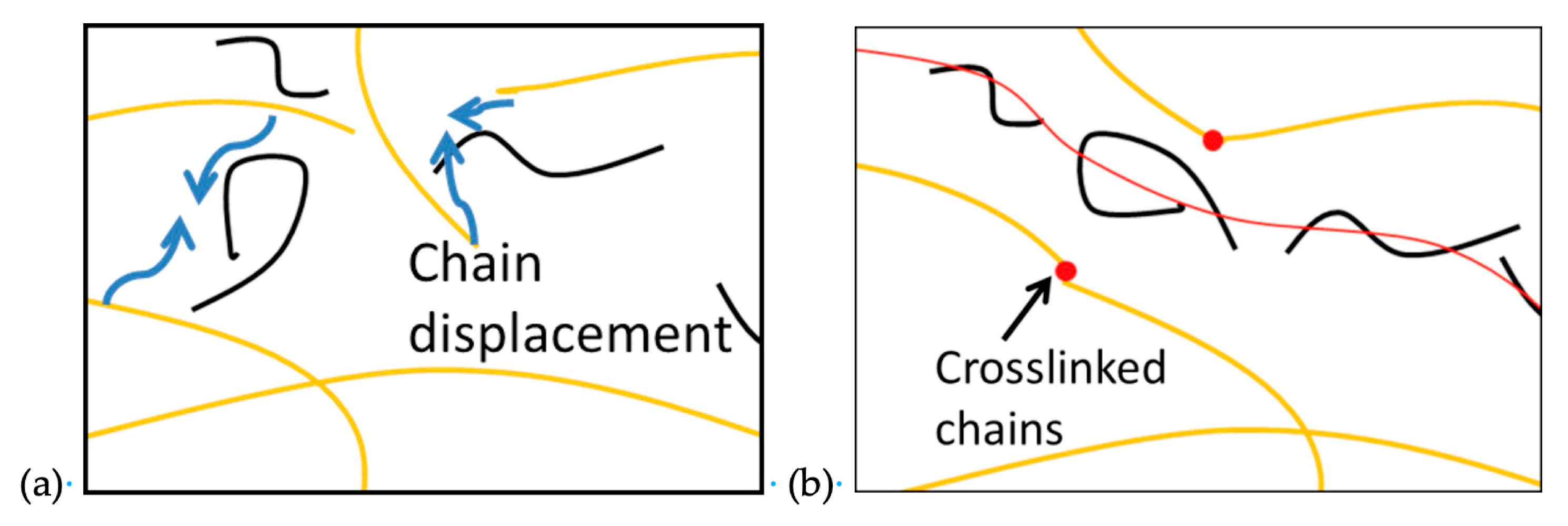
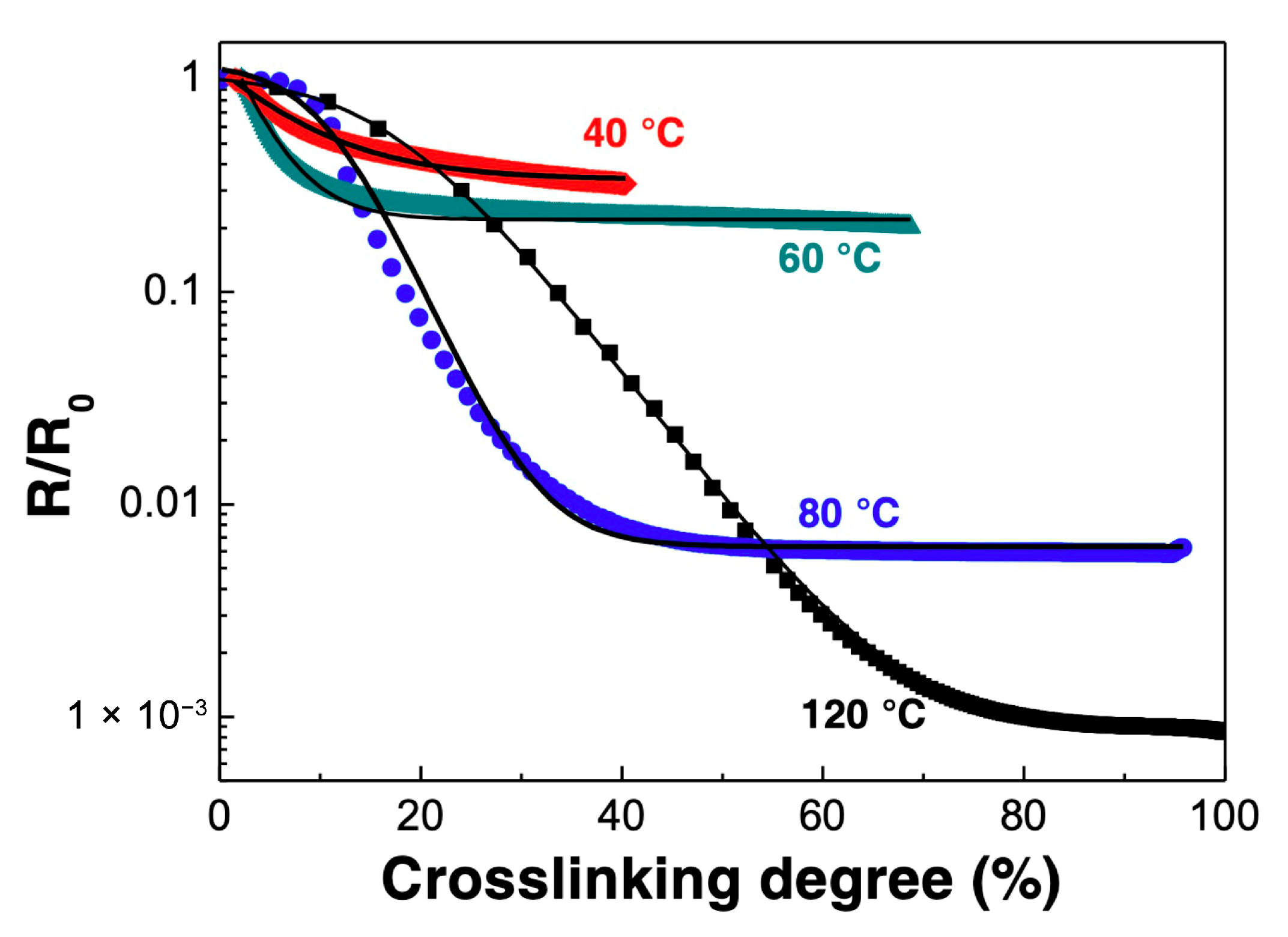
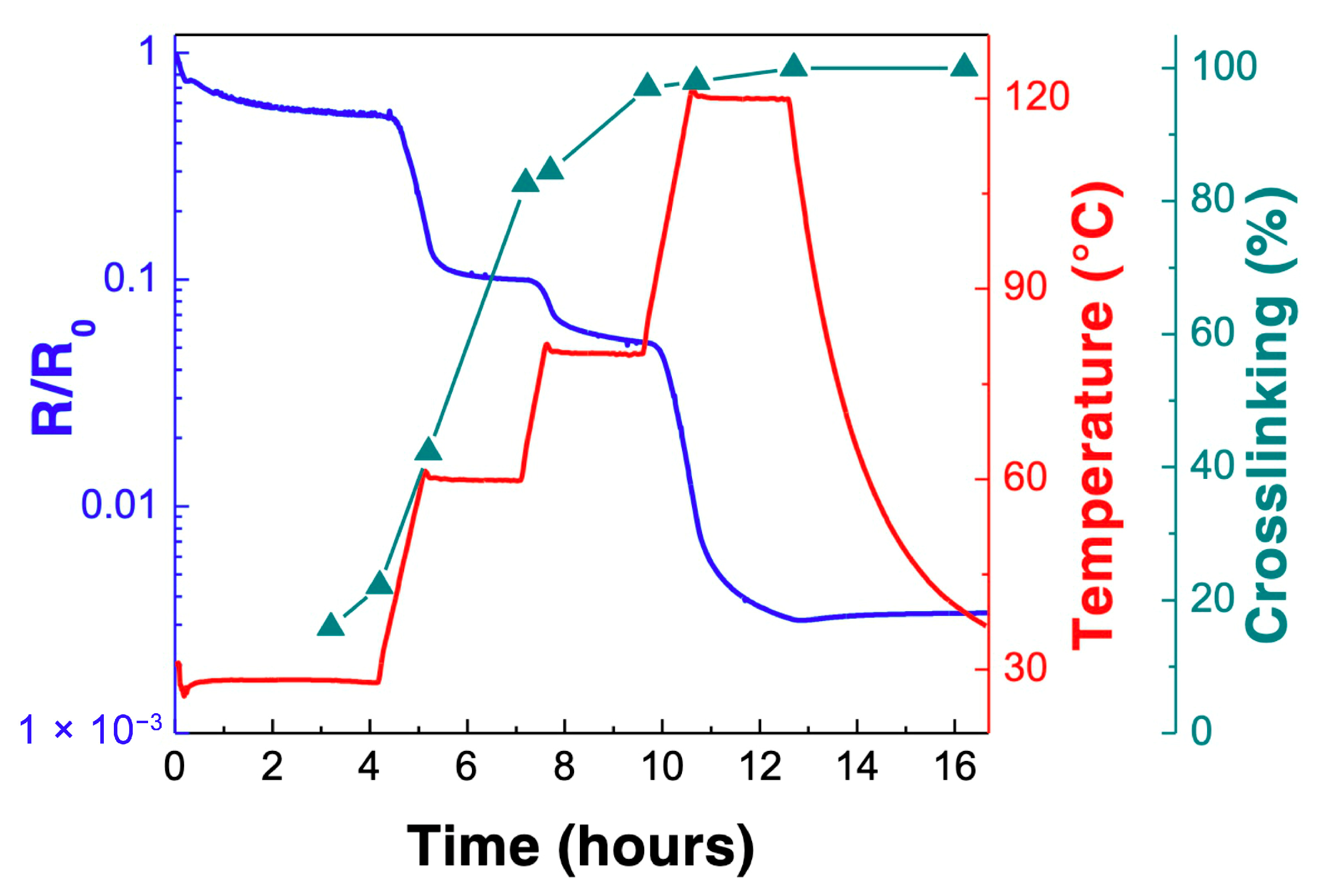
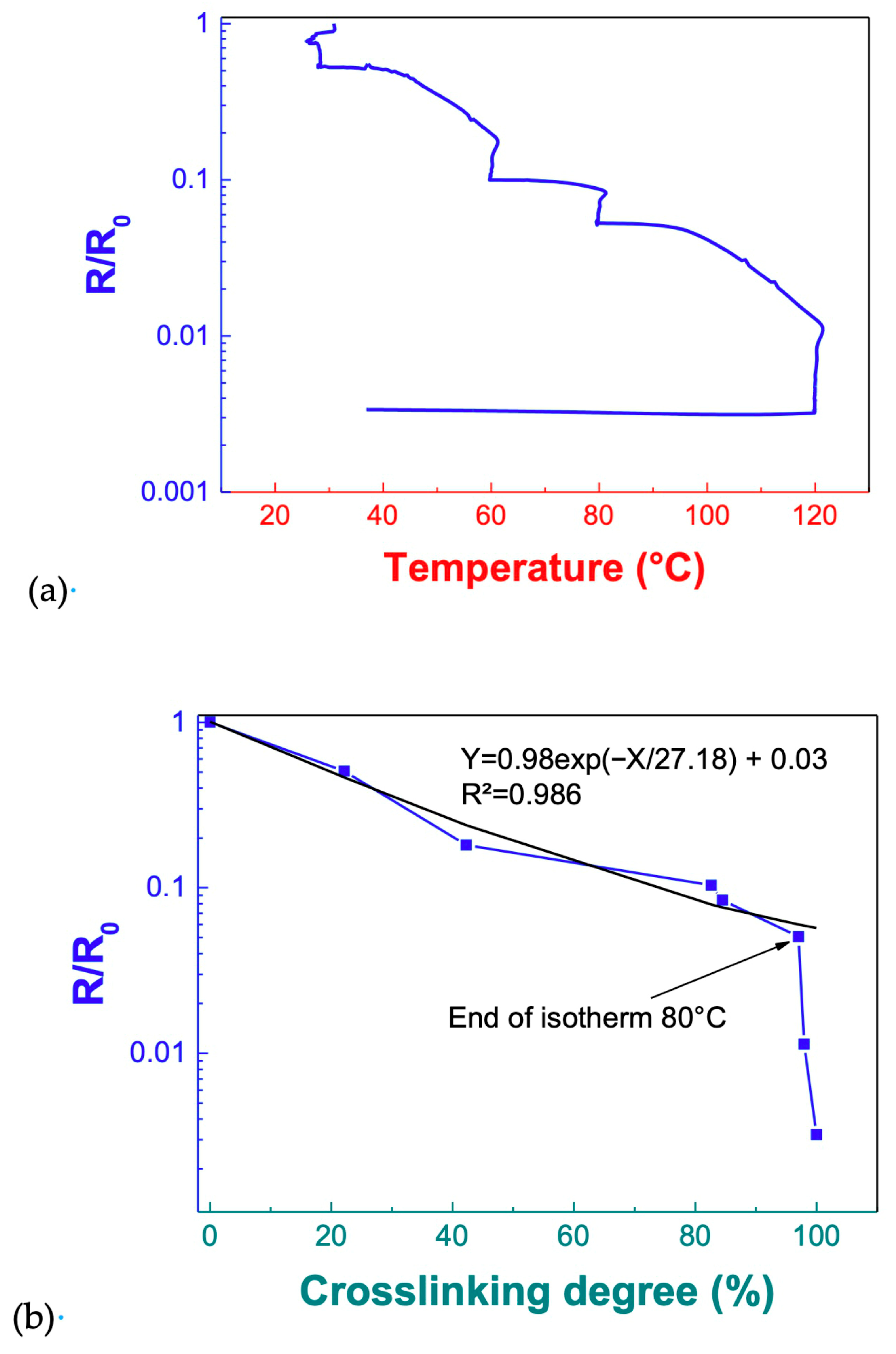
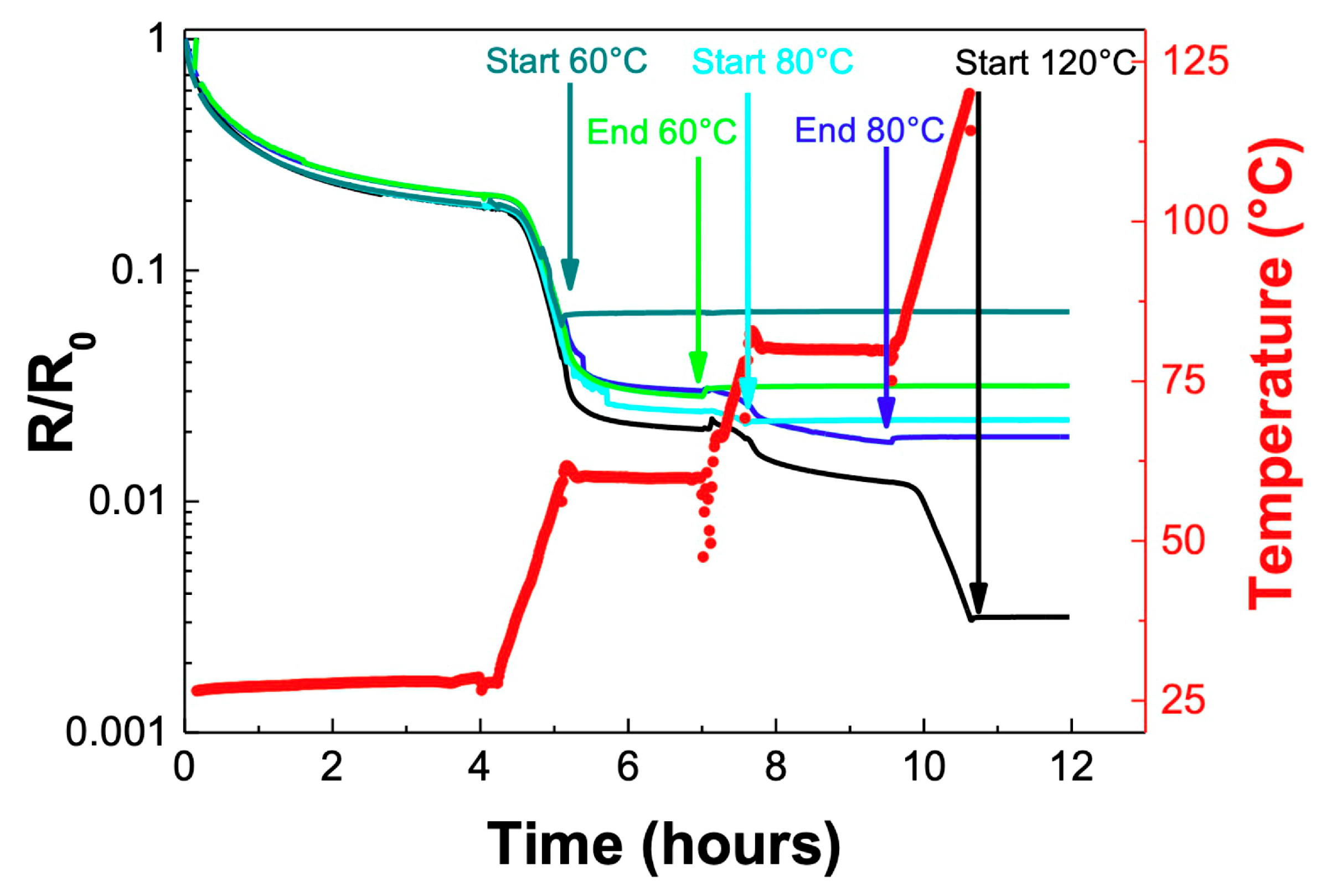
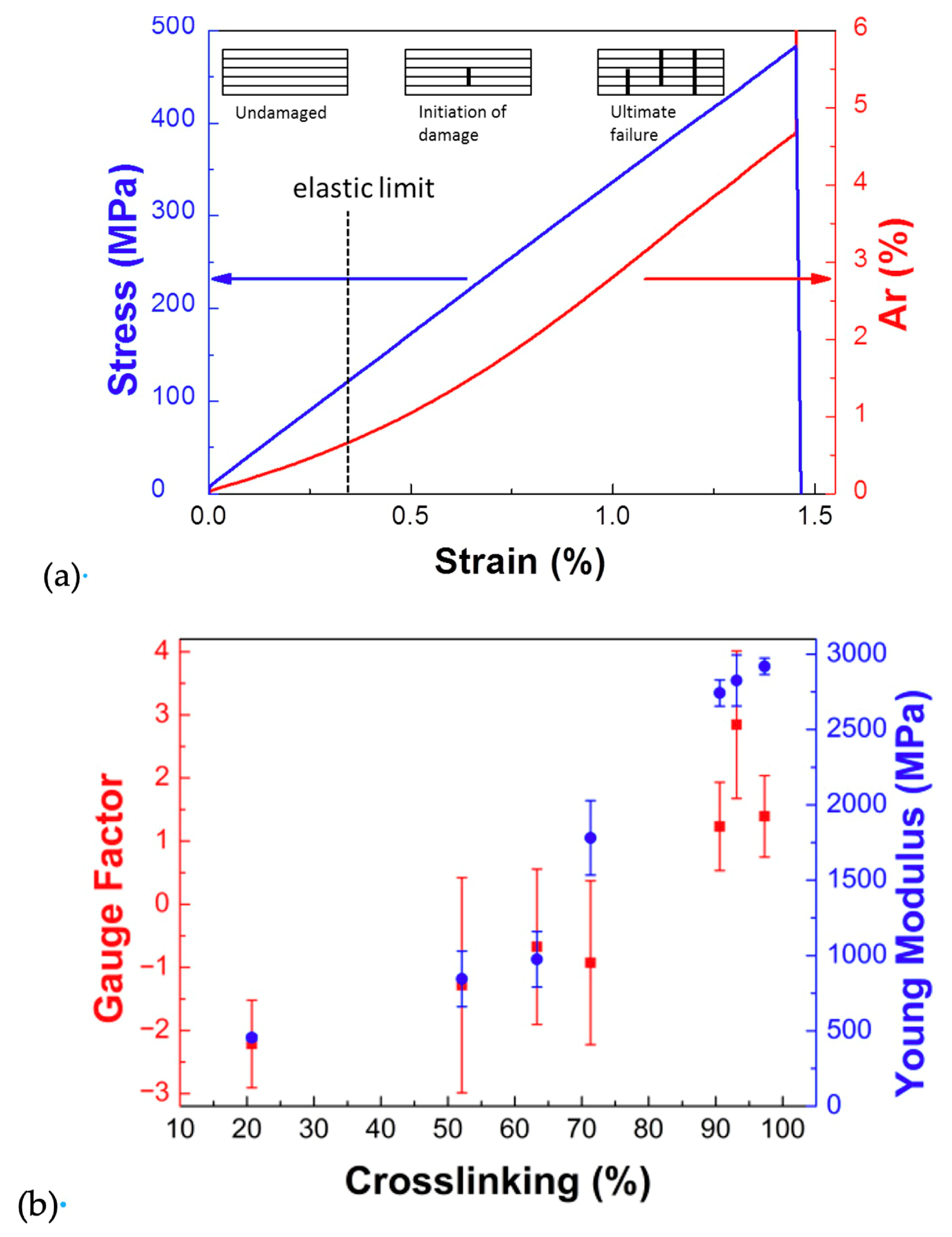
| Reference | n | m | E1 (kJ·mol−1) | E2 (kJ·mol−1) | A1 (s−1) | A2 (s−1) |
|---|---|---|---|---|---|---|
| Present study | 2.0–2.3 | 0.5 | 3.8 × 101 | 8.8 × 101 | 2.9 × 102 | 9.7 × 109 |
| [71] | 1.5–1.9 | 0.6–0.8 | 1.6 × 102 | 6.3 × 101 | 1.3 × 1014 | 3.0 × 104 |
| [80] | 2 | 1 | 6.9 × 101 | 7.3 × 101 | 1.3 × 105 | 2.1 × 107 |
| Isothermal Curing Temperature (°C) | 40 | 60 | 80 | 120 | |
|---|---|---|---|---|---|
| Onset time of percolation (s) | Without crosslinking | 400 | 260 | 100 | 30 |
| With crosslinking | 160 | 100 | 70 | 15 | |
| Ratio Rt = 4000s/Rt = 0s | Without crosslinking | 4.6 × 10−2 | 2.7 × 10−2 | 4.0 × 10−3 | 7.9 × 10−4 |
| With crosslinking | 3.3 × 10−1 | 2.0 × 10−1 | 5.9 × 10−3 | 8.4 × 10−4 | |
| Boltzmann Parameters | 40 | 60 | 80 | 120 |
|---|---|---|---|---|
| A | 0.3377 | 0.2190 | 0.0063 | 0.0008 |
| B | 2328 | 2332 | 1 | 1 |
| C | −64.5 | −27.1 | 11.7 | 17.1 |
| D | 8.06 | 3.67 | 3.93 | 7.06 |
| R2 | 0.986 | 0.983 | 0.997 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemartinel, A.; Castro, M.; Feller, J.-F. Core Monitoring of Thermoset Polymer Composites’ Curing with Embedded Nanocomposite Sensors: A Key Step Towards Process 4.0. J. Compos. Sci. 2025, 9, 435. https://doi.org/10.3390/jcs9080435
Lemartinel A, Castro M, Feller J-F. Core Monitoring of Thermoset Polymer Composites’ Curing with Embedded Nanocomposite Sensors: A Key Step Towards Process 4.0. Journal of Composites Science. 2025; 9(8):435. https://doi.org/10.3390/jcs9080435
Chicago/Turabian StyleLemartinel, Antoine, Mickaël Castro, and Jean-Francois Feller. 2025. "Core Monitoring of Thermoset Polymer Composites’ Curing with Embedded Nanocomposite Sensors: A Key Step Towards Process 4.0" Journal of Composites Science 9, no. 8: 435. https://doi.org/10.3390/jcs9080435
APA StyleLemartinel, A., Castro, M., & Feller, J.-F. (2025). Core Monitoring of Thermoset Polymer Composites’ Curing with Embedded Nanocomposite Sensors: A Key Step Towards Process 4.0. Journal of Composites Science, 9(8), 435. https://doi.org/10.3390/jcs9080435







